斜齿轮例题
从动轮斜齿轮判断左右旋向例题

从动轮斜齿轮判断左右旋向例题摘要:I.斜齿轮的基本概念和分类A.斜齿轮的定义B.斜齿轮的分类II.斜齿轮的旋向判断A.斜齿轮的旋向定义B.判断斜齿轮旋向的方法C.斜齿轮旋向判断的实例III.斜齿轮的应用领域A.斜齿轮在机械传动中的应用B.斜齿轮在汽车传动系统中的应用IV.斜齿轮的发展趋势和展望A.斜齿轮技术的创新和发展B.斜齿轮在未来的应用前景正文:斜齿轮,作为一种常见的机械传动元件,广泛应用于各种工业领域。
斜齿轮的旋向判断,是机械工程中一个基本的问题。
本文将详细介绍斜齿轮的基本概念、旋向判断方法以及在实际应用中的具体运用。
首先,我们需要了解斜齿轮的基本概念和分类。
斜齿轮,是指齿轮的齿廓线与轴线之间有一定的倾斜角度。
根据倾斜角度的不同,斜齿轮可以分为多种类型,例如:螺旋斜齿轮、圆锥斜齿轮、蜗杆斜齿轮等。
其次,我们需要掌握斜齿轮的旋向判断方法。
斜齿轮的旋向,是指斜齿轮在传动过程中,齿轮的旋转方向。
判断斜齿轮旋向的方法,通常有两种:一种是根据左右手定则,另一种是根据轴向力的方向。
在实际操作中,我们可以通过以上方法,快速准确地判断斜齿轮的旋向。
接着,我们来看一下斜齿轮的应用领域。
斜齿轮在机械传动中,有着广泛的应用。
例如,在汽车传动系统中,斜齿轮被广泛应用于变速器、驱动桥等关键部件。
此外,斜齿轮还在工业机器人、数控机床等领域中,有着重要的应用价值。
最后,我们来展望一下斜齿轮的发展趋势和展望。
随着科技的不断发展,斜齿轮技术也在不断创新和发展。
在未来,斜齿轮将在更多领域得到广泛应用,为人类社会的发展做出更大的贡献。
齿轮传动例题(直齿、斜齿)

da1 d1 2ha1 70.16 2 2.5 75.16mm da 2 d2 2ha 2 259.84 2 2.5 264.84mm
YF1=2.52 YF2=2.17 YS1=1.625 YS2=1.80 Yε =0.68 σ σ =420MPa Flim2=160MPa
b d d1 1 77 77mm
取
b1 b2 5 77 5 82mm b2 b 77mm
5.按齿根弯曲疲劳强度校核 (1)齿形系数
YF
与应力修正系数
YF1 2.57 , YS1 1.60
Y
YS
。
查图 7-15 得 查图 7-14 得 (2)重合度系数
[例 7.1]
设计一对单级支持圆柱齿轮减速器中的齿轮。电动机驱动,转向不变。
已知传动功率 P=10kW,小齿轮转速 n1=960r/min。传动比 i=3.7,齿轮为对称布置, 载荷平稳,设双班制工作,每班 8 小时,寿命 10 年,每年 250 工作日。
设计与说明
1、 选择齿轮材料、热处理方式、精度等级 因为是普通减速器,速度不高,由表 7-9 选 8 级精度。 该齿轮传动无特殊要求,为制造方便,所以选软齿面齿轮。 查表 7-1 选择小齿轮硬度范围为 240-HBS, 大齿轮硬度范围为 180-210HBS。 大小齿轮均用 45 钢: 小齿轮选用 45 钢调质,硬度为 229-286HBS; 大齿轮选用 45 钢正火,硬度为 162-217HBS。 取小齿轮的齿数 z1 为 27,则大齿轮齿数 z2=z1i=27×3.7=99.9 圆整取 z2=100。
(4)由式(7-12)计算弯曲应力:
b1 b2
2 KT1 2 1.499 99479 YF YS Y 2.57 1.60 0.68 44.57 MPa 2 bm z1 77 32 27 Y Y 2 KT1 2.18 1.79 Yb1YS 2Y b1 b 2 S 2 44.57 42.28MPa 2 bm z1 Yb1YS1 2.57 1.60
斜齿轮设计(史上最详细的计算过程,有图有表有计算)

12
相对齿根表面状况系数 根据齿面粗糙度
?? :查式 16.2-21 , ??????????
Ra1= R a2=1.6, ?? ?????????? 1 = ?? ?????????? 2 = 1 Yx: 查图 16.2-28 , Yx1 = Y x2 =1
弯曲强度计算的尺寸系数
将各参数代入公式计算安全系数
=
= 2.46
?? ?? 2 =
=
= 2.37
根据表 16.2-46 ,高可靠度 SFin =2,S H> SFmin, 故安全。
26) 斜齿轮主要几何参数 m n =4mm, β =9° 22 ′, Z1 =36, Z2 =112 4 × 36 = = 145.946 ???? ????????0.98667 ???? ?? 1 ???? ?? 2 = = 454.053 ???? ????????0.98667 4 ×112
=36,Z 2=112 实际传动比 i
=Z2/Z 1 =112/36=3.111
4
cos β =
?? ?? ?? 1 + ?? 2 2??
=
4× 36+112 2× 300
= 0.98667 , 所以 β =9° 22’
11)计算分度圆直径: ???? ?? 4 × 36 1 ?? = = = 145.946 ???? 1 0.98667 cos β ???? ?? 4 × 112 2 ?? = = 454.053 ???? 2 = 0.98667 cos β 12)确定齿宽: b= Ф α × ??=0.4 × 300=120mm 13)计算齿轮圆周速度: ??= = = 5.58 ??/ ?? 60 × 1000 60 × 100 根据齿轮圆周速度,参考表 16.2-73 ,选择齿轮精度等级为 ???? 1 ?? 1 ??× 145.946 ×730
11 斜齿轮例题

斜齿轮传动例题
齿数Z —必须为整数;
分度圆直径d —保留准确的计算值,精确到小数点 后三位;
斜齿轮中心距a —必须圆整为整数;
齿宽b —必须圆整为整数;
螺旋角β —保留准确的计算值,精确到秒。
齿轮传动中各个参数是相互制约的,即要满足上述 要求,又要满足齿轮正确啮合的几何关系,在设计 计算中必须进行相关参数的协调工作。
另一种方法
σ F1
=
2 KT1 bd1mn
YFa 1YSa 1Yε Yβ
= 2×1.71× 6.59×104 × 2.63×1.59× 0.625× 0.913 54× 53.200× 2
= 93.6MPa < [σ F1] = 420MPa
σF2
=
σ
F
1
×
YFa 2YSa 2 YFa1YSa1
= 93.6× 2.14×1.79 2.63 × 1.59
d1
=3
2KT1 ψd
⋅
u
+ u
1
⎜⎜⎝⎛
Z
E
⋅
ZH [σ
⋅ Zε H]
⋅ Zβ
⎟⎟⎠⎞2
=3
2×1.71× 6.59×104 × 4 + 1 × ⎜⎛ 189.8× 2.45× 0.79 × 0.988 ⎟⎞2
1
4⎝
520
⎠
= 51.379mm
10. 验算圆周速度
V = πd1n1 = π × 51.379 × 1450 = 3.9m / s
1
= 0.79
0.95× 1.685
7.螺旋角系数Zβ Zβ = cos β = cos12.5o = 0.988
斜齿轮传动例题
斜齿轮练习题

斜齿轮练习题
斜齿轮是一种常见的传动装置,由于其结构和工作原理的特殊性,常常被用于各种机械和工业设备中。
为了更好地了解斜齿轮的工作原理和计算方法,下面将介绍一些斜齿轮的练习题,以帮助读者更好地理解和应用相关知识。
1. 问题描述:
一台设备的主动轴和从动轴之间通过一对斜齿轮进行传动。
主动轴上的齿轮有20个齿,从动轴上的齿轮有35个齿。
要求计算主动轴每转一圈,从动轴转动多少圈?
2. 解题思路:
由于斜齿轮的传动比等于两个齿轮之间齿数的比值,我们可以通过计算齿数比值来求得转动圈数的关系。
3. 解题步骤:
步骤1: 计算传动比
传动比等于从动轴齿数除以主动轴齿数,即35/20 = 1.75
步骤2: 计算从动轴的转动圈数
从动轴每转一圈,主动轴就要转动1/1.75圈。
因此,从动轴的转动圈数是主动轴转动圈数的1.75倍。
4. 计算结果:
主动轴每转一圈,从动轴转动1.75圈。
5. 总结:
本题通过计算斜齿轮的传动比来求取主动轴和从动轴之间的转动圈数关系,了解并应用了计算斜齿轮传动比和转动圈数的方法。
6. 扩展练习:
如果主动轴上的齿轮有16个齿,从动轴上的齿轮有28个齿,请计算主动轴每转一圈,从动轴转动多少圈?
解答同上,传动比等于28/16 = 1.75。
从动轴的转动圈数是主动轴转动圈数的1.75倍。
通过以上练习题,我们对斜齿轮传动比和转动圈数的计算方法有了更深入的理解。
希望读者能够通过练习题的学习,掌握并应用斜齿轮传动的相关知识和计算方法,提高对斜齿轮的理解和应用能力。
斜齿轮设计(史上最详细的计算过程,有图有表有计算)

例题:已知小齿轮传递的额定功率P=95 KW,小斜齿轮转速n1=730 r/min,传动比i=3.11,单向运转,满载工作时间35000h。
1.确定齿轮材料,确定试验齿轮的疲劳极限应力参考齿轮材料表,选择齿轮的材料为:小斜齿轮:38S i M n M o,调质处理,表面硬度320~340HBS(取中间值为330HBS)大斜齿轮:35S i M n, 调质处理, 表面硬度280~300HBS(取中间值为290HBS)注:合金钢可提高320~340HBS由图16.2-17和图16.2-26,按MQ级质量要求选取值,查得齿轮接触疲劳强度极限σHlim及基本值σFE:σHlim1=800Mpa, σHlim2=760MpaσFE1=640Mpa, σFE2=600Mpa2.按齿面接触强度初步确定中心距,并初选主要参数:按公式表查得:a≥476(u+1)√KT1φa σHP2u3 1)小齿轮传递扭矩T1:T1=9550×Pn1=9549×95730=1243N.m2)载荷系数K:考虑齿轮对称轴承布置,速度较低,冲击负荷较大,取K=1.63)查表16.2-01齿宽系数φα:取φα=0.44)齿数比u=Z2/Z1=3.115)许用接触应力σHP:σHP =σHlimS Hmin查表16.2-46,取最小安全系数s Hmin=1.1,按大齿轮计算σHP2=σHlim2S Hmin2=7601.1MPa=691MPa6)将以上数据代入计算中心距公式:a≥476(3.11+1)√ 1.6×12430.4×6912×3.113=292.67mm取圆整为标准中心距a =300mm7)确定模数:按经验公式m n=(0.007~0.02)α=(0.007~0.02)x300mm=2.1~6mm 取标准模数m n=4mm8)初选螺旋角β=9°,cosβ= cos9°=0.9889)确定齿数:z1=2acosβm n(u+1)=2×300×0.9884×(3.11+1)=36.06Z2=Z1i=36.03×3.11=112.15 Z1=36,Z2=112 实际传动比i实=Z2/Z1=112/36=3.111 10)求螺旋角β:cosβ=m n(Z1+Z2)2a =4×(36+112)2×300=0.98667,所以β=9°22’11)计算分度圆直径:d1=m n Z1cosβ=4×360.98667=145.946mmd2=m n Z2cosβ=4×1120.98667=454.053mm12)确定齿宽:b=Фα×a =0.4×300=120mm 13)计算齿轮圆周速度:V=πd1n160×1000=π×145.946×73060×100=5.58m/s根据齿轮圆周速度,参考表16.2-73,选择齿轮精度等级为8-7-7 (GB10095-2002)3.校核齿面接触疲劳强度根据σH=Z H Z E Zεβ√F1bd1u+1uK A×K V×K Hβ×K Ha1)分度圆上的圆周F1:F1=2T1d1=2×1243×103145.946=17034N2)使用系数K A:查表16.2-36,K A=1.5 3)动载荷系数K V:K V=1+(K1K A F1b+K2)Z1V100√u21+u2查表16.2-39得K1=23.9,K2=0.0087代入上式得K V =1+(23.91.5×17034120+0.0087)36×5.58100√ 3.1121+3.112 =1.234)接触强度计算的齿向载荷分布系数K H β,根据表16.2-40,装配时候检验调整:K Hβ=1.15+0.18×(b d 1)2+0.31×10−3×b=1.15+0.18×(120145.946)2+0.31×10−3×120=1.2695)齿间载荷分配系数K H α:查表16.2-42,得:K A F t b=1.5×17034120=213 N/mm 2,K H α=1.16)节点区域系数Z H ,查图16.2-15,Z H =2.477)弹性系数Z E ,查表16.2-43,Z E =189.8√MPa8)接触强度计算的重合度与螺旋角系数Zεβ:当量齿数:Z V1=Z1COS3β=360.986673=37.5Z V2=Z2COS3β=1120.986673=116.6当量齿轮的端面重合度εav:εav=εaI+εaII ,查图16.2-10,分别得到εaI=0.83,εaII=0.91,εav:εav=εaI+εaII=0.83+0.91=1.74按 φm=bm =1204=30, β=9°22’,查图16.2-11,得εβ=1.55按εav= 1.74,εβ=1.55,β=9°22`,查图16.2-16,得Zεβ=0.76 9)将以上数据代入公式计算接触应力σH=2.47×189.8×0.76×√17034120×145.946×3.11+13.11× √1.5×1.23×1.27×1.1=649MPa10)计算安全系数S H根据表16.2-34,S H=σHlimZ HT Z LVR Z W Z XσH寿命系数Z NT:按式16.2-10N1=60n1K h=60×730×1×35000=1.533×109N2=N1i=1.533×1093.11=4.93×108对调质钢(允许有一点的点蚀),查图16.2-18,Z NT1=0.98,Z NT2=1.04滑油膜影响系数Z LVR ,:按v=5.58m/s选用220号齿轮油,其运动粘度V40=220mm2/s查图16.2-19, Z得LVR =0.95工作硬化系数Z W,:因小齿轮未硬化处理,齿面未光整,故Z W=1尺寸系数Z X:查图16.2-22,Z X =1 将各参数代入公式计算安全系数S HS H1=σHlim1Z NT1Z LVRσH Z w Z X=800×0.98×0.95×1649=1.13S H2=σHlim2Z NT2Z LVRσH Z w Z X=760×1.04×0.95×1649=1.16根据表16.2-46,一般可靠度S Hmin=1~1.1,S H>S Hmin,故安全。
机械设计-蜗轮蜗杆斜齿锥齿轮传动受力分析例题
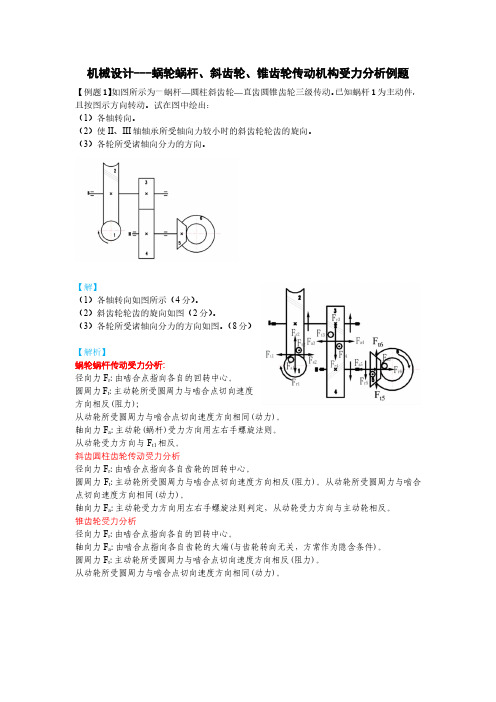
机械设计---蜗轮蜗杆、斜齿轮、锥齿轮传动机构受力分析例题【例题1】如图所示为一蜗杆—圆柱斜齿轮—直齿圆锥齿轮三级传动。
已知蜗杆1为主动件,且按图示方向转动。
试在图中绘出:
(1)各轴转向。
(2)使II、III轴轴承所受轴向力较小时的斜齿轮轮齿的旋向。
(3)各轮所受诸轴向分力的方向。
【解】
(1)各轴转向如图所示(4分)。
(2)斜齿轮轮齿的旋向如图(2分)。
(3)各轮所受诸轴向分力的方向如图。
(8分)
【解析】
蜗轮蜗杆传动受力分析:
径向力F r:由啮合点指向各自的回转中心。
圆周力F t:主动轮所受圆周力与啮合点切向速度
方向相反(阻力);
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
轴向力F a:主动轮(蜗杆)受力方向用左右手螺旋法则。
从动轮受力方向与F t1相反。
斜齿圆柱齿轮传动受力分析
径向力F r:由啮合点指向各自齿轮的回转中心。
圆周力F t:主动轮所受圆周力与啮合点切向速度方向相反(阻力)。
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
轴向力F a:主动轮受力方向用左右手螺旋法则判定,从动轮受力方向与主动轮相反。
锥齿轮受力分析
径向力F r:由啮合点指向各自的回转中心。
轴向力F a:由啮合点指向各自齿轮的大端(与齿轮转向无关,方常作为隐含条件)。
圆周力F t:主动轮所受圆周力与啮合点切向速度方向相反(阻力)。
从动轮所受圆周力与啮合点切向速度方向相同(动力)。
斜齿轮例题

试设计电动机驱动的闭式外啮合单级斜齿圆柱齿轮传动。
已知输入功率P=10kW,小齿轮转速n1=960r/min,传动比i=5,中等冲击,双向运转,齿轮相对轴承对称布置。
解:1、选择齿轮材料,确定许用应力由教材P152表10—1选小齿轮材料为45钢调质,齿面硬度230HBW;大齿轮材料为45钢正火,齿面硬度190HBW;查教材P159图10—6得σHlim1=570MPa,σHlim2=530MPa 查教材P160图10—7得σFlim1=190MPa,σFlim2=170MPa由教材P160表10—5,取S H=1.1,S F=1.4故[σH1]= σHlim1/ S H=518 MPa,[σH2]= σHlim2/ S H=482 MPa,[σF1]=0.7 σFlim1/ S F=95MPa,[σF2]=0.7 σFlim2/ S F=85MPa,2、按齿面接触疲劳强度设计由教材P154表10—2,齿轮按8级精度设计,由教材P155表10—3,取载荷系数K=1.5,由教材P161取齿宽系数ψa=0.4。
作用在小齿轮上的转矩T1为:T1=9.55×106P/ n1=9.95×104Nmm取小齿轮齿数Z1=25,则大齿轮齿数Z2=i Z1=125。
因为[σH1]>[σH2],所以用[σH2])u=i=5计算得a ≥186 取a=235mm 初选β=15°计算m n得m n =3.026mm查教材P84表6—1 取m n =3mm重新确定β β=16.77° 合适3、验算齿根弯曲疲劳强度计算当量齿数Z V1=28.48 Z V2=142.43 查教材P158表10—4 得Y FS1=4.105 Y FS2=3.90 b=ψa ×a=94mm 取b 1=100mm b 2=94mm计算得:σF1=46.34 MP a <[σF1]=95MPa 合适 σF2=44.0 MP a <[σF2]= 85MPa 合适[]312305)1(u KT u a a H φσ⎪⎪⎭⎫ ⎝⎛±≥βcos 2)(21z z m a n +=][cos 6.1121F n FS F Z bm Y KT σβσ≤=4、计算齿轮的圆周速度V=3.94m/s ≤9 m/s 合适5、计算几何尺寸(略)6、结构设计(略) 10006011⨯=n d V π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y Fa 1Y Sa 1
= =
270 2 ×1 .58
= 85 .44 = 55 .70
[σ F 2 ]
Y Fa 2Y Sa 2
220 2 .17 ×1 .82
由弯曲强度公式: 由弯曲强度公式:
F2 220 T ≤ bd m ε = × 115 × 76.67 × 3 × 2.79 1F 2 KY Y Y 1 n α 2 × 1.2 × 2.17 × 1.82 × 0.941 Fa 2 Sa 2 β = 1.8 × 106 N − mm
由接触强度公式, 由接触强度公式,
T1H ≤
(
[σ H ]
ZEZH
2 K (u +1)
) bd
2
2 1 uε α
=
(189.5752.48 )2 ×115×76.672 ×5×2.79 8×
2×1.2×(5+1)
= 9.8 × 10 N − mm
5
2、讨论弯曲强度 、 比较: 比较:
[σ F 1 ]
= 440 N
= 440 N
Fa 2 = − Fa 3 = Ft 3tgβ 3 =
tgβ 3 =
sin β 3 =
440×mn 3Z 3 2 T2
=
440×5×21 2×1.64×105
= 0.14085
β 3 = 8°5′50′′
(3)自行完成 )
举例1 一斜齿圆柱齿轮减速器、已知: r/min, 举例1、一斜齿圆柱齿轮减速器、已知:n1=955 r/min, 25, =125, mm, mm, 11.98° Z1=25,Z2=125,mn=3 mm,b=115 mm,β=11.98°,
K=l.2 ,[σ H1] =600 MPa ,[σ H2] =550 MPa,[σ F1] =270 =2, =2.17, =1.58, MPa ,[σ H2] =220 MPa , YFa1=2, YFa2=2.17, Ysa1=1.58, =1.82, Ysa2=1.82, ZE=189.8 (MPa)1/2 ,ZH=2.48, εα=2.79, =0.941, Yβ=0.941, 附公式: 附公式:
σ
比较 T1H 与 T1F,
T1H < T1F
9.8×105 ×955 95.5×105
P≤
T1n1 95.5×105
=
= 98kW
举例2、如图所示的两级斜齿圆柱齿轮减速器,己知高速级齿轮 Z1=21,Z2=52,mn1=3mm,β=12°7′43″;低速级齿轮Z3=21, Z4=52,mnⅡ=5mm,输入功率P1=10KW,n1=1450rpm, 齿 轮Z1的齿向为右旋。 试求: (1)为使中间轴Ⅱ上的轴承所受的轴向 力较小,低速级的齿轮Z3和Z4的齿向 n1 为右旋还是左旋? (2)为使中间轴Ⅱ上的轴承所受的轴向 力完全抵消,低速级的齿轮Z3和Z4 的分度圆螺旋角为多少? (3)分别画出各齿轮在啮合点三个力的 方向。
Z1
Ⅱ
Z2
Ⅲ
Z3
Z4
举例2(续)
Fa 2 = − Fa1 = Ft1tgβ1 = =
2 T1 sin β1 mn 1 Z 1
2 T1 d1
tgβ1 =
2T2 sin β 3 mn 3Z 3
2 T1tgβ 1
mn 1Z1 cos β1
=
2×6.6×10 4 ×sin(12.129° ) 3× 21
2 T2 d3
σ H = ZE ZH
σF =
2 KT 1 ( u ± 1 ) bd 1 2 uε α ≤ [σ ] H
求该减速器的许用传递功率。 求该减速器的许用传递功率。
α
2 KT1 YFα Yβ YSα ≤ [σ ]F bd1mnε α
解:1、讨论接触强度: 、讨论接触强度: [σH] =( [σH1] +[σH2] )/2=(600+550)/2=575 Mpa ( ( ) d1=mnZ1/cosβ=3×25/cos(11.98º)=76.67 mm × ( ) u=z2/z1=5
Z3 Z4
Ⅰ
Ⅱ
Z2
Ⅲ
解:(1)Z2—左旋,Z3—左旋,Z4—右旋 (2)T1=95.5×105P/n1= 95.5×105×10/1450 =6.6×104 N-mm u12=Z2 /Z1=52/21=2.48 T2= u12 T1= 2.48× 6.6×104 =1.64×105 N-mm Ⅰ
