第二章习题参考答案(5版)(可编辑修改word版)
(完整word版)电力电子技术第五版课后习题答案
电力电子技术第五版课后习题答案第二章 电力电子器件2. 使晶闸管导通的条件是什么?答:使晶闸管导通的条件是:晶闸管承受正向阳极电压,并在门极施加触发电流(脉冲)。
或:u AK >0且u GK >0。
3. 维持晶闸管导通的条件是什么?怎样才能使晶闸管由导通变为关断? 答:维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
要使晶闸管由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
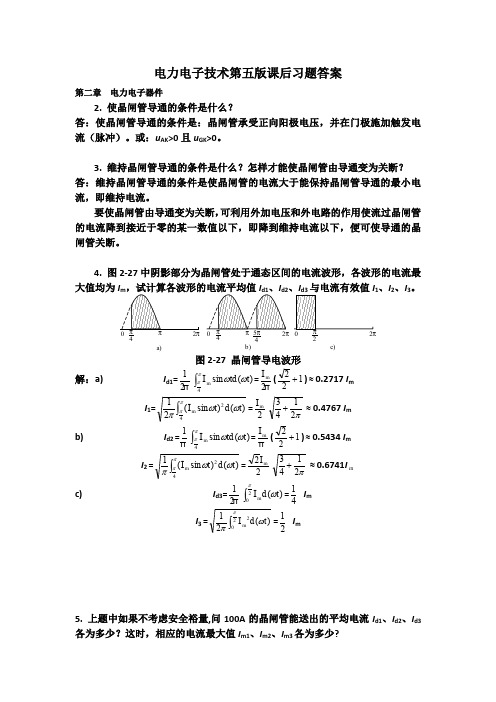
4. 图2-27中阴影部分为晶闸管处于通态区间的电流波形,各波形的电流最大值均为I m ,试计算各波形的电流平均值I d1、I d2、I d3与电流有效值I 1、I 2、I 3。
002π2π2ππππ4π4π25π4a)b)c)图1-430图2-27 晶闸管导电波形解:a) I d1=π21⎰ππωω4)(sin t td I m =π2m I (122+)≈0.2717 I m I 1=⎰ππωωπ42)()sin (21t d t I m =2m I π2143+≈0.4767 I m b) I d2 =π1⎰ππωω4)(sin t td I m =πm I (122+)≈0.5434 I m I 2 =⎰ππωωπ42)()sin (1t d t I m =22mI π2143+≈0.6741I m c) I d3=π21⎰20)(πωt d I m =41 I m I 3 =⎰202)(21πωπt d I m =21 I m5. 上题中如果不考虑安全裕量,问100A 的晶闸管能送出的平均电流I d1、I d2、I d3各为多少?这时,相应的电流最大值I m1、I m2、I m3各为多少?解:额定电流I T(AV) =100A 的晶闸管,允许的电流有效值I =157A ,由上题计算结果知a) I m1≈4767.0I≈329.35, I d1≈0.2717 I m1≈89.48 b) I m2≈6741.0I≈232.90, I d2≈0.5434 I m2≈126.56 c) I m3=2 I = 314,I d3=41 I m3=78.5第三章 整流电路1. 单相半波可控整流电路对电感负载供电,L =20mH ,U 2=100V ,求当α=0︒和60︒时的负载电流I d ,并画出u d 与i d 波形。
(完整版)第二章货币资金习题及答案解析

第二章货币资金一、单项选择题1.甲股份有限公司2010年度正常生产经营过程中发生的下列事项中,不影响其2010年度利润表中营业利润的是( )。
A.有确凿证据表明存在某金融机构的款项无法收回,该款项已计提过准备。
B.期末计提带息应收票据利息C.外币应收账款发生汇兑损失D.无法查明原因的现金短缺2.下列情形中,不违背《内部会计控制规范——货币资金》规定的“确保办理货币资金业务的不相容岗位相互分离、制约和监督”原则的是( )。
A.由出纳人员兼任会计档案保管工作B.由出纳人员兼任固定资产明细账及固定资产总账的登记工作C.由出纳人员兼任收入总账和明细账的登记工作D.由出纳人员保管签发支票所需全部印章3.下列经济业务中,企业不得动用库存现金支付的是( )。
A.支付职工奖金65000元B.购买办公用品付款300元C.预付出差人员携带的差旅费5000元D.支付购买设备款1200元4.企业用于办理日常转账结算和现金收付的银行存款户是( )。
A.临时存款户B.基本存款户C.专用存款户D.一般存款户5.企业将准备用于有价证券投资的现金存入证券公司指定的账户时,应借记的会计科目是( )。
A.银行存款B.其他货币资金C.其他应收款D.短期投资6.企业发现现金短缺属于无法查明的其他原因,按照管理权限经批准处理时,应在以下科目核算( )。
A.其他应收款B.管理费用C.其他应付款D.财务费用7.企业采用托收承付方式销售商品,其销售收入确认的时间是( )。
A.发出商品时B.发出商品时并向银行办妥托收手续时C.发出商品时并办妥托运手续时D.购买单位承付全部货款8.企业进行外币存款核算时,使用的会计科目是 ( )。
.A.其他货币资金B.银行存款C.备用金D.其他应收款9.下列各项中,不通过“其他货币资金”科目核算的是( )。
A.信用证存款B.银行本票存款C.信用卡存款D.备用金10.下列款项中,可以采用托收承付方式结算的有()。
A.商品交易的货款B.提供劳务的款项C.代销商品的款项D.赊销商品的款项11.企业将款项汇往外地开立采购专用账户时,应借记的会计科目是()。
国际经济学第五版第二章答案

第二章复习题及第三章预习题参考答案1、什么是制度?举例说明什么是正式制度和非正式制度,并解释制度和组织的区别。
答:一制度是一套行为规则。
它设置关于社会、政治和经济行为的限制或约束规则。
这些规则可以以法律,行政规则或一个组织的标准守则等形式被正式承认。
制度的规则可能还是非正式的,例如,在餐桌礼仪和社会习俗等。
示例,正规的制度包括民法,商法,和大学标准或行为(例如,认定抄袭或性骚扰)。
非正式制度的例子包括对生日礼物交换和餐桌礼仪,在拥挤的公交车上给老人让座。
制度和组织机构的区别,就如宪法和美国政府的区别。
后者宪法是一组管辖前者政府的规则。
组织机构是个人或团体的联合,制度是对他们行为的限制和他们必要遵守的规则。
2,支持国际组织的观点是什么?反对国际组织的观点是什么?你认为那种观点更具有说服力?答:赞成观点:国际组织在控制国家或区域性危机及避免其国际传播方面,是至关重要的。
他们通过提供一系列的确定的和已知的(透明)规则(制度),减少了国际经济的不确定性和增加稳定性。
在许多情况下,他们解决了在国际经济中搭便车的问题,以确保提供(国际)公共物品,如融资解决流动性危机的最后贷款人,或在经济衰退时开放市场。
反对论点:国际机构提供的解决问题的条件,超出了主权范围(可能会迫使采取不同于国家意愿或利益的国内政策),透明度(决策的机构可能被别人追求自己的利益所控制),意识形态(建议可能是不好的或有偏见的),以及执行和调整成本(不对称议价能力和承受能力,实行费用)。
总体而言,批评者质疑国际制度产生经济上的不平等和加剧弱势群体的风险。
这个问题的争论是强的并没有一个明确的结果。
那一观点可以被看作是更有说服力呢?最关键的是要学生理解两种争论,并且学生能够发展一套他们自己的理由来支持自己的观点。
3. Give the arguments for and against free trade agreements. How might the signing of a free trade agreement between the United States, Central America, and the Dominican Republic have harmed Bangladesh? 3、自由贸易协定的好处和害处分别是什么?如果美国、中美国家和多米尼加共和国签订自由贸易协定对孟加拉国(亚洲)有什么影响?Answer:Proponents of RTAs view them as building blocks for freer, more open world trade. They are able to perform this function because it is easier for a few countries to reach agreement on difficult trade matters than it is for a large number of countries. Furthermore, the domestic effects of a reduction of trade barriers are less dramatic since fewer countries are involved. Import flows and job losses and displacements are smaller and more easily managed. In addition, RTA members can experiment with new agreements, such as labor and environmental standards, that are too contentious in a larger set of negotiations. Opponents question these assumptions and argue that RTAs undermine progress toward multilateral agreements, such as the Doha Round of the WTO. They argue that RTAs polarize countries because they are discriminatory against nonmembers and because they disadvantage smaller countries that enter into agreements with large ones, since the small countries lack the ability to negotiate effectively and they are often unable to take advantage of the market opening of the larger country due to their limited infrastructure and other resources.区域贸易协定的支持者视其为更自由,更开放的世界贸易的基石。
(完整word版)《电子技术基础》第五版课后答案

第一章数字逻辑习题1.1数字电路与数字信号1。
1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms频率为周期的倒数,f=1/T=1/0。
01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1。
2数制21.2。
2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2。
718)D=(10。
1011)B=(2。
54)O=(2.B)H1。
4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1。
4。
3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@(3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+"的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331。
6逻辑函数及其表示方法1。
6.1在图题1。
6。
1中,已知输入信号A,B`的波形,画出各门电路输出L的波形.解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB A B A B ⊕AB AB A B ⊕ AB +AB 0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
同济第五版线性代数 课后题解析第二章

第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x , 求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解 由已知:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x ,故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635.(2)⎪⎪⎭⎫⎝⎛123)321(;解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛;解 )21(312-⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142.(4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ;解 ⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876.(5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x 322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA . 因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗? 解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A ,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148,但⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610,所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗? 解 (A +B)(A -B)≠A 2-B 2. 因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0; 解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ; 解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k.解⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k .8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k.解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA k k kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以 (AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以 AB =(AB)T =B T A T =BA . 11. 求下列矩阵的逆矩阵: (1)⎪⎭⎫ ⎝⎛5221; 解⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225.(2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解 ⎪⎭⎫⎝⎛-=θθθθc o s s in s in c o s A . |A|=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A ,所以 *||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121;解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012. (4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程: (1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ;解⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232.(2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ;解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; 解11110210132141--⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=21010366121⎪⎪⎭⎫⎝⎛=04111. (4)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012.13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A)-1(E -A). 另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A), 两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1. 证明 由A 2-A -2E =O 得 A 2-A =2E , 即A(A -E)=2E ,或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或 E A E E A =-⋅+)3(41)2( 由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-. 证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得|A 2-A|=2,即 |A||A -E|=2,故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆.由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-, 又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-. 16. 设A 为3阶矩阵, 21||=A , 求|(2A)-1-5A*|. 解 因为*||11A A A =-, 所以 |||521||*5)2(|111----=-A A A A A |2521|11---=A A =|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16.17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明 由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有 |A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以(A*)-1=|A|-1A . 又*)(||)*(||1111---==A A A A A , 所以(A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*.18. 设n 阶矩阵A 的伴随矩阵为A*, 证明:(1)若|A|=0, 则|A*|=0;(2)|A*|=|A|n -1.证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾,故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到 |A||A*|=|A|n .若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立.因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B . 解 由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330. 20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B . 解 由AB +E =A 2+B 得(A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B .解 由A*BA =2BA -8E 得(A*-2E)BA =-8E ,B =-8(A*-2E)-1A -1=-8[A(A*-2E)]-1=-8(AA*-2A)-1=-8(|A|E -2A)-1=-8(-2E -2A)-1=4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-= =2diag(1, -2, 1). 22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫ ⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A*|=|A|3=8, 得|A|=2.由ABA -1=BA -1+3E 得AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A11*)2(6*)21(3---=-=A E A E ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P , 而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 24. 设AP =P Λ, 其中⎪⎪⎭⎫ ⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0).ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114. 25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆. (A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B , 则 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A , 所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠. 解 41001200210100101002000021010010110100101==--=--=D C B A , 而 01111|||||||| ==D C B A , 故 |||||||| D C B A D C B A ≠.28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A , 则 ⎪⎭⎫ ⎝⎛=21A O O A A ,故 8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A , 1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则 ⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C , 所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321.由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D , 所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫ ⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--853*******B . 于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛----850032000052002125003800001200251111B A B A . (2)⎪⎪⎪⎭⎫ ⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛------1111114121031200210001B CA B O A B C O A⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=411212458103161210021210001.。
计算机网络安全基础(第5版)习题参考答案.doc

计算机网络安全基础(第5版)习题参考答案第1章习题:1.举出使用分层协议的两条理由?1.通过分层,允许各种类型网络硬件和软件相互通信,每一层就像是与另一台计算机对等层通信;2.各层之间的问题相对独立,而且容易分开解决,无需过多的依赖外部信息;同时防止对某一层所作的改动影响到其他的层;3.通过网络组件的标准化,允许多个提供商进行开发。
2.有两个网络,它们都提供可靠的面向连接的服务。
一个提供可靠的字节流,另一个提供可靠的比特流。
请问二者是否相同?为什么?不相同。
在报文流中,网络保持对报文边界的跟踪;而在字节流中,网络不做这样的跟踪。
例如,一个进程向一条连接写了1024字节,稍后又写了另外1024字节。
那么接收方共读了2048字节。
对于报文流,接收方将得到两个报文,、每个报文1024字节。
而对于字节流,报文边界不被识别。
接收方把全部的2048字节当作一个整体,在此已经体现不出原先有两个不同的报文的事实。
3.举出OSI参考模型和TCP/IP参考模型的两个相同的方面和两个不同的方面。
OSI模型(开放式系统互连参考模型):这个模型把网络通信工作分为7层,他们从低到高分别是物理层、数据链路层、网络层、传输层、会话层、表示层和应用层。
第一层到第三层属于低三层,负责创建网络通信链路;第四层到第七层为高四层,具体负责端到端的数据通信。
每层完成一定的功能,每层都直接为其上层提供服务,并且所有层次都互相支持。
TCP/IP模型只有四个层次:应用层、传输层、网络层、网络接口层。
与OSI功能相比,应用层对应的是OSI的应用层、表示层、会话层;网络接口层对应着OSI的数据链路层和物理层。
两种模型的不同之处主要有:(1) TCP/IP在实现上力求简单高效,如IP层并没有实现可靠的连接,而是把它交给了TCP层实现,这样保证了IP层实现的简练性。
OSI参考模型在各层次的实现上有所重复。
(2) TCP/IP结构经历了十多年的实践考验,而OSI参考模型只是人们作为一种标准设计的;再则TCP/IP有广泛的应用实例支持,而OSI参考模型并没有。
C语言程序设计第五版谭浩强课后答案(第二章答案)

C语⾔程序设计第五版谭浩强课后答案(第⼆章答案)⽬录1. 什么是算法?试从⽇常⽣活中找3个例⼦,描述它们的算法2. 什么叫结构化的算法?为什么要提倡结构化的算法?3. 试述3种基本结构的特点,请另外设计两种基本结构(要符合基类结构的特点)。
4. ⽤传统流程图表⽰求解以下问题的算法。
5. ⽤N-S图表⽰第4题中各题的算法6. ⽤伪代码表⽰第4题中各题的算法7. 什么叫结构化程序设计?它的主要内容是什么?8. ⽤⾃顶向下、逐步细化的⽅法进⾏以下算法的设计:1. 什么是算法?试从⽇常⽣活中找3个例⼦,描述它们的算法算法:简⽽⾔之就是求解问题的步骤,对特定问题求解步骤的⼀种描述。
⽐如⽣活中的例⼦:考⼤学⾸先填报志愿表、交报名费、拿到准考证、按时参加考试、收到录取通知书、按照⽇期到指定学校报到。
去北京听演唱会⾸先在⽹上购票、然后按时坐车到北京,坐车到演唱会会场。
把⼤象放进冰箱先打开冰箱门,然后将⼤象放进冰箱,关冰箱。
2. 什么叫结构化的算法?为什么要提倡结构化的算法?结构化算法:由⼀些顺序、选择、循环等基本结构按照顺序组成,流程的转移只存在于⼀个基本的范围之内。
结构化算法便于编写,可读性⾼,修改和维护起来简单,可以减少程序出错的机会,提⾼了程序的可靠性,保证了程序的质量,因此提倡结构化的算法。
3. 试述3种基本结构的特点,请另外设计两种基本结构(要符合基类结构的特点)。
结构化程序设计⽅法主要由以下三种基本结构组成:顺序结构:顺序结构是⼀种线性、有序的结构,它依次执⾏各语句模块选择结构:选择结构是根据条件成⽴与否选择程序执⾏的通路。
循环结构:循环结构是重复执⾏⼀个或⼏个模块,直到满⾜某⼀条件位置重新设计基本结构要满⾜以下⼏点:只有⼀个⼊⼝只有⼀个出⼝结构内的每⼀部分都有机会执⾏到结构内不存在死循环因此给出以下复习结构:while型和until型循环复合以及多选择结构4. ⽤传统流程图表⽰求解以下问题的算法。
第2章习题分析解析(可编辑修改word版)

第二章习题一、判断题1.计算机的性能指标完全由CPU 决定。
2.RAM 中的信息在计算机断电后会全部丢失。
3.存储地址是存储器存储单元的编号,CPU 要存取某个存储单元的信息,一定要知道这个存储单元的地址。
4.通常把计算机的运算器、控制器及内存储器称为主机。
5.由于硬盘的外部传输速率要小于内部传输速率,所以外部传输速率的高低是评价一个硬盘整体性能的决定性因素。
6.存储容量是数码相机的一项重要性能,不论拍摄质量如何,存储容量大的数码相机可拍摄的相片数量肯定比存储容量小的相机多。
7.计算机硬件从逻辑上讲包括CPU、内存储器、外存储器、输入设备和输出设备等,它们通过系统总线互相连接。
8.PC 机主板上有一个集成电路芯片是CMOS 存储器,主要存放着计算机硬件工作时所设置的一些参数,这个存储器是非易失性存储器。
9.CD-R 光盘是一种能够多次读出和反复修改已写入数据的光盘。
10.计算机的性能主要由CPU 决定,CPU 的运算速度又与CPU 的工作频率密切相关。
因此,主频为2GHz Pentium4 作为CPU 的一台PC 机,比使用主频为1GHz Pentium4 作为CPU 的PC机速度高一倍。
11.PC 机的主板上有电池,它的作用是在计算机断电后,给CMOS 芯片供电,保持该芯片中的信息不丢失。
12.大部分数码相机采用CCD 成像芯片,芯片中像素越多,可拍摄的图像最高分辨率(清晰度)就越高。
13.计算机中总线的重要指标之一是带宽,它指的是总线中数据线的宽度,用二进位数目来表示(如16 位,32 位总线)。
14.计算机常用的输入设备为键盘、鼠标,常用的输出设备有显示器、打印机。
15.目前市场上有些PC 机的主板已经集成了许多扩充卡(如声卡、以太网卡、显示卡)的功能,因此不再需要插接相应的适配卡。
16.I/O 操作的启动需要CPU 通过指令进行控制。
17.为了提高CPU 访问硬盘的工作效率,硬盘通过将数据存储在一个比其速度快得多的缓冲区来提高与CPU 交换的速度,这个区就是高速缓冲区,它是由DRAM 芯片构成的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章运算方法和运算器习题参考答案1.写出下列各数的原码、反码、补码、移码表示(用8 位二进制数)。
其中MSB 是最高位(又是符号位)LSB 是最低位。
如果是小数,小数点在MSB 之后;如果是整数,小数点在LSB 之后。
(1) -35 (2) 128 (3) -127 ( 4) -1解:(1)先把十进制数-35/64 写成二进制小数:(注意位数为8 位)x=(-35)10=(-100011)2[x]原=10100011 [x]反=11011100 [x]补=11011101(2)128 写成二进制小数:x=(128)10=(10000000)2[x]原=10000000 [x]反=10000000 [x]补=10000000(3)先把十进制数-127 写成二进制小数:x=(-127)10=(-1111111)2[x]原=11111111 [x]反=10000000 [x]补=10000001(4) 令Y=-1=-0000001B[Y]原=10000001 [Y]反=11111110 [Y]补=111111112. 设[X]补= a7,a6,a5…a0 , 其中a i取0 或1,若要x>-0.5,求a0,a1,a2,…,a6 的取值。
解:若a7= 0,则:x>0, 所以:a1= 0,a2,…,a6 任意;若a7= 1,则:a1= 1,a2,…,a6 不全为0。
3.有一个字长为32 位的浮点数,符号位1 位,阶码8 位,用移码表示;尾数23 位(包括1 位尾符)用补码表示,基数R=2。
请写出:(1)最大数的二进制表示;(2)最小数的二进制表示;(3)规格化数所能表示的数的范围;解:(1) 111111111 0 111111111111111111111(2)111111111 1000000000000000000000(3)111111111 0111111111111111111111~011111111 1000000000000000000000(4)000000000 00000000000000000000001~000000000 111111111111111111111114.将下列十进制数表示成浮点规格化数,阶码3 位,用补码表示;尾数9 位,用补码表示。
(1)27/64(2)-27/64解:(1)x=27/64=11011B×2-6=0.011011B=1.1011B×2-2S=0 M=0.10110000000000000000000E=e+127=-2+127=125=01111101[x]浮= 0011 1110 1 101 1000 0000 0000 0000 0000=(3ED80000)16(2)x=-27/64= -11011B×2-6= -0.011011B= -1.1011B×2-2S=1 M=0.10110000000000000000000E=e+127=-2+127=125=01111101[x]浮= 1011 1110 1 101 1000 0000 0000 0000 0000 =(BED80000)16浮点规格化数:[x]浮= 1111 10010100005.已知X 和Y, 用变形补码计算X+Y, 同时指出运算结果是否溢出。
(1)X=11011 Y=00011解:先写出x 和y 的变形补码再计算它们的和[x]补=00 11011 [y]补=00 00011[x+y]补=[x]补+[y]补=00 11011+00 00011=00 11110无溢出。
(2)X= 11011 Y= -10101解:先写出x 和y 的变形补码再计算它们的和[x]补=00 11011 [y]补=11 01011[x+y]补=[x]补+[y]补=00 11011+11 01011=00 00110∴x+y=00 00110B 无溢出。
(3)X= -10110 Y= -00001解:先写出x 和y 的变形补码再计算它们的和[x]补=11 01010 [y]补=11 11111[x+y]补=[x]补+[y]补=11.01010+11.11111=11 01001∴ x+y= - 10111 无溢出6.已知X 和Y, 用变形补码计算X-Y, 同时指出运算结果是否溢出。
(1) X=11011 Y= -11111解:先写出x 和y 的变形补码,再计算它们的差[x]补=00 11011 [y]补=11 00001 [-y]补=00 11111[x-y]补=[x]补+[-y]补=00 11011+00 11111=01 11010∵运算结果双符号不相等∴ 为正溢出(2) X=10111 Y=11011解:先写出x 和y 的变形补码,再计算它们的差[x]补=00 10111 [y]补=00 11011 [-y]补=11 00101[x-y]补=00 10111+11 00101=11 11100∴ x-y= -1 无溢出(3) X=0.11011 Y=-10011解:先写出x 和y 的变形补码,再计算它们的差[x]补=00 11011 [y]补=11 01101 [-y]补=00 10011[x-y]补=[x]补+[-y]补=00 11011+00 10011=01 01110∵运算结果双符号为01 不相等∴ 为正溢出7.用原码阵列乘法器、补码阵列乘法器分别计算X×Y。
(1)X= 11011 Y= -11111(2)X=-11111 Y=-11011解:(1)用原码阵列乘法器计算x,y 都取绝对值,符号单独处理[X]原=0.11011 [Y]原=1.11111积的符号为X f ⊕Y f= 0 ⊕1= 11 1 0 1 1× 1 1 1 1 1110111101111011110111 10110.1101000101[X×Y]原=1.1101000101 X×Y=-0.1101000101(2)X=-11111 Y=-11011解:用原码阵列乘法器计算[X]原=1 11111 [Y]原=1 11011积的符号为X f ⊕Y f=1⊕1 = 011111×110111 1 1 1 11 1 1 1 10 0 0 0 01 1 1 1 11 1 1 1 10.1101000101[X×Y]原=0.1101000101X×Y=0.11010001018.用原码阵列除法器计算X÷Y。
(1)X=0.11000Y=-0.11111(2)X=-0.01011Y=0.11001解:(1)[x]原=[x]补=0.11000 [|y|]补=0.11111[-∣y∣]补=1.00001被除数X 0.1100000000[-|y|]补1.00001余数为负 1.110010→q0=0+[|y|]补0.011111余数为正0.0100010→q1=1[-|y|]补 1.1100001余数为正0.00000110→q2=1[-|y|]补 1.11100001余数为负 1.111001110→q3=0+[|y|] 0. 000011111余数为负 1. 1111011010→q4=0+[|y|] 0. 00000111111. 1111111001 →q5=0商|q|=q0.q1q2q3q4q5=0.11000Xf ⊕Yf= 0 ⊕1 =1余数r=0.00000110=0.11×2-101 [x/y]原=1.11000(2)X =-0.01011 Y = 0.11001解:(1)[|x|]原=[|x|]补=0.01011 [|y|]补=0.11001[-|y|]补=1.00111被除数 X 0.010*******[-|y|]补 1.00111余数为负 1.100100 →q0=0+[|y|]补 0.011001余数为负 1.1111010 →q1=0[|y|]补 0.0011001余数为正 0.00100110 →q2=1[-|y|]补 1.11100111余数为正 0.000011010 →q3=1+[-|y|] 1.111100111余数为负 0. 0000000010 →q4=1+[|y|] 1. 11111001111. 1111101001 →q5=0|q|=q0.q1q2q3q4q5=0.01110r=0.000000001=0.1×21000X f ⊕ Y f = 1⊕ 0 = 1[x/y]原=1.011109.设阶为3 位((不包括阶符位), 尾数为6 位(不包括数符位), 阶码、尾数均用补码表示, 完成下列取值的[X+Y],[X-Y]运算:(1)x=2-011×0.100101 y=2-010×(-0.011110)解:① 对阶:因x 阶码小,所以调整x 指数向y 看齐x=2-010×0.0100101② 尾数相加减x+y=2-010×(0.0100101-0.011110)=2-010× (-0.0010111)x-y=2-010×0.1100001③规格化处理x+y=2-010× (-0.0010111)=2-101× (-1.011100)x-y=2-010×0.1100001=2-011×1.100001④溢出检查-126≤x+y的指数=-5,x-y的指数=-3≤127没有溢出(2) x=2-101×(-0.010110)y=2-100×(0.010110)解:① 对阶:因x 阶码小,所以调整x 指数向y 看齐x=2-100×(-0.0010110)② 尾数相加减x+y=2-100×(-0.0010110+0.010110)=2-100× (0.001011)x-y=2-100×(-0.100001)③规格化处理X+y=2-111× (1.011000)X-y=2-101×(-1.000010)④溢出检查-126≤x+y的指数=-7,x-y的指数=-5≤127没有溢出10.设数的阶码为3 位,尾数为6 位,用浮点运算方法,计算下列各式(1) (23⨯13) ⨯[2416⨯(-9)]16解: x=2010×1.10100, y=2011×(-1.00100) ①阶码求和ex+ey =010+011=101 (+5)移码表示为Ex+Ey=127+5=132②尾数相乘,可以采用原码阵列乘法实现(用绝对值)Mx ×My=1.10100 ×1.00100=1.1101010000③规格化处理与溢出检查Mx ×My= -1.1101010000(已是规格化数)-126≤指数5≤127,故没溢出④舍入处理(保留6 位小数)Mx ×My =1.110101⑤确定积的符号,异号相乘为负[x×y]浮=2101×(-1.110101)(2) (2-2⨯13) ÷(23⨯15) 32 16解: x=2-100×1.101000, y=2010×(1.111000) Mx = 1.101000 My= 1.111000①阶码求差ex-ey =-100-010 = -110 (-6)移码Ex-Ey=127+(-6)=121②尾数相除,可以采用无符号阵列除法实现Mx/My=1.101000 ÷ 1.111000=0. 110111③规格化处理及溢出判断---尾数左移1 位,阶码减1ex-ey = -111 (-7)-126≤指数-7≤127,故没溢出[Mx/My]= 1.101110④舍入处理(保留6 位小数)Mx ×My = 1.101110⑤确定商的符号,同号相除为正[x ÷y]浮=2-111×1.10111011.某加法器进位链小组信号为C4C3C2C1 ,低位来的信号为C0 ,请分别按下述两种方式写出C4C3C2C1 的逻辑表达式。
