二次曲线的配极原理
数学(本科)毕业论文题目汇总

数学毕业(学位)论文题目汇总一、数学理论1.试论导函数、原函数的一些性质。
2。
有界闭区域中连续函数的性质讨论及一些推广。
3。
数学中一些有用的不等式及推广。
4.函数的概念及推广.5.构造函数证明问题的妙想.6.对指数函数的认识.7。
泰勒公式及其在解题中的应用。
8。
导数的作用。
9。
Hilbert空间的一些性质。
10。
Banach空间的一些性质。
11.线性空间上的距离的讨论及推广。
12.凸集与不动点定理。
13.Hilbert空间的同构。
14。
最佳逼近问题.15。
线性函数的概念及推广。
16。
一类椭圆型方程的解。
17.泛函分析中的不变子空间.18.线性赋范空间上的模等价。
19.范数的概念及性质。
20.正交与正交基的概念。
21。
压缩映像原理及其应用。
22.隐函数存在定理的再证明。
23。
线性空间的等距同构。
24.列紧集的概念及相关推广.25.Lebesgue控制收敛定理及应用.26.Lebesgue积分与Riemann积分的关系。
27。
重积分与累次积分的关系.28.可积函数与连续函数的关系。
29.有界变差函数的概念及其相关概念。
30。
绝对连续函数的性质。
31。
Lebesgue测度的相关概念。
32。
可测函数与连续函数的关系.33.可测函数的定义及其性质。
34。
分部积分公式的推广。
35.Fatou引理的重要作用。
36.不定积分的微分的计算.37.绝对连续函数与微积分基本定理的关系。
38.Schwartz不等式及推广。
39.阶梯函数的概念及其作用.40.Fourier级数及推广。
41。
完全正交系的概念及其作用。
42。
Banach空间与Hilbert空间的关系。
43。
函数的各种收敛性及它们之间的关系。
44。
数学分析中的构造法证题术,45。
用微积分理论证明不等式的方法46.数学分析中的化归法47.微积分与辩证法48. 积分学中一类公式的证明49。
在上有界闭域的D中连续函数的性质50.二次曲线中点弦的性质51。
用射影的观点指导中学初等几何内容52。
高等几何

第五章高等几何第一节课程概论1、本课程的起源与发展早自欧洲文艺复兴时期,由于绘图和建筑等的需要,透视画的理论逐步形成,以后便建立了画法几何。
法国数学家蒙日(GaspardMonge,1746-1818)在1768到1799年之间和1809年分别出版了画法几何和微分几何两部经典著作,由于画法几何理论的发展,他的学生彭色列(JeanPoncelet,1788-1867)继承了这两部著作中的综合思想,于1822年写了一本书,它是射影几何方面最早的专者。
继彭色列之后,法国人沙尔(Michel Chasles,1793-1880) 等对射影几何的研究都做出了重要贡献。
出生于德国数学家史坦纳(Jacob Steiner,1796-1863)改进了射影几何的研究工具,并且把它们应用到各种几何领域,因而得到了丰硕结果。
到了19世纪上半叶,几何学的发展经历了它的黄金时代。
在这期间,古典的欧几里得几何学不再是几何学的唯一对象,射影几何学正式成为一门新学科。
英国人凯莱(Cayley,1821-1895)和德国人克莱因(Christian Felix Klein,1849-1925)等人用变换群的方法研究了这个分支,射影几何便成为完整独立的学科。
射影几何的诞生诱发于透视理论,一个射影平面就是由欧几里得平面添加所谓无穷远直线而得到的。
克莱因对于几何学理论的统一性有着执著的追求,他在成功地把几种度量几何统一于射影几何之后,就立即在更深层次上寻求统一各种几何学理论的基础。
在19世纪,人们开始把几何中图形的一些性质看作是一种“变换”运动的结果。
如正方形的“中心对称性”,就是将正方形绕其两条对角线的交点O“旋转”180°后仍重合的结果。
正方形的“轴对称性”,就是将正方形绕过O点的水平轴“反射”(即翻转)180°后仍重合的结果。
这里的“旋转”、“反射”就可以分别被看作是一种“变换”。
更为重要的是,数学家们进一步发现,这个正方形上的所有旋转、反射、平移等变换所构成的集合,满足群的条件,因而构成一个“变换群”。
极化曲线的测定
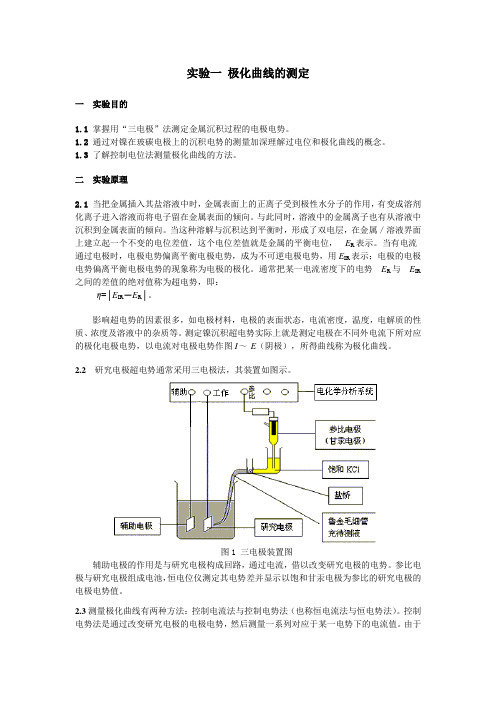
实验一极化曲线的测定一实验目的1.1掌握用“三电极”法测定金属沉积过程的电极电势。
1.2 通过对镍在玻碳电极上的沉积电势的测量加深理解过电位和极化曲线的概念。
1.3 了解控制电位法测量极化曲线的方法。
二实验原理2.1当把金属插入其盐溶液中时,金属表面上的正离子受到极性水分子的作用,有变成溶剂化离子进入溶液而将电子留在金属表面的倾向。
与此同时,溶液中的金属离子也有从溶液中沉积到金属表面的倾向。
当这种溶解与沉积达到平衡时,形成了双电层,在金属/溶液界面上建立起一个不变的电位差值,这个电位差值就是金属的平衡电位,E R表示。
当有电流通过电极时,电极电势偏离平衡电极电势,成为不可逆电极电势,用E IR表示;电极的电极电势偏离平衡电极电势的现象称为电极的极化。
通常把某一电流密度下的电势E R与E IR 之间的差值的绝对值称为超电势,即:η=│E IR-E R│。
影响超电势的因素很多,如电极材料,电极的表面状态,电流密度,温度,电解质的性质、浓度及溶液中的杂质等。
测定镍沉积超电势实际上就是测定电极在不同外电流下所对应的极化电极电势,以电流对电极电势作图I~E(阴极),所得曲线称为极化曲线。
2.2研究电极超电势通常采用三电极法,其装置如图示。
图1 三电极装置图辅助电极的作用是与研究电极构成回路,通过电流,借以改变研究电极的电势。
参比电极与研究电极组成电池,恒电位仪测定其电势差并显示以饱和甘汞电极为参比的研究电极的电极电势值。
2.3测量极化曲线有两种方法:控制电流法与控制电势法(也称恒电流法与恒电势法)。
控制电势法是通过改变研究电极的电极电势,然后测量一系列对应于某一电势下的电流值。
由于电极表面状态在未建立稳定状态前,电流会随时间改变,故一般测出的曲线为“暂态”极化曲线。
本实验采用控制电势法测量极化曲线:控制电极电势以较慢的速度连续改变,并测量对应该电势下的瞬时电流值,以瞬时电流对电极电势作图得极化曲线。
图2 阴极极化曲线三仪器与试剂LK98A微机电化学分析系统一台;甘汞电极一枝;铂电极一枝;玻碳电极一枝;100ml 烧杯3个,500ml烧杯1个;瓦特型镀镍液50ml;稀硝酸50ml;乙醇50ml;蒸馏水500ml。
二次线原理

二次线原理
二次线原理是指在电力系统中,通过二次线圈感应电流,从而实现对电流、电
压等参数的测量和保护控制。
在电力系统中,二次线原理扮演着非常重要的角色,它为电力系统的运行和管理提供了重要的技术支持。
首先,二次线原理在电流互感器中起到了至关重要的作用。
电流互感器是用于
测量电流的一种装置,它通过二次线圈感应电流,将高压侧的电流转化为低压侧的电流,从而方便进行测量和保护控制。
二次线原理保证了电流互感器的准确性和可靠性,为电力系统的安全运行提供了重要的保障。
其次,二次线原理也应用于电压互感器中。
电压互感器是用于测量电压的一种
装置,它同样通过二次线圈感应电压,将高压侧的电压转化为低压侧的电压,以便进行测量和保护控制。
二次线原理的应用使得电压互感器能够准确地反映系统的电压状况,为电力系统的稳定运行提供了重要的支持。
除此之外,二次线原理还广泛应用于各种保护装置和控制装置中。
通过二次线
圈感应电流、电压等参数,这些装置能够及时地感知电力系统的运行状态,并根据需要进行保护和控制。
二次线原理的有效应用,使得这些装置能够在电力系统发生故障或异常情况时迅速作出反应,保障了电力系统的安全稳定运行。
总的来说,二次线原理是电力系统中不可或缺的重要原理之一。
它通过二次线
圈感应电流、电压等参数,为电力系统的测量、保护和控制提供了重要的技术支持,保障了电力系统的安全稳定运行。
因此,我们需要深入理解和应用二次线原理,不断提高其在电力系统中的应用水平,为电力系统的可靠运行贡献力量。
高等几何中的对偶方法doc4(2)

通化师范学院本科生毕业论文(2012 届)题目: 高等几何中的对偶方法系别:数学系专业:数学与应用数学班级:三班作者姓名:马玉晶学号: ************ 指导教师:赵建红职称:副教授学历:研究生论文成绩:2011年12月目录摘要 (II)Abstract (II)1引言 (1)2高等几何中的对偶方法 (1)2.1对偶原理的相关概念 (1)2.2对偶原理及其一般模式 (2)2.3射影几何中的配极原则 (2)2.4 射影几何中的对偶方法 (3)2.5代数中对偶原理的应用 (4)2.6其他数学领域中的对偶应用 (5)3结束语 (5)致谢语 (6)参考文献 (6)指导教师评语.................................................................................................... 评阅人评语........................................................................................................高等几何中的对偶方法数学系2008级3班马玉晶摘要:这篇文章阐述了对偶原理及相关内容,如对偶图形、对偶元素、对偶命题和对偶运算等等,诠释了对偶方法,论述了对偶原理及对偶方法在高等几何、代数学和其他数学领域的作用以及广泛应用.关键词:对偶原理;对偶运算;对偶方法;对偶原理;方法及应用Dual method in the higherClass3, 2008, Department of Mathematics Ma YujingAbstract:This article explains the princile of duality and related content ,such as dual graphics,dual element,dual proposition and dual operation etc.,interpretation of the dual method,discusses the principle of duality and dual method in higher geometry,algebra and other field effect and wide application.Key words:The principle of duality; dual operation; dual method; dual theory; method and Application1.引言为了使几何学能够形成一个完整的公理化体系,古希腊学家欧几里得运用了亚里士多德的《分析篇》中公里方法,因而著有《几何原本》.由于这本著作有很多的不足,于是数学家们又开始了更深一层的研究.十九世纪末,大数学家希尔伯特(Hilbert)把“点、直线、面”作为基本对象,把“点结合线、点结合面、两点之间的一点”等作为基本关系,进而完善了《几何原本》中的公理化体系,又著成《几何基础》.2.高等几何中的对偶方法2.1对偶原理的相关概念对偶原理是射影几何中具有的重要的原理和方法,在欧氏几何当中,我们总是在研究“点”和“直线”之间的关系.定义1 (对偶命题)假设一个命题由点和直线构成,如果把命题中的各个元素换成它的对偶元素,各个运算换成它的对偶运算,这样形成了一个新的命题,这两个命题就叫做对偶命题.例如“两条直线相交于唯一点”与“两点能连接唯一直线”是一个对偶命题.定义2 (对偶元素)在平面射影几何中,我们将“点”和“线”称为平面上的对偶元素.定义3 (对偶运算)“过一个点作一条直线”与“在一条直线上取一个点”称作对偶运算.定义4(对偶图形)假设有点和直线组成的一个图形,将此图的各个元素改为它的对偶元素,各个运算改为它的对偶运算,结果得到了另一个新的图形,我们把得到的这个图形就叫做对偶图形。
高等几何

《高等几何》课程教学大纲课程名称:高等几何英文名称:课程代码: 课程类别: 专业必修学分: 3 学时: 48开课单位: 数学系适用专业: 数学与应用制订人:制订日期: 2011.11.18审核人:(教研室主任签字)审核日期:审定人: (分管教学副主任签字)审定日期:一、课程性质与目的(一)课程的性质高等几何是高等师范院校数学与应用数学专业的一门选修课程。
高等几何课程更是大学“数学与应用数学”专业的重要基础课程,在人才培养中有着最基本的重要性,是大学、研究生阶段的数学学习和未来从事数学教学、研究的重要基础。
(二)课程的目的本课程的目的是使学生在已学习初等几何,解析几何和高等代数的基础上,系统地学习射影几何的知识。
并通过学习实射影平面几何的基础知识,使学生认识射影空间、欧氏空间的内在联系。
从而发展空间概念,更深入地掌握初等几何,解析几何和高等代数的知识,在数学思想上得到启发,在数学方法上得到初步训练,为教好中学数学打下较坚实的基础。
二、与相关课程的联系与分工高等几何、高等数学、数学分析统称为“三高”,它们是高等师范院校数学专业的三门基础课程。
但是,本课程与其他两门课程相比,地位就相形见绌了。
同时本课程是以射影几何学为理论基础,因此学习本课程的学生应具备相应的初等几何、解析几何、高等代数等课程的基础知识。
三、教学内容及要求第一章仿射坐标与仿射变换【教学要求】本章是基于变换群的观点,对几何学的高度抽象概括,给出研究几何学的变换群观点。
要求掌握透视仿射对应、仿射对应与仿射变换、仿射坐标系,并能熟练地求出仿射变换的代数表示式,区别什么是射影平面,仿射平面,欧氏平面【教学重点】仿射坐标系;仿射变换的代数表示【教学难点】仿射性质;射影观点的建立;仿射变换的应用【教学内容】第一节透视放射对应第二节仿射对应与仿射变换第三节仿射坐标一、仿射坐标系二、放射变换的代数表示三、几种特殊的仿射变换第四节仿射的性质第二章射线平面【教学要求】本章作为学习全课程的基础和中心内容,重点讲解欧氏平面的拓展过程,在此基础上给出射影直线和影射平面的概念和模型,使得学生明确了解欧氏直线和射影直线、欧氏平面和影射平面的区别和联系。
二次贝塞尔曲线的计算公式
二次贝塞尔曲线的计算公式
B(t) = (1-t)^2 P0 + 2(1-t)tP1 + t^2 P2。
其中,t为参数,取值范围一般是0到1之间。
当t=0时,曲
线取P0点的值;当t=1时,曲线取P2点的值;当t在0到1之间
变化时,曲线呈现出平滑的变化。
这个公式可以通过代入不同的t值来计算曲线上的点的位置,
从而绘制出二次贝塞尔曲线。
在计算机图形学和计算机辅助设计中,二次贝塞尔曲线被广泛应用于曲线的绘制和动画效果的实现中。
除了计算公式外,二次贝塞尔曲线还有其他相关的概念和性质,比如曲线的凸包性质、切线方向的计算等,这些都是在实际应用中
需要考虑的问题。
因此,在使用二次贝塞尔曲线时,除了掌握计算
公式,还需要深入理解其原理和特性,以便更好地应用于实际场景中。
总的来说,二次贝塞尔曲线的计算公式是一个重要的基础知识点,对于计算机图形学和计算机辅助设计领域的从业者来说,掌握
这个公式及其应用是非常重要的。
二次曲线极点极线定理
二次曲线极点极线定理,又称极坐标定理,是指在二次曲线的极坐标方程中,通过极坐标的极点(即原点)作的切线,垂直于这些切线的直线所过的点构成的直线,称为二次曲线的极线。
具体来说,对于具有极坐标方程r = f(θ)的二次曲线,其中r 表示极径,θ表示极角,f(θ)是一个关于极角的函数,极点(0,0)是二次曲线的焦点。
在极坐标方程r = f(θ)的曲线上,以极点为起点的各切线的斜率等于f(θ)的导数f'(θ)。
而极线则是与切线垂直通过极坐标方程所给定的极点的直线。
极线可以用直角坐标系中的方程表示,并且通过二次曲线的对称中心(焦点)。
二次曲线的极点极线定理可以用于求解二次曲线的相关性质,如对称性、切线和法线等。
该定理在极坐标系中给出了二次曲线的极线的几何性质,为分析和绘制二次曲线提供了重要的工具。
此外,二次曲线的极点极线定理还可以用于求解二次曲线的方程。
一般地,给定二次曲线上三个不共线的点,可以通过求解它们的极坐标方程,然后利用极点极线定理,求出二次曲线的方程。
具体做法如下:1. 以已知的三个点中的任意一个点为极点,建立极坐标系。
2. 将其他两个点的坐标换算成极坐标形式,即r = sqrt(x^2 + y^2),θ= arctan (y/x)。
3. 列出三个点的极坐标方程,即r1 = f(θ1)、r2 = f(θ2)、r3 = f(θ3),其中f(θ)是待求的二次函数。
4. 对上述三个方程求导,即可得到f'(θ1)、f'(θ2)和f'(θ3)。
5. 利用极点极线定理,将上述导数值代入相应的式子中,得到三条直线的解析式。
6. 这三条直线的交点即为二次曲线的对称中心,对称中心的坐标即为二次曲线的焦点,进而可以利用焦点和其他几何性质,求出二次曲线的方程。
总之,二次曲线的极点极线定理是一种有力的工具,可以用于研究二次曲线的性质和方程,对于二次曲线的分析和应用具有实际意义。
二次曲线的定义
二次曲线的射影定义
定理2的证明. 设 Γ 由 O(P) O′(P) 生成,需证 A(M ) B(M ).
设
AM OP BM OP
K K
则有 A(M ) OP(K )
B(M ) OP(K )
所以只要证 OP(K ) OP(K ).
设 OA BM A,OB AM B.
O(P) O(P), O(A, B, P, M ) O(A, B, P, M ).
定义3′ 在射影平面上,称 两个射影点列对应点连线的集 合为一条二级曲线。
思考:试研究本定义是如何包含退化二次曲线的。
提示:考虑透视对应、射影变换的情况。
二次曲线的射影定义
例1 求由两个射影线束 x1 – λx3 = 0, x2 – μx3 = 0 ( λ + μ = 1) 生 成的二阶曲线方程。
由本定理的证明可知,[u1,u2,u3] 为 Γ上一点处的切线
a11 a12 a13 u1
a12 a22 a23 u2 0
(13)
a13 a23 a33 u3
u1 u2 u3 0
展开, 得 T Aijuiu j 0. 且Aij Aji ,| Aij || aij |2 0.
这里Aij是aij的代数余子式.
特殊 ( l 属于 Γ′ ):
Tl 0
(6' )
二次曲线的射影定义
例2 如果两个三点形 ABC 与 A′B′C′ 同时内接于一条二次曲线, 求证它们也同时外切于一条二次曲线。
证. 设交点 D, E; D′, E′ 如图。 因为 A, B, C, A′, B′, C′ 在同一条二次曲线 上,据二阶曲线的射影定义有
推论2′ 任一二级曲线可由 两个射影点列生成。
大纲高等几何
高纲0870江苏省高等教育自学考试大纲29790高等几何江苏教育学院编江苏省高等教育自学考试委员会办公室一、课程性质及其设置目的与要求(一)课程性质与特点《高等几何》是高等师范院校数学与应用数学专业的重要基础课程之一,本课程在学生具备初等几何、解析几何与高等代数知识的基础上,系统地学习射影几何的基本知识,使他们能用变换群观点来看待几何学,加深对几何学和几何空间概念的理解。
本课程的主旨在于拓展读者的几何空间知识,学习了解变换群观点,进而达到训练理性思维的能力,提高数学修养的目的。
本课程包括了许多著名的定理,奇妙的图形。
通过本课程的学习,可以有效地提高数学审美意识。
本大纲要求本课程的内容处理上实行解析法与综合法并用,以解析法为主。
(二)课程设置目的与要求课程内容包括:变换群与几何学;射影平面;射影变换;二次曲线的射影理论;射影几何的子几何。
课程设置目的和要求:一方面使得学生拓宽眼界,扩大知识领域,提高抽象思维能力,为进一步学习其他课程打下基础。
另一方面使学生加深对中学几何特别是解析几何的理论与方法的理解, 使得学生加深对中学几何特别是解析几何的理论与方法的理解,从而获得用高观点来处理中学几何问题的能力,为未来的中学几何教学打下基础。
二、课程内容与考核目标第一章变换群与几何学(一)课程内容1.变换与变换群2.仿射坐标和仿射平面3.仿射变换4.欧氏平面和保距变换5.几何学与变换群的关系(二)学习与考核要求本章是基于变换群的观点,对几何学的高度抽象概括,给出研究几何学的变换群观点。
掌握仿射变换的定义、性质和代数表达式;理解仿射坐标和图形的仿射性质,掌握仿射对应图形;掌握保距变换的性质和代数表达式;特别是基本仿射不变性---平行性和基本仿射不变量---单比,及其计算方法。
第二章射影平面(一)课程内容1.扩大仿射平面2.射影平面3.交比与调和共轭4.对偶原理(二)学习与考核要求本章作为学习全课程的基础和中心内容,重点讲解欧氏平面的拓展过程,在此基础上给出射影直线和影射平面的概念和模型,使得学生明确了解欧氏直线和射影直线、欧氏平面和影射平面的区别和联系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
配极变换
A11 (u1 , u2 , u3 ) A12 A 13 A12 A22 A23 A13 v1 A23 v2 0. A33 v3 (3)
3. 极点与极线的计算 (1). 已知P(pi), 求极线, 直接求Sp=0. (2). 已知u(ui), 求极点, 将[ui]代入(2), 解出(pi). (注:在实际 计算时, 可取ρ=1.)
证明 只要证后半. 设直线u: u1x1+u2x2+u3x3=0, 求u关于Γ的 极点.设P(pi)为其一个极点, 由于P(pi)的极线唯一存在为Sp=0, 从 而u与Sp=0为同一直线, 由此可以推知
u1 a11 u2 a12 u a 3 13 a12 a22 a23 a13 p1 a23 p2 . a33 p3 (2)
定理13 点P关于Γ的共轭点的轨迹为一条直线Sp=0.
证明 设P(pi), Q(qi). 则PQ与Γ: S=0的交点M(pi+λqi)满足
Sqq2 2S pq S pp 0. 设其两根为λ1, λ2. 则交点为Mj( pi+λjqi), (j=1,2).
于是 (PQ, M1M2) = –1 λ1/λ2 = –1 λ1+λ2 = 0 S pq 2 0 S pq 0. Sqq 将qi改为流动坐标xi, 得P关于Γ的共轭点的轨迹为直线Sp=0.
注1. 注2. 注3. 轭。 例1.
Γ的自极三点形的任一顶点必不在Γ上. Γ的自极三点形恰有一个顶点在Γ的“内部”. Γ的自极三点形任意两顶点相互共轭; 任意两边相互共 给定不在Γ上的一点P(pi), 任求Γ的一个自极三点形PQR.
解. (i) 求P(pi)的极线p: Sp=0. (ii) 在p上任取不属于Γ的一点Q(qi), 求Q的极线q: Sq=0.
因为|aij|≠0, 故(2)对于(p1,p2,p3)有唯一解, 即u的极点P唯一存在. (2)表示直线u与它的极点P之间的关系, 称为极点方程组.
配极变换 根据推论6′, 可以对偶地给出下列定义: 定义8 相互通过对方极点的直线称为关于Γ的共轭直线. 注. 利用Maclaurin定理及对偶原则有: 两直线u[ui], v[vi]关于 Γ: S=0共轭Tuv=0
配极变换
2. 极点与极线 共轭点轨迹p P 定义7 对于点P, 若 则称P关于Γ的 切线p 为 P P关于Γ的极线, 方程为Sp=0. 反之, 称P为直线p关于Γ的极点. 由推论5, 我们给出共轭点的一个等价定义: 定义6′ 相互在对方极线上的两点称为关于Γ的共轭点.
配极变换 推论6 平面上任一点P关于Γ的极线存在唯一, 其方程为Sp=0. 反之, 平面上任一直线u关于Γ的极点存在唯一.
配极变换 配极在二次曲线理论中十分重要, 二次曲线的大部分重要性 质均与配极有关. 只讨论二阶曲线, 总假定:非退化.
设 :
S aij xi x j 0
i , j 1 3
aij a ji , | aij | 0.
(1)
配极变换
一、极点与极线
1. 引入 定义6 两点P, Q关于Γ共轭 (如图),如 果(PQ,M1M2) = -1.
推论7 两点连线的极点为此二点极线的交点; 两直线交点的极线为此二直线极点的连线. 推论8 共线点的极线必共点;共点线的极 点必共线. 推论9 关于非退化二阶曲线Γ的配极变换使得点列对应于线 束, 线束对应于点列;图形对应于其对偶图形.
推论10 关于非退化二阶曲线Γ的配极变换使得共线四点的 交比等于其对应共点四直线的交比. 因此, 配极变换规定了一个点 列与其对应线束之间的一个射影对应.
综上: 非退化二阶曲线Γ 二维异素射影变换 从而 配极变换 二维异素射影变换
对偶变换
配极原则
特殊的对偶原则
配极变换 2. 自极三点形 定义10 若一个三点形关于Γ每个顶点是其对边的极点(则每 边是其对顶的极线), 则称此三点形为关于Γ的一个自极三点形.
定理15 内接于非退化二阶曲线Γ的完全四点形的对边三点 形是关于Γ的一个自极三点形.
配极变换
推论5 两点P, Q关于Γ共轭Spq=0. 注1. P在Γ上, 则Spp=0。我们规定 Γ上的点关于Γ自共轭. 注2. 验证两点P, Q关于Γ共轭, 只要验证
a11 ( p1 , p2 , p3 ) a12 a 13 a12 a22 a23 a13 q1 a23 q2 0. a33 q3
注. 方程(2)是一个非奇异线性变换, 是由Γ: S=0通过关于它 的极点极线关系规定的同底点场与线场之间的一个一一变换.
配极变换Βιβλιοθήκη 二、配极变换1. 配极变换的概念 定义 称由
ui aij x j
j 1 3
i 1, 2,3, aij a ji ,| aij | 0.
(4)
决定的同底点场与线场之间的变换为关于非退化二阶曲线Γ: S=0 的配极变换.
(iii) 求p与q的交点R(ri), 则PQR必为Γ的一个自极三点形.
配极变换 3. 配极变换的基本应用 (1). 几何证明题 灵活运用配极原则以及自极三点形等概念
(2). 极点极线作图 例2. 已知非退化二阶曲线Γ及不在Γ 上一点P, 求作P关于Γ的极线p. 例3. 已知非退化二阶曲线Γ以及一直 线p, 求作p关于Γ的极点P. 作法. 在p上任取不在Γ上两相异点 Q,R, 利用上例, 作Q,R关于Γ的极线q,r. 则 q×r=P. 例4. 已知非退化二阶曲线Γ及Γ外一 点P, 过P求作Γ的两切线. 作法一. 利用例2, 设p交于E,F, 连PE, PF即可. 作法二. 如图. 过P任作三割线, 可得切线.
