课后作业答案
部编人教版三年级语文上册课后作业《金色的草地》(含答案)

部编版三年级上册语文16.金色的草地课后作业一、选择题1.《金色的草地》一文写的主要事情是()A.兄弟俩在草地上玩耍,互相往对方脸上吹蒲公英的绒毛B.“我”和弟弟早晨起床去钓鱼。
C.“我”发现了草地会变颜色及其变颜色的原因。
D.“我”和弟弟在草地上种蒲公英。
2.对下列句中加点词的理解,有误的一项是()A.弟弟一本正经....地对我说:“你也要做个诚实的孩子。
”(“一本正经”指的是弟弟对“我”说话的时候很规矩,很认真。
)B.蒲公英成了我们最喜爱..的一种花。
(句中的“喜爱”表示作者对蒲公英感兴趣,可以换成“喜欢”。
)C.猪八戒假装..肚子疼,然后偷偷地跑去找西瓜吃。
(句中的“假装”说明猪八戒的肚子疼是一种故意行为,和“假如”意思相近。
)3.下列不是教育我们要“关爱别人,礼貌待人”的一项是()A.不迁怒,不贰过。
B.与人善言,暖于布帛;伤人以言,深于矛戟。
C.有理走遍天下,无理寸步难行。
D.仁者爱人,有礼者敬人。
4.下面的句子不是祈使句的是()A.请您给我讲讲吧!B.橘子、柿子你挤我碰,争着要让人们去摘呢!C.咱们捉迷藏玩吧!D.谁偷了嘴,罚扫地三天,不给东西吃!5.“绒”字的书写笔顺正确的一项是( )。
A.撇折、撇折、提、横、横、撇、斜钩、撇、点B.撇折、撇折、提、横、撇、横、斜钩、撇、点C.撇折、撇折、提、横、斜钩、横、撇、撇、点D.撇折、撇折、提、横、横、撇、斜钩、点、撇二、填空题6.在括号里填上合适的词语。
(___)(___)的草地(___)(___)的花瓣(___)(___)的蒲公英7.根据拼音写词语,不要写错别字。
shèng kāi wán shuǎ hé lǒng(_______)(________)(________)diào yú guān chá yǒu qù(______)(_______)(________)8.读课文《金色的草地》,完成填空。
《大学化学》课后习题答案大全

《⼤学化学》课后习题答案⼤全第⼀章课后作业答案1-4.判断下列⼏种说法是否正确,并说明理由。
(1)原⼦是化学变化中最⼩的微粒,它由原⼦核和核外电⼦组成;正确原⼦是化学变化中的最⼩粒⼦。
原⼦是由居于原⼦中⼼的原⼦核和核外电⼦构成,原⼦核⼜由质⼦和中⼦两种粒⼦构成的。
构成原⼦的基本粒⼦是电⼦、质⼦、中⼦。
(2)相对原⼦质量就是⼀个原⼦的质量;错误相对原⼦质量是指以⼀个碳-12原⼦质量的1/12作为标准,任何⼀个原⼦的真实质量与⼀个碳-12原⼦质量的1/12的⽐值。
(3)4g H2和4g O2所含分⼦数⽬相等;错误4g H2含有2mol氧⽓分⼦。
氢⽓相对分⼦质量2,4g/(2g/mol)=2mol。
4g O2含有0.125mol氧⽓分⼦。
氧⽓相对分⼦质量32,4g/(32g/mol)=0.125mol。
所以分⼦数⽬不相等。
(4)0.5mol的铁和0.5mol的铜所含原⼦数相等;正确铁和铜都是由原⼦构成的⾦属,摩尔是物质的量的单位,物质的量相同,即摩尔数相同,就表⽰原⼦数相同。
(5)物质的量就是物质的质量;错误物质的量:表⽰物质所含微粒数(N)(如:分⼦,原⼦等)与阿伏加德罗常数(NA)之⽐,即n=N/NA。
物质的量是⼀个物理量,它表⽰含有⼀定数⽬粒⼦的集体,符号为n。
物质的量的单位为摩尔,简称摩,符号为mol。
物质的质量:质量不随物体的形状和空间位置⽽改变,是物质的基本属性之⼀,通常⽤m表⽰物质的量=物质的质量/物质的摩尔质量(6)化合物的性质是元素性质的加合。
错误化合物的性质是由组成该化合物的微观结构决定的,例如CO和CO2,组成元素相同,性质却不同。
1-5.硫酸铵(NH4)2SO4、碳酸氢铵NH4HCO3和尿素CO(NH2)2三种化肥的含氮量各是多少?哪种肥效最⾼?答:①硫酸铵(NH4)2SO4,含氮量为(14*2)/(14*2+1*8+32*1+16*4)≈0.212②碳酸氢铵NH4HCO3,含氮量为14/(14+1*5+12+16*3)≈0.177③尿素CO(NH2)2,含氮量为(14*2)/(12+16+14*2+1*4)≈0.467综上,0.177<0.212<0.467,这三种肥料中,尿素的含氮量最⾼,所以尿素的肥效最⾼。
部编版小学五年级语文上册第七单元第21课《古诗词三首》课后作业及答案(含两套题)

部编版小学五年级语文上册第七单元第21课《古诗词三首》课后作业及答案1.结合诗词句判断下列加点字的解释是否正确,正确的打“√”。
(1)山一程,水一程,身向榆关..(那边,指关外)行。
..(山海关)那畔()(2)随意春芳歇.(休息),王孙..(原指贵族子弟,此处指诗人自己)自可留。
()(3)姑苏...(枫桥附近的一座寺庙),夜半..(苏州的别称)城外寒山寺钟声到客船。
()2.下列加点字的读音有误的一项是()。
A.江畔.(pàn)B.聒.噪(kuō)C.寺.庙(sì)D.榆.树(yú)3.下列关于《山居秋暝》的说法,不正确的一项是()。
A.全诗描绘了秋雨初晴后傍晚时分山村的旖旎风光和山居村民的淳朴风尚,表现了诗人寄情山水田园,对隐居生活怡然自得的满足心情B.一个“空”字,渲染出天高云淡,万物空灵之美。
诗人隐居于此是何等的闲适,如此描绘山水田园的环境,流露出诗人的喜爱之情C.这首诗通过写山水田园的清新宜人,表达了作者思念家乡的思想感情D.诗句“明月松间照,清泉石上流”中,前一句写静景,后一句写动景,动静结合,写出了山间的静谧感4.补全词句,完成练习。
长相思山一程,水一程,,夜深千帐灯。
风一更,雪一更,,故园无此声。
(1)写出下列字的意思。
程:聒:(2)《长相思》的作者是代的。
词的上阕描写的是的情景,下阕描写了将士们的情景。
(3)“故园无此声”中“故园”指,“此声”指词中的,表达了诗人的感情。
(4)下列对这首词的理解,不正确的一项是()。
A.众多的帐幕里深夜还亮着灯,出行在外的人们久久不能入睡,苦不堪言B.词人随着大队人马向山海关外进发,一路上跋山涉水,历尽辛苦C.这首词描绘了词人出行关外的艰辛和凄苦,抒发了词人浓郁的思乡之情D.一阵风过后接着一阵雪,使家乡无风无雪的词人心烦意乱,思乡之情油然而生5.根据古诗文填空。
《枫桥夜泊》的作者是代的,《山居秋暝》的作者是代的,两首诗写的都是季的景色。
线性代数课后习题1-4作业答案(高等教育出版社)

第一章 行列式1. 利用对角线法则计算下列三阶行列式:(1)381141102---;解381141102--- =2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4.(3)222111c b a cb a ;解222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)7110025*******214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---=143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====cc 041203212213041224--=====rr000003212213041214=--=====r r .(3)efcf bf decd bd ae ac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b ec b e c b ad f ---=a b c d e fa d fbc e 4111111111=---=.(4)dc b a 100110011001---.解dc b a100110011001---dc b a ab ar r 10011001101021---++=====d c a ab 101101)1)(1(12--+--=+01011123-+-++=====cdc ad a ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213ab a b a a b a ab ac c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)yx z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式):(1)aaD n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解a a a a a D n 0 0010 000 00 0000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n行展开))1()1(10 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a a n n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1 )1()1(=an-a n -2=a n -2(a 2-1).(2)xa a a x aa a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0 ,再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n 第二章 矩阵及其运算 1. 计算下列乘积: (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B ,求3AB -2A 及A T B .解⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503,⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T.3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问:(1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0.(2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y . 解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y . 7.设⎪⎪⎭⎫⎝⎛=λλλ001001A ,求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ,⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫.用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫⎝⎛5221;解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为⎪⎭⎫⎝⎛--=⎪⎭⎫⎝⎛=1225*22122111A A A A A , 故 *||11A A A =-⎪⎭⎫⎝⎛--=1225.(3)⎪⎪⎭⎫ ⎝⎛---145243121;解⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以*||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解⎪⎪⎪⎭⎫ ⎝⎛=n a a a A0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=-n a a a A 10011211 .12. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有⎪⎩⎪⎨⎧===001321x x x . 19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511,求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)]=diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫ ⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章 矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫ ⎝⎛--340313021201;解⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. ) ~⎪⎪⎭⎫ ⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311;解⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011.3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y ,求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换. 解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛323513123;解⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001 故逆矩阵为⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解⎪⎪⎪⎭⎫⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010********* 故逆矩阵为⎪⎪⎪⎭⎫ ⎝⎛-------10612631110104211.5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫⎝⎛-=132321B , 求X 使XA =B .解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫ ⎝⎛---411007101042001 ~r ,所以⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量. 12.设⎪⎪⎭⎫⎝⎛----=32321321k k k A ,问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3. 解⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r .(1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明 由⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r⎪⎪⎪⎭⎫ ⎝⎛------531400251552000751610421301~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示. 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明 由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a ,知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组: (1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~r r r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---14011313021512012211. 解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~r r r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~r r r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x . 解 对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x . 取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解 对增广矩阵进行初等行变换, 有 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。
管理学课后作业参考答案

第一章管理与管理学p003 前三个问题参考答案1.什么是管理,为什么需要管理?管理是人们通过综合运用人力资源和其他资源,以有效地实现目标的过程(本教材定义)。
为什么需要管理主要在于人的欲望的无限性与人所拥有的资源的有限性之间的矛盾,管理的功能就在于通过科学的方法来提高资源的利用率,力求以有限的资源实现尽可能多或高的目标。
2.如何衡量管理的好坏?可以用管理的有效性来衡量管理的好坏,有效性包括效率与效益。
效率是指投入与产出之比,效益是指目标的大程度。
有效的管理要求既讲求效益,又讲求效率。
3.怎样进行有效的管理?要进行有效的管理,必须履行管理的四大基本职能:计划、组织、领导、控制。
并且必须遵循管理的基本过程,即必须系统地开展计划、组织、领导、控制等各项工作。
单纯地就计划谈计划,就组织论组织、为领导而领导、为控制而控制,是达不到应有的管理效果的。
第二章管理者p026前三个问题参考答案1.管理者是干什么的?他在组织中充当什么角色?管理者是在一个组织中从事管理工作、履行管理四大职能,并且拥有下属、负责指挥下属开展各项工作的人员。
管理者在一个组织中充当着三个方面10种角色:人际关系方面(形象代言人、领导者、联络员);信息传递方面(组织发言人、信息监督者、信息传递者);决策活动方面(企业家、资源分配者、矛盾排除者、谈判者)。
2.在一个组织中有哪几类管理者?他们的职责有什么不同?组织中管理者的类型可以按照地位以及作用两种方式进行划分,不同类型管理者的职责有所不同。
按地位可以分为高层、中层和基层管理者。
高层管理者的主要职责是对组织负有全部责任,主要侧重于决定组织的大政方针,沟通组织与外界的交往联系,为组织创造良好的内外部环境;中层管理者的主要职责是正确理解高层的指示精神,创造性地结合本部门的实际情况,贯彻落实高层所确定的大政方针,指挥各基层管理者开展工作;基层管理者的主要职责是直接指挥和监督现场作业人员,保证完成上级下达的各项计划和指令。
机械设计课后作业及部分解答
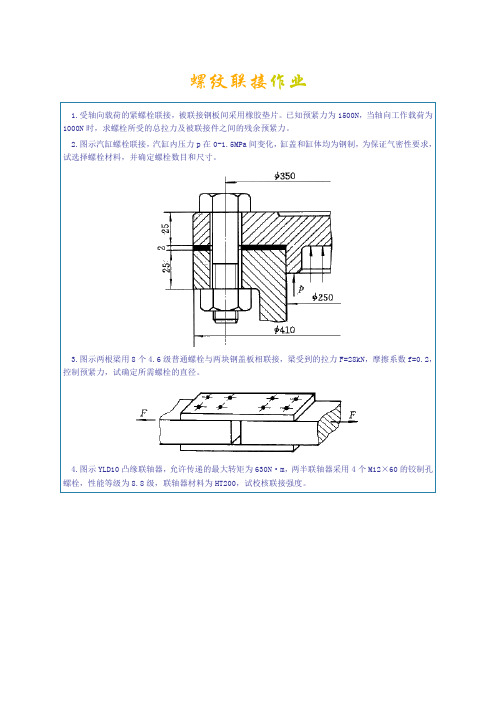
螺纹联接作业1.受轴向载荷的紧螺栓联接,被联接钢板间采用橡胶垫片。
已知预紧力为1500N,当轴向工作载荷为1000N时,求螺栓所受的总拉力及被联接件之间的残余预紧力。
2.图示汽缸螺栓联接,汽缸内压力p在0-1.5MPa间变化,缸盖和缸体均为钢制,为保证气密性要求,试选择螺栓材料,并确定螺栓数目和尺寸。
3.图示两根梁用8个4.6级普通螺栓与两块钢盖板相联接,梁受到的拉力F=28kN,摩擦系数f=0.2,控制预紧力,试确定所需螺栓的直径。
4.图示YLD10凸缘联轴器,允许传递的最大转矩为630N·m,两半联轴器采用4个M12×60的铰制孔螺栓,性能等级为8.8级,联轴器材料为HT200,试校核联接强度。
5.铰制孔用螺栓组联接的三种方案如图所示,已知L=300mm,a=60mm,试求三个方案中,受力最大的螺栓所受的力各为多少?哪个方案较好?6.图示底板螺栓组联接受外力F e作用,外力F e作用在包含x轴并垂直于底板结合面的平面内。
试分析螺栓组受力情况,并判断哪个螺栓受载最大?保证联接安全的必要条件有哪些?7.指出下列图中的错误结构,并画出正确的结构图。
8.图示刚性联轴器取4个M16小六角头铰制孔用螺栓,螺栓材料为45钢,受剪面处螺栓直径为φ17mm,其许用最大扭矩T=1.5kN·m(设为静载荷),试校核其强度。
联轴器材料HT250。
提示9.上题的刚性联轴器中,若采用M16受拉螺栓,靠两半联轴器的接合面间产生的摩擦力来传递扭矩,螺栓材料为45钢,接合面间的摩擦系数f=0.16,安装时不控制欲紧力,试决定螺栓数(螺栓数应为双数)。
10.如图,缸径D=500mm,蒸汽压力p=1.2MPa,螺栓分布圆直径D0=640mm。
为保证气密性要求,螺栓间距不得大于150mm。
试设计此汽缸盖螺栓组联接。
螺纹联接作业解答1~8 (略)解:(1)、求预紧力'F 查手册GB196-81 得113.835d =(M16) p=2H=0.866 p=1.732则:1 1.73213.83513.54666c Hd d =-=-= 查表6.3 取 []4S S =选6.8级:600B a Mp σ=480S a Mp σ=许用拉应力:480[]120[]4sa S Mp S σσ=== 24 1.3'[]c F d σπ⨯≤22[]13.546120'13303.014 1.34 1.3c d F N πσπ⨯⨯∴≤==⨯⨯(2) '2Sf DzF k T μ= 取保 1.3f k =23 1.31500100011.82'13303.010.16155f S k T z F Dμ⨯⨯⨯∴===⨯⨯取 z=12 (双数)解:1、确定螺栓数目z 取间距t =12564016.09125125D z ππ⨯=== 取=162、选螺栓性能等级6.8级 45钢600B a Mp σ= 480S a Mp σ=480S a Mp σ= 3、计算螺栓载荷(1)、气钢盖载荷:225001.2235619.4544D Q p N ππ⨯===(2)、螺栓工作载荷:14726.2216QF N == (3)、残余预紧力: "1.5 1.514726.2222089.33F F N =⨯=(4)、螺栓最大拉力:0"14726.2222089.3336815.55F F F N =+=+=(5)、许用拉力:取安全系数:[]3S S = (不控制预紧力)480[]16033Sa Mp σσ=== 4、计算螺栓尺寸19.5156c d mm ≥==选 M24查 124,20.752,3d d p === 0.866, 2.598H p ==1 2.59820.75220.31919.515666c Hd d =-=-=> (满足要求) 若选M22 122,19.294, 2.5d d p === 则: H=0.866 p=2.1651 2.16519.29418.93366c Hd d =-=-= (不满足) 轴毂联接作业1.图示减速器的低速轴与凸缘联轴器及圆柱齿轮之间分别采用键联接。
大学生心理健康课后作业及答案

1.绪论走进心理学已完成成绩:100.0分1【单选题】心理学是在()模式下研究人的问题的。
∙A、简单∙B、健康∙C、通约∙D、一般我的答案:C得分:25.0分2【单选题】心理学学科的发展迄今是()的局面。
∙A、稳步向前∙B、曲折坎坷∙C、百花齐放∙D、停滞不前我的答案:C得分:25.0分3【单选题】学习心理学要追求()、不要苛求()。
∙A、正确有效∙B、有效正确∙C、真理逻辑∙D、逻辑真理我的答案:B得分:25.0分4【判断题】科学不代表真实,只是行走在逼近真实的道路上。
我的答案:√什么是心理学已完成成绩:100.0分1【单选题】心理学是:研究个体感觉、()、情绪、意识与精神活动之间关系的科学∙A、思想∙B、行为∙C、外形∙D、动作我的答案:B得分:25.0分2【多选题】我们能理解美国人“嗷嗷”是在学狗叫,是因为()(多选)∙A、美国人养大狗∙B、关于狗叫声形成了通约∙C、这是不同情境下的不同标准∙D、中国人智商较高我的答案:ABC得分:25.0分3【判断题】主观是由我们的感知和觉知之间构成的现实。
我的答案:√得分:25.0分4【判断题】你理解的事物就是事物的本身。
我的答案:×心理学讨论什么已完成成绩:100.0分1【判断题】完全凭自己的好恶去评价一个人,就失去了社会的客观标准。
我的答案:√得分:25.0分2【判断题】心理学认为人过分强调表达自己某种特质时恰恰说明这个人缺少这种特质。
我的答案:√得分:25.0分3【判断题】心理学是研究人类如何更好地生活,如何幸福的科学。
我的答案:√得分:25.0分4【判断题】马丁·布伯的前半生主要致力于用哲学的方法研究宗教。
我的答案:√古典心理学已完成成绩:100.0分1【单选题】不属于亚里士多德的逻辑三段论的是∙A、大前提∙B、中前提∙C、小前提∙D、结论我的答案:B得分:20.0分2【单选题】马丁·布伯是()家∙A、政治∙B、历史学∙C、宗教哲学∙D、军事我的答案:C得分:20.0分3【单选题】科学世界有三大未解之谜:物质起源、生命起源、()∙A、意识起源∙B、生物起源∙C、文化起源∙D、宇宙起源我的答案:A得分:20.0分4【多选题】有效的争论技巧都有哪些?(多选)∙A、善于并愿意表达自己观点∙B、注重分享、真诚很重要∙C、不要轻易放弃、坚持自己我的答案:ABC得分:20.0分5【判断题】电影《金刚》中金刚和女主角的爱情是柏拉图式的爱情。
大学生创业基础(李肖鸣)课后作业及答案

大学生创业基础(李肖鸣)课后作业及全对答案1.1经历挫折与坚持:创业精神与创业结果已完成成绩:100.0分1 创业是不拘泥于当前资源约束,寻求机会、进行价值创造的行为过程。
()我的答案:√得分:33.3分2 从理论上讲,创业是在资源完备的情况下进行的一种价值整合。
()我的答案:×得分:33.3分3 创业过程中遇到挫折是必然的,创业精神是引领创业的支柱。
()我的答案:√得分:33.3分1.2创业的动机、类型、流程与创业者的特点已完成成绩:100.0分1 创业的本质是什么?()A、创业的本质是成功。
B、创业的本质是赚钱。
C、创业是一种生活方式。
D、创业是一种职业。
我的答案:C 得分:20.0分2 关于创业,下列说法错误的是()。
A、创业可以挖掘个人潜力,有助于实现自身价值。
B、在创业过程中考验的是综合素质和创业精神。
C、创业者的动机是多种多样的,可能是生理需求、安全需求、尊重需求等等。
D、就职业的稳定性而言,创业没有就业稳定。
我的答案:D 得分:20.0分3 自主创业的优点不包括()。
A、决策的自由B、时间的自由C、精神的自由D、财务的自由我的答案:C 得分:20.0分4 按创业主体分类,创业的类型不包括()。
A、智慧型B、关系型C、机会型D、传统型我的答案:D 得分:20.0分5创业的机会成本越低越容易创业。
()我的答案:√得分:20.0分1.3创业精神的本质、职业生涯规划与自我认识已完成成绩:100.0分1 以下哪一项不属于创业者必须具备的能力:()A、人际协调能力B、开拓创新能力C、组织管理能力D、自我执行能力我的答案:D 得分:20.0分2 关于创业与创业者,下列说法错误的是()。
A、创业者在创业前要做好准备,包括正确认识自己B、并不是每个人都适合创业C、创业精神是与生俱来的,与后天培养无关D、创业与职业生涯规划息息相关我的答案:C 得分:20.0分3 决定创业成败的是()。
A、资金B、人脉C、创业精神D、市场我的答案:C 得分:20.0分4 创业精神的本质是创新意识和主动精神。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
产品数据库Product(maker, model, type)PC(model, speed, ram, hd, price)Laptop(model, speed, ram, hd, screen, price)Printer(model, color, type, price)关系Product给出了各种产品的制造厂商、型号和产品类型(PC、笔记本电脑或者打印机)。
为了简单起见,假设所有产品的型号都唯一,而不管它是由哪个制造商生产的。
关系PC对于不同型号给出了如下属性:速度(处理器的速度,单位是GHz)、RAM的大小(单位是MB)、硬盘的容量(单位是GB)以及价格。
关系Laptop与关系PC类似,它在PC的基础上增加了属性screen,即显示器的尺寸(以英寸为单位)。
关系Printer对于每种型号有如下属性:是否彩色(如果是的话,这个值是true)、处理类型(激光的还是喷墨的)以及价格。
关系PC的数据关系Laptop的数据关系Printer的数据二战中的大型舰船数据库Classes(class, type, country, numGuns, bore, displacement) Ships(name, class, launched)Battles(name, date)Outcomes(ship, battle, result)相同设计的舰船组成一个“类”,类别的名称通常就是这个类的第一艘船的名字。
关系Classes 记录了“类”的名字、型号(bb代表主力舰,bc代表巡洋舰)、生产国家、火炮的门数、火炮的尺寸(口径,单位是英寸)和排水量(重量,单位是吨)。
关系Ships记录了舰船的名字、舰船类属名字、开始服役的日期。
关系Battles给出了这些舰船参加的战役的时间。
关系Outcomes给出了各个舰船在各场战役中的结果(是沉没,还是受伤,或者完好)关系Classes的数据关系Battles的数据关系Outcomes的数据需要注意的是:这个数据库中存在着“悬浮元组”,比如,在关系Outcomes中出现的船只可能在关系Ships中查不到。
※作业一:习题1.11.对于产品数据库中的4个关系,写出它们的关系模式定义语句。
CREATE TABLE Product (maker char(3),model char(4) primary key,type char(10));CREATE TABLE PC (model char(4) primary key,speed decimal(3,2),ram int,hd int,price int);CREATE TABLE Laptop (model char(4) primary key,speed decimal(3,2),ram int,hd int,screen decimal(3,1),price int);CREATE TABLE Printer (model char(4) primary key,color char(5),type char(10),price int);2.修改关系Printer,删掉属性color。
ALTER TABLE Printer DROP COLUMN color;3.修改关系Laptop,增加属性od(光驱类型,比如CD、DVD)。
如果某个笔记本电脑没有光驱,则该属性的默认值为‘none’。
ALTER TABLE Laptop ADD od char(10) DEFAULT ‘none’;习题1.2 [选做]1.对于二战中的大型舰船数据库中的4个关系,写出它们的关系模式定义语句。
CREATE TABLE Classes (class char(20) primary key,type char(2),country char (20),numGuns smallint,bore smallint,displacement int);CREATE TABLE Ships (name char(20) primary key,class char(20),launched int);CREATE TABLE Battles (name char(20) primary key,date datetime);CREATE TABLE Outcomes (ship char(20),battle char(20),result char(7),primary key (ship, battle));2.修改关系Classes,删掉属性bore。
ALTER TABLE Classes DROP COLUMN bore;3.修改关系Ships,增加属性yard,它给出了该船的船坞。
ALTER TABLE Ships ADD yard char(30);※作业二:(写关系代数表达式)习题2.1 对于产品数据库,试写出下列查询的关系代数表达式。
1.哪种PC型号具有最少3.00的速度?πmodel(σspeed>=3.00(PC))2.哪个生产厂商的笔记本电脑的硬盘容量至少100GB?πmaker (Product ∞(σhd>=100 (Laptop)))3.查询厂商B生产的所有产品的型号和价格。
πmodel, price(σmaker=’B’ (Product) ∞ PC) ⋃πmodel, price(σmaker=’B’ (Product) ∞Laptop) ⋃πmodel, price(σmaker=’B’ (Product) ∞ Printer)4.查询所有彩色激光打印机的型号。
πmodel (σcolor=’true’∧type=’laser’ (Printer))5.查询那些只生产笔记本电脑,不生产PC的厂商。
πmaker(σtype=’laptop’(Product)) - πmaker(σtype=’pc’(Product))※习题2.2 (关系代数计算)已知关系R(A,B):{(0,1), (2,3), (0,1), (2,4), (3,4)}S(B,C):{(0,1), (2,4), (2,5), (3,4), (0,2), (3,4)}计算下面的表达式:1. πB+1, C-1(S)2. τB,A(R)3. δ(R)4. γB,A VG(C)(S)5. γA,A VG(C)(R∞S) (注:∞此处代表自然连接)6. R与S的自然左外连接7. R与S的自然右外连接答:1. {(1,0), (3,3), (3,4), (4,3), (1,1), (4,3)}2. {(0,1), (0,1), (2,3), (2,4), (3,4)}3. {(0,1), (2,3), (2,4), (3,4)}4. {(0,1.5), (2,4.5), (3,4)}5. {(2, 4)}6. {(2,3,4), (2,3,4), (0,1,NULL), (0,1,NULL),(2,4,NULL),(3,4,NULL)}7. {(2,3,4), (2,3,4), (NULL,0,1), (NULL,2,4), (NUL,2,5), (NULL,0,2)}习题2.3 [选做]对于二战中的大型舰船数据库,试写出下列查询的关系代数表达式。
1.查询那些火炮口径大于16英寸的舰船类属和生产国。
πclass,country(σbore>16 (Classes))2.查询在丹麦海峡(Denmark Strait)战役中沉没的舰船。
πship (σbattle=’Denmark Strait’∧result=’sunk’(Outcomes)3.1921年签署的华盛顿条约禁止制造超过35000吨的大型军舰,请列出那些违背华盛顿条约的军舰。
πname(σdisplacement>35000 (Classes) ∞σlaunched>1921(Ships))4.列出参加了瓜达康纳尔岛(Guadalcanal)海战的战舰的名称、排水量及火炮的数目。
πname,displacement,numGuns(σbattle=’Guadalcanal’(Outcomes)∞σOutcomes.ship=(Ships) ∞ Classes)5.列出那些既有主力舰又有巡洋舰的国家。
πcountry(σtype=’bb’ (Classes)) ⋂πcountry(σtype=’bc’ (Classes))作业三:(写SQL语句)习题3.1 对于产品数据库,用SQL写出下面的查询:以下4小题要求使用连接查询1.查询硬盘容量至少30G的笔记本电脑制造商及该电脑的速度。
SELECT maker,speedFROM Product, LaptopWHERE Product.model=Laptop.model and hd>=30;2.查询制造商B生产的任意类型的所有产品的型号和价格。
(SELECT Product.model, priceFROM Product, PCWHERE Product.model = PC.model AND maker = 'B')UNION(SELECT Product.model, priceFROM Product, LaptopWHERE Product.model = Laptop.model AND maker = 'B')UNION(SELECT Product.model, priceFROM Product, PrinterWHERE Product.model = Printer.model AND maker = 'B');3.查询出现在两种或两种以上PC中的硬盘大小。
SELECT DISTINCT X.hdFROM PC X, PC YWHERE X.hd=Y.hd and X.model<Y.model;4.查询每对具有相同速度和RAM的PC的型号。
每一对只能列出一次;例如,若(i, j)已被列出,则(j, i)就不能再被列出。
SELECT X.model,Y.modelFROM PC X, PC YWHERE X.speed=Y.speed and X.ram=Y.ram and X.model<Y.model;以下4小题要求使用子查询(使用IN、EXISTS、ANY、ALL)5.找出速度在3.0以上的PC制造商。
SELECT DISTINCT makerFROM ProductWHERE model IN (SELECT modelFROM PCWHERE speed>=3.0);6.找出价格最高的打印机。
