第五章 固体电子论基础解析
合集下载
固体物理-金属电子理论解析

N’ N(EF)f(EF)E N(EF0)(2kBT)/2= N(EF0) kBT
1
由于:N EF0 C EF0 2
及
N 2C 3
EF0
3 2
N
EF0
3N 2EF0
于是,
N
3N 2EF0
kBT
而每个电子热运动的平均能量为
3 2 kBT
由于热激发,系统所获得的能量为
E T
N
3 2
3. 能态密度
E k
2k 2
2
2m 2m
kx2
k
2 y
kz2
这表明,在k空间中,自由电子的等能面为球面,在能 量为E的球体中,波矢k的取值总数为
k 4k3
3
每一个k的取值确定一个电子能级,若考虑电子自旋, 根据Pauli原理每一个能级可以填充自旋方向相反的两 个电子。如将每一个自旋态看作一个能态,那么,能 量为E的球体中,电子能态总数为
另一方面,电子由于碰撞而失去其定向运动。设电
子相邻两次碰撞之间的时间间隔为,且一旦发生碰撞, 电子就完全失去其定向运动。粗略假想,所有电子都在 时间内同时发生碰撞,其结果使分布回到平衡状态, 这样反复循环。于是,可求出费米球心移动的距离为
k dk e
dt
所以,电子的定向漂移速度为
1
d
m
2. Pauli顺磁 这里只考虑T 0的极端情况。
当B=0时,由于电子 自旋方向相反的两种 取向的几率相等,所 以,整个系统不显示 磁性,即M=0。
E
- B
E0
F
当B 0时,自旋磁矩 在磁场中的取向能:
N(E)/2
0
B=0
B
N(E)/2
B平行于B: -BB; B反平行于B: + BB
1
由于:N EF0 C EF0 2
及
N 2C 3
EF0
3 2
N
EF0
3N 2EF0
于是,
N
3N 2EF0
kBT
而每个电子热运动的平均能量为
3 2 kBT
由于热激发,系统所获得的能量为
E T
N
3 2
3. 能态密度
E k
2k 2
2
2m 2m
kx2
k
2 y
kz2
这表明,在k空间中,自由电子的等能面为球面,在能 量为E的球体中,波矢k的取值总数为
k 4k3
3
每一个k的取值确定一个电子能级,若考虑电子自旋, 根据Pauli原理每一个能级可以填充自旋方向相反的两 个电子。如将每一个自旋态看作一个能态,那么,能 量为E的球体中,电子能态总数为
另一方面,电子由于碰撞而失去其定向运动。设电
子相邻两次碰撞之间的时间间隔为,且一旦发生碰撞, 电子就完全失去其定向运动。粗略假想,所有电子都在 时间内同时发生碰撞,其结果使分布回到平衡状态, 这样反复循环。于是,可求出费米球心移动的距离为
k dk e
dt
所以,电子的定向漂移速度为
1
d
m
2. Pauli顺磁 这里只考虑T 0的极端情况。
当B=0时,由于电子 自旋方向相反的两种 取向的几率相等,所 以,整个系统不显示 磁性,即M=0。
E
- B
E0
F
当B 0时,自旋磁矩 在磁场中的取向能:
N(E)/2
0
B=0
B
N(E)/2
B平行于B: -BB; B反平行于B: + BB
固体物理 第五章 固体电子论基础1

5
5.一些金属元素的自由电子密度 一些金属元素的自由电子密度
元 素 Li Na K Cu Ag Mg Ca Zn Al In Sn Bi z 1 1 1 1 1 2 2 2 3 3 4 5 n/1028m-3 4.70 2.65 1.4 8.47 5.86 8.61 4.61 13.2 18.1 11.5 14.8 14.1 rs/10-10m 1.72 2.08 2.57 1.41 1.60 1.41 1.73 1.22 1.10 1.27 1.17 1.19 rs/a0 3.25 3.93 4.86 2.67 3.02 2.66 3.27 2.30 2.07 2.41 2.22 2.25
n= z
ρNA
M
ne2E j = nev = τ 2m
设电子平均自由程为l, 设电子平均自由程为 ,则 τ
2
zρNAe2E j= τ 2mM
(A m )
2
=l v
电流密度可写成
zρNAe E l j= × 2mM v
6.电导率σ 电导率
(A m )
2
j zρNAe l σ= = × 2mM v E
2
1.必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动 电子的运动不同于气体分子的运动, 电子的运动不同于气体分子的运动,不能用经典 理论来描述。 理论来描述。 2.电子的分布服从量子统计 即费米 狄拉克分布。 电子的分布服从量子统计, 即费米-狄拉克分布 狄拉克分布。 电子的分布服从量子统计 电子的分布不再服从经典的统计分布规律。 电子的分布不再服从经典的统计分布规律。 3.电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的 4.电子的能级是由一些能带组成。 电子的能级是由一些能带组成。 电子的能级是由一些能带组成
5.一些金属元素的自由电子密度 一些金属元素的自由电子密度
元 素 Li Na K Cu Ag Mg Ca Zn Al In Sn Bi z 1 1 1 1 1 2 2 2 3 3 4 5 n/1028m-3 4.70 2.65 1.4 8.47 5.86 8.61 4.61 13.2 18.1 11.5 14.8 14.1 rs/10-10m 1.72 2.08 2.57 1.41 1.60 1.41 1.73 1.22 1.10 1.27 1.17 1.19 rs/a0 3.25 3.93 4.86 2.67 3.02 2.66 3.27 2.30 2.07 2.41 2.22 2.25
n= z
ρNA
M
ne2E j = nev = τ 2m
设电子平均自由程为l, 设电子平均自由程为 ,则 τ
2
zρNAe2E j= τ 2mM
(A m )
2
=l v
电流密度可写成
zρNAe E l j= × 2mM v
6.电导率σ 电导率
(A m )
2
j zρNAe l σ= = × 2mM v E
2
1.必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动。 必须用薛定谔方程来描述电子的运动 电子的运动不同于气体分子的运动, 电子的运动不同于气体分子的运动,不能用经典 理论来描述。 理论来描述。 2.电子的分布服从量子统计 即费米 狄拉克分布。 电子的分布服从量子统计, 即费米-狄拉克分布 狄拉克分布。 电子的分布服从量子统计 电子的分布不再服从经典的统计分布规律。 电子的分布不再服从经典的统计分布规律。 3.电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的。 电子的运动是在一个周期性势场中进行的 4.电子的能级是由一些能带组成。 电子的能级是由一些能带组成。 电子的能级是由一些能带组成
《固体电子论基础》课件

课件的编写目的和意义
课件的结构和内容安排
课件目的
掌握固体电子论的基本概念和原理 了解固体电子论在材料科学中的应用 掌握固体电子论的数学基础 了解固体电子论在物理、化学等领域的应用
适用人群
固体电子论专业本 科生
固体电子论爱好者
电子工程、材料科 学等领域的研究人 员
对固体电子论感兴 趣的其他人员
课件结构
固体电子论在器 件设计中的应用
半导体技术 太阳能电池 电子器件 磁学和光学应用
应用领域
固体电子结构与性质
固体电子结构
固体电子论的 概述
固体电子的能 级结构
固体电子的态 密度
固体电子的输 运性质
电子性质
电子的电荷与质 量
电子的能级与跃 迁
电子的波粒二象 性
电子在固体中的 行为
固体能带结构的定义
固体电子论概述
固体电子论的定义
定义与概念
固体电子论的研究对象
固体电子论的基本概念
固体电子论与量子力学、固体物理学的关系
固体电子论的起源
发展历程
固体电子论的发展阶段
固体电子论的应用领域
固体电子论的未来展望
研究内容
固体电子论的基 本概念和原理
固体电子论的研 究对象和方法
固体电子论在材 料科学中的应用
单击此处输入你的 项正文
电流方向:单向 导电
单击此处输入你的 项正文
伏安特性:正向和 反向伏安特调幅 信号解调为音频信
号
单击此处输入你的
项正文
开关电路:控制 电路的通断
单击此处输入你的 项正文
晶体管工作原理及应用
晶体管基本结构与工作原理 晶体管类型与特性 晶体管在电路中的应用 晶体管在固体电子器件中的重要性
第五章 固体电子论基础3

dω 波包中心的位置: x E h 波包中心的位置: = t; = ω dk 0
dx dω 1 dE v(k0 ) = = = dt dk 0 h dk 0
5.结果分析 结果分析 波包在空间集中在∆ 范围内 范围内, 的大小为 的大小为: 波包在空间集中在∆x范围内, ∆x的大小为:
22
由量子力学得到的平均速度关系式: 附一 由量子力学得到的平均速度关系式
r r r r v k = vxi + vy j + vzk 1 ∂E(k) r ∂E(k) r ∂E(k) r i+ j+ k = h ∂kx ∂ky ∂kz r 1 = ∇k E k h
19
(3)d2E/dk2=0, m*→∞,相当 , 于外力对晶体中电子不产生 任何作用 。 加速度为零 , 电 子的速度也不再发生变化。 子的速度也不再发生变化。
d2E m*(k) = h2 / 2 dk
1 d E ax 2 = ⋅ Fx 2 h dkx
2
20
(4)能带的上半部的电子有效质量 能带的上半部的电子有效质量 m*<0 在能带的上半部,由于 dE/dk随k增加而减少, 加速度变 随 增加而减少 增加而减少, 为负值,在外力方向保持不变的 为负值, 情况下, 情况下,这个结果等效于有效质 量的符号从正号变为负号,即 m*<0,电子从外力场获得的动量 , 小于传递给晶格的动量; 小于传递给晶格的动量;
电子的速度
1 dE v(k) = h dk
2Ja vk = sinka h
2
有效质量
d E m*(k) = h / 2 dk
2
m*(k) = h / 2Ja cos ka
固体物理 第五章 固体电子论基础2(2)
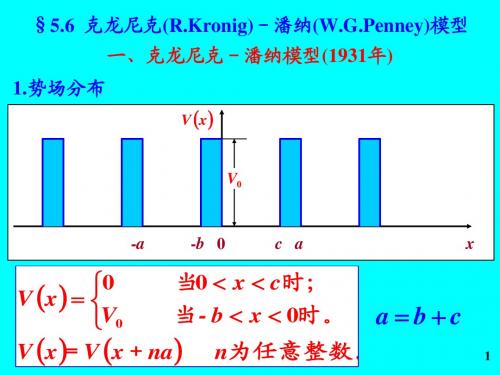
d u du 2 2 可得: + ik 2 -k u 0 2 dx dx
2
4
(2)特征方程为:
2
r 2ikr -k 0
2 2
r
- ik 2
2ik -4 -k -ik i
2 2 2
r1 -i k ,r2 i -k
i -k e
i -k c
= -ik e
A0 i k e -
-i k c
- -ik b
C 0 ik e -
B0 D0
ik b
(4)
16
(3)方程组
A0 B0 C 0 D0 0 - - = = i -k A0 - i k B0 - -ik C 0 + ik D0 0 i -k c e A0 e-i k c B0 - e - -ik bC 0 - e ik b D0 0 = i -k e i -k c A0 i k e-i k c B0 -ik e - -ik bC 0 - - ik e ik b D = + 0 0
2.波函数和薛定谔方程 (1)波函数 根据布罗赫定理可得:
x e ikxux
(2)薛定谔方程 把波函数代入薛定谔方程可得:
2 d 2 V x ψ x Eψ x 2 2m dx
d 2 2m + 2 E - V 0 2 dx
Dne
u x 是周期函数
u x u x na
C0e
-ik x
D0e
e
- ik x
C ne
固体物理-第五章3

SiO2的能带结构
特征:价带全满,且与下一个能带被一个大的禁带隔开
➢能带理论
➢半导体的能带结构
导
图(d)表示能隙间隔很小
体 的情况,这类晶体在0K时是绝缘
绝 体,但在不很高的温度下,热能
缘 可以将电子由满带激发越过不宽
体 的
的能隙,进入上面的空带中而成 为自由电子,对电导做出贡献。 这种电导叫做本征电导,这种半
➢固体能带理论基础
➢ 满带中的电子对导电的贡献
✓无外场作用时
电 因为K状态和 -K状态中电子的速度大小相等、方向相反
子 每个电子产生的电流 –qv,对电流的贡献相互抵消
的 热平衡状态下,电子占据波
运
矢为K的状态和占据波矢为-K
动 的状态的几率相等
晶体中的满带在无外场 作用时,不产生电流
➢固体能带理论基础
➢ 满带中的电子对导电的贡献
✓有外场E作用时
电 电子受到的作用力 F qE
子 的
电子动量的变化
d
(k
)
F
运 动
dt
所有电子状态以相同的速度沿着电场的反方向运动
dk
1
qE
dt
满带的情形中,电子的运动不改变布里渊区中电 子的分布, 满带中的电子不产生宏观的电流
➢固体能带理论基础
带 一般规律: 及 1. 越是外层电子,能带越宽,E越大。 一 般 2. 点阵间距越小,能带越宽,E越大。
性 3. 两个能带有可能重叠。
质
5.4.1 固体能带理论基础
能带中电子的排布
能 晶体中的一个电子只能处在某个能带中的某一能级上。
带 中
排布原则:
沈阳工业大学《固体物理》(李新)第五章

第五章固体电子论基础物理现象或实验结果物理模型决定因素理论解释第一阶段自由电子学说德鲁特和洛伦兹第二阶段量子自由电子学说fs电子理论第三阶段能带理论单电子近似求解电子能谱的理论固体电子论基础电子在运动中存在一定的散射机制
第五章 固体电子论基础
固体电子论基础 决定因素
修 改
物理现象 或实验结果
物理模型
v e
x
1 2 ( mv x ) / kT 2
dvx
m 2kT kT E0 / kT 2e( ) 3 e EF / kT e AT 2 e / kT h m m
此即里查孙-杜师曼公式;其中即功函数 因为
j 1 ln 2 ln A k T T
2 E0 m
2m dZ 4Vc 2 h
3/ 2
2m dE dk 2 E
3/ 2
E 1 / 2 dE
3/ 2
能态密度为:
dZ 2m N E 4Vc 2 dE h
E 1 / 2 CE1 / 2
2m C 4Vc 2 h
每个量子态k在波矢空间体积:
2 2 2 2 L L L L
3
k 空间中的状态分布
3
单位体积中的量子态数为:
L 2
1 .索末菲自由电子论
1.2运动方程及其解 在能量E到E+dE之间的区域,是半径为k到k+dk两个球面
之间的球壳层,它的体积为:
理论解释
验 证
结果与预言
第一阶段、自由电子学说-德鲁特和洛伦兹 第二阶段、量子自由电子学说-F-S电子理论 第三阶段、能带理论-单电子近似求解电子能谱的理论
第五章 固体电子论基础
固体电子论基础 决定因素
修 改
物理现象 或实验结果
物理模型
v e
x
1 2 ( mv x ) / kT 2
dvx
m 2kT kT E0 / kT 2e( ) 3 e EF / kT e AT 2 e / kT h m m
此即里查孙-杜师曼公式;其中即功函数 因为
j 1 ln 2 ln A k T T
2 E0 m
2m dZ 4Vc 2 h
3/ 2
2m dE dk 2 E
3/ 2
E 1 / 2 dE
3/ 2
能态密度为:
dZ 2m N E 4Vc 2 dE h
E 1 / 2 CE1 / 2
2m C 4Vc 2 h
每个量子态k在波矢空间体积:
2 2 2 2 L L L L
3
k 空间中的状态分布
3
单位体积中的量子态数为:
L 2
1 .索末菲自由电子论
1.2运动方程及其解 在能量E到E+dE之间的区域,是半径为k到k+dk两个球面
之间的球壳层,它的体积为:
理论解释
验 证
结果与预言
第一阶段、自由电子学说-德鲁特和洛伦兹 第二阶段、量子自由电子学说-F-S电子理论 第三阶段、能带理论-单电子近似求解电子能谱的理论
第五章 固体电子论基础

§5.2.2索末菲电子气的能量状态
• 索末菲认为金属中的价电子好比理想气 体,彼此之间没有相互作用,各自独立 地在势能等于平均势能的场中运动。如 果取平均势能为能量零点,那么要使金 属中的自由电子逸出,就必须对它作相 当的功,所以每个电子的能量状态就是 在一定深度的势阱中运动的粒子所具有 的能量状态。
(5.1-7)
• 经典自由电子理论推导的电导率公式表明,电导率的大小正比于 电荷浓度 ne (单位体积固体中的自由电子数)和单位电场强度产 生的加速度 e n 以及弛豫时间 τ 的乘积。 • 根据经典自由电子理论,即自由电子的行为如同理想气体一样, 服从玻耳兹曼统计。因此应用理想气体定律可以计算电子的动能 1 3 2 (5.1-8) 5.1-8 E = mv = k B T 2 2 • 式中 v 为自由电子平均速度;kB为玻耳兹曼常数;T为热力学温 度;m为电子质量。 • 由式(5.1-8)可以估计电子平均热运动速度。当T=0(K) 时, = 0 ;当T=300(K)时,电子动能为0.04eV,其热运动速 v 度为105m/s。由测不准关系知,电子“轨道”运动速度测不准 时约为107m/s,比所求值还大。其原因是即使在T→0(K)时, 电子运动速度也不为零,而且运动速度在106m/s。由此可见经 典自由电子理论在处理电子问题的局限性。
• 用这种模型描述的自由电子,通常称为特鲁德-洛仑兹电子,或 简称特鲁德电子。特鲁德和洛仑兹利用这一模型导出了金属电导 率和热导率,并得到了维德曼-夫兰兹定律。在没有外电场作用 时,固体中的自由电子沿着各个方向运动的几率相等,故不会产 生电流。当给固体施加外电场后,自由电子获得附加速度,于是 便沿外加电场方向发生定向运动,从而形成了电流。自由电子在 定向运动过程中,因不断与正离子发生碰撞,而使电子运动受阻, 这便是产生电阻的原因。 • 利用这一模型还可以定性地解释金属的某些性质,如金属块的不 透明性和特有的光泽,主要是由于入射光波被金属表面层电子吸 收所致,而电子吸收光波后产生强迫振动又发出光波来,因此出 现金属光泽。 • 总之,经典自由电子理论的基本内容是:金属中存在着大量能够 自由运动的电子,这些自由电子的行为象理想气体一样;正离子 所形成的电场是均匀的,电子气体除了在同离子实发生不断碰撞 的瞬间外,其余时间在离子实之间的运动被认为是自由的;电子 1τ τ 和电子之间的相互作用(碰撞)忽略不计,电子和离子之间的碰 撞过程可以用一个电子与离子实相继作用两次碰撞之间所间隔的 平均时间 (碰撞)来描述( 表示电子和离子实之间的碰撞 几率);电子气体是通过和离子实组成的晶格的热碰撞达到热平 衡,自由电子运动速度的热平衡分布遵循麦克斯韦-玻耳兹曼统 计规律。
