2014年第五届启智杯真题及试题分析(中学组)
蓝天教育(启智杯希望杯)报名表

2014年第五届“启智杯”竞赛
2015年第十三届小学“希望杯”全国邀请赛
2015年第二十六届中学“希望杯”全国邀请赛
蓝天教育报名登记表
赛区:广东省深圳市报名站:蓝天教育
1、在是否报名启智杯与希望杯比赛的选项栏中,是的请打“√”;
2、启智杯报名费50元,资料费20元(参考资料看家长选择)
3、希望杯报名费蓝天教育收取28元,资料费费用见附件,其中资料费均邮购价收取
4、居住片区为合理安排考点使用,请按照以下15个片区就近选填:
罗湖翠竹、罗湖黄贝岭、福田莲花、福田益田、福田竹子林、南山蛇口、南山华侨城、南山西丽、盐田、宝安、光明、龙华、龙岗、坪山、大鹏
5、蓝天教育9月9日上午10点起接受报名
附件:
第十三届小学“希望杯”全国数学邀请赛资料介绍。
试卷:2014年上海市新知杯初中数学试题(含答案解析)

2014上海市初三数学竞赛试卷(2014年12月7日 上午9:00—11:00)解答本试卷可以使用科学计算器一、填空题(每小题10分,共80分)1.化简:3223222a a b ab b a ab b--+=-+ 2. 若y xa x z+=,z y b y x +=,x z c z y +=,则()()()b c a c a b a b c +-+-+-的值为3. 已知ABCD 是等腰梯形, ABIICD ,AB=6,CD=16,△ACE 是直角三角形,∠AEC=900,CE=BC=AD ,则AE 的长为4. 方程2014xyz xy yz zx x y z ++++++=的非负整数解(x ,y ,z )的组数为5.在三角形ABC 中,∠ABC=440,D 是边BC 上的一点,满足DC=2AB, ∠BAD=240,则∠ACB 的大小为6. 在直角坐标平面xOy 上,由不等式221x y x y ⎧≤⎪≤⎨⎪-≤⎩确定的区域的面积为7. 使得关于x 的方程2221130a x ax a ++-=有两个整数根的所有正实数a 是8. 设20142的所有正约数为d 1,d 2,…,d k ,则12111 (201420142014)k d d d +++=+++二、解答题(第9、10 题,每题15 分,第11、12 题,每题20 分,共70 分) 9. 解关于x 的方程:(1)xx x x x a x x+--=++10.如图,在凸四边形ABCD 中,已知∠ABC +∠CDA =3000,AB CD BC AD ⨯=⨯, 求证:AB CD AC BD ⨯=⨯11. 已知边长为a 的正方形ABCD 的内部有n 个圆,每个圆的面积都不大于1,且与正方形ABCD 的边平行的直线都至多与一个圆相交,求证:这n 个圆的面积之和小于a 。
12. (1)证明:可以将全体正整数分成3组A 1,A 2,A 3,使得对每一个整数15n ≥,在A 1,A 2,A 3的每一组中都能取出两个不同的数,它们的和为n(2)证明:将全体正整数任意分成4组A 1,A 2,A 3,A 4,则存在整数15n ≥,在A 1,A 2,A 3 ,A 4中一定有一组A i ,在A i 中不存在两个不同的数,它们的和为n2014上海市初三数学竞赛试卷解答(2014年12月7日上午9:00—11:00)解答本试卷可以使用科学计算器一、填空题(每小题10分,共80分)1.化简:3223222a ab ab ba ab b--+= -+2. 若y xax z+=,z yby x+=,x zcz y+=,则()()()b c a c a b a b c+-+-+-的值为3. 已知ABCD是等腰梯形,ABIICD,AB=6,CD=16,△ACE是直角三角形,∠AEC=900,CE=BC=AD,则AE的长为4. 方程2014xyz xy yz zx x y z ++++++=的非负整数解(x ,y ,z )的组数为5.在三角形ABC 中,∠ABC=440,D 是边BC 上的一点,满足DC=2AB, ∠BAD=240,则∠ACB 的大小为6. 在直角坐标平面xOy 上,由不等式221x y x y ⎧≤⎪≤⎨⎪-≤⎩确定的区域的面积为7. 使得关于x 的方程2221130a x ax a ++-=有两个整数根的所有正实数a 是8. 设20142的所有正约数为d 1,d 2,…,d k ,则12111 (201420142014)k d d d +++=+++二、解答题(第9、10 题,每题15 分,第11、12 题,每题20 分,共70 分) 9. 解关于x 的方程:(1)xx x x x a x x+--=++⨯=⨯, 10.如图,在凸四边形ABCD中,已知∠ABC+∠CDA =3000,AB CD BC AD⨯=⨯求证:AB CD AC BD11. 已知边长为a的正方形ABCD的内部有n个圆,每个圆的面积都不大于1,且与正方形ABCD的边平行的直线都至多与一个圆相交,求证:这n个圆的面积之和小于a。
第三届启智杯数学思维及应用能力竞赛试卷(小学组)

参考答案及评分标准本卷共12题,每题10分,满分120分。
答题时间120分钟。
如图所示的算式中,相同的汉字表示相同的一位数字,不同的汉字表示不同的一位数字,则我+爱+启+智+杯= 或。
写出你的推算过程。
杯智杯启智杯爱启智杯+ 爱启智杯我爱启智杯参考答案:25或29五个杯字之和的个位数为杯,说明杯 = 0或5(进2);若杯=0,则四个智字之和的个位数为智,智=0;从而三个启字之和的个位数为启,启=0;两个爱字之和的个位为爱,进位为我,无解。
因此,杯=5(进2),由此推出智字之和加2的个位数为智,智=6(进2);三个启字之和加2的个位数为启,启=4(进1)或9(进2),进而得知爱等于9或8,而我=1.因此:我爱启智杯= 19465或18965,而我+爱+启+智+杯=25或29评分标准:只写出正确答案而未加说明,给5分;基本思路正确,而答案错误,给5分;答案写成19365或18965给8分。
其他情况酌情给分。
有三个封口的袋子,里面都装着同样重量和大小的小球,A袋子内装着红球,B袋子内装着白球,C袋子内混合装着红球和白球。
三个袋子分别贴有“红色”、“白色”、“混合色”的标签,可惜每一个标签都与袋子中球的实际颜色不符。
现在允许你只打开一个袋子,从中摸出一球(不准看袋子里面),看着这个球的颜色,你能立刻为三个袋子贴上正确标签吗?请说明你的具体操作方法。
参考答案:打开“混合色”标签的袋子由于三个袋子都标错了标签,所以三种标签构成一种“轮换”,不会出现“对换”。
打开“混合色”标签的袋子,由于依据假设,该袋子内必然是单色的,若拿出的是红色球,则该袋子应该标注“红色”;而原来标注红色的必然是“白色”,白色标签的也就是混合色了。
若拿出的是白色球,则该袋子应该标注“白色”;而原来标注白色的必然是“红色”,红色标签的也就是混合色了。
评分标准:只写出正确答案而未加说明,给5分;分析正确,而说明不清晰或者不简练,给7分;其他情况酌情给分。
2014年第五届启智杯真题及试题分析(中学组)讲诉

8 8x811 1 1 1 11\(1)(n 2) n13 511 3 12 4 7 9 11 13 15 17321(n 1 (n 1)3 5 12 5 7 9222014年(第五届)启智杯数学思维及应用能力竞赛(初中组)试卷特别注意:(1 )请把解答写在答题纸上,不要在本卷上答题。
(2 )本试卷在考试结束时请考生带走。
(3)本卷共12题,每题10分,满分120分。
答题时间120分钟。
1、观察如下几个灯饰:你发现了什么规律?请据此规律写出第 100个式子。
(2 )求 a<i + a 2 + a 3 +...+ a 353 的值。
写出答案和理由4、已知正整数n 满足:质的最小的六位数,写出答案和理3、一个数列 a 1 ,a 2 ,a 3,...,a n ,...,已知a 1 =8,之后的每一项有如下规律: a n 为奇数时,1an 1 =5 a n +1 ; a n 为偶数时,an 1 =2 。
(1 )求a 2014的值,2011 1 -20132、数“ 11125 ”具有这样的性质:它的各位数码之和等于它的各位数码之积。
求满足该性求正整数n 的值,写出答案和计算过程。
5、如右图所示,一个长方形 ABCD 中嵌入三个大小相同的小正方形构成一个“品”字,如 果AB=26mm ,BC=28mm ,问每个小正方形的面积是多少?ABC 中,延长BC 至D , ABC 与 ACD 的角平分线相交于点 A !, A i BC 与A i CD 的角平分线相交于点A 2,……,以此类推, A 5BC 与A 5CD 的角平分线相交于点A 6,若 A 6 2,求 A 的度数。
8、如右图所示,在矩形 ABCD 中,已知 AD=2AB , AF=5cm ,且DE 丄AF , E 为垂足,DE=3.6cm 。
你能求出图中哪些线段的长度?请写出求出线段的长度及解答过程。
6、如右图,正方形 为49,那么四边形7、如图所示,在△BDEF 的面积最小为多少?ABCD 的面积为1,延长BC 至E ,延长DC 至F ,如果矩形CEGF 面积9、如图所示的乘法竖式中,“我爱启智杯”分别代表 0~9中的一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么“我爱启智杯”代表的数字分别是多少?写□9□□□□ 匸□□□□□ □ □□□□□ □□□□10、右图中ABCD 和DEFG 是两个不等的正方形,连接 BG 交DE 于H ,如果A BHE 面积为11、有2014颗旗子,甲乙二人做如下游戏:甲将旗子分为数目不等的两堆交给乙,乙将其中较少数目的一堆留下,另一堆再分为数目不等的两堆交给甲,如此往复进行下去。
2013年第四届启智杯数学思维及应用能力竞赛试卷(初中组,pdf版,含答案)

数n ,当n≥9时,总能将正三角形分割成 n 个正三角形。
8.将1、2、3、…、10、11、12这12个数填入如图所示66的某些方格中,要求同时满足 (1)每一行、每一列都只有一个奇数、一个偶数; (2)每一行、每一列和两条对角线上都恰好各有2个数,而且两数之和均不小于9。
部确定再得 2 分。
2. 请完成以下两个问题:
(1)将 999 表示成 9 个连续的奇数之和的形式;
(2)将 7n1 表示成 7 个连续的奇数之和的形式时,则其中最小的奇数是多少?(用含有字母 n 的代 数式表示,其中字母 n 正整数)
【参考答案】 (1)由于 999 9 = 111,所取 9 个奇数的中间数应该是 111,这个表示为 999 = 103 +105 +107 +109 + 111 + 113 +115 +117 +119。
或
图 1,
图2
【评分标准】发现重叠阴影部分面积不变性(正方形面积的 1 )占 5 分;算出正方形边长占 5 分。 4
第四届启智杯数学思维及应用能力竞赛试卷(初学组) 第 4 页 共 8 页
7. 把一个边长为 9 的正三角形分割成若干正三角形(不要求每个正三角形边长相等)。 (1)最少能分割成多少个正三角形? (2) 你还能把一个正三角形分割成 5,6,7,8,9,10,11个正三角形吗?能做到的分别画
SAED:SABD= 2:3,SAED= 8cm2,
(3)
第四届启智杯数学思维及应用能力竞赛试卷(初学组) 第 3 页 共 8 页
而△CDG 相似于△AEG,相似比为 CD: AE=3:2,故 DG:EG = 3:2,SDGA : SEGA= 3:2,
2014年全国初中数学竞赛试题参考答案及评分标准

2014年全国初中数学竞赛试题参考答案及评分标准一、选择题(共10小题,每小题6分,满分60分.) 1.已知x 、y 、z 满足2x =3y-x =5z+x ,则5x-yy+2z的值为( )(A )1 (B )13 (C )-13 (D )12【答】B .解:设 2x =3y-x =5z+x =1k 则x=2k ,y-z=3k ,z+x=5k ,即x=2k ,y=6k ,z=3k 。
所以5x-y y+2z =5·2k-6k 6k+6k =13,故选B.2.已知等腰三角形的周长为12,则腰长a 的取值范围是( )(A )a >3 (B )a <6 (C )3<a <6 (D )4<a <7 【答】C.解:腰长为a ,则底长为12-2a ,由2a >12-2a 及12-2a >0可得3<a <6 故选C. 3.设 21x x 、 是一元二次方程032=-+x x的两根,则 1942231+-x x 等于( )(A )-4 (B )8 (C )6 (D )0 【答】D.解:将21x x 、代入方程,将目标整式降次,利用两根之和求解.4.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ) (A )1 (B )214a - (C )12 (D )14【答】D.解:由题设知,1112a a b a b <+<++<+,所以这四个数据的平均数为1(1)(1)(2)34244a ab a b a b+++++++++=, 中位数为 (1)(1)44224a ab a b++++++=, 于是 4423421444a b a b ++++-=. 故选D.5. 如图,正方形A BCD 和EFGC 中,正方形EFGC 的边长为a ,用a 的代数式表示阴影部分△AEG 的面积为( )(A )232a (B )223a (C )212a (D )2a【答】C .6.若△ABC 的三条边a,b,c 满足关系式a 4+b 2c 2- a 2c 2-b 4=0,则△ABC 的形状是( ) (A )等腰三角形 (B )等边三角形(C )直角三角形 (D )等腰三角形或直角三角形 【答】D.解法一:原方程左边变形为 (a 4-b 4)+(b 2c 2-a 2c 2)=0, (a 2+b 2)(a 2-b 2)+(b 2-a 2+)c 2=0,∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a=b 或c 2=a 2+b 2.∴△ABC 为等腰三角形或直角三角形. 解法二:应用配方法a 4+b 2c 2- a 2c 2-b 4=0, (a 4-a 2c 2)-(-b 2c 2+b 4)=0 (a 2-22c )2 -(22c -b 2)2=0 ∴(a 2-b 2)(a 2+b 2-c 2)=0, ∴a 2-b 2=0,或a 2+b 2-c 2=0. ∴a=b 或c 2=a 2+b 2. ∴△ABC 为等腰三角形或直角三角形. 故选D.7.一批志愿者组成了一个“爱心团队”,以募集爱心基金.第一个月他们就募集到资金1万元,随着影响的扩大,第n (n ≥2)个月他们募集到的资金都将会比上个月增加20%,则当该月所募集到的资金首次突破10万元时(参考数据: 51.22.5≈,61.2 3.0≈,71.2 3.6≈),相应的n 的值为( )(A )11 (B )12 (C )13 (D )14 【答】D.8.如图:点D 是△ABC 的边BC 上一点,若∠CAD = ∠DAB = 60°,AC = 3 ,AB = 6,则AD 的长度是( )(A )2 (B )2.5 (C )3 (D )3.5 【答】A.解:如图,作BE ⊥AC 交CA 的延长线于E ,在Rt △ABE 中, ∠BAE= 60° ∴∠ABE= 30° ∴AE=21AB = 3 由勾股定理得BE =33∴21BCA s △AC ·BE =329 ∵∠CAD = ∠DAB = 60°同理得△ADC 和△ABD 中AD 边上的高分别是323和33 ∴=CD A s △343AD ,=B DA s △323AD 又CD A s △+B DA s △=BC A s △ ∴343AD + 323AD =329 ∴AD = 2 故选A9.若m=20132+20132×20142+20142,则m ( )(A )是完全平方数,还是奇数 (B )是完全平方数,还是偶数 (C )不是完全平方数,但是奇数 (D )不是完全平方数,但是偶数 【答】A.解 :原式=20132-2×2013×2014+20142+2×2013×2014+20132×20142=(2013-2014)2+2×2013×2014+(2013×2014)2=1+2×2013×2014+(2013×2014)2=(2013×2014+1)2所以(2013×2014+1)2是一个完全平方数,末尾数字是9,所以也是奇数. 故选A. 10、设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,,则222ab bc caa b c ++++的值为( ) (A )12-(B )0 (C )12(D )1 【答】A.解:由已知得(234)(23)0a b c a b c a b c ++=++-++=,故 2()0a b c ++=.于是 2221()2ab bc ca a b c ++=-++, 所以22212ab bc ca a b c ++=-++.故选A.二、填空题(共5小题,每小题6分,满分30分)11.已知整数1234a a a a ⋅⋅⋅,,,,满足下列条件:10a =,21|1|a a =-+,32|2|a a =-+,43|3|a a =-+,…,依次类推,则2012a 的值为 .【答】1006-12.如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°, BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则BE = .【答】解:.如图,可以通过旋转变换将△ABE 绕点B 逆时针旋转90°,得到△CBF.证明出四边形BFDE 是正方形,且它的面积是8,则边长是或者过点B 作BF ⊥BE ,交DC 延长线于F. 证明△ABE ≌△CBF ,其余思路同上。
2014年全国高中数学联赛试题及答案详解(A卷)

2013
解:由题设
an
2(n 1) n
an1
2(n 1) n
2n n 1 an2
2(n 1) n
2n n 1
23 2
a1
2n1 (n
1)
.
记数列{an} 的前 n 项和为 Sn ,则
Sn =
2 + 2 × 3 + 22 × 4 + + 2n−1(n +1)
2015 2013
2015
.
2013
5. 正四棱锥 P ABCD 中,侧面是边长为 1 的正三角形,M , N 分别是边 AB, BC 的中
点,则异面直线 MN 与 PC 之间的距离是
.
答案: 2 . 4
解:设底面对角线 AC, BD 交于点 O ,过点 C 作直
线 MN 的垂线,交 MN 于点 H . 由 于 PO 是 底 面 的 垂 线 , 故 PO CH , 又
解:记 f (z) (z )2 z .则
f (z1) f (z2 ) (z1 )2 z1 (z2 )2 z2
(z1 z2 2)(z1 z2 ) z1 z2 .
①
假如存在复数 z1, z2 ( z1 , z2 1, z1 ≠ z2 ) ,使得 f (z1) f (z2 ) ,则由①知,
连接的情况数.
(1) 有 AB 边:共 25 32 种情况.
(2) 无 AB 边,但有 CD 边:此时 A , B 可用折线连接当且仅当 A 与 C , D 中至少一
点相连,且 B 与 C , D 中至少一点相连,这样的情况数为 (22 1)(22 1) 9 .
第1~6届启智杯真题+答案
6.已知 a 1 1 1 23
1 ,b 1 2 4 5 7 8
672
369
2014 2015 .求 a b 的值,写出计算过程. 2016
7.下图左边是一个 4 4 的正方形去掉六个1 1的小正方形后剩下的“十字”形图形,右边的六个图形也是有 1 1的小正方形拼成的图形,这些图形中,选择两块可以在平面上移动(可转动,但不翻动)拼成左边“十 字”形图形,请把所有可能选出两块的拼法画在“十字”形图形上,并标出拼图组件所对应的字母.
7.在一个孤岛上生活着三种怪物:奇虎、奇狮、奇豹,数量分别为 2010、2015、2020 个.这些怪物有一种 古怪的习性:它们任何两种怪物一旦见面,就双方都变成第三种怪物(比如,一个奇虎和一个奇狮见面,就 都变成奇豹),见一种怪物见面则不会产生变化.问,如此下去,它们是否有可能到某种时刻全部变成同一 种怪物?请说明理由.
10.右边乘法算式中,只有四个位置源自的数已知,它们分别是 2,0,1,5,请你在空白位置填上数字,使 得算式能够成立,写出所有可能成立的算式.
3
11.如下图,在正方形 ABCD 的四个顶点 A 、 B 、 C 、 D 上按照顺时针方向依次进行如下标注:首先在顶 点 A 、 B 上分别标注数 1、2,之后将 AB 两点的标注数之和(1+2=3)标注在下一个顶点 C 处,再将 BC 两 点的标注数之和(2+3=5)标注在下一个顶点 D 处.接下来再把 A 点的标注数 1 擦去,将 CD 两点的标注数 之和(3+5=8)标注在 A 点,如此下去,请问:对 A 点进行第 2015 次标注的数被 3 除的余数是多少?说明 你的依据.
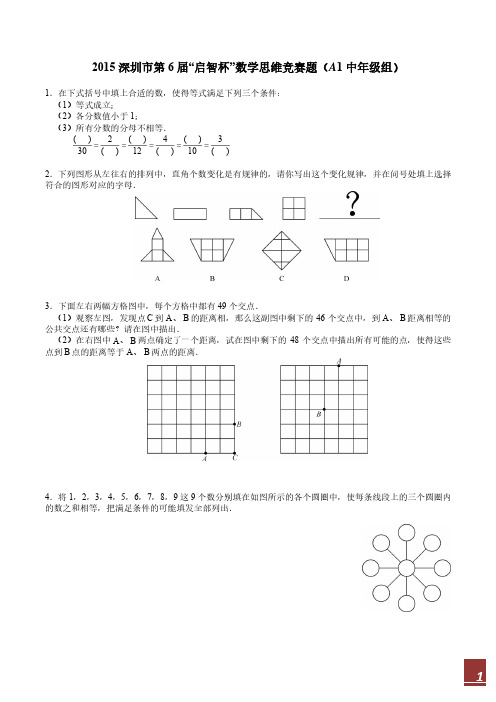
2015 深圳市第 6 届“启智杯”数学思维竞赛题(A1 中年级组)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年(第五届)启智杯数学思维及应用能力竞赛(初中组)试卷特别注意:(1)请把解答写在答题纸上,不要在本卷上答题。
(2)本试卷在考试结束时请考生带走。
(3)本卷共12题,每题10分,满分120分。
答题时间120分钟。
1、观察如下几个灯饰: (1)21853=+; (2)228975=++; (3)2381715131197=+++++;......你发现了什么规律?请据此规律写出第100个式子。
2、数“11125”具有这样的性质:它的各位数码之和等于它的各位数码之积。
求满足该性质的最小的六位数,写出答案和理由。
3、一个数列1a ,2a ,3a ,...,n a ,...,已知1a =8,之后的每一项有如下规律:n a 为奇数时,1+n a =5n a +1;n a 为偶数时,1+n a =n a21。
(1)求2014a 的值,(2)求1a +2a +3a +...+353a 的值。
写出答案和理由 4、已知正整数n 满足:201320111)1(111211......531142113111+=⎪⎪⎭⎫⎝⎛+⨯-+⨯⎪⎭⎫ ⎝⎛⨯-+⨯⨯⎪⎭⎫ ⎝⎛⨯+⨯⎪⎭⎫ ⎝⎛⨯+⨯⎪⎭⎫ ⎝⎛⨯+n n n n )()(求正整数n 的值,写出答案和计算过程。
5、如右图所示,一个长方形ABCD 中嵌入三个大小相同的小正方形构成一个“品”字,如果AB=26mm ,BC=28mm ,问每个小正方形的面积是多少?6、如右图,正方形ABCD 的面积为1,延长BC 至E ,延长DC 至F ,如果矩形CEGF 面积为49,那么四边形BDEF 的面积最小为多少?7、如图所示,在△ABC 中,延长BC 至D ,ABC ∠与ACD ∠的角平分线相交于点1A ,BC A 1∠与CD A 1∠的角平分线相交于点2A ,......,以此类推,BC A 5∠与CD A 5∠的角平分线相交于点6A ,若︒=∠2A 6,求A ∠的度数。
8、如右图所示,在矩形ABCD 中,已知AD=2AB ,AF=5cm ,且DE ⊥AF ,E 为垂足,DE=3.6cm 。
你能求出图中哪些线段的长度?请写出求出线段的长度及解答过程。
9、如图所示的乘法竖式中,“我爱启智杯”分别代表0~9中的一个数字,相同的汉字代表相同的数字,不同的汉字代表不同的数字,那么“我爱启智杯”代表的数字分别是多少?写出答案,并在各方框内填写正确的数字。
10、右图中ABCD和DEFG是两个不等的正方形,连接BG交DE于H,如果△BHE面积为10,问△DHF面积为多少?11、有2014颗旗子,甲乙二人做如下游戏:甲将旗子分为数目不等的两堆交给乙,乙将其中较少数目的一堆留下,另一堆再分为数目不等的两堆交给甲,如此往复进行下去。
在进程中,一旦谁将较少数目的一堆留下后,剩下的一堆旗子不能再按要求分为数目不等的两堆,则该人为负。
问:甲是否有必胜的策略?如果没有,请说明理由;如果有,请给出你的策略。
12、某班有50位同学,要推选班长,现在有三位候选人A、B、C,没人可以将三位候选人进行排序,如果有人认为A第一、B第二、C第三,我们记之为A>B>C(下同)。
民意测评的结果是:有15人认为A>B>C;有9人认为B>C>A;有9人认为A>C>B;有17人认为C>B>A;现在采用评分方式推选班长。
如果规定每个人给自己认为的第一、第二、第三名分别打3分、2分、1分,容易算出:A得98分,B得100分,C得102分,C当选。
请你分别设计两种不同的但却是合理的评分标准,分别让A当选,B当选。
给出你的方案,并算出各自的得分,指出当选人。
2014 年(第五届)启智杯数学思维及应用能力竞赛(初中组)参考答案与评分标准1.观察如下几个等式:……你发现了什么规律?请据此规律写出第100个式子。
解:第n个式子是2n个连续奇数之和被8除等于n的平方,其中开始的奇数为2n+1,结束的奇数为6n-1.—————————————————————————6分第100个式子为2.“11125”具有这样的性质:它的各位数码之和等于它的各位数码之积。
求满足该性质的最小的六位数。
写出答案和理由。
解答:依题意可知这六位数的数码都不是0,且因为所求满足该性质的最小六位数,故1的个数越多越好;————————————————————2分(1)若六位数的数码都是1,则各位数码之和等于6,但它的各位数码之积是 1.不合题意;————————————————————+1 = 3分(2)若六位数的数码中有5个都是1,另一个设为a,(其中2≤a≤9),则各位数码之和等于5+a,但它的各位数码之积是a,而5+a>a,不合题意;——+1= 4 分(3)若六位数的数码中有4个都是1,另2个设为a和b,(其中2≤a≤9,2≤b≤9 且a≥b),则各位数码之和等于4+a+b,但它的各位数码之积是ab,则4 +a+b=ab⇒(a-1)(b-1)=5 ⨯1,于是a-1 = 5 ,b-1 = 1。
即a=6,b=2。
——————————+3 =7分满足该性质且有4个的最小六位数是111162。
————————+1 = 8分(4)若六位数中有3个或3个以下的1,则其值都大于111162。
————+1 = 9分故满足该性质的最小六位数是111162。
————+1 = 10分3.一个数列a1、a2、a3,、a n,,已知a1=8,之后的每一项有如下规律:a n为奇数时,a n+1=5a n+1;a n为偶数时,a n+1=12 a n.(1)求a2014的值。
(2)求a1+a2+a3+ +a353的值。
写出答案和理由。
解:根据已知条件,数列是一个周期为7的数列,各项依次为:8,4,2,1,6,3,16,8,4,2,1,6,......——————————————————————————— 4 分(2)= 50 ⨯ (8 + 4 + 2 +1 + 6 + 3 +16) + 8 + 4 + 2=50 ⨯ 40 +14=2014———————+3 =10分4.已知正整数n满足:A B 5.如右图所示,一个长方形ABCD中嵌入三个大小相同的小正方形构成一个“品”字。
如果AB = 26mm,BC = 28mm,问每个小正 方形的面积是多少?【参考答案】DC解:(1)如图,从每个小正方形各顶点引垂直线或水平虚线,两条第 5 题图相交虚线和小正方形的一条边可以构成一个直角三角形,其中小正方形的一条边为斜边 c ,记该直角三角形的两个直角边分别为 a 和 b ,a >b , 则根据勾股定理,小正方形的面积为 c 2 = a 2 + b 2。
—————————-4 分AB = 3a + b = 26(2)从图中容易看出, BC = 2 a + 2b = 28 ,由此解出 a = 6,b =8,—-------— +4 = 8 分 因此小正方形的面积为 c 2= 62+82=100mm 2。
—-------— + 2 = 10 分A Bcc b a ccDC6. 如右图。
正方形 ABCD 面积为 1,延长 BC 至 E ,延长DC 至 F ,如果矩形 CEGF 面积为 49,那么四边形 BDEF的面积最小为多少?解:记正方形边长 AB = a ,长方形边长 CF = b ,CE = c 。
则a 2 =1, bc = 49, ———————————2 分四边形 BDEF 可以分割为四个三角形,其中 ∆ BCD 和 ∆ ECF A DBCEF G第 6 题面积分别是(定值),而 ∆ DCE 和 ∆ BCF 都是直角三角形,其面积之和 。
———————————— + 3 = 5 分问题转化为:当 bc = 49 时,何时使21(b + c ) 最小? —————————— + 1 = 6 分由于两个正数和一定,两数相等时乘积最大,所以当两个正数乘积一定,两数相等时和最小,因此b = c =7 —————————— + 2 = 8 分所以四边形BDEF的最小面积为:1 + 49 + 1 (b+c) = 25 + 7 = 32———— + 2 = 10 分2 2 237.如图所示,在∆ABC中,延长BC至D,∠ABC与∠ACD的角平分线相交于点A1,∠A1 BC 与∠A`1CD 的角平分线相交于点A2,……,以此类推,∠A5BC与∠A`5CD 的角平分线相交于点A6,若∠A6=2︒,求∠A的度数。
解答:因为∠A11∠A 。
∠A21 ⎛ 1⎫2 1∠A2⎛ 1 ⎫ 3=2=2∠A1= ⎪ ∠A ,∠A3 =2= ⎪ ∠A ,……,⎝ 2 ⎭ ⎝ 2 ⎭————————————————----------6分⎛ 1 ⎫ 6∠A ⇒∠A=64∠A6 = 128︒。
------------------ +4 = 10 分归纳出∠A6= ⎪⎝ 2 ⎭A1A A2A3B C D,8 .如右图所示,在矩形ABCD中,已知AD=2AB, A DAF =5cm ,且DE⊥AF,E为垂足,DE =3.6 cm 。
你能求出图中哪些线段的长度,请写出所求线段的长度及解答过程。
答案:可以求出AB=CD=3cm; EBC =AD=2AB=6 cm ;BF =4cm ;FC =2 cm ;B F C24 1第8题AE =5cm ;EF=5;(每正确写出一个正确答案得1分,共6分)解答过程:连结DF,则S∆AFD= 1 AF ⨯ DE = 1 AD ⨯ AB,于是DE⨯AF=AB⨯AD。
2 2又AD=2AB,所以3.6⨯5=2AB2 ⇒ AB 2=9⇒ AB =3(cm )。
AD=2AB=6(cm )。
——————————————————————————————+ 2 = 8 分在直角∆ABF中,根据勾股定理得:BF2=AF2 -AB 2=52 - 32 = 42,BF=4cm,FC = BC - BF =6-4=2( cm ) -------------------------- +1 = 9 分在直角∆AED中,根据勾股定理得:2 2 2 2 ⎛18 ⎫ 2 62(52- 32) ⎛ 24 ⎫2 24AE = AD - ED = 6 - ⎪ = = ⎪ . AE= ,52 5⎝ 5 ⎭ ⎝ 5 ⎭所以,EF=AF-AE=5- 24 = 1 (cm)。
(10分)--------------- +1 = 10 分5 59.如图所示的乘法竖式中,“我爱启智杯”分别代表 0~9 中的一个数字,相同的汉字代 表相同的数字,不同的汉字代表不同的数字, 那么“我爱启智杯”代表的数字分别是多少?写出答案和分析过程。
9 解:根据最后一步的进位情况,说明“我⨯我爱启智杯 = 9☐☐☐☐”,因此“我=3”; -------- 2 分 根据“启⨯我爱启智杯 = 0”,因此“启=0”;—————————————— +2 =4 分根据第二步、第三步,“爱⨯我爱启智杯”、“智⨯ 我爱启智杯 ⨯我爱启智杯9第 9 题图我爱启智杯”均为五位数,因此“爱”“智”只能为 1、2、3,但由于“我=3”,所以“爱”“智”只能为 1、2。
