福建省泉州市2019年中考数学试题

合集下载

【2019年中考数学】福建省泉州市2019年5月初中毕业班质量检测数学试题(含答案解析)

2019年福建省泉州市初中学业质量检查数学试题(试卷满分：150分；考试时间：120分钟)友情提示：所有答案必须填写在答题卡相应的位置上．一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上相应题目的答题区域内作答．1. 下列各式正确的是( )A. －(－2019)＝2019B. |－2019|＝±2019C. 20190＝0D. 2019－1＝－20192. 计算(－2a 2)3的结果是( )A. －6a 2B. －9a 5C. 9a 5D. －9a 63. 某几何体如下左图所示，该几何体的右视图是( )第3题图4. 一个正多边形的边长为2，每个外角都为60°，则这个多边形的周长是( )A. 9B. 12C. 16D. 195. 不等式组⎩⎪⎨⎪⎧x －1≤0－x ＜2，的整数解的个数为( ) A. 0个 B. 2个 C. 3个 D. 无数个6. 如图，▱ABCD 的对角线AC 与BD 相交于点O ，要使它成为矩形，需再添加的条件是( )A. OA ＝OCB. AC ＝BDC. AC ⊥BDD. BD 平分∠ABC第6题图9. 在学校演讲比赛中，10名选手的成绩折线统计图如图所示，则下列说法正确的是( )A. 最高分90B. 众数是5C. 中位数是90D. 平均分为99.5第9题图9. 如图，在△ABC 中，点D 、E 分别是边AB 、AC 上的点，且DE ∥BC ，若AD DB ＝12，DE ＝3，则BC 的长度是( )A. 6B. 9C. 9D. 10第9题图 9. 实数a 、b 、c 、d 在数轴上的对应点从左到右依次是A 、B 、C 、D ，若b ＋d ＝0，则a ＋c 的值( )A. 小于0B. 等于0C. 大于0D. 与a 、b 、c 、d 的取值有关10. 已知双曲线y ＝k x 经过点(m ，n )，(n ＋1，m －1)，(m 2－1，n 2－1)，则k 的值为( )A. 0或3B. 0或－3C. －3D. 3二、填空题：本大题共6小题，每小题4分，共24分．把答案填在答题卡的相应位置．11. 已知x ＝0是方程x 2－5x ＋2m －1＝0的解，则m 的值是________．12. 分解因式：x 3－4x ＝________．13. 某口袋中装有2个红球和若干个黄球，每个球除颜色外其它都相同，搅匀后从中摸出一个球恰为红球的概率是15，则袋中黄球的个数为________．14. 抛物线y ＝x 2－6x ＋9的顶点坐标是________．15. 在直角坐标系中，点M (3，1)绕着原点O 顺时针旋转60°后的对应点的坐标是________．16. 如图，在面积为16的四边形ABCD 中，∠ADC ＝∠ABC ＝90°，AD ＝CD ，DP ⊥AB 于点P ，则DP 的长是________．第16题图三、解答题：本大题共9小题，共96分．解答应写出文字说明，证明过程或演算步骤．在答题卡的相应位置内作答．19. (9分)先化简，再求值：x (x ＋2)＋(x －1)(x ＋1)－2x ，其中x ＝ 2.19. (9分)解方程组：⎩⎪⎨⎪⎧x －y ＝13x ＋y ＝7.19. (9分)如图，在四边形ABCD 中，AB ＝AD ＝3，DC ＝4，∠A ＝60°，∠D ＝150°，试求BC 的长度．第19题图。

2019年福建省中考数学试题及答案

2019年福建省初中学业水平考试数学(试卷满分：150分考试时间：120分钟)一、选择题：本题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的. 1.计算22＋(－1)0的结果是( )A .5B .4C .3D .22.北京故宫的占地面积约为720 000m 2，将720 000用科学记数法表示为( ) A .72×104 B .7.2×105 C .7.2×106 D .0.72×1063.下列图形中，一定既是轴对称图形又是中心对称图形的是( ) A .等边三角形 B .直角三角形 C .平行四边形 D .正方形4.右图是由一个长方体和一个球组成的几何体，它的主视图是( )A .B .C .D .5.已知正多边形的一个外角是36°，则该正多边形的边数为( ) A .12 B .10 C .8 D .66.如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是( ).A .甲的数学成绩高于班级平均分，且成绩比较稳定B .乙的数学成绩在班级平均分附近波动，且比丙好C .丙的数学成绩低于班级平均分，但成绩逐次提高D .就甲、乙、丙三个人而言，乙的数学成绩最不稳定 7.下列运算正确的是( ).A .a ·a 3＝a 3B .(2a )3＝6a 3C .a 6÷a 3＝a 2D .(a 2)3－(－a 3)2＝08.《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问君每日读多少?”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字?已知《孟子》一书共有34 685个字，设他第一天读x 个字，则下面所列方程正确的是( ) A .x ＋2x ＋4x ＝34 685 B .x ＋2x ＋3x ＝34 685 C .x ＋2x ＋2x ＝34 685 D .x ＋12x ＋14x ＝34 685次数主视图9.如图，P A 、PB 是⊙O 的两条切线，A 、B 为切点，点C 在⊙O 上，且∠ACB ＝55°，则∠APB 等于( ) A .55° B .70° C .110° D .125°10.若二次函数y ＝|a |x 2＋bx ＋c 的图象过不同的五点A (m ，n )，B (0，y 1)，C (3－m ，n )，D (2，y 2)，E (2，y 3)，则y 1， y 2，y 3的大小关系是( )A .y 1＜y 2＜y 3B .y 1＜y 3＜y 2C .y 3＜y 2＜y 1D .y 2＜y 3＜y 1 二、填空题(每小题4分，共24分) 11.因式分解：x 2－9＝ .12.如图，数轴上A 、B 两点所表示的数分别是－4和2，点C 是线段AB 的中点，则点C 所表示的数是 . 13.某校征集校运会会徽图案，遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎，随机调查了该校100位学生，其中60位学生喜欢甲图案，若该校共有学生2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有人.14.在平面直角坐标系xOy 中，□OABC 的三个顶点分别为O (0，0)，A (3，0)，B (4，2)，则其第四个顶点C 的坐标是 .15.如图，边长为2的正方形ABCD 的中心与半径为2的⊙O 的圆心重合，E 、F 分别是AD 、BA 的延长与⊙O 的交点，则图中阴影部分的面积为 .(结果保留π)16.如图，菱形ABCD 顶点A 在例函数y ＝3x (x >0)的图象上，函数y ＝kx (k >3，x >0)的图象关于直线AC 对称，且经过点B 、D 两点，若AB ＝2，∠DAB ＝30°，则k 的值为 .第15题图第16题图三、解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分8分)解方程组：⎩⎪⎨⎪⎧x －y ＝52x ＋y ＝4.18.(本小题满分8分)如图，点E 、F 分别是矩形ABCD 的边 AB 、CD 上的一点，且DF ＝BE . 求证：AF ＝CE .A19.(本小题满分8分)先化简，再求值：(x －1)÷(x －2x －1x )，其中x ＝2＋1已知△ABC为和点A'，如图，(1)以点A'为一个顶点作△A'B'C'，使得△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC面积的4倍；(要求：尺规作图，不写作法，保留作图痕迹)(2)设D，E，F分别是△ABC三边AB，BC，CA的中点，D'，E'，F'分别是你所作的△A'B'C'三边A'B'，B'C'，A'C'的中点，求证：△DEF∽△D'E'F'.AA'21.(本小题满分8分)在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转一个角度α得到△DEC，点A，B的对应点分别为D，E.(1)若点E恰好落在边AC上，如图1，求∠ADE的大小；(2)若α＝60°，F为AC的中点，如图2，求证：四边形BEDF是平行四边形.图1 图2某工厂为贯彻落实“绿水青山就是金山银山”的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理.但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理.已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元。

福建省泉州市2019届中考数学试题特色题型突破含答案

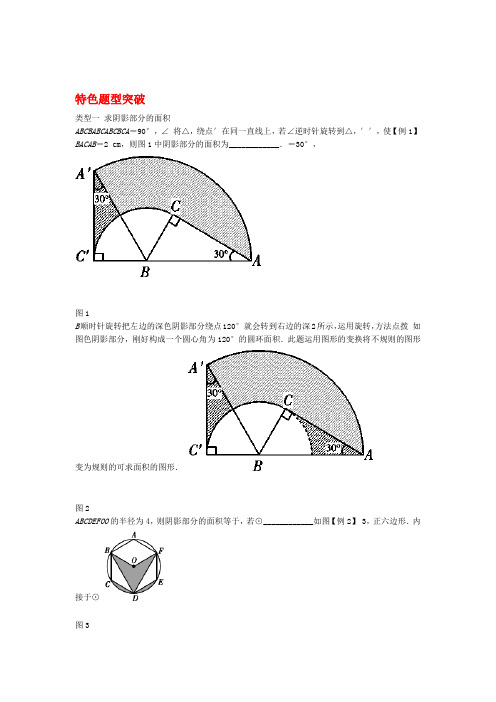
特色题型突破类型一求阴影部分的面积ABCBABCABCBCA＝90°，∠将△，绕点′在同一直线上，若∠逆时针旋转到△，′′，使【例1】BACAB＝2 cm，则图1中阴影部分的面积为____________．＝30°，图1B顺时针旋转把左边的深色阴影部分绕点120°就会转到右边的深2所示，运用旋转，方法点拨如图色阴影部分，刚好构成一个圆心角为120°的圆环面积．此题运用图形的变换将不规则的图形变为规则的可求面积的图形．图2ABCDEFOO的半径为4，则阴影部分的面积等于，若⊙____________如图【例2】 3，正六边形．内接于⊙图3ODSSSDEBC的面积，，弓形方法点拨连接，根据正多边形的对称性可得的面积＝弓形＝＝BCDBDOFDO△△△BOD的面积．此题运用图象的面积相等替换求不规则图象的面积．则不规则的阴影部分的面积刚好拼成扇形ABCABABC为圆心，以2，分别以＝2为半径作，，，△如图(2016·滨州】【例3 )4是等边三角形，弧，则图中阴影部分的面积是____________．图4此题运用面积的差求阴影部分的面积．方法点拨．1OABOOO为上的两个四等分点的直径为圆心，，1．(2016·赤峰)如图5，⊙1的半径为，分别以⊙212)( 半径作圆，则图中阴影部分的面积为11 ππ D．2 A．π B．π C．425图1ABBCABCDBDBCG上一点，的面积为16，点，点，△是边上一点，且是＝62．(2016·淄博)如图4BDHGHABC)是平行四边形，则图中阴影部分的面积是内部，且四边形点( 在△6图6． D 3 B．4 C．5 A．ACBDCABOBACOO若∠，．(2016·临沂)如图7，是⊙，与⊙的切线，.为切点，经过点分别相交于点3AB)＝30°，( ＝3，则阴影部分的面积是7 图π3ππ33．DA.－C ．－ B．6622634．如图8，方格纸中4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为____________(结果保留π)．图8ABCDACOOAAC＝2＝，将正方形绕点对角线9)5．(2016·黄石如图所示，正方形所在直线上有一点，O．____________60°，在旋转过程中，正方形扫过的面积是顺时针旋转图9ABCCAOABO的⊙中，∠在斜边＝90°，∠2＝30°，点6．(2016·重庆C)如图10，Rt△上，半径为DECEBCECDBACD围成的阴影部分的面积为____________，，切．边于点及，交边于点 .则由线段过点图10ABCDAAD的长为半径画弧，再以中，先以点，在边长为4的正方形为圆心，7．(2016·安顺)如图11ABAB长的一半为半径画弧，则阴影部分面积是____________(结果保留π)．边的中点为圆心，图11ACBCACBCBCOCBCAB，为圆心，4，以为半径作弧8．如图12，为直径作半圆，圆心为⊥.，＝以点＝OACDE，则阴影部分的面积是____________作．的平行线交两弧于点过点，图12类型二规律问题【例1】 (2016·宁波)下列图案是用长度相同的火柴棒按一定规律拼搭而成，图13①需8根火柴棒，图②需15根火柴棒，…，按此规律，图⑦需____________根火柴棒．图13ABCABCAC为直角边，画第的斜边1的等腰直角三角形，以Rt，已知△】【例2 如图14△是腰长为ACDACDADADE，……依此类推，则第2 013△为直角边，画第三个等腰RtRt二个等腰△，再以△的斜边Rt．____________个等腰直角三角形的斜边长是图141．(2016·娄底)“数学是将科学现象升华到科学本质认识的重要工具”，比如在化学中，甲烷的化学nn为正整数)(，丙烷的化学式是CH，…，设碳原子的数目为，则它们的化学H式CH，乙烷的化学式是C83246式都可以用下列哪个式子来表示( )A．CH B．CH C．CH D．CH nnnnnnnn3＋2－＋2222343222．已知A＝3×2＝6，A＝5×4×3＝60，A＝5×4×3×2＝120，A＝6×5×4×3＝360，依此规律A＝75635____________.149163．按一定规律排列的一列数依次为：，，，，…，按此规律排列下去，这列数中的第5个数是3579n个数是____________．____________，第4．如图15，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形；……按这样的规律下去，第6幅图中有____________个正方形．图15ABOAABCBO，顺时针旋转到△绕点的位置，点如图5．(2016·梅州)16，在平面直角坐标系中，将△11BCBxABCBABCCx轴上，将轴上，再将△在处，点绕点在的位置，点分别落在点，顺时针旋转到△21112111113????BAxAAABCCBC0，(0,2)绕点，则顺时针旋转到△轴上，依次进行下去….若点△，的位置，点在22222112??2B的坐标为____________．点 2 016图166．观察下列等式：311a＝－＝第一个等式：；1222×21×2×21×2411a＝＝－；第二个等式：23323×22×3×22×2511a＝＝－第三个等式：；×23×23×4×2．34344611a ＝＝－；第四个等式：45545×24×24×5×2……按上述规律，回答以下问题：nna ＝____________＝____________个等式：；(1)用含的代数式表示第naaaaa ＝＋…＋＋(2)式子____________. ＋202314类型三阅读理解1bbaa ，这里等式右边是实数?”为：(2016·梅州)对于实数＝，?，定义一种新运算“【例1】2ba －211x ＝－2)?(( 运算．例如：1?3＝－1的解是 ) ＝－.则方程 2x 48－1－3xxxx 7．B ．5＝C ．＝＝6 DA ．＝4【例2】先阅读理解下面的例题，再按要求解答下列问题：2x 0. ＞－例题：解一元二次不等式42xxx 2)＋2)(∵解：，－4＝(－2xxx 0.－2)4＞0可化为(＞＋2)(∴－由有理数的乘法法则“两数相乘，同号得正”，得xx 2<0＋2>0＋????. ，②①?? xx 2<0－2>0－????x ＞2，解不等式组①，得x ＜－2，解不等式组②，得xxxx ＜－或的解集为2. ＞(2)(＋2－2)＞0∴2xxx 2.2或4＞0的解集为＜－＞即一元二次不等式－2x ；＞0的解集为________________________(1)一元二次不等式16－x 1－ ________________________；>0(2)分式不等式的解集为x 3－2xx 0.＜3－2解一元二次不等式(3)．nn －134xyxxynxyy .，规定4′＝′＝则有给出一种运算：对于函数＝，＝若函数例如：.1．(2016·深圳)3yyx )的解是′＝已知函数12＝( ，则方程xxxx 2 ＝－A ．＝4，，＝－4 ＝B ．22121xxxx 3＝0 ＝ D ．32 ＝2 ，＝－C ．2112．阅读下列材料：2yxxyyx ＜＋的取值范围”有如下解法：0，试确定，解答“已知2－＝且1＞， yxxy 2. ∵解：＋－＝2，∴＝yyx 1. －∴＞＋21.＞，∴又∵＞1 yy 0.①，∴－又∵＜01＜＜x ②＜2.同理得：1＜xy 2. ＋＜＋由①＋②得－11＋＜0yxyx 2. ＋＜＜∴＋的取值范围是0 请按照上述方法，完成下列问题：yxxxyy 的取值范围是1，23－(1)已知＝，且＞＜，则＋．____________axaxxyyy 成立，求＝，若1＜－，1已知(2)＞－结果用含(的取值范围＋)的式子表示．。

泉州市 2019 届初中毕业班中考模拟试卷(三)数学试题参考答案及评分标准

2019年泉州市初中毕业班中考模拟（三）数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．一、选择题（每小题4分，共40分）1．B 2．A 3．C 4．D 5．C 6．A 7．A 8．C 9．B 10．B 二、填空题（每小题4分，共24分）11．()()33−+x x x 12. 2113．9 14．＞ 15.π 16．27 三、解答题（共86分） 17．（本小题8分）解：原式ab b ab b ab a 22222+−−+−=………………………………………………………………4分ab a −=2………………………………………………………………………………………5分当12,12−=+=b a 时，原式()()()1212122−⨯+−+=………………………………………………………………7分1223−+=222+=……………………………………………………………………………………8分 18．（本小题8分）解：去分母得：()()1321−=−+x x x …………………………………………………………………2分331−=+−x x ……………………………………………………………………4分44=x1=x ………………………………………………………………………6分经检验：1=x 为增根，……………………………………………………………………………7分 ∴原方程无解. ………………………………………………………………………………………8分 19．（本小题8分）解：已知：如图AB CD ⊥于D ，BD AD =，求证：CB CA =.……………………………………………………………3分证明：∵AB CD ⊥，∴︒=∠=∠90CDB CDA .……………………………………………5分BCD A在ACD ∆和BCD ∆中，∵⎪⎩⎪⎨⎧=︒=∠=∠=DC DC BDC ADC BD AD 90 ∴ACD ∆≌BCD ∆（S A S ..）， ……………………………………………………………………7分 ∴CB CA =. …………………………………………………………………………………………8分20．（本小题8分）证明：（1）依题意得：()m m m m m 1618162241422−++=⨯⨯−+=∆ ……………………………………2分 ()22141816−=+−=m m m∵()0142≥−m ，∴方程总有实数根. ……………………………………………………………………………………4分（2）解方程()021422=++−m x m x 得： ()41414−±+=m m x ，∴m x x 2,2121==. ………………………………………………………………………………………6分 ∵方程的两个根中只有一个根小于1，1211<=x ， ∴12≥m ，即21≥m .…………………………………………………………………………………………………8分 21．（本小题8分）解：（1）如图线段AD 为所求作图形；………………………………………3分（2）过C 作CE ∥DA 交BA 延长线于E ，∴DCBDAE AB =，ACE DAC ∠=∠，AEC BAD ∠=∠ ………………5分又∵AD 平分BAC ∠，CAD BAD ∠=∠ ∴AEC ACE ∠=∠∴AE AC =…………………………………………………………7分 ∴CDBDAC AB =…………………………………………………………8分 22．（本小题10分）解：（1）9，3； ……………………………………………………………………………………………2分（2）略……………………………………………………………………………………………………4分（3）第一次调查，平均每天未吃早餐人数为 ()3958475635201⨯+⨯+⨯+⨯+⨯⨯=x …………………………………………………………7分7140201=⨯= ……………………………………………………………………………………9分 ∴30150010057=⨯−（人）答：通过宣传教育后，这所学校每天约还有30人未吃早餐. ………………………………………10分 23．（本小题10分）解：（1）连接OD ， ∵AB 为⊙O 直径∴︒=∠90ADB ， ………………………………………………………………………………………1分 ∵AC AB =，∴CD BD =，……………………………………………………………………………………………2分又∵OB OA =， ∴OD ∥AC ， ∵AC DF ⊥， ∴DF OD ⊥，∴FG 是⊙O 的切线；…………………………………………………………………………………4分（2）连接BE ． ∵AB 为⊙O 直径, ∴︒=∠90BEA .∴BE ∥GF ，DF 为BCE ∆中位线， …………………………………………………………………5分 ∴3==EF CF . ∵5=BG ，EFAEBG AB =, …………………………………………………………………………………6分 ∴35AEAB =，设x AE x AB 3,5==,由勾股定理得：x BE 4=，x DF 2=. ∵,90︒=∠=A ∠=∠DFC FD CDA 即︒=∠+∠=∠+∠90C CDF CDF ADF ∴ADF C ∠=∠.∴ADF ∆∽DCF ∆, ……………………………………………………………………………………8分 ∴AF DFDF CF =, ∴33223+=x xx , 解得：43,321−==x x （舍去）, ∴155==x AB .…………………………………………………………………………………………10分24．（本小题13分）解：（1）法一：∵︒=∠60BAC ，AB AC = ∴ABC ∆为等边三角形，∴BC AC AB ==，︒=∠=∠=∠60ABC ACB BAC ，由翻折可得：︒=∠=∠60ACD ACE ， ∴BAC ACE ∠=∠，∴AB EG //．……………………………………………………………………………………………………2分同理可得AC FG //，∴四边形ABGC 为平行四边形，………………………………………………………………………………3分又AC AB =，∴四边形ABGC 为菱形．………………………………………………………………………………………4分法二：∵︒=∠60BAC ，AB AC = ∴ABC ∆为等边三角形，∴BC AC AB ==，︒=∠=∠60ABC ACB ，由翻折可得：︒=∠=∠60ACD ACE ， ∴︒=∠60BCG ，同理可得︒=∠60CBG ， ∴GBC ∆为等边三角形，∴BC BG CG ==，……………………………………………………………………………………………2分又BC AC AB ==， ∴AC CG BG AB ===，∴四边形ABGC 为菱形．……………………………………………………………………………………4分（2）过点A 作EF AM ⊥交EF 于点M ， ∴︒=∠=∠90FMA EMA ．由翻折可得：CAE CAD ∠=∠，FAB DAB ∠=∠，AF AE AD ==， ∴EM EF 2=，∴()︒=︒⨯=∠=∠+∠=∠+∠=∠+∠=∠1206022222CAB DAB CAD DAB CAD DAF EAD EAF ， ∴︒=︒−︒=∠=∠302120180AFM AEM ．……………………………………………………………………6分在Rt AME ∆中，AE AE AEM AE EM 2330cos cos =︒⋅=∠⋅=， ∴AD AE AE EM EF 332322==⎪⎪⎭⎫⎝⎛==，……………………………………7分 ∴当AD 取最小值时，EF 最小.又∵当BC AD ⊥时，AD 取得最小值，即EF 最小.∴当EF 最小时，BC AD ⊥. ……………………………………………………8分M HECDBA（3）由（2）可知BC AD ⊥， ∴︒=∠=∠90ADB ADC ．∵EAC DAC ∠=∠，FAB DAB ∠=∠，∴()︒=︒⨯=∠=∠+∠=∠12060222BAC DAB DAC EAF ，……………………………………………………9分又AF AE AD ==，∴︒=−=∠=∠︒︒302120180AFE AEF ，又︒=∠=∠90ADB AFB ，∴︒=︒−︒=∠603090BFH ，…………………………………………………………10分 ∴BAC BFH ∠=∠，又ABC FBH ∠=∠， ∴BFH ∆∽BAC ∆， ∴BC BHBA BF =， ……………………………………………………………………………………………11分 ∴BCBABH BF =，又CBH ABF ∠=∠，∴ABF ∆∽CBH ∆，………………………………………………………………………………………12分 ∴︒=∠=∠90AFB CHB ，即AB CH ⊥． ……………………………………………………………………………………………13分 25．（本小题13分）解：（1）把),(1y m A 代入12++−=m x y 中，得：1121+=++−=m m m y ，…………………………………1分 ∴)1,(+m m A ……………………………………………………2分把)1,(+m m A 代入)0(>=k xky 中，得：m m m m k +=+=2)1(.………………………………………3分（2）法一：若1=m ，则反比例函数为xy 2=，一次函数为3+−=x y ，如图，过点P 作AB PM ⊥于点M ，过点P 作y PN //轴交直线AB 于点N ，在Rt PQM ∆中，︒=∠90PMQ ，︒=∠30PQM ，∴PM PQ 2=. …………………………………………………4分 ∵直线3+−=x y 与y 轴所夹的锐角为︒45，又y PN //轴， ∴︒=∠45PNM .在Rt PMN ∆中，︒=∠90PMN ，︒=∠45PNM ，HECDBA∴PN PM 22=, ∴PN PQ 2=. …………………………………………5分设点)0)(2,(>x xx P ，则)3,(+−x x N ，令t PN =∴xx t 2)3(−+−=，整理得()0232=+−+x t x ， ∴()0832≥−−=∆t ，即()()22223≥−t ，……………………………………………………………6分又∵3)2(32)3(<+−=−+−=xx x x t ， ∴223−<−t ，即223−≤t ， ∴PN 的最小值为223−，又∵PN PQ 2=，∴PQ 的最小值为423−.………………………………………………………………………………7分法二：如图，同上可得PN PQ 2=. …………………………………………………………………………5分设直线AB 平移后的表达式为b x y +−=，联立⎪⎩⎪⎨⎧+−==bx y xy ,2，得022=+−bx x ，由0=∆，解得22=b 或22−=b （舍去），…………………………………………………………6分即直线22+−=x y 与双曲线xy 2=在A 、B 之间曲线部分有且只有一个交点，当点P 与该交点重合时，PN 最大，此时223−=PN ，又PN PQ 2=，∴PQ 的最大值为423− (7)(3) 联立⎪⎩⎪⎨⎧++−=+=122m x y xm m y ，得0)12(22=+++−m m x m x ，解得m x =1，12+=m x …………………………………………………………………………………9分 ∴1+=m n ,∴当n x m <<时，即为1+<<m x m . ∵()2314+<−m mx x ，又10+<<<m x m ， ∴上式化为()xm m x2214+<−.…………………………………………………………………………10分令函数m x y 421−=，函数()xm y 221+=，其中10+<<<m x m ， ∵二次函数1y 的对称轴为y 轴且开口向上，∴当10+<<<m x m 时，函数值1y 随着x 的增大而增大，此时，函数值1y 的最大值()124122+−=−+<m m m m S .……………………………………………11分 ∵0)1(2>+m ，∴当10+<<<m x m 时，反比例函数2y 随着x 的增大而减小，此时，函数值2y 的最小值()1112+=++>m m m T .………………………………………………………12分由题意得1122+≤+−m m m ， ∴m m 32≤，又0>m ，∴30≤<m . ……………………………………………………………………………………………13分。

2019年福建中考数学试题(解析版)

先根据二次函数解析式确定抛物线的图象开口方向，再结合图象分别计算出自变量为0， 2 和 2的函数值，再比较函数值的大小.
{分值}4 {章节:[1-22-1-4]二次函数y=ax2+bx+c的图象和性质} {考点:二次函数y＝ax2+bx+c的性质} {考点:二次函数的系数与图象的关系} {难度:3-中等难度} {类别:易错题}
{答案} B
{解析}本题考查了多边形的内角和，解题的关键是多边形的外角和公式的记忆．先由正多边形
的一个外角是36゜，然后再套入 n 边形外角和公式列方程计算即可．由多边形的外角公式，得
36°n=360°, n =10，故选择 B.
{分值}4
{章节:[1-11-3]多边形及其内角和}
{考点:多边形}
{考点:多边形的内角和}
A. x+2x+4x=34 685
B. x+2x+3x=34 685
C. x+2x+2x=34 685
11 D. x+ x+ x=34 685
24
{答案}A
{解析}本题考查了一元一次方程的应用，关键是审清题意，抓住等量关系列方程即可
{分值}4
{章节:[1-3-3]实际问题与一元一次方程}
{考点:一元一次方程的应用（其他问题）}
{题目}14. （2019年福建）在平面直角坐标系xOy中，□OABC的三个顶点O(0,0)、A(3,0) 、
B(4,2),则其第四个顶点是是_______. {答案} (1,2) {解析}本题考查了用样本估计总体，解题的关键根据喜欢甲图案的学生60名和所占的百分比 60 ×100％＝60％，进而用样本估计总体2000×60％＝1200。 100 {分值}4 {章节:[1-10-1]统计调查} {考点:样本的代表性} {考点:用样本估计总体} {类别:常考题} {难度:2-简单}

2019年福建省中考数学试卷与解析

2019年福建省中考试卷及解析、选择题1•计算2斗（一 1尸的姑果是（、 A .5B.4C 3D.22•北京故宫的占地面駅约为720 0曲,将了20 00囲科芋记款进表示为（：＞. A.72xl04B.7.2xl （pC.7.2«10eD, 0.72^0®3.下列團形申，一定既是抽对蘇團形又逻申心对称困形的是（）. A.等过三角形 B 直角三用形C •平行西边形 D.正君形至已知正寥边彫的亠金外角为3护，剧该止多边形鬧边数为（）.A.12B.10C.ED.66一如图是某班甲、乙、丙三位同学査近弐次数学成绩及其曲在班级相应平均分的折践统计團，則下列割斷措误的是（）.I1CXA 甲的敖学成绩為于淮级平均分，且成纷比较穂定旷B 一乙的戲学咸绩在班圾平均分附近淡动’且比丙好 MC 芮的戟学戒绩低于班綴年均分，但嚴綺連次撮嘉 “D 一就甲r J 丙三个人而言，匸的歡芋成绩戴不穩（7.下列运牡正蹦的爰（＞,^.（1＜1~ aE_（2出戶亦C. a~^a= d口一（口子一（一J ）M ）8.《增删算法统宗》记载：“有金学生资性好，一部孟子三日了，琴日墙诟一倍多，问若毎B 读多少？9 其大意是：青金学生天赍廳三天读宪一部《孟子》,每天闻读的字数是前一天的两倨，问他莓天各读多少个字？已鈕《孟子》-书共有34阴玲字十设他第一天读x 个字，则下西所列方程正璋的是（）-A.A +2X +4尸弭 685B.X +2J +3J X =34 685C. rl-2.r+2v=34 685D. -d —JT + — x=34 6852 49如團，尸八出是0O 切嬪.，土 B 为切点，点（?在G ）O 上，且ZACB=55^ 则N/V 出等于（）. A.55c B.70d CU0& D125c壬视万向（第他10.若二次函敕的圏象经述AQn』）、巩。

莎卜C（3—injt）. 0（^2 :刃、E（2：yQ『则y“兀、旳的大小芙系是（）.A. ＞i＜护卫 E.厘弋邸卫U y3＜护月 D. y2＜护月二、填空题（每小题4分，共24分）11.____________________ 因式分解:A2-9-■*4 - ~亠亠、、/t C liL2.如图，数轴上仏呂两点所表示的数分别走一4和2, ---- ---------------x——L*_4 u 2点JT是线段川?的中点，則点「所羞示的数是___________ . （第12□ ■某校挺集校运会合徽，遲遶出甲、乙、丙三种图案-为了解轲4+圏案更登欢迎，随机调蚩了该校100名学生，其中60名同学專说甲因案，芝该校共有2000人，權据所学妁统计知识可以倍计该校喜欢1F图案的学生有人.14.中在平面直甬生昏系疋v中.n（）ABC的三个顶点0（00）、川30）、0（4,2）,则其弟四个顶点是是—・15.如图,边长为2的丘方形ABCD申心与半径为2的0O的国心董合，E、F分别是E1的延悅与0O的交点剧图中阴影部分的面积是 ________ .（结杲保蛰；T）316,如图，菱形ABCD顶点J在例函數尸-（.v＞0）的图象上，函数x尸±0tA3, Q0）的图象关于直茨片匚对称#且经过点以D x悶点.若八B=2, ZDAB=30°,则£的值为_______________________ ・三、解答题（共X6分）17-悔小题满分&分）解方旌组；$一2 '|2.r+v = 4(M15 (第1618.准小题满分8分)如因*点&厂分别是拒形ABCD的边皿、CD上的一点+且Dr=BE.求证：AF=CE-19.体小题满分呂分)先化简，再求值：a—i)F&—主二2),其中x-vT+i20*爲小题满分8分)如图，已知△ABC为和点(1)以点/T为顶点求作色AEC气使△片迟Cs^ ABC.(尺规作图，保留作團痕迹，不写作法)(2)设D. E. F分别是卫ABC三边人風BC. AC的中点，D\ E\F分剂是你所作的仏A7TC'三边ATT、B'C\ A r Cr的中点，求证：氐DEFS& D£F・21.界』卜题港分$分）A RtAABC中，ZABC-90Q f Z/?AC-30,J将厶ABC点/!顺时豺旗L轻一定的南更u得到△片E0 点B、C的对应点分别是氐D （I）如图1，書点Q恰好在片厂上甘＜求zrnr的度数；Q）如因2,若戊之小时*点尸是边申点，求证：V9z4^ BFDE是平行四边形.22■（本小懸満分10分）某工厂为费彻落实“绿水痛山就是金山锻山叫勺夏最遲念，投资组蹇了日茂贰处理蚩沟加吨的厦爪处邂车间，討该厂工业隕术谨行无害化处理.伸雀盍工厂¥产炖棧的扩丸」该牟间捋常无法完氏当天匚业废氷的处湮倍务，需姜将超出日暖水处理蚤的废水立给第三方企业处理.已知该车间处理厦於，毎天需固定成本⑷元，并且年处理一吨废水还需其他费用&元：将废水交给第三方企业处理，每吨需支付12无.根据记氧5^21 S,该厂产生工业废水笳吨+共花费废水处遽费370乙（1）求该牟间的日废水处理量期；（2）为实现可持渎发展*走綾色发曳之璐，工厂合理控鬣了生产规橫’使殍辛天废水赴理的平均赞用不超过JO元伽打试计算该厂一天产生的工业废水量的范亂2王（本小題满分10分）某种机器使用期为三年*买方在购进机器甘・可臥给各台机券分别一次性额外购买若干次錐修服务* 每次维修服务费为2000元.毎台机器在使用期间，如果维傷次数未超过购机时购买的维修腹务次数，毎次实陥绒修时还需向維修人员支甘工时费500元；如果维修次歎趨辻机时购买的线修服务次數，超出部分每矢雉修时需支付维修服务费MOO元，但无需支ft工时费某小司计划购窝1台该种机送，为决箕在购买机器时应同时一炭性额外购买几次维修服务，喪集并整理了100台这种机需在三年使用期內的维修次数，整理得下表；⑴以这100台机器为样直，佶计"台机器在二车使用取内维修次戟不尢于RT'的慨率；（2）试以这100杠器维修費用的平均數作为决策依据，说明购买1台该机器的同时应一次性额外购10次迁是11次维修狼务？24.宙小题满分12分)如图，四边形ABCD内接于0。

福建省泉州市2019年中考数学质检试题卷(含答案)

2019年年泉州市初中学业质量量检查数学试题(试卷满分:150分：考试时间:120分钟)⼀一、选择题：本⼤大题共10⼩小题，每⼩小题4分，共40分1.在－1、2、、这四个数中，⽆无理理数是()A.－1B.2C.D.2.下列列运算结果为a 3的是()A.a+a+aB.a 5－a 2C.a·a·aD.a 6÷a 23.⼀一个⼏几何体的三视图如图所示，则这个⼏几何体是()4.⼈人体中红细胞的直径约为0.0000077m ，将数字0.0000077⽤用⽉月科学记数法表示为A.7.7×10－5B.0.77×10－5C.7.7×10－6D.77×10－75.下列列事件中，是必然事件的是()A.从装有10个⿊黑球的不不透明袋⼦子中摸出⼀一个球，恰好是红球B.抛掷⼀一枚普通正⽅方体骰⼦子所得的点数⼩小于7C.抛掷⼀一枚普通硬币，正⾯面朝上D.从⼀一副没有⼤大⼩小王的扑克牌中抽出⼀一张牌，恰好是⽅方块6.⼩小王和⼩小丽下棋，⼩小王执圆⼦子，⼩小丽执⽅方⼦子，如图是在直⻆角坐标系中棋⼦子摆出的图案，若再摆放⼀一圆⼀一⽅方两枚棋⼦子，使9枚棋⼦子组成的图案既是轴对称图形⼜又是中⼼心对称图形，则这两枚棋⼦子的坐标分别是()A.圆⼦子(2,3)，⽅方⼦子(1,.3) B.圆⼦子(1,3)，⽅方⼦子(2,3)C.圆⼦子(2,3)，⽅方⼦子(4,0)D.圆⼦子(4,0)，⽅方⼦子(2,3)7.关于x 的⼀一元⼆二次⽅方程x 2－mx －1=0的根的情况是()A.有两个不不相等的实数根B.有两个相等的实数根C.⽆无实数根D.不不能确定8.⼀一次函数y =－2x +1的图象不不经过()A.第⼀一象限B.第⼆二象限C.第三象限D.第四象限9.如图，抛物线y=ax 2+bx+c (a >0)过原点O ，与x 轴另⼀一交点为A ，顶点为B ，若△AOB 为等边三⻆角形，则b 的值为()A.－B.2C.－3D.－4D ．C ．A ．B ．(第3题)(第6题)(第9题)10.如图，点E 为△ABC 的内⼼心，过点E 作MN ∥BC 交AB 于点M ，交AC 于点N ，若AB =7，AC =5，BC =6，则MN 的⻓长为()A.3.5B.4C.5D.5.5⼆二、填空题：本⼤大题共6⼩小题，每⼩小题4分，共24分11.计算：()－1+(－1)°＝________.12.若⼀一组数据1、3、x 、5、8的众数为8，则这组数据的中位数为________.13.在五边形ABCDE 中，若∠A +∠B +∠C +∠D =440°，则∠E ＝________.14.若是⽅方程组的解，则a +4b ＝________.15.如图，PA 切⊙O 于点A ，点B 是线段PO 的中点，若⊙O 的半径为，则图中阴影部分的⾯面积为________.16.在平⾯面直⻆角坐标系中，点A 的坐标为(4,0)，点B 为y 轴上的⼀一动点，将线段AB 绕点B 顺时针旋转90°得线段BC ，若点C 恰好落在反⽐比例例函数y =的图象上，则点B 的坐标为________.三、解答题：本⼤大题共9⼩小题，共86分，解答应写出⽂文字说明，证明过程或演算步骤17.(8分)解不不等式组，并将解集在数轴上表示出来.18.(8分)先化简，再求值：(a +)÷，其中a ＝－2.(第10题)(第15题)19.(8分)如图，在△ABC中，AB=AC，CD⊥AB于点D，BE⊥AC于点E.求证:BD=CE.20.(8分)《杨辉算法》中有这么⼀一道题：“直⽥田积⼋八百六⼗十四步，只云⻓长阔共六⼗十步，问⻓长多⼏几何?”意思是：⼀一块矩形⽥田地的⾯面积为864平⽅方步，只知道它的⻓长与宽共60步，问它的⻓长⽐比宽多了了多少步？21.(8分)如图，在□ABCD中，AC与BD交于点O，AC⊥BC于点C，将△ABC沿AC翻折得到△AEC，连接DE.(1)求证：四边形ACED是矩形；(2)若AC=4，BC=3，求sin∠ABD的值.22.(10分)电器器专营店的经营利利润受地理理位置、顾客消费能⼒力力等因素的影响某品牌电脑专营店设有甲、⼄乙两家分店，均销售A、B、C、D四种款式的电脑，每种款式电脑的利利润如表1所示.现从甲、⼄乙两店每⽉月售出的电脑中各随机抽取所记录的50台电脑的款式，统计各种款式电脑的销售数量量，如表2所示.表1：四种款式电脑的利利润电脑款式A B C D利利润(元/台)160200240320表2：甲、⼄乙两店电脑销售情况电脑款式A B C D甲店销售数量量(台)2015105⼄乙店销售数量量(台)88101418试运⽤用统计与概率知识，解决下列列问题：(1)从甲店每⽉月售出的电脑中随机抽取⼀一台，其利利润不不少于240元的概率为_______;(2)经市场调查发现，甲、⼄乙两店每⽉月电脑的总销量量相当.现由于资⾦金金限制，需对其中⼀一家分店作出暂停营业的决定，若从每台电脑的平均利利润的⻆角度考虑，你认为应对哪家分店作出暂停营业的决定?并说明理理由.23.(10分)在平⾯面直⻆角坐标系中，反⽐比例例函数y=(x>0,k>0图象上的两点(n,3n)、(n+1,2n).(1)求n的值；(2)如图，直线l为正⽐比例例函数y=x的图象，点A在反⽐比例例函数y=(x>0,k>0)的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的⾯面积为S1，△ABD的⾯面积为S2，求S1－S2的值.24.(13分)如图，在菱形ABCD中，点E是BC边上⼀一动点(不不与点C重合)对⻆角线AC与BD相交于点O，连接AE，交BD于点G.(1)根据给出的△AEC，作出它的外接圆⊙F，并标出圆⼼心F(不不写作法和证明，保留留作图痕迹)；(2)在(1)的条件下，连接EF.①求证:∠AEF=∠DBC；②记t=GF2+AG·GE，当AB=6，BD=6时，求t的取值范围.25.(13分)如图，⼆二次函数y=x2+bx－3的图象与x轴分别相交于A、B两点，点B的坐标为(3,0)，与y轴的交点为C，动点T在射线AB上运动，在抛物线的对称轴l上有⼀一定点D，其纵坐标为2，l与x轴的交点为E，经过A、T、D三点作⊙M.(1)求⼆二次函数的表达式；(2)在点T的运动过程中，①∠DMT的度数是否为定值?若是，请求出该定值：若不不是，请说明理理由；②若MT=AD，求点M的坐标；(3)当动点T在射线EB上运动时，过点M作MH⊥x轴于点H，设HT=a，当OH≤x≤OT时，求y的最⼤大值与最⼩小值(⽤用含a的式⼦子表示).2019年福建省泉州市初中学业质量检查数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．一、选择题（每小题4分，共40分）1．D 2．C 3．D 4．C 5．B 6. A 7．A 8．C 9．B 10．B 二、填空题（每小题4分，共24分）11．3 12. 5 13．100 14．6 15. 233π− 16．()1,0或()3,0 三、解答题（共86分） 17．（本小题8分）解：解不等式①得：x ≥2− …………………………………………………………………………3分解不等式②得： 3＜x ……………………………………………………………………………6分∴不等式组的解集是2−≤x 3<……………………………………………………………………8分 18．（本小题8分）解：原式aa a a a a +−÷−+−=2221212…………………………………………………………………1分()()()()111212+−+÷−−=a a a a a a ……………………………………………………………4分 ()()()()111212−++⋅−−=a a a a a a ……………………………………………………………5分()21−−=a a a ………………………………………………………………………………6分当2−=a 时，原式()2322122−=−−−−⨯−=…………………………………………………8分19．（本小题8分）证明：法一：∵AB CD ⊥,AC BE ⊥，∴90BDC CEB ∠=∠=︒.……………………………………………………………………………2分 ∵AB AC =，∴ABC ACB ∠=∠.……………………………………………………………………………………3分在BCD ∆与CBE ∆中，BDC CEB ∠=∠，DBC ECB ∠=∠，BC CB =,∴BCD ∆≌CBE ∆.……………………………………………………………………………………7分 ∴CE BD = . …………………………………………………………………………………………8分法二：∵AB CD ⊥,AC BE ⊥,∴︒=∠=∠90BEA CDA .………………………………………………………………………2分在ADC ∆与AEB ∆中，BEA CDA ∠=∠，A A ∠=∠，AC AB =∴ADC ∆≌AEB ∆. ……………………………………………………………………………………6分 ∴AE AD =∴AE AC AD AB −=−,∴CE BD = . ……………………………………………………………………………………………8分 20．（本小题8分）解：设矩形的长为x 步，则宽为()x −60步，依题意得：……………………………………………1分()86460=−x x ，……………………………………………………………………………………5分整理得：0864602=+−x x解得：36=x 或24=x （不合题意，舍去）………………………………………………………7分∴24366060=−=−x (步) ∴122436=−(步) 答：该矩形的长比宽多12步. ……………………………………………………………………………8分 21．（本小题8分）(1)由折叠性质得：CE BC = .…………………………………………………………………………1分在□ABCD 中，AD BC =，BC ∥AD ，∴AD CE =， ……………………………………………………………………………………………2分又AD ∥CE ，∴四边形ACED 是平行四边形. …………………………………………………………………………3分 ∵BC AC ⊥， ∴︒=∠90ACE . ∴□ACED 是矩形. ………………………………………………………………………………………4分 (2)法一：在矩形ACED 中，4==DE AC ，︒=∠=∠90ADE DEC . ∵︒=∠90ACE ，由折叠性质可知：B 、C 、E 三点共线 ∴633=+=+=CE BC BE . 在BED Rt ∆中，由勾股定理得：132524622==+=BD .………5分在ABC Rt ∆中，同理可得：5=AB . 如图1，过点A 作BD AF ⊥于点F ， ∴DE AD AF BD S ABD ⋅=⋅=∆2121，D∴432113221⨯⨯=⋅⨯AF ，13136=AF . ……………………………………………………6分在AFB Rt ∆中，65136513136sin ===∠AB AF ABF .………………………………………………8分法二：由(1)得︒=∠=∠90ACB BED ，4==AC DE ，3==BC CE ，在BED Rt ∆中，由勾股定理，得：132********==+=+=DE BE BD ，在ABC Rt ∆中，同理可得：5=AB .在□ABCD 中，242121=⨯==AC AO ，131322121=⨯==BD BO ……………………5分如图2，过点O 作AB OF ⊥于点F ，则︒=∠90OFA . ∵BAC OAF ∠=∠，︒=∠=∠90BCA OFA ， ∴OAF ∆∽BAC ∆，∴BA OA BC OF =，即523=OF ，∴56=OF ，………………………………6分在OFB Rt ∆中，651361356sin ===∠OB OF ABD .……………………8分 22．（本小题10分）解：(1)103；……………………………………………………………………………………………3分 (2) 甲店每售出一台电脑的平均利润值为：204505320102401520020160=⨯+⨯+⨯+⨯（元）， ………………………………………………………………………………………………………6分乙店每售出一台电脑的平均利润值为：248501832014240102008160=⨯+⨯+⨯+⨯（元）， ………………………………………………………………………………………………………9分 204248> ，即乙店每售出一台电脑的平均利润值大于甲店，又两店每月电脑的总销量相当，∴应对甲店作出暂停营业的决定. ………………………………………………………………10分 23．（本小题10分）解：(1)将)3,(n n 和)2,1(n n +代入x k y =得：n k n =3，12+=n kn ， ………………………1分 ()1232+=∴n n n ，……………………………………………………………………………………2分解得2=n 或0=n （舍去），2=∴n .…………………………………………………………………………………………………3分 (2)由(1)得：点)6,2(在反比例函数)0,0(>>=x k xky 的图象上，(第21题图2)将点()6,2代入x ky =，得12=k . ∴反比例函数为xy 12=.………………………………………………………………………………4分设OC a =，又点B 在直线x y =，∴点B ()a a ,.又x BC ⊥轴，∴BOC ∆为等腰直角三角形. ∵l AB ⊥，BC AD ⊥，∴ABD ∆为等腰直角三角形. …………………………………………………………………………6分设b BD =，则b AD =， ∴点()b a b a A −+,. 将点()b a b a A −+,代入x y 12=，得ba b a +=−12，即1222=−b a ，………………………………………………………………………………………8分又2121a S =，2221b S =， ()61221212221=⨯=−=−∴b a S S .…………………………………10分24．（本小题13分）(1) 如图1，⊙F 为所求作的圆；…………………………………………3分（若有其它作法，可参考以上评分标准） (2) ①证明：法一：如图2，连接AF .∵四边形ABCD 为菱形，∴BD AC ⊥.∴ACB DBC ∠−︒=∠90.…………………………………………………4分∵FE FA =，∴FAE AEF ∠=∠,∴()AFE AFE AEF ∠−︒=∠−︒=∠219018021.…………………………………………………5分又AFE ACB ∠=∠21,∴ACB AEF ∠−︒=∠90，……………………………………………………………………………7分又∵ACB DBC ∠−︒=∠90,∴DBC AEF ∠=∠.……………………………………………………………………………………8分法二：如图2，连接AF ,在菱形ABCD 中，CD CB =,AC 平分BCD ∠，∴ACB BCD ∠=∠2.………………………………………………………4分又ACE AFE ∠=∠2,∴AFE BCD ∠=∠.…………………………………………………………5分D(第24题图1)(第24题图2)在等腰三角形CBD 中，2180BCDCBD ∠−︒=∠，在等腰三角形FEA 中，2180AFEAEF ∠−︒=∠， ………………………………………………7分 ∴AEF CBD ∠=∠. …………………………………………………………………………………8分②法一：∵四边形ABCD 为菱形，∴CBD ABD ∠=∠,OC AO =，33362121=⨯===BD DO BO . ………………………9分在ABO Rt ∆中，3)33(62222=−=−=BO AB AO .又∵FGE AGB ∠=∠，FEG ABG ∠=∠，∴ABG ∆∽FEG ∆， ∴GEBGGF AG =，∴BG GF GE AG ⋅=⋅.………………………………………………………………10分 ∵FBE GEF ∠=∠，EFB GFE ∠=∠， ∴EFB ∆∽GFE ∆， ∴EFBFGF EF =, ∴2GF BF EF ⋅=， …………………………………………………………………………………11分 ∴GE AG GF t ⋅+=2=22)(EF BF GF BG GF GF BG GF GF =⋅=+=⋅+.在菱形ABCD 中，BD AC ⊥，AF EF =≥AO ,∴2EF ≥9322==AO .如图3，当点F 与点O 重合时，AF 最小.∴当3==AO EF 时，t 的最小值为9. ……………………………………………………………12分如图3，当点E 与点B 重合时，AF 最大.由题意可知：BF AF =，设x AF =，则x OF −=33，由勾股定理得：222AF OF AO =+，即()222333x x =−+，解得：32=x .∴当32=x 时，t 的最大值为12∴9≤t ≤12…………………………………………………………13分法二：如图4，设⊙F 的半径为r ，连接EQ 、AP 、AF . 在菱形ABCD 中，BD AC ⊥，则AF ≥OA ，即r ≥3.(第24题图3)(G(第24题图4)参考答案第 6 页共 8 页∵AQ =AQ ，∴APG QEG ∠=∠. 又PGA QGE ∠=∠，∴QEG ∆∽APG ∆，…………………………………………………………………………………10分 ∴AGQGPG EG =，即QG PG AG EG ⋅=⋅.……………………………………………………………11分 ∴()()2222222AF r GF r GF GF r GF r GF QG PG GF GE AG GF t ==−+=+⋅−+=⋅+=⋅+=. 如图4，当点F 与点O 重合时，AF 最小.∴当3=r 时，t 的最小值为9. ………………………………………………………………………12分 ......（以下同法一） 25．（本小题13分）解：(1)把点B ()0,3代入32−+=bx x y ，得：2−=b ，∴二次函数的解析式为：322−−=x x y ……………………………2分(2) ①DMT ∠为定值.…………………………………………………3分理由如下：如图1，连接AD ，∵抛物线()413222−−=−−=x x x y ，∴抛物线的对称轴为直线1=x .又点D 的纵坐标为32，∴()32,1D .………………………………………………………………4分在322−−=x x y 中，令0=y ，则0322=−−x x ，解得：11−=x ，32=x ，∴()0,1−A .在AED Rt ∆中，3232tan ===∠AEDE DAE ，……………………5∴︒=∠60DAE ，∴︒=∠=∠1202DAE DMT ，∴在点T 的运动过程中，DMT ∠为定值︒120.………………………6分②解法一：如图2， ∵AD MT 21=，又MD MT =， ∴AD MD 21=，∵ADT ∆的外接圆圆心M 在AD 的中垂线上，(第25题图2)C(第25题图1)参考答案第 7 页共 8 页∴当点M 是线段AD 的中点时，此时AD 为⊙M 的直径时，AD MD 21=.……………………7分 ∵()0,1−A ，()32,1D ，∴点M 的坐标为()3,0.………………………………………………8分解法二：如图3， ∵()0,1−A ，()32,1D ，∴线段AD 的中点P 的坐标为()3,0，32=AD .由题意得：圆心M 在AD 的中垂线上，设直线MP 交x 轴于点Q . ∴AD PQ ⊥,即︒=∠90APQ ，又︒=∠60DAQ ， ∴︒=∠30PQA . 在OPQ Rt ∆中，3=OP ，330tan =︒=OPOQ ，即()0,3Q ,∴Q 与点B 重合.由()3,0P 、()3,0Q 可求得直线333+−=x y . ……………………………………………7分设点⎪⎪⎭⎫ ⎝⎛+−333,m m M ，则1+=m HT ，()0,12+m T ，∵AD MT 21=，∴242121=⨯==AD MT . 作x MH ⊥轴于点H ，在MHT Rt ∆中，由勾股定理，得：222MT HT MH =+∴()22221333=++⎪⎪⎭⎫ ⎝⎛+−m m ，解得：0=m . ∴()3,0M .……………………………………………………………………………………………8分(3)如图4，作x MH ⊥轴于点H ，则AT HT AH 21==，又a HT =，∴()0,1−a H 、()0,12−a T ………………………9分 ∵OH ≤x ≤OT ，又动点T 在射线EB 上运动， ∴0≤1−a ≤x ≤12−a ， ∴0≤1−a ≤12−a ，∴a ≥1，∴12−a ≥1.…………………………………………10分(第25题图3)C(第25题图4)参考答案第 8 页共 8 页（i ）当()⎩⎨⎧−−≥−−≥−11211112a a a ，即1≤a ≤34时，当1−=a x 时，()()a a a a y 4312122max −=−−−−=；当1=x 时，4min −=y .………………………………………………………………………………11分（ii ）当()⎪⎩⎪⎨⎧−−<−−>−≤−<11211112110a a a a ，即a <34≤2时，当12−=a x 时，()()a a a a y 8431221222max −=−−−−=；当1=x 时，4min −=y .…………………………………………………………………………………………………………12分（iii ）当11>−a ，即2>a 时，当12−=a x 时，()()a a a a y 8431221222max −=−−−−=.当1−=a x 时，()()a a a a y 4312122min −=−−−−=.…………………………………………………………………………………………………………13分。

福建省泉州市2019秋南安初二年期中考数学科答案

南安市2019—2020学年度上学期初中期中教学质量监测初二数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一步没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确作完该步应得的累计分数．（四）评分最小单位是1分，得分或扣分都不出现小数．一、选择题（每小题4分，共40分）．1．D ； 2．C ； 3．B ； 4．A ； 5．C ；6．D ； 7．C ； 8．B ； 9．A ； 10．A ．二、填空题（每小题4分，共24分）．11、512； 12、3； 13、2；14、5； 15、2244m mn n ++； 16、3三、解答题（10题，共86分）．17．（8分）5(4)-- …………………………………………………6分1 ………………………………………………………8分18．（8分）解：原式＝22322969y x xy y x -- ……………………………………6分＝36xy - ……………………………………………………8分19．（8分）解：（1）原式＝2(9)x x -+ …………………………………………2分＝(3)(3)x x x +- ……………………………………4分（2）原式＝22(69)a x x -+ ……………………………………6分＝22(3)a x - …………………………………………8分20．（8分）解：原式＝32222324248x x y xy x y xy y ++--- ……………………4分＝338x y - ………………………………………………………6分当1x =-，12y =时， 333318(1)8()2x y -=--⨯ …………………………………………7分＝112--=- ……………………………………………8分21．（8分）解：（1） 4 ， 40 ………………………………4分（2）1.99 ……………………………………………………………6分（3）10000 ……………………………………………………………8分22．（10分）解：（1）16 …………………………………………………………………2分（2）333b c b c +=⋅ ……………………………………………………4分58=⨯40= ……………………………………………………6分（3）233a b -＝2333a b ÷ ………………………………………………7分＝23(3)(3)a b ÷ ……………………………………………8分＝2345÷ ＝16125 ……………………………………………………10分 23．（10分）解：（1）∵2236108=-，∴36是奇巧数． ……………………………………………………2分设两个连续偶数为m ，2m +（n 为偶数），则22(2)50m m +-=，解得11.5m =（不符合题意）∴50不是奇巧数． …………………………………………………4分（2）是. …………………………………………………………………5分理由如下：∵22(22)(2)n n +-＝224844n n n ++- ………………………8分＝84n + ………………………………9分＝4(21)n +∴这两个连续偶数构造的奇巧数是4的倍数 ………………………10分24．（13分）解：（1）2 4 6； ………………………………………………3分（2）log a MN ………………………………………………………………4分设log a M x =，log a N y =，则x a M =，y a N = ………………………………………………5分∴x y x y M N a a a +⋅=⋅=， …………………………………………6分根据对数的定义， log a x y MN +=，即log log log a a a M N MN += ……………………………………7分（3）（方法一）：log 9log (33)a a =⨯ …………………………………………………8分log 3log 3a a =+ ……………………………………………9分5510=+= …………………………………………………10分log 27a ＝log (93)a ⨯ ………………………………………………11分＝log 9log 3a a + ……………………………………………12分＝10515+= …………………………………………………13分（方法二）：由log 35a =，得53a =，∵5510933a a a =⨯=⋅=，5551527333a a a a =⨯⨯=⋅⋅=∴根据对数的定义， log 910a =，log 2715a =25．（13分）解：（1）ab b a b a 2)(222++=+ ………………………………… 3分备注：或者ab b a b a 2)()(222=+-+，)(2)(222b a ab b a +=-+（2）（法一）：设b m a m =-=-2019,2020 ，则ab m m =--)2019)(2020(，221,4039a b a b +=+= ……… 4分∵ab b a b a 2)(222++=+∴ a b 2403912+= …………………………………………………… 6分∴ 2019-=ab ……………………………………………………… 7分 ∴)2019)(2020(--m m 2019-= …………………………………… 8分（法二）：∵ab b a b a 2)(222++=+[])2019)(2020(2)2019()2020()2019()2020(222--+-+-=-+-∴m m m m m m………………………………………………………………………… 5分∴ )2019)(2020(2403912--+=m m …………………… 7分∴)2019)(2020(--m m 2019-= ………………………………… 8分（3）设正方形EFGH 的边长为x ，则x NG x PG -=-=32,8……… 9分∵ CQGN PBNG APGM S S S S 正方形长方形正方形阴++=2∴22)32()32)(8(2)8(x x x x S -+--+-=阴………………… 10分∵ab b a b a 2)(222++=+∴ []2)32()8(x x S -+-=阴 ………………………………………… 12分 224=576= ……………………………………………………………… 13分。

【2019年中考真题系列】福建省2019年中考数学真题试卷含答案(解析版)

福建省2019年中考数学试卷(解析版)一、选择题（每小题4分，共40分）1．（4分）计算22+（﹣1）0的结果是（）A．5B．4C．3D．22．（4分）北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（）A．72×104B．7.2×105C．7.2×106D．0.72×106 3．（4分）下列图形中，一定既是轴对称图形又是中心对称图形的是（）A．等边三角形B．直角三角形C．平行四边形D．正方形4．（4分）如图是由一个长方体和一个球组成的几何体，它的主视图是（）A．B．C．D．5．（4分）已知正多边形的一个外角为36°，则该正多边形的边数为（）A．12B．10C．8D．66．（4分）如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（）A．甲的数学成绩高于班级平均分，且成绩比较稳定B．乙的数学成绩在班级平均分附近波动，且比丙好C．丙的数学成绩低于班级平均分，但成绩逐次提高D．就甲、乙、丙三个人而言，乙的数学成绩最不稳7．（4分）下列运算正确的是（）A．a•a3＝a3B．（2a）3＝6a3C．a6÷a3＝a2D．（a2）3﹣（﹣a3）2＝08．（4分）《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）A．x+2x+4x＝34685B．x+2x+3x＝34685C．x+2x+2x＝34685D．x+x+x＝346859．（4分）如图，P A、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）A．55°B．70°C．110°D．125°10．（4分）若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1二、填空题（每小题4分，共24分）11．（4分）因式分解：x2﹣9＝．12．（4分）如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是．13．（4分）某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有人．14．（4分）在平面直角坐标系xOy中，▱OABC的三个顶点O（0，0）、A（3，0）、B（4，2），则其第四个顶点是．15．（4分）如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是．（结果保留π）16．（4分）如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k ＝．三、解答题（共86分）17．（8分）解方程组．18．（8分）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．19．（8分）先化简，再求值：（x﹣1）÷（x﹣），其中x＝+1．20．（8分）已知△ABC和点A'，如图．（1）以点A'为一个顶点作△A'B'C'，使△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC 面积的4倍；（要求：尺规作图，不写作法，保留作图痕迹）（2）设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点，求证：△DEF∽△D'E'F'．21．（8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．22．（10分）某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元．根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元．（1）求该车间的日废水处理量m；（2）为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围．23．（10分）某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；维修次数89101112频率（台数）1020303010（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；（2）试以这100机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？24．（12分）如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD 的延长线上，且DF＝DC，连接AF、CF．（1）求证：∠BAC＝2∠CAD；（2）若AF＝10，BC＝4，求tan∠BAD的值．25．（14分）已知抛物y＝ax2+bx+c（b＜0）与x轴只有一个公共点．（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．2019年福建省中考数学试卷(解析答案)一、选择题（每小题4分，共40分）1．【分析】分别计算平方、零指数幂，然后再进行实数的运算即可．【解答】解：原式＝4+1＝5故选：A．2．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：将720000用科学记数法表示为7.2×105．故选：B．3．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、等边三角形是轴对称图形，不是中心对称图形，故本选项错误；B、直角三角形不是轴对称图形，也不是中心对称图形，故本选项错误；C、平行四边形不是轴对称图形，是中心对称图形，故本选项错误；D、正方形既是轴对称图形，又是中心对称图形，故此选项正确．故选：D．4．【分析】从正面看几何体，确定出主视图即可．【解答】解：几何体的主视图为：故选：C．5．【分析】利用多边形的外角和是360°，正多边形的每个外角都是36°，即可求出答案．【解答】解：360°÷36°＝10，所以这个正多边形是正十边形．故选：B．6．【分析】折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好【解答】解：A．甲的数学成绩高于班级平均分，且成绩比较稳定，正确；B．乙的数学成绩在班级平均分附近波动，且比丙好，正确；C．丙的数学成绩低于班级平均分，但成绩逐次提高，正确D．就甲、乙、丙三个人而言，丙的数学成绩最不稳，故D错误．故选：D．7．【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式＝a4，不符合题意；B、原式＝8a3，不符合题意；C、原式＝a3，不符合题意；D、原式＝0，符合题意，故选：D．8．【分析】设他第一天读x个字，根据题意列出方程解答即可．【解答】解：设他第一天读x个字，根据题意可得：x+2x+4x＝34685，故选：A．9．【分析】根据圆周角定理构造它所对的弧所对的圆心角，即连接OA，OB，求得∠AOB ＝110°，再根据切线的性质以及四边形的内角和定理即可求解．【解答】解：连接OA，OB，∵P A，PB是⊙O的切线，∴P A⊥OA，PB⊥OB，∵∠ACB＝55°，∴∠AOB＝110°，∴∠APB＝360°﹣90°﹣90°﹣110°＝70°．故选：B．10．【分析】由点A（m，n）、C（3﹣m，n）的对称性，可求函数的对称轴为x＝，再由B （0，y1）、D（，y2）、E（2，y3）与对称轴的距离，即可判断y1＞y3＞y2；【解答】解：∵经过A（m，n）、C（3﹣m，n），∴二次函数的对称轴x＝，∵B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离B最远，D最近，∵|a|＞0，∴y1＞y3＞y2；故选：D．二、填空题（每小题4分，共24分）11．【分析】原式利用平方差公式分解即可．【解答】解：原式＝（x+3）（x﹣3），故答案为：（x+3）（x﹣3）．12．【分析】根据A、B两点所表示的数分别为﹣4和2，利用中点公式求出线段AB的中点所表示的数即可．【解答】解：∵数轴上A，B两点所表示的数分别是﹣4和2，∴线段AB的中点所表示的数＝（﹣4+2）＝﹣1．即点C所表示的数是﹣1．故答案为：﹣113．【分析】用总人数乘以样本中喜欢甲图案的频率即可求得总体中喜欢甲图案的人数．【解答】解：由题意得：2000×＝1200人，故答案为：1200．14．【分析】由题意得出OA＝3，由平行四边形的性质得出BC∥OA，BC＝OA＝3，即可得出结果．【解答】解：∵O（0，0）、A（3，0），∴OA＝3，∵四边形OABC是平行四边形，∴BC∥OA，BC＝OA＝3，∵B（4，2），∴点C的坐标为（4﹣3，2），即C（1，2）；故答案为：（1，2）．15．【分析】延长DC，CB交⊙O于M，N，根据圆和正方形的面积公式即可得到结论．【解答】解：延长DC，CB交⊙O于M，N，则图中阴影部分的面积＝×（S圆O﹣S正方形ABCD）＝×（4π﹣4）＝π﹣1，故答案为：π﹣1．16．【分析】连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG⊥x轴于点G，得O、A、C在第一象限的角平分线上，求得A点坐标，进而求得D 点坐标，便可求得结果．【解答】解：连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D 作DG⊥x轴于点G，∵函数y＝（k＞3，x＞0）的图象关于直线AC对称，∴O、A、C三点在同直线上，且∠COE＝45°，∴OE＝AE，不妨设OE＝AE＝a，则A（a，a），∵点A在在反比例函数y＝（x＞0）的图象上，∴a2＝3，∴a＝，∴AE＝OE＝，∵∠BAD＝30°，∴∠OAF＝∠CAD＝∠BAD＝15°，∵∠OAE＝∠AOE＝45°，∴∠EAF＝30°，∴AF＝，EF＝AE tan30°＝1，∵AB＝AD＝2，AE∥DG，∴EF＝EG＝1，DG＝2AE＝2，∴OG＝OE+EG＝+1，∴D（+1，2），故答案为：6+2．三、解答题（共86分）17．【分析】方程组利用加减消元法求出解即可．【解答】解：，①+②得：3x＝9，即x＝3，把x＝3代入①得：y＝﹣2，则方程组的解为．18．【分析】由SAS证明△ADF≌△BCE，即可得出AF＝CE．【解答】证明：∵四边形ABCD是矩形，∴∠D＝∠B＝90°，AD＝BC，在△ADF和△BCE中，，∴△ADF≌△BCE（SAS），∴AF＝CE．19．【分析】先化简分式，然后将x的值代入计算即可．【解答】解：原式＝（x﹣1）÷＝（x﹣1）•＝，当x＝+1，原式＝＝1+．20．【分析】（1）分别作A'C'＝2AC、A'B'＝2AB、B'C'＝2BC得△A'B'C'即可所求．（2）根据中位线定理易得∴△DEF∽△ABC，△D'E'F'∽△A'B'C'，故△DEF∽△D'E'F'【解答】解：（1）作线段A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，得△A'B'C'即可所求．证明：∵A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，∴△ABC∽△A′B′C′，∴（2）证明：∵D、E、F分别是△ABC三边AB、BC、AC的中点，∴DE＝，，，∴△DEF∽△ABC同理：△D'E'F'∽△A'B'C'，由（1）可知：△ABC∽△A′B′C′，∴△DEF∽△D'E'F'．21．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC 上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝25°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．22．【分析】（1）求出该车间处理35吨废水所需费用，将其与350比较后可得出m＜35，根据废水处理费用＝该车间处理m吨废水的费用+第三方处理超出部分废水的费用，即可得出关于m的一元一次方程，解之即可得出结论；（2）设一天产生工业废水x吨，分0＜x≤20及x＞20两种情况考虑，利用每天废水处理的平均费用不超过10元/吨，可得出关于x的一元一次不等式，解之即可得出结论．【解答】解：（1）∵35×8+30＝310（元），310＜350，∴m＜35．依题意，得：30+8m+12（35﹣m）＝370，解得：m＝20．答：该车间的日废水处理量为20吨．（2）设一天产生工业废水x吨，当0＜x≤20时，8x+30≤10x，解得：15≤x≤20；当x＞20时，12（x﹣20）+8×20+30≤10x，解得：20＜x≤25．综上所述，该厂一天产生的工业废水量的范围为15≤x≤20．23．【分析】（1）利用概率公式计算即可．（2）分别求出购买10次，11次的费用即可判断．【解答】解：（1）“1台机器在三年使用期内维修次数不大于10”的概率＝＝0.6．（2）购买10次时，某台机器使用期内维修次数89101112该台机器维修费用2400024500250003000035000此时这100台机器维修费用的平均数y1＝（24000×10+24500×20+25000×30+30000×30+35000×10）＝27300购买11次时，某台机器使用期内维修次数89101112该台机器维修费用2600026500270002750032500此时这100台机器维修费用的平均数y2＝（26000×10+26500×20+27000×30+27500×30+32500×10）＝27500，∵27300＜27500，所以，选择购买10次维修服务．24．【分析】（1）根据等腰三角形的性质得出∠ABC＝∠ACB，根据圆心角、弧、弦的关系得到＝，即可得到∠ABC＝∠ADB，根据三角形内角和定理得到∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∠ADB＝90°﹣∠CAD，从而得到∠BAC＝∠CAD，即可证得结论；（2）易证得BC＝CF＝4，即可证得AC垂直平分BF，证得AB＝AF＝10，根据勾股定理求得AE、CE、BE，根据相交弦定理求得DE，即可求得BD，然后根据三角形面积公式求得DH，进而求得AH，解直角三角函数求得tan∠BAD的值．【解答】解：（1）∵AB＝AC，∴＝，∠ABC＝∠ACB，∴∠ABC＝∠ADB，∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∵BD⊥AC，∴∠ADB＝90°﹣∠CAD，∴∠BAC＝∠CAD，∴∠BAC＝2∠CAD；（2）解：∵DF＝DC，∴∠DFC＝∠DCF，∴∠BDC＝2∠DFC，∴∠BFC＝∠BDC＝∠BAC＝∠FBC，∴CB＝CF，又BD⊥AC，∴AC是线段BF的中垂线，AB＝AF＝10，AC＝10．又BC＝4，设AE＝x，CE＝10﹣x，由AB2﹣AE2＝BC2﹣CE2，得100﹣x2＝80﹣（10﹣x）2，解得x＝6，∴AE＝6，BE＝8，CE＝4，∴DE＝＝＝3，∴BD＝BE+DE＝3+8＝11，作DH⊥AB，垂足为H，∵AB•DH＝BD•AE，∴DH＝＝＝，∴BH＝＝，∴AH＝AB﹣BH＝10﹣＝，∴tan∠BAD＝＝＝．25．【分析】（1）抛物线与x轴的公共点坐标即为函数顶点坐标，即可求解；（2）①y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），即可求解；②计算直线AD表达式中的k值、直线AC表达式中的k值，两个k值相等即可求解．【解答】解：（1）抛物线与x轴的公共点坐标即为函数顶点坐标，故：y＝a（x﹣2）2＝ax2﹣4ax+4a，则c＝4a；（2）y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），又△ABC为等腰直角三角形，∴点A为抛物线的顶点；①c＝1，顶点A（1，0），抛物线的解析式：y＝x2﹣2x+1，②，x2﹣（2+k）x+k＝0，x＝（2+k±），x D＝x B＝（2+k﹣），y D＝﹣1；则D，y C＝（2+k2+k，C，A（1，0），∴直线AD表达式中的k值为：k AD＝＝，直线AC表达式中的k值为：k AC＝，∴k AD＝k AC，点A、C、D三点共线．22．（15分）如图，已知抛物线y＝ax2+bx+5经过A（﹣5，0），B（﹣4，﹣3）两点，与x 轴的另一个交点为C，顶点为D，连结CD．（1）求该抛物线的表达式；（2）点P为该抛物线上一动点（与点B、C不重合），设点P的横坐标为t．①当点P在直线BC的下方运动时，求△PBC的面积的最大值；②该抛物线上是否存在点P，使得∠PBC＝∠BCD？若存在，求出所有点P的坐标；若不存在，请说明理由．【分析】（1）将点A、B坐标代入二次函数表达式，即可求解；（2）①S△PBC＝PG（x C﹣x B），即可求解；②分点P在直线BC下方、上方两种情况，分别求解即可．【解答】解：（1）将点A、B坐标代入二次函数表达式得：，解得：，故抛物线的表达式为：y＝x2+6x+5…①，令y＝0，则x＝﹣1或﹣5，即点C（﹣1，0）；（2）①如图1，过点P作y轴的平行线交BC于点G，将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝x+1…②，设点G（t，t+1），则点P（t，t2+6t+5），S△PBC＝PG（x C﹣x B）＝（t+1﹣t2﹣6t﹣5）＝﹣t2﹣t﹣6，∵＜0，∴S△PBC有最大值，当t＝﹣时，其最大值为；②设直线BP与CD交于点H，当点P在直线BC下方时，∵∠PBC＝∠BCD，∴点H在BC的中垂线上，线段BC的中点坐标为（﹣，﹣），过该点与BC垂直的直线的k值为﹣1，设BC中垂线的表达式为：y＝﹣x+m，将点（﹣，﹣）代入上式并解得：直线BC中垂线的表达式为：y＝﹣x﹣4…③，同理直线CD的表达式为：y＝2x+2…④，联立③④并解得：x＝﹣2，即点H（﹣2，﹣2），同理可得直线BH的表达式为：y＝x﹣1…⑤，联立①⑤并解得：x＝﹣或﹣4（舍去﹣4），故点P（﹣，﹣）；当点P（P′）在直线BC上方时，∵∠PBC＝∠BCD，∴BP′∥CD，则直线BP′的表达式为：y＝2x+s，将点B坐标代入上式并解得：s＝5，即直线BP′的表达式为：y＝2x+5…⑥，联立①⑥并解得：x＝0或﹣4（舍去﹣4），故点P（0，5）；故点P的坐标为P（﹣，﹣）或（0，5）．【点评】本题考查的是二次函数综合运用，涉及到一次函数、等腰三角形性质、图形的面积计算等，其中（2），要主要分类求解，避免遗漏．。

福建泉州2019中考试题-数学

福建泉州2019中考试题-数学【一】选择题〔每题3分，共21分〕1、－7的相反数是【】A、－7B、7C、－17D、172、(a2)4等于【】A、2a3B、4a2C、a8D、a63、把不等式x＋1≥0的解集在数轴上表示出来，那么正确的选项是【】4、下面左图是两个长方体堆成的物体，那么那个物体的主视图是【】5、假设y＝kx－4的函数值y随x的增大而增大，那么k的值可能是以下的【】A、－4B、－12C、0D、36、以下图形中，有且只有两条对称轴的中心称轴图形是【】A、正三角形B、正方形C、圆D、菱形7、如图，O是△ABC的内心，过点O作EF∥AB，分别交AC、BC于点E、F，那么【】A、EF＞AE＋BFB、EF＜AE＋BFC、EF＝AE＋BFD、EF≤AE＋BF【二】填空题〔每题4分，共10分〕8、比较大小：－50〔用“＞”或“＜”号填空〕、9、分解因式：x2－5x＝、10、光的速度大约是300000000m/s，将300000000用科学记数法表示为、11、某校初一年级进行科技创新竞赛活动，各班选送的学生数分别为3、2、2、6、6、5，那么这组数据的平均数是、12、n边形的内角和为900º，那么n＝、13、计算：mm－1－1m－1＝、14、如图，在△ABC中，AB＝AC，BC＝6，AD⊥BC于D，那么BD＝、15、如图，在△ABC中，∠A＝60º，∠B＝40º，点D、E分别在BC、AC的延长线上，那么∠1＝、16、如图，在矩形ABCD中，AB＝1，AD＝2，AD绕点A顺时针旋转，当点D落在BC上的点D′时，AD′＝，∠AD′B＝º、17、在△ABC中，P是AB上异于A、B的动点，过点P的直线截△ABC，使截得三角形与△ABC相似，我们不妨称这种直线为过点．．P．的△．．ABC．．．的相似线．．．．，简记为P(l x)(x为自然数)、(1)如图1，∠A＝90º，∠B＝∠C，当BP＝2PA时，P(l1)、P(l2)基本上．．．过点P的△ABC 的相似线(其中l1⊥BC，l2∥AC)，此外，还有条；(2)如图2，∠C＝90º，∠B＝30º，当BPBA＝时，P(l x)截得三角形的面积为△ABC面积的14、【三】解答题〔共89分〕18、(9分)计算：错误!未找到引用源。

福建省泉州市2019届中考数学试题：函数探究题_含答案

函数探究【例1】 1.抛物线y=ax 2+bx+c 的图象如图所示，则一次函数y=ax+b 与反比例函数y=在同一平面直角坐标系内的图象大致为（）A ．B ．C ．D ．2.已知x=2m+n+2和x=m+2n 时，多项式x 2+4x+6的值相等，且m ﹣n+2≠0，则当x=3（m+n+1）时，多项式x 2+4x+6的值等于．3.已知二次函数y=ax 2﹣2ax+1（a ＜0）图象上三点A （﹣1，y 1），B （2，y 2）C （4，y 3），则y 1、y 2、y 3的大小关系为（）A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 1＜y 3＜y 2D ．y 3＜y 1＜y 2方法总结 1．将抛物线解析式写成y ＝a(x －h)2＋k 的形式，则顶点坐标为(h ，k)，对称轴为直线x ＝h ，也可应用对称轴公式x ＝－，顶点坐标（-，)来求对称轴及顶点坐标．2．比较两个二次函数值大小的方法： (1)直接代入自变量求值法；(2)当自变量在对称轴两侧时，看两个数到对称轴的距离及函数值的增减性判断； (3)当自变量在对称轴同侧时，根据函数值的增减性判断．举一反三 1.已知点A （a ﹣2b ，2﹣4ab ）在抛物线y=x 2+4x+10上，则点A 关于抛物线对称轴的对称点坐标为（） A ．（﹣3，7）B ．（﹣1，7）C ．（﹣4，10）D ．（0，10）2.已知关于x 的函数y=（2m ﹣1）x 2+3x+m 图象与坐标轴只有2个公共点，则m= ．3.设A 1(2)y -，，B 2(1)y ，，C 3(2)y ，是抛物线2(1)y x a =-++上的三点，则1y ，2y ，3y 的大小关系为（）A ．312y y y >>B ．312y y y >>C ．321y y y >>D ．213y y y >> 考点二、二次函数系数的符号及其之间的关系【例2】二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①2a+b＞0；②b＞a＞c；③若﹣1＜m＜n＜1，则m+n＜﹣；④3|a|+|c|＜2|b|．其中正确的结论是（写出你认为正确的所有结论序号）．方法总结根据二次函数的图象确定有关代数式的符号，是二次函数中的一类典型的数形结合问题，具有较强的推理性．解题时应注意a决定抛物线的开口方向，c决定抛物线与y轴的交点，抛物线的对称轴由a，b共同决定，b2－4ac决定抛物线与x轴的交点情况．当x＝1时，决定a＋b＋c的符号，当x＝－1时，决定a－b＋c的符号．在此基础上，还可推出其他代数式的符号．运用数形结合的思想更直观、更简捷．举一反三 1.二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①b2﹣4ac＞0；②4a+c＞2b；③（a+c）2＞b2；④x（ax+b）≤a﹣b．其中正确结论的是．（请把正确结论的序号都填在横线上）2.一次函数y=ax+b（a≠0）、二次函数y=ax2+bx和反比例函数y=（k≠0）在同一直角坐标系中的图象如图所示，A点的坐标为（﹣2，0），则下列结论中，正确的是（）A．b=2a+k B．a=b+k C．a＞b＞0 D．a＞k＞0考点三、二次函数图象的平移【例3】二次函数y＝－2x2＋4x＋1的图象怎样平移得到y＝－2x2的图象( )A．向左平移1个单位，再向上平移3个单位B．向右平移1个单位，再向上平移3个单位C．向左平移1个单位，再向下平移3个单位D．向右平移1个单位，再向下平移3个单位方法总结二次函数图象的平移实际上就是顶点位置的变换，因此先将二次函数解析式转化为顶点式确定其顶点坐标，然后按照“左加右减、上加下减”的规律进行操作．举一反三将二次函数y＝x2的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数解析式是( )A．y＝(x－1)2＋2 B．y＝(x＋1)2＋2 C．y＝(x－1)2－2 D．y＝(x＋1)2－2考点四、确定二次函数的解析式【例4】如图，四边形ABCD是菱形，点D的坐标是(0，3)，以点C为顶点的抛物线y＝ax2＋bx＋c恰好经过x轴上A，B两点．(1)求A，B，C三点的坐标；(2)求经过A，B，C三点的抛物线的解析式．方法总结用待定系数法求二次函数解析式，需根据已知条件，灵活选择解析式：若已知图象上三个点的坐标，可设一般式；若已知二次函数图象与x轴两个交点的横坐标，可设交点式；若已知抛物线顶点坐标或对称轴与最大(或小)值，可设顶点式．举一反三已知抛物线p：y=ax2+bx+c的顶点为C，与x轴相交于A、B两点（点A在点B左侧），点C关于x轴的对称点为C′，我们称以A为顶点且过点C′，对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线，直线AC′为抛物线p的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2，则这条抛物线的解析式为．考点五、二次函数的实际应用【例5】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．方法总结运用二次函数的性质解决生活和实际生产中的最大值和最小值问题是最常见的题目类型，解决这类问题的方法是：1．列出二次函数的关系式，列关系式时，要根据自变量的实际意义，确定自变量的取值范围．2．在自变量取值范围内，运用公式法或配方法求出二次函数的最大值和最小值．举一反三大学毕业生小王响应国家“自主创业”的号召，利用银行小额无息贷款开办了一家饰品店．该店购进一种今年新上市的饰品进行销售，饰品的进价为每件40元，售价为每件60元，每月可卖出300件．市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件．为了获得更大的利润，现将饰品售价调整为60+x（元/件）（x＞0即售价上涨，x＜0即售价下降），每月饰品销量为y（件），月利润为w（元）．（1）直接写出y与x之间的函数关系式；（2）如何确定销售价格才能使月利润最大？求最大月利润；（3）为了使每月利润不少于6000元应如何控制销售价格？考点六、二次函数的面积问题【例6】如图，对称轴为x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．（1）求点B的坐标．（2）已知a=1，C为抛物线与y轴的交点．①若点P在抛物线上，且S△POC=4S△BOC，求点P的坐标．②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．方法总结对于此类二次函数题型考查了待定系数法求二次函数、一次函数的解析式，二次函数的性质以及三角形面积、线段长度问题，解题的关键是运用方程思想与数形结合思想．其次就是应用到二次函数常见的水平宽铅垂高．举一反三如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B 的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．（1）求A、B两点的坐标；（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；（3）当△BDM为直角三角形时，求m的值．考点七、二次函数的综合应用【例7】如图抛物线y=ax2+bx+3与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C，顶点为D，连接AC、CD、AD．（1）求该二次函数的解析式；（2）求△ACD的面积；（3）若点Q在抛物线的对称轴上，抛物线上是否存在点P，使得以A、B、Q、P四点为顶点的四边形为平行四边形？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．方法总结此类题型主要考查二次函数与其他知识点的综合应用，利用待定系数法求函数解析式，利用勾股定理、勾股定理的逆定理求三角形的形状；利用平行四边形的性质：对角线互相平分，对边相等是求出题中P点的关键．所以对于考查二次函数与三角形、四边形、圆、相似等相关知识的结合性题目时一定要把握好它们的性质及其常考定理与推理的综合应用．举一反三在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是直线y=﹣x 上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．一、选择题1．已知抛物线()3y k x 1x k ⎛⎫=+ ⎪⎝⎭-与x 轴交于点A ，B ，与y 轴交于点C ，则能使△ABC 为等腰三角形的抛物线的条数是（）A ．2B ．3C ．4D ．5 2．已知下列命题：①对于不为零的实数c ，关于x 的方程1+=+c xcx 的根是c ； ②在反比例函数xy 2=中，如果函数值y ＜1时，那么自变量x ＞2； ③二次函数 2222-+-=m mx x y 的顶点在x 轴下方；④函数y= kx 2+(3k+2)x+1，对于任意负实数k ，当x<m 时，y 随x 的增大而增大，则m 的最大整数值为2-.其中真命题为（）A ．①③B ．③C ．②④D ．③④ 3．(2013杭州，10)给出下列命题及函数x y =，2x y =和xy 1=的图象 ①如果21a a a>>，那么10<<a ； ②如果aa a 12>>，那么1>a ；③如果a a a>>21，那么01<<-a ；④如果a aa >>12时，那么1-<a 。

2019年福建省泉州市初中毕业

经典精品试卷2019年福建省泉州市初中毕业、升学考试数学试题（满分：150分；考试时间：120分钟）毕业学校姓名考生号一、选择题（每小题4分，共24分）每小题有四个答案，其中有且只有一个答案是正确的．请在答题卡上相应题目的答题区域内作答，答对的得4分，答错、不答或答案超过一个的一律得0分．1．计算：=-0)5(（）．A ．1B ．0C ．-1D ．-5 2．一组数据2, 6, 2, 8, 4, 2的众数是（）．A ．8B ．6C ．4D ．2 3. 右边物体的俯视图．．．是（）．4．方程组⎩⎨⎧=-=+24y x y x 的解是（）．A ．⎩⎨⎧==3,1y x B ．⎩⎨⎧==1,3y x C ．⎩⎨⎧==2,2y x D ．⎩⎨⎧==0,2y x5．已知两圆的半径分别为2和3，圆心距为5，则这两圆的位置关系是（）．A.外离B.外切C.相交D.内切6．点A 1、 A 2、 A 3、 …、 A n （n 为正整数）都在数轴上.点A 1在原点O 的左边，且A 1O=1；点A 2在点A 1的右边，且A 2A 1=2；点A 3在点A 2的左边，且A 3A 2=3；点A 4在点A 3的右边，且A 4A 3=4；……，依照上述规律，点A 2008 、 A 2019所表示的数分别为（）. A.2008、-2019 B.-2008、 2019 C.1004、-1005 D.1004、 -1004 二、填空题（每小题3分，共36分）在答题卡上相应题目的答题区域内作答．7．计算：（-4）÷2= ． 8．计算： a 3·a 4= ． 9．宝岛台湾的面积约为36 000平方公里，用科学记数法表示约为平方公里．10．计算： acb a • = ．11．分解因式： =++962x x ．12．八边形的内角和等于度．13．在分别写有数字1、 2、 3、 4、 5的5张小卡片中，随机地抽出1张卡片，则抽出卡片上的数字是1的概率为．14．如图，方格纸中每个最小正方形的边长为1，则两平行直线AB 、CD 之间的距离是．15．如图，△ABC 的中位线DE 长为10,则BC= ．16．已知反比例函数y=kx(k 是常数，k ≠0)的图象在第一、三象限，请写出符合上述条件的k 的一个值：．17．已知圆锥的底面半径长为5，侧面展开后所得的扇形的圆心角为120°，则该圆锥的母线长等于．18．如图，在△ABC 中，BC 边上的垂直平分线DE 交边BC 于点D ，交边AB 于点E.若△EDC 的周长为24，△ABC 与四边形AEDC 的周长之差为12，则线段DE 的长为．三、解答题（共90分）在答题卡上相应题目的答题区域内作答． 19．（8分）计算：212221-+--． 20．（8分）先化简下面的代数式，再求值：)3)(3()3(-++-x x x x ，其中.32+=x21．（8分）如图，已知∠1=∠2,AO=BO.求证：AC=BC.22. 右图为我国2004—2008年税收收入及其增长速度的不完整统计图.请你根据图中已有信息，解答下列问题：（1）这5年中，哪一年至哪一年的年税收收入增长率持续上升？（2）求出2008年我国的年税收收入.（精确到1亿元）23. (8分）如图所示，一棵大树在一次强烈的地震中于C处折断倒下，树顶落在地面B处，测得B处与树的底端A相距25米，∠ABC=24°.(1)求大树折断倒下部分BC的长度；（精确到1米）（2）问大树在折断之前高多少米?（精确到1米）24.（8分）将形状和大小都一样的红、白两种颜色的小球分装在甲、乙两个口袋中，甲袋装有1个红球和1个白球，乙袋装有2个红球和1个白球，现从每个口袋中各随机摸出1个小球.(1) 请你用画树状图或列表的方法表示所有等可能的结果；（2）有人说：“摸出‘两红’和摸出‘一红一白’这两个事件发生的概率相等.”你同意这种说法吗？为什么？25.（8分）如图，△ABC与△ADE都是等腰直角三角形，∠ACB和∠E都是直角，点C在AD上，把△ABC绕点A按顺时针方向旋转n度后恰好与△ADE重合.(1)请直接写出n的值；(2)若BC=2，试求线段BC在上述旋转过程中所扫过部分的面积.26．（8分）已知：直线y=kx(k≠0)经过点（3，-4）.(1)求k的值；(2)将该直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相离（点O为坐标原点）,试求m的取值范围.27．（13分）如图，等腰梯形花圃ABCD的底边AD靠墙，另三边用长为40米的铁栏杆围成，设该花圃的腰AB的长为x米.(1)请求出底边BC的长（用含x的代数式表示）；（2）若∠BAD=60°, 该花圃的面积为S米2.①求S与x之间的函数关系式（要指出自变量x的取值范围），并求当93时x的值；S=3②如果墙长为24米，试问S有最大值还是最小值？这个值是多少？28．（13分）在直角坐标系中，点A（5，0）关于原点O的对称点为点C.(1)请直接写出点C的坐标；（2）若点B在第一象限内，∠OAB=∠OBA，并且点B关于原点O的对称点为点D.①试判断四边形ABCD的形状，并说明理由；②现有一动点P从B点出发，沿路线BA—AD以每秒1个单位长的速度向终点D运动，另一动点Q从A点同时出发，沿AC方向以每秒0.4个单位长的速度向终点C运动，当其中一个动点到达终点时，另一个动点也随之停止运动.已知AB=6，设点P、Q的运动时间为t秒，在运动过程中，当动点Q在以PA为直径的圆上时，试求t的值.四、附加题（共10分）在答题卡上相应题目的答题区域内作答．友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分．填空：1.（5分）写出一个比0小的实数：.2.（5分）如右图，直线AB 、CD 相交于点O ，∠1=50°，则∠2= 度.2019年福建省泉州市初中毕业、升学考试数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．一、选择题（每小题4分，共24分）1．A ； 2．D ； 3．D ； 4．B ； 5．B ； 6．C ．二、填空题（每小题3分，共36分）7．-2； 8．7a ； 9．4106.3⨯； 10．bc； 11．2)3(+x ； 12．1080；13．51； 14．3； 15．20； 16．例如：“2”； 17．15； 18．6．三、解答题（共90分） 19.（本小题8分）解：原式=42121-+ ……………………………………………………（6分）=1-4 ………………………………………………………… （7分）=-3 ……………………………………………………………（8分）20.（本小题8分）解：原式＝9322-+-x x x ………………………………………… （4分）＝93-x ………………………………………………………（5分）当2=a +3时，原式＝9)32(3-+ ……………………………(6分） =9923-+ ……………………………（7分）=23………………………………… （8分） 21．（本小题8分）证明：证明：在△AOC 与△BOC 中∵AO=BO,∠1=∠2,OC=OC …………………………… （3分） ∴△AOC ≌△BOC ………………………………………（6分）∴AC=BC ………………………………………… （8分）22.（本小题8分）解：（1）这5年中，2005年至2007年的年税收收入增长率持续上升. ……………………………………………………………（4分）(2)49443×(1+17%)≈57848(亿元），即2008年我国的年税收收入约为57848亿元. …………………………………………………………………（8分）23.（本小题8分）解：如图，在Rt △ABC 中，∠CAB=90°,∠ABC=24°,AB=25米（1）∵cos ∠ABC=BCAB ……………………………………………（2分）∴BC=ABC AB cos =024cos 25≈27（米）即大树折断倒下部分BC 的长度约为27米. ……………………（4分）(2)∵tan ∠ABC=ABAC∴AC=AB ·tan ∠ABC=25·tan24°≈11.1(米）…………（7分）∴BC+AC ≈27+11.1≈38（米）即大树折断之前高约为38米. ……………………………（8分） 24.（本小题8分）解：（1）（解法一）列举所有等可能的结果，画树状图：…………………………………………（4分）（解法二）列表如下：（略）（2）不同意这种说法……………………………………………………………（5分）由（1）知，P （两红）=62=31，P （一红一白）=63=21∴P （两红）＜P （一红一白） …………………………………………（8分） 25.（本小题8分）解：（1）n=45 ……………………………………………………（3分）（2）设在旋转过程中，线段BC 所扫过部分的面积（即图中阴影部分面积）为S ，则 S=S 扇形ABD -S △ABC +S △ADE -S 扇形ACE又S △ABC =S △ADE∴S=S 扇形ABD -S 扇形ACE …………………………………………………（5分）在Rt △ABC 中，BC=2，由（1）得∠BAC=45°, ∴AB=045sin BC =222=2…………………………………………………（6分）∵AC=BC=2 ∴S=4442360)2(4536024522πππππ=-=•-•…………………………（8分）26.（本小题8分）解：（1）依题意得：-4=3k ，∴k=34- …………………………（3分）（2）由（1）及题意知，平移后得到的直线l 所对应的函数关系式为y=34-x+m(m ＞0) …………………………………………（4分）设直线l 与x 轴、y 轴分别交于点A 、B ，（如左图所示）当x=0时，y=m;当y=0时，x=43m.∴A(43m,0),B(0,m)，即OA=43m ，OB=m 在Rt△OAB中，AB=22OB OA +2=m m m 4516922=+…………（5分）过点O 作OD ⊥AB 于D ，∵S △ABO =21OD ·AB=21OA ·OB ∴21OD ·m 45=21·43m ·m∵m ＞0,解得OD=53m …………………………………………………（6分）依题意得：53m ＞6，解得m ＞10即m 的取值范围为m ＞10……………………………………………（8分） 27.（本小颗13分）解：（1）∵AB=CD=x 米，∴BC=40-AB-CD=（40-2x ）米.……………………………………………………（3分） (2)①如图，过点B 、C 分别作BE ⊥AD 于E ，CF ⊥AD 于F ，在Rt △ABE 中，AB=x,∠BAE=60°∴AE=21x,BE=23x.同理DF=21x,CF=23x又EF=BC=40-2x∴AD=AE+EF+DF=21x+40-2x+21x=40-x ……………………………（4分）∴S=21(40-2x+40-x)·23x=43x(80-3x)=3203432+-x (0＜x ＜20)…………………………………（6分）当S=393时，3203432+-x =393 解得：x 1=6,x 2=3220（舍去）.∴x=6………………………………（8分）②由题意，得40-x ≤24,解得x ≥16，结合①得16≤x ＜20………………………………………………………………（9分）由①，S=3203432+-x =33400)340(3432+--x ∵a=433-＜0 ∴函数图象为开口向下的抛物线的一段（附函数图象草图如左）.其对称轴为x=340，∵16＞340,由左图可知，当16≤x ＜20时，S 随x 的增大而减小……………………………（11分） ∴当x=16时，S 取得最大值，………………………………………（12分）此时S 最大值=312816320163432=⨯+⨯-.…………………（13分）28.（本小题13分）解:（1）C （-5，0）…………………………………………（3分）（2）①四边形ABCD 为矩形，理由如下：如图，由已知可得：A 、O 、C 在同一直线上，且 OA=OC ；B 、O 、D 在同一直线上，且OB=OD ，∴四边形ABCD 是平行四边形.…………………………………………………………（5分）∵∠OAB=∠OBA ∴OA=OB,即AC=2OA=2OB=BD∴四边形ABCD 是矩形.……………………………………（7分） ②如图，由①得四边形ABCD 是矩形∴∠CBA=∠ADC=90°………………………………………（8分）又AB=CD=6，AC=10∴由勾股定理，得BC=AD==2222610-=-AB AC =8…………………………………（9分）∵254.010=，14186=+，∴0≤t ≤14.……………………（10分）当0≤t ≤6时，P 点在AB 上，连结PQ. ∵AP 是直径，∴∠PQA=90°…………………………………（11分）又∠PAQ=∠CAB ，∴△PAQ ∽△CAB∴AB AQ CA PA =，即64.0106tt =-,解得t=3.6…………………………（12分）当6＜t ≤14时，P 点在AD 上，连结PQ ，同理得∠PQA=90°，△PAQ ∽△CAD ∴AD AQ CA PA =，即84.0106t t =-t-6,解得t=12. 综上所述，当动点Q 在以PA 为直径的圆上时，t 的值为3.6或12.……………………………………………………………（13分）四、附加题（共10分，每小题5分）1. 如：-1（答案不唯一）；2. 50.文档说明(Word 文档可以删除这部分)专注于精品小学试卷教案合同协议施工组织设计、期中、期末等测试文档解放你双手，时间就是生命，工作之外我们应该拥有更多享受生活的时间，本文档目的是为了节省读者的工作时间，提高读者的工作效率，读者可以放心下载文档进行编辑使用.文档来源网络，由于文档太多，审核有可能疏忽，如果有错误或侵权，请联系本店马上删除。

2019年福建省中考数学试题及参考答案(word解析版)

2019年福建省中考数学试题（满分150分，考试时间120分钟）第Ⅰ卷一、选择题：本题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合要求的。

1．计算22+（﹣1）0的结果是（）A．5 B．4 C．3 D．22．北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（）A．72×104B．7.2×105C．7.2×106D．0.72×1063．下列图形中，一定既是轴对称图形又是中心对称图形的是（）A．等边三角形B．直角三角形C．平行四边形D．正方形4．如图是由一个长方体和一个球组成的几何体，它的主视图是（）A．B．C．D．5．已知正多边形的一个外角为36°，则该正多边形的边数为（）A．12 B．10 C．8 D．66．如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（）A．甲的数学成绩高于班级平均分，且成绩比较稳定B．乙的数学成绩在班级平均分附近波动，且比丙好C．丙的数学成绩低于班级平均分，但成绩逐次提高D．就甲、乙、丙三个人而言，乙的数学成绩最不稳7．下列运算正确的是（）A．a•a3＝a3B．（2a）3＝6a3C．a6÷a3＝a2D．（a2）3﹣（﹣a3）2＝08．《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）A．x+2x+4x＝34685 B．x+2x+3x＝34685 C．x+2x+2x＝34685 D．x+x+x＝34685 9．如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）A．55°B．70°C．110°D．125°10．若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E （2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1第Ⅱ卷二、填空题：本题共6小题，每小题4分，共24分。

2019年福建省中考数学试题(原卷+解析)含答案

2019年福建省中考数学试卷一、选择题（每小题4分，共40分）1．（4分）计算22+（﹣1）0的结果是（）A．5B．4C．3D．22．（4分）北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（）A．72×104B．7.2×105C．7.2×106D．0.72×106 3．（4分）下列图形中，一定既是轴对称图形又是中心对称图形的是（）A．等边三角形B．直角三角形C．平行四边形D．正方形4．（4分）如图是由一个长方体和一个球组成的几何体，它的主视图是（）A．B．C．D．5．（4分）已知正多边形的一个外角为36°，则该正多边形的边数为（）A．12B．10C．8D．66．（4分）如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（）A．甲的数学成绩高于班级平均分，且成绩比较稳定B．乙的数学成绩在班级平均分附近波动，且比丙好C．丙的数学成绩低于班级平均分，但成绩逐次提高D．就甲、乙、丙三个人而言，乙的数学成绩最不稳7．（4分）下列运算正确的是（）A．a•a3＝a3B．（2a）3＝6a3C．a6÷a3＝a2D．（a2）3﹣（﹣a3）2＝08．（4分）《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）A．x+2x+4x＝34685B．x+2x+3x＝34685C．x+2x+2x＝34685D．x+x+x＝346859．（4分）如图，P A、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）A．55°B．70°C．110°D．125°10．（4分）若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1二、填空题（每小题4分，共24分）11．（4分）因式分解：x2﹣9＝．12．（4分）如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是．13．（4分）某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有人．14．（4分）在平面直角坐标系xOy中，▱OABC的三个顶点O（0，0）、A（3，0）、B（4，2），则其第四个顶点是．15．（4分）如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是．（结果保留π）16．（4分）如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k ＝．三、解答题（共86分）17．（8分）解方程组．18．（8分）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．19．（8分）先化简，再求值：（x﹣1）÷（x﹣），其中x＝+1．20．（8分）已知△ABC和点A'，如图．（1）以点A'为一个顶点作△A'B'C'，使△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC 面积的4倍；（要求：尺规作图，不写作法，保留作图痕迹）（2）设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点，求证：△DEF∽△D'E'F'．21．（8分）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．22．（10分）某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元．根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元．（1）求该车间的日废水处理量m；（2）为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围．23．（10分）某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；（2）试以这100机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？24．（12分）如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD 的延长线上，且DF＝DC，连接AF、CF．（1）求证：∠BAC＝2∠CAD；（2）若AF＝10，BC＝4，求tan∠BAD的值．25．（14分）已知抛物y＝ax2+bx+c（b＜0）与x轴只有一个公共点．（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．2019年福建省中考数学试卷参考答案与试题解析一、选择题（每小题4分，共40分）1．【分析】分别计算平方、零指数幂，然后再进行实数的运算即可．【解答】解：原式＝4+1＝5故选：A．2．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：将720000用科学记数法表示为7.2×105．故选：B．3．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、等边三角形是轴对称图形，不是中心对称图形，故本选项错误；B、直角三角形不是轴对称图形，也不是中心对称图形，故本选项错误；C、平行四边形不是轴对称图形，是中心对称图形，故本选项错误；D、正方形既是轴对称图形，又是中心对称图形，故此选项正确．故选：D．4．【分析】从正面看几何体，确定出主视图即可．【解答】解：几何体的主视图为：故选：C．5．【分析】利用多边形的外角和是360°，正多边形的每个外角都是36°，即可求出答案．【解答】解：360°÷36°＝10，所以这个正多边形是正十边形．故选：B．6．【分析】折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好【解答】解：A．甲的数学成绩高于班级平均分，且成绩比较稳定，正确；B．乙的数学成绩在班级平均分附近波动，且比丙好，正确；C．丙的数学成绩低于班级平均分，但成绩逐次提高，正确D．就甲、乙、丙三个人而言，丙的数学成绩最不稳，故D错误．故选：D．7．【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式＝a4，不符合题意；B、原式＝8a3，不符合题意；C、原式＝a3，不符合题意；D、原式＝0，符合题意，故选：D．8．【分析】设他第一天读x个字，根据题意列出方程解答即可．【解答】解：设他第一天读x个字，根据题意可得：x+2x+4x＝34685，故选：A．9．【分析】根据圆周角定理构造它所对的弧所对的圆心角，即连接OA，OB，求得∠AOB ＝110°，再根据切线的性质以及四边形的内角和定理即可求解．【解答】解：连接OA，OB，∵P A，PB是⊙O的切线，∴P A⊥OA，PB⊥OB，∵∠ACB＝55°，∴∠AOB＝110°，∴∠APB＝360°﹣90°﹣90°﹣110°＝70°．故选：B．10．【分析】由点A（m，n）、C（3﹣m，n）的对称性，可求函数的对称轴为x＝，再由B （0，y1）、D（，y2）、E（2，y3）与对称轴的距离，即可判断y1＞y3＞y2；【解答】解：∵经过A（m，n）、C（3﹣m，n），∴二次函数的对称轴x＝，∵B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离B最远，D最近，∵|a|＞0，∴y1＞y3＞y2；故选：D．二、填空题（每小题4分，共24分）11．【分析】原式利用平方差公式分解即可．【解答】解：原式＝（x+3）（x﹣3），故答案为：（x+3）（x﹣3）．12．【分析】根据A、B两点所表示的数分别为﹣4和2，利用中点公式求出线段AB的中点所表示的数即可．【解答】解：∵数轴上A，B两点所表示的数分别是﹣4和2，∴线段AB的中点所表示的数＝（﹣4+2）＝﹣1．即点C所表示的数是﹣1．故答案为：﹣113．【分析】用总人数乘以样本中喜欢甲图案的频率即可求得总体中喜欢甲图案的人数．【解答】解：由题意得：2000×＝1200人，故答案为：1200．14．【分析】由题意得出OA＝3，由平行四边形的性质得出BC∥OA，BC＝OA＝3，即可得出结果．【解答】解：∵O（0，0）、A（3，0），∴OA＝3，∵四边形OABC是平行四边形，∴BC∥OA，BC＝OA＝3，∵B（4，2），∴点C的坐标为（4﹣3，2），即C（1，2）；故答案为：（1，2）．15．【分析】延长DC，CB交⊙O于M，N，根据圆和正方形的面积公式即可得到结论．【解答】解：延长DC，CB交⊙O于M，N，则图中阴影部分的面积＝×（S圆O﹣S正方形ABCD）＝×（4π﹣4）＝π﹣1，故答案为：π﹣1．16．【分析】连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG⊥x轴于点G，得O、A、C在第一象限的角平分线上，求得A点坐标，进而求得D 点坐标，便可求得结果．【解答】解：连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D 作DG⊥x轴于点G，∵函数y＝（k＞3，x＞0）的图象关于直线AC对称，∴O、A、C三点在同直线上，且∠COE＝45°，∴OE＝AE，不妨设OE＝AE＝a，则A（a，a），∵点A在在反比例函数y＝（x＞0）的图象上，∴a2＝3，∴a＝，∴AE＝OE＝，∵∠BAD＝30°，∴∠OAF＝∠CAD＝∠BAD＝15°，∵∠OAE＝∠AOE＝45°，∴∠EAF＝30°，∴AF＝，EF＝AE tan30°＝1，∵AB＝AD＝2，AE∥DG，∴EF＝EG＝1，DG＝2AE＝2，∴OG＝OE+EG＝+1，∴D（+1，2），故答案为：6+2．三、解答题（共86分）17．【分析】方程组利用加减消元法求出解即可．【解答】解：，①+②得：3x＝9，即x＝3，把x＝3代入①得：y＝﹣2，则方程组的解为．18．【分析】由SAS证明△ADF≌△BCE，即可得出AF＝CE．【解答】证明：∵四边形ABCD是矩形，∴∠D＝∠B＝90°，AD＝BC，在△ADF和△BCE中，，∴△ADF≌△BCE（SAS），∴AF＝CE．19．【分析】先化简分式，然后将x的值代入计算即可．【解答】解：原式＝（x﹣1）÷＝（x﹣1）•＝，当x＝+1，原式＝＝1+．20．【分析】（1）分别作A'C'＝2AC、A'B'＝2AB、B'C'＝2BC得△A'B'C'即可所求．（2）根据中位线定理易得∴△DEF∽△ABC，△D'E'F'∽△A'B'C'，故△DEF∽△D'E'F'【解答】解：（1）作线段A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，得△A'B'C'即可所求．证明：∵A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，∴△ABC∽△A′B′C′，∴（2）证明：∵D、E、F分别是△ABC三边AB、BC、AC的中点，∴DE＝，，，∴△DEF∽△ABC同理：△D'E'F'∽△A'B'C'，由（1）可知：△ABC∽△A′B′C′，∴△DEF∽△D'E'F'．21．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC 上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝25°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．22．【分析】（1）求出该车间处理35吨废水所需费用，将其与350比较后可得出m＜35，根据废水处理费用＝该车间处理m吨废水的费用+第三方处理超出部分废水的费用，即可得出关于m的一元一次方程，解之即可得出结论；（2）设一天产生工业废水x吨，分0＜x≤20及x＞20两种情况考虑，利用每天废水处理的平均费用不超过10元/吨，可得出关于x的一元一次不等式，解之即可得出结论．【解答】解：（1）∵35×8+30＝310（元），310＜350，∴m＜35．依题意，得：30+8m+12（35﹣m）＝370，解得：m＝20．答：该车间的日废水处理量为20吨．（2）设一天产生工业废水x吨，当0＜x≤20时，8x+30≤10x，解得：15≤x≤20；当x＞20时，12（x﹣20）+8×20+30≤10x，解得：20＜x≤25．综上所述，该厂一天产生的工业废水量的范围为15≤x≤20．23．【分析】（1）利用概率公式计算即可．（2）分别求出购买10次，11次的费用即可判断．【解答】解：（1）“1台机器在三年使用期内维修次数不大于10”的概率＝＝0.6．（2）购买10次时，此时这100台机器维修费用的平均数y1＝（24000×10+24500×20+25000×30+30000×30+35000×10）＝27300购买11次时，此时这100台机器维修费用的平均数y2＝（26000×10+26500×20+27000×30+27500×30+32500×10）＝27500，∵27300＜27500，所以，选择购买10次维修服务．24．【分析】（1）根据等腰三角形的性质得出∠ABC＝∠ACB，根据圆心角、弧、弦的关系得到＝，即可得到∠ABC＝∠ADB，根据三角形内角和定理得到∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∠ADB＝90°﹣∠CAD，从而得到∠BAC＝∠CAD，即可证得结论；（2）易证得BC＝CF＝4，即可证得AC垂直平分BF，证得AB＝AF＝10，根据勾股定理求得AE、CE、BE，根据相交弦定理求得DE，即可求得BD，然后根据三角形面积公式求得DH，进而求得AH，解直角三角函数求得tan∠BAD的值．【解答】解：（1）∵AB＝AC，∴＝，∠ABC＝∠ACB，∴∠ABC＝∠ADB，∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∵BD⊥AC，∴∠ADB＝90°﹣∠CAD，∴∠BAC＝∠CAD，∴∠BAC＝2∠CAD；（2）解：∵DF＝DC，∴∠DFC＝∠DCF，∴∠BDC＝2∠DFC，∴∠BFC＝∠BDC＝∠BAC＝∠FBC，∴CB＝CF，又BD⊥AC，∴AC是线段BF的中垂线，AB＝AF＝10，AC＝10．又BC＝4，设AE＝x，CE＝10﹣x，由AB2﹣AE2＝BC2﹣CE2，得100﹣x2＝80﹣（10﹣x）2，解得x＝6，∴AE＝6，BE＝8，CE＝4，∴DE＝＝＝3，∴BD＝BE+DE＝3+8＝11，作DH⊥AB，垂足为H，∵AB•DH＝BD•AE，∴DH＝＝＝，∴BH＝＝，∴AH＝AB﹣BH＝10﹣＝，∴tan∠BAD＝＝＝．25．【分析】（1）抛物线与x轴的公共点坐标即为函数顶点坐标，即可求解；（2）①y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），即可求解；②计算直线AD表达式中的k值、直线AC表达式中的k值，两个k值相等即可求解．【解答】解：（1）抛物线与x轴的公共点坐标即为函数顶点坐标，故：y＝a（x﹣2）2＝ax2﹣4ax+4a，则c＝4a；（2）y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），又△ABC为等腰直角三角形，∴点A为抛物线的顶点；①c＝1，顶点A（1，0），抛物线的解析式：y＝x2﹣2x+1，②，x2﹣（2+k）x+k＝0，x＝（2+k±），x D＝x B＝（2+k﹣），y D＝﹣1；则D，y C＝（2+k2+k，C，A（1，0），∴直线AD表达式中的k值为：k AD＝＝，直线AC表达式中的k值为：k AC＝，∴k AD＝k AC，点A、C、D三点共线．。

2019年福建省中考数学试卷和答案解析

2019年福建省中考数学试卷一、选择题（每小题4分，共40分）1．（4分）（2019•福建）计算22+（﹣1）0的结果是（）A．5 B．4 C．3 D．22．（4分）（2019•福建）北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（）A．72×104B．7.2×105C．7.2×106D．0.72×1063．（4分）（2019•福建）下列图形中，一定既是轴对称图形又是中心对称图形的是（）A．等边三角形B．直角三角形C．平行四边形D．正方形4．（4分）（2019•福建）如图是由一个长方体和一个球组成的几何体，它的主视图是（）A．B．C．D．5．（4分）（2019•福建）已知正多边形的一个外角为36°，则该正多边形的边数为（）A．12 B．10 C．8 D．66．（4分）（2019•福建）如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（）A．甲的数学成绩高于班级平均分，且成绩比较稳定B．乙的数学成绩在班级平均分附近波动，且比丙好C．丙的数学成绩低于班级平均分，但成绩逐次提高D．就甲、乙、丙三个人而言，乙的数学成绩最不稳7．（4分）（2019•福建）下列运算正确的是（）A．a•a3＝a3B．（2a）3＝6a3C．a6÷a3＝a2D．（a2）3﹣（﹣a3）2＝08．（4分）（2019•福建）《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）A．x+2x+4x＝34685 B．x+2x+3x＝34685C．x+2x+2x＝34685 D．x+x+x＝346859．（4分）（2019•福建）如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB ＝55°，则∠APB等于（）A．55°B．70°C．110°D．125°10．（4分）（2019•福建）若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C （3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1二、填空题（每小题4分，共24分）11．（4分）（2019•福建）因式分解：x2﹣9＝．12．（4分）（2019•福建）如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是．13．（4分）（2019•福建）某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有人．14．（4分）（2019•福建）在平面直角坐标系xOy中，▱OABC的三个顶点O（0，0）、A（3，0）、B（4，2），则其第四个顶点是．15．（4分）（2019•福建）如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是．（结果保留π）16．（4分）（2019•福建）如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y ＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k＝．三、解答题（共86分）17．（8分）（2019•福建）解方程组．18．（8分）（2019•福建）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．19．（8分）（2019•福建）先化简，再求值：（x﹣1）÷（x﹣），其中x＝+1．20．（8分）（2019•福建）已知△ABC和点A'，如图．（1）以点A'为一个顶点作△A'B'C'，使△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC 面积的4倍；（要求：尺规作图，不写作法，保留作图痕迹）（2）设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点，求证：△DEF∽△D'E'F'．21．（8分）（2019•福建）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．22．（10分）（2019•福建）某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元．根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元．（1）求该车间的日废水处理量m；（2）为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围．23．（10分）（2019•福建）某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；维修次数8 9 10 11 12频率（台数）10 20 30 30 10（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；（2）试以这100机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？24．（12分）（2019•福建）如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD的延长线上，且DF＝DC，连接AF、CF．（1）求证：∠BAC＝2∠CAD；（2）若AF＝10，BC＝4，求tan∠BAD的值．25．（14分）（2019•福建）已知抛物y＝ax2+bx+c（b＜0）与x轴只有一个公共点．（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．2019年福建省中考数学试卷参考答案与试题解析一、选择题（每小题4分，共40分）1．（4分）（2019•福建）计算22+（﹣1）0的结果是（）A．5 B．4 C．3 D．2【考点】有理数的加法；有理数的乘方；零指数幂．【分析】分别计算平方、零指数幂，然后再进行实数的运算即可．【解答】解：原式＝4+1＝5故选：A．2．（4分）（2019•福建）北京故宫的占地面积约为720000m2，将720000用科学记数法表示为（）A．72×104B．7.2×105C．7.2×106D．0.72×106【考点】科学记数法—表示较大的数．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：将720000用科学记数法表示为7.2×105．故选：B．3．（4分）（2019•福建）下列图形中，一定既是轴对称图形又是中心对称图形的是（）A．等边三角形B．直角三角形C．平行四边形D．正方形【考点】轴对称图形；中心对称图形．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、等边三角形是轴对称图形，不是中心对称图形，故本选项错误；B、直角三角形不是轴对称图形，也不是中心对称图形，故本选项错误；C、平行四边形不是轴对称图形，是中心对称图形，故本选项错误；D、正方形既是轴对称图形，又是中心对称图形，故此选项正确．故选：D．4．（4分）（2019•福建）如图是由一个长方体和一个球组成的几何体，它的主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】从正面看几何体，确定出主视图即可．【解答】解：几何体的主视图为：故选：C．5．（4分）（2019•福建）已知正多边形的一个外角为36°，则该正多边形的边数为（）A．12 B．10 C．8 D．6【考点】多边形内角与外角．【分析】利用多边形的外角和是360°，正多边形的每个外角都是36°，即可求出答案．【解答】解：360°÷36°＝10，所以这个正多边形是正十边形．故选：B．6．（4分）（2019•福建）如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图，则下列判断错误的是（）A．甲的数学成绩高于班级平均分，且成绩比较稳定B．乙的数学成绩在班级平均分附近波动，且比丙好C．丙的数学成绩低于班级平均分，但成绩逐次提高D．就甲、乙、丙三个人而言，乙的数学成绩最不稳【考点】折线统计图；方差．【分析】折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好【解答】解：A．甲的数学成绩高于班级平均分，且成绩比较稳定，正确；B．乙的数学成绩在班级平均分附近波动，且比丙好，正确；C．丙的数学成绩低于班级平均分，但成绩逐次提高，正确D．就甲、乙、丙三个人而言，丙的数学成绩最不稳，故D错误．故选：D．7．（4分）（2019•福建）下列运算正确的是（）A．a•a3＝a3B．（2a）3＝6a3C．a6÷a3＝a2D．（a2）3﹣（﹣a3）2＝0【考点】合并同类项；同底数幂的乘法；幂的乘方与积的乘方；同底数幂的除法．【分析】各项计算得到结果，即可作出判断．【解答】解：A、原式＝a4，不符合题意；B、原式＝8a3，不符合题意；C、原式＝a3，不符合题意；D、原式＝0，符合题意，故选：D．8．（4分）（2019•福建）《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）A．x+2x+4x＝34685 B．x+2x+3x＝34685C．x+2x+2x＝34685 D．x+x+x＝34685【考点】由实际问题抽象出一元一次方程．【分析】设他第一天读x个字，根据题意列出方程解答即可．【解答】解：设他第一天读x个字，根据题意可得：x+2x+4x＝34685，故选：A．9．（4分）（2019•福建）如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB ＝55°，则∠APB等于（）A．55°B．70°C．110°D．125°【考点】圆周角定理；切线的性质．【分析】根据圆周角定理构造它所对的弧所对的圆心角，即连接OA，OB，求得∠AOB＝110°，再根据切线的性质以及四边形的内角和定理即可求解．【解答】解：连接OA，OB，∵PA，PB是⊙O的切线，∴PA⊥OA，PB⊥OB，∵∠ACB＝55°，∴∠AOB＝110°，∴∠APB＝360°﹣90°﹣90°﹣110°＝70°．故选：B．10．（4分）（2019•福建）若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C （3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1【考点】二次函数图象上点的坐标特征．【分析】由点A（m，n）、C（3﹣m，n）的对称性，可求函数的对称轴为x＝，再由B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离，即可判断y1＞y3＞y2；【解答】解：∵经过A（m，n）、C（3﹣m，n），∴二次函数的对称轴x＝，∵B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离B最远，D最近，∵|a|＞0，∴y1＞y3＞y2；故选：D．二、填空题（每小题4分，共24分）11．（4分）（2019•福建）因式分解：x2﹣9＝（x+3）（x﹣3）．【考点】因式分解﹣运用公式法．【分析】原式利用平方差公式分解即可．【解答】解：原式＝（x+3）（x﹣3），故答案为：（x+3）（x﹣3）．12．（4分）（2019•福建）如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是﹣1 ．【考点】数轴．【分析】根据A、B两点所表示的数分别为﹣4和2，利用中点公式求出线段AB的中点所表示的数即可．【解答】解：∵数轴上A，B两点所表示的数分别是﹣4和2，∴线段AB的中点所表示的数＝（﹣4+2）＝﹣1．即点C所表示的数是﹣1．故答案为：﹣113．（4分）（2019•福建）某校征集校运会会徽，遴选出甲、乙、丙三种图案．为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人，根据所学的统计知识可以估计该校喜欢甲图案的学生有1200 人．【考点】用样本估计总体．【分析】用总人数乘以样本中喜欢甲图案的频率即可求得总体中喜欢甲图案的人数．【解答】解：由题意得：2000×＝1200人，故答案为：1200．14．（4分）（2019•福建）在平面直角坐标系xOy中，▱OABC的三个顶点O（0，0）、A（3，0）、B（4，2），则其第四个顶点是（1，2）．【考点】坐标与图形性质；平行四边形的性质．【分析】由题意得出OA＝3，由平行四边形的性质得出BC∥OA，BC＝OA＝3，即可得出结果．【解答】解：∵O（0，0）、A（3，0），∴OA＝3，∵四边形OABC是平行四边形，∴BC∥OA，BC＝OA＝3，∵B（4，2），∴点C的坐标为（4﹣3，2），即C（1，2）；故答案为：（1，2）．15．（4分）（2019•福建）如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是π﹣1 ．（结果保留π）【考点】正方形的性质；扇形面积的计算．【分析】延长DC，CB交⊙O于M，N，根据圆和正方形的面积公式即可得到结论．【解答】解：延长DC，CB交⊙O于M，N，则图中阴影部分的面积＝×（S圆O﹣S正方形ABCD）＝×（4π﹣4）＝π﹣1，故答案为：π﹣1．16．（4分）（2019•福建）如图，菱形ABCD顶点A在函数y＝（x＞0）的图象上，函数y ＝（k＞3，x＞0）的图象关于直线AC对称，且经过点B、D两点，若AB＝2，∠BAD＝30°，则k＝6+2．【考点】反比例函数与一次函数的交点问题．【分析】连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG⊥x 轴于点G，得O、A、C在第一象限的角平分线上，求得A点坐标，进而求得D点坐标，便可求得结果．【解答】解：连接OC，AC过A作AE⊥x轴于点E，延长DA与x轴交于点F，过点D作DG ⊥x轴于点G，∵函数y＝（k＞3，x＞0）的图象关于直线AC对称，∴O、A、C三点在同直线上，且∠COE＝45°，∴OE＝AE，不妨设OE＝AE＝a，则A（a，a），∵点A在在反比例函数y＝（x＞0）的图象上，∴a2＝3，∴a＝，∴AE＝OE＝，∵∠BAD＝30°，∴∠OAF＝∠CAD＝∠BAD＝15°，∵∠OAE＝∠AOE＝45°，∴∠EAF＝30°，∴AF＝，EF＝AE tan30°＝1，∵AB＝AD＝2，AE∥DG，∴EF＝EG＝1，DG＝2AE＝2，∴OG＝OE+EG＝+1，∴D（+1，2），故答案为：6+2．三、解答题（共86分）17．（8分）（2019•福建）解方程组．【考点】解二元一次方程组．【分析】方程组利用加减消元法求出解即可．【解答】解：，①+②得：3x＝9，即x＝3，把x＝3代入①得：y＝﹣2，则方程组的解为．18．（8分）（2019•福建）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．【考点】全等三角形的判定与性质；矩形的性质．【分析】由SAS证明△ADF≌△BCE，即可得出AF＝CE．【解答】证明：∵四边形ABCD是矩形，∴∠D＝∠B＝90°，AD＝BC，在△ADF和△BCE中，，∴△ADF≌△BCE（SAS），∴AF＝CE．19．（8分）（2019•福建）先化简，再求值：（x﹣1）÷（x﹣），其中x＝+1．【考点】分式的化简求值．【分析】先化简分式，然后将x的值代入计算即可．【解答】解：原式＝（x﹣1）÷＝（x﹣1）•＝，当x＝+1，原式＝＝1+．20．（8分）（2019•福建）已知△ABC和点A'，如图．（1）以点A'为一个顶点作△A'B'C'，使△A'B'C'∽△ABC，且△A'B'C'的面积等于△ABC 面积的4倍；（要求：尺规作图，不写作法，保留作图痕迹）（2）设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点，求证：△DEF∽△D'E'F'．【考点】三角形的面积；三角形中位线定理；作图—复杂作图；相似三角形的判定．【分析】（1）分别作A'C'＝2AC、A'B'＝2AB、B'C'＝2BC得△A'B'C'即可所求．（2）根据中位线定理易得∴△DEF∽△ABC，△D'E'F'∽△A'B'C'，故△DEF∽△D'E'F' 【解答】解：（1）作线段A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，得△A'B'C'即可所求．证明：∵A'C'＝2AC、A'B'＝2AB、B'C'＝2BC，∴△ABC∽△A′B′C′，∴（2）证明：∵D、E、F分别是△ABC三边AB、BC、AC的中点，∴DE＝，，，∴△DEF∽△ABC同理：△D'E'F'∽△A'B'C'，由（1）可知：△ABC∽△A′B′C′，∴△DEF∽△D'E'F'．21．（8分）（2019•福建）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．（1）当点E恰好在AC上时，如图1，求∠ADE的大小；（2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．【考点】平行四边形的判定；旋转的性质．【分析】（1）如图1，利用旋转的性质得CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC ＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余和计算出∠ADE的度数；（2）如图2，利用直角三角形斜边上的中线性质得到BF＝AC，利用含30度的直角三角形三边的关系得到AB＝AC，则BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，从而得到DE＝BF，△ACD和△BCE为等边三角形，接着证明△CFD≌△ABC得到DF＝BC，然后根据平行四边形的判定方法得到结论．【解答】（1）解：如图1，∵△ABC绕点A顺时针旋转α得到△DEC，点E恰好在AC上，∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°，∵CA＝CD，∴∠CAD＝∠CDA＝（180°﹣30°）＝75°，∴∠ADE＝90°﹣75°＝15°；（2）证明：如图2，∵点F是边AC中点，∴BF＝AC，∵∠ACB＝30°，∴AB＝AC，∴BF＝AB，∵△ABC绕点A顺时针旋转60得到△DEC，∴∠BCE＝∠ACD＝60°，CB＝CE，DE＝AB，∴DE＝BF，△ACD和△BCE为等边三角形，∴BE＝CB，∵点F为△ACD的边AC的中点，∴DF⊥AC，易证得△CFD≌△ABC，∴DF＝BC，∴DF＝BE，而BF＝DE，∴四边形BEDF是平行四边形．22．（10分）（2019•福建）某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元．根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元．（1）求该车间的日废水处理量m；（2）为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围．【考点】一元一次方程的应用；一元一次不等式的应用．【分析】（1）求出该车间处理35吨废水所需费用，将其与350比较后可得出m＜35，根据废水处理费用＝该车间处理m吨废水的费用+第三方处理超出部分废水的费用，即可得出关于m的一元一次方程，解之即可得出结论；（2）设一天产生工业废水x吨，分0＜x≤20及x＞20两种情况考虑，利用每天废水处理的平均费用不超过10元/吨，可得出关于x的一元一次不等式，解之即可得出结论．【解答】解：（1）∵35×8+30＝310（元），310＜350，∴m＜35．依题意，得：30+8m+12（35﹣m）＝370，解得：m＝20．答：该车间的日废水处理量为20吨．（2）设一天产生工业废水x吨，当0＜x≤20时，8x+30≤10x，解得：15≤x≤20；当x＞20时，12（x﹣20）+8×20+30≤10x，解得：20＜x≤25．综上所述，该厂一天产生的工业废水量的范围为15≤x≤20．23．（10分）（2019•福建）某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；维修次数8 9 10 11 12频率（台数）10 20 30 30 10（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；（2）试以这100机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？【考点】总体、个体、样本、样本容量；用样本估计总体；加权平均数；列表法与树状图法；利用频率估计概率．【分析】（1）利用概率公式计算即可．（2）分别求出购买10次，11次的费用即可判断．【解答】解：（1）“1台机器在三年使用期内维修次数不大于10”的概率＝＝0.6．（2）购买10次时，某台机器使用期内维修次数8 9 10 11 12 该台机器维修费用24000 24500 25000 30000 35000 此时这100台机器维修费用的平均数y1＝（24000×10+24500×20+25000×30+30000×30+35000×10）＝27300购买11次时，某台机器使用期内维修次数8 9 10 11 12该台机器维修费用26000 26500 27000 27500 32500 此时这100台机器维修费用的平均数y2＝（26000×10+26500×20+27000×30+27500×30+32500×10）＝27500，∵27300＜27500，所以，选择购买10次维修服务．24．（12分）（2019•福建）如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD的延长线上，且DF＝DC，连接AF、CF．（1）求证：∠BAC＝2∠CAD；（2）若AF＝10，BC＝4，求tan∠BAD的值．【考点】等腰直角三角形；圆心角、弧、弦的关系；圆周角定理；解直角三角形．【分析】（1）根据等腰三角形的性质得出∠ABC＝∠ACB，根据圆心角、弧、弦的关系得到＝，即可得到∠ABC＝∠ADB，根据三角形内角和定理得到∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∠ADB＝90°﹣∠CAD，从而得到∠BAC＝∠CAD，即可证得结论；（2）易证得BC＝CF＝4，即可证得AC垂直平分BF，证得AB＝AF＝10，根据勾股定理求得AE、CE、BE，根据相交弦定理求得DE，即可求得BD，然后根据三角形面积公式求得DH，进而求得AH，解直角三角函数求得tan∠BAD的值．【解答】解：（1）∵AB＝AC，∴＝，∠ABC＝∠ACB，∴∠ABC＝∠ADB，∠ABC＝（180°﹣∠BAC）＝90°﹣∠BAC，∵BD⊥AC，∴∠ADB＝90°﹣∠CAD，∴∠BAC＝∠CAD，∴∠BAC＝2∠CAD；（2）解：∵DF＝DC，∴∠DFC＝∠DCF，∴∠BDC＝2∠DFC，∴∠BFC＝∠BDC＝∠BAC＝∠FBC，∴CB＝CF，又BD⊥AC，∴AC是线段BF的中垂线，AB＝AF＝10，AC＝10．又BC＝4，设AE＝x，CE＝10﹣x，由AB2﹣AE2＝BC2﹣CE2，得100﹣x2＝80﹣（10﹣x）2，解得x＝6，∴AE＝6，BE＝8，CE＝4，∴DE＝＝＝3，∴BD＝BE+DE＝3+8＝11，作DH⊥AB，垂足为H，∵AB•DH＝BD•AE，∴DH＝＝＝，∴BH＝＝，∴AH＝AB﹣BH＝10﹣＝，∴tan∠BAD＝＝＝．25．（14分）（2019•福建）已知抛物y＝ax2+bx+c（b＜0）与x轴只有一个公共点．（1）若抛物线与x轴的公共点坐标为（2，0），求a、c满足的关系式；（2）设A为抛物线上的一定点，直线l：y＝kx+1﹣k与抛物线交于点B、C，直线BD垂直于直线y＝﹣1，垂足为点D．当k＝0时，直线l与抛物线的一个交点在y轴上，且△ABC为等腰直角三角形．①求点A的坐标和抛物线的解析式；②证明：对于每个给定的实数k，都有A、D、C三点共线．【考点】二次函数综合题．【分析】（1）抛物线与x轴的公共点坐标即为函数顶点坐标，即可求解；（2）①y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），即可求解；②计算直线AD表达式中的k值、直线AC表达式中的k值，两个k值相等即可求解．【解答】解：（1）抛物线与x轴的公共点坐标即为函数顶点坐标，故：y＝a（x﹣2）2＝ax2﹣4ax+4a，则c＝4a；（2）y＝kx+1﹣k＝k（x﹣1）+1过定点（1，1），且当k＝0时，直线l变为y＝1平行x轴，与轴的交点为（0，1），又△ABC为等腰直角三角形，∴点A为抛物线的顶点；①c＝1，顶点A（1，0），抛物线的解析式：y＝x2﹣2x+1，②，x2﹣（2+k）x+k＝0，x＝（2+k±），x D＝x B＝（2+k﹣），y D＝﹣1；则D，y C＝（2+k2+k，C，A（1，0），∴直线AD表达式中的k值为：k AD＝＝，直线AC表达式中的k值为：k AC＝，∴k AD＝k AC，点A、C、D三点共线．。