2019-2020年高考数学一轮复习第8章平面解析几何第6讲双曲线增分练
2020版高考数学大一轮复习第八章平面解析几何第6节双曲线讲义理含解析新人教A版
第节 双曲线考试要求 了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线).知 识 梳 理.双曲线的定义平面内与两个定点，(＝＞)的距离差的绝对值等于常数(小于且大于零)的点的轨迹叫双曲线.这两个定点叫双曲线的焦点，两焦点间的距离叫焦距.其数学表达式：集合＝{－＝}，＝，其中，为常数且>，>：()若<时，则集合为双曲线；()若＝时，则集合为两条射线；()若>时，则集合为空集..双曲线的标准方程和几何性质[微点提醒].过双曲线的一个焦点且与实轴垂直的弦的长为..离心率＝＝＝..等轴双曲线的渐近线互相垂直，离心率等于.基础自测.判断下列结论正误(在括号内打“√”或“×”)()平面内到点(，)，(，－)距离之差的绝对值等于的点的轨迹是双曲线.( )()平面内到点(，)，(，－)距离之差等于的点的轨迹是双曲线.( )()方程－＝(>)表示焦点在轴上的双曲线.( )()双曲线－＝λ(>，>，λ≠)的渐近线方程是±＝.( )()若双曲线－＝(>，>)与－＝(>，>)的离心率分别是，，则)＋)＝(此条件中两条双曲线称为共轭双曲线).( )解析()因为－＝＝，表示的轨迹为两条射线.()由双曲线的定义知，应为双曲线的一支，而非双曲线的全部.()当＞，＞时表示焦点在轴上的双曲线，而＜，＜时则表示焦点在轴上的双曲线.答案()×()×()×()√()√.(选修－改编)经过点(，－)，且对称轴都在坐标轴上的等轴双曲线方程为.解析设双曲线方程为：－＝λ(λ≠)，把点(，－)代入，得λ＝，故所求双曲线方程为－＝.答案－＝.(选修－改编)已知双曲线－＝上一点到它的一个焦点的距离等于，那么点到另一个焦点的距离等于.解析设双曲线的焦点为，，＝，则－＝，故＝或，又双曲线上的点到焦点的距离的最小值为－＝－，故＝.答案.(·浙江卷)双曲线－＝的焦点坐标是( ).(－，)，(，) .(－，)，(，).(，－)，(，) .(，－)，(，)解析由题可知双曲线的焦点在轴上，又＝＋＝＋＝，所以＝，故焦点坐标为(－，)，(，). 答案.(·全国Ⅲ卷)双曲线－＝(>)的一条渐近线方程为＝，则＝.解析由题意可得＝，所以＝.答案.(·北京卷)若双曲线－＝(>)的离心率为，则＝.解析由题意可得，＝，即＝，又>，所以＝.答案考点一双曲线的定义及应用【例】 ()已知，为双曲线：－＝的左、右焦点，点在上，＝，则∠＝( )()(·济南调研)已知圆：(＋)＋＝和圆：(－)＋＝，动圆同时与圆及圆相外切，则动圆圆心的轨迹方程为.解析()由－＝，知＝＝，＝.由双曲线定义知，－＝＝，又＝，∴＝，＝，在△中，＝＝，由余弦定理，得∠＝＝.()如图所示，设动圆与圆及圆分别外切于和.根据两圆外切的条件，得－＝，－＝，因为＝，所以－＝－，所以点到两定点，的距离的差是常数且小于＝.又根据双曲线的定义，得动点的轨迹为双曲线的左支(点与的距离大，与的距离小)，其中＝，＝，则＝.故点的轨迹方程为－＝(≤－).答案() ()－＝(≤－)规律方法.利用双曲线的定义判定平面内动点的轨迹是否为双曲线，进而根据要求可求出曲线方程；.在“焦点三角形”中，常利用正弦定理、余弦定理，经常结合－＝，运用平方的方法，建立与，的联系.【训练】 ()已知双曲线：－＝(>，>)的离心率为，左、右焦点分别为，，点在双曲线上，若△的周长为，则△的面积为( )()(·杭州质检)双曲线的渐近线方程为＝±，一个焦点为(，－)，点(，)，点为双曲线第一象限内的点，则当点的位置变化时，△周长的最小值为( )＋＋解析()由双曲线的对称性不妨设在双曲线的右支上，由＝＝，得＝，∴△的周长为＋＋＝＋＋，又△的周长为，∴＋＝，又∵－＝，∴＝，＝，在△中，＝，∴ ∠＝＝＝.又<∠<π，∴ ∠＝，∴△＝·· ∠＝×××＝.()由已知得双曲线方程为－＝，设双曲线的另一个焦点为′，则＝′＋，△的周长为＋＋＝′＋＋＋，当′，，三点共线时，′＋有最小值，为′＝，故△的周长的最小值为.答案() ()考点二双曲线的标准方程【例】()(·全国Ⅲ卷)已知双曲线：－＝(>，>)的一条渐近线方程为＝，且与椭圆＋＝有公共焦点，则的方程为( )－＝－＝()(·天津卷)已知双曲线－＝(>，>)的离心率为，过右焦点且垂直于轴的直线与双曲线交于，两点.设，到双曲线的同一条渐近线的距离分别为和，且＋＝，则双曲线的方程为( ) －＝－＝－＝－＝解析()由题设知＝，①又由椭圆＋＝与双曲线有公共焦点，易知＋＝＝，②由①②解得＝，＝，则双曲线的方程为－＝.()由＋＝，得双曲线的右焦点到渐近线的距离为，所以＝.因为双曲线－＝(>，>)的离心率为，所以＝，所以＝，所以＝，解得＝，所以双曲线的方程为－＝.答案() ()规律方法.利用待定系数法求双曲线标准方程的关键是：设出双曲线方程的标准形式，根据已知条件，列出关于参数，，的方程并求出，，的值..与双曲线－＝有相同渐近线时可设所求双曲线方程为－＝λ(λ≠).【训练】()(·海南二模)已知双曲线：－＝(>，>)过点(，)，且实轴的两个端点与虚轴的一个端点组成一个等边三角形，则双曲线的标准方程是( )－＝－＝－＝－＝()已知双曲线的渐近线方程为±＝，且双曲线经过点(，)，则双曲线的方程为.解析()由双曲线：－＝(>，>)过点(，)，且实轴的两个端点与虚轴的一个端点组成一个等边三角形，可得解得∴双曲线的标准方程是－＝.()由双曲线的渐近线方程为＝±，可设双曲线方程为－＝λ(λ≠).因为双曲线过点(，)，所以－＝λ，λ＝－，故所求双曲线方程为－＝.答案() ()－＝考点三双曲线的性质多维探究角度求双曲线的渐近线【例－】 (一题多解)(·全国Ⅱ卷)双曲线－＝(>，>)的离心率为，则其渐近线方程为( ) ＝±＝±＝±＝±解析法一由题意知，＝＝，所以＝，所以＝＝，即＝，所以该双曲线的渐近线方程为＝±＝±.法二由＝＝＝，得＝，所以该双曲线的渐近线方程为＝±＝±.答案角度求双曲线的离心率【例－】()(·全国Ⅲ卷)设，是双曲线：－＝(>，>)的左、右焦点，是坐标原点.过作的一条渐近线的垂线，垂足为.若＝，则的离心率为( )()(·泰安联考)已知双曲线：－＝(>，>)，圆：＋－＋＝，若双曲线的一条渐近线与圆有两个不同的交点，则双曲线的离心率的取值范围是( ).(，) .(，＋∞)解析()不妨设一条渐近线的方程为＝，则到＝的距离＝＝，在△中，＝，所以＝，所以＝，又＝，所以在△与△中，根据余弦定理得∠＝＝－∠＝－，则＋－()＝，得＝，所以＝＝.()由双曲线方程可得其渐近线方程为＝±，即±＝，圆：＋－＋＝可化为(－)＋＝，圆心的坐标为(，)，半径＝，由双曲线的一条渐近线与圆有两个不同的交点，得<，即>，即>，又知＝－，所以>(－)，即<，所以＝<，又知>，所以双曲线的离心率的取值范围为.答案() ()角度与双曲线有关的范围(最值)问题【例－】已知(，)是双曲线：－＝上的一点，，是的两个焦点，若·<，则的取值范围是( )解析因为(－，)，(，)，)－＝，所以·＝(－－，－)·(－，－)＝＋－<，即－<，解得－<<.答案规律方法.求双曲线离心率或其取值范围的方法()求，，的值，由＝＝＋直接求.()列出含有，，的齐次方程(或不等式)，借助于＝－消去，然后转化成关于的方程(或不等式)求解..与双曲线有关的取值范围问题的解题思路()若条件中存在不等关系，则借助此关系直接变换转化求解.()若条件中没有不等关系，要善于发现隐含的不等关系或借助曲线中不等关系来解决. 【训练】()(·上海崇明区调研)在平面直角坐标系中，双曲线：－＝(>，>)的一条渐近线与圆(－)＋(－)＝相切，则的离心率为( )()已知焦点在轴上的双曲线＋＝，它的焦点到渐近线的距离的取值范围是.解析()双曲线的渐近线方程为±＝，结合图形易知与圆相切的只可能是－＝，又圆心坐标为(，)，则＝，得＝，所以＝＝(－)，则＝，又>，故＝.()对于焦点在轴上的双曲线－＝(>，>)，它的一个焦点(，)到渐近线－＝的距离为＝.本题中，双曲线＋＝即－＝，其焦点在轴上，则解得<<，则焦点到渐近线的距离＝∈(，).答案() ()(，)[思维升华].与双曲线－＝ (>，>)有公共渐近线的双曲线的方程可设为－＝(≠)..已知双曲线的标准方程求双曲线的渐近线方程时，只要令双曲线的标准方程中“”为“”就得到两渐近线方程，即方程－＝就是双曲线－＝ (>，>)的两条渐近线方程.[易错防范].双曲线方程中＝＋，说明双曲线方程中最大，解决双曲线问题时不要忽视了这个结论，不要与椭圆中的知识相混淆..求双曲线离心率及其范围时，不要忽略了双曲线的离心率的取值范围是(，＋∞)这个前提条件，否则很容易产生增解或扩大所求离心率的取值范围致错..双曲线－＝ (>，>)的渐近线方程是＝±，－＝ (>，>)的渐近线方程是＝±.基础巩固题组(建议用时：分钟)一、选择题.(·郑州模拟)设双曲线－＝(＞，＞)的虚轴长为，焦距为，则双曲线的渐近线方程为( ) ＝±＝±＝±＝±解析因为＝，所以＝，因为＝，所以＝，所以＝＝，所以双曲线的渐近线方程为＝±＝±. 答案.双曲线：－＝(>，>)的一个焦点为，过点作双曲线的一条渐近线的垂线，垂足为，且交轴于，若为的中点，则双曲线的离心率为( )解析由题易知双曲线的一条渐近线与轴的夹角为，故双曲线的离心率＝(π)))＝.答案.(·全国Ⅲ卷)已知双曲线：－＝(>，>)的离心率为，则点(，)到的渐近线的距离为( )解析法一由离心率＝＝，得＝，又＝－，得＝，所以双曲线的渐近线方程为＝±.由点到直线的距离公式，得点(，)到的渐近线的距离为＝.法二离心率＝的双曲线是等轴双曲线，其渐近线方程是＝±，∴点(，)到的渐近线的距离为＝.答案.(·天津和平区一模)已知双曲线－＝(>，>)的离心率为，过右焦点作渐近线的垂线，垂足为.若△的面积为，其中为坐标原点，则双曲线的方程为( )－＝－＝－＝－＝解析由题意可知＝＝，可得＝，取一条渐近线为＝，可得到渐近线＝的距离＝＝，在△中，由勾股定理可得＝＝＝，由题意可得＝，联立解得所以双曲线的方程为－＝.答案.已知，是双曲线－＝(>，>)的上、下两个焦点，过的直线与双曲线的上下两支分别交于点，，若△为等边三角形，则双曲线的渐近线方程为( )＝±＝±＝±＝±解析根据双曲线的定义，可得－＝，∵△为等边三角形，∴＝，∴－＝＝，又∵－＝，∴＝＋＝，∵在△中，＝，＝，∠＝°，∴＝＋－· °，即＝＋－×××＝，亦即＝，则＝＝＝，由此可得双曲线的渐近线方程为＝±.答案二、填空题.直线：＝＋过双曲线－＝(>，>)一个焦点且与其一条渐近线平行，则双曲线方程为.解析由题意得一个焦点为(－，)，＝，＝，又＋＝，所以＝，＝，所以双曲线方程为－＝.答案－＝.设双曲线－＝的右顶点为，右焦点为.过点且平行于双曲线的一条渐近线的直线与双曲线交于点，则△的面积为.解析＝，＝，故＝.∴(，)，(，)，不妨设直线的方程为＝(－)，代入双曲线方程解得.∴△＝·＝··＝.答案.(·梅州质检)已知双曲线：－＝(>，>)的左、右焦点分别为，，为坐标原点是双曲线在第一象限上的点，直线，分别交双曲线左、右支于，.若＝，且∠＝°，则双曲线的离心率为. 解析由题意，＝，由双曲线的定义可得，－＝，可得＝，＝，又＝，＝，得四边形为平行四边形，又∠＝°，可得∠＝°，在△中，由余弦定理可得，＝＋－··· °，即＝－，＝，可得＝，所以＝＝.答案三、解答题.(·安徽江南十校联考)已知双曲线的中心在原点，焦点，在坐标轴上，离心率为，且过点(，－).()求双曲线的方程；()(一题多解)若点(，)在双曲线上，求证：·＝.()解∵＝，∴可设双曲线的方程为－＝λ(λ≠).∵双曲线过点(，－)，∴－＝λ，即λ＝.∴双曲线的方程为－＝，即－＝.()证明法一由()可知，＝＝，∴＝，∴(－，)，(，)，∴＝，＝，·＝＝－.∵点(，)在双曲线上，∴－＝，＝，故·＝－，∴⊥.∴·＝.法二由()可知，＝＝，∴＝，∴(－，)，(，)，＝(－－，－)，＝(－，－)，∴·＝(＋)×(－)＋＝－＋，∵点(，)在双曲线上，∴－＝，即－＝，∴·＝..设，分别为双曲线－＝(>，>)的左、右顶点，双曲线的实轴长为，焦点到渐近线的距离为. ()求双曲线的方程；()已知直线＝－与双曲线的右支交于，两点，且在双曲线的右支上存在点，使＋＝，求的值及点的坐标.解()由题意知＝，∵一条渐近线为＝，即－＝.∴由焦点到渐近线的距离为，得＝.又∵＝＋，∴＝，∴双曲线的方程为－＝.()设(，)，(，)，(，)，其中≥.又＋＝，即(，)＋(，)＝(，)，则＋＝，＋＝.将直线方程＝－代入双曲线方程－＝得－＋＝，其中Δ＝()－×>，则＋＝，＋＝(＋)－＝.∴)－()＝.))解得∴＝，点的坐标为(，).能力提升题组(建议用时：分钟).(·河南适应测试)已知，分别是双曲线－＝(>，>)的左、右焦点，是双曲线上一点，若＋＝，且△的最小内角为，则双曲线的渐近线方程为( )＝±＝±＝±＝±解析不妨设为双曲线右支上一点，则>，由双曲线的定义得－＝，又＋＝，所以＝，＝.又因为所以∠为最小内角，故∠＝.由余弦定理，可得＝，即(－)＝，所以＝，则＝，所以双曲线的渐近线方程为＝±.答案.已知点为双曲线：－＝(>，>)的右焦点，直线＝(>)与交于不同象限内的，两点，若⊥，设∠＝β，且β∈，则该双曲线的离心率的取值范围是( ).[，＋] .[，＋].[，＋] .[，＋]解析如图，设左焦点为′，连接′，′，令＝，′＝，则＝′＝，由双曲线定义可知－＝①，∵点与点关于原点对称，且⊥，∴＝＝＝，∴＋＝②，由①②得＝(－)，又知△＝△，∴＝·· β，∴－＝·β，∴＝β)，又∵β∈，∴ β∈，∴＝β)∈[，(＋)].又>，∴∈[，＋].答案.(·北京卷)已知椭圆：＋＝(>>)，双曲线：－＝.若双曲线的两条渐近线与椭圆的四个交点及椭圆的两个焦点恰为一个正六边形的顶点，则椭圆的离心率为；双曲线的离心率为.解析设椭圆的右焦点为(，)，双曲线的渐近线与椭圆在第一象限内的交点为，由题意可知，由点在椭圆上得，＋＝，∴＋＝，∵＝－，∴(－)＋＝(－)，∴－＋＝，∴－＋＝，∴＝±，∴椭＝＋(舍去)或椭＝－，∴椭圆的离心率为－.∵双曲线的渐近线过点，∴渐近线方程为＝，∴＝，故双曲线的离心率双＝＝.答案－.已知椭圆的方程为＋＝，双曲线的左、右焦点分别是的左、右顶点，而的左、右顶点分别是的左、右焦点.()求双曲线的方程；()若直线：＝＋与双曲线恒有两个不同的交点和，且·＞(其中为原点)，求的取值范围. 解()设双曲线的方程为－＝(＞，＞)，则＝，＝，再由＋＝，得＝.故的方程为－＝.()将＝＋代入－＝，得(－)－－＝.由直线与双曲线交于不同的两点，得∴≠且＜.①设(，)，(，)，则＋＝，＝－.∴＋＝＋(＋)(＋)＝(＋)＋(＋)＋＝.又∵·＞，得＋＞，∴＞，即＞，解得＜＜.②由①②得＜＜，故的取值范围为∪.新高考创新预测.(多填题)已知椭圆＋＝与双曲线－＝的离心率分别为，，且有公共的焦点，，则－＝，若为两曲线的一个交点，则·＝.解析由题意得椭圆的半焦距满足＝－，双曲线的半焦距满足＝＋，又因为两曲线有相同的焦点，所以－＝＋，即＋＝，则－＝×－(＋)＝－(＋)＝.不妨设，分别为两曲线的左、右焦点，点为两曲线在第一象限的交点，则解得则·＝.答案。
2020版高考数学一轮复习第8章平面解析几何第6讲双曲线讲义理含解析20190420166
第6讲 双曲线[考纲解读] 1.掌握双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线)．(重点)2.掌握直线与双曲线位置关系的判断，并能求解与双曲线有关的简单问题，理解数形结合思想在解决问题中的应用．(难点)[考向预测] 从近三年高考情况来看，本讲是高考中的热点．预测2020年高考会考查：①双曲线定义的应用与标准方程的求解；②渐近线方程与离心率的求解．试题以客观题的形式呈现，难度不大，以中档题为主.对应学生用书P149 1．双曲线的定义平面内与两个定点F 1，F 2(|F 1F 2|＝2c >0)的距离的差的绝对值为常数(小于|F 1F 2|且不等于零)的点的轨迹叫做□01双曲线．这两个定点叫做双曲线的□02焦点，两焦点间的距离叫做双曲线的□03焦距． 集合P ＝{M |||MF 1|－|MF 2||＝2a }，|F 1F 2|＝2c ，其中a ，c 为常数且a >0，c >0： (1)当□04a <c 时，P 点的轨迹是双曲线； (2)当□05a ＝c 时，P 点的轨迹是两条□06射线； (3)当□07a >c 时，P 点不存在． 2．双曲线的标准方程和几何性质3．必记结论(1)焦点到渐近线的距离为b .(2)等轴双曲线：实轴长和虚轴长相等的双曲线叫等轴双曲线，其方程可写作：x 2－y 2＝λ(λ≠0)．(3)等轴双曲线⇔离心率e ＝2⇔两条渐近线y ＝±x 相互垂直．1．概念辨析(1)平面内到点F 1(0,4)，F 2(0，－4)距离之差等于6的点的轨迹是双曲线．( )(2)双曲线方程x 2m 2－y 2n 2＝λ(m >0，n >0，λ≠0)的渐近线方程是x 2m 2－y 2n 2＝0，即x m ±yn＝0.( )(3)等轴双曲线的渐近线互相垂直，离心率等于 2.( )(4)若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)与y 2b 2－x 2a 2＝1(a >0，b >0)的离心率分别是e 1，e 2，则1e 21＋1e 22＝1(此结论中两条双曲线为共轭双曲线)．( )答案 (1)× (2)√ (3)√ (4)√ 2．小题热身(1)已知双曲线x 2a2－y 2＝1(a >0)两焦点之间的距离为4，则双曲线的渐近线方程是( )A ．y ＝±33x B ．y ＝±3x C ．y ＝±233x D ．y ＝±32x答案 A解析 双曲线x 2a2－y 2＝1(a >0)两焦点之间的距离为4，∴2c ＝4，解得c ＝2；∴c 2＝a 2＋1＝4，∴a ＝3； ∴双曲线的渐近线方程是y ＝±13x ，即y ＝±33x .故选A. (2)设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线左、右两个焦点，若|PF 1|＝9，则|PF 2|＝________.答案 17解析 由题意知|PF 1|＝9<a ＋c ＝10，所以P 点在双曲线的左支，则有|PF 2|－|PF 1|＝2a ＝8，故|PF 2|＝|PF 1|＋8＝17.(3)经过点A (5，－3)，且对称轴都在坐标轴上的等轴双曲线方程为________． 答案x 216－y 216＝1 解析 设双曲线的方程为x 2－y 2＝λ(λ≠0)，把点A (5，－3)代入，得λ＝16，故所求方程为x 216－y 216＝1.(4)(2018·北京高考)若双曲线x 2a 2－y 24＝1(a >0)的离心率为52，则a ＝________.答案 4解析 由已知，b 2＝4，e ＝c a ＝52，即c 2a 2＝⎝ ⎛⎭⎪⎫522＝54，又因为a 2＋b 2＝c 2，所以a 2＋4a 2＝54，a 2＝16，a ＝4.题型 一 双曲线的定义及应用1．若双曲线x 24－y 212＝1的左焦点为F ，点P 是双曲线右支上的动点，A (1,4)，则|PF |＋|PA |的最小值是( )A ．8B ．9C ．10D ．12 答案 B解析 由题意知，双曲线x 24－y 212＝1的左焦点F 的坐标为(－4,0)，设双曲线的右焦点为B ，则B (4,0)，由双曲线的定义知|PF |＋|PA |＝4＋|PB |＋|PA |≥4＋|AB |＝4＋4－12＋0－42＝4＋5＝9，当且仅当A ，P ，B 三点共线且P 在A ，B 之间时取等号．∴|PF |＋|PA |的最小值为9.故选B.2．已知F 1，F 2为双曲线C ：x 2－y 2＝2的左、右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝________.答案 34解析 ∵由双曲线的定义有|PF 1|－|PF 2|＝|PF 2|＝2a ＝22， ∴|PF 1|＝2|PF 2|＝42，则cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝422＋222－422×42×22＝34. 条件探究 举例说明2中，若将条件“|PF 1|＝2|PF 2|”改为“∠F 1PF 2＝60°”，求△F 1PF 2的面积．解 不妨设点P 在双曲线的右支上，则|PF 1|－|PF 2|＝2a ＝22，在△F 1PF 2中，由余弦定理，得cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝12，∴|PF 1|·|PF 2|＝8，∴S △F 1PF 2＝12|PF 1|·|PF 2|·sin60°＝2 3.(1)应用双曲线的定义需注意的问题在双曲线的定义中，要注意双曲线上的点(动点)具备的几何条件，即“到两定点(焦点)的距离之差的绝对值为一常数，且该常数必须小于两定点间的距离”．若定义中的“绝对值”去掉，点的轨迹是双曲线的一支．同时需注意定义的转化应用．(2)在焦点三角形中，注意定义、余弦定理的活用，常将||PF 1|－|PF 2||＝2a 平方，建立与|PF 1|·|PF 2|间的联系．1．F 1，F 2分别是双曲线C ：x 29－y 27＝1的左、右焦点，P 为双曲线C 右支上一点，且|PF 1|＝8，则△PF 1F 2的周长为( )A ．15B ．16C ．17D ．18 答案 D解析 由已知得a ＝3，b ＝7，c ＝a 2＋b 2＝4，所以|F 1F 2|＝2c ＝8.由双曲线的定义可知，|PF 1|－|PF 2|＝2a ＝6，又|PF 1|＝8，所以|PF 2|＝2.所以△PF 1F 2的周长是|PF 1|＋|PF 2|＋|F 1F 2|＝18.2．方程 x ＋102＋y 2－x －102＋y 2＝12的化简结果为( )A.x 236－y 264＝1 B.x 264－y 236＝1 C.x 236－y 264＝1(x >0) D.x 264－y 236＝1(x >0) 答案 C解析 由已知得点P (x ，y )到点F 1(－10,0)和点F 2(10，0)的距离之差为12，显然12<|F 1F 2|，所以点P 的轨迹是以F 1(－10,0)，F 2(10,0)为焦点，实轴长为12的双曲线的右支，已知方程是点P 的轨迹方程，由a ＝6，c ＝10得b ＝c 2－a 2＝8，所以点P 的轨迹方程可化为x 236－y 264＝1(x >0)．题型 二 双曲线的标准方程及应用1．已知动圆M 与圆C 1：(x ＋4)2＋y 2＝2外切，与圆C 2：(x －4)2＋y 2＝2内切，则动圆圆心M 的轨迹方程为( )A.x 22－y 214＝1(x ≥ 2)B.x 22－y 214＝1(x ≤－2)C.x 22＋y 214＝1(x ≥ 2) D.x 22＋y 214＝1(x ≤－2) 答案 A解析 设动圆的半径为r ，由题意可得MC 1＝r ＋2，MC 2＝r －2，所以MC 1－MC 2＝22＝2a ，故由双曲线的定义可知动点M 在以C 1(－4,0)，C 2(4,0)为焦点，实轴长为2a ＝22的双曲线的右支上，即a ＝2，c ＝4⇒b 2＝16－2＝14，故其标准方程为x 22－y 214＝1(x ≥2)．2．根据下列条件，求双曲线的标准方程： (1)虚轴长为12，离心率为54；(2)焦距为26，且经过点M (0,12)；(3)经过两点P (－3,27)和Q (－62，－7)．解 (1)设双曲线的标准方程为x 2a 2－y 2b 2＝1或y 2a 2－x 2b2＝1(a >0，b >0)．由题意知，2b ＝12，e ＝c a ＝54，∴b ＝6，c ＝10，a ＝8.∴双曲线的标准方程为x 264－y 236＝1或y 264－x 236＝1.(2)∵双曲线经过点M (0,12)，∴M (0,12)为双曲线的一个顶点，故焦点在y 轴上，且a ＝12.又2c ＝26，∴c ＝13，∴b 2＝c 2－a 2＝25. ∴双曲线的标准方程为y 2144－x 225＝1. (3)设双曲线方程为mx 2－ny 2＝1(mn >0)．∴⎩⎪⎨⎪⎧9m －28n ＝1，72m －49n ＝1，解得⎩⎪⎨⎪⎧m ＝－175，n ＝－125.∴双曲线的标准方程为y 225－x 275＝1.求双曲线标准方程的两种方法(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a ，b ，c 的方程并求出a ，b ，c 的值．与双曲线x 2a 2－y 2b 2＝1有相同渐近线时，可设所求双曲线方程为x 2a 2－y 2b2＝λ(λ≠0)．(2)定义法：依定义得出距离之差的等量关系式，求出a 的值，由定点位置确定c 的值． 注意：求双曲线的标准方程时，若焦点位置不确定，要注意分类讨论．也可以设双曲线方程为mx 2＋ny 2＝1(mn <0)求解．1．设F 1和F 2分别为双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，若F 1，F 2，P (0,2b )为等边三角形的三个顶点，且双曲线经过Q (5，3)点，则该双曲线的方程为( )A ．x 2－y 23＝1B.x 22－y 22＝1C.x 23－y 29＝1D.x 24－y 212＝1 答案 D解析 F 1和F 2分别为双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，F 1，F 2，P (0,2b )构成正三角形，∴2b ＝3c ，即有3c 2＝4b 2＝3(a 2＋b 2)，∴b 2＝3a 2；双曲线x 2a 2－y 2b2＝1过点Q (5，3)，∴5a 2－33a2＝1，解得a 2＝4，∴b 2＝12， ∴双曲线方程为x 24－y 212＝1.故选D.2．已知双曲线过点(4，3)，且渐近线方程为y ＝±12x ，则该双曲线的标准方程为________．答案x 24－y 2＝1解析 因为此双曲线的渐近线方程为y ＝±12x ，即x 2±y ＝0，所以可设此双曲线方程为x24－y 2＝λ(λ≠0)．又因为此双曲线过点(4，3)，所以424－(3)2＝λ，λ＝1，所以此双曲线的标准方程为x 24－y 2＝1. 题型 三 双曲线的几何性质角度1 与双曲线有关的范围问题1．(2015·全国卷Ⅰ)已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1上的一点，F 1，F 2是C 的两个焦点．若MF 1→·MF 2→<0，则y 0的取值范围是( )A.⎝ ⎛⎭⎪⎫－33，33 B.⎝ ⎛⎭⎪⎫－36，36 C.⎝ ⎛⎭⎪⎫－223，223D.⎝ ⎛⎭⎪⎫－233，233答案 A解析 不妨令F 1为双曲线的左焦点，则F 2为右焦点，由题意可知a 2＝2，b 2＝1，∴c2＝3，∴F 1(－3，0)，F 2(3，0)，则MF 1→·MF 2→＝(－3－x 0)·(3－x 0)＋(－y 0)·(－y 0)＝x 20＋y 20－3.又知x 202－y 20＝1，∴x 20＝2＋2y 20，∴MF 1→·MF 2→＝3y 20－1<0.∴－33<y 0<33.故选A. 角度2 与双曲线渐近线有关的问题2．(2018·全国卷Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |＝( )A.32 B ．3 C ．2 3 D ．4 答案 B解析 因为双曲线x 23－y 2＝1的渐近线方程为y ＝±33x ，所以∠MON ＝60°.不妨设过点F 的直线与直线y ＝33x 交于点M ，由△OMN 为直角三角形，不妨设∠OMN ＝90°，则∠MFO ＝60°，又直线MN 过点F (2,0)，所以直线MN 的方程为y ＝－3(x －2)，由⎩⎪⎨⎪⎧y ＝－3x －2，y ＝33x ，得⎩⎪⎨⎪⎧x ＝32，y ＝32，所以M ⎝ ⎛⎭⎪⎫32，32，由⎩⎪⎨⎪⎧y ＝－3x －2，y ＝－33x ，得⎩⎨⎧x ＝3，y ＝－3，所以N (3，－3)，所以|MN |＝⎝ ⎛⎭⎪⎫3－322＋⎝ ⎛⎭⎪⎫－3－322＝3. 角度3 与双曲线离心率有关的问题3．双曲线x 2a 2－y 2b2＝1(a >0，b >0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界)，若点(2,1)在“右”区域内，则双曲线离心率e 的取值范围是( )A.⎝ ⎛⎭⎪⎫1，52 B.⎝⎛⎭⎪⎫52，＋∞ C.⎝ ⎛⎭⎪⎫1，54D.⎝ ⎛⎭⎪⎫54，＋∞ 答案 B解析 依题意，注意到题中的双曲线x 2a 2－y 2b 2＝1的渐近线方程为y ＝±bax ，且“右”区域是由不等式组⎩⎪⎨⎪⎧y <b ax ，y >－ba x所确定，又点(2,1)在“右”区域内，于是有1<2b a ，即b a >12，因此题中的双曲线的离心率e ＝1＋⎝ ⎛⎭⎪⎫b a2∈⎝ ⎛⎭⎪⎫52，＋∞，选B.1．与双曲线有关的范围问题的解题思路(1)若条件中存在不等关系，则借助此关系直接转化求解．(2)若条件中没有不等关系，要善于发现隐含的不等关系，如借助双曲线上点的坐标范围，方程中Δ≥0等来解决．2．与双曲线离心率、渐近线有关问题的解题策略(1)双曲线的离心率e ＝ca是一个比值，故只需根据条件得到关于a ，b ，c 的一个关系式，利用b 2＝c 2－a 2消去b ，然后变形成关于e 的关系式，并且需注意e >1.(2)双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的渐近线是令x 2a 2－y 2b 2＝0，即得两渐近线方程x a ±yb＝0.(3)渐近线的斜率也是一个比值，可类比离心率的求法解答．1．(2016·全国卷Ⅰ)已知方程x2m 2＋n －y23m 2－n＝1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是( )A ．(－1,3)B ．(－1，3)C ．(0,3)D ．(0，3)答案 A解析 由题意可知，c 2＝(m 2＋n )＋(3m 2－n )＝4m 2，其中c 为半焦距， ∴2c ＝2×2|m |＝4，∴|m |＝1，∵方程x 2m 2＋n －y 23m 2－n＝1表示双曲线，∴(m 2＋n )·(3m 2－n )>0， ∴－m 2<n <3m 2，∴－1<n <3.故选A.2．设双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的两条渐近线互相垂直，顶点到一条渐近线的距离为1，则双曲线的一个焦点到一条渐近线的距离为( )A ．2 B. 2 C ．2 2 D ．4答案 B解析 因为双曲线C ：x 2a 2－y 2b2＝1的两条渐近线互相垂直，所以渐近线方程为y ＝±x ，所以a ＝b .因为顶点到一条渐近线的距离为1，所以22a ＝1，所以a ＝b ＝2，双曲线C 的方程为x 22－y 22＝1，所以双曲线的一个焦点到一条渐近线的距离为b ＝ 2.3．(2018·全国卷Ⅲ)设F 1，F 2是双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，O 是坐标原点．过F 2作C 的一条渐近线的垂线，垂足为P .若|PF 1|＝6|OP |，则C 的离心率为( )A. 5 B ．2 C. 3 D. 2答案 C解析 由题可知|PF 2|＝b ，|OF 2|＝c ，∴|PO |＝a . 在Rt △POF 2中，cos ∠PF 2O ＝|PF 2||OF 2|＝bc， ∵在△PF 1F 2中，cos ∠PF 2O ＝|PF 2|2＋|F 1F 2|2－|PF 1|22|PF 2||F 1F 2|＝bc，∴b 2＋4c 2－6a 22b ·2c＝b c⇒c 2＝3a 2，∴e ＝ 3.故选C.题型 四 直线与双曲线的综合问题已知双曲线C ：x 2－y 2＝1及直线l ：y ＝kx －1.(1)若l 与C 有两个不同的交点，求实数k 的取值范围；(2)若l 与C 交于A ，B 两点，O 是坐标原点，且△AOB 的面积为2，求实数k 的值． 解 (1)若双曲线C 与直线l 有两个不同的交点，则方程组⎩⎪⎨⎪⎧x 2－y 2＝1，y ＝kx －1有两个不同的实数根，整理得(1－k 2)x 2＋2kx －2＝0，所以⎩⎪⎨⎪⎧1－k 2≠0，Δ＝4k 2＋81－k 2>0，解得－2<k <2且k ≠±1.即双曲线C 与直线l 有两个不同的交点时，k 的取值范围是(－2，－1)∪(－1,1)∪(1，2)．(2)设交点A (x 1，y 1)，B (x 2，y 2)，直线l 与y 轴交于点D (0，－1)，由(1)知，C 与l 联立的方程为(1－k 2)x 2＋2kx －2＝0，所以⎩⎪⎨⎪⎧x 1＋x 2＝－2k1－k 2，x 1x 2＝－21－k 2.当A ，B 在双曲线的一支上且|x 1|>|x 2|时，S △OAB ＝S △OAD －S △OBD ＝12(|x 1|－|x 2|)＝12|x 1－x 2|；当A ，B 在双曲线的两支上且x 1>x 2时，S △OAB ＝S △ODA ＋S △OBD ＝12(|x 1|＋|x 2|)＝12|x 1－x 2|.所以S △OAB ＝12|x 1－x 2|＝2，所以(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2＝(22)2， 即⎝⎛⎭⎪⎫－2k 1－k 22＋81－k 2＝8，解得k ＝0或k ＝±62.又因为－2<k <2，且k ≠±1， 所以当k ＝0或k ＝±62时，△AOB 的面积为 2.1．判断直线与双曲线位置关系的三个步骤2．一个易错点联立直线与双曲线方程消元后，一定要注意二次项系数是否为零的判断或讨论． 3．一组常用结论过双曲线x 2m －y 24＝1的右焦点F 作x 轴的垂线与双曲线交于A ，B 两点，O 为坐标原点，若△AOB 的面积为8，则双曲线的渐近线方程为( )A ．y ＝±32xB ．y ＝±22xC ．y ＝±3xD ．y ＝±2x 答案 C解析 由右焦点F (c,0)，∴c 2m －y 24＝1，∴y ＝±4m，∴|AB |＝8m，∵△AOB 的面积为8，∴12×8m ×m ＋4＝8，解得m ＝43， ∴双曲线的渐近线方程为y ＝±223x ，即y ＝±3x . 高频考点 双曲线的离心率、渐近线问题考点分析 高考题对双曲线的考查，通常以选择或填空题的形式出现，考查内容以离心率、渐近线问题为主．[典例1] (2019·安徽皖江模拟)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)，四点P 1(4,2)，P 2(2,0)，P 3(－4,3)，P 4(4，3)中恰有三点在双曲线上，则该双曲线的离心率为( )A.52B.52C.72D.72答案 C解析 由双曲线的对称性可知P 3(－4,3)，P 4(4,3)在双曲线上，且P 1(4,2)一定不在双曲线上，∴P 2(2,0)也在双曲线上，∴a ＝2，b ＝3，c ＝7，∴e ＝72. [典例2] 如果双曲线x 2a 2－y 2b2＝1(a >0，b >0)两渐近线的夹角是60°，则该双曲线的离心率是________．答案233或2 解析 易知双曲线的渐近线的斜率是±b a .又两渐近线的夹角为60°，则b a ＝tan30°或b a＝tan60°，即e 2－1＝13或e 2－1＝3，又e >1，所以e ＝233或e ＝2，故该双曲线的离心率为233或2.[典例3] (2018·华南师大附中二模)已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，点F 2关于直线y ＝bax 的对称点为M ，若点M 在双曲线C 上，则双曲线C 的渐近线方程为________．答案 y ＝±2x解析 设点F 2关于直线y ＝b ax 的对称点是M 在双曲线的左支上，MF 2交渐近线于点N ，则|MN |＝|NF 2|＝|bc |b 2＋a2＝b ，|ON |＝|OF 2|2－|NF 2|2＝c 2－b 2＝a ，又因为O 是F 1F 2的中点，N 是MF 2的中点，所以|MF 1|＝2a ，又由双曲线的定义知|MF 2|－|MF 1|＝2a ，所以2b －2a ＝2a⇒b a＝2，所以双曲线C 的渐近线方程为y ＝±2x .。
2019版高考数学(文)高分计划一轮课件：第8章 平面解析几何 8-6
2．已知双曲线1x62 －y92＝1 上有一点 P，F1，F2 是双曲线 的焦点，且∠F1PF2＝3π，则△PF1F2 的面积为__9___3___．
解析 由题意，得|F1F2|＝2 16＋9＝10. ||PF1|－|PF2||＝8，
因为|PF1|2＋|PF2|2－2|PF1|·|PF2|cosπ3＝100， 所以|PF1|·|PF2|＝36. 所以 S△PF1F2＝12|PF1|·|PF2|sinπ3＝9 3.
(1)当 a<c 时，P 点的轨迹是双曲线； (2)当 a＝c 时，P 点的轨迹是两条 射线 ； (3)当 a>c 时，P 点不存在．
2．双曲线的标准方程和几何性质
标准 方程
ax22－by22＝1(a>0，b>0)
ay22－bx22＝1(a>0，b>0)
图形
3．必记结论 (1)焦点到渐近线的距离为 b. (2)等轴双曲线：实轴长和虚轴长相等的双曲线叫等轴 双曲线，其方程可写作：x2－y2＝λ(λ≠0)． (3)等轴双曲线⇔离心率 e＝ 2⇔两条渐近线 y＝±x 相 互垂直．
()
A. 3
B．3
C. 3m
D．3m
解析 由题意知，双曲线的标准方程为3xm2 －y32＝1，其
中 a2＝3m，b2＝3，故 c＝ a2＋b2＝ 3m＋3，不妨设 F 为
双曲线的右焦点，故 F( 3m＋3，0)．其中一条渐近线的方
程为
y＝
1 m
x，即 x－
my＝0，由点到直线的距离公式可
得
d＝
| 3· m＋1| ＝ 1＋－ m2
解析 设点 A(1,0)，因为△PF1F2 的内切圆与 x 轴切于 点(1,0)，则|PF1|－|PF2|＝|AF1|－|AF2|，所以 2a＝(c＋1)－(c －1)，则 a＝1.因为点 P 与点 F1 关于直线 y＝－bax对称，所 以∠F1PF2＝2π，且||PPFF12||＝ba＝b，结合|PF1|－|PF2|＝2，|PF1|2 ＋|PF2|2＝4c2＝4＋4b2，可得 b＝2.所以双曲线的方程为 x2 －y42＝1.
数学(理)一轮复习 第八章 平面解析几何 第讲 双曲线
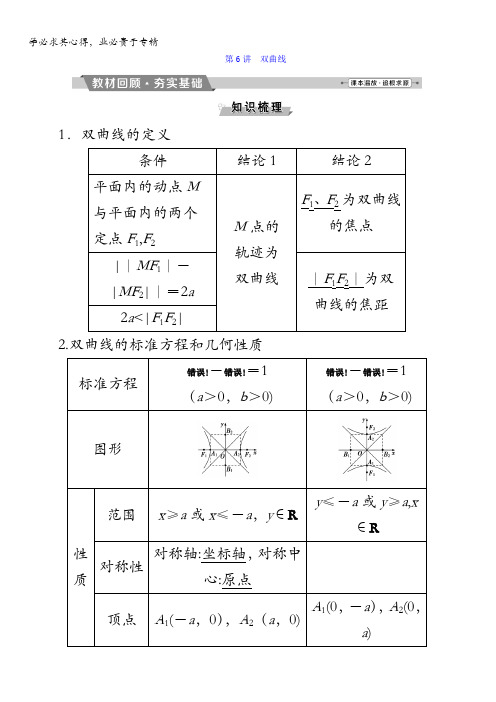
第6讲 双曲线1．双曲线的定义 条件 结论1 结论2 平面内的动点M与平面内的两个定点F 1,F 2M 点的 轨迹为 双曲线 F 1、F 2为双曲线的焦点 |｜MF 1｜－|MF 2|｜＝2a｜F 1F 2｜为双曲线的焦距 2a <|F 1F 2|2.双曲线的标准方程和几何性质 标准方程 错误!－错误!＝1 （a ＞0，b ＞0) 错误!－错误!＝1 （a ＞0，b ＞0)图形性质 范围x ≥a 或x ≤－a ，y ∈R y ≤－a 或y ≥a ,x ∈R 对称性 对称轴:坐标轴，对称中心:原点顶点 A 1(－a ，0），A 2（a ，0) A 1(0，－a ），A 2(0，a )渐近线y＝±ba xy＝±错误!x离心率e＝错误!,e∈（1，＋∞)实虚轴线段A1A2叫做双曲线的实轴，它的长｜A1A2|＝2a；线段B1B2叫做双曲线的虚轴，它的长｜B1B2|＝2b；a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长a、b、c的关系c2＝a2＋b2(c＞a＞0，c＞b＞0）1．辨明三个易误点（1）双曲线的定义中易忽视2a＜|F1F2|这一条件．若2a＝|F1F2|,则轨迹是以F1,F2为端点的两条射线，若2a＞｜F1F2|,则轨迹不存在．（2）区分双曲线中a，b,c的关系与椭圆中a，b，c的关系，在椭圆中a2＝b2＋c2，而在双曲线中c2＝a2＋b2。
(3）双曲线的离心率e∈（1，＋∞)，而椭圆的离心率e∈(0，1)．2．求双曲线标准方程的两种方法（1）定义法根据题目的条件,判断是否满足双曲线的定义，若满足,求出相应的a，b，c，即可求得方程．（2）待定系数法①与双曲线错误!－错误!＝1共渐近线的可设为错误!－错误!＝λ（λ≠0);②若渐近线方程为y ＝±b ax ,则可设为错误!－错误!＝λ（λ≠0)； ③若过两个已知点，则可设为错误!＋错误!＝1(mn ＜0）．3．双曲线几何性质的三个关注点（1)“六点”:两焦点、两顶点、两虚轴端点;(2)“四线”：两对称轴（实、虚轴）、两渐近线；（3）“两形”:中心、顶点、虚轴端点构成的三角形;双曲线上的一点（不包括顶点）与两焦点构成的三角形．1。
高考数学一轮复习第8章解析几何第6讲双曲线
1．判断下列结论是否正确(请在括号中打“√”或“×”
(1平面内到点F1(0,4,F2(0,－4距离之差的绝对值等于8的点的轨迹是双曲线．( × )
(2方程 － ＝1(mn＞0表示焦点在x轴上的双曲线．( × )
(3双曲线方程 － ＝λ(m＞0,n＞0,λ≠0的渐近线方程是 － ＝0,即 ± ＝0．( √ )
(4等轴双曲线的渐近线互相垂直,离心率等于 ．( √ )
(5若双曲线 － ＝1(a＞0,b＞0与 － ＝1(a＞0,b＞0的离心率分别是e1,e2,则 ＋ ＝1(此条件中两条双曲线称为共轭双曲线．( √ )
题组二 走进教材
2．(必修2P61T1若双曲线 － ＝1(a＞0,b＞0的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( A )
∴||PF2|－|PF1||＝||PF2|－|PM||＝|MF2|＝2＜|F1F2|,
∴由双曲线的定义可得,点P的轨迹是以F1,F2为焦点的双曲线．
(2设双曲线的右焦点为F1,则由双曲线的定义,可知|PF|＝4＋|PF1|,所以当|PF1|＋|PA|最小时满足|PF|＋|PA|最小．由双曲线的图形可知,当点A,P,F1共线时,满足|PF1|＋|PA|最小,|AF1|即|PF1|＋|PA|的最小值．又|AF1|＝5,故所求的最小值为9．
(4过双曲线焦点F1的弦AB与双曲线交在同支上,则AB与另一个焦点F2构成的△ABF2的周长为4a＋2|AB|．
(5双曲线的离心率公式可表示为e＝ ．
(6双曲线的形状与e的关系：|k|＝ ＝ ＝ ,e越大,即渐近线斜率的绝对值就越大,双曲线开口就越开阔．
(7 － ＝1(a＞0,b＞0与 － ＝1(a＞0,b＞0互为共轭双曲线,其离心率倒数的平方和为1．
(新课标)2020年高考数学一轮总复习第八章平面解析几何8_6双曲线课件理新人教A版
间的距离为4，得m2＋n＋3m2－n＝4，即m2＝1，所以－1<n<3.
(2)根据圆和双曲线的对称性，可知四边形ABCD为矩形．双曲线的渐近线方程为y
＝±b2x，圆的方程为x2＋y2＝4，不妨设交点A在第一象限，由y＝b2x，x2＋y2＝4得xA
＝
4 4＋b2
，yA＝
2b 4＋b2
，故四边形ABCD的面积为4xAyA＝
[答案] (1)B (2)C
名师点拨 利用双曲线的定义解决问题时，要注意三点： 1．距离之差的绝对值； 2．2a<|F1F2|； 3．焦点所在坐标轴的位置．
跟踪训练
(1)设F1，F2是双曲线x2－
y2 24
＝1的两个焦点，P是双曲线上的一点，且
|PF1|＝43|PF2|，则△PF1F2的面积等于(
(2)已知F1，F2为双曲线
x2 5
－
y2 4
＝1的左，右焦点，P(3，1)为双曲线内一点，点A在
双曲线上，则|AP|＋|AF2|的最小值为( )
A. 37＋4
B． 37－4
C. 37－2 5
D． 37＋2 5
[解析] (1)如图，由双曲线的定义
可得||PQFF22||－－||PQFF11|＝|＝22aa，， ②
32b 4＋b2
＝2b，解得b2＝
12，故所求的双曲线方程为x42－1y22 ＝1，故选D.
(3)∵双曲线的一条渐近线方程为y＝
b a
x，则由题意得
b a
>2，∴e＝
c a
＝
1＋ba2
> 1＋4＝ 5.
(4)∵e＝ac ＝
3
，∴
b2 a2
＝
c2－a2 a2
2020版高考数学一轮复习第8章平面解析几何第6节双曲线教学案含解析理
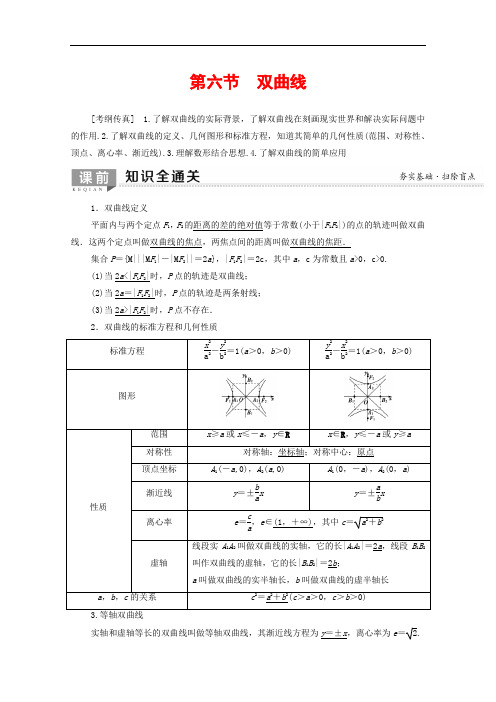
第六节双曲线[考纲传真] 1.了解双曲线的实际背景，了解双曲线在刻画现实世界和解决实际问题中的作用.2.了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线).3.理解数形结合思想.4.了解双曲线的简单应用1．双曲线定义平面内与两个定点F1，F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P＝{M|||M F1|－|M F2||＝2a}，|F1F2|＝2c，其中a，c为常数且a>0，c>0.(1)当2a<|F1F2|时，P点的轨迹是双曲线；(2)当2a＝|F1F2|时，P点的轨迹是两条射线；(3)当2a>|F1F2|时，P点不存在．2．双曲线的标准方程和几何性质标准方程x2a2－y2b2＝1(a＞0，b＞0)y2a2－x2b2＝1(a＞0，b＞0) 图形性质范围x≥a或x≤－a，y∈R x∈R，y≤－a或y≥a对称性对称轴：坐标轴；对称中心：原点顶点坐标A1(－a,0)，A2(a,0)A1(0，－a)，A2(0，a)渐近线y＝±bax y＝±abx离心率e＝ca，e∈(1，＋∞)，其中c＝a2＋b2虚轴线段实A1A2叫做双曲线的实轴，它的长|A1A2|＝2a，线段B1B2叫作双曲线的虚轴，它的长|B1B2|＝2b；a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长a，b，c的关系c2＝a2＋b2(c＞a＞0，c＞b＞0)实轴和虚轴等长的双曲线叫做等轴双曲线，其渐近线方程为y＝±x，离心率为e＝ 2.[常用结论]三种常见双曲线方程的设法(1)若已知双曲线过两点，焦点位置不能确定，可设方程为Ax 2＋By 2＝1(AB <0)． (2)当已知双曲线的渐近线方程为bx ±ay ＝0，求双曲线方程时，可设双曲线方程为b 2x 2－a 2y 2＝λ(λ≠0)．(3)与双曲线x 2a 2－y 2b 2＝1有相同的渐近线的双曲线方程可设为x 2a 2－y 2b2＝λ(λ≠0)．(4)过双曲线的一个焦点且与实轴垂直的弦长为2b2a.[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面内到点F 1(0,4)，F 2(0，－4)距离之差的绝对值等于8的点的轨迹是双曲线．( )(2)方程x 2m －y 2n＝1(mn >0)表示焦点在x 轴上的双曲线． ( )(3)双曲线x 2m 2－y 2n 2＝λ(m >0，n >0，λ≠0)的渐近线方程是x 2m 2－y 2n 2＝0，即x m ±yn＝0.( )(4)等轴双曲线的渐近线互相垂直，离心率等于 2. ( ) [答案] (1)× (2)× (3)√ (4)√ 2．双曲线x 23－y 22＝1的焦距为( ) A ．5 B. 5C ．2 5D ．1C [由双曲线x 23－y 22＝1，易知c 2＝3＋2＝5，所以c ＝5，所以双曲线x 23－y 22＝1的焦距为25]3．(教材题改编)已知双曲线x 2a 2－y 23＝1(a >0)的离心率为2，则a ＝( )A ．2 B.62C.52D ．1 D [依题意，e ＝c a ＝a 2＋3a＝2，∴a 2＋3＝2a ，则a 2＝1，a ＝1.]4．设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线左、右两个焦点，若|PF 1|＝9，则|PF 2|＝________.17 [由题意知|PF 1|＝9＜a ＋c ＝10，所以P 点在双曲线的左支，则有|PF 2|－|PF 1|＝2a＝8，故|PF2|＝|PF1|＋8＝17.]5．已知双曲线x2a 2－y 2b2＝1(a＞0，b＞0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y＝0垂直，则双曲线的方程为________．x24－y2＝1[由题意可得⎩⎪⎨⎪⎧b a＝12，a2＋b2＝5，a＞0，b＞0，解得a＝2，则b＝1，所以双曲线的方程为x24－y2＝1.]双曲线的定义及应用1. 已知F1，F2为双曲线C：x2－y2＝2的左、右焦点，点P在C上，|PF1|＝2|PF2|，则cos∠F1PF2＝( )A.14B.35C.34D.45C[∵由双曲线的定义有|PF1|－|PF2|＝|PF2|＝2a＝22，∴|PF1|＝2|PF2|＝42，则cos∠F1PF2＝|PF1|2＋|PF2|2－|F1F2|22|PF1|·|PF2|＝422＋222－422×42×22＝34.选C.]2．若双曲线x24－y212＝1的左焦点为F，点P是双曲线右支上的动点，A(1,4)，则|PF|＋|PA|的最小值是( )A．8 B．9 C．10 D．12B[由题意知，双曲线x24－y212＝1的左焦点F的坐标为(－4,0)，设双曲线的右焦点为B，则B(4,0)，由双曲线的定义知|PF|＋|PA|＝4＋|PB|＋|PA|≥4＋|AB|＝4＋4－12＋0－42＝4＋5＝9，当且仅当A，P，B三点共线且P在A，B之间时取等号．] [规律方法]双曲线定义的两个应用一是判定平面内动点的轨迹是否为双曲线，进而根据要求可求出曲线方程；二是在“焦点三角形”中，常利用正弦定理、余弦定理，结合||PF1|－|PF2||＝2a，运用平方的方法，建立与|PF1|，|PF2|的联系.双曲线的标准方程【例1】 设双曲线与椭圆x 227＋y 236＝1有共同的焦点，且与椭圆相交，其中一个交点的坐标为(15，4)，则此双曲线的标准方程是________．y 24－x 25＝1 [法一：椭圆x 227＋y 236＝1的焦点坐标是(0，±3)，设双曲线方程为y 2a 2－x 2b2＝1(a >0，b >0)，根据双曲线的定义知2a ＝|15－02＋4－32－15－02＋4＋32|＝4，故a ＝2.又b 2＝32－22＝5，故所求双曲线的标准方程为y 24－x 25＝1.法二：椭圆x 227＋y 236＝1的焦点坐标是(0，±3)．设双曲线方程为y 2a 2－x 2b2＝1(a >0，b >0)，则a 2＋b 2＝9，①又点(15，4)在双曲线上，所以16a 2－15b2＝1，②联立①②解得a 2＝4，b 2＝5.故所求双曲线的标准方程为y 24－x 25＝1.法三：设双曲线的方程为x 227－λ＋y 236－λ＝1(27<λ<36)，由于双曲线过点(15，4)，故1527－λ＋1636－λ＝1，解得λ1＝32，λ2＝0， 经检验λ1＝32，λ2＝0都是方程的根，但λ＝0不符合题意，应舍去，所以λ＝32. 故所求双曲线的标准方程为y 24－x 25＝1.][规律方法] 求双曲线标准方程的一般方法1待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a ，b ，c 的方程并求出a ，b ，c 的值.与双曲线有相同渐近线时，可设所求双曲线方程为2定义法：依定义得出距离之差的等量关系式，求出a 的值，由定点位置确定c 的值.(1)已知双曲线a 2－b2＝1(a ＞0，b ＞0)的一个焦点为F (2,0)，且双曲线的渐近线与圆(x －2)2＋y 2＝3相切，则双曲线的方程为( )A.x 29－y 213＝1 B.x 213－y 29＝1C.x 23－y 2＝1 D ．x 2－y 23＝1(2)(2019·郑州质量预测)已知双曲线的一个焦点与抛物线x 2＝24y 的焦点重合，其一条渐近线的倾斜角为30°，则该双曲线的标准方程为( )A.x 29－y 227＝1 B.y 29－x 227＝1 C.y 212－x 224＝1 D.y 224－x 212＝1 (1)D (2)B [(1)由题意知，双曲线的渐近线方程为y ＝±b ax ，即bx ±ay ＝0，因为双曲线的渐近线与圆(x －2)2＋y 2＝3相切，所以|2b |a 2＋b 2＝3，由双曲线的一个焦点为F (2,0)可得a 2＋b 2＝4，所以|b |＝3，即b 2＝3，所以a 2＝1，故双曲线的方程为x 2－y 23＝1.(2)∵x 2＝24y ，∴焦点为(0,6)，∴可设双曲线的方程为y 2a 2－x 2b2＝1(a ＞0，b ＞0)．∵渐近线方程为y ＝±a bx ， 其中一条渐近线的倾斜角为30°， ∴a b ＝33，c ＝6，∴a 2＝9，b 2＝27. 其方程为y 29－x 227＝1.]双曲线的几何性质►考法1 【例2】 (1)(2017·全国卷Ⅱ)若a >1，则双曲线x 2a2－y 2＝1的离心率的取值范围是( )A ．(2，＋∞)B ．(2，2)C ．(1，2)D ．(1,2)(2)(2018·全国卷Ⅲ)设F 1，F 2是双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左，右焦点，O 是坐标原点．过F 2作C 的一条渐近线的垂线，垂足为P .若|PF 1|＝6|OP |，则C 的离心率为( )A. 5 B ．2C. 3D. 2(1)C (2)C [(1)由题意得双曲线的离心率e ＝a 2＋1a.∴e 2＝a 2＋1a 2＝1＋1a2.∵a ＞1，∴0＜1a 2＜1，∴1＜1＋1a2＜2，∴1＜e ＜ 2. 故选C.(2)不妨设一条渐近线的方程为y ＝ba x ，则F 2到y ＝b ax 的距离d ＝|bc |a 2＋b 2＝b ，在Rt△F 2PO中，|F 2O |＝c ，所以|PO |＝a ，所以|PF 1|＝6a.又|F 1O |＝c ，所以在△F 1PO 与Rt△F 2PO 中，根据余弦定理得cos∠POF 1＝a 2＋c 2－6a22ac＝－cos∠POF 2＝－ac，即3a 2＋c 2－(6a )2＝0，得3a 2＝c 2，所以e ＝c a＝ 3.]►考法2 双曲线的渐近线问题【例3】 (1)(2019·合肥质检)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的离心率为3，则该双曲线的渐近线方程为________．(2)已知F 1，F 2是双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的两个焦点，P 是C 上一点，若|PF 1|＋|PF 2|＝6a ，且△PF 1F 2最小内角的大小为30°，则双曲线C 的渐近线方程是________．(1)y ＝±2x (2)2x ±y ＝0 [(1)因为e ＝ca＝3，所以c 2＝a 2＋b 2＝3a 2，故b ＝2a ，则此双曲线的渐近线方程为y ＝±b ax ＝±2x .(2)由题意，不妨设|PF 1|>|PF 2|，则根据双曲线的定义得，|PF 1|－|PF 2|＝2a ，又|PF 1|＋|PF 2|＝6a ，解得|PF 1|＝4a ，|PF 2|＝2a.在△PF 1F 2中，|F 1F 2|＝2c ，而c >a ，所以有|PF 2|<|F 1F 2|，所以∠PF 1F 2＝30°，所以(2a )2＝(2c )2＋(4a )2－2·2c ·4a cos 30°，得c ＝3a ，所以b ＝c 2－a 2＝2a.所以双曲线的渐近线方程为y ＝±bax ＝±2x ，即2x ±y ＝0.]►考法3 求双曲线的方程【例4】 已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左焦点为F ，离心率为 2.若经过F 和P (0,4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( )A.x 24－y 24＝1B.x 28－y 28＝1C.x 24－y 28＝1 D.x 28－y 24＝1B [由离心率为2，可知a ＝b ，c ＝2a ，所以F (－2a,0)，由题意知k PF ＝4－00－－2a ＝42a＝1，所以2a ＝4，解得a ＝22，所以双曲线的方程为x 28－y 28＝1.][规律方法] 与双曲线几何性质有关问题的解题策略1求双曲线的离心率或范围.依据题设条件，将问题转化为关于a ，c 的等式或不等式，解方程或不等式即可求得.2求双曲线的渐近线方程.依据题设条件，求双曲线中a ，b 的值或a 与b 的比值，进而得出双曲线的渐近线方程.(1)已知方程x 2m 2＋n －y 23m 2－n＝1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是( )A ．(－1,3)B ．(－1，3)C ．(0,3)D ．(0，3)(2)已知双曲线E ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)，若矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是________．(1)A (2)2 [(1)若双曲线的焦点在x 轴上，则⎩⎪⎨⎪⎧m 2＋n ＞0，3m 2－n ＞0.又∵(m 2＋n )＋(3m 2－n )＝4，∴m 2＝1，∴⎩⎪⎨⎪⎧1＋n ＞0，3－n ＞0，∴－1<n <3.若双曲线的焦点在y 轴上，则双曲线的标准方程为y 2n －3m 2－x 2－m 2－n ＝1，即⎩⎪⎨⎪⎧n －3m 2＞0，－m 2－n ＞0，即n >3m 2且n <－m 2，此时n 不存在．故选A.(2)由已知得|AB |＝2b2a，|BC |＝2c ，∴2×2b 2a＝3×2c .又∵b 2＝c 2－a 2，整理得2c 2－3ac－2a 2＝0，两边同除以a 2，得2⎝ ⎛⎭⎪⎫c a 2－3c a－2＝0，即2e 2－3e －2＝0，解得e ＝2.]1．(2018·全国卷Ⅱ)双曲线x 2a 2－y 2b2＝1(a >0，b >0)的离心率为3，则其渐近线方程为( )A ．y ＝±2xB ．y ＝±3xC ．y ＝±22x D ．y ＝±32x A [因为双曲线的离心率为3，所以c a＝3，即c ＝3a.又c 2＝a 2＋b 2，所以(3a )2＝a 2＋b 2，化简得2a 2＝b 2，所以b a ＝ 2.因为双曲线的渐近线方程为y ＝±bax ，所以y ＝±2x .故选A]2．(2018·全国卷Ⅲ)已知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为2，则点(4,0)到C 的渐近线的距离为( )A. 2 B ．2C.322D ．2 2D [法一：由离心率e ＝ca＝2，得c ＝2a ，又b 2＝c 2－a 2，得b ＝a ，所以双曲线C 的渐近线方程为y ＝±x .由点到直线的距离公式，得点(4,0)到C 的渐近线的距离为41＋1＝2 2.故选D.法二：离心率e ＝2的双曲线是等轴双曲线，其渐近线方程是y ＝±x ，由点到直线的距离公式得点(4,0)到C 的渐近线的距离为41＋1＝2 2.故选D.]3．(2017·全国卷Ⅲ)双曲线x 2a 2－y 29＝1(a ＞0)的一条渐近线方程为y ＝35x ，则a ＝________.5 [∵双曲线的标准方程为x 2a 2－y 29＝1(a >0)，∴双曲线的渐近线方程为y ＝±3ax .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5]自我感悟：______________________________________________________ ________________________________________________________________ ________________________________________________________________。
2020高考数学一轮总复习第8章平面解析几何8-6双曲线模拟演练文
【2019最新】精选高考数学一轮总复习第8章平面解析几何8-6双曲线模拟演练文[A级基础达标](时间：40分钟)1．[2017·唐山统考]“k<9”是“方程＋＝1表示双曲线”的( )A．充分不必要条件B．必要不充分条件D．既不充分也不必要条件C．充要条件答案A解析∵方程＋＝1表示双曲线，∴(25－k)(k－9)<0，∴k<9或k>25，∴“k<9”是“方程＋＝1表示双曲线”的充分不必要条件，故选A.2．[2017·北京模拟]若双曲线－＝1的离心率为，则其渐近线方程为( )B．y＝±xA．y＝±2xC．y＝±xD．y＝±x答案B解析由离心率为，可知＝.又c2＝a2＋b2，b＝a.因此双曲线的渐近线方程为y＝±x＝±x，故选B. 3．已知双曲线x2＋my2＝1的虚轴长是实轴长的2倍，则实数m的值是( )B.A．4D．－4C．－答案C 解析依题意得m<0，双曲线方程是x2－＝1，于是有＝2×1，m＝－. 4．已知双曲线－＝1(a>0，b>0)的两条渐近线均和圆C：x2＋y2－6x＋5＝0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为( )B.－＝1A.－＝1D.－＝1C.－＝1答案A解析圆心的坐标是(3,0)，圆的半径是2，双曲线的渐近线方程是bx±ay＝0，根据已知得＝2，即＝2，解得b＝2，则a2＝32－22＝5，故所求的双曲线方程是－＝1.5．已知双曲线－＝1与直线y ＝2x 有交点，则双曲线离心率的取值范围为( )A ．(1，)B ．(1，]C ．(，＋∞)D ．[，＋∞)答案 C解析 ∵双曲线的一条渐近线方程为y ＝x ，则由题意得>2，∴e＝＝>＝. 6．[2017·海口调研]已知点F1，F2分别为双曲线－＝1(a>0，b>0)的左、右焦点，P 为双曲线左支上的任意一点，且|PF2|＝2|PF1|，若△PF1F2为等腰三角形，则双曲线的离心率为________．答案 2解析 ∵|PF2|－|PF1|＝2a ，|PF2|＝2|PF1|，∴|PF2|＝4a ，|PF1|＝2a ，∵△PF1F2为等腰三角形，∴|PF2|＝|F1F2|，即4a ＝2c ，∴＝2.7．[2016·浙江高考]设双曲线x2－＝1的左、右焦点分别为F1，F2.若点P 在双曲线上，且△F1PF2为锐角三角形，则|PF1|＋|PF2|的取值范围是________．答案 (2，8)解析 由题意不妨设点P 在双曲线的右支上，现考虑两种极限情况：当PF2⊥x 轴时，|PF1|＋|PF2|有最大值8；当∠P 为直角时，|PF1|＋|PF2|有最小值2.因为△F1PF2为锐角三角形，所以|PF1|＋|PF2|的取值范围为(2，8)．8．已知双曲线－y2＝1的左、右焦点为F1，F2，点P 为左支上一点，且满足∠F1PF2＝60°，则△F1PF2的面积为________．答案3解析 设|PF1|＝m ，|PF2|＝n ，所以⎩⎪⎨⎪⎧m2＋n2－mn ＝20，m2＋n2－2mn ＝16，所以mn ＝4，所以S△F1PF2＝mnsin60°＝.9．已知双曲线焦距为4，焦点在x 轴上，且过点P(2,3)．(1)求该双曲线的标准方程；(2)若直线m 经过该双曲线的右焦点且斜率为1，求直线m 被双曲线截得的弦长．解 (1)设双曲线方程为－＝1(a ，b>0)，由已知可得左、右焦点F1、F2的坐标分别为(－2,0)，(2,0)，则|PF1|－|PF2|＝2＝2a ，所以a ＝1，又c＝2，所以b＝，所以双曲线方程为x2－＝1.(2)由题意可知直线m方程为y＝x－2，联立双曲线及直线方程消去y，得2x2＋4x－7＝0，设两交点为A(x1，y1)，B(x2，y2)，所以x1＋x2＝－2，x1x2＝－，由弦长公式得|AB|＝|x1－x2|＝·＝6. 10．已知双曲线Γ：－＝1(a>0，b>0)经过点P(2,1)，且其中一焦点F到一条渐近线的距离为1.(1)求双曲线Γ的方程；(2)过点P作两条相互垂直的直线PA，PB分别交双曲线Γ于A，B两点，求点P到直线AB距离的最大值．解(1)∵双曲线－＝1过点(2,1)，∴－＝1.不妨设F为右焦点，则F(c,0)到渐近线bx－ay＝0的距离d＝＝b，∴b＝1，a2＝2，∴所求双曲线的方程为－y2＝1. (2)设A(x1，y1)，B(x2，y2)，直线AB的方程为y＝kx＋m.将y＝kx＋m代入x2－2y2＝2中，整理得(2k2－1)x2＋4kmx＋2m2＋2＝0.∴x1＋x2＝，①x1x2＝.②∵·＝0，∴(x1－2，y1－1)·(x2－2，y2－1)＝0，∴(x1－2)(x2－2)＋(kx1＋m－1)(kx2＋m－1)＝0，∴(k2＋1)x1x2＋(km－k－2)(x1＋x2)＋m2－2m＋5＝0.③将①②代入③，得m2＋8km＋12k2＋2m－3＝0，∴(m＋2k－1)(m＋6k＋3)＝0.而P∉AB，∴m＝－6k－3，从而直线AB的方程为y＝kx－6k－3.将y＝kx－6k－3代入x2－2y2－2＝0中，判别式Δ＝8(34k2＋36k＋10)>0恒成立，∴y＝kx－6k－3即为所求直线．∴P到AB的距离d＝＝.∵2＝＝1＋≤2.∴d≤4，即点P到直线AB距离的最大值为4.[B级知能提升](时间：20分钟)11．[2016·全国卷Ⅱ]已知F1，F2是双曲线E：－＝1的左，右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1＝，则E的离心率为( )B.A.C.D．2答案A解析∵sin∠MF2F1＝，∴|MF2|＝3|MF1|.∵2c＝＝2|MF1|，∴c＝|MF1|，∵2a＝|MF2|－|MF1|，∴a＝|MF1|，∴e＝＝.故选A. 12．[2017·河北模拟]已知双曲线E的中心为原点，F(3,0)是E的焦点，过F的直线l与E相交于A，B两点，且AB的中点为N(－12，－15)，则E的方程为( )B.－＝1A.－＝1D.－＝1C.－＝1答案B解析由已知kAB＝kFN＝＝1.设E：－＝1(a>0，b>0)，A(x1，y1)，B(x2，y2)，∴－＝1，－＝1，则－＝0，而∴＝＝1，∴b2＝a2.①又c2＝a2＋b2＝9，②联立①②解得a2＝4，b2＝5，∴E的方程为－＝1. 13．已知F1，F2为双曲线－＝1(a>0，b>0)的焦点，过F2作垂直于x轴的直线交双曲线于点P和Q，且△F1PQ为正三角形，则双曲线的渐近线方程为________________．答案y＝±x解析设F2(c,0)(c>0)，P(c，y0)，Q(c，－y0)，代入双曲线方程，得y0＝±，∵PQ⊥x轴，∴|PQ|＝.在Rt△F1F2P中，∠PF1F2＝30°，∴|F1F2|＝|PF2|，即2c＝·.又∵c2＝a2＋b2，∴b2＝2a2或2a2＝－3b2(舍去)．∵a>0，b>0，∴＝.故所求双曲线的渐近线方程为y＝±x.14．已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为(，0)．(1)求双曲线C的方程；(2)若直线l：y＝kx＋与双曲线C恒有两个不同的交点A和B，且·>2(其中O为原点)，求k的取值范围．解(1)设双曲线C的方程为－＝1(a>0，b>0)．由已知得a＝，c＝2，再由c2＝a2＋b2，得b2＝1.所以双曲线C的方程为－y2＝1.(2)将y＝kx＋代入－y2＝1中，整理得(1－3k2)x2－6kx－9＝0.由题意得故k2≠且k2<1.①设A(xA，yA)，B(xB，yB)，则xA＋xB＝，xAxB＝.由·>2，得xAxB＋yAyB>2. xAxB＋yAyB＝xAxB＋(kxA＋)(kxB＋)＝(k2＋1)·xAxB＋k(xA＋xB)＋2＝(k2＋1)·＋k·＋2＝，于是>2，即>0，解得<k2<3.②由①②得<k2<1，所以k的取值范围为∪.。
2020高考数学一轮复习第8章平面解析几何第6讲双曲线增分练
【2019最新】精选高考数学一轮复习第8章平面解析几何第6讲双曲线增分练板块四 模拟演练·提能增分[A 级 基础达标]1．[2018·安徽模拟]下列双曲线中，焦点在y 轴上且渐近线方程为y ＝±2x 的是( )A ．x2－＝1B.－y2＝1 C ．y2－＝1D.－x2＝1 答案 D解析 由题意，选项A ，B 的焦点在x 轴，故排除A ，B ；D 项的渐近线方程为－x2＝0，即y ＝±2x.2．[2018·湖北模拟]若双曲线－＝1的一条渐近线经过点(3，－4)，则此双曲线的离心率为( )53C. D. A. B. 答案 D解析 由已知可得双曲线的渐近线方程为y ＝±x，点(3，－4)在渐近线上，∴＝，又a2＋b2＝c2，∴c2＝a2＋a2＝a2，∴e＝＝.故选D.3．[2017·全国卷Ⅰ]已知F 是双曲线C ：x2－＝1的右焦点，P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1,3)，则△APF 的面积为( )32A. B. C. D. 答案 D解析 因为F 是双曲线C ：x2－＝1的右焦点，所以F(2,0)．因为PF⊥x 轴，所以可设P 的坐标为(2，yP)．因为P 是C 上一点，所以4－＝1，解得yP ＝±3，所以P(2，±3)，|PF|＝3.又因为A(1,3)，所以点A 到直线PF 的距离为1，所以S△APF＝×|PF|×1＝×3×1＝.故选D.4．[2018·广东模拟]已知双曲线C ：－＝1的离心率e ＝，且其右焦点为F2(5,0)，则双曲线C 的方程为( )A.－＝1B.－＝1C.－＝1D.－＝1 答案 C解析 因为双曲线C 的右焦点为F2(5,0)，所以c ＝5.因为离心率e ＝＝，所以a＝4.又a2＋b2＝c2，所以b2＝9.故双曲线C 的方程为－＝1.5．P 为双曲线－＝1(a>0，b>0)右支上的一点，且|PF1|＝2|PF2|，则双曲线的离心率的取值范围是( )A ．(1,3)B ．(1,3]C ．(3，＋∞)D ．[3，＋∞) 答案 B⎩⎪⎨⎪⎧4a ＋2a>2c ，a<c ，如图，由题意可知 解析 ∴1<e<3.当P 在x 轴上时，4a ＋2a ＝2c ，∴e ＝3.综合e∈(1,3]．6．已知双曲线－＝1(a>0，b>0)的左、右焦点分别为F1、F2，过点F2作与x 轴垂直的直线与双曲线一个交点为P ，且∠PF1F2＝，则双曲线的渐近线方程为________．答案 y ＝±x解析 根据已知可得，|PF1|＝且|PF2|＝，故－＝2a ，所以＝2，＝，双曲线的渐近线方程为y ＝±x.7．[2018·海口调研]已知点F1，F2分别为双曲线－＝1(a>0，b>0)的左、右焦点，P 为双曲线左支上的任意一点，且|PF2|＝2|PF1|，若△PF1F2为等腰三角形，则双曲线的离心率为________．答案 2解析 ∵|PF2|－|PF1|＝2a ，|PF2|＝2|PF1|，∴|PF2|＝4a ，|PF1|＝2a ，∵△PF1F2为等腰三角形，∴|PF2|＝|F1F2|，即4a ＝2c ，∴＝2.8．[2016·北京高考]双曲线－＝1(a>0，b>0)的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝________.答案 2解析 由OA ，OC 所在直线为渐近线，且OA⊥OC，知两条渐近线的夹角为90°，从而双曲线为等轴双曲线，则其方程为x2－y2＝a2.OB 是正方形的对角线，且点B 是双曲线的焦点，则c ＝2，根据c2＝2a2可得a ＝2.9．设A ，B 分别为双曲线－＝1(a>0，b>0)的左、右顶点，双曲线的实轴长为4，焦点到渐近线的距离为.(1)求双曲线的方程；(2)已知直线y ＝x －2与双曲线的右支交于M ，N 两点，且在双曲线的右支上存在点D ，使＋＝t ，求t 的值及点D 的坐标．解 (1)由题意知a ＝2，又∵一条渐近线为y ＝x ，即bx －ay ＝0.∴由焦点到渐近线的距离为，得＝.∴b2＝3，∴双曲线的方程为－＝1.(2)设M(x1，y1)，N(x2，y2)，D(x0，y0)，则x1＋x2＝tx0，y1＋y2＝ty0.将直线方程y ＝x －2代入双曲线方程－＝1得x2－16x ＋84＝0，则x1＋x2＝16，y1＋y2＝(x1＋x2)－4＝12.⎩⎨⎧x0＝43，y0＝3，∴∴ ∴t ＝4，点D 的坐标为(4，3)．10．[2018·广西模拟]已知双曲线方程2x2－y2＝2.(1)求以A(2,1)为中点的双曲线的弦所在的直线方程；(2)求过点B(1,1)能否作直线l ，使l 与所给双曲线交于Q1，Q2两点，且点B 是弦Q1Q2的中点？这样的直线l 如果存在，求出它的方程；如果不存在，说明理由． 解 (1)由2·22－12＝7>2可知点A 在双曲线内部(含焦点的区域内)，设以A(2,1)为中点的弦两端点分别为P1(x1，y1)，P2(x2，y2)，则有x1＋x2＝4，y1＋y2＝2.由对称性知x1≠x2.∵P1、P2在双曲线上，∴两式相减得2(x1＋x2)(x1－x2)－(y1＋y2)(y1－y2)＝0.∵x1＋x2＝4，y1＋y2＝2.∴＝4.所求中点弦所在直线方程为y－1＝4(x－2)，即4x－y－7＝0.(2)由2·12－12＝1<2知B(1,1)在双曲线的外部(双曲线两支之间)．可假定直线l存在，采用(1)的方法求出l的方程为y－1＝2(x－1)，即2x－y－1＝0.联立方程组消y，得2x2－4x＋3＝0.∵Δ＝(－4)2－4×2×3＝－8<0，无实根，因此直线l与双曲线无交点，这一矛盾说明了满足条件的直线l不存在．[B级知能提升]1．[2017·天津高考]已知双曲线－＝1(a>0，b>0)的右焦点为F，点A在双曲线的渐近线上，△OAF是边长为2的等边三角形(O为原点)，则双曲线的方程为( )B.－＝1A.－＝1D．x2－＝1C.－y2＝1答案D解析根据题意画出草图如图所示.由△AOF是边长为2的等边三角形得到∠AOF＝60°，c＝|OF|＝2.又点A在双曲线的渐近线y＝x上，∴＝tan60°＝.又a2＋b2＝4，∴a＝1，b＝，∴双曲线的方程为x2－＝1.故选D. 2．已知双曲线E的中心为原点，F(3,0)是E的焦点，过F的直线l与E相交于A，B两点，且AB的中点为M(－12，－15)，则E的方程为( )B.－＝1A.－＝1D.－＝1C.－＝1答案B解析由已知易得l的斜率为k＝kFM＝1.设双曲线方程为－＝1(a>0，b>0)，A(x1，y1)，B(x2，y2)，则有两式相减并结合x1＋x2＝－24，y1＋y2＝－30，得＝，从而＝1，即4b2＝5a2.又a2＋b2＝9，解得a2＝4，b2＝5，故选B. 3．[2018·武汉模拟]过双曲线－＝1(a>0，b>0)的一个焦点F的直线与双曲线相交于A，B两点，当AB⊥x轴，称|AB|为双曲线的通径．若过焦点F的所有焦点弦AB中，其长度的最小值为，则此双曲线的离心率的范围为( )B．(1，]A．(1，)D．[，＋∞)C．(，＋∞)答案B解析当经过焦点F的直线与双曲线的交点在同一支上，可得双曲线的通径最小，令x＝c，可得y＝±b＝±，即有最小值为；当直线与双曲线的交点在两支上，可得直线的斜率为0时，即为实轴，最小为2a.由题意可得2a≥，即为a2≥b2＝c2－a2，即有c≤a，则离心率e＝∈(1，]．4．[2018·承德模拟]已知点M(－2,0)，N(2,0)，动点P满足条件|PM|－|PN|＝2，记动点P的轨迹为W.(1)求W的方程；(2)若A和B是W上的不同两点，O是坐标原点，求·的最小值．解(1)由|PM|－|PN|＝2知动点P的轨迹是以M，N为焦点的双曲线的右支，实半轴长a＝.又焦距2c＝4，所以虚半轴长b＝＝.所以W的方程为－＝1(x≥)．(2)设A，B的坐标分别为(x1，y1)，(x2，y2)．当AB⊥x轴时，x1＝x2，y1＝－y2，从而·＝x1x2＋y1y2＝x－y＝2.当AB与x轴不垂直时，设直线AB的方程为y＝kx＋m(k≠±1)，与W的方程联立，消去y得(1－k2)x2－2kmx－m2－2＝0，则x1＋x2＝，x1x2＝，所以·＝x1x2＋y1y2＝x1x2＋(kx1＋m)(kx2＋m)＝(1＋k2)x1x2＋km(x1＋x2)＋m2＝＋＋m2＝＝2＋.又因为x1x2>0，所以k2－1>0.所以·>2.综上所述，当AB⊥x轴时，·取得最小值2. 5．已知双曲线Γ：－＝1(a>0，b>0)经过点P(2,1)，且其中一焦点F到一条渐近线的距离为1.(1)求双曲线Γ的方程；(2)过点P作两条相互垂直的直线PA，PB分别交双曲线Γ于A，B两点，求点P到直线AB距离的最大值．解(1)∵双曲线－＝1过点(2,1)，∴－＝1.不妨设F为右焦点，则F(c,0)到渐近线bx－ay＝0的距离d＝＝b，∴b＝1，a2＝2，∴所求双曲线的方程为－y2＝1. (2)设A(x1，y1)，B(x2，y2)，直线AB的方程为y＝kx＋m.将y＝kx＋m代入x2－2y2＝2中，整理得(2k2－1)x2＋4kmx＋2m2＋2＝0.∴x1＋x2＝，①x1x2＝.②∵·＝0，∴(x1－2，y1－1)·(x2－2，y2－1)＝0，∴(x1－2)(x2－2)＋(kx1＋m－1)(kx2＋m－1)＝0，∴(k2＋1)x1x2＋(km－k－2)(x1＋x2)＋m2－2m＋5＝0.③将①②代入③，得m2＋8km＋12k2＋2m－3＝0，∴(m＋2k－1)(m＋6k＋3)＝0.而P∉AB，∴m＝－6k－3，从而直线AB的方程为y＝kx－6k－3.将y＝kx－6k－3代入x2－2y2－2＝0中，判别式Δ＝8(34k2＋36k＋10)>0恒成立，∴y＝kx－6k－3即为所求直线．∴P到AB的距离d＝＝.∵2＝＝1＋≤2.∴d≤4，即点P到直线AB距离的最大值为4.。
2019版高考数学(文)培优增分一轮全国经典版培优讲义：第8章 平面解析几何 第6讲双曲线
第6讲 双曲线板块一 知识梳理·自主学习[必备知识]考点1 双曲线的概念平面内与两个定点F1，F2(|F1F2|＝2c>0)的距离的差的绝对值为常数(小于|F1F2|且不等于零)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a、c为常数且a>0，c>0：(1)当a<c时，P点的轨迹是双曲线；(2)当a＝c时，P点的轨迹是两条射线；(3)当a>c时，P点不存在．考点2 双曲线的标准方程和几何性质[必会结论]双曲线中的几个常用结论(1)焦点到渐近线的距离为b .(2)实轴长和虚轴长相等的双曲线叫做等轴双曲线．(3)双曲线为等轴双曲线⇔双曲线的离心率e ＝⇔双曲线的两2条渐近线互相垂直(位置关系)．(4)过双曲线的一个焦点且与实轴垂直的弦的长为.2b 2a (5)过双曲线焦点F 1的弦AB 与双曲线交在同支上，则AB 与另一个焦点F 2构成的△ABF 2的周长为4a ＋2|AB |.(6)双曲线的离心率公式可表示为e ＝.1＋b 2a 2[考点自测] 1．判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面内到两点F 1(－1,0)，F 2(1,0)的距离之差等于1的点的轨迹是双曲线．( )(2)方程－＝1(mn >0)表示焦点在x 轴上的双曲线．( )x 2m y 2n (3)与双曲线－＝1(mn >0)共渐近线的双曲线方程可设为－x 2m y 2n x 2m ＝λ(λ≠0)．( )y 2n (4)等轴双曲线的离心率等于，且渐近线互相垂直．( )2(5)若双曲线－＝1(a >0，b >0)与－＝1(a >0，b >0)的离x 2a 2y 2b 2x 2b 2y 2a 2心率分别是e 1，e 2，则＋＝1(此结论中两条双曲线为共轭双曲线)1e 211e 2．( )答案 (1)× (2)× (3)√ (4)√ (5)√2．[课本改编]双曲线y 2－x 2＝2的渐近线方程是( )A ．y ＝±xB ．y ＝±x 2C ．y ＝±xD ．y ＝±2x3答案 A解析 由题意知－＝1，y ＝±x .y 22x 223．[2018·广东模拟]已知中心在原点的双曲线C 的右焦点为F (3,0)，离心率等于，则C 的方程是( )32A.－＝1B.－＝1x 24y 25x 24y 25C.－＝1 D.－＝1x 22y 25x 22y 25答案 B解析 由题意设C 的方程为－＝1(a >0，b >0)．x 2a 2y 2b 2由右焦点为F (3,0)，可知c ＝3，又因为离心率等于，所以32＝，所以a ＝2.由c 2＝a 2＋b 2，知b 2＝5，故双曲线C 的方程为c a 32－＝1.故选B.x 24y 254．[2018·福州质检]设F 1、F 2分别是双曲线x 2－＝1的左、右y 29焦点．若点P 在双曲线上，且|PF 1|＝5，则|PF 2|＝( )A ．5B ．3C ．7D ．3或7答案 D解析 ∵||PF 1|－|PF 2||＝2，∴|PF 2|＝7或3.5．[2017·北京高考]若双曲线x 2－＝1的离心率为，则实数y 2m 3m ＝________.答案 2解析 由双曲线的标准方程知a ＝1，b 2＝m ，c ＝，1＋m 故双曲线的离心率e ＝＝＝，ca 1＋m 3∴1＋m ＝3，解得m ＝2.6．[2017·全国卷Ⅲ]双曲线－＝1(a >0)的一条渐近线方程为x 2a 2y 29y ＝x ，则a ＝________.35答案 5解析 ∵双曲线的标准方程为－＝1(a ＞0)，x 2a 2y 29∴双曲线的渐近线方程为y ＝±x .3a 又双曲线的一条渐近线方程为y ＝x ，∴a ＝5.35板块二 典例探究·考向突破考向 双曲线的定义及标准方程 例1 (1)[2017·天津高考]已知双曲线－＝1(a ＞0，b ＞0)的x 2a 2y 2b 2左焦点为F ，离心率为.若经过F 和P (0,4)两点的直线平行于双曲2线的一条渐近线，则双曲线的方程为( )A.－＝1B.－＝1 x 24y 24x 28y 28C.－＝1 D.－＝1x 24y 28x 28y 24答案 B解析 由题意可得＝，即c ＝a .ca 22又左焦点F (－c,0)，P (0,4)，则直线PF 的方程为＝，y －04－0x ＋c0＋c 化简即得y ＝x ＋4.结合已知条件和图象易知直线PF 与y ＝x4c ba 平行，则＝，即4a ＝bc .4c ba 故Error!解得Error!故双曲线方程为－＝1.故选B.x 28y 28(2)[2017·全国卷Ⅲ]已知双曲线C ：－＝1(a ＞0，b ＞0)的一x 2a 2y 2b 2条渐近线方程为y ＝x ，且与椭圆＋＝1有公共焦点，则C 的52x 212y 23方程为( )A.－＝1B.－＝1x 28y 210x 24y 25C.－＝1 D.－＝1x 25y 24x 24y 23答案 B解析 由y ＝x 可得＝.①52ba 52由椭圆＋＝1的焦点为(3,0)，(－3,0)，x 212y 23可得a 2＋b 2＝9.②由①②可得a 2＝4，b 2＝5.所以C 的方程为－＝1.故选B.x 24y 25触类旁通(1)若涉及双曲线上的点，在解题时要首先想到双曲线上的任意点均满足双曲线的定义．(2)利用求待定系数法求双曲线标准方程的关键是：设出双曲线方程的标准形式，根据已知条件，列出关于参数a ，b ，c 的方程并求出a ，b ，c 的值．与双曲线－＝1，有相同渐近线时可设所求x 2a 2y 2b 2双曲线方程为－＝λ(λ≠0)．x 2a 2y 2b 2【变式训练1】 (1)已知双曲线C ：－＝1的焦距为10，x 2a 2y 2b 2点P (2,1)在C 的渐近线上，则C 的方程为( )A.－＝1B.－＝1x 220y 25x 25y 220C.－＝1 D.－＝1x 280y 220x 220y 280答案 A解析 由已知可得双曲线的焦距2c ＝10，a 2＋b 2＝25，排除C ，D ，又由渐近线方程为y ＝x ＝x ，得＝，解得a 2＝20，b 2＝5.ba 1212ba (2)求与双曲线－＝1有共同渐近线，并且经过点(－3,2)x 29y 2163的双曲线的方程．解 设所求双曲线方程为－＝λ，将点(－3,2)代入双曲线x 29y 2163方程，得－＝λ，解得λ＝，99121614∴所求双曲线方程为－＝1.4x 29y 24考向 双曲线的几何性质命题角度1 双曲线的离心率问题 例2 (1)[2017·全国卷Ⅱ]若a ＞1，则双曲线－y 2＝1的离心x 2a 2率的取值范围是( )A ．(，＋∞)B ．(，2)22C ．(1，)D ．(1,2)2答案 C解析 由题意得双曲线的离心率e ＝.a 2＋1a∴e 2＝＝1＋.a 2＋1a 21a 2∵a >1，∴0<<1，∴1<1＋<2，∴1<e <.1a 21a 22故选C.(2)[2016·山东高考]已知双曲线E ：－＝1(a >0，b >0)．若矩x 2a 2y 2b 2形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是________．答案 2解析 由已知得|AB |＝|CD |＝，|BC |＝|AD |＝|F 1F 2|＝2c .2b 2a 因为2|AB |＝3|BC |，所以＝6c ，4b 2a 又b 2＝c 2－a 2，所以2e 2－3e －2＝0，解得e ＝2，或e ＝－(舍去)．12命题角度2 双曲线的渐近线问题 例3 (1)已知双曲线C ：－＝1(a >0，b >0)的离心率为，x 2a 2y 2b 252则C 的渐近线方程为( )A ．y ＝±xB ．y ＝±x 1413C ．y ＝±x D ．y ＝±x 12答案 C解析 ∵e ＝，∴＝，即＝.52ca 52c 2a 254∵c 2＝a 2＋b 2，∴＝，∴＝.b 2a 214b a 12∵双曲线的渐近线方程为y ＝±x ，b a ∴渐近线方程为y ＝±x .故选C.12(2)[2018·深圳调研]在平面直角坐标系xOy 中，双曲线的中心在原点，焦点在y 轴上，一条渐近线方程为x －2y ＝0，则它的离心率为( )A. B. C. D ．25523答案 A解析 依题意设双曲线的方程是－＝1(其中a >0，b >0)，则y 2a 2x 2b 2其渐近线方程是y ＝±x ，由题知＝，即b ＝2a ，因此其离心率e ＝a b a b 12＝＝.a 2＋b 2a5a a 5触类旁通与双曲线的几何性质有关的问题(1)双曲线的几何性质中重点是渐近线方程和离心率，在双曲线－＝1(a >0，b >0)中，离心率e 与双曲线的渐近线的斜率k ＝±x 2a 2y 2b 2满足关系式e 2＝1＋k 2.ba (2)求双曲线的离心率时，将提供的双曲线的几何关系转化为关于双曲线基本量a ，b ，c 的方程或不等式，利用b 2＝c 2－a 2和e ＝转化为关于e 的方程或不等式，通过解方程或不等式求得离心率的ca 值或取值范围．【变式训练2】 (1)若双曲线C ：－＝1的焦点分别为x 2a 2y 2b 2F 1，F 2，以F 1F 2为直径的圆与双曲线的一个交点为M ，且sin ∠MF 1F 2＝，则双曲线的离心率为( )15A. B. C ．2 D.235答案 D解析 由题意知，∠F 1MF 2＝，不妨设点M 在第一象限，则π2Error!解得Error!又|MF 1|2＋|MF 2|2＝|F 1F 2|2，即16a 2＋4a 2＝4c 2，所以e ＝＝.ca 5故选D.(2)已知双曲线－＝1的两条渐近线与以椭圆＋＝1的左y 2a 2x 29x 225y 29焦点为圆心、为半径的圆相切，则渐近线方程为________．165答案 4x ±3y ＝0解析 双曲线的渐近线方程为ax ±3y ＝0，椭圆的左焦点为F (－4,0)，因为渐近线ax ＋3y ＝0与以F 为圆心、为半径的圆相切，165所以＝，解得a ＝±4，故渐近线方程为4x ±3y ＝0.|－4a ＋0|a 2＋9165考向 双曲线中焦点三角形 例4 (1)已知F 1，F 2是双曲线－y 2＝1的两个焦点，P 是双曲x 24线上一点，且∠F 1PF 2＝90°，则△F 1PF 2的面积是( )A ．1 B. C ．2 D.525答案 A解析 解法一：设|PF 1|＝d 1，|PF 2|＝d 2，由双曲线的定义可知|d 1－d 2|＝4.又∠F 1PF 2＝90°，于是有d ＋d ＝|F 1F 2|2＝20，212因此，S △F 1PF 2＝d 1d 2＝(d ＋d －|d 1－d 2|2)＝1.1214212解法二：由－y 2＝1，知|F 1F 2|＝2.x 245设P 点的纵坐标为y P ，由于∠F 1PF 2＝90°，则P 在以|F 1F 2|为直径的圆上，即在x 2＋y 2＝5上．由Error!消去x 得|y P |＝.55故△F 1PF 2的面积S ＝|F 1F 2|·|y P |＝1.12(2)已知F 1，F 2为双曲线C ：x 2－y 2＝1的左、右焦点，P 点在C 上，∠F 1PF 2＝60°，则P 到x 轴的距离为( )A. B. C. D.326236答案 B解析 设|PF 1|＝m ，|PF 2|＝n ，不妨设m >n ，P (x ，y )，|PF 1|－|PF 2|＝m －n ＝2.在△F 1PF 2中，由余弦定理得(2)2＝m 2＋n 2－2mn cos60°，2∴8＝(m －n )2＋mn .∴mn ＝4.由△F 1PF 2的面积相等，得 ×2×|y |＝mn sin60°，即|y |＝×4×.1221221232∴|y |＝.62即P 到x 轴的距离为.62触类旁通【变式训练3】 (1)[2018·哈尔滨质检]已知双曲线x 2－＝1y 224的两个焦点为F 1，F 2，P 为双曲线右支上一点．若|PF 1|＝|PF 2|，则43△F 1PF 2的面积为( )A ．48 B ．24 C ．12 D ．6答案 B解析 由双曲线的定义可得|PF 1|－|PF 2|＝|PF 2|＝2a ＝2，13解得|PF 2|＝6，故|PF 1|＝8，又|F 1F 2|＝10，由勾股定理可知三角形PF 1F 2为直角三角形，因此S △PF 1F 2＝|PF 1|×|PF 2|＝24.12(2)[2016·全国卷Ⅰ]已知方程－＝1表示双曲线，x 2m 2＋n y 23m 2－n 且该双曲线两焦点间的距离为4，则n 的取值范围是( )A ．(－1,3)B ．(－1，)C ．(0,3)D ．(0，)33答案 A解析 解法一：由题意可知：c 2＝(m 2＋n )＋(3m 2－n )＝4m 2，其中c 为半焦距，∴2c ＝2×2|m |＝4，∴|m |＝1.∵方程－＝1表示双曲线，x 2m 2＋n y 23m 2－n ∴(m 2＋n )·(3m 2－n )>0，∴－m 2<n <3m 2，∴－1<n <3.故选A.解法二：∵原方程表示双曲线，且焦距为4，∴Error! ①或Error! ②由①得m 2＝1，n ∈(－1,3)．②无解．故选A.考向 直线与双曲线的综合问题 例5 直线l ：y ＝(x －2)和双曲线C ：－＝1(a >0，b >0)交3x 2a 2y 2b 2于A ，B 两点，且|AB |＝，又l 关于直线l 1：y ＝x 对称的直线l 23b a 与x 轴平行．(1)求双曲线C 的离心率e ；(2)求双曲线C 的方程．解 (1)设双曲线C ：－＝1过第一、三象限的渐近线x 2a 2y 2b 2l 1：－＝0的倾斜角为α.x a yb 因为l 和l 2关于l 1对称，记它们的交点为P ，l 与x 轴的交点为M .而l 2与x 轴平行，记l 2与y 轴的交点为Q .依题意有∠QPO ＝∠POM ＝∠OPM ＝α.又l ：y ＝(x －2)的倾斜角为60°，则2α＝60°，3所以tan30°＝＝.ba 33于是e 2＝＝1＋＝1＋＝，c 2a 2b 2a 21343所以e ＝.233(2)由于＝，于是设双曲线方程为－＝1(k ≠0)，ba 33x 23k 2y 2k 2即x 2－3y 2＝3k 2.将y ＝(x －2)代入x 2－3y 2＝3k 2中，3得x 2－3×3(x －2)2＝3k 2.化简得到8x 2－36x ＋36＋3k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则|AB |＝|x 1－x 2|1＋3＝2(x 1＋x 2)2－4x 1x 2＝2×362－4×8×(36＋3k 2)8＝.9－6k 23解得k 2＝1.故所求双曲线C 的方程为－y 2＝1.x 23触类旁通求解双曲线综合问题的主要方法双曲线的综合问题主要为直线与双曲线的位置关系．解决这类问题的常用方法是：(1)设出直线方程或双曲线方程，然后把直线方程和双曲线方程组成方程组，消元后转化成关于x (或y )的一元二次方程，利用根与系数的关系及整体代入的思想解题．(2)利用点差法．【变式训练4】 设双曲线C ：－y 2＝1(a >0)与直线x 2a 2l ：x ＋y ＝1相交于两个不同点A ，B .(1)求双曲线C 的离心率e 的取值范围；(2)设直线l 与y 轴的交点为P ，取＝，求a 的值．PA → 512PB→ 解 (1)将y ＝－x ＋1代入双曲线－y 2＝1(a >0)中，得(1－a 2)x 2a 2x 2＋2a 2x －2a 2＝0.所以Error!解得0<a <且a ≠1.2又双曲线的离心率e ＝＝，1＋a 2a1a 2＋1所以e >且e ≠，即e ∈∪(，＋∞)．622(62，2)2(2)设A (x 1，y 1)，B (x 2，y 2)，P (0,1)，因为＝，所以(x 1，y 1－1)＝(x 2，y 2－1)，PA → 512PB→512由此得x 1＝x 2.512由于x 1，x 2是方程(1－a 2)x 2＋2a 2x －2a 2＝0的两根，且1－a 2≠0，所以x 1＋x 2＝x 2＝－，17122a 21－a 2x 1x 2＝x ＝－，51222a 21－a 2消去x 2得－＝，由a >0，解得a ＝.2a 21－a 2289601713核心规律1.当已知双曲线的焦点不明确而又无法确定时，其标准方程可设为＋＝1(mn <0)，这样可避免讨论和复杂的计算；也可设为x 2m y 2n Ax 2＋By 2＝1(AB <0)，这种形式在解题时更简便．2.与双曲线－＝1(a >0，b >0)有公共渐近线的双曲线的方程x 2a 2y 2b 2可设为－＝λ(λ≠0)．x 2a 2y 2b 23.已知双曲线的标准方程求双曲线的渐近线方程时，只要令双曲线的标准方程中“1”为“0”就得到两渐近线方程，即方程－＝0x 2a 2y 2b 2就是双曲线－＝1(a >0，b >0)的两条渐近线方程．x 2a 2y 2b2满分策略1.双曲线的标准方程的两种形式的区分要结合x 2，y 2前系数的正负．2.关于双曲线中离心率范围问题，不要忘记双曲线离心率固有范围e >1.3.双曲线－＝1(a >0，b >0)的渐近线方程是x 2a 2y 2b 2y ＝±x ，－＝1(a >0，b >0)的渐近线方程是y ＝±x .b a y 2a 2x 2b 2a b 4.若利用弦长公式计算，在设直线斜率时要注意说明斜率不存在的情况．5.当直线与双曲线交于一点时，不一定相切，例如：当直线与双曲线的渐近线平行时，直线与双曲线相交于一点，但不是相切；反之，当直线与双曲线相切时，直线与双曲线仅有一个交点.板块三 启智培优·破译高考题型技法系列 15——函数方程数学思想方法的应用(1)[2015·全国卷Ⅰ]已知F 是双曲线C ：x 2－＝1的右焦点，P y 28是C 的左支上一点，A (0,6)．当△APF 周长最小时，该三角形的6面积为________．解题视点 利用双曲线定义寻求△APF 周长最小时P 点位置．解析 设F 1为双曲线的左焦点，由双曲线方程x 2－＝1可知，y 28a ＝1，c ＝3，故F (3,0)，F 1(－3,0)．当点P 在双曲线左支上运动时，由双曲线定义知|PF |－|PF 1|＝2，所以|PF |＝|PF 1|＋2，从而△APF 的周长为|AP |＋|PF |＋|AF |＝|AP |＋|PF 1|＋2＋|AF |.因为|AF |＝＝15为定值，所以当|AP |＋|PF 1|最小时，△APF 的周长32＋(66)2最小，由图象可知，此时点P 在线段AF 1与双曲线的交点处(如图所示)．由题意可知直线AF 1的方程为y ＝2x ＋6，由Error!66得y 2＋6y －96＝0，解得y ＝2或y ＝－8(舍去)，所以S △666APF ＝S △AF 1F －S △PF 1F ＝×6×6－×6×2＝12.1261266答案 6(2)已知双曲线－＝1，其中a >1，求e 的取值范围．x 2a 2y 2(a ＋1)2解题视点 带参量的双曲线问题，需寻找e 与参量的依存关系，即函数关系，e 的范围由e ＝f (a )来确定．解 e 2＝＝＝1＋2，c 2a 2a 2＋(a ＋1)2a 2(1＋1a )∵a >1，∴1＋0<1＋<1＋1，1a ∴1<2<4，即2<e 2<5，(1＋1a )<e <.25答题启示 解决解析几何问题，先通过已知条件和几何性质确定圆锥曲线的方程，再通过方程研究直线与圆锥曲线的位置关系，解析几何中的计算比较复杂，解决此类问题的关键要熟记圆锥曲线的定义、标准方程、几何性质及直线与圆锥曲线位置关系的常见思路.注意应用数学思想方法.跟踪训练[2015·山东高考]过双曲线C ：－＝1(a >0，b >0)的右焦点作x 2a 2y 2b 2一条与其渐近线平行的直线，交C 于点P .若点P 的横坐标为2a ，则C 的离心率为________．答案 2＋3解析 不妨设过右焦点与渐近线平行的直线为y ＝(x －c )，与ba C 交于P (x 0，y 0)．∵x 0＝2a ，∴y 0＝(2a －c )．ba 又P (x 0，y 0)在双曲线C 上，∴－＝1，(2a )2a 2b 2a 2(2a －c )2b 2∴整理得a 2－4ac ＋c 2＝0，设双曲线C 的离心率为e ，则1－4e ＋e 2＝0.∴e 1＝2－(舍去)，e 2＝2＋，33即双曲线C 的离心率为2＋.3板块四 模拟演练·提能增分 [A 级 基础达标]1．[2018·安徽模拟]下列双曲线中，焦点在y 轴上且渐近线方程为y ＝±2x 的是( )A ．x 2－＝1B.－y 2＝1y 24x 24C ．y 2－＝1 D.－x 2＝1x 24y 24答案 D解析 由题意，选项A ，B 的焦点在x 轴，故排除A ，B ；D 项的渐近线方程为－x 2＝0，即y ＝±2x .y 242．[2018·湖北模拟]若双曲线－＝1的一条渐近线经过点x 2a 2y 2b 2(3，－4)，则此双曲线的离心率为( )A. B. C. D.73544353答案 D解析 由已知可得双曲线的渐近线方程为y ＝±x ，点(3，－4)ba 在渐近线上，∴＝，又a 2＋b 2＝c 2，∴c 2＝a 2＋a 2＝a 2，∴e ＝b a 43169259＝.故选D.c a 533．[2017·全国卷Ⅰ]已知F 是双曲线C ：x 2－＝1的右焦点，y 23P 是C 上一点，且PF 与x 轴垂直，点A 的坐标是(1,3)，则△APF 的面积为( )A. B. C. D.13122332答案 D解析 因为F 是双曲线C ：x 2－＝1的右焦点，所以F (2,0)．y 23因为PF ⊥x 轴，所以可设P 的坐标为(2，y P )．因为P 是C 上一点，所以4－＝1，解得y P ＝±3，y 2P 3所以P (2，±3)，|PF |＝3.又因为A (1,3)，所以点A 到直线PF 的距离为1，所以S △APF ＝×|PF |×1＝×3×1＝.故选D.1212324．[2018·广东模拟]已知双曲线C ：－＝1的离心率e ＝，x 2a 2y 2b 254且其右焦点为F 2(5,0)，则双曲线C 的方程为( )A.－＝1B.－＝1x 24y 23x 29y 216C.－＝1 D.－＝1x 216y 29x 23y 24答案 C解析 因为双曲线C 的右焦点为F 2(5,0)，所以c ＝5.因为离心率e ＝＝，所以a ＝4.c a 54又a 2＋b 2＝c 2，所以b 2＝9.故双曲线C 的方程为－＝1.x 216y 295．P 为双曲线－＝1(a >0，b >0)右支上的一点，且x 2a 2y 2b 2|PF 1|＝2|PF 2|，则双曲线的离心率的取值范围是( )A ．(1,3)B ．(1,3]C ．(3，＋∞)D ．[3，＋∞)答案 B解析 如图，由题意可知Error!∴1<e <3.当P 在x 轴上时，4a ＋2a ＝2c ，∴e ＝3.综合e ∈(1,3]．6．已知双曲线－＝1(a >0，b >0)的左、右焦点分别为x 2a 2y 2b 2F 1、F 2，过点F 2作与x 轴垂直的直线与双曲线一个交点为P ，且∠PF 1F 2＝，则双曲线的渐近线方程为________．π6答案 y ＝±x2解析 根据已知可得，|PF 1|＝且|PF 2|＝，故2b 2a b 2a －＝2a ，所以＝2，＝，双曲线的渐近线方程为y ＝±x .2b 2a b 2a b 2a 2ba 227．[2018·海口调研]已知点F 1，F 2分别为双曲线－＝1(a >0，b >0)的左、右焦点，P 为双曲线左支上的任意一点，x 2a 2y 2b 2且|PF 2|＝2|PF 1|，若△PF 1F 2为等腰三角形，则双曲线的离心率为________．答案 2解析 ∵|PF 2|－|PF 1|＝2a ，|PF 2|＝2|PF 1|，∴|PF 2|＝4a ，|PF 1|＝2a ，∵△PF 1F 2为等腰三角形，∴|PF 2|＝|F 1F 2|，即4a ＝2c ，∴＝2.ca 8．[2016·北京高考]双曲线－＝1(a >0，b >0)的渐近线为正x 2a 2y 2b 2方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝________.答案 2解析 由OA ，OC 所在直线为渐近线，且OA ⊥OC ，知两条渐近线的夹角为90°，从而双曲线为等轴双曲线，则其方程为x 2－y 2＝a 2.OB 是正方形的对角线，且点B 是双曲线的焦点，则c ＝2，根据c 2＝2a 2可得a ＝2.29．设A ，B 分别为双曲线－＝1(a >0，b >0)的左、右顶点，x 2a 2y 2b 2双曲线的实轴长为4，焦点到渐近线的距离为.33(1)求双曲线的方程；(2)已知直线y ＝x －2与双曲线的右支交于M ，N 两点，且在33双曲线的右支上存在点D ，使＋＝t ，求t 的值及点D 的坐OM → ON → OD→ 标．解 (1)由题意知a ＝2，3又∵一条渐近线为y ＝x ，即bx －ay ＝0.ba ，得＝.3|bc |b 2＋a 23∴b 2＝3，∴双曲线的方程为－＝1.x 212y 23(2)设M (x 1，y 1)，N (x 2，y 2)，D (x 0，y 0)，则x 1＋x 2＝tx 0，y 1＋y 2＝ty 0.将直线方程y ＝x －2代入双曲线方程－＝1得33x 212y 23x 2－16x ＋84＝0，3则x 1＋x 2＝16，y 1＋y 2＝(x 1＋x 2)－4＝12.333∴Error!∴Error!∴t ＝4，点D 的坐标为(4，3)．310．[2018·广西模拟]已知双曲线方程2x 2－y 2＝2.(1)求以A (2,1)为中点的双曲线的弦所在的直线方程；(2)求过点B (1,1)能否作直线l ，使l 与所给双曲线交于Q 1，Q 2两点，且点B 是弦Q 1Q 2的中点？这样的直线l 如果存在，求出它的方程；如果不存在，说明理由．解 (1)由2·22－12＝7>2可知点A 在双曲线内部(含焦点的区域内)，设以A (2,1)为中点的弦两端点分别为P 1(x 1，y 1)，P 2(x 2，y 2)，则有x 1＋x 2＝4，y 1＋y 2＝2.由对称性知x 1≠x 2.∵P 1、P 2在双曲线上，∴Error!两式相减得2(x 1＋x 2)(x 1－x 2)－(y 1＋y 2)(y 1－y 2)＝0.∵x 1＋x 2＝4，y 1＋y 2＝2.∴＝4.y 1－y 2x 1－x 2所求中点弦所在直线方程为y －1＝4(x －2)，即4x －y －7＝0.(2)由2·12－12＝1<2知B (1,1)在双曲线的外部(双曲线两支之间)．可假定直线l 存在，采用(1)的方法求出l 的方程为y －1＝2(x －1)，即2x －y －1＝0.联立方程组Error!消y ，得2x 2－4x ＋3＝0.∵Δ＝(－4)2－4×2×3＝－8<0，无实根，因此直线l 与双曲线无交点，这一矛盾说明了满足条件的直线l 不存在．[B 级 知能提升]1．[2017·天津高考]已知双曲线－＝1(a >0，b >0)的右焦点x 2a 2y 2b 2为F ，点A 在双曲线的渐近线上，△OAF 是边长为2的等边三角形(O 为原点)，则双曲线的方程为( )A.－＝1B.－＝1x 24y 212x 212y 24C.－y 2＝1 D ．x 2－＝1x 23y 23答案 D解析 根据题意画出草图如图所示.(不妨设点A 在渐近线y ＝ba x 上)由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2.又点A 在双曲线的渐近线y ＝x 上，ba ∴＝tan60°＝.ba 3又a 2＋b 2＝4，∴a ＝1，b ＝，3∴双曲线的方程为x 2－＝1.故选D.y 232．已知双曲线E 的中心为原点，F (3,0)是E 的焦点，过F 的直线l 与E 相交于A ，B 两点，且AB 的中点为M (－12，－15)，则E 的方程为( )A.－＝1B.－＝1x 3y 26x 24y 25C.－＝1 D.－＝1x 26y 23x 25y 24答案 B解析 由已知易得l 的斜率为k ＝k FM ＝1.设双曲线方程为－＝1(a >0，b >0)，A (x 1，y 1)，B (x 2，y 2)，则有Error!两式相减并x 2a 2y 2b 2结合x 1＋x 2＝－24，y 1＋y 2＝－30，得＝，从而＝1，y 1－y 2x 1－x 24b 25a 24b 25a 2即4b 2＝5a 2.又a 2＋b 2＝9，解得a 2＝4，b 2＝5，故选B.3．[2018·武汉模拟]过双曲线－＝1(a >0，b >0)的一个焦点x 2a 2y 2b 2F 的直线与双曲线相交于A ，B 两点，当AB ⊥x 轴，称|AB |为双曲线的通径．若过焦点F 的所有焦点弦AB 中，其长度的最小值为，2b 2a 则此双曲线的离心率的范围为( )A ．(1，)B ．(1，]22C ．(，＋∞)D ．[，＋∞)22答案 B解析 当经过焦点F 的直线与双曲线的交点在同一支上，可得双曲线的通径最小，令x ＝c ，可得y ＝±b ＝±，即c 2a 2－1b 2a有最小值为；2b 2a 当直线与双曲线的交点在两支上，可得直线的斜率为0时，即为实轴，最小为2a .由题意可得2a ≥，2b 2a 即为a 2≥b 2＝c 2－a 2，即有c ≤a ，2则离心率e ＝∈(1，]．ca 24．[2018·承德模拟]已知点M (－2,0)，N (2,0)，动点P 满足条件|PM |－|PN |＝2，记动点P 的轨迹为W .2(1)求W 的方程；(2)若A 和B 是W 上的不同两点，O 是坐标原点，求·的OA → OB→ 最小值．解 (1)由|PM |－|PN |＝2知动点P 的轨迹是以M ，N 为焦点的2双曲线的右支，实半轴长a ＝.2又焦距2c ＝4，所以虚半轴长b ＝＝.c 2－a 22所以W 的方程为－＝1(x ≥)．x 22y 222(2)设A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)．当AB ⊥x 轴时，x 1＝x 2，y 1＝－y 2，从而·＝x 1x 2＋y 1y 2＝x －y ＝2.OA → OB→ 2121当AB 与x 轴不垂直时，设直线AB 的方程为y ＝kx ＋m (k ≠±1)，与W 的方程联立，消去y 得(1－k 2)x 2－2kmx －m 2－2＝0，则x 1＋x 2＝，x 1x 2＝，2km1－k 2m 2＋2k 2－1所以·＝x 1x 2＋y 1y 2OA → OB→ ＝x 1x 2＋(kx 1＋m )(kx 2＋m )＝(1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝＋＋m 2(1＋k 2)(m 2＋2)k 2－12k 2m 21－k 2＝＝2＋.2k 2＋2k 2－14k 2－1又因为x 1x 2>0，所以k 2－1>0.所以·>2.OA → OB → 综上所述，当AB ⊥x 轴时，·取得最小值2.OA → OB→ 5．已知双曲线Γ：－＝1(a >0，b >0)经过点P (2,1)，且其中x 2a 2y 2b 2一焦点F 到一条渐近线的距离为1.(1)求双曲线Γ的方程；(2)过点P 作两条相互垂直的直线PA ，PB 分别交双曲线Γ于A ，B 两点，求点P 到直线AB 距离的最大值．解 (1)∵双曲线－＝1过点(2,1)，∴－＝1.x 2a 2y 2b 24a 21b 2不妨设F 为右焦点，则F (c,0)到渐近线bx －ay ＝0的距离d ＝＝b ，∴b ＝1，a 2＝2，|bc |a 2＋b 2∴所求双曲线的方程为－y 2＝1.x 22(2)设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝kx ＋m .将y ＝kx ＋m 代入x 2－2y 2＝2中，整理得(2k 2－1)x 2＋4kmx ＋2m 2＋2＝0.∴x 1＋x 2＝，①－4km2k 2－1x 1x 2＝.②2m 2＋22k 2－1∵·＝0，PA → PB→ ∴(x 1－2，y 1－1)·(x 2－2，y 2－1)＝0，∴(x 1－2)(x 2－2)＋(kx 1＋m －1)(kx 2＋m －1)＝0，∴(k 2＋1)x 1x 2＋(km －k －2)(x 1＋x 2)＋m 2－2m ＋5＝0.③将①②代入③，得m 2＋8km ＋12k 2＋2m －3＝0，∴(m ＋2k －1)(m ＋6k ＋3)＝0.而P ∉AB ，∴m ＝－6k －3，从而直线AB 的方程为y ＝kx －6k －3.将y ＝kx －6k －3代入x 2－2y 2－2＝0中，判别式Δ＝8(34k 2＋36k ＋10)>0恒成立，∴y ＝kx －6k －3即为所求直线．∴P 到AB 的距离d ＝＝.|2k －6k －3－1|1＋k 24|k ＋1|k 2＋1∵2＝＝1＋≤2.(d 4)k 2＋1＋2kk 2＋12kk 2＋1∴d ≤4，即点P 到直线AB 距离的最大值为4.22。
近年届高考数学一轮复习第八章平面解析几何第6讲双曲线演练直击高考文(2021年整理)
（江苏专版）2019届高考数学一轮复习第八章平面解析几何第6讲双曲线分层演练直击高考文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（江苏专版）2019届高考数学一轮复习第八章平面解析几何第6讲双曲线分层演练直击高考文）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（江苏专版）2019届高考数学一轮复习第八章平面解析几何第6讲双曲线分层演练直击高考文的全部内容。
第6讲双曲线1．双曲线错误!－错误!＝1的焦距为________．［解析] 由双曲线定义易知c2＝5.［答案] 2错误!2．（2018·江苏省重点中学领航高考冲刺卷（二））已知方程错误!＋错误!＝1表示双曲线，则实数m的取值范围是________．［解析] 因为方程错误!＋错误!＝1表示双曲线,所以当焦点在x轴上时，错误!，解得－1〈m〈0；当焦点在y轴上时,错误!，解得m<－1.所以实数m的取值范围是m〈－1或－1〈m<0.［答案］（－∞,－1)∪（－1,0）3．双曲线错误!－y2＝1的顶点到其渐近线的距离为________．[解析］双曲线错误!－y2＝1的渐近线方程为y＝±错误!，即x±2y＝0，所以双曲线的顶点(±2，0）到其渐近线距离为错误!＝错误!。
[答案］错误!4．(2018·江苏省重点中学领航高考冲刺卷（五))在平面直角坐标系xOy中,双曲线错误!－y2b2＝1(a>0,b>0）的一条渐近线方程为y＝错误!x，则双曲线的离心率为________．［解析] 由题意得，错误!＝错误!，又a2＋b2＝c2，所以错误!＝错误!，所以错误!＝错误!，所以e＝错误!。
19版高考数学一轮复习第8章平面解析几何8.6双曲线学案文
19版高考数学一轮复习第8章平面解析几何8.6双曲线学案文D(3)当a>c 时，P点不存在．2．双曲线的标准方程和几何性质标准方程x2a2－y2b2＝1(a>0，b>0)y2a2－x2b2＝1(a>0，b>0)图形续表3．必记结论(1)焦点到渐近线的距离为b.(2)等轴双曲线：实轴长和虚轴长相等的双曲线叫等轴双曲线，其方程可写作：x2－y2＝λ(λ≠0)．(3)等轴双曲线⇔离心率e＝2⇔两条渐近线y＝±x相互垂直．[诊断自测]1．概念思辨(1)平面内到点F1(0,4)，F2(0，－4)距离之差等于6的点的轨迹是双曲线．( )(2)双曲线方程x2m2－y2n2＝λ(m>0，n>0，λ≠0)的渐近线方程是x2m2－y2n2＝0，即xm±yn＝0.( )(3)等轴双曲线的渐近线互相垂直，离心率等于 2.( )(4)若双曲线x2a2－y2b2＝1(a>0，b>0)与y2b2－x2a2＝1(a>0，b>0)的离心率分别是e1，e2，则1e21＋1e22＝1(此结论中两条双曲线为共轭双曲线)．( ) 答案(1)×(2)√(3)√(4)√2．教材衍化(1)(选修A1－1P53T3)已知椭圆x28＋y25＝1和双曲线x2m－y2＝1有公共的焦点，那么双曲线的渐近线方程是( )A．x＝±36y B．y＝±36xC．x＝±22y D．y＝±22x答案 D解析由椭圆x28＋y25＝1和双曲线x2m－y2＝1有公共的焦点，得m＋1＝8－5.所以m＝2，所以双曲线方程为x22－y2＝1，所以双曲线的渐近线方程为y＝±22x.故选D.(2)(选修A1－1P51例3)已知中心在原点，焦点在y轴的双曲线的渐近线方程为y＝±12x，则此双曲线的离心率为________．答案 5解析因为焦点在y轴的双曲线的渐近线方程为y＝±12x，所以ab＝12，即b＝2a.由c2＝a2＋b2，得c2＝a2＋4a2＝5a2，即c2a2＝5，所以e＝ca＝5.3．小题热身(1)(2014·全国卷Ⅰ)已知F为双曲线C：x2－my2＝3m(m>0)的一个焦点，则点F到C的一条渐近线的距离为( )A. 3 B．3C.3m D．3m答案 A解析由题意知，双曲线的标准方程为x23m－y23＝1，其中a2＝3m，b2＝3，故c＝a2＋b2＝3m＋3，不妨设F为双曲线的右焦点，故F(3m＋3，0)．其中一条渐近线的方程为y＝1 mx，即x－my＝0，由点到直线的距离公式可得d＝|3·m＋1|1＋(－m)2＝3，故选A.(2)(2016·山东高考)已知双曲线E：x2a2－y2b2＝1(a>0，b>0)．若矩形ABCD的四个顶点在E上，AB，CD的中点为E的两个焦点，且2|AB|＝3|BC|，则E的离心率是________．答案 2解析由已知得|AB|＝|CD|＝2b2a，|BC|＝|AD|＝|F1F2|＝2c.因为2|AB|＝3|BC|，所以4b2a＝6c，又b2＝c2－a2，所以2e2－3e－2＝0，解得e＝2或e＝－12(舍去)．题型1 双曲线的定义及应用典例1(2017·湖北武汉调研)若双曲线x2 4－y212＝1的左焦点为F，点P是双曲线右支上的动点，A(1,4)，则|PF|＋|PA|的最小值是( )A．8 B．9C．10 D．12利用双曲线定义得到|PF|＋|PA|＝2a＋|PB|＋|PA|，再利用|PA|＋|PB|≥|AB|求出最小值．答案 B解析由题意知，双曲线x24－y212＝1的左焦点F的坐标为(－4,0)，设双曲线的右焦点为B，则B(4,0)，由双曲线的定义知|PF|＋|PA|＝4＋|PB|＋|PA|≥4＋|AB|＝4＋(4－1)2＋(0－4)2＝4＋5＝9，当且仅当A，P，B三点共线且P在A，B之间时取等号．∴|PF|＋|PA|的最小值为9.故选B.典例2(2018·河北邯郸模拟)设动圆C 与两圆C1：(x＋5)2＋y2＝4，C2：(x－5)2＋y2＝4中的一个内切，另一个外切，则动圆圆心C 的轨迹方程为________．根据圆与圆相切关系求动圆圆心到两个定圆圆心的距离之差，然后用定义法求解．答案x24－y 2＝1解析 设圆C 的圆心C 的坐标为(x ，y )，半径为r ，由题设知r ＞2，于是有⎩⎨⎧|CC 1|＝r ＋2，|CC 2|＝r －2或⎩⎨⎧|CC 1|＝r －2，|CC 2|＝r ＋2，∴||CC 1|－|CC 2||＝4＜25＝|C 1C 2|，即圆心C 的轨迹L 是以C 1，C 2为焦点，4为实轴长的双曲线，∴L 的方程为x2⎝ ⎛⎭⎪⎫422－y2(5)2－⎝ ⎛⎭⎪⎫422＝1，即x24－y 2＝1. 方法技巧1．“焦点三角形”中常用到的知识点及技巧(1)常用知识点：在“焦点三角形”中，正弦定理、余弦定理、双曲线的定义经常使用．(2)技巧：经常结合||PF1|－|PF2||＝2a，运用平方的方法，建立它与|PF1|·|PF2|的联系．2．应用双曲线定义需注意的问题(1)在双曲线的定义中一是不能漏掉“绝对值”，否则轨迹是双曲线的一支；二是“常数”小于|F1F2|，否则轨迹是线段或不存在．(2)求双曲线方程时，注意用标准形式．冲关针对训练1．(2017·衡水模拟)已知△ABP的顶点A，B分别为双曲线C：x216－y29＝1的左、右焦点，顶点P在双曲线上，则|sin A－sin B|sin P的值等于( )A.45B.74C.54D.7答案 A解析 由x216－y29＝1得a ＝4，b ＝3，c ＝5.结合双曲线定义及正弦定理得|sin A －sin B |sin P ＝||PA |－|PB |||AB |＝2a 2c ＝45，故选A.2．已知双曲线x 216－y 29＝1上有一点P ，F 1，F 2是双曲线的焦点，且∠F 1PF 2＝π3，则△PF 1F 2的面积为________．答案 9 3解析 由题意，得|F 1F 2|＝216＋9＝10. 因为⎩⎪⎨⎪⎧||PF 1|－|PF 2||＝8，|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|cos π3＝100，所以|PF 1|·|PF 2|＝36.所以S △PF 1F 2＝12|PF 1|·|PF 2|sin π3＝9 3.题型2 双曲线的标准方程及应用典例 (2018·兰州检测)已知双曲线x 24－y 2b2＝1(b >0)，以原点为圆心，双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于A ，B ，C ，D 四点，四边形ABCD 的面积为2b ，则双曲线的方程为( )A.x 24－3y24＝1 B.x 24－4y23＝1 C.x24－y24＝1 D.x24－y212＝1 本题采用方程法．答案 D解析 不妨设A (x 0，y 0)在第一象限，由题意得⎩⎪⎨⎪⎧x 20＋y 20＝22，①2x 0·2y 0＝2b ，②y 0＝b 2x 0，③由①③得x 20＝164＋b2，④ 所以y 20＝b 24×164＋b 2＝4b 24＋b2，⑤ 由②④⑤可得b 2＝12.所以双曲线的方程为x24－y212＝1.故选D.[条件探究1] 若将典例中条件变为“以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4)”，求双曲线的方程．解 因为以|F 1F 2|为直径的圆与双曲线渐近线的一个交点为(3,4)，所以c ＝5，b a ＝43.又c2＝a 2＋b 2，所以a ＝3，b ＝4，所以此双曲线的方程为x29－y216＝1.[条件探究2] 若将典例中变为“双曲线过点(2,1)，且双曲线与椭圆x24＋y2＝1共焦点”，求双曲线的方程．解椭圆x24＋y2＝1的焦点坐标是(±3，0)．设双曲线方程为x2a2－y2b2＝1(a>0，b>0)，所以4 a2－1b2＝1，a2＋b2＝3，解得a2＝2，b2＝1，所以所求双曲线方程是x22－y2＝1.方法技巧双曲线标准方程的求解方法1．定义法．2．待定系数法．提醒：利用求待定系数法求双曲线标准方程的关键是：设出双曲线方程的标准形式，根据已知条件，列出关于参数a，b，c的方程并求出a，b，c的值．与双曲线x2a2－y2b2＝1，有相同渐近线时可设所求双曲线方程为x2a2－y2b2＝λ(λ≠0)．冲关针对训练1．已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为( )A.x24－y 2＝1 B ．x 2－y24＝1C.3x 220－3y25＝1 D.3x 25－3y220＝1 答案 A解析 由题意得c ＝5，b a ＝12，则a ＝2，b＝1，所以双曲线的方程为x24－y 2＝1.故选A.2．(2018·福建漳州模拟)已知双曲线C ：x2a 2－y2b2＝1(a ＞0，b ＞0)的左、右焦点为F 1，F 2，P 为双曲线C 右支上异于顶点的一点，△PF 1F 2的内切圆与x 轴切于点(1,0)，且P 与点F 1关于直线y ＝－bxa对称，则双曲线的方程为________________．答案 x 2－y 24＝1解析 设点A (1,0)，因为△PF 1F 2的内切圆与x 轴切于点(1,0)，则|PF 1|－|PF 2|＝|AF 1|－|AF 2|，所以2a ＝(c ＋1)－(c －1)，则a ＝1.因为点P 与点F 1关于直线y ＝－bxa对称，所以∠F 1PF 2＝π2，且|PF 1||PF 2|＝b a ＝b ，结合|PF 1|－|PF 2|＝2，|PF 1|2＋|PF 2|2＝4c 2＝4＋4b 2，可得b ＝2.所以双曲线的方程为x 2－y 24＝1.题型3 双曲线的几何性质角度 1 与双曲线有关的范围问题(多维探究)典例(2015·全国卷Ⅰ)已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1上的一点，F 1，F 2是C 的两个焦点．若MF 1→·MF 2→<0，则y 0的取值范围是( )A.⎝⎛⎭⎪⎫－33，33B.⎝⎛⎭⎪⎫－36，36C.⎝ ⎛⎭⎪⎫－223，223D.⎝⎛⎭⎪⎫－233，233 根据已知MF1→·MF 2→<0，列出y 0的不等式求解．答案 A解析 不妨令F 1为双曲线的左焦点，则F 2为右焦点，由题意可知a 2＝2，b 2＝1，∴c 2＝3，∴F 1(－3，0)，F 2(3，0)，则MF1→·MF 2→＝(－3－x 0)·(3－x 0)＋(－y 0)·(－y 0)＝x 20＋y 20－3.又知x 202－y 20＝1，∴x 20＝2＋2y 20，∴MF 1→·MF 2→＝3y 2－1<0.∴－33<y 0<33，故选A.[条件探究] 将本例中条件“MF 1→·MF 2→<0”改为“MF1→·MF 2→＝0”，求△MF 1F 2的面积． 解 由MF1→·MF 2→＝0得MF 1⊥MF 2，知△MF 1F 2为直角三角形．设M 为双曲线右支上一点，则|MF 1|－|MF 2|＝22，|MF 1|2＋|MF 2|2＝(|MF 1|－|MF 2|)2＋2|MF 1|·|MF 2|＝12，得|MF 1|·|MF 2|＝2，所以S △MF 1F 2＝12·|MF 1|·|MF 2|＝1.角度2 与双曲线渐近线有关的问题 典例(2017·山东高考)在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的右支与焦点为F 的抛物线x 2＝2py (p ＞0)交于A ，B 两点．若|AF |＋|BF |＝4|OF |，则该双曲线的渐近线方程为________．涉及曲线交点时，考虑用设而不求的方法．答案 y ＝±22x解析 设A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧x 2a 2－y 2b2＝1，x 2＝2py ，得a 2y 2－2pb 2y ＋a 2b 2＝0，∴y1＋y2＝2pb2 a2.又∵|AF|＋|BF|＝4|OF|，∴y1＋p2＋y2＋p2＝4×p2，即y1＋y2＝p，∴2pb2a2＝p，即b2a2＝12，∴ba＝22，∴双曲线的渐近线方程为y＝±22x.角度3 与双曲线离心率有关的问题典例(2016·全国卷Ⅱ)已知F1，F2是双曲线E：x2a2－y2b2＝1的左、右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1＝13，则E的离心率为( )A. 2B.3 2C. 3 D．2将等式sin ∠MF 2F 1＝13转化为关于a ，b ，c 的等式．答案 A解析 由MF 1⊥x 轴，可得M ⎝⎛⎭⎪⎫－c ，b 2a ，∴|MF 1|＝b 2a .由sin ∠MF 2F 1＝13，可得cos ∠MF 2F 1＝1－⎝ ⎛⎭⎪⎫132＝223，又tan ∠MF 2F 1＝|MF 1||F 1F 2|＝b 22ac ，∴b 22ac ＝13223，∴b 2＝22ac ，∵c 2＝a 2＋b 2⇒b 2＝c 2－a 2，∴c 2－a 2－22ac ＝0⇒e 2－22e －1＝0，∴e ＝ 2.故选A.方法技巧与双曲线离心率、渐近线有关问题的解题策略1．双曲线的离心率e ＝ca是一个比值，故只需根据条件得到关于a，b，c的一个关系式，利用b2＝c2－a2消去b，然后变形成关于e的关系式，并且需注意e＞1.2．求双曲线离心率或其范围的方法(1)求a，b，c的值，由c2a2＝a2＋b2a2＝1＋b2a2直接求e.(2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝c2－a2消去b，然后转化成关于e的方程(或不等式)求解．3．求双曲线x2a2－y2b2＝1(a＞0，b＞0)的渐近线的方法是令x2a2－y2b2＝0，即得两渐近线方程xa±yb＝0.冲关针对训练1．(2015·全国卷Ⅱ)已知A，B为双曲线E 的左、右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为( )A. 5 B．2C. 3D. 2 答案 D解析设双曲线E的标准方程为x2a2－y2b2＝1(a>0，b>0)，则A(－a,0)，B(a,0)，不妨设点M在第一象限内，则易得M(2a，3a)，又M点在双曲线E上，于是(2a)2a2－(3a)2b2＝1，可得b2＝a2，∴e＝1＋b2a2＝ 2.故选D.2．(2018·成都统考)已知a>b>0，椭圆C1的方程为x2a2＋y2b2＝1，双曲线C2的方程为x2a2－y2b2＝1，C1与C2的离心率之积为32，则C2的渐近线方程为( )A．x±2y＝0 B.2x±y＝0C．x±2y＝0 D．2x±y＝0答案 A解析设椭圆C1和双曲线C2的离心率分别为e 1和e 2，则e 1＝a 2－b 2a ，e 2＝a 2＋b2a.因为e 1·e 2＝32，所以a 4－b 4a 2＝32，即⎝ ⎛⎭⎪⎫b a 4＝14，所以b a ＝22. 故双曲线的渐近线方程为y ＝±b a x ＝±22x ，即x ±2y ＝0.故选A.题型4 直线与双曲线的综合问题 典例1以P (1,8)为中点作双曲线为y 2－4x 2＝4的一条弦AB ，求直线AB 的方程．本题采用“点差法”．解 设A (x 1，y 1)，B (x 2，y 2)，则⎩⎨⎧y 21－4x 21＝4，y 22－4x 22＝4，∴(y 1＋y 2)(y 1－y 2)＝4(x 1＋x 2)(x 1－x 2)， ∵弦AB 的中点是P (1,8)，∴x 1＋x 2＝2，y 1＋y 2＝16.∴16(y1－y2)＝8(x1－x2)，∴直线AB的斜率为y1－y 2x1－x2＝12，∴直线AB的方程为y－8＝12(x－1)，即直线AB的方程为x－2y＋15＝0.典例2已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为(3，0)．(1)求双曲线C的方程；(2)若直线l：y＝kx＋2与双曲线C恒有两个不同的交点A和B，且OA→·OB→>2(其中O为原点)，求k的取值范围．(2)直线与双曲线联立，用设而不求的方法，列出不等式，然后求解．解(1)设双曲线方程为x2a2－y2b2＝1(a>0，b>0)．由已知得a＝3，c＝2，于是a2＋b2＝22，b2＝1，故双曲线C的方程为x23－y2＝1.(2)将y ＝kx ＋2代入x23－y 2＝1，得(1－3k 2)x 2－62kx －9＝0.由直线l 与双曲线交于不同的两点，得⎩⎨⎧1－3k 2≠0，Δ＝(62k )2＋36(1－3k 2)＝36(1－k 2)>0，即k 2≠13且k 2<1.设A (x A ，y A )，B (x B ，y B )， 则x A ＋x B ＝62k 1－3k 2，x A x B ＝－91－3k 2. 由OA →·OB →>2，得x A x B ＋y A y B >2.x A x B ＋y A y B ＝x A x B ＋(kx A ＋2)(kx B ＋2)＝(k 2＋1)x A x B ＋2k (x A ＋x B )＋2 ＝(k 2＋1)－91－3k 2＋2k ·62k 1－3k2＋2 ＝3k 2＋73k 2－1. 于是3k 2＋73k 2－1>2，即－3k 2＋93k 2－1>0，解得13<k 2<3，又∵k 2<1，∴13<k 2<1， 故k 的取值范围为⎝ ⎛⎭⎪⎫－1，－33∪⎝ ⎛⎭⎪⎫33，1.方法技巧直线y ＝kx ＋m 与双曲线x 2a 2－y2b2＝1(a >0，b >0)的位置关系的分析：1．代数法⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2a 2－y2b2＝1，消去y ，得(b2－a 2k 2)x 2－2kma 2x －a 2(m 2＋b 2)＝0.(1)二次项系数为0时，直线L ⎝⎛⎭⎪⎫k ＝±b a 与双曲线的渐近线平行或重合．重合：无交点；平行：有一个交点． (2)二次项系数不为0时，上式为一元二次方程，Δ>0⇔直线与双曲线相交(两个交点)；Δ＝0⇔直线与双曲线相切； Δ<0⇔直线与双曲线相离．2．几何法：运用数形结合思想考查直线与渐近线的位置关系，转化为其斜率的大小关系．冲关针对训练若双曲线E ：x2a2－y 2＝1(a ＞0)的离心率等于2，直线y ＝kx －1与双曲线E 的右支交于A ，B 两点．(1)求k 的取值范围；(2)若|AB |＝63，点C 是双曲线上一点，且OC →＝m (OA →＋OB →)，求k ，m 的值．解 (1)由⎩⎪⎨⎪⎧c a＝2，a 2＝c 2－1，得⎩⎨⎧a 2＝1，c 2＝2，故双曲线E 的方程为x 2－y 2＝1.设A (x 1，y 1)，B (x 2，y 2)，由⎩⎨⎧y ＝kx －1，x 2－y 2＝1，得(1－k 2)x 2＋2kx －2＝0.(*)∵直线与双曲线右支交于A ，B 两点，故⎩⎨⎧k ＞1，Δ＝(2k )2－4(1－k 2)×(－2)＞0，即⎩⎨⎧k ＞1，－2＜k ＜2，所以1＜k ＜ 2.故k 的取值范围是{k |1＜k ＜2}． (2)由(*)得x 1＋x 2＝2k k 2－1，x 1x 2＝2k 2－1，∴|AB |＝1＋k 2·(x 1＋x 2)2－4x 1x 2 ＝2(1＋k 2)(2－k 2)(k 2－1)2＝63， 整理得28k 4－55k 2＋25＝0，∴k 2＝57或k 2＝54，又1＜k ＜2，∴k ＝52，所以x 1＋x 2＝45，y 1＋y 2＝k (x 1＋x 2)－2＝8.设C (x 3，y 3)，由OC →＝m (OA →＋OB →)， 得(x 3，y 3)＝m (x 1＋x 2，y 1＋y 2) ＝(45m,8m )．∵点C 是双曲线上一点，∴80m2－64m2＝1，得m＝±14 .故k＝52，m＝±14.1.(2016·全国卷Ⅰ)已知方程x2m2＋n－y23m2－n＝1表示双曲线，且该双曲线两焦点间的距离为4，则n的取值范围是( )A．(－1,3) B．(－1，3)C．(0,3) D．(0，3)答案 A解析由题意可知：c2＝(m2＋n)＋(3m2－n)＝4m2，其中c为半焦距，∴2c＝2×2|m|＝4，∴|m|＝1，∵方程x2m2＋n－y23m2－n＝1表示双曲线，∴(m2＋n)·(3m2－n)>0，∴－m2<n<3m2，∴－1<n<3.故选A.2．(2017·全国卷Ⅲ)已知双曲线C ：x 2a 2－y2b2＝1(a ＞0，b ＞0)的一条渐近线方程为y ＝52x ，且与椭圆x 212＋y 23＝1有公共焦点，则C 的方程为( )A.x28－y210＝1 B.x24－y25＝1 C.x 25－y 24＝1 D.x 24－y 23＝1 答案 B解析 解法一：由双曲线的渐近线方程可设双曲线方程为x24－y25＝k (k >0)，即x 24k －y25k＝1，∵双曲线与椭圆x 212＋y 23＝1有公共焦点，∴4k ＋5k ＝12－3，解得k ＝1，故双曲线C 的方程为x24－y25＝1.故选B.解法二：∵椭圆x 212＋y 23＝1的焦点为(±3,0)，双曲线与椭圆x212＋y23＝1有公共焦点，∴a 2＋b 2＝(±3)2＝9①，∵双曲线的一条渐近线为y ＝52x ，∴b a ＝52②，联立①②可解得a 2＝4，b 2＝5.∴双曲线C 的方程为x24－y25＝1.故选B.3．(2017·全国卷Ⅰ)已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点．若∠MAN ＝60°，则C 的离心率为________．答案 233解析 如图，由题意知点A (a,0)，双曲线的一条渐近线l的方程为y＝bax，即bx－ay＝0，∴点A到l的距离d＝aba2＋b2.又∠MAN＝60°，MA＝NA＝b，∴△MAN为等边三角形，∴d＝32MA＝32b，即aba2＋b2＝32b，∴a2＝3b2，∴e＝ca＝a2＋b2a2＝233.4．(2018·兰州诊断)若双曲线x2a2－y2b2＝1(a>0，b>0)一条渐近线的倾斜角为π3，离心率为e，则a2＋eb的最小值为________．答案26 3解析由题意，可得k＝ba＝tanπ3＝ 3.∴b＝3a，则a2＝b23，∴e＝1＋b2a2＝2.∴a2＋eb＝b23＋2b＝b3＋2b≥2b3×2b＝263.当且仅当b2＝6，a2＝2时取“＝”．[重点保分两级优选练]A级一、选择题1．(2018·唐山统考)“k<9”是“方程x2 25－k ＋y2k－9＝1表示双曲线”的( )A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 A解析∵方程x225－k＋y2k－9＝1表示双曲线，∴(25－k)(k－9)<0，∴k<9或k>25，∴“k<9”是“方程x225－k＋y2k－9＝1表示双曲线”的充分不必要条件，故选A.2．(2017·湖北黄冈二模)已知双曲线x 2－y23＝1的左、右焦点分别为F 1，F 2，双曲线的离心率为e ，若双曲线上存在一点P 使sin ∠PF 2F 1sin ∠PF 1F 2＝e ，则F 2P →·F 2F 1→的值为( )A ．3B ．2C ．－3D ．2答案 B解析 由题意及正弦定理得sin ∠PF 2F 1sin ∠PF 1F 2＝|PF 1||PF 2|＝e ＝2，∴|PF 1|＝2|PF 2|，由双曲线的定义知|PF 1|－|PF 2|＝2，∴|PF 1|＝4，|PF 2|＝2，又|F 1F 2|＝4，由余弦定理可知cos ∠PF 2F 1＝|PF 2|2＋|F 1F 2|2－|PF 1|22|PF 2|·|F 1F 2|＝4＋16－162×2×4＝14，∵F 2P →·F 2F 1→＝|F 2P →|·|F 2F 1→|cos ∠PF 2F 1＝2×4×14＝2.故选B.3．已知双曲线中心在原点且一个焦点为F (7，0)，直线y ＝x －1与其相交于M ，N 两点，MN 中点的横坐标为－23，则此双曲线的方程是( )A.x23－y24＝1 B.x24－y23＝1 C.x 25－y 22＝1 D.x 22－y 25＝1 答案 D解析 设双曲线方程x 2a 2－y2b2＝1，M (x 1，y 1)，N (x 2，y 2)，∴⎩⎪⎨⎪⎧x 21a 2－y 21b2＝1，①x 22a 2－y 22b2＝1.②①－②，得y 1－y 2x 1－x 2＝b 2a 2·x 1＋x 2y 1＋y 2.∴1＝b 2a 2·－23－53，∴5a 2＝2b 2.又a 2＋b 2＝7，∴a 2＝2，b 2＝5，故选D. 4．过双曲线x 2－y22＝1的右焦点F 作直线l交双曲线于A ，B 两点，若|AB |＝4，则这样的直线l 有( )A ．1条B ．2条C ．3条D ．4条答案 C解析 解法一：设A (x 1，y 1)，B (x 2，y 2)，当直线l 的斜率不存在时，其方程为x ＝3，由⎩⎪⎨⎪⎧x ＝3，x 2－y22＝1，得y ＝±2，∴|AB |＝|y 1－y 2|＝4满足题意．当直线l 的斜率存在时，其方程为y ＝k (x －3)，由⎩⎪⎨⎪⎧y ＝k (x －3)，x 2－y22＝1，得(2－k 2)x 2＋23k 2x －3k 2－2＝0.当2－k 2≠0时，x 1＋x 2＝23k2k 2－2，x 1x 2＝3k 2＋2k 2－2， |AB |＝1＋k 2(x 1＋x 2)2－4x 1x 2＝1＋k 2⎝ ⎛⎭⎪⎫23k 2k 2－22－12k 2＋8k 2－2＝1＋k216(k 2＋1)(k 2－2)2＝4(1＋k 2)|k 2－2|＝4， 解得k ＝±22，故这样的直线有3条．故选C.解法二：当直线l 无斜率时同解法一，且此时与双曲线一支交于两点的情况只有一种，其他直线得到的|AB |>4.由于双曲线的实轴长为2小于4，因此与双曲线两支分别相交得到的两点都在x 轴上方或x 轴下方两种情况．综上所述，共有三条直线满足条件，故选C.5．(2016·浙江高考)已知椭圆C 1：x 2m2＋y2＝1(m >1)与双曲线C 2：x2n2－y 2＝1(n >0)的焦点重合，e 1，e 2分别为C 1，C 2的离心率，则( )A ．m >n 且e 1e 2>1B ．m >n 且e 1e 2<1C ．m <n 且e 1e 2>1D ．m <n 且e 1e 2<1 答案 A解析 在椭圆中，a 1＝m ，c 1＝m 2－1，e 1＝m 2－1m.在双曲线中，a 2＝n ，c 2＝n 2＋1，e 2＝n 2＋1n.因为c 1＝c 2，所以n 2＝m 2－2.由n >0，m >1可得m >n ，且m 2－2>0.从而e 21·e 22＝(m 2－1)(n 2＋1)m 2·n2＝(m 2－1)2m 2·(m 2－2)，则e 21e 22－1＝(m 2－1)2m 2(m 2－2)－1＝1m 2(m 2－2)>0，即e 1e 2>1.故选A. 6．(2017·福建龙岩二模)已知离心率为52的双曲线C ：x 2a 2－y2b2＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，M 是双曲线C 的一条渐近线上的点，且OM⊥MF2，O为坐标原点，若S△OMF2＝16，则双曲线的实轴长是( )A．32 B．16C．84 D．4答案 B解析由题意知F2(c,0)，不妨令点M在渐近线y＝bax上，由题意可知|F2M|＝bca2＋b2＝b，所以|OM|＝c2－b2＝a.由S△OMF2＝16，可得12 ab＝16，即ab＝32，又a2＋b2＝c2，ca＝52，所以a＝8，b＝4，c＝45，所以双曲线C的实轴长为16.故选B.7．(2018·湖南十校联考)设双曲线x2a2－y2b2＝1的两条渐近线与直线x＝a2c分别交于A，B两点，F为该双曲线的右焦点．若60°＜∠AFB＜90°，则该双曲线的离心率的取值范围是( ) A．(1，2) B．(2，2)C ．(1,2)D ．(2，＋∞)答案 B解析 双曲线x 2a 2－y2b2＝1的两条渐近线方程为y ＝±b a x ，x ＝a 2c 时，y ＝±abc ，不妨设A ⎝ ⎛⎭⎪⎫a 2c，ab c ，B ⎝ ⎛⎭⎪⎫a 2c，－ab c ，∵60°＜∠AFB ＜90°，∴33＜k FB ＜1，∴33＜abc c －a 2c＜1，∴33＜a b ＜1，∴13＜a 2c 2－a 2＜1，∴1＜e 2－1＜3，∴2＜e ＜2.故选B.8．(2017·福建漳州八校联考)已知椭圆C 1：x 2a 21＋y 2b 21＝1(a 1＞b 1＞0)与双曲线C 2：x 2a 22－y2b 22＝1(a 2＞0，b 2＞0)有相同的焦点F 1，F 2，点P 是两曲线的一个公共点，e 1，e 2分别是两曲线的离心率，若PF 1⊥PF 2，则4e 21＋e 22的最小值为( )A.52B．4C.92D．9答案 C解析由题意设焦距为2c，令P在双曲线的右支上，由双曲线的定义知|PF1|－|PF2|＝2a2，①由椭圆定义知|PF1|＋|PF2|＝2a1，②又∵PF1⊥PF2，∴|PF1|2＋|PF2|2＝4c2，③①2＋②2，得|PF1|2＋|PF2|2＝2a21＋2a22，④将④代入③，得a21＋a22＝2c2，∴4e21＋e22＝4c2a21＋c2a22＝4(a21＋a22)2a21＋a21＋a222a22＝52＋2a22a21＋a212a22≥52＋22a22a21·a212a22＝92，当且仅当2a22a21＝a212a22，即a21＝2a22时，取等号．故选C.9．(2017·青州市模拟)已知中心在坐标原点的椭圆与双曲线有公共焦点，且左、右焦点分别为F1，F2，这两条曲线在第一象限的交点为P，△PF 1F 2是以PF 1为底边的等腰三角形．若|PF 1|＝10，记椭圆与双曲线的离心率分别为e 1，e 2，则e 1·e 2的取值范围是( )A.⎝ ⎛⎭⎪⎫13，＋∞B.⎝ ⎛⎭⎪⎫15，＋∞ C.⎝ ⎛⎭⎪⎫19，＋∞ D ．(0，＋∞)答案 A解析 设椭圆和双曲线的半焦距为c ，|PF 1|＝m ，|PF 2|＝n (m >n )，由于△PF 1F 2是以PF 1为底边的等腰三角形．若|PF 1|＝10，即有m ＝10，n ＝2c ，由椭圆的定义可得m ＋n ＝2a 1， 由双曲线的定义可得m －n ＝2a 2， 即有a 1＝5＋c ，a 2＝5－c (c <5)， 再由三角形的两边之和大于第三边，可得2c ＋2c >10，可得c >52，即有52<c <5.由离心率公式可得e1·e2＝ca1·ca2＝c225－c2＝125 c2－1，由于1<25c2<4，则有125c2－1>13.则e1·e2的取值范围为⎝⎛⎭⎪⎫13，＋∞.故选A. 10．已知椭圆C：x2a2＋y2b2＝1(a>b>0)的离心率为32.双曲线x2－y2＝1的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为( )A.x28＋y22＝1 B.x212＋y26＝1C.x216＋y24＝1 D.x220＋y25＝1答案 D解析∵椭圆的离心率为32，∴c a ＝a 2－b 2a ＝32，∴a ＝2b .∴椭圆的方程为x 2＋4y 2＝4b 2.∵双曲线x 2－y 2＝1的渐近线方程为x ±y ＝0，∴渐近线x ±y ＝0与椭圆x 2＋4y 2＝4b 2在第一象限的交点为⎝ ⎛⎭⎪⎫255b ，255b ，∴由圆锥曲线的对称性得四边形在第一象限部分的面积为255b ×255b ＝4，∴b 2＝5，∴a 2＝4b 2＝20. ∴椭圆C 的方程为x220＋y25＝1.故选D. 二、填空题11．若点P 在曲线C 1：x216－y29＝1上，点Q在曲线C 2：(x －5)2＋y 2＝1上，点R 在曲线C 3：(x ＋5)2＋y 2＝1上，则|PQ |－|PR |的最大值是________．答案 10解析依题意得，点F1(－5,0)，F2(5,0)分别为双曲线C1的左、右焦点，因此有|PQ|－|PR|≤|(|PF2|＋1)－(|PF1|－1)|≤||PF2|－|PF1||＋2＝2×4＋2＝10，故|PQ|－|PR|的最大值是10.12．过双曲线x2a2－y2b2＝1(a>0，b>0)的左焦点F(－c,0)(c>0)，作圆x2＋y2＝a24的切线，切点为E，延长FE交曲线右支于点P，若OE→＝12(OF→＋OP→)，则双曲线的离心率为________．答案10 2解析圆x2＋y2＝a24的半径为a2，由OE→＝12(OF→＋OP→)知，E是FP的中点，设F′(c,0)，由于O是FF′的中点，所以OE⊥PF，|OE|＝12|PF′|⇒|PF′|＝2|OE|＝a.由双曲线定义，|FP|＝3a，因为FP是圆的切线，切点为E ，所以FP ⊥OE ，从而∠FPF ′＝90°.由勾股定理，得|FP |2＋|F ′P |2＝|FF ′|2⇒9a 2＋a 2＝4c 2⇒e ＝102.13．(2018·安徽江南十校联考)已知l 是双曲线C ：x22－y24＝1的一条渐近线，P 是l 上的一点，F 1，F 2是C 的两个焦点，若PF1→·PF 2→＝0，则P 到x 轴的距离为________．答案 2解析 由题意取F 1(－6，0)，F 2(6，0)，不妨设l 的方程为y ＝2x ，则可设P (x 0，2x 0)，由PF1→·PF 2→＝(－6－x 0，－2x 0)·(6－x 0，－2x 0)＝3x 2－6＝0，得x 0＝±2，故P 到x 轴的距离为2|x 0|＝2.14．(2018·贵州六校联考)我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F 1，F 2是一对相关曲线的焦点，P 是它们在第一象限的交点，当∠F 1PF 2＝60°时，这一对相关曲线中双曲线的离心率是________．答案 3解析 设椭圆的半长轴为a 1，椭圆的离心率为e 1，则e 1＝c a 1，a 1＝c e 1.设双曲线的实半轴为a ，双曲线的离心率为e ，e ＝c a ，a ＝c e.|PF 1|＝x ，|PF 2|＝y (x >y >0)，则由余弦定理得4c 2＝x 2＋y 2－2xy cos60°＝x 2＋y 2－xy ，当点P 看作是椭圆上的点时， 有4c 2＝(x ＋y )2－3xy ＝4a 21－3xy ，① 当点P 看作是双曲线上的点时， 有4c 2＝(x －y )2＋xy ＝4a 2＋xy ，② ①②联立消去xy ，得4c 2＝a 21＋3a 2，即4c 2＝⎝ ⎛⎭⎪⎫c e 12＋3⎝ ⎛⎭⎪⎫c e 2，所以⎝ ⎛⎭⎪⎫1e 12＋3⎝ ⎛⎭⎪⎫1e 2＝4，又因为1e 1＝e ，所以e 2＋3e2＝4，整理得e 4－4e 2＋3＝0，解得e 2＝3，所以e ＝3，即双曲线的离心率为 3.B 级三、解答题15．已知点M (－2,0)，N (2,0)，动点P 满足条件|PM |－|PN |＝22，记动点P 的轨迹为W .(1)求W 的方程；(2)若A 和B 是W 上的不同两点，O 是坐标原点，求OA →·OB →的最小值．解 (1)由|PM |－|PN |＝22知动点P 的轨迹是以M ，N 为焦点的双曲线的右支，实半轴长a ＝ 2.又焦距2c ＝4，所以虚半轴长b ＝c 2－a 2＝2.。
2020版高考数学一轮复习第8章平面解析几何第6节双曲线教学案理含解析新人教A版
第六节双曲线[考纲传真] 1.了解双曲线的实际背景，了解双曲线在刻画现实世界和解决实际问题中的作用.2.了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线).3.理解数形结合思想.4.了解双曲线的简单应用．1．双曲线的定义(1)平面内与两个定点F1，F2(|F1F2|＝2c>0)的距离之差的绝对值为非零常数2a(2a <2c )的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点．(2)集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数且a>0，c>0.①当2a<|F1F2|时，M点的轨迹是双曲线；②当2a＝|F1F2|时，M点的轨迹是两条射线；③当2a>|F1F2|时，M点不存在．2．双曲线的标准方程和几何性质标准方程x2a2－y2b2＝1(a>0，b>0)y2a2－x2b2＝1 (a>0，b>0)图形性质范围x≥a或x≤－a，y∈R y≤－a或y≥a，x∈R 对称性对称轴：坐标轴，对称中心：原点顶点A1(－a,0)，A2(a,0)A1(0，－a)，A2(0，a) 渐近线y＝±bax y＝±abx 离心率e＝ca，e∈(1，＋∞)实、虚轴线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a；线段B1B2叫做双曲线的虚轴，它的长|B1B2|＝2b；a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长a，b，c的关系c2＝a2＋b2(c>a>0，c>b>0)实轴和虚轴等长的双曲线叫做等轴双曲线，其渐近线方程为y＝±x，离心率为e＝ 2.[常用结论]1．双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)中，过焦点垂直于实轴所在直线的弦长为2b2a.2．双曲线的焦点到渐近线的距离等于其虚半轴长．3．已知双曲线x 2a 2－y 2b2＝λ(a ＞0，b ＞0，λ≠0)，求其渐近线的方程，只需把λ改写为0整理即可．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面内到点F 1(0,4)，F 2(0，－4)距离之差的绝对值等于8的点的轨迹是双曲线．( )(2)方程x 2m －y 2n＝1(mn >0)表示焦点在x 轴上的双曲线．( )(3)双曲线x 2m 2－y 2n 2＝λ(m >0，n >0，λ≠0)的渐近线方程是x 2m 2－y 2n 2＝0，即x m ±yn＝0.( )(4)等轴双曲线的渐近线互相垂直，离心率等于 2.( ) [答案] (1)× (2)× (3)√ (4)√ 2．双曲线3x 2－y 2＝1的渐近线方程是( ) A ．y ＝±3x B ．y ＝±13xC ．y ＝±3xD ．y ＝±33x C [由3x 2－y 2＝0得y ＝±3x .故选C.]3．(教材改编)若双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的焦点到其渐近线的距离等于实轴长，则该双曲线的离心率为( ) A. 5 B ．5 C. 2D ．2A [由题意可知b ＝2a ，∴e ＝c a ＝1＋b 2a2＝5，故选A.] 4．若双曲线E ：x 29－y 216＝1的左、右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝3，则|PF 2|等于( ) A ．11 B ．9 C ．5 D ．3B [由题意知a ＝3，b ＝4，∴c ＝5.由双曲线的定义||PF 1|－|PF 2||＝|3－|PF 2||＝2a ＝6，∴|PF 2|＝9.]5．已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为________．x24－y2＝1[由题意可得⎩⎪⎨⎪⎧b a＝12，a2＋b2＝5，a＞0，b＞0，解得a＝2，b＝1，所以双曲线的方程为x24－y2＝1.]双曲线的定义及其应用【例1】(1)已知圆C1：(x＋3)2＋y2＝1和圆C2：(x－3)2＋y2＝9，动圆M同时与圆C1及圆C2相外切，则动圆圆心M的轨迹方程为________．(2)已知F1，F2为双曲线C：x2－y2＝2的左、右焦点，点P在C上，|PF1|＝2|PF2|，则cos∠F1PF2＝________.(1)x2－y28＝1(x≤－1) (2)34[(1)如图所示，设动圆M与圆C1及圆C2分别外切于点A和B. 根据两圆外切的条件，得|MC1|－|AC1|＝|MA|，|MC2|－|BC2|＝|MB|.因为|MA|＝|MB|，所以|MC1|－|AC1|＝|MC2|－|BC2|，即|MC2|－|MC1|＝|BC2|－|AC1|＝2，所以点M到两定点C1，C2的距离的差是常数且小于|C1C2|.根据双曲线的定义，得动点M的轨迹为双曲线的左支(点M与C2的距离大，与C1的距离小)，其中a＝1，c＝3，则b2＝8.故点M的轨迹方程为x2－y28＝1(x≤－1)．(2)因为由双曲线的定义有|PF1|－|PF2|＝|PF2|＝2a＝22，所以|PF1|＝2|PF2|＝42，所以cos∠F1PF2＝|PF1|2＋|PF2|2－|F1F2|22|PF1|·|PF2|＝422＋222－422×42×22＝34.][母题探究] (1)将本例(2)中的条件“|PF1|＝2|PF2|”改为“∠F1PF2＝60°”，则△F1PF2的面积是多少？(2)将本例(2)中的条件“|PF1|＝2|PF2|”改为“PF1→·PF2→＝0”，则△F1PF2的面积是多少？[解] (1)不妨设点P 在双曲线的右支上， 则|PF 1|－|PF 2|＝2a ＝22， 在△F 1PF 2中，由余弦定理，得cos∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝12，∴|PF 1|·|PF 2|＝8，∴S △F 1PF 2＝12|PF 1|·|PF 2|·sin 60°＝2 3.(2)不妨设点P 在双曲线的右支上， 则|PF 1|－|PF 2|＝2a ＝22， ∵PF 1→·PF 2→＝0，∴PF 1→⊥PF 2→，∴在△F 1PF 2中，有|PF 1|2＋|PF 2|2＝|F 1F 2|2， 即|PF 1|2＋|PF 2|2＝16， ∴|PF 1|·|PF 2|＝4，∴S △F 1PF 2＝12|PF 1|·|PF 2|＝2.[规律方法] 1.利用双曲线的定义判定平面内动点的轨迹是否为双曲线，进而根据要求可求出曲线方程；2．在“焦点三角形”中，常利用正弦定理、余弦定理，经常结合||PF 1|－|PF 2||＝2a ，运用平方的方法，建立与|PF 1|·|PF 2|的联系．(1)方程x ＋102＋y 2－x －102＋y 2＝12的化简结果为( )A.x 236－y 264＝1B.x 264－y 236＝1 C.x 236－y 264＝1(x ＞0) D.x 264－y 236＝1(x ＞0) (2)设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线左、右两个焦点，若|PF 1|＝9，则|PF 2|等于________．(1)C (2)17 [(1)设F 1(－10,0)，F 2(10,0)，动点P (x ，y )，则由题意可知 |PF 1|－|PF 2|＝12，又|F 1F 2|＝20，∴动点P 的轨迹是以F 1，F 2为焦点的双曲线的右支． 又2a ＝12,2c ＝20，∴a ＝6，c ＝10，b ＝8. 即所求方程为x 236－y 264＝1(x ＞0)．(2)由题意知|PF 1|＝9＜a ＋c ＝10，所以P 点在双曲线的右支，则有|PF 2|－|PF 1|＝2a ＝8，故|PF 2|＝|PF 1|＋8＝17.]双曲线的标准方程【例2】 (1)(2018·天津高考)已知双曲线x 2a2－y 2b2＝1(a ＞0，b ＞0)的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点．设A ，B 到双曲线的同一条渐近线的距离分别为d 1和d 2，且d 1＋d 2＝6，则双曲线的方程为( ) A.x 24－y 212＝1 B.x 212－y 24＝1 C.x 23－y 29＝1 D.x 29－y 23＝1 (2)已知双曲线过点(2,3)，渐近线方程为y ＝±3x ，则该双曲线的标准方程是( ) A.7x 216－y212＝1 B.y 23－x 22＝1 C ．x 2－y 23＝1D.3y 223－x223＝1 (1)C (2)C [(1)由d 1＋d 2＝6，得双曲线的右焦点到渐近线的距离为3，所以b ＝3.因为双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率为2，所以c a ＝2，所以a 2＋b 2a 2＝4，所以a 2＋9a2＝4，解得a 2＝3，所以双曲线的方程为x 23－y 29＝1，故选C.(2)因为双曲线的渐近线方程为y ＝±3x, 即y3＝±x .所以可设双曲线的方程是x 2－y 23＝λ(λ≠0)，将点(2,3)代入，得λ＝1，所以该双曲线的标准方程为x 2－y 23＝1，故选C.][规律方法] 求双曲线标准方程的主要方法1定义法：由条件判定动点的轨迹是双曲线，求出a 2，b 2，得双曲线方程.2待定系数法：即“先定位，后定量”，如果不能确定焦点的位置，应注意分类讨论或恰当设置简化讨论.(1)(2017·全国卷Ⅲ)已知双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的一条渐近线方程为y ＝52x ，且与椭圆x 212＋y23＝1有公共焦点，则C 的方程为( )A.x 28－y 210＝1 B.x 24－y 25＝1 C.x 25－y 24＝1 D.x 24－y 23＝1 (2)已知点A (－1,0)，B (1,0)为双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右顶点，点M 在双曲线上，△ABM 为等腰三角形，且顶角为120°，则该双曲线的标准方程为( )A ．x 2－y 24＝1B ．x 2－y 23＝1C ．x 2－y 22＝1D ．x 2－y 2＝1(1)B (2)D [(1)由y ＝52x 可得b a ＝52.① 由椭圆x 212＋y 23＝1的焦点为(3,0)，(－3,0)，可得a 2＋b 2＝9.② 由①②可得a 2＝4，b 2＝5. 所以C 的方程为x 24－y 25＝1.故选B.(2)由题意知a ＝1.不妨设点M 在第一象限，则由题意有|AB |＝|BM |＝2，∠ABM ＝120°.过点M 作MN ⊥x 轴于点N ，则|BN |＝1，|MN |＝3，所以M (2，3)，代入双曲线方程得4－3b2＝1，解得b ＝1，所以双曲线的方程为x 2－y 2＝1，故选D.]双曲线的几何性质►考法1 双曲线的离心率问题【例3】 (2018·广州一模)如图，在梯形ABCD 中，已知|AB |＝2|CD |，AE →＝25AC →，双曲线过C ，D ，E 三点，且以A ，B 为焦点，则双曲线的离心率为( ) A.7 B ．2 2 C ．3D.10A [如图，以AB 所在直线为x 轴，以线段AB 的垂直平分线为y 轴建立平面直角坐标系，则由梯形的性质与双曲线的对称性知C ，D 关于y 轴对称．设A (－c,0)，则B (c,0)，C ⎝ ⎛⎭⎪⎫c2，h (其中h 为梯形的高)，因为AE →＝25AC →，所以x E ＝－25c ，y E ＝25h .设双曲线的方程为x 2a 2－y 2b2＝1(a＞0，b ＞0)，因为点C ，E 在双曲线上，则⎩⎪⎨⎪⎧425·c 2a 2－425·h2b2＝1，14·c 2a 2－h2b 2＝1，解得c 2a2＝7，所以双曲线的离心率e ＝c a＝7，故选A.]►考法2 双曲线的渐近线问题【例4】 (2019·福州模拟)过双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点分别作双曲线的两条渐近线的平行线，若这4条直线所围成的四边形的周长为8b ，则该双曲线的渐近线方程为( ) A ．y ＝±x B ．y ＝±2x C ．y ＝±3xD ．y ＝±2xA [由双曲线的对称性得该四边形为菱形，因为该四边形的周长为8b ，所以菱形的边长为2b ，由勾股定理得4条直线与y 轴的交点到x 轴的距离为4b 2－c 2＝3b 2－a 2，又4条直线分别与两条渐近线平行，所以b a ＝3b 2－a2a 2＋b 2，解得a ＝b ，所以该双曲线的渐近线的斜率为±1，所以该双曲线的渐近线方程为y ＝±x ，故选A.] ►考法3 双曲线几何性质的综合应用【例5】 (1)(2019·福州模拟)已知双曲线x 2a 2－y 2b2＝1与直线y ＝2x 有交点，则双曲线离心率的取值范围为( ) A ．(1，5) B ．(1，5] C ．(5，＋∞)D ．[5，＋∞)(2)已知双曲线C 1：x 24－y 2＝1，双曲线C 2：x 2a 2－y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，点M 在双曲线C 2的一条渐近线上，且OM ⊥MF 2(O 为坐标原点)，若S △OMF 2＝16，且双曲线C 1，C 2的离心率相同，则双曲线C 2的实轴长为( ) A ．32 B ．16 C ．8D ．4(1)C (2)B [(1)∵双曲线的一条渐近线方程为y ＝ba x ，则由题意，得b a ＞2，∴e ＝c a＝1＋⎝ ⎛⎭⎪⎫b a2＞1＋4＝5，即双曲线离心率的取值范围为(5，＋∞)．(2)双曲线C 1：x 24－y 2＝1的离心率为52，设F 2(c,0)，双曲线C 2的一条渐近线方程为y ＝b a x ，可得|MF 2|＝bc a 2＋b 2＝b ，|OM |＝c 2－b 2＝a .由S △OMF 2＝16，可得12ab ＝16，即ab ＝32.又a 2＋b 2＝c 2，且ca＝52，得a ＝8，b ＝4，c ＝45，所以双曲线C 2的实轴长为16.] [规律方法] 与双曲线几何性质有关问题的解题策略1求双曲线的离心率或范围.依据题设条件，将问题转化为关于a ，c 的等式或不等式，解方程或不等式即可求得.2求双曲线的渐近线方程.依据题设条件，求双曲线中a ，b 的值或a 与b 的比值，进而得出双曲线的渐近线方程.(1)(2019·海口模拟)在平面直角坐标系xOy 中，双曲线C ：y 2a 2－x 2b2＝1(a ＞0，b＞0)的一条渐近线与圆(x －2)2＋(y －1)2＝1相切，则C 的离心率为( ) A.43 B.54 C.169D.2516(2)若实数k 满足0＜k ＜9，则曲线x 225－y 29－k ＝1与曲线x 225－k －y 29＝1的( )A ．焦距相等B ．实半轴长相等C ．虚半轴长相等D ．离心率相等(3)已知双曲线C 1，C 2的焦点分别在x 轴、y 轴上，渐近线方程为y ＝±1ax (a ＞0)，离心率分别为e 1，e 2，则e 1＋e 2的最小值为________．(1)B (2)A (3)22 [(1)双曲线C 的渐近线方程为by ±ax ＝0，与圆相切的只能是直线by －ax ＝0，则|b －2a |a 2＋b 2＝1，化简得3a ＝4b ，所以9a 2＝16b 2＝16(c 2－a 2)，e 2＝2516，故e ＝54，故选B.(2)∵0＜k ＜9，∴9－k ＞0,25－k ＞0.∴x 225－y 29－k ＝1与x 225－k －y 29＝1均表示双曲线，又25＋(9－k )＝34－k ＝(25－k )＋9， ∴它们的焦距相等，故选A. (3)e 1＋e 2＝1＋1a 2＋a 2＋1＝a 2＋1·a ＋1a≥2a ×2a＝22，当且仅当a ＝1时取等号，故e 1＋e 2的最小值是2 2.]1．(2018·全国卷Ⅱ)双曲线x 2a2－y 2b2＝1(a ＞0，b ＞0)的离心率为3，则其渐近线方程为( ) A ．y ＝±2x B ．y ＝±3x C ．y ＝±22x D ．y ＝±32x A [法一：由题意知，e ＝c a ＝3，所以c ＝3a ，所以b ＝c 2－a 2＝2a ，所以b a＝2，所以该双曲线的渐近线方程为y ＝±b ax ＝±2x ，故选A.法二：由e ＝ca＝1＋⎝ ⎛⎭⎪⎫b a2＝3，得b a ＝2，所以该双曲线的渐近线方程为y ＝±b ax ＝±2x ，故选A.]2.(2018·全国卷Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |＝( ) A.32 B ．3 C ．2 3D ．4B [因为双曲线x 23－y 2＝1的渐近线方程为y ＝±33x ，所以∠MON ＝60°.不妨设过点F 的直线与直线y ＝33x 交于点M ，由△OMN 为直角三角形，不妨设∠OMN ＝90°，则∠MFO ＝60°，又直线MN 过点F (2,0)，所以直线MN 的方程为y ＝－3(x －2)，由⎩⎪⎨⎪⎧y ＝－3x －2，y ＝33x ，得⎩⎪⎨⎪⎧x ＝32，y ＝32，所以M ⎝ ⎛⎭⎪⎫32，32，所以|OM |＝⎝ ⎛⎭⎪⎫322＋⎝ ⎛⎭⎪⎫322＝3，所以|MN |＝3|OM |＝3，故选B.]3．(2016·全国卷Ⅰ)已知方程x 2m 2＋n －y 23m 2－n＝1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是( ) A ．(－1,3) B ．(－1，3) C ．(0,3)D ．(0，3)A [若双曲线的焦点在x 轴上，则⎩⎪⎨⎪⎧m 2＋n ＞0，3m 2－n ＞0.又∵(m 2＋n )＋(3m 2－n )＝4，∴m 2＝1，∴⎩⎪⎨⎪⎧1＋n ＞0，3－n ＞0，∴－1<n <3.若双曲线的焦点在y 轴上，则双曲线的标准方程为y 2n －3m 2－x 2－m 2－n ＝1，即⎩⎪⎨⎪⎧n －3m 2＞0，－m 2－n ＞0，即n >3m 2且n <－m 2，此时n 不存在．故选A.]4.(2017·全国卷Ⅰ)已知双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b >0)的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点．若∠MAN ＝60°，则C 的离心率为________．233 [如图，由题意知点A (a,0)，双曲线的一条渐近线l 的方程为y ＝bax ，即bx －ay ＝0，∴点A 到l 的距离d ＝aba 2＋b2. 又∠MAN ＝60°，MA ＝NA ＝b ，∴△MAN 为等边三角形， ∴d ＝32MA ＝32b ，即ab a 2＋b2＝32b ，∴a 2＝3b 2，∴e ＝c a ＝a 2＋b 2a 2＝233.] 5．(2015·全国卷Ⅰ)已知F 是双曲线C ：x 2－y 28＝1的右焦点，P 是C 的左支上一点，A (0,66)．当△APF 周长最小时，该三角形的面积为________．126 [由双曲线方程x 2－y 28＝1可知，a ＝1，c ＝3，故F (3,0)，F 1(－3,0)．当点P 在双曲线左支上运动时，由双曲线定义知|PF |－|PF 1|＝2，所以|PF |＝|PF 1|＋2，从而△APF 的周长＝|AP |＋|PF |＋|AF |＝|AP |＋|PF 1|＋2＋|AF |. 因为|AF |＝32＋662＝15为定值，所以当(|AP |＋|PF 1|)最小时，△APF 的周长最小，由图象可知，此时点P 在线段AF 1与双曲线的交点处(如图所示)．由题意可知直线AF 1的方程为y ＝26x ＋66，由⎩⎪⎨⎪⎧y ＝26x ＋66，x 2－y 28＝1，得y 2＋66y －96＝0，解得y ＝26或y ＝－86(舍去)， 所以S △APF ＝S △AF 1F －S △PF 1F ＝12×6×66－12×6×26＝12 6.]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020年高考数学一轮复习第8章平面解析几何第6讲双曲线增分练[A 级 基础达标]1．[xx·安徽模拟]下列双曲线中，焦点在y 轴上且渐近线方程为y ＝±2x 的是( ) A ．x 2－y 24＝1B.x 24－y 2＝1 C ．y 2－x 24＝1D.y 24－x 2＝1 答案 D解析 由题意，选项A ，B 的焦点在x 轴，故排除A ，B ；D 项的渐近线方程为y 24－x 2＝0，即y ＝±2x .2．[xx·湖北模拟]若双曲线x 2a 2－y 2b2＝1的一条渐近线经过点(3，－4)，则此双曲线的离心率为( )A.73 B.54 C.43 D.53答案 D解析 由已知可得双曲线的渐近线方程为y ＝±b a x ，点(3，－4)在渐近线上，∴b a ＝43，又a 2＋b 2＝c 2，∴c 2＝a 2＋169a 2＝259a 2，∴e ＝c a ＝53.故选D.3．[xx·全国卷Ⅰ]已知F 是双曲线C ：x 2－y 23＝1的右焦点，P 是C 上一点，且PF 与x轴垂直，点A 的坐标是(1,3)，则△APF 的面积为( )A.13B.12C.23D.32 答案 D解析 因为F 是双曲线C ：x 2－y 23＝1的右焦点，所以F (2,0)．因为PF ⊥x 轴，所以可设P 的坐标为(2，y P )． 因为P 是C 上一点，所以4－y 2P3＝1，解得y P ＝±3，所以P (2，±3)，|PF |＝3.又因为A (1,3)，所以点A 到直线PF 的距离为1， 所以S △APF ＝12×|PF |×1＝12×3×1＝32.故选D.4．[xx·广东模拟]已知双曲线C ：x 2a 2－y 2b 2＝1的离心率e ＝54，且其右焦点为F 2(5,0)，则双曲线C 的方程为( )A.x 24－y 23＝1B.x 29－y 216＝1C.x 216－y 29＝1 D.x 23－y 24＝1 答案 C解析 因为双曲线C 的右焦点为F 2(5,0)，所以c ＝5.因为离心率e ＝c a ＝54，所以a ＝4.又a 2＋b 2＝c 2，所以b 2＝9. 故双曲线C 的方程为x 216－y 29＝1.5．P 为双曲线x 2a 2－y 2b2＝1(a >0，b >0)右支上的一点，且|PF 1|＝2|PF 2|，则双曲线的离心率的取值范围是( )A ．(1,3)B ．(1,3]C ．(3，＋∞)D ．[3，＋∞)答案 B解析 如图，由题意可知⎩⎪⎨⎪⎧4a ＋2a >2c ，a <c ，∴1<e <3.当P 在x 轴上时，4a ＋2a ＝2c ， ∴e ＝3. 综合e ∈(1,3]．6．已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点分别为F 1、F 2，过点F 2作与x 轴垂直的直线与双曲线一个交点为P ，且∠PF 1F 2＝π6，则双曲线的渐近线方程为________．答案 y ＝±2x解析 根据已知可得，|PF 1|＝2b2a 且|PF 2|＝b 2a ，故2b 2a －b 2a ＝2a ，所以b 2a 2＝2，ba＝2，双曲线的渐近线方程为y ＝±2x .7．[xx·海口调研]已知点F 1，F 2分别为双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右焦点，P 为双曲线左支上的任意一点，且|PF 2|＝2|PF 1|，若△PF 1F 2为等腰三角形，则双曲线的离心率为________．答案 2解析 ∵|PF 2|－|PF 1|＝2a ，|PF 2|＝2|PF 1|，∴|PF 2|＝4a ，|PF 1|＝2a ，∵△PF 1F 2为等腰三角形，∴|PF 2|＝|F 1F 2|，即4a ＝2c ，∴c a＝2.8．[xx·北京高考]双曲线x 2a 2－y 2b2＝1(a >0，b >0)的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a ＝________.答案 2解析 由OA ，OC 所在直线为渐近线，且OA ⊥OC ，知两条渐近线的夹角为90°，从而双曲线为等轴双曲线，则其方程为x 2－y 2＝a 2.OB 是正方形的对角线，且点B 是双曲线的焦点，则c ＝22，根据c 2＝2a 2可得a ＝2.9．设A ，B 分别为双曲线x 2a 2－y 2b2＝1(a >0，b >0)的左、右顶点，双曲线的实轴长为43，焦点到渐近线的距离为 3.(1)求双曲线的方程； (2)已知直线y ＝33x －2与双曲线的右支交于M ，N 两点，且在双曲线的右支上存在点D ，使OM →＋ON →＝tOD →，求t 的值及点D 的坐标．解 (1)由题意知a ＝23，又∵一条渐近线为y ＝b ax ，即bx －ay ＝0. ∴由焦点到渐近线的距离为3，得|bc |b 2＋a 2＝ 3.∴b 2＝3，∴双曲线的方程为x 212－y 23＝1. (2)设M (x 1，y 1)，N (x 2，y 2)，D (x 0，y 0)， 则x 1＋x 2＝tx 0，y 1＋y 2＝ty 0.将直线方程y ＝33x －2代入双曲线方程x 212－y 23＝1得x 2－163x ＋84＝0，则x 1＋x 2＝163，y 1＋y 2＝33(x 1＋x 2)－4＝12. ∴⎩⎪⎨⎪⎧x 0y 0＝433，x 212－y 203＝1，∴⎩⎨⎧x 0＝43，y 0＝3，∴t ＝4，点D 的坐标为(43，3)．10．[xx·广西模拟]已知双曲线方程2x 2－y 2＝2. (1)求以A (2,1)为中点的双曲线的弦所在的直线方程；(2)求过点B (1,1)能否作直线l ，使l 与所给双曲线交于Q 1，Q 2两点，且点B 是弦Q 1Q 2的中点？这样的直线l 如果存在，求出它的方程；如果不存在，说明理由．解 (1)由2·22－12＝7>2可知点A 在双曲线内部(含焦点的区域内)，设以A (2,1)为中点的弦两端点分别为P 1(x 1，y 1)，P 2(x 2，y 2)，则有x 1＋x 2＝4，y 1＋y 2＝2.由对称性知x 1≠x 2.∵P 1、P 2在双曲线上，∴⎩⎪⎨⎪⎧2x 21－y 21＝2，2x 22－y 22＝2，两式相减得2(x 1＋x 2)(x 1－x 2)－(y 1＋y 2)(y 1－y 2)＝0. ∵x 1＋x 2＝4，y 1＋y 2＝2.∴y 1－y 2x 1－x 2＝4. 所求中点弦所在直线方程为y －1＝4(x －2)，即4x －y －7＝0.(2)由2·12－12＝1<2知B (1,1)在双曲线的外部(双曲线两支之间)．可假定直线l 存在，采用(1)的方法求出l 的方程为y －1＝2(x －1)，即2x －y －1＝0.联立方程组⎩⎪⎨⎪⎧2x 2－y 2＝2，2x －y －1＝0，消y ，得2x 2－4x ＋3＝0.∵Δ＝(－4)2－4×2×3＝－8<0，无实根，因此直线l 与双曲线无交点，这一矛盾说明了满足条件的直线l 不存在．[B 级 知能提升]1．[xx·天津高考]已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF 是边长为2的等边三角形(O 为原点)，则双曲线的方程为( )A.x 24－y 212＝1 B.x 212－y 24＝1 C.x 23－y 2＝1 D ．x 2－y 23＝1答案 D解析 根据题意画出草图如图所示⎝⎛⎭⎪⎫不妨设点A 在渐近线y ＝bax 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2. 又点A 在双曲线的渐近线y ＝b ax 上，∴b a＝tan60°＝ 3. 又a 2＋b 2＝4， ∴a ＝1，b ＝3，∴双曲线的方程为x 2－y 23＝1.故选D.2．已知双曲线E 的中心为原点，F (3,0)是E 的焦点，过F 的直线l 与E 相交于A ，B 两点，且AB 的中点为M (－12，－15)，则E 的方程为( )A.x 3－y 26＝1 B.x 24－y 25＝1 C.x 26－y 23＝1 D.x 25－y 24＝1 答案 B解析 由已知易得l 的斜率为k ＝k FM ＝1.设双曲线方程为x 2a 2－y 2b2＝1(a >0，b >0)，A (x 1，y 1)，B (x 2，y 2)，则有⎩⎪⎨⎪⎧x 21a 2－y 21b2＝1，x 22a 2－y22b 2＝1，两式相减并结合x 1＋x 2＝－24，y 1＋y 2＝－30，得y 1－y 2x 1－x 2＝4b 25a 2，从而4b 25a2＝1，即4b 2＝5a 2.又a 2＋b 2＝9，解得a 2＝4，b 2＝5，故选B. 3．[xx·武汉模拟]过双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的一个焦点F 的直线与双曲线相交于A ，B 两点，当AB ⊥x 轴，称|AB |为双曲线的通径．若过焦点F 的所有焦点弦AB 中，其长度的最小值为2b2a，则此双曲线的离心率的范围为( )A ．(1，2)B ．(1，2]C ．(2，＋∞)D ．[2，＋∞)答案 B解析 当经过焦点F 的直线与双曲线的交点在同一支上， 可得双曲线的通径最小，令x ＝c ，可得y ＝±bc 2a 2－1＝±b 2a ，即有最小值为2b 2a； 当直线与双曲线的交点在两支上，可得直线的斜率为0时， 即为实轴，最小为2a . 由题意可得2a ≥2b2a，即为a 2≥b 2＝c 2－a 2， 即有c ≤2a ，则离心率e ＝c a∈(1，2]．4．[xx·承德模拟]已知点M (－2,0)，N (2,0)，动点P 满足条件|PM |－|PN |＝22，记动点P 的轨迹为W .(1)求W 的方程；(2)若A 和B 是W 上的不同两点，O 是坐标原点，求OA →·OB →的最小值．解 (1)由|PM |－|PN |＝22知动点P 的轨迹是以M ，N 为焦点的双曲线的右支，实半轴长a ＝ 2.又焦距2c ＝4，所以虚半轴长b ＝c 2－a 2＝ 2. 所以W 的方程为x 22－y 22＝1(x ≥2)．(2)设A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)． 当AB ⊥x 轴时，x 1＝x 2，y 1＝－y 2，从而OA →·OB →＝x 1x 2＋y 1y 2＝x 21－y 21＝2.当AB 与x 轴不垂直时，设直线AB 的方程为y ＝kx ＋m (k ≠±1)，与W 的方程联立，消去y 得(1－k 2)x 2－2kmx －m 2－2＝0，则x 1＋x 2＝2km 1－k 2，x 1x 2＝m 2＋2k 2－1， 所以OA →·OB →＝x 1x 2＋y 1y 2 ＝x 1x 2＋(kx 1＋m )(kx 2＋m ) ＝(1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝＋k2m 2＋k 2－1＋2k 2m 21－k2＋m 2＝2k 2＋2k 2－1＝2＋4k 2－1. 又因为x 1x 2>0，所以k 2－1>0.所以OA →·OB →>2.综上所述，当AB ⊥x 轴时，OA →·OB →取得最小值2.5．已知双曲线Γ：x 2a 2－y 2b2＝1(a >0，b >0)经过点P (2,1)，且其中一焦点F 到一条渐近线的距离为1.(1)求双曲线Γ的方程；(2)过点P 作两条相互垂直的直线PA ，PB 分别交双曲线Γ于A ，B 两点，求点P 到直线AB 距离的最大值．解 (1)∵双曲线x 2a 2－y 2b 2＝1过点(2,1)，∴4a 2－1b2＝1.不妨设F 为右焦点，则F (c,0)到渐近线bx －ay ＝0的距离d ＝|bc |a 2＋b2＝b ，∴b ＝1，a2＝2，∴所求双曲线的方程为x 22－y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝kx ＋m .将y ＝kx ＋m 代入x 2－2y 2＝2中，整理得(2k 2－1)x 2＋4kmx ＋2m 2＋2＝0. ∴x 1＋x 2＝－4km2k 2－1，①x 1x 2＝2m 2＋22k 2－1.②∵PA →·PB →＝0，∴(x 1－2，y 1－1)·(x 2－2，y 2－1)＝0，∴(x 1－2)(x 2－2)＋(kx 1＋m －1)(kx 2＋m －1)＝0，∴(k 2＋1)x 1x 2＋(km －k －2)(x 1＋x 2)＋m 2－2m ＋5＝0.③将①②代入③，得m 2＋8km ＋12k 2＋2m －3＝0， ∴(m ＋2k －1)(m ＋6k ＋3)＝0. 而P ∉AB ，∴m ＝－6k －3，从而直线AB 的方程为y ＝kx －6k －3. 将y ＝kx －6k －3代入x 2－2y 2－2＝0中， 判别式Δ＝8(34k 2＋36k ＋10)>0恒成立， ∴y ＝kx －6k －3即为所求直线．∴P 到AB 的距离d ＝|2k －6k －3－1|1＋k 2＝4|k ＋1|k 2＋1. ∵⎝ ⎛⎭⎪⎫d 42＝k 2＋1＋2k k 2＋1＝1＋2k k 2＋1≤2.∴d ≤42，即点P 到直线AB 距离的最大值为4 2.2019-2020年高考数学一轮复习第8章平面解析几何第6讲抛物线知能训练轻松闯关文北师大版1．(xx·合肥质量检测)抛物线x 2＝12y 的焦点坐标为( )A.⎝ ⎛⎭⎪⎫12，0B.⎝ ⎛⎭⎪⎫0，12C.⎝ ⎛⎭⎪⎫18，0D.⎝ ⎛⎭⎪⎫0，18 解析：选D.抛物线x 2＝12y 的焦点坐标是⎝ ⎛⎭⎪⎫0，18.2．若抛物线y 2＝2x 上一点M 到它的焦点F 的距离为32，O 为坐标原点，则△MFO 的面积为( )A.22 B.24 C.12 D.14 解析：选B.由题意知，抛物线准线方程为x ＝－12.设M (a ，b )，由抛物线的定义可知，点M 到准线的距离为32，所以a ＝1，代入抛物线方程y 2＝2x ， 解得b ＝±2，所以S △MFO ＝12×12×2＝24.3．若抛物线y 2＝2x 上一点P 到准线的距离等于它到顶点的距离，则点P 的坐标为( )A.⎝ ⎛⎭⎪⎫14，±22 B.⎝ ⎛⎭⎪⎫14，±1C.⎝ ⎛⎭⎪⎫12，±22 D.⎝ ⎛⎭⎪⎫12，±1解析：选A.设抛物线的顶点为O ，焦点为F ，P (x P ，y P )，由抛物线的定义知，点P 到准线的距离即为点P 到焦点的距离，所以|PO |＝|PF |，过点P 作PM ⊥OF 于点M (图略)，则M 为OF的中点，所以x P ＝14，代入y 2＝2x ，得y P ＝±22，所以P ⎝ ⎛⎭⎪⎫14，±22.4．直线l 过抛物线y 2＝－2px (p >0)的焦点，且与抛物线交于A 、B 两点，若线段AB 的长是8，AB 的中点到y 轴的距离是2，则此抛物线的方程是( )A ．y 2＝12xB ．y 2＝－8xC ．y 2＝6xD ．y 2＝－4x解析：选B.设A (x 1，y 1)、B (x 2，y 2)，由抛物线定义可得|x 1|＋|x 2|＋p ＝8，又AB 的中点到y 轴的距离为2，即|x 1|＋|x 2|＝4，所以p ＝4，所以y 2＝－8x .故选B.5．(xx·云南省第一次检测)已知抛物线C 的顶点是原点O ，焦点F 在x 轴的正半轴上，经过F 的直线与抛物线C 交于A ，B 两点，如果OA →·OB →＝－12，那么抛物线C 的方程为( )A ．x 2＝8yB ．x 2＝4yC ．y 2＝8xD ．y 2＝4x解析：选C.由题意，设抛物线方程为y 2＝2px (p >0)，直线方程为x ＝my ＋p2，联立得y 2－2pmy－p 2＝0，设A (x 1，y 1)，B (x 2，y 2)，得OA →·OB →＝x 1x 2＋y 1y 2＝⎝⎛⎭⎪⎫my 1＋p 2⎝ ⎛⎭⎪⎫my 2＋p 2＋y 1y 2＝m 2y 1y 2＋pm 2(y 1＋y 2)＋p 24＋y 1y 2＝－34p 2＝－12⇒p ＝4，即抛物线C 的方程为y 2＝8x . 6．(xx·衡水调研)已知等边△ABF 的顶点F 是抛物线C 1：y 2＝2px (p ＞0)的焦点，顶点B 在抛物线的准线l 上且AB ⊥l ，则点A 的位置( ) A ．在C 1开口内 B ．在C 1上 C ．在C 1开口外 D ．与p 值有关 解析：选B.设B ⎝ ⎛⎭⎪⎫－p2，m ，由已知有AB 中点的横坐标为p2，则A ⎝ ⎛⎭⎪⎫3p 2，m ，△ABF 是边长|AB |＝2p 的等边三角形， 即|AF |＝⎝ ⎛⎭⎪⎫3p 2－p 22＋m 2＝2p ，所以p 2＋m 2＝4p 2，所以m ＝±3p ，所以A ⎝ ⎛⎭⎪⎫3p 2，±3p ，代入y 2＝2px 中，得点A 在抛物线上，故选B.7．(xx·资阳模拟)顶点在原点，对称轴是y 轴，并且经过点P (－4，－2)的抛物线方程是________．解析：设抛物线方程为x 2＝my ，将点P (－4，－2)代入x 2＝my ，得m ＝－8.所以抛物线方程是x 2＝－8y .答案：x 2＝－8y8．(经典考题)如图所示是抛物线形拱桥，当水面在l 时，拱顶离水面2 m ，水面宽4 m ．水位下降1 m 后，水面宽________m.解析：建立如图所示的平面直角坐标系，设抛物线方程为x 2＝－2py (p >0)，则A (2，－2)，将其坐标代入x 2＝－2py ，得p ＝1.所以x 2＝－2y .当水面下降1 m ，得D (x 0，－3)(x 0>0)，将其坐标代入x 2＝－2y ，得x 20＝6， 所以x 0＝ 6.所以水面宽|CD |＝2 6 m. 答案：2 69．(xx·南昌质检)已知抛物线y 2＝2x 的焦点是F ，点P 是抛物线上的动点，若点A (3，2)，则|PA |＋|PF |取最小值时，点P 的坐标为________．解析：将x ＝3代入抛物线方程y 2＝2x ，得y ＝± 6.因为6>2，所以A 在抛物线内部．如图，设抛物线上点P 到准线l ：x ＝－12的距离为d ，由定义知|PA |＋|PF |＝|PA |＋d ，当PA ⊥l 时，|PA |＋d 有最小值，最小值为72，即|PA |＋|PF |的最小值为72，此时点P 的纵坐标为2，代入y 2＝2x ，得x ＝2，所以点P 的坐标为(2，2)． 答案：(2，2)10．(xx·豫东、豫北十校联考)已知抛物线的顶点在原点，焦点在x 轴的正半轴上，若抛物线的准线与双曲线5x 2－y 2＝20的两条渐近线围成的三角形的面积为45，则抛物线方程为________．解析：由双曲线方程5x 2－y 2＝20知其渐近线方程为y ＝±5x ，由题意可设抛物线方程为y 2＝2px (p >0)，故其准线方程为x ＝－p2，设准线与双曲线的两条渐近线的交点为A ，B ，则不妨令A ⎝ ⎛⎭⎪⎫－p 2，52p ，B ⎝ ⎛⎭⎪⎫－p 2，－52p ，故S △ABO ＝12×5p ×p 2＝54p 2＝45，解得p 2＝16，又因为p >0，所以p ＝4，故抛物线方程为y 2＝8x .答案：y 2＝8x11．已知抛物线y 2＝2px (p >0)的焦点为F ，A 是抛物线上横坐标为4，且位于x 轴上方的点，A 到抛物线准线的距离等于5，过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M . (1)求抛物线的方程；(2)若过M 作MN ⊥FA ，垂足为N ，求点N 的坐标． 解：(1)抛物线y 2＝2px 的准线为x ＝－p2，于是4＋p2＝5，所以p ＝2.所以抛物线方程为y 2＝4x . (2)因为点A 的坐标是(4，4)， 由题意得B (0，4)，M (0， 2)．又因为F (1，0)，所以k FA ＝43，因为MN ⊥FA ，所以k MN ＝－34.又FA 的方程为y ＝43(x －1)，①MN 的方程为y －2＝－34x ，②联立①②，解得x ＝85，y ＝45，所以点N 的坐标为⎝ ⎛⎭⎪⎫85，45.1．已知抛物线x 2＝2y ，过抛物线的焦点F 的直线l 交抛物线于P ，Q 两点，过P ，Q 分别作抛物线的切线，两切线交于点A ，则点A 的纵坐标为________．解析：由x 2＝2y ，得y ＝12x 2， 所以y ′＝x .设P (x 1，y 1)，Q (x 2，y 2)，所以抛物线在P ，Q 两点处的切线的斜率分别为x 1，x 2，所以过点P 的抛物线的切线方程为y －y 1＝x 1(x －x 1)，又x 21＝2y 1， 所以切线方程为y ＝x 1x －x 212，同理可得过点Q 的切线方程为y ＝x 2x －x 222， 两切线方程联立解得⎩⎪⎨⎪⎧x A ＝x 1＋x 22，y A ＝x 1x 22. 又抛物线焦点F 的坐标为⎝ ⎛⎭⎪⎫0，12，易知直线l 的斜率存在，可设直线l 的方程为y ＝mx ＋12，由⎩⎪⎨⎪⎧y ＝mx ＋12，x 2＝2y ，得x 2－2mx －1＝0， 所以x 1x 2＝－1，所以y A ＝－12. 答案：－122．已知圆C 过定点F ⎝ ⎛⎭⎪⎫－14，0，且与直线x ＝14相切，圆心C 的轨迹为E ，曲线E 与直线l ：y ＝k (x ＋1)(k ∈R )相交于A ，B 两点．(1)求曲线E 的方程；(2)当△OAB 的面积等于10时，求k 的值．解：(1)由题意，点C 到定点F ⎝ ⎛⎭⎪⎫－14，0和直线x ＝14的距离相等， 故点C 的轨迹E 的方程为y 2＝－x .(2)由方程组⎩⎪⎨⎪⎧y 2＝－x ，y ＝k （x ＋1），消去x 后， 整理得ky 2＋y －k ＝0.设A (x 1，y 1)，B (x 2，y 2)，由根与系数的关系有y 1＋y 2＝－1k，y 1y 2＝－1. 设直线l 与x 轴交于点N ，则N (－1，0)．所以S △OAB ＝S △OAN ＋S △OBN＝12|ON ||y 1|＋12|ON ||y 2|， ＝12|ON ||y 1－y 2| ＝12×1×（y 1＋y 2）2－4y 1y 2 ＝12 ⎝ ⎛⎭⎪⎫1k 2＋4. 因为S △OAB ＝10，所以12 ⎝ ⎛⎭⎪⎫1k 2＋4＝10， 解得k ＝±16. 3．(xx·石家庄一模)在平面直角坐标系xOy 中，一动圆经过点⎝ ⎛⎭⎪⎫12，0且与直线x ＝－12相切，设该动圆圆心的轨迹为曲线E .(1)求曲线E 的方程；(2)设P 是曲线E 上的动点，点B ，C 在y 轴上，△PBC 的内切圆的方程为 (x －1)2＋y 2＝1，求△PBC 面积的最小值．解：(1)由题意可知圆心到⎝ ⎛⎭⎪⎫12，0的距离等于到直线x ＝－12的距离， 由抛物线的定义可知圆心的轨迹方程为y 2＝2x .(2)设P (x 0，y 0)，B (0，b )，C (0，c )，直线PB 的方程为(y 0－b )x －x 0y ＋x 0b ＝0，又圆心(1，0)到PB 的距离为1， |y 0－b ＋x 0b |（y 0－b ）2＋x 20＝1，整理得(x 0－2)b 2＋2y 0b －x 0＝0， 同理可得(x 0－2)c 2＋2y 0c －x 0＝0，所以b ，c 是方程(x 0－2)x 2＋2y 0x －x 0＝0的两根，所以b ＋c ＝－2y 0x 0－2，bc ＝－x 0x 0－2， 依题意得bc <0，即x 0>2，则(b －c )2＝4x 20＋4y 20－8x 0（x 0－2）2， 因为y 20＝2x 0，所以|b －c |＝⎪⎪⎪⎪⎪⎪2x 0x 0－2， 所以S ＝12|b －c ||x 0|＝(x 0－2)＋4（x 0－2）＋4≥8， 当x 0＝4时，不等式等号成立，所以△PBC 面积的最小值为8.。