青岛理工大学概率统计期末试卷—B(附答案)
2007级理工科概率统计期末考试试题B机答案

B 卷 第 1页 共2页华侨大学07~08学年第一学期《概率统计》期末考试试卷(B 卷) 考试日期:2008年 月 日上午8:30-10:30一、填空题(每空3分,共30分)1. 已知随机事件A ,B 有概率7.0)(=A P ,8.0)(=B P ,条件概率6.0)|(=A B P ,则=⋃)(B A P .2. 社会上定期发行某中奖劵,中奖率为p .某人每次购买一张,若没有中奖,接着再买一张,直到中奖为止,X 为总共购买的奖券张数,则对1,2,k = ,==)(k X P ,EX = .3. 已知随机变量),(Y X 的联合分布密度函数如下, 则常数=K=),(y x f ⎩⎨⎧≤≤≤≤-其它。
,0;0,10),1(x y x x y K 4. 设随机变量Y X ,满足 ()4,()1,D X D Y ==28)23(=-Y X D ,则XY ρ= . 5. 设X 为总体)4,3(~N X 中抽取的样本(4321,,,X X X X )的均值, 则)51(<<-X P = .6. 设321,,X X X 是取自N (,)μ1的样本,3211)22(3ˆX k X kX -++=μ是μ的无偏 估计量,则常数=k .7. 设随机变量()~0,2X U ,则2X Y =的概率密度函数为 . 8. 设某种保险丝熔化时间),(~2σμN X (单位:秒),取16=n 的样本,得 样本均值和方差分别为36.0,152==S X ,则μ的置信度为95%的单侧 置信区间上限为 .9. 原假设0H 为真时,作出拒绝0H 的决策,称为犯第 类错误.B 卷 第 2页 共2页二、(10分) 已知一批产品中96 %是合格品. 检查产品时,一件合格品被误认为是次品的概率是0.02;一件次品被误认为是合格品的概率是0.05.求在被检查后认为是合格品的产品确实是合格品的概率.三、(10分) 学校某课程的考试,成绩分优秀,合格,不合格三种,优秀者得3分,合格者得2分,不合格者得1分.根据以往的统计,每批参加考试的学生中考得优秀、合格、不合格的,各占10%、70%、20%.现有100位学生参加考试,试用中心极限定理估计100位学生考试的总分在180至200分之间的概率.四、(15分) 设二维随机变量( X , Y )的联合密度函数为:⎩⎨⎧+∞<<<<=+-.,0,0,10,),()(他其y x be y x f y x试求(1)常数b ; (2) X 和Y 各自的边缘密度函数;(3)函数),max(Y X U =的分布函数.五、(15分) 设总体X 的概率密度为(1),(0,1),(,)0,(0,1),x x f x x θθθ⎧+∈=⎨∉⎩ 其中1θ>-为未知参数.已知12,,,n X X X 是取自总体X 的一个样本.求:(1)未知参数θ的矩估计量;(2)未知参数θ的最大似然估计量;(3))(X E 的最大似然估计量.六、(10分)国际市场每年对我国某种出口商品的需求量X 是一个随机变量,它在区间[2000,4000](单位:吨)上服从均匀分布,若每出售一吨,可得外汇3万美元,如销售不出而积压,则每吨需保养费1万美元,问应组织多少货源,才能使平均收益最大?七、(10分) 某电子产品的一个指标服从正态分布,从某天生产的产品中抽取15个产品,测得该指标的样本均值为2.60,样本标准差为1.20.(1) 取显著性水平α =0.05,问是否可以认为该指标的平均值显著地不等于2? (2) 求该指标的方差的置信水平为0.95的置信区间.附常用分布的分布表值:(2)0.9772Φ= 9680.0)856.1(=Φ 0.0250.05 1.96, 1.645z z ==1448.2)14(025.0=t , ()0.0515 1.7531t = 629.5)14(,119.26)14(2975.02025.0==χχB 卷 第 3页 共2页华侨大学07-08第一学期 概率统计期末考试(B 卷)答案一、填空题:(每空3分,共30分)1.62.0; 2.()11k p p --⋅,1p; 3.24; 4.0.5; 5.0.9544; 6.4;7.⎩⎨⎧<<=;他其)(0,)40(/25.0)(y yy f 8.上限为 15.2630; 9.一.二、【10分】设A 为被查后认为是合格品的事件,B 为抽查的产品为合格品的事件. …………… 2分9428.005.004.098.096.0)()()()()(=⨯+⨯=+=B A P B P B A P B P A P ,…………… 4分.998.09428.0/9408.0)(/)()()(===A P B A P B P A B P…………… 4分三、【10分】 设i X 为第i 位学生的得分)100,2,1( =i ,则总得分∑==1001i i X X ,且9.1)(=i X E29.0)(=i X D 199.1100)(=⨯=X E29.0100)(⨯=X D …………… 6分由中心极限定理,)29190180()29190200()200180(-Φ--Φ=<<X P 936.01)856.1(2=-Φ= ……… 4分四、【15分】(本大题(1)-(2)小题各6分,(3)小题3分)(1)()()101,x y f x y dxdy dx bedy+∞+∞-+-∞==⎰⎰⎰()1101x y b e dx e dy b e +∞---==-⎰⎰,故111b e-=-(2)()()10,01,10,xx y X e be dy x f x e-+∞-+-⎧= <<⎪=-⎨⎪ ⎩⎰其它,B 卷 第 4页 共2页()()10,0,0,x y y Y bedx e y f y -+-⎧= <⎪=⎨⎪ ⎩⎰其它.(3) 由于()()(),X Y f x y f x f y =⋅,因此X 和Y 相互独立,故()()()()()()(),U X Y F u P U u P X u Y u P X u P Y u f u f u =≤=≤≤=≤≤=⋅从而当u <时,()0U F u =.当01u ≤<时,()()()()211.1u uuU X Y e F u f x dx f y dy e---==-⎰⎰当1u ≥时,()()()101uuU X Y F u f x dx f y dy e -==-⎰⎰,综上()()210,0,1,1,11,.u U u u e F u u e e u --- <⎧⎪-⎪= 0≤<⎨-⎪⎪- 1≤⎩X 与Y相互独立,因为)()(),(y f x f y x f Y X =. …………… 本大题每小题各5分五、【15分】(1) 矩估计量12ˆ1XX θ-=- …………… 6分 (2)极大似然估计量11ˆ11ln ni i X n θ==--∑…………… 6分 (3))(X E 的极大似然估计量∑=-=++=ni in X X E 11ln 112ˆ1ˆ)(ˆθθ …………… 3分六、【10分】B 卷 第 5页 共2页设组织t 吨货源时,收益为()()3,,3,,3,4,.t t X t t X t W X X t X X t X t X t >⎧ >⎧⎪==⎨⎨-- ≤- ≤⎪⎩⎩又()~2000,4000X U ,则()1,20020000,.X x f x ⎧ <<⎪=⎨⎪ ⎩其它 …………… 4分从而()()()()2400020004374000200020001000tt t X t x t t t E W X W x f x dx dx dx t +∞-∞-==+=-+-⎰⎰⎰,易知当()()70500t dE W X tdt=-=即3500t =时,平均收益最大.故应组织3500吨货源. ……… 6分七、【10分】(1)设2:,2:10≠=μμH H,则(14)X Y t =,且拒绝域D 为:1448.2)14(15/2025.0=>-=t S X T1.93652.1448X =≈<, 因此不能拒绝0H ,不可以认为该指标的平均值显著地不等于2; …………… 5分 (2)因为222(1)(14)n S χσ- ,令2220.9750.0252(1)(14)(14)n S χχσ-<<则该指标的方差的置信水平为0.95 的置信区间为22220.0250.975(1)(1),(0.7719,3.5815)(14)(14)n S n S χχ⎛⎫--= ⎪⎝⎭. …………… 5分。
概率论试卷BB 附具体答案解析

D.12
4、如果函数
f
(x)
x, 0,
a x b 是某连续随机变量 X 的概率密度,则区间[a, b] 可以是(
其他
)
题号 一 二 三
总分
A [0,1]
B [0.2]
C [ 0,2 ]
D[1,2]
分数
一、填空题(每题 3 分,共 24 分)
1、若 A,B 为随机事件,且 P( A) 0.6 , P(B A) 0.2 ,当 A 与 B 互不相容时, P(B)
5. 设总体 X , X1, X 2 ,, X n 是取自总体 X 的一个样本, X 为样本均值,则不是总体期望 的无偏
估计量的是( )
n
。
(A) X ; (B) X1 X 2 X 3 ; (C) 0.2 X1 0.3X 2 0.5X 3 ; (D) X i
i 1
2、若每次试验时 A 发生的概率都是 0.2 , X 表示 50 次独立试验中事件 A 发生的次数, D(X ) 3、若随机变量 X1, X 2 相互独立,且 X1 ~ N (3, 32 ) , X 2 ~ N (1, 22 ) 。令 X X1 2X 2 ,则 D( X )
2008 至 2009 第 1 学期 课程名称 概率论与数理统计 试卷
专业: 理工科各专业
考试性质: 闭卷
考试时间 120 分钟
(B)
3、.已知随机变量 X 和 Y 相互独立,且它们分别在区间[ 1,3]和[2,4]上服从均匀分布,则
E(XY)= ( )
A. 3 B.6
C.10
概率为_ ____
7、设随机变量 X 的数学期望 E( X ) 7 ,方差 D( X ) 5 ,用切比雪夫不等式估计得
(完整word版)青岛理工大学《理论力学》期末考试试题(未知学年)(A卷)
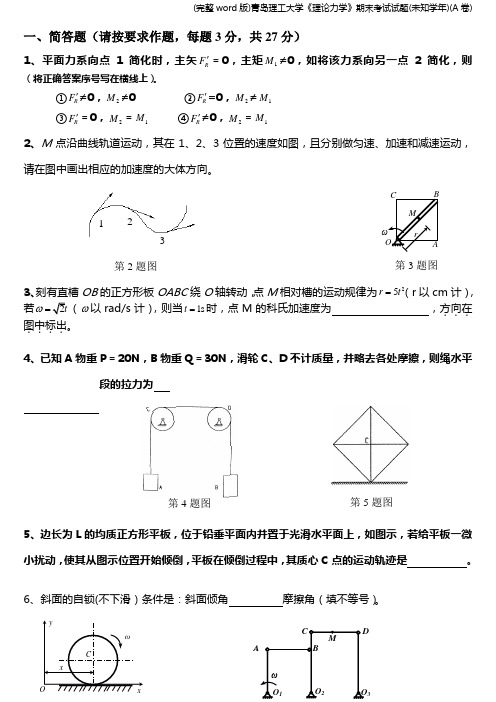
一、简答题(请按要求作题,每题3分,共27分)1、平面力系向点1简化时,主矢R F '=0,主矩1M ≠0,如将该力系向另一点2简化,则(将正确答案序号写在横线上)。
①R F '≠0,2M ≠0 ②R F '=0,2M ≠1M ③R F '=0,2M =1M ④R F '≠0,2M =1M2、M 点沿曲线轨道运动,其在1、2、3位置的速度如图,且分别做匀速、加速和减速运动,请在图中画出相应的加速度的大体方向。
3、刻有直槽OB 的正方形板OABC 绕O 轴转动,点M 相对槽的运动规律为25r t =(r 以cm 计),若2t ω=(ω以rad/s 计),则当1s t =时,点M 的科氏加速度为 ,方向在...图中标出....。
4、已知A 物重P =20N ,B 物重Q =30N ,滑轮C 、D 不计质量,并略去各处摩擦,则绳水平段的拉力为5、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是 。
6、斜面的自锁(不下滑)条件是:斜面倾角 摩擦角(填不等号)。
O 1ω O 2 O 3ABCDMωO yCxxωOA B CMr123第2题图第3题图第4题图第5题图7、滚轮半径r =5cm ,沿水平轨道向右作纯滚动,轮心C 的运动规律为32331419x t t t =--+(t 以s 为单位,x 以cm 为单位),则t =2s 时轮子的角速度为 ,角加速度为 。
8、图示机构中已知12O A O B =,23O C O D =,1O A 杆长为l ,绕1O 轴匀速转动的角速度为ω,2O C 杆长为1.2l ,则M 点的速度v= ,加速度a = 。
9、已知曲柄连杆机构中的OA =r, AB=L ,曲柄以匀角速度o ω转动,则图示位置连杆的角加速度AB α= 。
二、计算题(14分)构架ABC由AB,BC,DF组成,杆DF上的销子E,可在杆BC的光滑槽内滑动,在杆DF上作用一力偶,其矩为M,A为固定端,C为可动铰支座。
概率统计B(48学时)练习题(演示版)

概率统计习题习题一一填空题(1)设C B A ,,为三事件,试用C B A ,,的运算表示下列事件:C B A ,,中不多C B A ,,中至少有两个发生:BC AC AB ⋃⋃(2)设B A ,为二事件,试用B A ,的运算分别表示下列事件及其对立事件:B A ,都发生:,AB(2)设B A ,注:1A :两件均不合格,2A :一件合格,两件中有一件是不合格品即21A A ⋃; 两件中有一件是不合格品,另一件也是不合格即1A ,故516466)())(())((1614244221211211=⋅+=+=⋃⋃=⋃=C C C C A A P A A A P A A A P P (5)生产产品直到有10件正品为止,记录生产产品的总件数,写出该试验的样本空间。
{10,11,……}(6)假设7.0)(,4.0)(=⋃=B A P A P ,若B A 与互不相容,则3.0)()()(=-⋃=A P B A P B P ,若B A 与相互独立,则5.0)(),(4.04.07,0)()()()()(=+-=⋅+-⋃=B P B P B P A P A P B A P B P2甲乙丙三人各射一次靶,记-A “甲中靶”;-B “乙中靶”;-C “丙中靶”则用上述三事件的运算分别表示下列事件 (1)甲未中靶:A ; (2)甲中靶而乙未中靶B A(3)三人中只有丙未中靶:C AB (4)三人中恰好一人中靶:C B A C B A C B A ⋃⋃(5)三人中至少一人中靶C B A ⋃⋃ (6)三人中至少一人未中靶C B A ⋃⋃ (7)三人中恰好两人中靶:C B A BC A C AB ⋃⋃(8)三人中至少两人中靶AC BC AB ⋃⋃ (9)三人中均未中靶:C B A (10)三人中至多一人中靶C B A C B A C B A C B A ⋃⋃⋃ (11)三人中至多两人中靶C B A ABC ⋃⋃=3 20个运动队,任意分成甲乙两组(每组10队)进行比赛,已知其中有两个队是一级队,求这两个一级队: (1) 被分在不同组(A )的概率,;(2)被分在同一组(B )的概率。
概率论与数理统计期末考试试卷答案

《概率论与数理统计》试卷A(考试时间:90分钟; 考试形式:闭卷)(注意:请将答案填写在答题专用纸上,并注明题号。
答案填写在试卷和草稿纸上无效)一、单项选择题(本大题共20小题,每小题2分,共40分) 1、A ,B 为二事件,则AB =()A 、AB B 、A BC 、A BD 、A B2、设A ,B ,C 表示三个事件,则A B C 表示()A 、A ,B ,C 中有一个发生 B 、A ,B ,C 中恰有两个发生C 、A ,B ,C 中不多于一个发生D 、A ,B ,C 都不发生 3、A 、B 为两事件,若()0.8P AB =,()0.2P A =,()0.4P B =,则()成立A 、()0.32P AB = B 、()0.2P A B =C 、()0.4P B A -=D 、()0.48P B A = 4、设A ,B 为任二事件,则()A 、()()()P AB P A P B -=- B 、()()()P AB P A P B =+C 、()()()P AB P A P B =D 、()()()P A P AB P AB =+ 5、设事件A 与B 相互独立,则下列说法错误的是()A 、A 与B 独立 B 、A 与B 独立C 、()()()P AB P A P B =D 、A 与B 一定互斥 6、设离散型随机变量X 的分布列为其分布函数为()F x ,则(3)F =()A 、0B 、0.3C 、0.8D 、17、设离散型随机变量X 的密度函数为4,[0,1]()0,cx x f x ⎧∈=⎨⎩其它 ,则常数c =()A 、15 B 、14C 、4D 、58、设X ~)1,0(N,密度函数22()x x ϕ-=,则()x ϕ的最大值是()A 、0B 、1 C、9、设随机变量X 可取无穷多个值0,1,2,…,其概率分布为33(;3),0,1,2,!k p k e k k -==,则下式成立的是()A 、3EX DX ==B 、13EX DX == C 、13,3EX DX == D 、1,93EX DX ==10、设X 服从二项分布B(n,p),则有()A 、(21)2E X np -=B 、(21)4(1)1D X np p +=-+C 、(21)41E X np +=+D 、(21)4(1)D X np p -=-11、独立随机变量,X Y ,若X ~N(1,4),Y ~N(3,16),下式中不成立的是()A 、()4E X Y +=B 、()3E XY =C 、()12D X Y -= D 、()216E Y += 12、设随机变量X 的分布列为:则常数c=()A 、0B 、1C 、14 D 、14- 13、设X ~)1,0(N ,又常数c 满足{}{}P X c P X c ≥=<,则c 等于()A 、1B 、0C 、12D 、-1 14、已知1,3EX DX =-=,则()232E X ⎡⎤-⎣⎦=()A 、9B 、6C 、30D 、36 15、当X 服从( )分布时,EX DX =。
青岛理工大学系统工程复习题B期末试题及参考答案

答:动态系统是系统的状态随时间而变化的系统;而静态系统则是表征系统运行规律的模型中不含时间因素,即模型中的量不随时间而变化,它可视作动态系统的一种特殊情况,即状态处于稳定的系统。实际上多数系统是动态系统,但由于动态系统中各种参数之间的相互关系非常复杂,要找出其中的规律性有时是非常困难的,这时为了简化起见而假设系统是静态的,或使系统中的各种参数随时间变化的幅度很小,而视为稳态的。
系统分析系统仿真决策控制系统效用系统工程
系统分析:系统分析是运用建模及预测、优化、仿真、评价等技术对系统的各个方面进行定性与定量相结合的分析,为选择最优或满意的系统方案提供决策依据的分析研究过程。
系统仿真:所谓系统仿真,就是根据系统分析的目的,在分析系统各要素性质及其相互关系的基础上,建立能描述系统结构或行为过程,且具有一定逻辑关系或数学方程的仿真模型,据此进行实验或定性分析,以获得正确决策所需的各种信息。
效用:评价主体根据个人的性格特点以及对未来的展望等因素,对于某种利益和损失有自己独到的感觉和反应,这种感觉和反应就是效用。
系统工程:用定量与定性相结合的系统思想和方法处理大型复杂系统的问题,无论是系统的设计或组织的建立,还是系统的经营管理,都可以统一的看成是一类工程实践,统称为系统工程。
三简答题(40分)
4答:系统方法告诉我们要以系统的观点去看整个世界,不能片面、孤立地看问题。系统方法主张以思辨原则代替实验原则,不能机械看问题,尤其是在处理复杂、有机程度高地系统时,这一点尤为重要。系统方法论主张以整体论代替还原论。系统方法启示我们以目的论代替因果论。人类经济社会不是偶然事件的产物,而是有目的性的复杂系统,研究问题的出发点是认识其目的,服务于目的。
教师试做时间
出题教师
青岛理工大学2010年概率论与数理统计试卷

一、填空题(每题3分,共15分)1、对于随机事件A 与B ,已知()0.5,()0.6,P A P B ==且8.0)(=⋃B A P ,则(|)PB A = 。
. 2、已知~(3,1),~(2,1)X N Y N -,且X 与Y 相互独立,设323--=Y X Z ,则~Z 。
3随机变量X 的分布函数为0, 10.4, 11()0.8, 131, 3x x F x x x <-⎧⎪-≤<⎪=⎨≤<⎪⎪≤<+∞⎩,则随机变量X 的分布律为 。
4、随机变量X 服从参数为λ的泊松分布,D(-2X+1)=_____________。
5、设),,,(21n X X X 是来自总体),(~2σμN X 的样本,2,σμ均为未知参数,则置信水平为α-1的关于2σ的双侧置信区间为 。
二、选择题(每题2分,共20分)1、设A n 是n 次独立重复试验中事件A 发生的次数,且(,) (01)A n B n p p <<~,则当n 很大时,下列选项不正确的是( )A .An n依概率收敛于p (B)(,(1))A n N np np p -~ C .(1)(,)A n p p N p n n -~(0,1)N 2、如果()0,()0,(|)()P A P B P A B P A >>=,则下列结论不成立的是( )。
A .(|)()P B A P B = B .(|)()P A B P A = C .A 、B 相容 D . A 、B 不相容 3、A 、B 为两事件,若()0.8P A B = ,()0.2P A =,()0.4P B =,则()成立A .()0.32P AB = B .()0.2P AB =C .()0.4P B A -=D .()0.48P B A = 4、设)1,0(~N X ,又常数c 满足{}{}P X c P X c ≥=<,则c 等于()A .1B .0C .12D .-1 5、已知1,3EX DX =-=,则()232E X ⎡⎤-⎣⎦=()A .9B .6C .30D .36 6、当X 服从( )分布时,EX DX =。
统计学期末考试试题库和答案解析

第一章绪论一、填空题1.标志是说明特征的,指标是说明数量特征的。
2.标志可以分为标志和标志。
3.变量按变量值的表现形式不同可分为变量和变量。
4.统计学是研究如何、、显示、统计资料的方法论性质的科学。
5.配第在他的代表作《》中,用数字来描述,用数字、重量和尺度来计量,为统计学的创立奠定了方法论基础。
二、判断题1.企业拥有的设备台数是连续型变量。
()2.学生年龄是离散型变量。
()3.学习成绩是数量标志。
()4.政治算术学派的创始人是比利时的科学家凯特勒,他把概率论正式引进统计学。
()5.指标是说明总体的数量特征的。
()6.对有限总体只能进行全面调查。
()7.总体随着研究目的的改变而变化。
()8.要了解某企业职工的文化水平情况,总体单位是该企业的每一位职工。
()9.数量指标数值大小与总体的范围大小有直接关系。
()10.某班平均成绩是质量指标。
()三、单项选择题1.考察全国的工业企业的情况时,以下标志中属于数量标志的是( )。
A.产业分类B.劳动生产率C.所有制形式D.企业名称2.要考察全国居民的人均住房面积,其统计总体是( )。
A.全国所有居民户B.全国的住宅C.各省市自治区D.某一居民户3.若要了解全国石油企业采油设备情况,则总体单位是( )。
A.全国所有油田B.每一个油田C.每一台采油设备D.所有采油设备4.关于指标下列说法正确的是( )。
A.指标是说明总体单位数量特征的B.指标都是用数字表示的C.数量指标用数字表示,质量指标用文字表示D.指标都是用文字表示的5.政治算术学派的代表人物是 ( )。
A.英国人威廉·配第B.德国人康令C.德国人阿亨瓦尔D.比利时人凯特勒6.关于总体下列说法正确的是( )。
A.总体中的单位数都是有限的B.对于无限总体只能进行全面调查C.对于有限总体只能进行全面调查D.对于无限总体只能进行非全面调查7.关于总体和总体单位下列说法不正确的是( )。
A.总体和总体单位在一定条件下可以相互转换B.总体和总体单位是固定不变的C.构成总体的个别单位是总体单位D.构成总体的各个单位至少具有某种相同的性质8.关于标志下列说法不正确的是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学号:姓名:班级:..........................................................密.......................................................封...........................................................线..........................................................专业本科各专业年级2007级班2008~2009学年第 1 学期概率论与数理统计课程期末试卷试卷类型:B 卷青岛理工大学试卷纸共 4 页第 1 页试题要求:1、试题后标注本题得分;2、试卷应附有评卷用标准答案,并有每题每步得分标准;3、试卷必须装订,拆散无效;4、试卷必须..........................................................密.......................................................封..........................................................线....................................................................................................................密.......................................................封..........................................................线....................................................................................................................密.......................................................封..........................................................线..........................................................2008年下学期概率统计试卷(B)参考答案1. 设A, B, C 是三个随机事件. 事件:A 发生, B , C 中至少有一个不发生表示为(空1) .2. 从1,2,3,4中任取一个数, 记为X , 再从1,2,…,X 中任取一个数, 记为Y . 则P {Y =2}=(空2) . 解 P {Y =2}=P {X =1}P {Y =2|X =1}+P {X =2}P {Y =2|X =2}+P {X =3}P {Y =2|X =3}+P {X =4}P {Y =2|X =4} =41×(0+21+31+41)=4813. 3. 已知随机变量X 只能取-1,0,1,2四个值, 且取这四个值的相应概率依次为cc c c 167,85,43,21. 则常数c = (空3) . 概率}0|1{≠<X X P =(空4) .解 由离散型随机变量的分布律的性质知,13571,24816c c c c+++=所以3516c =. 所求概率为P {X <1| X 0≠}=258167852121}0{}1{=++=≠-=cc c c X P X P . 4. 设随机变量X , Y 的数学期望分别是2和-4, 方差分别是1和4, 而相关系数为0.5. 则根据切比雪夫不等式估计{|2|P X Y +≥12}=(空5) .解 {2}2()()22(4)E X Y E X E Y +=+=⨯+-=,{2}4()()22Cov(,)D X Y D X D Y X Y +=+-⨯840.5124=-⨯⨯⨯=. 所以, {|2|P X Y +≥12}≤2411236=. 5. 若1X ,2X ,3X 为来自总体2(,)X N μσ 的样本, 且Y 1231134X X kX =++为μ的无偏估计量, 则常数k =(空6) . 解 要求1231111()3434E X X kX k μμμμ++=++=, 解之, k =512.1.设A, B 为任二事件, 则下列关系正确的是( ).(A) ()()()P A P AB P AB =+. (B)()()()P A B P A P B =+ . (C) ()()()P A B P A P B -=-. (D) ()()()P AB P A P B =.解 由文氏图易知本题应选(D).2. 设事件A 与B 独立, 则下面的结论中错误的是( ).(A) A 与B 独立. (B) A 与B 独立. (C) ()()()P P P B =. (D) A 与B 一定互斥.解 因事件A 与B 独立, 故A B 与,A 与B 及A 与B 也相互独立. 因此本题应选(D).3. 设随机变量X 的概率密度为()f x , 且()()f x f x =-, 又F (x )为随机变量X 的分布函数, 则对任意实数a , 有( ).(A) 0()1d ()∫aF a x f x -=-. (B) 01()d 2()∫aF a x f x -=-. (C) ()()F a F a -=. (D) ()2()1F a F a -=-.解 由分布函数的几何意义及概率密度的性质知答案为(B).4. 设随机变量X 服从标准正态分布N (0,1), 对给定的正数)10(<<αα, 数αu 满足{}P X u αα>=. 若{}P X x α<=, 则x 等于( ).(A) /2u α . (B) 1/2u α- . (C) (1)/2u α-. (D) α-1u . 解 答案是(C).5. 设连续型随机变量X 的概率密度为f (x ), 则31Y X =+的概率密度为g (y )为( ).(A)111()333f y -. (B) 3(31)f y +. (C) 3()1f y +. (D) 1133()f y -.解 由随机变量函数的分布可得, 本题应选(A). 6. 在下列结论中, 错误的是( ).(A) 若随机变量X 服从参数为n ,p 的二项分布,则().E X np =(C) 若X 服从泊松分布, 则()()D X E X =. (D) 若2~(,),X N μσ 则~(0,1)X N μσ-.解 )1,1(~-U X , 则3112212)()(22==-=a b X D . 选(B). 7. 在下列结论中, ( )不是随机变量X 与Y 不相关的充分必要条件(A) E (XY )=E (X )E (Y ). (B) D (X +Y )=D (X )+D (Y ). (C) Cov(X ,Y )=0. (D) X 与 Y 相互独立.解 X 与 Y 相互独立是随机变量X 与Y 不相关的充分条件,而非必要条件. 选(D). 8. 已知X 1,X 2,…,X n 是来自总体2(,)X N μσ 的样本, 则下列结论中正确的是( ).(A) ().E X n μ= (B) 2().D X σ=(C) 22().E S σ= (D) 以上全不对.解 选(C).9. 设随机变量X 与Y 都服从标准正态分布, 则下列结论中正确的是( ).(A) X +Y 服从标准正态分布. (B) X 2+Y 2服从2χ分布.(C) X 2和Y 2都服从2χ分布. (D)22X Y服从F 分布.解 因为随机变量X 与Y 都服从标准正态分布, 但X 与Y 不一定相互独立,所以(A),(B),(D)都不对, 故选(C).10. 设总体X 的均值μ与方差σ2都存在但未知, 而12,,,n X X X 为来自X 的样本, 则均值μ与方差σ2的矩估计量分别是( ) .(A) X 和S 2. (B) X 和211()nii X nμ=-∑. (C) μ和σ2. (D) X 和211()nii X X n=-∑.解 选(D).三、(10分)在三个箱子中, 第一箱装有4个黑球, 1个白球; 第二箱装有3个黑球, 3个白球; 第三箱装有3个黑球, 5个白球. 现任取一箱, 再从该箱中任取一球.(1) 求取出的球是白球的概率;(2) 若取出的为白球, 求该球取自第二箱的概率. 解 以A 表示“取得的球是白球”,i H 表示“取得的球来自第i 个箱子”,i =1,2,3. 则P (i H )=13, i =1,2,3, 123115(|),(|),(|)528P A H P A H P A H ===. ...................... 4分 (1) 由全概率公式知P (A )=112233()(|)()(|)()(|)P H P A H P H P A H P H P A H ++=12053. ............ 4分(2) 由贝叶斯公式知 P (2|H A )=222()()(|)20()()53P AH P H P A H P A P A ==. .................. 2分 四、(10分) 设二维随机变量(X , Y )的概率密度为(,)1,01,02,0,.f x y x y x =<<<<⎧⎨⎩其它 求:(1) (X , Y )的边缘概率密度(),()X Y f x f y ;(2)11{}22P Y X ≤≤;(3) X 与Y 是否独立?并说明理由. 解 (1) 当01x <<时,20()(,)d d 2xX f x f x y y y x +∞-∞===⎰⎰;当x ≤0时或x ≥1时, ()0X f x =.故 2,01,()0,其它.X x x f x <<=⎧⎨⎩ ............................. 2分当0<y <2时,12()(,)d d 12y Y y f y f x y x x +∞-∞===-⎰⎰; 当y ≤0时或y ≥2时, ()0Y f y =.故 1,02,()20,.Y yy f y -<<=⎧⎪⎨⎪⎩其它 ............................... 2分(2) {}{}11311322161122442≤,≤≤≤≤P X Y P Y X P X ===⎧⎫⎨⎬⎩⎭. ............................. 4分 (3) 因为(,)()()X Y f x y f x f y ≠,所以X 与Y 是否独立. …………………………………2分 五、(10分)设随机变量(X , Y )的分布律为若E (XY )=0.8, 求常数a ,b 和协方差Cov(X ,Y ). 解 首先,由∑∑∞=∞==111i j ijp得4.0=+b a . 其次,由0.8()100.420110.2210.22E XY a b b ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=+,得3.0=b . 进而1.0=a . ...................................................... 2分由此可得边缘分布律于是 4.14.026.01)(=⨯+⨯=X E , 5.05.015.00)(=⨯+⨯=Y E .故 Cov(,)()()()0.8 1.40.50.1X Y E XY E X E Y =-=-⨯=. ...................... 4分六、(10分)设某种商品每周的需求量X 是服从区间[10,30]上均匀分布的随机变量,而经销商店进货量为区间[10,30]中的某一整数. 该经销商店每销售一单位该种商品可获利500元; 若供大于求则削价处理, 每处理一单位该种商品亏损100元; 若供不应求, 则可从外部调剂供应, 此时每一单位商品仅获利300元. 为实现该商店所获利润期望值不小于9280元的目标, 试确定该经销商店对该种商品的进货量范围.解 设进货量为a 单位, 则经销商店所获利润为500300()300200,30,500100()600100,10.a a X a X a a X M X a X X a X a +-=+<=--=-⎧⎨⎩≤≤≤ ............ 4分 需求量X 的概率密度为()1,1030,200,.f x x =⎧<<⎪⎨⎪⎩其它 ........................... 2分 由此可得利润的期望值为30301010111()(600100)(300200)202020a a a aE M M dx x a dx x a dx =-++=⎰⎰⎰ .............. 2分 21535052502a a =-++依题意, 有21535052502a a -++≥9280,即21535040302a a -+≤0, 解得623≤a ≤26. 故期望利润不少于9280元的进货量范围为21单位~26单位. ................................................................ 2分七、(10分) 设总体X 服从参数为λ的指数分布, 即X 的概率密度为e ,0,(,)0,0,x x f x x λλλ->=⎧⎨⎩≤ 其中0λ>为未知参数, X 1, X 2, …, X n 为来自总体X 的样本, 试求:(1) 未知参数λ的矩估计量; (2) 极大似然估计量.解 因为E (X )=1λ =X , 所以λ的矩估计量为1ˆXλ=. ................................ 4分 设x 1, x 2,…, x n 是相应于样本X 1, X 2,… ,X n 的一组观测值, 则似然函数11nii inxx nni L eeλλλλ=--=∑==∏, ...................... 2分取对数1ln ln ()ni i L n x λλ==-∑.令1d ln 0,d ni i L n x λλ==-=∑ 得λ的极大似然估计值为1ˆx λ=,λ的极大似然估计量为1ˆX λ=. 4分八、(12分)已知一批零件的长度X (单位:cm)服从正态分布(,1)N μ, 从中随机地抽取16个零件, 得到长度的平均值为40cm.(1) 取显著性水平α=0.05时, 是否可以认为μ=41? (2) 求μ的置信水平为0.95的置信区间;(3) 问题(1)和(2)的条件与结论之间有什么关系? 解 (1) 提出假设 H 0: μ=μ0=41; H 1:μ≠μ0 . ................................... 2分 对于α=1-0.95= 0.05, 选取检验统计量X z =拒绝域为|z |>z 0.025=1.96 ............... 2分代入数据n =16, x =40, σ=1, 得到||x z ===4>1.96. 所以拒绝原假设, 不能认为μ=41 2分(2) 已知x =40, σ =1,α = 0.05, 查表可得0.025 1.96,z z α==所求置信区间为22()(40 1.96,40 1.96),x z x αα+=(39.51,40.49).= ..... 4分(3) 假设检验中的显著性水平α=0.05与置信区间估计的置信水平0.95满足关系0.95=1-α; .. 1分μ的双侧假设检验的接受域与μ的置信水平为0.95的置信区间相同...................... 1分 注意:题目参考数据: t 0.025(24)=2.0639, t 0.025(23)=2.0687, t 0.05(24)=1.7109, t 0.05(23)=1.7139z 0.025=1.96, z 0.05=1.65。
