板(膜)理论吸声公式及声强反射系数
初学者:声学计算公式大全
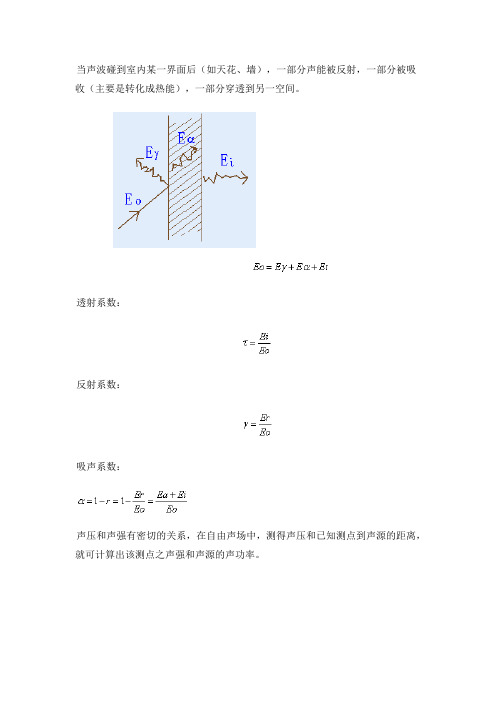
当声波碰到室内某一界面后(如天花、墙),一部分声能被反射,一部分被吸收(主要是转化成热能),一部分穿透到另一空间。
透射系数:反射系数:吸声系数:声压和声强有密切的关系,在自由声场中,测得声压和已知测点到声源的距离,就可计算出该测点之声强和声源的声功率。
1、声压级Lp取参考声压为Po=2*10-5N/m2为基准声压,任一声压P的Lp为:听觉下限: p=2*10-5N/m2 为0dB能量提高100倍的 P=2*10-3N/m2 为20dB听觉上限: P=20N/m2 为120dB2、声功率级Lw取Wo为10-12W,基准声功率级任一声功率W的声功率级Lw为:3、声强级:3、声压级的叠加几个声源同时作用时,某点的声能是各个声源贡献的能量的代数和。
因此其声压是各声源贡献的声压平方和的开根号。
即:声压级为:声压级的叠加•两个数值相等的声压级叠加后,总声压级只比原来增加3dB,而不是增加一倍。
这个结论对于声强级和声功率级同样适用。
•此外,两个声压级分别为不同的值时,其总的声压级为问题:10dB+10dB=? 0dB+0dB=? 0dB+10dB=?答案分别是:13dB,3dB,10dB.两个声强级获声功率级的叠加公式与上式相同在建筑声学中,频带划分的方式通常不是在线性标度的频率轴上等距离的划分频带,而是以各频率的频程数n都相等来划分。
声波在室内的反射与几何声学3.2.1 反射界面的平均吸声系数(1)吸声系数:用以表征材料和结构吸声能力的基本参量通常采用吸声系数,以α表示,定义式:材料和结构的吸声特性和声波入射角度有关。
声波垂直入射到材料和结构表面的吸声系数,成为“垂直入射(正入射)吸声系数”。
这种入射条件可在驻波管中实现。
其吸声系数的大小可通过驻波管法来测定。
当声波斜向入射时,入射角度为θ,这时的吸声系数称为斜入射吸声系数,。
建筑声环境中,出现垂直入射和斜入射的情况较少,而普遍情况是声波从各个方向同时入射到材料和结构表面,如果入射声波在半空间中均匀分布,,则称这种入射情况为“无规则入射”或“扩散入射”。
声学计算公式

声学计算公式当声波碰到室内某⼀界⾯后(如天花、墙),⼀部分声能被反射,⼀部分被吸收(主要是转化成热能),⼀部分穿透到另⼀空间。
透射系数:反射系数:吸声系数:声压和声强有密切的关系,在⾃由声场中,测得声压和已知测点到声源的距离,就可计算出该测点之声强和声源的声功率。
声压级Lp取参考声压为Po=2*10-5N/m2为基准声压,任⼀声压P的Lp为:听觉下限: p=2*10-5N/m2 为0dB能量提⾼100倍的 P=2*10-3N/m2 为20dB听觉上限: P=20N/m2 为120dB2、声功率级Lw取Wo为10-12W,基准声功率级任⼀声功率W的声功率级Lw为:3、声强级:3、声压级的叠加10dB+10dB=? 0dB+0dB=? 0dB+10dB=? 答案分别是:13dB,3dB,10dB.⼏个声源同时作⽤时,某点的声能是各个声源贡献的能量的代数和。
因此其声压是各声源贡献的声压平⽅和的开根号。
即:声压级为:声压级的叠加两个数值相等的声压级叠加后,总声压级只⽐原来增加3dB,⽽不是增加⼀倍。
这个结论对于声强级和声功率级同样适⽤。
此外,两个声压级分别为不同的值时,其总的声压级为两个声强级获声功率级的叠加公式与上式相同在建筑声学中,频带划分的⽅式通常不是在线性标度的频率轴上等距离的划分频带,⽽是以各频率的频程数n都相等来划分。
声波在室内的反射与⼏何声学3.2.1 反射界⾯的平均吸声系数(1)吸声系数:⽤以表征材料和结构吸声能⼒的基本参量通常采⽤吸声系数,以α表⽰,定义式:材料和结构的吸声特性和声波⼊射⾓度有关。
声波垂直⼊射到材料和结构表⾯的吸声系数,成为“垂直⼊射(正⼊射)吸声系数”。
这种⼊射条件可在驻波管中实现。
其吸声系数的⼤⼩可通过驻波管法来测定。
当声波斜向⼊射时,⼊射⾓度为θ,这是的吸声系数称为斜⼊射吸声系数,。
建筑声环境中,出现垂直⼊射和斜⼊射的情况较少,⽽普遍情况是声波从各个⽅向同时⼊射到材料和结构表⾯,如果⼊射声波在半空间中均匀分布,,则称这种⼊射情况为“⽆规则⼊射”或“扩散⼊射”。
微孔板吸声原理

一、微孔板吸声结构的理论在板厚小于1.0mm的薄板上穿以孔径小于等于1.0mm的微孔,穿孔率为1~5%,后部留有一定的厚度(5-20cm)空气层,该层不填任何吸声材料 ,这样即构成了微穿孔板吸声结构。
它是一种低声质量,高声阻的共振吸声结构,其研究表明,表征微穿孔板吸声特性的吸声系数和频带宽度,主要由微穿孔板的声质量m和声阻r来决定,而这两个因素又与微孔直径d及穿孔率p有关。
微穿孔板吸声结构的相对声阻抗Z(以空气的特性阻抗ρC为单位)用式(1)计算:Z=r+jwm=jctg(WD/C)(1)式中:ρ--空气密度(kg/cm3);C--空气中声速(m/s);D--腔深(mm);m--相对声质量;r--相对声阻;w--角频率,W=2πf(f为频率);而r和m分别由式(2)(3)表达:r=atkr/dzp(2)m=(0.294)×10-3tkm/p(3)式中:t--板厚(毫米)d--孔径(毫米)p--穿孔率(%)kr--声阻系数kr=(1+x2/32)1/2+(2x)1/2/8×d/tkm--声质量系数km=1+{1+[1/(9+(x2/2))]}+0.85d/t其中x=abf,a和b为常数,对于绝热板a=0.147,b=0.32;对于导热板a=0.235,b=0.21。
声吸收的角频带宽度,近似地由r/m决定,此值越大,吸声的频带越宽。
r/m=(l/d2)×(kr/km)(4)式中l--常数,对于金属板l=1140,而隔热板l=500。
上式也可以用式(5)表达:r/m=50f((kr/km)/x2)(5)而kr/km的近似计算式为:kr/km=0.5+0.1x+0.005x2(6)利用以上各式就可以从要求的r、m、f求出微穿孔板吸声结构的x、d、t、p等参量。
由于微穿孔板的孔径很小且稀,基声阻r值比普通穿孔板大得多,而声质量m又很小,故吸声频带比普通穿孔板共振吸声结构大得多,一般性能较好的单层或双层微穿孔板吸声结构的吸声频带宽度可以达到6~10个1/3信频程以上。
声学计算公式大全

声学计算公式大全1.声压级公式:声压级(Lp) = 20 * log10(p/p0)其中,p为声压,p0为参考声压(通常取20微帕)。
2.声强级公式:声强级(Lw)= 10 * log10(I/10^-12)其中,I为声强。
3.声强公式:声强(I)=p*v其中,p为声压,v为声速。
4.声能级公式:声能级(Le)= Lu - 10 * log10(S/S0)其中,Lu为声能,S为参考面积,S0为参考面积(1平方米)。
5.声能公式:声能(Lu)=P*T其中,P为声功率,T为时间。
6.声功率级公式:声功率级(Lw)= 10 * log10(W/10^-12)其中,W为声功率。
7.声功率公式:声功率(W)=p*S*v其中,p为声压,S为振动面积,v为振动速度。
8.声深度公式:声深度(Ld)= 20 * log10(d/d0)其中,d为距离,d0为参考距离。
9.声暴公式:声暴(SN)= 20 * log10(sqrt(L1/L0) * (R0/R1)^2)其中,L1和L0为两个声级的差值,R0和R1为两个距离的比值。
10.波长公式:波长(λ)=v/f其中,v为声速,f为频率。
11.反射系数公式:反射系数(R)=(Z2-Z1)/(Z2+Z1)其中,Z1和Z2为两个介质的声阻抗。
12.驻波公式:驻波(λ/2)=L/n其中,L为管道长度,n为节点数。
13.声阻抗公式:声阻抗(Z)=p/v其中,p为声压,v为声速。
14.声频公式:声频(ν)=f/N其中,f为频率,N为周期。
这些公式只是声学领域中的一部分,用于基本的声学计算。
在实际应用中,还需要综合考虑各种因素,如温度、湿度、介质特性等,才能获得准确的结果。
同时,不同的声学计算问题可能需要采用不同的公式和方法,因此深入学习声学计算方法和理论是非常重要的。
[VIP专享]声学计算公式大全[1]
![[VIP专享]声学计算公式大全[1]](https://img.taocdn.com/s3/m/56f3a7b99e314332396893d7.png)
噪声分析常用计算公式汇总(二)吸声降噪

噪声分析常用计算公式汇总(二)吸声降噪在上一篇文章中,我们介绍了噪声分析的一些常用计算公式。
在本文中,我们将继续探讨一些吸声降噪方面的常用计算公式。
1. 吸声材料的吸声系数计算公式(Sabine公式)Sabine公式是用来计算吸声材料的吸声系数的常用公式,其表达式为:α=1-(1/R)其中,α为吸声系数,R为反射系数。
2.单层吸声材料的声阻抗计算公式单层吸声材料的声阻抗可通过以下公式计算:Z=ρc/α其中,Z为声阻抗,ρ为吸声材料的密度,c为声速,α为吸声系数。
3.多层吸声材料的等效吸声系数计算公式多层吸声材料的等效吸声系数可通过以下公式计算:αeq = 1 - (1 - α1)(1 - α2)/(1 - α1α2)其中,αeq为等效吸声系数,α1和α2分别为两层吸声材料的吸声系数。
4.噪声源的声压级计算公式噪声源的声压级可通过以下公式计算:Lp = Lw + 10log(Q)其中,Lp为噪声源的声压级,Lw为噪声源的声功率级,Q为噪声源的辐射效率。
5.高分子材料(如聚酯纤维、蓝胶等)吸声材料的等效吸声系数计算公式高分子材料的等效吸声系数可通过以下公式计算:αeq = αi/hi其中,αeq为等效吸声系数,αi为高分子材料的吸声系数,hi为高分子材料的厚度。
6.扩散法降噪效果计算公式扩散法是一种常用的降噪方法,可通过以下公式计算其降噪效果:D = 10log(A/A0)其中,D为降噪效果,A为扩散以后的声能流密度,A0为扩散之前的声能流密度。
7.双壁屏蔽材料的声传递损失计算公式双壁屏蔽材料的声传递损失可通过以下公式计算:TL = 10log(1 + (M/R))其中,TL为声传递损失,M为主要隔声体积,R为面阻抗。
以上是一些吸声降噪方面常用的计算公式,通过这些公式可以对吸声材料的性能和降噪效果进行评估和分析。
对于噪声控制和降噪工程来说,准确地计算和评估吸声材料的性能是非常重要的,有助于选择合适的吸声材料和设计有效的降噪方案。
声学计算公式大全

当声波碰到室内某一界面后(如天花、墙),一部分声能被反射,一部分被吸收(主要是转化成热能),一部分穿透到另一空间。
透射系数:反射系数:吸声系数:声压和声强有密切的关系,在自由声场中,测得声压和已知测点到声源的距离,就可计算出该测点之声强和声源的声功率。
声压级Lp取参考声压为Po=2*10-5N/m2为基准声压,任一声压P的Lp为:听觉下限: p=2*10-5N/m2 为0dB能量提高100倍的 P=2*10-3N/m2 为20dB听觉上限: P=20N/m2 为120dB1、声压级Lp取参考声压为Po=2*10-5N/m2为基准声压,任一声压P的Lp为:听觉下限: p=2*10-5N/m2 为0dB能量提高100倍的 P=2*10-3N/m2 为20dB听觉上限: P=20N/m2 为120dB2、声功率级Lw取Wo为10-12W,基准声功率级任一声功率W的声功率级Lw为:3、声强级:3、声压级的叠加10dB+10dB=? 0dB+0dB=? 0dB+10dB=? 答案分别是:13dB,3dB,10dB.几个声源同时作用时,某点的声能是各个声源贡献的能量的代数和。
因此其声压是各声源贡献的声压平方和的开根号。
即:声压级为:声压级的叠加•两个数值相等的声压级叠加后,总声压级只比原来增加3dB,而不是增加一倍。
这个结论对于声强级和声功率级同样适用。
•此外,两个声压级分别为不同的值时,其总的声压级为两个声强级获声功率级的叠加公式与上式相同在建筑声学中,频带划分的方式通常不是在线性标度的频率轴上等距离的划分频带,而是以各频率的频程数n都相等来划分。
声波在室内的反射与几何声学3.2.1 反射界面的平均吸声系数(1)吸声系数:用以表征材料和结构吸声能力的基本参量通常采用吸声系数,以α表示,定义式:材料和结构的吸声特性和声波入射角度有关。
声波垂直入射到材料和结构表面的吸声系数,成为“垂直入射(正入射)吸声系数”。
穿孔板和薄板吸声系数和频谱经验公式

1. 序言
穿孔板和薄板及膜材料是常用的吸声材料。传统理论认为穿孔板的吸声来自于其穿孔对 于共振时声波空气粒子的粘滞消耗。而薄板和膜材料的吸声来自于材料自身的振动。本文的 两个实验证明,穿孔板吸声结构的吸声来也自于板材在声波作用下的振动。根据这个原理, 作者得出了穿孔板和薄板及膜材料共振吸声系数经验公式吸声频谱经验公式。
穿孔板和薄板吸声系数和频谱经验公式
张新安
西安工程大学,西安(710048)
E-mail:zxafafa.my265@
摘 要:作者在分析实验结果的基础上得出了穿孔板共振吸声系数公式和吸声频谱经验公 式,并推演出薄板(膜)共振吸声系数公式和吸声频谱经验公式。通过验证,这些公式可以 较好的反映实际测试情况。 关键词:穿孔板,薄板(膜),共振吸声系数经验公式,吸声频谱经验公式。
1000
0.61 0.63 0.320.7 1.2
1250
0.52 0.43
1600
0.37 0.35
2000
0.31 0.28
注:吸声系数1为穿孔铝板背后5cm空腔内填充4.8cm厚多孔材料时的情况;
吸声系数2为穿孔铝板背后5cm空腔内填充5.2cm厚多孔材料时的情况;
本次测试材料
m
=
m1
=
ρo D 3S
(10)
面积为 s = 7.85 ×10−3 ,根据式(10)可求得4.8cm厚多
孔材料层与穿孔板
Za
=
1 jωC
+
jωm =
j(ω(0.1 −
ρ
0
c
2 0
)
=
j(0.1 − 3.67 ×108
/ω)
ωV
之间的空气层质量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在建筑吸声和噪声控制领域,板材料和膜材料是常用的吸声材料之一。关于板材料和膜 材料的吸声性能国内外已有大量研究 (1−10) 。本根据动量守恒定律、牛顿力学分析、膜振动 理论推导出板(膜)材料的吸声理论公式。通过分析,该公式与板(膜)材料的吸声规律吻 合较好。
作者曾在相关文献中证明,纤维材料的吸声也是来自于材料的振动 (11−14) 。以此概念为 前提,板(膜)材料吸声理论公式也被应用于纤维材料当中。通过分析证明,板(膜)材料 吸声理论公式也适合于表达纤维材料吸声性能。
2
=
∂2 ∂x 2
+
∂2 ∂y 2
从而有,
∇ r 2η
−
1 c2
∂ 2η ∂t 2
=
−p c 2σ
……………………….(7)
-2-
其中
∇r
=
∂2 ∂r 2
+
1 r
∂ ∂r
令解为
η(t, r) = R(r)e jωt
带入(7)式可得
……………………….(8)
弹簧位移也就是材料波动的振幅。由此,我们令
s=η (t, r) = η a e j(ωt+π / 2) , v = va e jωt ,
将此带入(6)式可解得
a = 1 − ( kη a )2 ωmva
………………………………….(12)
根据前面的定义。驻波管内作用于材料的 1/4 波长的质量可表示为, m = πr 2 ρ0c0 ,( r 为 4f
设材料表面受到声压为
p = pa2e jωt
的声压作用,其中 pa2 为声压振幅
(N/m 2 ), ω 为声波的圆频率,那么在 dxdy 单元上就受到如下的外力作用。
FF = p2dxdy
将上式带入膜波动方程
∇ 2η = 1 ∂ 2η , c 2 ∂t 2
式中
c=
T σ
,T 为膜的张力,σ
为膜的面密度。∇
句话说。由此可以得出以下结论:自由声场中的中间媒质层可以看做是膜和弹簧组成的一个
简单模型,这个模型所得出的声强反射系数,与由小振幅声波的一维物态方程所得到的声强
反射系数的误差小于万分之一。若 sin 函数的角度值无限精确的取下去,则误差将趋于 0。 然而由膜-弹簧模型却能得到随入射声波的波动而变化的精细的声强反射系数公式。
得 (2) ε =
p
2 a
。则声强 I ' =
p
2 a
。由此,对于自由声场中的中间媒质层,声强反射系
2 ρ 0 c02
2ρ0c0
数为
I ' = pa22 / 2ρ0c0
p
2 a1
/
2ρ
0c0
(18)
根据上述讨论,式(18)表达的是声波传递中的平均声能变化情况。对比式(17)和
式(18),当式(17)中的 sin 函数取平均值时(角度值取一位小数), I = 1.0000735I ' 。换
-4-
吸声系数 吸声系数
10cm空腔
塑料膜 纤维板
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0
125 200 315 500 800 1250 2000 3150
频率/Hz
图 4 10cm 空腔时两种材料的吸声频谱
20cm空腔
碰撞后空气速度为 v 1 ,材料速度为 v 2 根据动 量守恒定律。
mv = Mv2 + mv1
(1)
根据吸声系数的定义
a = 1 − ( par )2 pai
式中 pai , par 分别为
入射声压和反射声压。
1本课题得到陕西省重点实验室项目(05JS07)的资助。 -1-
图 1 声波与材料相互作用示意图 图 2 动量守恒分析图
层的吸声情况。作者曾在文献(15,16)中证明,纤维层在声波作用下随声波波动做同频率
的振动。此时材料所受声波压力 pa2 及其变化都较小。那么,式(15)中吸声系数的变化就
主 要 来 自 于 公 式 右 侧 第 2 项 的 分 母 的 变 化 , 即 , D = (2n − 1) λ , n = 1,2,3,⋅ ⋅ ⋅ 时 , 4
sin(
2πD λ
)
=
1 ,式(15)中的第
2
项达到极小,吸声系数为极大值。而
D
=
n
λ 2
,n
=
1,2,3,⋅ ⋅ ⋅
时,sin( 2πD ) = 0 ,式(15)中的第 2 项达到极大,吸声系数为极小值。另外,在 D = n λ
λ
2
时,声波波幅为零,材料波幅也为零,它们的振动速度和加速度均为零,那么材料所受到的
由于
par
=
Fr s
, pai
=
Fi s
,
所以,
a
=
1−
⎜⎜⎝⎛
Fr Fi
⎟⎟⎠⎞
2
…………………………(2)
Fi 为声波对材料的作用力, Fr 为材料对空气的反作用力。
将 Fr = m dv dt
带入(2)并推导可得
Fi = m dv1 dt
v1 = v 1 − a
参考文献
[1] Kuttruff,H. H.,Room Acoustics (Fourth edition)[M],London:published by Spon Press 11 New Fetter Lane,2000,163-173,39-44 [2] 杜功焕,朱哲民,龚秀芬.声学基础.第二版,南京:南京大学出版社,2001,271-278,98-102.168-193。 [3] Hansen, Colin H.,Solutions to problems in engineering noise control, South Australia: Department of Mechanical Engineering University of Adelaide,1996,178-181. [4] Sound Research Laboratories, Noise control in industry Sound Research Laboratories(3rd ed), London E. & FN. Spon,1991,245-247. [5] Rettinger, M.,Handbook of architectural acoustics and noise control a manual for architects and engineers,Blue Ridge Summit TAB Professional and Reference Books, 1988,184-186. [6] Barber,A., Handbook of noise and vibration control(6th ed.),Oxford, UK : Elsevier Advanced Technology,1992,315-323 [7] Barron, Randall F. Industrial noise control and acoustics, New York : Marcel Dekker,2003,269-273. [8] cavanaugh h,W.J,Wikes,W.J. 建筑声学-理论与实践,赵樱译,北京:机械工业出版社,2004,56-57 [9] 赵松龄.噪声的降低与隔.上海:同济大学出版社,1985,133-137. [10] 马大猷.现代声学理论基础.北京:科学出版社,2004, 210-237 [11] 张新安.振动吸声理论及声学设计.西安:西安交通大学出版社,2007,131-170 [12] 张新安,中国科技论文在线,薄纤维层吸声原理分析 200609-13 [13] ZHANG xian an,The fiber Viberation Sound absorptin theory, SAE Technical Papers,2007-01-2188 [14] 张新安,纤维层材料振动吸声理论,中国科技论文在线,200609-22 [15] Xin an Zhang,The Formula of Sound Absorption Spectrum For Fibrous Material,12th,International Meeting, on Low Frequency Noise and Vibration and its Control,Bristol, UK 18 – 20 September 2006,371-380 [16] 张新安,纤维性材料经验吸声公式,中国科技论文在线,200608-350
驻波管内半径,ρ0 , c0 分别为空气密度和声速)。而 ω
= 2πf
,同时,对空气来说 va
=
pa1 ρ0c0
,
通过对(11)式求解 (2) ,膜的振幅可表达为η a
=
r 2 pa2 8T
。设 k
=
pa2 ⋅ πr 2 ηa
将上述表达式带入(12)式可得
式中 式
a = 1− (2 pa2 )2
.(13)
4f
λ
则式(14)变为
a
=
1
−
0.41(
pa2 sin( 2πD
)
)
2
λ
(15)
下面对式(15)进行讨论。
(1)材料在不同声波作用力下的情况。
通常情况下,当板(膜)已经波动而表面变成凸字形时,再加反方向的力使其往回振动
时,由于板(膜)材料自身的应力,材料会对施力者产生一种“顶”的力量,这就使材料上所
1.板(膜)材料吸声理论公式的建立
在最大吸声系数对应频率处,材料背后空腔距离为 1/4 波长。如图 1,取频率为 400Hz,则背后空腔为 22cm.。
