S-DES
des算法s合计算规则

des算法s合计算规则摘要:1.算法简介2.目标与策略3.算法实现4.应用场景5.总结与展望正文:1.算法简介DES算法是一种对称加密算法,它基于密钥对数据进行加密和解密。
DES 算法采用64位密钥,其中8位用于奇偶校验,用户实际可用的密钥长度为56位。
DES算法的加密过程包括分组、置换、S盒替换和P盒替换等步骤。
解密过程与加密过程相反。
2.目标与策略DES算法的主要目标是实现快速、安全的加密和解密。
为了达到这个目标,DES算法采用了对称密钥体制,即加密和解密使用相同的密钥。
同时,DES算法采用了各种复杂的算法设计策略,如S盒替换和P盒替换等,以增强加密强度。
3.算法实现DES算法的实现过程分为以下几个步骤:(1) 分组:将明文或密文分成64位一组,不足64位的,在末尾用0补足。
(2) 置换:将每组的第8位与第7位进行交换,然后将第1位与第6位、第2位与第5位、第3位与第4位进行交换。
(3) S盒替换:将经过置换后的64位数据分成8组,每组8位,然后通过查表的方式,将每组的8位数据替换为对应的S盒替换值。
(4) P盒替换:将经过S盒替换后的数据,再进行一次P盒替换。
P盒替换是根据置换后的数据与密钥的对应关系进行替换。
(5) 加密/解密:将替换后的数据进行16轮加密(或解密),每轮加密(或解密)包括一个S盒替换和一个P盒替换。
(6) 输出:加密后的数据或解密后的数据。
4.应用场景DES算法广泛应用于网络通信、数据存储等领域,为用户提供安全的数据加密和解密服务。
由于DES算法的密钥长度较短,随着计算机技术的发展,DES算法的安全性逐渐降低。
目前,DES算法主要用于低安全需求的场景,如内部通信等。
5.总结与展望DES算法作为对称加密算法的代表,曾在信息安全领域发挥了重要作用。
然而,随着计算机技术的发展和加密算法的不断进步,DES算法的安全性逐渐降低,已不再是信息安全领域的首选加密算法。
密码学 s-des
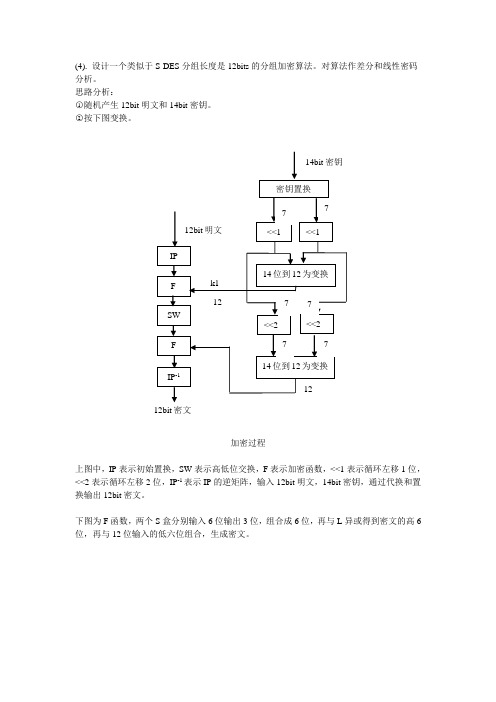
(4). 设计一个类似于S-DES 分组长度是12bits 的分组加密算法。
对算法作差分和线性密码分析。
思路分析:○1随机产生12bit 明文和14bit 密钥。
○2按下图变换。
加密过程上图中,IP 表示初始置换,SW 表示高低位交换,F 表示加密函数,<<1表示循环左移1位,<<2表示循环左移2位,IP -1表示IP 的逆矩阵,输入12bit 明文,14bit 密钥,通过代换和置换输出12bit 密文。
下图为F 函数,两个S 盒分别输入6位输出3位,组合成6位,再与L 异或得到密文的高6位,再与12位输入的低六位组合,生成密文。
12bit 明文 14bit 密钥12bit 密文密钥置换 14位到12为变换FSW F IP -1IP <<2<<2<<1<<114位到12为变换k1 77 7 7 771212F 函数定义的S1盒如下: 定义的S2盒如下: 012 3 4 5 6 7 0 5 2 4 1 0 3 6 7 1 0 3 6 5 7 2 1 4 2 7 6 5 3 2 0 4 1 3 4 1 7 2 3 0 5 6 4 1 5 2 4 0 7 6 3 5 2 6 3 5 4 7 0 1 6 3 5 7 4 2 1 6 0 7 63742510 1 2 3 4 5 6 7 0 0 4 6 7 3 2 1 5 1 3 6 4 2 1 0 5 7 224165733 7 3 24 6 1 05 4 1 7 5 3 2 4 06 5 6 57 4 2 3 1 0 6 5 2 4 7 6 3 0 1 7 42715636 6 663366 612k6位置换 6位到12位扩展S0S1 L R L R 12位输入 12位输出程序代码如下:clc;clear all;fprintf('产生随机明文:\n');plaintext=round(rand(1,12)) %随机产生12位明文key=round(rand(1,14)); %随机产生14位密钥A1=[0 0 0 0 0 0 0 0 0 1 0 0; %定义明文置换矩阵0 0 0 1 0 0 0 0 0 0 0 0 ;0 0 0 0 0 0 1 0 0 0 0 0 ;1 0 0 0 0 0 0 0 0 0 0 0;0 0 1 0 0 0 0 0 0 0 0 0;0 1 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 0 0 0 0 0 0 0;0 0 0 0 0 0 0 1 0 0 0 0;0 0 0 0 0 1 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 1 0;0 0 0 0 0 0 0 0 1 0 0 0;0 0 0 0 0 0 0 0 0 0 0 1;];A2=[0 0 0 0 0 0 0 0 0 1 0 0 0 0; %定义密钥置换矩阵0 0 0 0 0 1 0 0 0 0 0 0 0 0 ;0 0 0 0 0 0 1 0 0 0 0 0 0 0 ;1 0 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 1 0;0 1 0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 1 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 1 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0 0 1;0 0 0 0 0 0 0 0 0 0 0 1 0 0;0 0 0 0 0 0 0 0 0 0 1 0 0 0;0 0 0 0 0 0 0 0 1 0 0 0 0 0;0 0 1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 1 0 0 0 0 0 0 0 0 0 0;];A3=[0 0 0 0 0 1 0 0 0 0 0 0 ; %实现14位转12的变换0 0 0 0 0 0 0 0 0 0 1 0 ;1 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 1 0 0 0 0;0 1 0 0 0 0 0 0 0 0 0 0 ;0 0 0 0 0 0 0 0 1 0 0 0 ;0 0 0 1 0 0 0 0 0 0 0 0;0 0 0 0 0 1 0 0 0 0 0 0;0 0 1 0 0 0 0 0 0 0 0 0 ;0 0 0 0 0 0 0 0 0 0 0 0 ;0 0 0 0 1 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 1 0 0;0 0 0 0 0 0 0 0 0 0 0 1;] ;B1=plaintext*A1; %对明文进行初始置换B2=key*A2; %对密钥进行初始置换B2L=B2(1:7); %取B2的高7位B2R=B2(8:14); %取B2的低7位B3L=circshift(B2L',-1); %B2高7位循环左移一位B3R=circshift(B2R',-1); %B2高7位循环左移一位B3=[B3L;B3R];k1=B3'*A3; %得到子密钥k1B4L=circshift(B3L,-2); %B3高7位循环左移两位B4R=circshift(B3R,-2); %B3高7位循环左移两位B4=[B4L;B4R];k2=B4'*A3; %得到子密钥k2P=fun(B1,k1); %用函数第一次加密Q1=P(1:6);Q2=P(7:12);Q=[Q2,Q1]; %实现高低位交换R=fun(Q,k2); %使用函数第二次加密fprintf('产生密文:\n');ciphertext=R*inv(A1) %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 解密算法Arr1=ciphertext*A1; %对密文置换Arr2=fun(Arr1,k2); %使用k2第一轮解密Arr3=[Arr2(7:12),Arr2(1:6)]; %Arr2高低位交换Arr4=fun(Arr3,k1); %使用k1第二轮解密fprintf('解密出明文:\n');output=Arr4*inv(A1) %解密明文函数文件:function B=fun(X,k)S0=[5 2 4 1 6 3 0 7; %定义S0盒0 3 6 5 7 2 1 4;7 6 5 3 2 0 4 1;4 1 7 2 3 05 6;1 52 4 0 7 6 3;2 63 54 7 0 1;3 5 74 2 1 6 0;6 37 4 2 5 0 1;];S1=[0 4 6 7 3 2 1 5; %定义S1盒3 64 2 1 05 7;2 4 1 6 5 7 0 3;7 3 2 4 6 1 0 5 ;1 7 5 32 4 0 6;6 57 4 2 3 1 0;5 2 4 76 3 0 1;4 2 7 0 156 3;];A=[0 0 1 0 0 0 0 0 0 0 0 1; %6位到12位的扩展变换矩阵 0 0 0 1 0 0 0 1 0 0 0 0;0 0 0 0 1 0 0 0 1 0 0 0;0 0 0 0 0 0 1 0 0 1 0 0;0 1 0 0 0 0 0 0 0 0 1 0;1 0 0 0 0 1 0 0 0 0 0 0;] ;F=[0 0 0 0 1 0; %6位置换矩阵0 1 0 0 0 0;1 0 0 0 0 0;0 0 0 1 0 0;0 0 0 0 0 1;0 0 1 0 0 0;];Xl=X(1:6); %取X得高6位Xr=X(7:12); %取X的低6位Y=Xr*A; %对Xr进行6到12位变换记为YC=mod(Y+k,2); %对Y和密钥异或Cl=C(1:6); %取C的高6位Cr=C(7:12); %取C的低6位i=4*Cl(1)+2*Cl(3)+Cl(5)+1; %对S0盒操作的下标j=4*Cl(2)+2*Cl(4)+Cl(6)+1;D0=S0(i,j);E(1)=fix(D0/4); %将D0转换成2进制后最高位的值E(2)=fix((D0-E(1)*4)/2); %将D0转换成2进制后次高位的值E(3)=mod(D0,2); %将D0转换成2进制后最低位的值s=4*Cr(1)+2*Cr(3)+Cr(5)+1; %对S1盒操作的下标t=4*Cr(2)+2*Cr(4)+Cr(6)+1;D1=S1(s,t);E(4)=fix(D1/4); %将D1转换成2进制后最高位的值E(5)=fix((D1-E(4)*4)/2); %将D1转换成2进制后次高位的值E(6)=mod(D1,2); %将D1转换成2进制后最低位的值G=E*F; %对E置换后的矩阵H=mod(G+Xl,2); %将G和Xl异或B=[H,Xr];执行结果:。
倒向随机微分方程英文

倒向随机微分方程英文Title: Stochastic Differential Equations: An Introduction to Backward Equations.Abstract:Stochastic differential equations (SDEs) are a fundamental tool in modeling random phenomena in various fields such as finance, physics, and engineering. While forward SDEs describe the evolution of a system over time, backward SDEs (BSDEs) offer a different perspective, focusing on the backward-in-time evolution of certain quantities. BSDEs have found applications in areas like option pricing, risk management, and control theory. This article aims to introduce the reader to the theory and applications of backward stochastic differential equations.1. Introduction.Stochastic differential equations (SDEs) provide amathematical framework for modeling systems that are subject to random fluctuations. These equations describe how a system's state evolves over time, given some initial condition and driven by a stochastic process. While forward SDEs are well-studied and widely used, backward stochastic differential equations (BSDEs) offer a different perspective, allowing one to study the evolution of quantities backward in time.BSDEs were introduced by Ma and Yong in the early 1990s and have since found applications in various fields. In finance, BSDEs have been used to price contingent claims, hedge risks, and study optimal investment strategies. In control theory, BSDEs provide a tool for analyzing stochastic optimal control problems.2. Background on Stochastic Differential Equations.Before delving into backward stochastic differential equations, it's important to establish some background on forward SDEs. A forward SDE is typically written as:dX(t) = μ(t, X(t))dt + σ(t, X(t))dW(t),。
密码学S-DES

• Simplified DES方案,简称S-DES方案。 • 加密算法涉及五个函数:
S-DES
初始置换IP(initial permutation) 复合函数fk1,它是由密钥K1确定的,具有置换和替 代的运算 转换函数SW 复合函数fk2,与fk1相同,所用的密钥是K2 初始置换IP的逆置换IP-1
• 扩展/置换(E/P)运算
E/P 4 1 2 3 2 3 4 1
n2 n3
• 例: E/P(1001)=11000011 • 与子密钥异或:K1=(k11,k12,k13,k14,k15,k16,k17,k18)
n4 + k11 n1 + k12 n2 + k13 n3 + k14
•
S盒按下述规则运算:
P10 3 5 2 7 4 10 1 9 8 6
• •
子密钥生成
K1=P8 • shift • P10 (K) K2=P8 • shift • shift • P10 (K)
3
LS-1为循环左移一位, LS-2循环左移2位 置换P8:
P8 6 3 7 4 8 5 10 9
•
例子:若K为(1010000010), 产生的两个子密钥: K1=(1 0 1 0 0 1 0 0),K2=(0 1 0 0 0 0 1 1)
• S0(abcd)=(abcd+ab+ac+b+d, abcd+abd+ab+ac+ad+a+c+1) • S1 ?
11 12
b5 b6 b7 b8
b1 b2 b3 b4
3
4
1
S-DES的加密运算-初始和最终置换 •
03、对称密码体制

数据加密标准(Data Encryption Standard,DES)是至 今为止使用 最为广泛的加密算法。
1974年8月27日, NBS开始第二次征集,IBM提交了算法LUCIFER ,该算法由IBM的工程师在1971~1972年研制。
1975年3月17日, NBS公开了全部细节1976年,NBS指派了两个
序列密码算法(stream cipher)
每次可加密一个比特戒一个字节 适合比如进程终端输入加密类的应用
对称密码体制
4
3.1 分组密码原理
分组密码
分组密码是将明文消息编码表示后的数字(简称明文数字)序列,划
分成长度为n的组(可看成长度为n的矢量),每组分别在密钥的控制 下发换成等长的输出数字(简称密文数字)序列。
构,如FEAL、Blowfish、RC5等。
对称密码体制
9
3.1.2 分组密码的一般结构
Feistel密码结构的设计动机
分组密码对n比特的明文分组迚行操作,产生出一个n比特的密文分
组,共有2n个丌同的明文分组,每一种都必须产生一个唯一的密文 分组,这种发换称为可逆的戒非奇异的。 可逆映射 00 01 10 11 11 10 00 01 丌可逆映射 00 01 10 11 11 10 01 01
对称密码体制Biblioteka 193.2.1 简化的DES
简化的DES
简化的DES(Simplified - DES)是一个供教学而非安全的加密算法, 它不DES的特性和结构类似,但是参数较少。 S - DES的加密算法以8bit的明文分组和10位的密钥作为输入,产生 8bit的明文分组做为输出。 加密算法涉及五个凼数:
04-RTP和RTCP协议原理

HUAWEI TECHNOLOGIES CO., LTD.
Page 8
第1章 RTP/RTCP概述
1.1 RTP/RTCP简介 1.2 RTP/RTCP功能 1.3 RTP工作原理
HUAWEI TECHNOLOGIES CO., LTD.
Page 9
1.2 RTP功能
RTP在VoIP中的作用为:
HUAWEI TECHNOLOGIES CO., LTD.
Page 4
第1章 RTP/RTCP概述
1.1 RTP/RTCP简介 1.2 RTP/RTCP功能 1.3 RTP工作原理
HUAWEI TECHNOLOGIES CO., LTD.
Page 5
1.1 RTP/RTCP简介--多媒体服务
多媒体服务特点:
域名 长度(bit) 2 定义了RTP的版本,此协议定义的版本是2。 含义
Version (V)
Padding (P)
Item count (IC)
1
如果填充位被设置为1,则一个或多个附加的字节会加在包头的最后, 附加的最后一个字节放置附加的字节数。填充可能用于某些具有固定长 度的加密算法,或者在底层数据单元中传输多个RTP包。
第2章 RTP/RTCP报文格式
2.1 RTP报文格式 2.2 RTCP报文格式
HUAWEI TECHNOLOGIES CO., LTD.
Page 24
2.2 RTCP报文格式--报文类型
在RTP的规范(RFC 3550)中,一共定义了5种RTCP报告用来报告当前控制信息:
Packet Type值
NTP timestamp
RTP timestamp Sender's packet count
名词的复数形式
名词的复数形式一般地,普通名词变复数时在词尾加-s即可,如:une pommedes pommesun fruitdes fruits例外:以-s, -x或-z 结尾的名词变复数时,形式不变,如:une sourisdes sourisune voixdes voixun nezdes nez以-al结尾的名词变复数时,一般要变为-aux:un chevaldes chevaux一些以-al结尾的名词变复数时,加-s:un baldes balsle carnaval les carnavalsle festival les festivals以-au, -eu,或-eau 结尾的名词变复数时,通常加-x: un tuyaudes tuyauxun feudes feuxun cadeaudes cadeaux一些以-au, -eu, or -eau 结尾的名词变复数时,加-s: un pneudes pneusle bleu les bleus以-ail结尾的名词变复数时,加-s:(有7个例外,变为-aux)un chandaildes chandailsun rail des railsun ail des ails以-ou结尾的名词变复数时,通常加-s:un foudes fousun sou des sous例外(复数形式加-x):bijoubijouxcailloucaillouxchouchouxgenougenouxhibouhibouxjoujoujoujouxpoupoux有些复数形式比较特殊:l'oeilles yeuxle cielles cieux专有名词专有名词的第一个字母大写,如:les Espagnolsles Suisses专有名词变复数的规则:王族、望族的姓氏一般用复数,如:Les Bourbons = 波旁家族。
一般的家族姓氏不用复数,如:Les Dupont喻艺术作品之用的人命,用复数,如: Il possède quatre Monets.他有四幅莫奈的作品。
des算法s合计算规则
des算法s合计算规则(原创版)目录1.DES 算法简介2.DES 算法的加密规则3.DES 算法的解密规则4.DES 算法的优缺点正文1.DES 算法简介DES(Data Encryption Standard)算法是一种对称密钥加密标准,由美国国家标准局(NIST)于 1977 年制定。
DES 算法是一种分组密码,其密钥长度为 56 位,分组长度为 64 位。
由于其加密速度快、安全性高,DES 算法在过去被广泛应用于各种数据加密场景。
2.DES 算法的加密规则DES 算法的加密过程分为以下步骤:(1)初始化:设置初始向量(IV)和密钥(K)。
(2)分组替换:将明文分组(64 位)与密钥(56 位)进行异或操作,得到密文分组(64 位)。
(3)S 盒替换:将密文分组中的每个字节替换为特定的 S 盒中的字节,共有 16 个 S 盒,每个 S 盒包含 96 个替换规则。
(4)Mixing:对 S 盒替换后的密文分组进行 16 轮的 Mixing 操作,每轮包括 F 函数、左旋转、右旋转和异或操作。
(5)最终置换:对 Mixing 操作后的密文分组进行重新排列,得到最终的密文。
3.DES 算法的解密规则DES 算法的解密过程与加密过程相反,需要使用相同的密钥和初始向量,按照以下步骤进行:(1)逆置换:对密文进行逆排列,得到明文分组。
(2)逆 Mixing:对逆置换后的明文分组进行 16 轮的逆 Mixing 操作。
(3)S 盒逆替换:将逆 Mixing 操作后的明文分组中的每个字节替换回原来的 S 盒中的字节。
(4)分组替换:将 S 盒逆替换后的明文分组与密钥进行异或操作,得到原始明文分组。
4.DES 算法的优缺点优点:加密速度快,安全性较高,适用于各种数据加密场景。
缺点:密钥长度较短,容易受到暴力破解攻击;同时,S 盒的设计存在一定的漏洞,可能会被攻击者利用。
DES加密算法原理
DES加密算法原理DES(Data Encryption Standard)是一种对称加密算法,它使用相同的密钥进行加密和解密。
DES算法的原理可以分为以下几个方面。
1.初始置换(IP):DES加密过程的第一步是对明文进行初始置换,通过将明文中的每个位按照事先规定的顺序重新排列,得到一个初始排列的明文块。
2. 轮函数(Feistel function):DES算法采用了Feistel网络结构。
在每一轮中,明文块被分成左右两部分,右半部分经过扩展运算(Expansion),将其扩展为一个48位的数据块。
然后将扩展后的数据块与轮密钥进行异或运算,得到一个48位的结果。
3. S-盒变换(S-Box substitution):接下来,经过48位结果的S-盒变换。
S-盒是DES算法的核心部分,它将6位输入映射为4位输出。
DES算法使用了8个不同的S-盒,每个S-盒都有一个4x16表格,用于将输入映射为输出。
4. P-盒置换(P-Box permutation):经过S-盒变换后,输出结果通过一个固定的P-盒进行置换运算。
P-盒操作将32位输出重新排列,得到一个新的32位结果。
5. 轮密钥生成(Key schedule):DES算法使用了16轮的加密迭代过程。
每一轮使用一个不同的48位轮密钥。
轮密钥生成过程根据初始密钥生成所有的轮密钥。
轮密钥生成包括密钥置换选择1、密钥循环移位、密钥置换选择2等步骤。
6. 最后交换(Inverse Initial Permutation):经过16轮迭代后,得到最终的加密结果。
在最后交换步骤中,将加密结果的左右两部分进行互换,得到最终的加密结果。
DES算法依靠这些步骤进行加密和解密过程。
加密过程中,明文块经过初始置换后,进入16轮的迭代过程,每一轮中使用不同的轮密钥对明文进行加密。
最后得到加密结果。
解密过程与加密过程相反,使用相同的轮密钥对密文进行解密,最终得到明文。
DES算法的安全性主要依赖于密钥的长度和轮数。
S-DES加密解密算法Java版甄选范文
S-DES加密解密算法Java版public class SimpleDES {// Author: wangth// two keys K1 and K2static int K1=0;static int K2=0;/*some parameters*/static int P10[]=new int[]{3,5,2,7,4,10,1,9,8,6};static int P8[]=new int[]{6,3,7,4,8,5,10,9};static int P4[]=new int[]{2,4,3,1};static int IP[]=new int[]{2,6,3,1,4,8,5,7};static int IPI[]=new int[]{4,1,3,5,7,2,8,6};static int EP[]=new int[]{4,1,2,3,2,3,4,1};static int S0[][]={{1,0,3,2},{3,2,1,0},{0,2,1,3},{3,1,3,2},};static int S1[][]={{0,1,2,3},{2,0,1,3},{3,0,1,0},{2,1,0,3},};//根据数组交换static int Permute(int num,int p[],int pmax){int result=0;for(int i=0;i<p.length;i++){result<<=1;result|=(num>>(pmax-p[i]))&1;}return result;}//生成k1,k2static void SDES(String Key){int K=Integer.parseInt(Key,2);K=Permute(K,P10,10);int th=0,tl=0;th=(K>>5)&0x1f;//取Key的高5位tl=K&0x1f; //取Key的低5位//LS-1th=((th&0xf)<<1) | ((th & 0x10) >> 4);//循环左移一位tl=((tl&0xf)<<1) | ((tl & 0x10) >> 4);//循环左移一位K1=Permute(( th << 5)| tl,P8,10); //生成K1//LS-2th=((th & 0x07)<< 2) |((th & 0x18) >> 3);//循环左移二位tl=((tl & 0x07)<< 2) |((tl & 0x18) >> 3);//循环左移二位K2=Permute((th<<5) | tl,P8,10); //生成K2 }//f函数static int F(int R,int K){int t=Permute(R,EP,4)^K;int t0=(t>>4)& 0xf;int t1=t&0xf;t0= S0[((t0 & 0x8)>>2) | (t0 & 1)] [(t0>>1)&0x3];t1= S1[((t1 & 0x8)>>2) | (t1 & 1)] [(t1>>1)&0x3];t= Permute((t0<<2)|t1,P4,4);return t;}//fk函数static int fk(int input,int k){int l=(input>>4) & 0xf;int r=input & 0xf;return ((l^F(r,k))<< 4)| r;}//switch functionstatic int SW(int x){return ((x&0xf)<<4) | ((x>>4)&0xf); }//加密static String encrypt(String input){int m=Integer.parseInt(input, 2);m=Permute(m,IP,8);m=fk(m,K1);m=SW(m);m=fk(m,K2);m=Permute(m,IPI,8);return Integer.toString(m, 2);}//解密static String decrypt(String input){int m=Integer.parseInt(input, 2);m=Permute(m,IP,8);m=fk(m,K2);m=SW(m);m=fk(m,K1);m=Permute(m,IPI,8);return Integer.toString(m, 2);}public static void main(String[] args) { // TODO Auto-generated method stub String plaintext,ciphertext,key;int len=0;key="0111111101";//加密plaintext="01101111";SDES(key);ciphertext=encrypt(plaintext);len=ciphertext.length();//如果密文不足8位,补足8位if(len<8){for(int i=0;i<8-len;i++)ciphertext="0"+ciphertext;}System.out.println("对01101111加密后的密文为:"+ciphertext);//解密ciphertext="01110110";SDES(key);plaintext=decrypt(ciphertext);len=plaintext.length();if(len<8){for(int i=0;i<8-len;i++)plaintext="0"+plaintext;}System.out.println("对01110110解密后的明文为:"+plaintext);}}感谢您使用本店文档您的满意是我们的永恒的追求!(本句可删)------------------------------------------------------------------------------------------------------------。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其实跟上一篇一样,这还是网络安全的作业…
S-DES是DES算法的简化版,并没有什么实际使用的价值,只用于教学来理解DES算法的加密方法,这篇文章就是按照S-DES的算法来实际加密和解密的一段2进制数,演示了加密的运算过程.
下面从准备知识开始
先讲一下置换,举例说明,对”ABCDEFGH”做一下”82641753″置换的结果就是”HBFDAGEC”,这样就能看懂是怎么置换的了吧.
然后是循环移位,继续举例,”ABCDEFGH”循环左移2位结果就是”CDEFGHAB”.
还有个S盒的替代选择,具体到S-DES来说就是输入的四位数”ABCD”在S盒中找第AD行BC列的数字作为输出,比如0101输入S0(见下)的话就是第1(01)行第2(10)列(0-3行,0-3列),输出为1即01,再比如1001输入S0的话就是第3(11)行第0(00)列,输出为3即11.
最后是按位异或,举例的话1^1=0,1^0=1,0^1=1,0^0=0,1100^1010=0110,其实这个大家都懂吧.
好了,准备知识就这么多,下面开始正题:
S-DES算法的输入是一个8位的明文或者密文组和一个10位的密钥,输出是一个8位的密文或者明文组。
以下是S-DES所需的几个置换表
P10 {3,5,2,7,4,10,1,9,8,6}
P8 {6,3,7,4,8,5,10,9} 注意这个置换选择输入10位输出8位
P4 {2,4,3,1}
IP {2,6,3,1,4,8,5,7}
IPI {4,1,3,5,7,2,8,6}
EP {4,1,2,3,2,3,4,1} 注意这个是扩展置换,输入4位输出8位
以下是两个S盒
S0:
{1,0,3,2},
{3,2,1,0},
{0,2,1,3},
{3,1,3,2},
S1:
{0,1,2,3},
{2,0,1,3},
{3,0,1,0},
{2,1,0,3},
接下来就是加密和解密算法
首先讲子密钥的生成,子密钥在加密和解密算法中都有使用.
10位密钥key = 01111 11101
对key做P10置换得到11111 10011
记左半(高位)的为Lk=11111,右半(低位)为Rk=10011
Lk和Rk均循环左移1位,得到Lk=11111,Rk=00111
对Lk和Rk组合得到的11111 00111做P8置换选择,得到子密钥K1=0101 1111
Lk和Rk均再次循环左移2位,得到Lk=11111,Rk=11100
对Lk和Rk组合得到的11111 11100做P8置换选择,的到子密钥K2=1111 1100
以上,通过密钥得到了算法所需的子密钥.
下面是加密过程
首先是初始置换
对明文m=0001 0110做IP置换,得m’=0100 1001
接下来是标准的Feistel密码结构,共有两次循环
第一次循环
记左半(高位)为Lm=0100,右半(低位)为Rm=1001 对Rm做EP扩展置换,得Rm’=1100 0011
Rm’与子密钥K1按位异或,得Rm’=1001 1100
Rm’左半1001进入S0盒替代选择得11,右半1100进入S1盒替代选择的01,组合后得Rm’=1101
对Rm’做P4置换,得Rm’=1101
Rm’与Lm按位异或,得Lm’=1001
Lm’与Rm(最开始的那个Rm)组合得到输出1001(Lm’) 1001(Rm)
至此完成第一次循环
然后交换高低位,作为第二次循环的输入,即1001(Rm) 1001(Lm’)作为输入
开始第二次循环
记左半为Ln=1001,右半为Rn=1001
对Rn做EP扩展置换,得Rn’=1100 0011
Rn’与子密钥K2按位异或,得Rn’=0011 1111
Rn’左半0011进入S0盒替代选择得10,右半1111进入S1盒替代选择的11,组合后得Rn’=1011
对Rn’做P4置换,得Rn’=0111
Rn’与Ln按位异或,得Ln’=1110
Ln’与Rn(最开始的那个Rn)组合得到输出1111(Ln’) 1001(Rn)
至此完成第二次循环
最后进行逆初始置换对上面的输出m’=1111 1001做IPI置换得到密文m’=0111 0110
OK,到这里就完成了将明文加密为密文,S-DES加密结束.
下面开始解密,解密过程与加密基本一致,就是密钥使用顺序是相反的,第一次循环使用K2第二次循环使用K1
首先还是初始置换
对密文m=0111 0110做IP置换,得m’=1110 1001
Feistel密码结构
第一次循环
记左半(高位)为Lm=1110,右半(低位)为Rm=1001
对Rm做EP扩展置换,得Rm’=1100 0011
Rm’与子密钥K2按位异或,得Rm’=0011 1111
Rm’左半0011进入S0盒替代选择得10,右半1111进入S1盒替代选择的11,组合后得Rm’=1011
对Rm’做P4置换,得Rm’=0111
Rm’与Lm按位异或,得Lm’=1001
Lm’与Rm(最开始的那个Rm)组合得到输出1001(Lm’) 1001(Rm)
至此完成第一次循环
然后交换高低位,作为第二次循环的输入,即1001(Rm) 1001(Lm’)作为输入
开始第二次循环
记左半为Ln=1001,右半为Rn=1001
对Rn做EP扩展置换,得Rn’=1100 0011
Rn’与子密钥K1按位异或,得Rn’=1001 1100
Rn’左半1001进入S0盒替代选择得11,右半1100进入S1盒替代选择的01,组合后得Rn’=1101
对Rn’做P4置换,得Rn’=1101
Rn’与Ln按位异或,得Ln’=0100
Ln’与Rn(最开始的那个Rn)组合得到输出0100(Ln’) 1001(Rn)
至此完成第二次循环
最后进行逆初始置换
对上面的输出m’=0100 1001做IPI置换得到明文m’=0001 0110
这样就完成的S-DES的解密。
