高二数学圆锥曲线
高二圆锥曲线基本知识点

高二圆锥曲线基本知识点圆锥曲线是高中数学中的一个重要内容,主要包括椭圆、双曲线和抛物线。
它们有着广泛的应用和深刻的数学内涵。
本文将介绍高二学生需要掌握的圆锥曲线基本知识点。
一、椭圆椭圆是平面上一个固定点F(焦点)与平面上的一条固定距离之和等于常数2a的动点M(动点到焦点的距离之和等于2a)所构成的图形。
其数学表达式如下:(x - h)² / a² + (y - k)² / b² = 1其中(h,k)为椭圆的中心坐标,a与b分别为椭圆的长半轴和短半轴。
椭圆的性质有很多,比如对称性、离心率、焦点与准线等等。
在解决实际问题中,我们可以利用椭圆的性质进行分析和计算。
二、双曲线双曲线是平面上一个固定点F(焦点)与平面上的一条距离之差的绝对值等于常数2a的动点M(动点到焦点的距离之差的绝对值等于2a)所构成的图形。
其数学表达式如下:(x - h)² / a² - (y - k)² / b² = 1其中(h,k)为双曲线的中心坐标,a与b分别为双曲线的半轴长度。
双曲线同样具有很多性质,比如渐近线、离心率、焦点与准线等。
对于双曲线上的点,我们可以通过运用这些性质来求解和描述。
三、抛物线抛物线是一种二次曲线,其形状像一个开口朝上或朝下的U字形。
其数学表达式如下:y = ax² + bx + c其中a,b,c为常数,a不等于0。
抛物线也有很多重要的性质,比如焦点、准线、对称性等。
抛物线在物理学、工程学等领域有广泛的应用,如抛物线轨道、抛物线反射。
四、曲线的参数方程以上所述的椭圆、双曲线和抛物线都可以用参数方程表示,参数方程以参数t作为自变量,通过给定参数t的取值范围,可以得到曲线上的点的坐标。
以椭圆为例,其参数方程为:x = a cos(t)y = b sin(t)对于双曲线和抛物线,其参数方程的表达式类似,通过参数方程,我们可以更加灵活地描述曲线上的点和曲线的性质。
高二数学圆锥曲线知识点整理
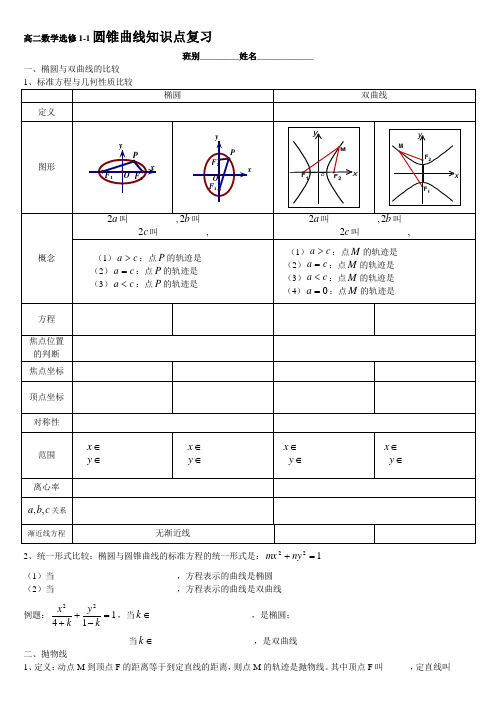
高二数学选修1-1圆锥曲线知识点复习班别_________姓名_____________一、椭圆与双曲线的比较2、统一形式比较:椭圆与圆锥曲线的标准方程的统一形式是:122=+ny mx (1)当____________________________,方程表示的曲线是椭圆 (2)当____________________________,方程表示的曲线是双曲线例题:11422=-++ky k x ,当∈k _______________________,是椭圆; 当∈k _______________________,是双曲线二、抛物线 1、定义:动点M 到顶点F 的距离等于到定直线的距离,则点M 的轨迹是抛物线。
其中顶点F 叫______,定直线叫_____2、焦半径MF :抛物线上点M 到焦点F 的距离3、焦点弦AB :直线AB 过焦点F ,与抛物线交于点A 、B三、圆锥曲线常见问题1、求相交弦AB 中点坐标问题步骤:(1)设点:()11,y x A ,()22,y x B ;(2)联立方程,得出:02=++c bx ax ;(3)利用韦达定理:abx x -=+21 (4)利用直线方程,求出:21y y +;(5)中点M 坐标为⎪⎭⎫⎝⎛++2,22121y y x x练习:已知直线1:-=x y l ,与抛物线x y C 12:21=相交于点A 、B ,与椭圆145:222=+y x C 相交于点M 、N 则AB 中点坐标为_________________,MN 中点坐标为_______________ 2、已知中点M (00,y x ),求中点弦(过中点的相交弦)方程问题步骤:(1)设点:()11,y x A ,()22,y x B ,则2102x x x +=,2102y y y += (2)把()11,y x A ,()22,y x B 代入曲线方程;(3)作差;(4)求斜率k (5)求直线方程AB :)(00x x k y y -=-练习:(1)、已知抛物线x y 82=的弦AB 被)1,1(-平分,则AB 方程为_____________________(2)、椭圆193622=+y x 的的弦AB 被)2,4(平分,则AB 方程为_____________________ 3、求弦长AB步骤:(1)设点:()11,y x A ,()22,y x B ;(2)联立方程,得出:02=++c bx ax ;(3)利用韦达定理:a b x x -=+21,acx x =21 (4)求弦长AB =()21221241x x x x k-++练习:(1)已知直线1:-=x y l 与抛物线x y C 12:21=相交于点A 、B ,则AB =____________(2)已知直线1:-=x y l 与椭圆145:222=+y x C 相交于点M 、N ,则MN =___________ 4、直线与圆锥曲线的位置关系判断交点情况,一般步骤:(1)联立方程,得出:02=++c bx ax ;(2)判断ac b 42-=∆的符号 ①0<∆,直线与圆锥曲线没有交点,相离②0=∆,直线与圆锥曲线有1个交点,相切 ③0>∆,直线与圆锥曲线有2个交点,相交练习:已知直线过定点()3,0,斜率为k ,当k 为何值时,直线与抛物线x y 82=有(1)1个交点 (2)0个交点 (3)2个交点。
数学高二圆锥曲线知识点

数学高二圆锥曲线知识点在高中数学中,圆锥曲线是一个重要的数学概念,它在几何图形和代数方程中都有广泛的应用。
在高二数学学习过程中,我们会接触到圆锥曲线的基本知识和性质。
本文将详细介绍高二数学中的圆锥曲线知识点,帮助你更好地理解和掌握这一概念。
一、圆锥曲线的定义和分类圆锥曲线是在平面直角坐标系中描述的一类曲线,它们由一个平面和一个与其不重合的点(称为焦点)以及到这个点的距离之比(称为离心率)所确定。
根据离心率的不同取值,圆锥曲线可分为以下三类:1. 椭圆:离心率小于1的圆锥曲线。
在平面上的图形是一个闭合曲线,它以两个焦点为中心,轨迹上的所有点到两个焦点的距离之和等于一个常数。
2. 抛物线:离心率等于1的圆锥曲线。
在平面上的图形是一个开放曲线,它以一个焦点为中心,轨迹上的所有点到焦点的距离等于到其直角坐标轴的距离。
3. 双曲线:离心率大于1的圆锥曲线。
在平面上的图形是一个开放曲线,它以两个焦点为中心,轨迹上的所有点到两个焦点的距离之差等于一个常数。
二、椭圆的性质和方程表示椭圆是一种常见的圆锥曲线,在几何问题和工程应用中经常遇到。
以下是椭圆的一些基本性质和方程表示:1. 长轴和短轴:椭圆的长轴是连接两个焦点并通过中心的线段,短轴是与长轴垂直并通过中心的线段。
2. 焦距和离心率:椭圆的焦距是指两个焦点之间的距离,离心率则是焦距与椭圆长轴之间的比值。
3. 方程表示:椭圆的一般方程形式为(x-h)²/a² + (y-k)²/b² = 1,其中(h,k)是椭圆的中心坐标,a和b分别是椭圆长半轴和短半轴的长度。
三、抛物线的性质和方程表示抛物线是另一种常见的圆锥曲线,其形状和特性与开口朝上或朝下的碗形相似。
以下是抛物线的一些基本性质和方程表示:1. 焦点和准线:抛物线的焦点是与准线的距离相等的点,准线是与焦点之间距离相等的直线。
2. 抛物线开口方向:抛物线开口朝上时,其准线在抛物线的上方;开口朝下时,准线在抛物线的下方。
高二-数学-《圆锥曲线方程》知识点总结

高二-数学-《圆锥曲线方程》知识点总结
圆锥曲线是一类近似椭圆的曲线,也叫双曲曲线或鱼眼曲线。
它们的性质与椭圆十分接近,形状近似椭圆,但是椭圆的离心率为常数,而圆锥曲线的离心率是一个变量。
一般圆锥曲线的方程是这样的:
$$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$
其中,a和b是变量,称为离心率。
离心率的大小决定了曲线的形状,a大于b表示离心率大,它的处处突出,而a小于b则表示离心率小,它就会把曲线变得更加平缓。
圆锥曲线的概念和椭圆类似,只是离心率不再是常数而是变量,这使得曲线得到更多的灵活性,可以满足更多类型的用途。
圆锥曲线的准确表达式是:
$$x=acosθ, y=bsinθ, 0 ≤ θ ≤ π$$
其中,θ是由变量a,b决定的,而a和b也可以理解成点(a,0)和点(0,b)。
由于它的形状和椭圆类似,可以用同样的方法来进行求积分。
圆锥曲线也经常用在绘图中,比如地球影像分析中,常常需要使用圆锥曲线来作为地球表面的近似曲线。
圆锥曲线还有很多其他的应用,比如飞行轨迹的分析、流体动力学计算中的重力变形应用、测试反差图的绘制等等。
总之,圆锥曲线是一类强大的数学曲线,可以用来描述很多实际情况,可以给我们带来很多的想象空间。
高二数学课本《选修11第二章圆锥曲线与方程》

高二数学课本《选修1-1第二章圆锥曲线与方程》高二数学课本《选修1-1》第二章圆锥曲线与方程在本章中,我们将探索圆锥曲线与方程之间的关系。
圆锥曲线是平面几何中的重要主题,而通过引入方程,我们可以更精确地描述这些曲线的性质。
一、引言圆锥曲线是平面几何中的一个基本主题。
椭圆、双曲线和抛物线等圆锥曲线都是平面上的点满足某种条件的轨迹。
通过引入方程,我们可以对这些曲线进行精确的描述和分类。
二、基本概念1.圆锥曲线的定义:圆锥曲线是指在平面直角坐标系中,一个动点在满足某种条件的限制下,沿着一条具有特殊形状的轨迹运动所形成的图形。
2.圆锥曲线的方程:对于每种圆锥曲线,我们可以使用一个二元二次方程来表示。
例如,椭圆方程可以表示为(x-a)^2/b^2 + (y-c)^2/d^2 = 1,其中a、b、c、d是椭圆的主要参数。
三、主要内容1.椭圆的定义和方程:椭圆是一种常见的圆锥曲线,它描述了一个动点在两个固定点(焦点)之间移动的轨迹。
椭圆的方程可以写为(x-a)^2/b^2 + (y-c)^2/d^2 = 1,其中(a, c)是焦点位置,b和d是半轴长度。
2.双曲线的定义和方程:双曲线也是一种圆锥曲线,描述了一个动点在一个固定点(焦点)和无穷远点之间的轨迹。
双曲线的方程可以写为(x-a)^2/b^2 - (y-c)^2/d^2 = 1,其中(a, c)是焦点位置,b和d是半轴长度。
3.抛物线的定义和方程:抛物线是一种圆锥曲线,描述了一个动点在一个固定点(焦点)和一条直线(准线)之间的轨迹。
抛物线的方程可以写为y^2 = 2px或x^2 = 2py,其中p是抛物线的焦参数。
4.圆锥曲线的性质:通过观察圆锥曲线的方程,我们可以得出一些重要的性质,例如范围、对称性和离心率等。
这些性质有助于我们更好地理解和应用圆锥曲线。
四、方法与技巧1.代数方法:通过代入坐标到圆锥曲线的方程中,我们可以得到点的位置,从而通过代数方法解决问题。
第3章圆锥曲线的方程(复习课件)高二数学(人教A版选择性必修第一册)

x=ty+a,
由 2
y =2x,
消去 x,得 y2-2ty-2a=0.
设A(x1,y1),B(x2,y2),则y1+y2=2t,y1y2=-2a.
y21y22
因为 OA⊥OB,所以 x1x2+y1y2=0,即 4 +y1y2=0,
解得y1y2=0(舍去)或y1y2=-4.
所以-2a=-4,解得a=2.
我们把平面内与两个定点F1,F2的距离之和(2a)等于常数
(大于|F1F2|)的点的轨迹叫做椭圆。这两个定点叫做椭圆的
焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦
距。
对椭圆定义的理解
①当2a=|F1F2|时,其轨迹为线段;
②当2a<|F1F2|时,其轨迹不存在.
椭圆的简单几何性质:
焦点位置
x2 y2
∴椭圆的方程为 4 + 3 =1.
1
(2)若直线 l:y=-2x+m 与椭圆交于 A,B 两点,与以 F1F2 为直径的圆交于 C,
|AB| 5 3
D 两点,且满足|CD|= 4 ,求直线 l 的方程.
解
由(1)知,以F1F2为直径的圆的方程为x2+y2=1,
2|m|
∴圆心到直线 l 的距离 d=
焦点坐标
y 2 2 px ( p 0)
p
F ( ,0)
2
y 2 2 px ( p 0)
F (
x 2 py( p 0)
p
F (0, )
2
y
p
F (0, )
2
y
2
x 2 2 py( p 0)
p
,0)
2
准线方程
x
x
p
高二圆锥曲线知识点

高二圆锥曲线知识点圆锥曲线是数学中的重要概念,广泛应用在几何、物理和工程学中。
在高二阶段,学生需要掌握圆锥曲线的基本知识点,包括椭圆、双曲线和抛物线。
椭圆是一种圆锥曲线,它具有两个焦点和一个长轴。
椭圆的定义是所有到两个焦点距离之和等于常数的点的集合。
椭圆可以看作是一个拉伸的圆,其长轴与短轴之比称为离心率,离心率小于1。
在学习椭圆时,我们需要掌握椭圆的标准方程、焦点、顶点、长轴、短轴,以及椭圆的性质。
双曲线也是一种圆锥曲线,它具有两个焦点和两个分离的极限位置。
双曲线的定义是所有到两个焦点距离之差等于常数的点的集合。
双曲线可以看作是一个拉伸的开口向左右两个方向的椭圆,其离心率大于1。
学习双曲线时,我们需要了解双曲线的标准方程、焦点、顶点、渐近线、分支、离心率,以及双曲线的性质。
抛物线是一种特殊的圆锥曲线,它具有一个焦点和一个直线。
抛物线的定义是所有到焦点和直线距离相等的点的集合。
抛物线可以看作是一个拉伸的开口向上或向下的U形曲线。
在学习抛物线时,我们需要了解抛物线的标准方程、焦点、顶点、焦半径、准线,以及抛物线的性质。
在学习圆锥曲线时,我们还需要掌握一些基本的图像特征、方程的转化与图像的转变,以及曲线与直线的位置关系。
圆锥曲线的应用非常广泛,例如在天文学中描述行星的轨道、在物理学中描述物体的抛射运动、在工程学中描述天线的方向性等等。
高二阶段的圆锥曲线知识点包括椭圆、双曲线和抛物线的定义、方程、焦点、顶点、长轴、短轴、渐近线、准线、离心率以及性质等。
掌握这些知识点将帮助我们更好地理解和应用圆锥曲线。
高二圆锥曲线相关知识点

高二圆锥曲线相关知识点圆锥曲线是数学中重要的概念,在高二数学课程中也是一个重要的内容。
本文将介绍高二圆锥曲线相关的知识点,包括椭圆、双曲线和抛物线的定义、性质和方程等内容。
一、椭圆椭圆是圆锥曲线中最常见的一种类型。
它的定义可以用两个焦点和到焦点的距离之和等于定值的性质来描述。
椭圆还具有以下性质:1. 焦点和直径:椭圆的焦点是椭圆的特殊点,它与椭圆的离心率有关。
椭圆的直径是椭圆上两个对称的点之间的最长距离。
2. 焦点与半轴:椭圆有两个主轴,分别与两个焦点相垂直,长度分别为2a和2b。
其中,a和b是椭圆的两个半轴长度。
3. 椭圆的方程:椭圆的方程可以用标准形式和一般形式表示。
标准形式为x^2/a^2 + y^2/b^2 = 1,其中a和b是椭圆的半轴长度。
二、双曲线双曲线也是圆锥曲线的一种类型。
它的定义可以用两个焦点和到焦点的距离之差等于定值的性质来描述。
双曲线还具有以下性质:1. 焦点和直径:双曲线的焦点是双曲线的特殊点,它与双曲线的离心率有关。
双曲线的直径是双曲线上两个对称的点之间的最长距离。
2. 焦点与渐近线:双曲线有两条互相垂直的渐近线,它们与双曲线的曲线趋势无限接近。
3. 双曲线的方程:双曲线的方程可以用标准形式和一般形式表示。
标准形式为x^2/a^2 - y^2/b^2 = 1,其中a和b是双曲线的参数。
三、抛物线抛物线也是圆锥曲线中的一种类型。
它的定义可以用一个焦点和到焦点的距离等于到准线的距离的性质来描述。
抛物线还具有以下性质:1. 焦点和准线:抛物线的焦点是抛物线的特殊点,它与抛物线的离心率有关。
抛物线的准线是与焦点和抛物线对称并与抛物线平行的直线。
2. 焦点与顶点:抛物线有一个顶点,它是抛物线的最高点或最低点,与焦点的距离等于焦准距的一半。
3. 抛物线的方程:抛物线的方程可以用顶点形式和一般形式表示。
顶点形式为y = a(x-h)^2 + k,其中(h, k)是抛物线的顶点坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、双曲线的定义 :
平面内与两定点F1、F2的距离的差的绝对 值是常数(小于|F1F2|)的点的轨迹叫做双曲 线.这两个定点F1、F2叫做双曲线的焦点, 两个焦点之间的距离叫做焦距.
说明:若动点M到两定点的距离之差的 绝对值为2a ,| F1 F2| = 2c 当c > a >0时,动点M的轨迹是双曲线; 当a = c>0时,动点M的轨迹是两条射线; 当 0 < c < a时,动点M无轨迹
例4.(课本P24练习 2)已知定点F和定 直线l,点F不在直线l 上,动圆M过F点 且与直线l相切,求证:圆心M的轨迹是 一条抛物线.
练习1. (1)方程
| ( x 5) y ( x 5) y | 6
2 2 2 2
表示什么曲线?
(2)方程 ( x 5) y ( x 5) y 6
2 2 2 2
表示什么曲线?
(6)方程 ( x 5) y ( x 5) y 10
2 2 2 2
表示什么曲线?
(7)方程 ( x 5) y ( x 5) y 8
2 2 2 2
表示什么曲线?
(8)方程 ( x 5) y ( x 5) y 12
例1、试用适当的方法作出以两 个定点F1、F2为焦点的一个椭圆。
例2、曲线上的点到两个定点F1(-5,0)、 F2(5,0)的距离之差的绝对值分别等于 ①6 ②10 ③12 满足条件的曲线若存在, 是什么样曲线?若不存在,请说明 理由
例3、到定点F(1,1)和定直线l: x+y-2 = 0的距离相等的点的轨 迹是什么?
2 2 2 2
表示什么曲线?
(3)方程 ( x 5) y ( x 5) y -6
2 2 2 2
表示什么曲线?
(4)方程 ( x 5) y ( x 5) y 10
2 2 2 2
表示什么曲线?
(5)方程 ( x 5) y ( x 5) y -10
抛物线的定义:
• 平面内与一个定点F的距离和一条定直线l (F不在l上)的距离相等的点的轨迹叫做抛物 线,定点F叫做抛物线的焦点,定直线l叫 做抛物线的准线 说明:(1)点F不能在直线l上, 否则其轨迹是过点F且与l垂直的直线 (2)与椭圆、双曲线不同, 抛物线只有一个焦点和一条准线
圆锥曲线: 椭圆、双曲线、抛物线统称为圆锥 曲线
A
如图,球与圆锥面相切, 切点轨迹是⊙O,同时球 与截面切于点F.设M是截 线上任意一点,则MF是由 点 M 向球所作的切线的长 又圆锥过点 M 的母线与球 切于点P.
设⊙ O 所在的平面为 α , MH⊥α 于 H ,截面与平面 α 交 于 l , HN⊥l 于 N , 则 MN⊥l .
MF = MP= MN
V
Q
F1
O2
F2
M P
O1
如图,两个球都与圆锥面相切, 切点轨迹分别是⊙ O1 和⊙ O2 ; 同时两球分别与截面切于点 F1 、 F2.设M是截线上任意一点,则 MF1、 MF2是由点 M向两个球所 作的切线的长,又圆锥过点M的 母线与两球分别切于P、Q两 点.
|MF2-MF1| =| MQ-MP | =QP (常数)
已知ABC中,B、C是两个定点,并且 sin B SinC 2sin A,则该动点的轨迹是
小结:
(1) 椭圆、双曲线、抛物线的定义。 (2) 圆锥曲线的概念。
•; 新宝5
ath74cwb
•颜,问表 的安。”乐韵似嗅着猫的老鼠,一声都不敢发,至宝音足边跪下,攥着宝音裙角,不断叩头,是真心急了。宝音就着邱妈妈手里的 帕子印了印眼睛,抬起头来,对乐韵极低道:“去。”乐韵退开一点点。满地都是瓷碴,再退就要跪到瓷碴上了,她只好站起来。宝音方对洛 月轻声道:“请进来罢。”嘉颜迈进屋内,但觉表 这儿一屋子药味、一屋子萧然,举目,见地上滚着铜镜、碎着瓷碴、还湿了一大滩水,表 头发蓬乱,满面泪痕,不由得大大生出“太过分了”的心情,口中问洛月:“姑娘这儿是怎么了?”眼睛已经剜到乐韵身上。乐韵只觉一股冷 气从脊骨往头盖骨上冒。宝音却赶在洛月开口前,小声道:“我碰掉了杯子。”乐韵低着头,还不敢抬起来,眼睛却瞪大了:碰掉?才不是! 明明摔掉!由摔到碰,一言超生,分明在维护她了。为什么忽的勃然大怒、推她到悬崖边上,为什么忽而又轻言温语,维护于她?乐韵心里乱 如一团麻,分毫也看不清 路数。她只知道一件事:识相的,她还是老实闭嘴别说话罢,否则,恐怕 真有法子叫她死无全尸。今日 ,已绝非从 前的 。嘉颜仍盯着乐韵,看出乐韵藏着忐忑,知道今日之事,怎会是“失手摔了杯子”这么简单。看表 有意息事宁人,她也乐得大事化小, 小事化了,冲乐韵冷冷道:“还不替姑娘扫地?这般躲懒,且扣去半月的月银。”宝音目光微妙的顿了一顿。乐韵连忙行动。这辈子她拿笤帚 都没这么快过。宝音亲手开了妆盒,替表 理妆,看着韩玉笙消瘦的脸、湿漉漉低垂的长睫毛,还有虽然苍白干裂了、但弧度仍然可爱的唇线。 这两片嘴唇里喘气低微、似乎无意的逸出一句问候:“宝音姐姐侍候老太太登高去了么?”嘉颜唇边那训练有素的笑意顿时一僵,几乎碎得比 地上的瓷碴儿还要碎。宝音在镜子里看她,只看了一眼。一眼之后,嘉颜重新微笑,宝音也错开眼睛。这一眼,宝音读出来的信息已经太多。 而嘉颜甚至没有发现宝音曾经抬起眼睛。妆盒中拿起一把掠子,嘉颜替宝音整理发鬓,口中夸道:“表 发质真好,又柔又润。”真的,大病经 年,未损青丝,也算得上天垂怜。嘉颜手不停,道:“表 ,这些婢子不懂事,您尽快同我讲,切莫宠惯她们,损了您的千金体。”乐韵扫着地, 大气都不敢出。韩玉笙原梳的是垂挂髻,未嫁女孩儿的双分辫儿,折上去成两鬟,鬟底留出盘平的、小小的髻,似花萼,不失少女的俏皮,而 下头温婉的双鬟,又显得宁静大方,嘉颜拆下照原样重盘,插上玳瑁如意錾花短簪,退后一步看看,不错了,转头对乐韵道:“呆站着做什么? 没看见你姑娘裙脚都打湿了?”乐韵连忙上来,蹲下去替 擦抹。嘉颜又斥道:“湿成这样,怎么擦?你还不给你姑娘拿裙子来换?”第十四章
2 2 2 2
表示什么曲线?
2.P24习题1.ΔABC中,B(-3,0),C(3,0),且 AB,BC,AC成等差数列. (1)求证:点A在一个椭圆上运动; (2)写出这个椭圆的焦点坐标. 习题2. ΔABC中,BC的长为6,周长为16,那么 顶点A在怎样的曲线上运动?
变题
已知ABC中,B、C是两个定点,并且 1 sin B SinC sin A,则该动点的轨迹是 2
圆锥曲线
• 用一个平面去截取一个圆锥面,当平面经 过圆锥面的顶点时,可得到两条相交直线; 当平面与圆锥面的轴垂直时,截得的图形 是一个圆。改变上述平面的位置,观察截 得的图形的变换情况。 • 问题:平面截得圆锥面还能得到哪些不同 曲线?
古希腊数学家 Dandelin 在圆锥截 面的两侧分别放置一球,使它们 都与截面相切(切点分别为F1, F2),又分别与圆锥面的侧面相 切(两球与侧面的公共点分别构 成圆 O1和圆 O2).过 M点作圆锥 面的一条母线分别交圆O1,圆O2 与 P , Q 两点,因为过球外一点 作球的切线长相等,所以 MF1 = MP,MF2 = MQ, MF1 + MF2 =MP + MQ = PQ=定值
1、推导说明(1)中截法中,截线 上任意一点到两个定点的距离的 和等于常数。
2、椭圆的定义:
平面内到两定点F1、F2的距离之和等于 常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点叫做椭圆的焦点,两焦点 间的距离叫做焦距.
说明: 若动点M到的距离之和为2a , | F1 F2| = 2c 则当a>c>0时,动点M的轨迹是椭圆; 当a = c>0时,动点M的轨迹是线段F1 F2 ; 当 0 < a < c时,动点M无轨迹
