第四章讲义稳定性分析
信号与系统讲义第四章5系统频率特性及稳定性汇总

(系统的串联)
2020/3/10
信号与系统
2020/3/10
信号与系统
4.11 线性系统的稳定性
1、稳定系统
有限(界)激励,产生有限(界)输出,稳定系统 有限(界)激励,产生无限(界)输出,为不稳定系统
r(t) h(t)*e(t) h( )e(t )d
4.8由系统函数零、极点分布分析频响特性
一、系统的频响特性
1、频响特性
在正弦信号激励下稳态响应随频率的变化
H( j) H( j) e j()
幅频特性 相频特性
2020/3/10
信号与系统
分析正弦信号e(t) Em sin 0t u(t)激励下系统的响应?
H (s)为稳定系统,极点在左半开平面,自由响应为暂态响应
➢ 系统的极零点图 ➢ 确定系统的时域响应特性、系统稳定性分析 ➢ 绘制系统的幅频响应和相频响应特性曲线,通频特性分析
2020/3/10
信号与系统
作业
4-39(a)(e) 4-42 (b) 4-45
自读4.9节内容 预习 4.12 4.13章节内容
2020/3/10
信号与系统
H ( j)
K
0
系统的零、极点分布→系统的频率响应特性 零、极点分布特点??
2020/3/10
信号与系统
全通系统的零、极点分布
•极点在S左半平面,零点在右半平面 •极点数=零点数,且与虚轴成镜像对称
2020/3/10
信号与系统
幅频特性: 相频特性:
2020/3/10
信号与系统
二、最小相移系统
e(t) Me
李雅普洛夫稳定性分析精品PPT课件

2.2 状态向量范数
符号 称为向量的范数,
为状态向量端点至
平衡状态向量端点的范数,其几何意义为“状态偏差
向量”的空间距离的尺度,其定义式为:
①范数 X 0 X e 表示初始偏差都在以Xe 为中心,δ为半径的 闭球域S(δ)内.
(2) 求系统的特征方程:
det(I
A)
1
求得:1 2,2 3
系统不是渐近稳定的。
6
1
(
2)(
3)
0
3.2 非线性系统的李亚普洛夫第一法
对非线性系统 X f (X ,t)
当f (X,t)为与X 同维的矢量函数,且对X 具有连续偏导数,则可将
向于无穷大时,有:
lim x
t
xe
0
即收敛于平衡状态xe,则称平衡状态xe为渐近稳定的。
如果 与初始时刻 t0无关,则称平衡状态xe为一致渐近稳定。
渐近稳定几何表示法:
Hale Waihona Puke 3、大范围渐近稳定如果对状态空间的任意点,不管初始偏差有多大,都有渐
近稳定特性,即:lim x t
xe
0
对所有点都成立,称平衡状态xe为大范围渐近稳定的。其
渐近稳定的最大范围是整个状态空间。
必要性:整个状态空间中,只有一个平衡状态。 (假设有2个平衡状态,则每个都有自己的稳定范 围,其稳定范围不可能是整个状态空间。)
结论:如果线性定常系统是渐近稳定的,则它一定是大范 围渐近稳定的。
4、不稳定 如果对于某一实数 0 ,不论 取得多么小,由 S( )内
域 S( ) ,当初始状态 x0 满足 x0 xe ( , t0 ) 时,对由此出发
第四章稳定性分析——劳讲义斯判据4-1
21
THANKS
第二步:建立劳斯表(又叫劳斯阵列)。 例:五阶系统,其特征方程:
a 5 s 5 a 4 s 4 a 3 s 3 a 2 s 2 a 1 s a 0 0
9
s5
a5
a3
a1
s4
a4
a2
a0
s3
A1
a4a3 a5a2 a4
A2
a4a1 a5a0 a4
0
s2
B1
A1a 2 a 4 A2 A1
13
s5
1
52
s4
1
51
s3
0 ( )
10
s2
5 1
10
s1 5 1 2 0 0
5 1
s0
1
00
5 1 0
5 12
0
5 1
劳斯表中第一列元素符号的变化两次, 说明特征方程有两个正实部的根,所以系统不 稳定。
14
(2)某一行元素全为零 在劳斯表中,如果出现某一行元素全为零,
说明特征方程存在大小相等符号相反的实根 和(或)共轭虚根,或者共轭复根。
s0 2 0
因劳斯表中第一列元素无符号变化,所以系统稳 定。 令: ss1 1
20
原特征方程,经过整理,得到 s1 特征方程:
s1 35s1 23s110
s
3 1
1
3
s
2 1
5
1
s
1 1
2.8
0
s
0 1
1
0
劳斯表中第一列元素符号变化一次,所以有一 个特征方程根在垂线 s1右边。即有一个根在阴影 区内。
即输出增量收敛于原平衡工作点,线性系统稳定 。
生物新案同步三苏教讲义:第四章 生态系统的稳态 第二节 第1课时 含答案

第二节生态系统的稳态第1课时生态系统中的能量流动[学习目标]1。
概述能量流动的概念,描述能量在生态系统中的流动过程。
2.分析总结能量流动的特点。
3。
结合生态农业实例,阐明研究能量流动的意义。
方式一请大家做一个快乐竞猜游戏。
假设你像鲁滨逊那样流落在不毛的荒岛上,只有15 kg玉米和一只母鸡可以食用,那么使自己活的最长的办法是:1.先吃鸡,然后吃玉米。
2.先吃玉米,同时用部分玉米喂鸡,吃鸡生产的蛋,最后再吃鸡。
学生:每组学生各选一名代表,做出选择。
(绝大部分学生选择的是2)教师:真理往往掌握在少数人手里。
我们共同来看看鲁滨逊的选择是—-先吃鸡,然后吃玉米。
但母鸡提出抗议。
教师:对于母鸡的抗议,我们是可以理解的.我们必须给母鸡一个合理的解释,消除母鸡的不满情绪,这就得用到我们这节课的内容“生态系统中的能量流动”.方式二播放影片:非洲草原上鹰捕食兔子的过程.提问:刚才这部短片的主角是谁?(过渡)对了,兔子、鹰,不要忘了还有小草,在非洲大草原上主要的生产者就是小草,草原上几乎所有的动物都是由小草养活的,没有小草,也就不会有兔子和鹰了.现在小草有问题要问了:1.我们的能量来自哪里?2.照射在草地上的太阳能都被我们吸收了吗?3.我们吸收了太阳能后,这些能量有哪些去向?总结:导入生态系统中的能量流动。
一、能量流动的概念和过程1.能量流动的概念:是指生态系统中能量的输入、传递、转化和散失的过程。
2.能量流经第一营养级的过程(1)输入:生产者通过光合作用把太阳能转化为化学能,固定在光合作用制造的有机物中。
(2)能量去向:①在生产者的呼吸作用中以热能形式散失。
②随着植物体的衰老死亡以枯枝落叶的形式被分解者分解而散失。
③被初级消费者取食同化,流入第二营养级。
3.能量流经第二营养级的过程(1)输入:通过取食生产者获得。
(2)能量去向:①通过呼吸作用以热能形式散失.②随遗体、排泄物流向分解者。
③被次级消费者取食同化,流入下一营养级. 4.能量在某个生态系统中流动过程图解知识整合1.能量流入某营养级的定时定量的分析(1)流入某一营养级的能量在一定时间内的去路有4条,它们分别是:a.自身呼吸消耗;b.流入下一个营养级;c。
第4章 稳定性分析

分析举例,判断下列函数是否为正定的? 正定的 半正定的 负定的 半负定的 不定的
信息与控制工程学院
2. 二次型标量函数 设 x =[ x1, x2, ···, xn]T,则实二次型标量函数记为:
V(x)=V(x1, x2, ···, xn)=xTPx
其中,P称为二次型的矩阵(实对称矩阵)
p11
信息与控制工程学院
⑴李亚普诺夫意义下一致稳定
通常时变系统的d与t0有关,时不变系 统的d与t0无关。只要d与t0无关,这种平
衡状态称为一致稳定的。
⑵时不变系统的稳定属性
时不变系统李亚普诺夫意义下的稳定和一致稳定必为等价。
⑶李亚普诺夫意义下稳定的实质上是工程意义下的临界稳定。
信息与控制工程学院
2、渐近稳定性
信息与控制工程学院
x&1 f1(x1, x2 ) x1 - x1x2
在xe1=[0, 0]T 处将其线性化有
x&2 f2 (x1, x2 ) -x2 x1x2
x&1
x&2
A
x1 x2
其中雅可比矩阵A为
f1
A
x1 f2
x1
f1
x2 f2
1
- x2 x2
x2
D1 p11,
D2
p11 p21
p12 , p22
,
Dn P
信息与控制工程学院
矩阵P定号的充要条件是:
(1)若Di> 0 (i=1,2,…,n),则P为正定的。
(2)若Di
>0 <0
i为偶数 i为奇数
,则P为负定的。
(3)若Di
0 i= (1,2,…,n-1) ,则P为半正定的。 = 0 i=n
信号与系统讲义第四章5系统频率特性及稳定性

06.06.2019
信号与系统
例:图示反馈系统,求系统函数分析稳定性 Q(s)
稳定系统的充要条件: h()d<
06.06.2019
信号与系统
2、根据系统函数零、极点分布判断稳定性
系统稳定的条件
H(s)全部极点在s左半开平面,稳定 H(s)的极点在右半开平面,或虚轴上有二阶以
上高阶极点,不稳定 H(s)虚轴上单极点,不稳定(边界稳定)
06.06.2019
根据幅频特性的不同,可划分成如下几种
06.06.2019
截止频率--下降3dB的频率点
信号与系统
二、由极、零点分布分析频响特性
m
(s z j)
H (s) K
j 1 n
(s pi)
i 1
s沿 虚 轴 移s 动j
m
( j z j )
H ( j) K
j 1 n
信号与系统
1 1 R1C1 R2C2
06.06.2019
信号与系统
小结: (232页)
若函数有一对非常靠近jω轴的极点,则ω 在极点附近,幅频特性出现峰点,相频特性 迅速下降
若函数有一对非常靠近jω轴的零点,则ω 在零点附近,副频特性出现下陷,相频特性 迅速上升
若系统函数的零、极点远离jω轴,则对频 率响应特性曲线的影响较小,只是大小有所 增减。
信号与系统
4.11 线性系统的稳定性
1、稳定系统
有限(界)激励,产生有限(界)输出,稳定系统 有限(界)激励,产生无限(界)输出,为不稳定系统
幼儿园教育基础,讲义 第四章

第四章幼儿园教育的基本原则教育原则是教育工作必须遵循的基本准则,它反映教育原理的基本观点,是教育理论的具体化,体现教育理论对教育实践的指导。
幼儿园教育原则是根据幼儿身心发展规律和幼儿教育性质制定出来的,同时也是由幼儿教育实践总结而来的,更是今后的幼儿园教育工作行动的依据。
幼儿园教育的基本原则包括两个部分,一部分是与其他阶段教育如小学教育所共有的,是教育的一般原则,另一部分是它所独有的,与其他阶段教育不同的特殊原则。
第一节教育的一般原则一、尊重和保护儿童原则(一)尊重和保护儿童原则的含义尊重和保护儿童的原则,要求教师把儿童当作教育的主体,尊重其主体权利与地位,并为儿童的发展提供保护,消除教育活动过程中可能对儿童身心产生伤害的各种隐患,促进儿童健康持续的发展。
这一原则是依据我国教育目标、任务和儿童的身心发展特点,在长期的教育实践经验中总结而来的。
具体到幼儿园教育中,就是要将尊重和保护幼儿视为幼儿园教育工作的基本前提。
1.尊重幼儿尊重幼儿就是在幼儿园教育中要尊重作为主体的幼儿的生命、人格、地位与权利、身心发展特点和个性差异、学习特点等。
具体包括:(1)尊重幼儿的生命。
(2)尊重幼儿的人格。
(3)尊重幼儿的权利。
(4)尊重幼儿的身心发展特点和个性差异。
(5)尊重幼儿的学习特点。
2.保护幼儿保护幼儿,主要包括保护幼儿的健康、安全、自尊心、自信心、好奇心、求知欲或探究欲、创造力、想象力等。
(1)保护幼儿的健康和安全。
《纲要(试行)》指出:幼儿园必须把保护幼儿的生命和促进幼儿的健康放在工作的首位。
树立正确的健康观念,在重视幼儿身体健康的同时,要高度重视幼儿的心理健康。
《中华人民共和国未成年人保护法》指出:不得对幼儿实施体罚、变相体罚或者其他侮辱人格尊严的行为;幼儿园安排幼儿参加集会、文化娱乐、社会实践等集体活动,应当有利于幼儿的健康成长等。
(2)保护幼儿的自尊心和自信心。
《纲要(试行)》中还指出:“要从不同角度促进幼儿情感、态度、能力、知识、技能等方面的发展。
稳定性分析专业知识讲座
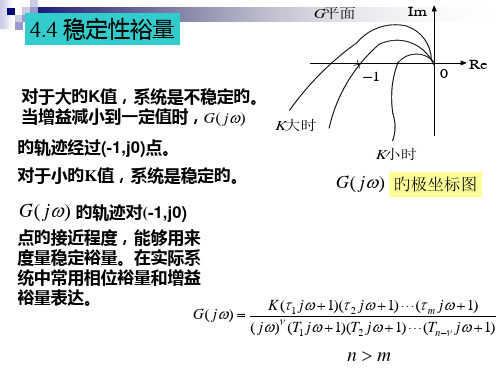
5.7.3 原则二阶系统中阶跃瞬 R ( s )
态响应与频率响应之间旳关系
_
书上例5-13p203
ω n2
C (s)
S (S + 2 ξω n)
图 3-8 标 准 形 式 的 二 阶 系 统 方 块 图
在图3-8所示旳原则二阶系统中,单位阶跃响应中 旳最大超调量能够精确地与频率响应中旳谐振峰值 联络在一起。所以,从本质上看,在频率响应中包 括旳系统动态特征信息与在瞬态响应中包括旳系统 旳动态特征信息是相同旳。
K (1 j )
G( j)
j(1 j
0.1
)(1 j )
0.01
5
看对数幅频特征
L()
80
dB
60
40
-20dB/dec
K (1 j )
G( j)
j(1 j
0.1
)(1
j
)
0.01
5
-40dB/dec
20
-20dB/dec
0
5
0.01 0.1
1
rad/s
-20
-40dB/dec
对于小旳阻尼比, 谐振频率与阻尼自 然频率旳值几乎是 相同旳。所以,对 于小旳阻尼比,谐 振频率旳值表征了 系统瞬态响应旳速 度。
r n 1 2 2
d n 1 2
旳值越小
M r 和 M p 旳值越大。
r M r 和 M p 与
之间旳函数关系如图5-52 所示。能够看出,当 0.4 时,M r 和 M p
相位交界频率 x
(x ) G( jx )H ( jx ) 180
(x ) 90 arctg0.2x arctg0.05x 180
即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/1/24
6
结构稳定性(续)
极限载荷
• 在实际结构中,要获得临界载荷非常困难。由于几何误 差和非线性特性,结构在低于临界载荷的力的作用下就 会变得不稳定。
F
歧点
实际结构的响应,
低于临界载荷就会
Fcr
出现不稳定。
2021/1/24
u
7
结构稳定性(续)
• 一般的非线性载荷位移曲线如下图所示。此图显示了理想的加载 路径,非理想结构的加载路径及结构的动态响应。
稳定
2021/1/24
不稳定
中性
5
结构稳定性(续)
临界载荷
• 当 F < Fcr时, 立柱处于稳定平衡状态。 如果先施加一个 小的扰动力 (P 0) 然后再删除掉,立柱将会恢复到原始 位置。当 F > Fcr 时,立柱处于非稳定平衡状态,任何扰 动力都将会引起失稳。当 F = Fcr时 ,立柱处于中性平衡 状态,这就是临界载荷。
F
线性特 征值屈曲
非线性屈曲
理想化加载路径 非理想结构的加载路径
前屈曲
u
2021/1/24
18
特征值屈曲
• 特征值屈曲分析 可预测一个理想线弹性
结构的理论屈曲强度(歧点)。
• 特征值公式决定了结构的歧点。此种方 法相当于教科书上的线弹性屈曲分析方 法。一个Euler 立柱的特征值屈曲解与经 典的Euler解相匹配。
轴向载荷(F)作用下,将显示出如下特性
。F F F
歧点
不稳定平衡
Fcr u
中性平衡 稳定平衡
2021/1/24
u
3
结构稳定性(续)
歧点
• 在加载历史中的某一点处,可能有两种分支的解,这一点就是所谓 的柱,在临界载 荷(Fcr)的作用下,它将有可能向左或向右 弯曲。因此会有两种可能的加载路径。在
第四章稳定性分析
精品
结构稳定性
• 许多结构需要评定它们的结构稳定性。 细立柱,受压杆件,真空容器都是需考 虑结构稳定性的例子。
• 在不稳定(失稳)发生时,结构在载荷
基本无变化F 的情况下(由F于小的载荷扰
动),位移 {u} 发生很大变化。
稳定
不稳定
2021/1/24
2
结构稳定性(续)
• 一个理想化的固定端柱子在逐渐增加的
– 相对经济(快速)的分析 – 失稳模态形状可用作非线性屈曲分析的初始
几何缺陷。
2021/1/24
21
特征值屈曲分析的基础
13
弧长法
• 弧长法是一种用于得到不稳定(KT 0)或负刚度矩阵(KT < 0)问题 的数值稳定解的方法。
• 弧长法可用于比例加载的静力问题。
F
• 尽管弧长法可求解复杂的力位移响 应问题,但它最适合求解不带突然
歧点的平滑响应问题。
u
2021/1/24
14
弧长法(续)
• 通过在求解时引入未知数-载荷因子l (-1 < l < 1)后,弧长法 可在 Newton-Raphson 方法中对载荷与位移同时求解。 Newton-Raphson 方程可重写为,
F
歧点
极限点
前屈曲
理想的静力 特性
后屈曲
2021/1/24
理想的加载路径 非理想结构的加载路径 实际动态响应
u
8
载荷控制,位移控制与弧长法
• 为计算结构的静态力位移响应,有不同 的分析技巧。这些技巧包括:
– 载荷控制 – 位移控制 – 弧长法
2021/1/24
9
载荷控制
• 分析如下所示的薄拱形结构突然弯折。当用增量加载(F)的方式完成
2021/1/24
Fapp Fcr
KT = 0
KT < 0
Fcr 只能用载荷控 制得到。
u
11
位移控制
• 弧形结构受到逐渐增大的位移载荷,对应于受力载荷,求解是使用
位移控制 完成的。位移控制的优点在于它在Fcr 点外产生一个稳定
求解。(施加的位移可在不稳定点添加约束。)
UY
Fapp
UY
UY
2021/1/24
[KT]{u} = l {Fa} - {Fnr}
• 为了适应增加的未知数,必须引入一个约束方程,弧长 。弧 长与载荷因子l以及Newton-Raphson 方程中的位移增量{u} 有关。
2021/1/24
15
弧长法(续)
弧长法是借助一条圆 弧将载荷因子增量l 和位移增量u关联起 来。图中所示的是用 于全NewtonRaphson法中的载荷 因子增量l和位移增 量u。
此问题的求解时,需使用载荷控制 。
F F F
Fapp
2021/1/24
可用载荷控制得到 Fapp 吗?
u
10
载荷控制(续)
• 在Newton-Raphson 法中使用载荷控制的困难在于求解无法越过不 稳定点。在不稳定点(Fcr) ,刚度矩阵KT 奇异 。使用载荷控制, Newton-Raphson 法将不收敛。但是,此种分析对描述结构的前屈 曲特性有益。
实际的结构中,由于几何误差或扰动载荷
(P 0) 的存在,它们会决定加载路径。
u
2021/1/24
4
结构稳定性(续)
稳定,不稳定与中性平衡
• 考虑下面所示的球的平衡。如果表面是向上凹的,则平衡是稳定的 。如果受到干扰,球将回到它的初始位置。如果表面是向上凸的, 则平衡是不稳定的,如果受到干扰,球将滚开。如果表面是平的, 则球处于中性平衡态,球将停留在新的平衡位置。
Fapp 可通过位移控制得 到。 (Fapp 现在是施加 位移UY 的反作用力。)
u
12
位移控制(续)
• 位移控制的缺点是只有你明确知道施加多大的位移时才可使用! 如果在弧形结构上施加的不是集中载荷而是压力载荷,则不可能 使用位移控制。
P
对于一些更复杂的加载情况,
通常不知道施加的位移大小。
2021/1/24
2021/1/24
19
特征值屈曲(续)
• 但是非理想性与非线性使大多数实际结构无法达到它们的理论弹性
屈曲强度。特征值屈曲通常得到非保守 结果,在使用时要小心。
F
歧点
前屈曲
2021/1/24
极限载荷
理想加载路径 非理想结构的加载路径
u
20
特征值屈曲(续)
• 尽管特征值屈曲分析经常得到非保守解 ,但进行线性失稳分析有两个优点:
2021/1/24
ArLcenRgath di uun 2sl2
16
弧长法(续)
• 强制Newton-Raphson 迭代沿 着与平衡路径相交的圆弧收敛, 可得到承受零或负刚度的结构的解。
F
ri
ri
ri
ri
ri 弧长半径 收敛子步
平衡路径
u
2021/1/24
17
前屈曲分析
前屈曲分析及破坏载荷分析的分析方法包括: • 线性特征值屈曲 • 非线性屈曲分析
