王淑华版固体物理第五章答案
固体物理第五章习题及答案

.
从上式可以看出,当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量 m* 变 为 . 此时电子的加速度
a= 1 F =0
m*
,
即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么?
[解答] 由本教科书的(5.53)式可知, 万尼尔函数可表示为
m* = 1 m 1 + 2Tn
Vn <1.
10. 电子的有效质量 m* 变为 的物理意义是什么?
[解答] 仍然从能量的角度讨论之. 电子能量的变化
(dE)外场力对电子作的功 = (dE)外场力对电子作的功 + (dE)晶格对电子作的功
m*
m
m
=
1 m
(dE ) 外场力对电子作的功
− (dE)电子对晶格作的功
i 2 nx
V (x) = Vne a
n
中, 指数函数的形式是由什么条件决定的?
[解答] 周期势函数 V(x) 付里叶级数的通式为
上式必须满足势场的周期性, 即
V (x) = Vneinx
n
显然
V (x + a) = Vnein (x+a) = Vneinx (eina ) = V (x) = Vneinx
Es (k)
=
E
at s
− Cs
−
Js
e ik Rn
n
即是例证. 其中孤立原子中电子的能量 Esat 是主项, 是一负值, − Cs和 − J s 是小量, 也是负 值. 13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?
物理化学第五版课后习题答案解析电子教案

物理化学第五版课后习题答案解析第五章 化学平衡5-1.在某恒定的温度和压力下,取n 0﹦1mol 的A (g )进行如下化学反应:A (g )B (g )若0B μ﹦0A μ,试证明,当反应进度﹦0.5mol 时,系统的吉布斯函数G 值为最小,这时A ,B 间达到化学平衡。
解: 设反应进度为变量A (g )B (g )t ﹦0 n A , 0﹦n 0 0 0﹦0t ﹦t 平 n A n B﹦BBn ν n B ﹦B,n A ﹦n 0-n B ﹦n 0-B,n ﹦n A +n B ﹦n 0气体的组成为:y A ﹦A n n ﹦00B n n νξ-﹦01n ξ-,y B ﹦B nn﹦0n ξ各气体的分压为:p A ﹦py A ﹦0(1)p n ξ-,p B ﹦py B ﹦p n ξ各气体的化学势与的关系为:0000ln ln (1)A A AA p p RT RT p p n ξμμμ=+=+- 0000lnln B B B B p p RT RT p p n ξμμμ=+=+⋅ 由 G =n AA+n BB=(n A 0A μ+n B 0B μ)+00ln(1)A p n RT p n ξ-+00ln B p n RT p n ξ⋅ =[n 0-A μ+0B μ]+n 00lnpRT p +00()ln(1)n RT n ξξ--+0ln RT n ξξ 因为 0B μ﹦0A μ,则G =n 0(0A μ+0lnpRT p)+00()ln(1)n RT n ξξ--+0ln RT n ξξ ,0()ln T p G RT n ξξξ∂=∂- 20,20()()T p n RT Gn ξξξ∂=-∂-<0 令 ,()0T p Gξ∂=∂011n ξξξξ==-- ﹦0.5 此时系统的G 值最小。
5-2.已知四氧化二氮的分解反应 N 2O 4 (g ) 2 NO 2(g )在298.15 K 时,0r m G ∆=4.75kJ ·mol -1。
物理化学答案——第五章-相平衡[1]
![物理化学答案——第五章-相平衡[1]](https://img.taocdn.com/s3/m/3b8b7eb9561252d381eb6e33.png)
第五章 相平衡一、基本公式和内容提要基本公式1. 克劳修斯—克拉贝龙方程m mH dp dT T V ∆=∆相相(克拉贝龙方程,适用于任何纯物质的两相平衡) 2ln m H d p dT RT ∆=相(克劳修斯—克拉贝龙方程,适用与其中一相为气相,且服从理想气体状态方程的两相间平衡)2.特鲁顿(Trouton)规则1188vap mvap m b H S J mol k T --∆=∆≈⋅⋅(T b 为该液体的正常沸点)3.相律f+Φ=C+n C=S-R-R ′f+Φ=C+2 (最普遍形式)f* +Φ=C+1 (若温度和压力有一个固定,f * 称为“条件自由度”)*4. Ehrenfest 方程2112()p p C C dp dT TV αα-=-(C p ,α为各相的恒压热容,膨胀系数)基本概念1. 相:体系中物理性质和化学性质完全均匀的部分,用Φ表示。
相的数目叫相数。
2.独立组分数C=S-R-R′,S为物种数,R为独立化学反应计量式数目,R′ 为同一相中独立的浓度限制条件数。
3.自由度:指相平衡体系中相数保持不变时,所具有独立可变的强度变量数,用字母f 表示。
单组分体系相图相图是用几何图形来描述多相平衡系统宏观状态与T、p、X B(组成)的关系。
单组分体系,因C=1 ,故相律表达式为f=3-Φ。
显然f最小为零,Φ最多应为 3 ,因相数最少为 1 ,故自由度数最多为 2 。
在单组分相图中,(如图5-1,水的相图)有单相的面、两相平衡线和三相平衡的点,自由度分别为f=2、f=1、f=0。
两相平衡线的斜率可由克拉贝龙方程求得。
图5-1二组分体系相图根据相律表达式f=C-Φ+2=4-Φ,可知f最小为零,则Φ最多为 4 ,而相数最少为 1 ,故自由度最多为 3 。
为能在平面上显示二组分系统的状态,往往固定温度或压力,绘制压力-组成(p-x、y)图或温度-组成(T-x、y)图,故此时相律表达式为f*=3-Φ,自然f*最小为 0 ,Φ最多为 3,所以在二组分平面图上最多出现三相共存。
物理化学第五版课后习题答案解析

第五章 化学平衡5-1.在某恒定的温度和压力下,取n 0﹦1mol 的A (g )进行如下化学反应:A (g )B (g )若0B μ﹦0A μ,试证明,当反应进度﹦0.5mol 时,系统的吉布斯函数G 值为最小,这时A ,B 间达到化学平衡。
解: 设反应进度为变量A (g )B (g )t ﹦0 n A , 0﹦n 0 0 0﹦0t ﹦t 平 n A n B﹦BBn ν n B ﹦B,n A ﹦n 0-n B ﹦n 0-B,n ﹦n A +n B ﹦n 0气体的组成为:y A ﹦A n n ﹦00B n n νξ-﹦01n ξ-,y B ﹦B nn﹦0n ξ各气体的分压为:p A ﹦py A ﹦0(1)p n ξ-,p B ﹦py B ﹦p n ξ各气体的化学势与的关系为:0000ln ln (1)A A AA p p RT RT p p n ξμμμ=+=+- 0000lnln B B B B p p RT RT p p n ξμμμ=+=+⋅ 由 G =n AA+n BB=(n A 0A μ+n B 0B μ)+00ln(1)A p n RT p n ξ-+00ln B p n RT p n ξ⋅ =[n 0-A μ+0B μ]+n 00lnpRT p +00()ln(1)n RT n ξξ--+0ln RT n ξξ 因为 0B μ﹦0A μ,则G =n 0(0A μ+0lnpRT p )+00()ln(1)n RT n ξξ--+0ln RT n ξξ ,0()ln T p G RT n ξξξ∂=∂- 20,20()()T p n RT Gn ξξξ∂=-∂-<0 令 ,()0T p Gξ∂=∂011n ξξξξ==-- ﹦0.5 此时系统的G 值最小。
5-2.已知四氧化二氮的分解反应 N 2O 4 (g) 2 NO 2(g )在298.15 K 时,0r m G ∆=4.75kJ ·mol -1。
《固体物理》第5章课后题目答案

1、什么是Peierl不稳定性和Peierls相变?【解答】:假设的晶格内原子状态:假定一维系统是由晶格常数为 a 的N个原子组成,每个晶格原胞只带一个传导电子,电子波函数满足周期条件;第一布里渊区边缘在±π/a,第一布里渊区可以填充2N个电子,因为N个价电子正好填充了最低能带的一半,费米能量恰好位于能带1/2处(Kf=±π/2a),空能级和占据能级各一半。
然而,Peierls指出这种等距离排列的一维晶格是不稳定的,在低温下,原子发生移动,晶格常数由a变为2a,即第一布里渊区边缘移至费米面且打开了一个能隙,系统总能量降低(。
这就说明,原来等距离排列的具有较高能量的一维晶格经原子移动后变成具有较低能量的畸变晶格,所以原来的晶格是不稳定的。
经过晶格畸变,从半满能带的导体变成为稳定的只有满带和空带的半导体,这就是Peierls不稳定性。
只有在0K时,体系才完全处于上述半导体基态中,当T升高,晶格原子的振动逐步加强以至畸变模糊。
存在相变温度Tp,T<Tp,体系呈现半导体;T≥Tp,体系相变为导体,这种半导体变为导体的相变称为Peierls相变。
2、简述金刚石、石墨的结构和物性,比较它们性质的异同?【解答】:金刚石和石墨的化学成分都是碳,科学家们称之为“同质多像变体”,也有人称“同素异形体”。
从这种称呼可以知道它们具有相同的“质”,但“形”或“性”却不同,且有天壤之别,金刚石是目前最硬的物质,而石墨却是最软的物质之一。
大家都知道铅笔芯就是用石墨粉和粘土配比而制成的,石墨粉多则软,用“B“表示,粘土掺多了则硬,用“H”表示。
矿物学家用摩氏硬度来表示相对硬度,金刚石为10,而石墨的摩氏硬度只有1。
它们的硬度差别那么大,关键在于它们的内部结构有很大的差异。
石墨内部的碳原子呈层状排列,一个碳原子周围只有3个碳原子与其相连,碳与碳组成了六边形的环状,无限多的六边形组成了一层。
层与层之间联系力非常弱,而层内三个碳原子联系很牢,因此受力后层间就很容易滑动,这就是石墨很软能写字的原因。
中山大学固体物理第五章参考答案
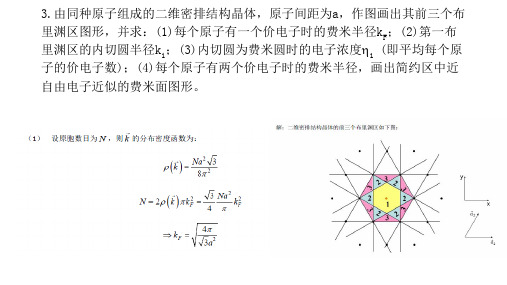
4.分别求出二维正方晶格简约区中沿M和XZM轴自由电子能量函数En(k) 能量
最低的前四条曲线的表达式,画出其示意图并给出各曲线的简并度。
二度简并
• 思考题
(1)对有限尺寸晶体(如量子点,量子线或量子井),你认为其晶体能带相 对于理想晶体会有什么变化?
周期性边界条件破坏,边界效应开始变得明显能带不再是准连续的。
反。
构造一虚拟的 空穴带,以描 述空穴动力学
k
逸失一电子 后的价带
2、能隙的由来?利用能带理论解释导体、 半导体以及绝缘体?
要点:本质是由于原子与原子的相互作用能 级分裂成能带,能带之间即是能隙。晶体中 是由于周期性势场的影响,在布里渊区边界 处bloch波的散射形成了能隙。
导体半导体绝缘体:电子的填充+能隙的大 小
(3)空穴:k(状态)空间的一种状态空缺,是存在这一空缺的整
个能带的描述,同其它电子一样,在真实空间的位置不确定,
在k空间的运动方向与其它电子相同,总带正电荷。
k 如果轨道中一个波矢为
能带是对称的,有
Ee
(ke
)
Ee
(ek的e ) 电Eh子(k逸e ) 失Eh,(k则h ),空显穴然的有波矢E为h (k-h
边界条件:波函数和它的一阶导数在x=c,和a处连续
U(x)
U0
1区 2区 3区
b x
0 ca Aeic Beic Cei 'c Dei 'c , ( Aeic Beic ) '(Cei 'c Dei 'c ) Cei 'a Dei 'a eika ( Aeia Beia ), '(Cei 'a Dei 'a ) eika ( Aeia Beia )
固体物理学1~6章习题解答

证明:由书可知
在高温时, ,则在整个积分范围内 为小量,因此可将上式中被积函数化简为
将上式代入 的表达式,得
将
代入上式得
3.10设晶格中每个振子的零点振动能为 ,试用德拜模型求三维晶格的零点振动能
解:由讨论由一个N个原子组成的二维晶格的比热,证明在低温下其比热正比于
(1)这种晶格属于哪种布拉维格子?
(2)原胞的体积和晶胞的体积各等于多少?
答:(1)因为a=3i,b=3j,而c=1.5(i+j+k)=1/2(3i+3j+3k)=1/2(a+b+c′)式中c′=3k。显然,a、b、c′构成一个边长为3*10-10m的立方晶胞,基矢c正处于此晶胞的体心上。因此,所述晶体属于体心立方布喇菲格子。
《固体物理学》习题解答
第一章
1.1有许多金属即可形成体心立方结构,也可以形成面心立方结构。从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以Rf和Rb代表面心立方和体心立方结构中最近邻原子间的距离,试问Rf/Rb等于多少?
答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:
(2)晶胞的体积= = =27*10-30(m3)
原胞的体积= = =13.5*10-30(m3)
1.7六方晶胞的基失为: , ,
求其倒格子基失,并画出此晶格的第一布里渊区.
答:根据正格矢与倒格矢之间的关系,可得:
正格子的体积Ω=a·(b*c)=
那么,倒格子的基矢为 , ,
其第一布里渊区如图所示:(略)
答:根据题意,由于OA、OB和OC分别与基失a1,a2和a3重合,那么
1.3二维布拉维点阵只有5种,试列举并画图表示之。
物理化学:第五章思考题解答

么? ①直接用下式计算
ln
o Δr Hm (298.15K) ⎛ K o(773.15K ) 1 1 ⎞ = − − ⎜ ⎟ o R 773 . 15 K 298 . 15 K K (298.15K ) ⎝ ⎠
o ②先算出 Δ r H m (773.15K ) ,然后用下式计算
ln
o (773.15K ) ⎛ 1 Δr Hm K o(773.15K ) 1 ⎞ = − − ⎜ ⎟ o R K (298.15K ) ⎝ 773.15K 298.15K ⎠
∗ eq ν B = − RT ln K o + ∑ν B ∫ o VB (l, s) dp + RT ln ∏B (a B ) B p
[
⎥ ⎦
]
=0
∴
p ⎧ ⎫ eq ν B ∗ K o = ∏ (a B ) × exp⎨∑ν B ∫ o V B (l, s) RT dp ⎬ p ⎩B ⎭ B p ⎧ ⎫ ∗ (l, s) ( RT ) dp ⎬ = K a exp⎨∑ν B ∫ o V B p ⎩B ⎭
第5章
化学平衡
·101·
o ③先求出 Δ r H m (T ) 与 T 的关系式,再代入下式进行积分 o dlnK o / dT = Δ r H m (T ) / RT 2 o 是温度的函数,故 解:第三种方法是正确的。因为该反应的 Δ r C p ,m o 也是温度的函数,不能用第一种或第二种方法计算 K o 。 Δr Hm
反应焓,后者用摩尔蒸发焓。固体物质的分解温度则与纯液体的正常沸 点类似,是平衡压力为 101325 Pa 时的温度。
2HgO (s) == 2Hg (l) + O 2 (g)
o o (298.15 K ) = −2Δ f G m (HgO,298.15 K ) Δ r Gm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姘去半V珩 留◇一泵Υ叩圉 ‘ 晔 首弼 壬 ‘ 弭弼 些驺匾町 佯 哭
裰 橛 擞 镢 黼
Cz=t手
〓 饣V=0Ⅱ 黟 r'昭 ″饣 〓
照叼 =’
'r
嘭鱼 嘭丁甲
r=凹 沪
・ 叼 曰钌击啷羽娣W苔 妊 ‘ 拐叩弼far钾 国汝△鹅 官 勹
r,c+【r-叫 江 C-,″ 歹 素
¢+,cJ9t罗 ¢-口 ″ 系
印
(z〉
~t~~~ˉ ~— — — 篙 鹅 豳 镙 灞 吝梨濠囤梁壬昏sJ唯 娶中鍪佯粥鹞 -孕 ‘ 吖鱼
(0%℃ 尸 +θ %艹 甲:挪 =(廴
(″ ~→ rz=fF9%(ε
,
・ ¥取叨早恶毒黎羿£昏 苔决 0~J 冫
(湃 塑sg舀 盥-赘 Vr,
=fF9%〈 乙 冫 ?tnα叩
仞 〓 %(1冫 t呷 ⑶
I【
`=,百
’ Jn〓 (→ Jh疵 ,《 → 。
0卜
→ fK《
,+FI%簿
。
r-`〓 J`
’ -Eq:o四 ″ -→
封
=t0丬
I【
f-D-丬F了 《″ +→ f否 《口 t硒 -’ +⒚
(ε 〉
¨ △ቤተ መጻሕፍቲ ባይዱ
¨ 冖
羽镁爸串笤弼留孕壬昏
ˉ
_
鼹 鼹 翻 髑 攫
(・
・ v=sl z饣
Jr7」 L-〓
ε
+sz
扌
珀乡
(・
z?勿 〓sl 犯
亻扌 丁廴
=冫
泊蟹
ar圉
″ ″ ″ 口 饣
(丢 +£
y(r+szl=″ ″ 澎 饣
')〓
f→ 【 =,.fv, 暂 壬
【
寻 fJ,j唧 9=lJ+|号
r→ =刃 u’
硇 衤・
FΞ 吓刀’ ″ =FΞ 叩 Ψ
lJ+下
〃→=
)吓 =lf妊 =崂 l灬
(‘
壬
〉
)⒑
lf,+r9号 ]御
‘ 口 竿濠筚,I , 吖漯囤取钾壬昏
砰 卒群熬华γ檗宗珂
黎茁柴铝 荨丁蒡
fF9%湃 碹取sg士
R∶
