正弦定理解三角形时解的个数
1.1正弦定理和余弦定理知识点

1.1正弦定理和余弦定理基本要求:1. 能证明正弦定理、余弦定理.2. 能理解正弦定理、余弦定理在讨论三角形边角关系时的作用.3. 能用正弦定理、余弦定理解斜三角形.4. 理解用正弦定理、余弦定理讨论三角形解的情形. 重点:正弦定理和余弦定理及其推导.难点:用正弦定理解三角形时解的个数的讨论. 考点结构分析:1. 正弦定理1:在一个三角形中各边和它所对角的正弦的比相等,即:CcB b A a sin sin sin ==. 2. 余弦定理2:三角形中任何一边的平方等于其他两边的平方和减去这两边与它们夹角余弦积的两倍,即:A bc c b a cos 2222-+=.B ca a c b cos 2222-+=.C ab b a c cos 2222-+=.3. 余弦定理推论:bc a c b A 2cos 222-+=.ca c a c B 2cos 222-+=.abc b a C 2cos 222-+=.4. 重要结论:(1) 在ABC ∆中,a 、b 、c 分别为A 、B 、C 的对边,C B A c b a C B A sin sin sin >>⇔>>⇔>>. (2) 在ABC ∆中,给定A 、B 的正弦或余弦值,则C 有解(即存在)的充要条件是0cos cos >+B A . 5. 解斜三角形的类型:(1) 已知两角一边,用正弦定理,有解时,只有一解.(2) 已知两边及其一边的对角,用正弦定理,有解的情况可分为以下情况,在ABC ∆中,已知a 、b 和角A 时,解的情况如下:上表中为锐角时,时,无解;为钝角或直角时,,均无解. (3) 已知三边,用余弦定理有解时,只有一解. (4) 已知两边及夹角,用余弦定理,必有一解.6. 三角形面积:(1) ah S 21=(h 为BC 边上的高); (2) C ab S sin 21=;(3) C B A R S sin sin sin 22=(R 为ABC ∆外接圆半径);(4) RabcS 4=(R 为ABC ∆外接圆半径); (5) ))()((c p b p a p p S ---=,)(21c b a p ++=.疑难点清单:判断三角形形状基本思想是:利用正弦定理进行角边统一.即将条件化为只含角的关系式,然后利用三角恒等变换得出内角之间的关系式;或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系.结论一般为特殊的三角形,如等边三角形,等腰三角形,直角三角形,等腰直角三角形等.另外,在变形过程中要注意A 、B 、C 内角的固定范围对三角函数数值的影响. 附:1. 正弦定理的证明: ① 定义法(教科书中给出)如图1,在ABC Rt ∆中,C ∠是最大的角,所对的斜边c 是最大的边,要考虑边长之间的数量关系,就涉及到了锐角三角函数.根据正弦函数的定义,Ac asin =, B cbsin =.所以c BbA a ==sin sin . 又1sin =C ,所以CcB b A a sin sin sin ==. 那么,对于一般的三角形,以上关系式是否仍然成立呢?如图2,当ABC ∆是锐角三角形时,设边AB 上的高是CD ,根据三角函数的定义,B a CD sin =,A b CD sin =,所以A bB a sin sin =, 得到BbA a sin sin =. 同理,在ABC ∆中, CcB b sin sin =. 所以CcB b A a sin sin sin ==. ② 向量法如图3,ABC ∆为锐角三角形时,过A 作三位向量→j 垂直于→AB ,则→j 与→AB 的夹角为︒90,→j 与→BC 的夹角为B -2π,→j 与→CA 的夹角为A +2π,设c AB =,a BC =,b AC =.因为→→→→=++0CA BC AB ,所以00=⋅=⋅+⋅+⋅→→→→→→→→j CA j BC j AB j . 即0)2cos(||||)2cos(||||2cos||||=++-+→→→→→→A CA jB BC j AB j πππ.所以A b B a sin sin =,即BbA a sin sin =. 同理可得:C cB b sin sin =,即CcB b A a sin sin sin ==.当ABC ∆为钝角三角形或者直角三角形时,利用同样的方法可以证得结论.(可以请学生来给出证明) ③ 几何法如图4,设O 为ABC ∆的外接圆的圆心,连接BO 并延长交 ⊙O 与点A ',连接C A ',则A A ='或A A -='π,∴=A sinR a B A BC A 2sin ='=',即R A a 2sin =,同理可证R B b2sin =, R C c 2sin =,故有CcB b A a sin sin sin ==. 注:在运用时,有时需要对它进行变形,如C B A c b a sin :sin :sin ::=; A R a sin 2=,B R b sin 2=,C R c sin 2=.如图5,当ABC ∆为钝角三角形时,设B 为钝角.过C 作AB 的垂线与AB 的延长线交于D 点,由三角函数的定义得A b CD sin =,B a B a CD sin )180sin(=-︒=,B a A b sin sin =∴,即BbA a sin sin =. 同理可得C c A a sin sin =,CcB b A a sin sin sin ==∴.2. 余弦定理证明:如图6,设→→=a CB ,→→=b CA ,→→=c AB ,那么→→→-=b a c ,→→→→→→→→→→→→→⋅-⋅-⋅=+⋅-=⋅=b a b b a a b a b a c c c 2)()(||2C ab b a cos 222-+=所以C ab b a c cos 2222-+=.同理可以证明:A bc c b a cos 2222-+=.B ca a c b cos 2222-+=.。
人教版高中数学高二人教A版必修5(正弦定理)

绝密★启用前1.1.1 正弦定理 (A 卷)考点:1.正弦定理解三角形 2.正弦定理判定三角形解的个数3.正弦定理边角互化的应用一、选择题:本题共8个小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【题文】在△ABC 中,6,60a b A ===,则sin B = ( )A . 23B .3.2 D .382.【题文】设△ABC 的内角A ,B ,C 所对的边分别为,,a b c ,若cos cos sin b C c B a A +=,则△ABC 的形状为( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不确定3.【题文】在△ABC 中, ,,A B C ∠∠∠所对的边分别为,,a b c ,若8,60,75a B C =∠=︒∠=︒,则实数b 等于( )A. B. D.3234.【题文】在△ABC 中,b =4B π∠=,tan A =,则实数a 的值是( )A .210B .C .10D .25.【题文】在△ABC 中,15,18,30a b A ===︒,则此三角形解的个数为( ) A .0 B . C . 2 D .不确定6.【题文】在△ABC 中,角,,A B C 所对的边分别为a b c 、、,已知π3,3a b A ===,则角B 等于( ) A.π4 B.3π4 C. π4或3π4D. 以上都不正确7.【题文】在△ABC 中,已知AB =,30B =︒,则A = ( ) A .45° B.15° C.45°或135° D.15°或105°8.【题文】在△ABC 中,已知1,15b c B ===,则边长a 等于 ( )A 1或21 C. 2 D.二、填空题:本题共3小题.9.【题文】在△ABC 中,已知a =4,B =60°,C =75°,则b = .10.【题文】在△ABC 中,角A , C 所对的边分别是a , c ,其中1=a ,33=c 3A π=,则角=C .11.【题文】如图所示,在一个坡度一定的山坡AC 的顶上有一高度为25m 的建筑物CD .为了测量该山坡相对于水平地面的坡角θ,在山坡的A 处测得15DAC ︒∠=,沿山坡前进50m 到达B 处,又测得45DBC ︒∠=.根据以上数据计算可得cos θ=__________.三、解答题:解答应写出文字说明,证明过程或演算步骤.12.【题文】△ABC 的内角A 、B 、C 所对的边分别为a 、b 、c .己知A −C =90°,a +c =2b ,求C .13.【题文】如图,在△ABC中,点D 在BC 边上,π72cos 42CAD AC ADB ∠==∠=-,,.(1)求sin C ∠的值; (2)若5BD =,求AD 的长.14.【题文】在△ABC 中,c b a 、、分别是角C B A 、、所对的边,且满足C b a cos 3=.(1)求BCtan tan 的值; (2)若3tan ,3==A a ,求边长b 的值.1.1.1 正弦定理 (A 卷)参考答案与解析1. 【答案】D【解析】∵6,60a b A ===,由sin sin a b A B =得sin 3sin .8b A B a ==故选D. 考点:正弦定理. 【题型】选择题 【难度】一般2. 【答案】B【解析】由已知可得2sin cos cos sin sin B C B C A +=,∴()2sin sin B C A +=, ∴sin 1A =,∴π2A =,三角形为直角三角形. 考点:判断三角形的形状. 【题型】选择题 【难度】较易3. 【答案】C【解析】∵60,75B C ︒︒∠=∠=,∴45A ∠=,∵sin sin a bA B =,=,∴b =考点:正弦定理解三角形. 【题型】选择题 【难度】较易4. 【答案】B【解析】因为sin tan cos AA A==22sin cos 1A A +=,∴sin A =,由正弦定πsin 43=,解得a = B. 考点:三角恒等式,正弦定理解三角形. 【题型】选择题 【难度】一般5. 【答案】C303=,因为b a >,所以30B A >=,所以角B 可能是锐角,也可能是钝角,所以此三角形有两解,故选C.考点:正弦定理判定三角形解的个数. 【题型】选择题 【难度】一般6. 【答案】A【解析】在△ABC 中,∵π3,3a b A ===,∴3πsin sin sin 3a b A B =⇒=sin B ⇒=,又∵3b a =<=,∴π03B A <<=,∴π4B =,故选A. 考点:正弦定理解三角形. 【题型】选择题 【难度】一般7. 【答案】D 【解析】由正弦定理得sinsin AB ACC B=,得sin sin 30AB B C AC ==︒=,由AB AC >,得C B >,所以45C =︒或135︒,从而105A =︒或15︒.故选D . 考点:正弦定理解三角形. 【题型】选择题 【难度】一般8. 【答案】A【解析】由正弦定理可得,sin 6sin153sin 31c B C b ⨯===-, 在△ABC 中,c b >,60C ∴=或120.当60C =时,105A =,sin 6sin10531sin sin 60c A a C ︒︒∴===+; 当120C =时,45A =,此时sin 6sin 452sin sin120c A a C ︒︒∴===. 综上可得31a =+或2a =. 考点:正弦定理解三角形. 【题型】选择题 【难度】一般9. 【答案】26【解析】∵B =60°,C =75°,∴A =45°,∴由正弦定理得b =oo sin 4sin 60=26sin sin 45a B A ⨯=考点:正弦定理解三角形. 【题型】填空题 【难度】较易10. 【答案】π6【解析】由正弦定理可得313πsin sin 3C =,即212333sin =⨯=C ,所以π6C =或5π6,又a c <,所以π6C =.考点:正弦定理解三角形. 【题型】填空题 【难度】一般11. 【解析】在△ABD 中,50m 15451530AB DAB ADB ︒︒︒︒=∠=∠=-=,,,由正弦定理得50sin 30sin 15BD ︒︒=,可得100sin 15m BD ︒=.在△DBC 中,25m CD =,45CBD ︒∠=,90BCD θ︒∠=+,由正弦定理得()100sin15sin 45295sin 0θ︒︒︒=+,()cos sin 90θθ︒︒∴=+==1. 考点:正弦定理解三角形. 【题型】填空题 【难度】较难12. 【答案】15【解析】由正弦定理可得sin sin A C B +=,又由于()o o 90=180,A C B A C -=-+,故()cos sin C C A C +=+()o 9022.C C =+=cos 2,C C C = ()o cos 45=cos 2C C -.因为o o 090C <<, 所以o 2=45C C -,o =15C .考点:正弦定理边角互化的应用,三角恒等变换. 【题型】解答题 【难度】一般13. 【答案】(1)45(2【解析】(1)因为cos ADB ∠=,所以sin ADB ∠=. 又因为π4CAD ∠=,所以π4C ADB ∠=∠-.所以πsin sin sin 4C ADB ADB⎛⎫∠=∠-=∠ ⎪⎝⎭ππ4cos cos sin 441021025ADB ⋅-∠⋅=+=.(2)在△ACD 中,由sin sin AD ACC ADC=∠∠考点:两角差的正弦公式,正弦定理解三角形. 【题型】解答题 【难度】一般14. 【答案】(1)2 (2【解析】(1)由正弦定理可得sin 3sin cos A B C =,πA B C ++=,sin sin()=3sin cos A B C B C ∴=+,即sin cos cos sin =3sin cos B C B C B C +,cos sin =2sin cos B C B C ∴,cos sin =2sin cos B CB C∴,故tan =2tan CB. (2)由πA B C ++=得tan()tan(π)3B C A +=-=-,即tan tan 31tan tan B C B C +=--⨯, 将tan 2tan C B =代入得23tan 312tan BB=--, 解得tan 1B =或1tan 2B =-,根据tan 2tan C B =得tan tan C B 、同正, 所以tan 1B =,又tan 3A =,可得sin sin 210B A ==102,∴b考点:正弦定理的运用,三角函数的恒等变换. 【题型】解答题【难度】一般。
解三角形(正弦定理、余弦定理、三角形面积公式)

授课班级:13级1班 授课时间:15年12月1日
2019年7月4日9时48分
1
余弦定理、正弦定理和三角形面积公 式
夯基释疑
概要
考点突破
考点一 考点二
例 1 训练1 例 2 训练2
课堂小结
考点三
例 3 训练3
2019年7月4日9时48分
2
夯基释疑
熟记公式是本节的基本要求。
所以sin A=
3=
3
3
3 2 1
12
12
12
2
因为a b,所以0 ∠A 2 ,则∠A= ,
3
6
因为∠C= 2
63 6
所以S
1 ABC = 2 ab sin C
14 2
3 12 1 12 2
3
2019年7月4日9时48分
19
余弦定理、正弦定理和三角形面积公 式
夯基释疑
概要
考点突破
考点一 考点二
例 1 训练1 例 2 训练2
课堂小结
考点三
例 3 训练3
2019年7月4日9时48分
17
考点突破 考点三 三角形面积公式的应用
【例3】(2013年高考题)在△ABC中,a 3,b=4,c= 37, 则△ABC的面积是 _________ .
解析
a2 b2 c2 9 16 37 1
21
请完成《学海领航课堂训练》
2019年7月4日9时48分
22
SUCCESS
THANK YOU
2019/7/4
5
所以cosA 1 ( 4)2 3 ,
5
§1.1.1正弦定理(2)
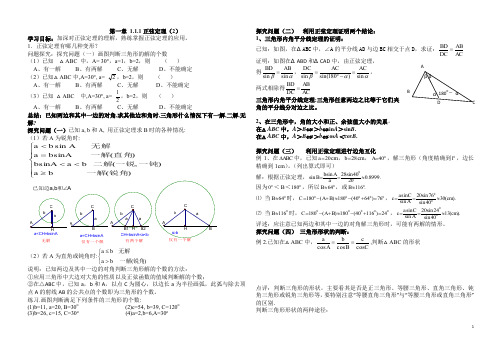
第一章 1.1.1正弦定理(2)学习目标:加深对正弦定理的理解,熟练掌握正弦定理的应用。
1.正弦定理有哪几种变形?问题探究:探究问题(一)画图判断三角形的解的个数 (1)已知 △ABC 中,A= 30°,a=1,b=2,则 ( ) A 、有一解 B 、有两解 C 、无解 D 、不能确定 (2)已知△ABC 中,A=30°, a= 2,b=2,则 ( )A 、有一解B 、有两解C 、无解D 、不能确定(3)已知 △ABC 中,A=30°, a= 21,b=2,则 ( )A 、有一解B 、有两解C 、无解D 、不能确定总结:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?探究问题(一)已知a, b 和A, 用正弦定理求B 时的各种情况: (1)若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ) ,(b a bsinA )( bsinAasin 锐角一解一钝一锐二解直角一解无解A b a已知边a,b 和∠A有两个解仅有一个解无解CH=bsinA<a<b a=CH=bsinA a<CH=bsinA(2)若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a说明:已知两边及其中一边的对角判断三角形解的个数的方法:①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数;②在△ABC 中,已知a ,b 和A ,以点C 为圆心,以边长a 为半径画弧,此弧与除去顶点A 的射线AB 的公共点的个数即为三角形的个数。
练习.画图判断满足下列条件的三角形的个数:(1)b=11, a=20, B=30o (2)c=54, b=39, C=120o (3)b=26, c=15, C=30o (4)a=2,b=6,A=30o探究问题(二) 利用正弦定理证明两个结论: 1、三角形内角平分线定理的证明:已知:如图,在ΔABC 中,∠A 的平分线AD 与边BC 相交于点D ,求证:BD ABDC AC=证明:如图在ΔABD 和ΔCAD 中,由正弦定理,得sin sin BD AB βα=,0sin sin(180)sin DC AC ACβαα==-,两式相除得BD ABDC AC = 三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比。
高考数学 二轮 专题六 三角函数与解三角形 第3讲 解三角形 理

专题六 三角函数与解三角形
3.辨明易错易混点 (1)利用正弦定理解三角形时,注意解的个数讨论,可能有一 解、两解或无解. (2)在判断三角形形状时,等式两边一般不要约去公因式,应 移项提取公因式,以免漏解.
栏目 导引
专题六 三角函数与解三角形
考点一 正、余弦定理的基本应用
(经典考题)已知锐角△ABC的内角A,B,C的对边分
专题六 三角函数与解三角形
栏目 导引
专题六 三角函数与解三角形
(3)由余弦定理得 b2+c2-bc=4,
配方得(b+c)2-3bc=4,③
∵b+c≥2 bc,④
将③代入④得
(b+
c)2≥
( 4×
b+
c)
2-
4,
3
解得 b+c≤4,当且仅当 b=c 时取等号,
又∵b+c>a=2,则 2<b+c≤4,
∴△ABC 的周长的范围为(4,6].
栏目 导引
专题六 三角函数与解三角形
2.在△ABC 中,角 A、B、C 所对的边分别为 a、b、c,已知 a =c.
3cos A sin C (1)求 A 的大小; (2)若 a=6,求 b+c 的取值范围. 解:(1)∵ a = c = a ,
3cos A sin C sin A
A. 3 2
C.1 2
B. 2 2
D.-1 2
解析:由余弦定理得
cos C=a2+b2-c2= c2 2ab 2ab
≥a2+c2 b2=2cc22=12.故选 C.
栏目 导引
专题六 三角函数与解三角形
栏目 导引
专题六 三角函数与解三角形
3.如图,在△ABC 中,D 是边 AC 上的点,且 AB=AD,2AB = 3BD,BC=2BD,则 sin C 的值为( D ) A. 3
解三角形题型分类讲解

解三角形知识点总结及题型分类讲解一、 知识点复习 1、正弦定理及其变形2(sin sin sin a b cR R A B C===为三角形外接圆半径)12sin ,2sin ,2sin a R A b R B c R C ===()(边化角公式)2sin ,sin ,sin 222a b cA B C R R R===()(角化边公式) 3::sin :sin :sin a b c A B C =() sin sin sin (4),,sin sin sin a A a A b Bb Bc C c C===2、正弦定理适用情况: (1)已知两角及任一边(2)已知两边和一边的对角(需要判断三角形解的情况) 已知a ,b 和A ,求B 时的解的情况:如果B A sin sin ≥,则B 有唯一解;如果1sin sin <<B A ,则B 有两解; 如果1sin =B ,则B 有唯一解;如果1sin >B ,则B 无解. 3、余弦定理及其推论2222222222cos 2cos 2cos a b c bc Ab ac ac B c a b ab C=+-=+-=+-222222222cos 2cos 2cos 2b c a A bc a c b B aca b c C ab+-=+-=+-=4、余弦定理适用情况:(1)已知两边及夹角;(2)已知三边. 5、常用的三角形面积公式(1)高底⨯⨯=∆21ABC S ; (2)B ca A bc C ab S ABC sin 21sin 21sin 21===∆(两边夹一角).6、三角形中常用结论(1),,(a b c b c a a c b +>+>+>即两边之和大于第三边,两边之差小于第三边); (2)sin sin (ABC A B a b A B ∆>⇔>⇔>在中,即大边对大角,大角对大边). (3)在△ABC 中,π=++C B A ,所以C B A sin )sin(=+;C B A cos )cos(-=+;C B A tan )tan(-=+.(4)2sin 2cos ,2cos 2sinCB AC B A =+=+. 二、典型例题题型1、计算问题(边角互换)例1、在ABC ∆中,若7:5:3sin :sin :sin =C B A ,则角C 的度数为 答案:=C 23π 例2、已知∆ABC 中,∠A 60=︒,3a =,则sin sin sin a b cA B C++++=.答案:2例3、在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2asinB=b .求角A 的大小; 答案:π3题型2、三角形解的个数例1.在△ABC 中,已知b=40,c=20,C=60。
重点突破:判断三角形解的个数问题

0
=
b sinB
,即 1 =
2
3
3 3 sinB
∴B=60°或 B=120°. 故选:C . 点睛:本题主要考查正弦定理解三角形,属于简单题.在解与三角形有关的问题时,正弦定理、余弦定理是两个
主要依据. 解三角形时, 有时可用正弦定理, 有时也可用余弦定理, 应注意用哪一个定理更方便、 简捷一般来说 , 当条件中同时出现 ab 及b2 、a2 时,往往用余弦定理,而题设中如果边和正弦、余弦函数交叉出现时,往往运 用正弦定理将边化为正弦函数再结合和、差、倍角的正余弦公式进行解答. 5.D 【解析】分析:利用正弦定理即可得出. 详解:由正弦定理可得:
5 1 , B 1500 符合两解。选 D. 9 2
bsinA 0 , A 中 sinB 1, B 90 , 1 解, 不符。 C 中 sinB 2 1 , a
【点睛】
在己知两边一对角的题型中,有钝角或直角最多一解,己知角所对边为大边,最多一解,其余情况根据三角形内 角和 180 ,大边对大角来判断。 4.C【解析】分析:利用正弦定理求出 sinB,得出 B,利用内角和定理进行检验. 详解:由正弦定理得 ∴sinB= .π 2π π源自)B.2π 3
C.
π 3
D.
π 4
2.已知 ABC 中, a A. 0 个 B. 1个
0
2, b 3, A 45 ,则三角形的解的个数(
D. 0 个或 1个
)
)
C. 2 个
3.在 ABC 中,利用正弦定理理解三角形时,其中有两解的选项是( A. a 3, b 6, A 30 B. a 6, b 5, A 150 D. a
三角形解的个数问题专题

解三角形专题2 【2 】三角形解的个数问题A 为锐角 A 为钝角或直角 图形关系 A<bsinAA=bsinA bsinA<a<b a ≥b a ≤b解的个数 无解 一解 两解 一解 无解1 已知下列三角形中的双方及个中一边的对角,断定三角形是否有解,并指出有几解?(1) 78105a ,b ,A ==∠= (2) 102080a ,b ,A ==∠=(3) 105660b ,c ,C ==∠=(4) 23630a ,b ,A ==∠=答案:(1) 90A ∠>而a b <,故无解(2) 90A ,a b sin A b ∠<<<,故有无解(3) c b >,故有一组解(4) 90A ,b sin A a b ∠<<<,故有两组解2在△ABC 中,A =45°,AB =3,则“BC=2”是“△ABC 只有一解且C =60°”的A .充分不必要前提B .必要不充分前提C .充要前提D .既为充分也不必要前提另解法法1:大角对大边在已知ABC ∆中的边长a ,b 和角A ,且已知a ,b 的大小关系,常运用正弦定理联合“大边对大角”来断定三角形解的个数,一般的做法如下,起首运用大边对大角,断定出角B 与角A 的大小关系,然后求出B 的值,依据三角函数的有界性求解.【例1】在ABC ∆中,已知a =b =45B =︒,求A .C 及c .解:由正弦定理,得sin sin a B A b ===,∵4590B =︒<︒,b a <,∴60A =︒或120︒. 当60A =︒时,75C =︒,sin 75sin sin 45b C c B ︒===︒;当120A =︒时,15C =︒,sin sin sin 452b C c B ︒===︒. 点评:在三角形中,sin sin a b A B A B >⇔>⇔>这是个隐含前提,在运用时我们要留意发掘. 法2:二次方程的正根个数一般地,在ABC ∆中的边长a ,b 和角A ,常常可对角A 运用余弦定理,并将其整顿为关于c 的一元二次方程2222cos 0c bc A b a -+-=,若该方程无解或只有负数解,则该三角形无解;若方程有一个正数解,则该三角形有一解;若方程有两个不等的正数解,则该三角形有两解. 【例2】如图,在四边形ABCD 中,已知AD CD ⊥,10AD =,14AB =, 60BDA ∠=︒,135BCD ∠=︒,求BC 的长.解:在ABD ∆中,设BD x =,由余弦定理得2221410210cos60x x =+-⋅︒, 整顿得210960x x --=,解得16x =.由正弦定理,得sin 16sin30sin sin135BD CDB BC BCD ∠︒===∠︒ A BCD点评:已知三角形双方和个中一边的对角,我们可以采用正弦定理或余弦定理求解,从上述例子可以看出,运用余弦定理联合二次方程来断定显得加倍简捷.法3:画圆法已知ABC ∆中,A 为已知角(90≠︒),先画出A ,肯定极点A ,再在A 的一边上肯定极点C ,使AC边长为已知长度,最后以极点C 为圆心,以CB 边长为半径画圆,看该圆与A 的另一边是否有交点,假如没有交点,则解释该三角形的解的个数为0;如有一个交点,则解释该三角形的解的个数为1;如有两个交点,则解释该三角形的解的个数为2.【例3】在ABC ∆中,60A ∠=︒,a =3b =,则ABC ∆解的情形()(A )无解(B )有一解(C )有两解(D )不能肯定解:在A 的一边上肯定极点C ,使3AC b ==,作60CAD ∠=︒, 以极点C 为圆心,认为CB a ==,看该圆与AD 没有交点,则解释该三角形的解的个数为0,故选A . A b C a D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修5-系列微课选题设计表
??44sinsin b?a,且B?sin44? 3 可为锐角也可为钝角,三角形有两解??B
:数形结合思想解析2.
:数形结合,右图所2解析第 3张PPT170秒以内
???122??24sin45CD?24sin44182解?24a?b24sin44??
若其他条件不变:
3.小结归纳:
a,b及角A,其三角形解的个数已知ΔABC的两边的判定方法如下:
b,然后再画角及角A的邻边A1.画示意图(先画角a,若A为锐角时,再画出垂线段CD,A对边其中︱CD︱bsin A)=
ababsin A的大小,从而边和邻边边和与比较2.第 4张PPT165秒以内判定三角形解的个数
?(1)当0<A<时,若a<b sin A,三角形无解2若a=b sin A,三角形1解若b sin A<a<b,三角形2解解三角形,?若ab 1
教学反思
?,若?ABC有两解,则45?x,b2,B?x的取值范围是( C )(2)?,ABC?中a A. (2,+?) B. (02C,). (2,22D). (2,2)。
