可靠性概率分布讲解
第二篇,可靠性概念和指标

e
其中,μ是随机 变量t的均值, σ是随机变量t的 标准离差。
tf t dt
1
2 2 t f t dt
注:1、一种常见的分布,它具有对称性;2、零件 的应力和强度、部件的寿命为正态分布。3、均值决 定正态分布的位臵,标准差决定正态曲线的形状。
《机械可靠性 设计》讲义
特征量:数学期望μ、方差σ2
1 1 b
2
2 2 1 1 1 b b
2
其中:
s
x
s 1
e
x
dx
0
《机械可靠性 设计》讲义
讨论:
1: b它是产品一致性的的一种度量,b越大离 散越小, b越小离散越大;
2:θ反映寿命与可靠度的关系; θ较小时可靠 度下降快。
3:b<1,可以描述零件早期失效分布;b>1 =1,此时λ(t)=1/ θ=常数,曲线呈指数 分布形状。 b>1, λ(t)的形状和零件的耗 损失效期的曲线形状相似。
《机械可靠性 设计》讲义
例:某重要零件,工作时承受对称循环应力 σ1=379N/mm2。根据试验知,该零件疲劳强度服从 威布尔分布,并测得形状参数β=2.65,最小应力 σmin=344.5N/mm2 ,尺度参数σ1a=531N/mm2 , 试计算该零件的可靠度。若可靠度时R=0.999, 其工作应力σ’-1为多少?
t
1 N R t t 时刻附近单位时间失效 t 时刻附近仍正常工作的 dN
Q
的产品数 产品数
t
f t R t
dt
《机械可靠性 设计》讲义
它反映某一时刻t残存的产品在其后紧接着的一个 单位时间内失效的产品数,对t时刻的残存的产品 数之比。它直观地反映了每一时刻的失效情况。
可靠性工程可靠性的概率统计知识培训课件

第2章 可靠性的概率统计知识
第2章 可靠性的概率统计知识
2.3.2 可信性 可信性是表示可用性及其影响因素。可靠
性、维修性、维修保障性的非定量综合描 述。 R.M.S综合反映
2.4 概率知识 随机事件、概率、事件关系及运算、概率运 算(加法、乘法、条件、全概、逆概Bayes)
第2章 可靠性的概率统计知识
第2章 可靠性的概率统计知识
2.1 可靠性基本概念和特征量
2.1.1 故障及其分类 条件、时间容易理解 功能→故障 产品或其一部分不能本将不完成预定的功能的事件
或状态称为故障。 对于不可修的产品也称失效。 故障——表现形式——故障模式 物理、化学变化的原因——机理
第2章 可靠性的概率统计知识
第2章 可靠性的概率统计知识
故障率、可靠度及故障密度函数的关系 四个函数之间的关系: R(t) F(t) f(t) λ( t ) 表2.1
第2章 可靠性的概率统计知识
2.1.5 平均寿命
概率含义——数学期望 统计含义——样本均值
μ= ∫ t f(t) dt = ∫ R(t) dt 平均故障前时间(MTTF)
R(t) =exp (-∫λ(t) dt ) λ(t)= λ0 —— 指数分布
第2章 可靠性的概率统计知识
浴盆曲线Leabharlann 第2章 可靠性的概率统计知识
①早期故障阶段 机械:跑合期(磨合期)、设计缺陷、 加工缺陷、安装缺陷 ②偶然:偶然因素,操作、负荷 ③耗损:老化、疲劳、磨损、腐蚀。可 通过维修、更换
第2章 可靠性的概率统计知识
2.5 随机变量的概率分布和数字特征 离散、连续随机变量 累计分布函数、分布密度函数 数字特征:期望、方差、矩(原点、中心)、
可靠性中常用的概率分布

(3-4)
指数分布的累积分布函数
F(x)=1-e-x
(3-5)
——若产品在一定时间区间内的失效数服从泊松分布,则该产品的 寿命服从指数分布。
3.5 正态分布
正态分布密度函数定义为:
f (x)
1
2
exp
1 2
x
2, x来自其中: -均值, -标准差。
(3-6)
标准正态分布
例如,对于图(下左)中所示的两种分布形式(一种为 Weibull分布,另一种为正态分布),虽然它们的概率密度 函数曲线差别很小,但其累积分布函数(反映可靠性特征) 在小概率区域的差别却十分显著,如图(下右)所示。
Probability density function
Probability
0.35
当 (t) 为常数时,满足上述条件的计数过程 {N (t),t 0} 为
时齐泊松随机过程。
泊松随机过程的概率密度分布
(t) 0.5 h 1
P(m, t )
n
t/h
3.4 指数分布
指数分布的定义
指数分布的密度函数为
e x
f (x) 0
式中为常数,是指数分布的失效率。
(x 0; 0)
(3-3)
P{X k} Cnk pk (1 p)nk
(k 0,1,2,..., n)
泊松过程
泊松随机过程作为一种重要的计数过程, 可以很好地用于描述“顾客流”、“粒子流” 、“信号流”等事件的概率特性。
设 {N(t),t 0} 为一计数过程,且满足以下条件: (1) N(0)=0; (2) {N (t),t 0} 是一个独立增量过程,即任取 0 t1 t2 tm
失效率函数
可靠性中常用的概率分布
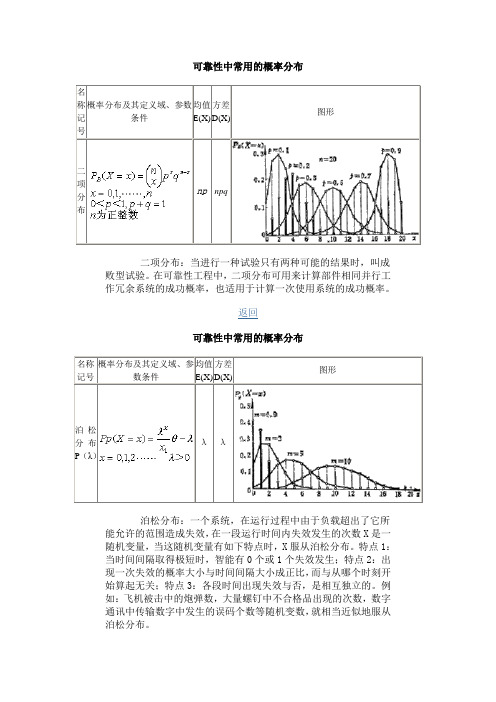
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形二项分布np npq二项分布:当进行一种试验只有两种可能的结果时,叫成败型试验。
在可靠性工程中,二项分布可用来计算部件相同并行工作冗余系统的成功概率,也适用于计算一次使用系统的成功概率。
返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形泊松分布P(λ)λλ泊松分布:一个系统,在运行过程中由于负载超出了它所能允许的范围造成失效,在一段运行时间内失效发生的次数X是一随机变量,当这随机变量有如下特点时,X服从泊松分布。
特点1:当时间间隔取得极短时,智能有0个或1个失效发生;特点2:出现一次失效的概率大小与时间间隔大小成正比,而与从哪个时刻开始算起无关;特点3:各段时间出现失效与否,是相互独立的。
例如:飞机被击中的炮弹数,大量螺钉中不合格品出现的次数,数字通讯中传输数字中发生的误码个数等随机变数,就相当近似地服从泊松分布。
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形超几何分布H(n,M,N)返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形指数分布e(λ)指数分布:许多电子产品的寿命分布一般服从指数分布。
有的系统的寿命分布也可用指数分布来近似。
它在可靠性研究中是最常用的一种分布形式。
指数分布是伽玛分布和威布尔分布的特殊情况,产品的失效是偶然失效时,其寿命服从指数分布。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形威布尔分布(Ⅲ型极值分布)W(k,a,b)威布尔分布:在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式。
由于它可以利用概率纸很容易地推断出它的分布参数,被广泛应用与各种寿命试验的数据处理。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形正态分布(高斯分布)N(μ,σ)μσ2正态分布:是在机械产品和结构工程中,研究应力分布和强度分布时,最常用的一种分布形式。
第3章 可靠性分布函数

6
车辆可靠性设计
第三章 可靠性常用分布函数
三、指数分布 e()
指数分布在质量可靠性工程中常用来描述产品在正常 运转期间的寿命。
密度函数 f (t ) e t
不可靠度函数 F(t) 1 et
可靠度函数 R(t) et
失效率函数 (t) f (t) / R(t)
平均寿命 寿命方差
E(T ) 1
14
车辆可靠性设计
第三章 可靠性常用分布函数
例6(教材例3-5):有100个某种材料的试件进行抗拉强 度试验,现测得试件材料的强度呈正态分布,均值 μ=600MPa ,标准差 σ=50MPa。求:(1)试件强度 =600MPa时的存活率、失效概率和失效试件数;(2)强 度落在(550~450)MPa 区间内的失效概率和失效试件数; (3)失效概率为 0.05时材料的强度值。
2
1)特征:
① 曲线关于x 对称。
x
1
② 在均值x 处有最大值,其值为 2 。
③ 标准差σ越小,曲线 f (x)的峰值越高,因而 X落在μ附近的概率越大。
10
车辆可靠性设计
第三章 可靠性常用分布函数
2)标准正态分布故障密度函数
0 , 1 的正态分布称为标准正态分布
(x)
1
x2
e2
D(T ) 2 1 2
可靠寿命
11
TR
ln R
特征寿命 T (e1) 1
7
车辆可靠性设计
第三章 可靠性常用分布函数
例3:某仪器的寿命T服从指数分布,其平均无故障连 续工 作时间MTBF为25h,试求其失效率为多少?若 要求 可靠性为90%,问应如何选择连续工作时间?
解:失效率为:
可靠性计算

可靠性计算一、概率与统计1、概率;这里用道题来说明这个数学问题(用WORD把这些烦琐的公式打出来太麻烦了,因为公司不重视品质管理,所以部门连个文员MM都没有,最后我只好使用CORELDRAW做的公式粘贴过来,如果你的电脑系统比较慢,需要耐心等待一会公式才会显示来,不过别着急,好东西往往是最后才出来的嘛!)。
题一、从含有D个不良品的N个产品中随机取出n个产品(做不放回抽样),求取出d个不良品的概率是多少?解:典型的超几何分布例题,计算公式如下(不要烦人的问我为什么是这样的公式计算,我虽然理解了一些,解释起来非常麻烦,别怪我不够意思,是你自己上学的时候只顾早恋,没有学习造成的,骂自己吧!):超几何分布:(最基本的了):最精确的计算,适用比较小的数据其中:N ——产品批量D ——N中的不合格数d ——n中的合格数n ——抽样数另外的概率计算的常用算法还有:二项分布:(最常用的了,是超几何分布的极限形式。
用于具备计件值特征的质量分布研究):只是估算,当N≥10n后才比较准确其中:n ——样本大小 d ——n中的不合格数ρ——产品不合格率泊松分布:(电子产品的使用还没有使用过,只是在学习的时候玩过一些题目,我也使用没有经验)具有计点计算特征的质量特性值其中:λ——n ρn ——样本的大小ρ——单位不合格率(缺陷率) e = 2.7182812、分布;各种随机情况,常见的分布有:二项分布、正态分布、泊松分布等,分位数的意义和用法也需要掌握;较典型的题目为:题三、要求电阻器的值为80+/-4欧姆;从某次生产中随机抽样发现:电阻器的阻值服从正态分布,其均值80.8欧姆、标准差1.3欧姆,求此次生产中不合格品率。
公式好麻烦的,而且还要查表计算,555555555555,我懒得写了,反正我也没有做过电阻。
3、置信区间:我们根据取得样品的参数计算出产品相应的参数,这个“计算值”到底跟产品的“真实值”有什么关系?一般这样去描述这两个量:把“计算值”扩充成“计算区间”、然后描述“真实值有多大的可能会落在这个计算区间里”,从统计学上看,就是“估计参数”的“置信区间”;较典型的题目为:题四、设某物理量服从正态分布,从中取出四个量,测量/计算后求得四个量的平均值为8.34,四个量的标准差为0.03;求平均值在95%的置信区间。
可靠性讲稿(2.2可靠性的基本公式)

随机变量 X 服从对数正态分布
1 1 ln x − µ f ( x) = exp(− ) 2 σ σ x 2π 其中ln x ~ N ( µ , σ 2 )
1 2 E ( X ) exp( µ + σ ) = 2 D( X ) = [exp(2µ + σ 2 )][exp(σ 2 ) − 1]
可靠度: Pr 失效概率: Pf 且: Pr + Pf = 1
Xiukai Yuan
• 结构可靠度(reliability)的普遍表达式
两类基本变量:强度变量,应力变量 与强度相关的基本变量:结构尺寸,表面粗糙 度,材料的性质,划痕,裂纹等。
R = R( xR1 , xR2 ,..., xRi )
∞
µln Z x2 1 Pr = Φ Φ(β ) exp(− )dx = µln Z = ∫−σ 2 2π σ ln Z ln Z
β =
µ 1 + V 2 1/ 2 S ln R 2 µ S 1 + VR µln R − µln S = 2 2 1/ 2 2 2 [ln(1 V ) ln(1 V + + + σ ln R + σ ln S R S )]
S0
(3)应力处在 dS 小区间内由干 涉引起的可靠概率(R和S独立):
f s ( S0 ) dS ∫ f R ( R ) dR
S0 ∞
Xiukai Yuan
(4)对应力的所有可能值,强度大于应力的概率,即
Pr = P ( R > S ) =
∫
∞
−∞
f s ( S )dS ∫ f R ( R )dR
可靠性基本概念

可靠性设计主要符号表可靠性的概念可靠性的经典定义:产品在规定条件下和规定时间内,完成规定功能的能力产品:指作为单独研究和分别试验对象的任何元件、设备或系统,可以是零件、部件,也可以是由它们装配而成的机器,或由许多机器组成的机组和成套设备,甚至还把人的作用也包括在内。
在具体使用“产品”这一词时,其确切含义应加以说明。
例如汽车板簧、汽车发动机、汽车整车等。
规定条件:一般指的是使用条件,环境条件。
包括应力温度、湿度、尘砂、腐蚀等,也包括操作技术、维修方法等条件。
规定时间:是可靠性区别于产品其他质量属性的重要特征,一般也可认为可靠性是产品功能在时间上的稳定程度。
因此以数学形式表示的可靠性各特征量都是时间的函数。
这里的时间概念不限于一般的年、月、日、分、秒,也可以是与时间成比例的次数、距离。
例如应力循环次数、汽车行驶里程。
规定功能:道德要明确具体产品的功能是什么,怎样才算是完成规定功能。
产品丧失规定功能称为失效,对可修复产品通常也称为故障。
怎样才算是失效或故障,有时很容易判定,但更多情况则很难判定。
当产品指的是某个螺丛,显然螺栓断裂就是失效;当产品指的是某个设备,对某个零件损坏而该设备仍能完成规定功能就不能算失效或故障,有时虽有某些零件损坏或松脱,但在规定的短时间内可容易地修复也可不算是失效或故障。
若产品指的是某个具有性能指标要求的机器,当性能下降到规定的指标后,虽然仍能继续运转,但已应算是失效或故障。
究竟怎样算是失效或故障,有时要涉及厂商与用户不同看法的协商,有时要涉及当时的技术水平和经济政策等而作出合理的规定。
能力:只是定性的理解是比较抽象的,为了衡量检验,后面将加以定量描述。
产品的失效或故障均具有偶然性,一个产品在某段时间内的工作情况并不很好地反映该产品可靠性的高低,而应该观察大量该种产品的工作情况并进行合理的处理后才能正确的反映该产品的可靠性,因此对能力的定量需用概率和数理统计的方法。
按产品可靠性的形成,可靠性可分为固有可靠性和使用可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于可靠性分布函数及其工程应用的讨论学号:*********姓名:***目录一、引言 (3)二、分布函数及其应用的讨论 (3)(一)、指数分布 (3)1.定义: (3)2.指数分布的可靠度与不可靠度函数 (4)3.图像分析 (4)4.应用 (5)(二)、正态分布 (6)1.定义: (6)2.正态分布的可靠度与不可靠度函数 (6)3.失效率函数 (6)4.图像分析 (7)5.应用 (8)(三)、对数正态分布 (9)1.定义: (9)2.对数正态分布的可靠度与不可靠度函数 (9)3.对数正态分布失效率 (9)4.图像分析 (9)5应用 (11)(四)、威布尔分布 (12)1.三参数威布尔分布的定义: (12)2.可靠度与不可靠度函数 (12)3.威布尔分布失效率 (12)4.图像分析 (12)5.应用 (15)三、小结 (16)参考文献 (17)附录 (18)一、引言可靠性是指产品在规定的条件下,规定时间内,完成规定功能的能力,是对产品无故障工作能力的度量。
可靠性作为衡量产品质量的一个重要的指标,已广泛的应用于各个工程领域。
与可靠性相反,产品丧失规定功能称为失效或故障。
工程机械系统是由零件和部件组成的,零件或部件的失效会导致系统的失效。
然而,失效的原因是多种多样的,如结构缺陷、工艺缺陷、使用不当、老化等等。
引起每种失效的原因也可能是不同的,如性能退化可能由于疲劳、蠕变、裂纹扩展、磨损或者腐蚀等导致的[1]。
实践表明,系统或零、部件的失效时间往往是不确定的,要定量描述系统或零、部件的失效时间,应当采用统计学方法。
将失效时间作为一个随机变量,用一个恰当的概率分布函数去描述它。
从数据的统计分析中找出产品寿命分布的规律,是进一步分析产品故障,预测故障发展,研究其失效机理及制定维修策略的重要手段。
可靠性分析与评估是可靠性分析中非常重要的一部分,它是指在产品的寿命周期内,根据产品的可靠性分布模型、结构,以及相关的可靠性信息,利用统计方法,对产品的可靠性指标做出估计的过程。
科学的可靠性评估方法不仅可以减少试验经费,提高分析结果的准确性,而且缩短了研制周期,成为现代工业生产所必须的工具。
在可靠性分析和评估中,对产品的寿命等数据的分散度进行的研究表明,其分散的形态,大多可用几种典型的分布模型来近似的模拟。
下面就针对指数分布、正态分布、对数正态分布、威布尔分布分析说明其中的参数对其分布函数形状、位置等的影响及它们在工程分析中的应用。
二、分布函数及其应用的讨论(一)、指数分布指数分布是由失效率为常量这一假设得出的,是可靠性理论中最基本、最常用的分布模型之一。
1、定义:若t 的概率密度函数为f (t )= ⎩⎨⎧<>≥-)0(0);0(t t e tλλλ (1.1)则称其服从参数为λ的指数分布,其中λ为常数,是指数分布的失效率。
2、指数分布的可靠度与不可靠度函数指数分布不可靠度为F (t )=⎰tdt t f )(=1-t-eλ t ≥0;λ>0 (1.2)可靠度为R (t )=1-F (t )=t-eλ t ≥0;λ>0 (1.3)3、图像分析(1)下图为指数分布概率密度函数图像图1-1 指数分布失效密度函数由图1-1可以看出失效概率密度均为下降趋势,为严格减函数,并且当t →0时f (t )→0。
另外,失效率对失效概率密度函数的影响:失效率越大,则起始时刻f (t )越大,且f (t )下降越快,这与实际直观认识是一致的。
(2)下图是指数分布不可靠度与可靠度函数图像从图中可以看到,失效率越底,不可靠度上升越慢(即可靠度下降越慢)。
若下降到到同一可靠度,失效率越低,所需时间越长,即零件工作时间越长,这和实际经验也是相一致的。
图1-2 指数分布可靠度与不可靠度变化曲线4、应用(1)原理指数分布是可靠性理论中最基本、最常用的一种分布,它最显著的特征是失效率等于常数。
正是因为此特点,它更适合描述许多产品在偶然失效期的有用寿命分布。
指数分布产生原理是无累积效应失效。
在工程实践中,大多数产品无累积效应的失效,基本可以认为其服从指数分布,多数电子产品的失效以及突发重大事故即属于此类。
指数分布的一个重要性质是无记忆性,即如果一产品寿命服从指数分布,则工作一段时间后若仍然正常,则它仍然和新的一样,再工作t时间的概率和已经工作过的时间长短无关,偶联系,又称为“无后效性”。
(2)工程应用在电子产品可靠性理论中,指数分布是最基本、最常用的分布,适用于失效率为常数的情况(当产品进入偶然失效期间,其失效率近似等于常数)。
由于大部分电子产品的使用寿命服从或近似服从指数分布,因此,可用指数分布描述其寿命分布。
指数分布作为可靠性工作中非常重要的一种分布,还经常用于描述由大量元器件组成的复杂系统寿命分布(如复杂的航空电子设备可靠性分析),分析元器件的筛选、老化, 系统的冗余设计等,在高可靠性的复杂部件、机器或系统的失效分布模型,特别是在部件或机器的整机试验中也有广泛应用。
但最主要的还是在电子元器件的可靠性研究中价值,通常用于描述对发生的缺陷数或系统故障数的测量结果[2]。
在日本的工业标准和美国军用标准中,半导体器件的抽验方案都是采用指数分布。
此外,指数分布还用来描述大型复杂系统(如计算机)的平均故障间隔时间MTBF的失效分布。
不仅如此,指数分布也可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔等。
(3)局限性但是,由于指数分布具有缺乏“记忆”的特性.因而限制了它在机械可靠性研究中的应用,指数分布的这种特性,与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的,它违背了产品损伤累积和老化这一过程。
所以,指数分布不能作为机械零件功能参数的分布形式。
再者,由于指数分布失效率为常数,对于失效率变化的情况,不能做到有效的模拟(浴盆曲线前后两个时期),这一点的限制了其在工程领域可的应用范围。
(二)、正态分布正态分布又称为“高斯分布”,是由高斯首先提出并应用的。
作为一种经典的概率分布模型,有着极其广泛的应用。
1、定义:若t 的概率密度函数为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛=2-t 21-ex p 21t f σμπσ)( +∞<<∞t - (2.1)则称其服从参数为μ和σ2的正态分布。
式中,σ和μ为两个参数,σ称为标准差;μ称为均值。
其中,μ反映了t 的分布的平均水平,而σ反映了分布的集中程度。
2、正态分布的可靠度与不可靠度函数 正态分布不可靠度为F (t )=dt -t 21-ex p 21t-2⎰∞⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσ (2.2)可靠度为R (t )=1-F (t )=dt -t 21-ex p 21t2⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσ (2.3)3、失效率函数 正态分布失效率为λ(t )=)()(t R t f =dt -t 21-exp 21-t 21-exp 21t 22⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσσμπσ (2.4)4、图像分析(1)图2-1为正态分布失效概率密度函数曲线图2-1 正态分布σ和μ对失效概率密度函数曲线的影响从图2-1中可以看到:①. 曲线关于x=μ对称,μ值大小影响曲线左右位置,即改变的值使曲线在水平方向上作平移;②. 当t=μ时取得最大值,且t离μ越远,函数值越小,在左右无穷远处,概率密度函数值趋于0;③. σ值影响曲线形状。
σ值越小,即标准差越小,图形变得越尖,分布越集中。
(2)下图为正态分布不可靠度和可靠度变化曲线(左边为可靠度,右边为不可靠度)图2-2 正态分布可靠度与不可靠度曲线从图2-2中可以看出均值若较小,可靠度会在t较小时开始显著降低(相应的不可靠度在t较小时开始显著上升);而标准差较小使可靠度下降变晚(相应的不可靠度上升变晚),但达到一定时间会快速下降,迅速趋近于0,而后稳定,相反,标准差较大者,使可靠度始终保持一个较稳定的速度平稳下降,逐渐趋于0。
(3)失效率下图为正态分布失效率曲线图2-3 正态分布失效率曲线可以看出,失效率总体趋势为先上升,后下降,最终接近0。
均值越大,失效率曲线相对向右移动,峰值出现晚,峰值提高;标准差对曲线没有左右位置影响,即出现峰值位置不变,而是只改变峰值大小,标准差越小,峰值越高。
5、应用(1)原理正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线。
正态分布是应用较广泛的分布之一,其失效机理是:多微因合成, 没有主导因素。
即它是由大量相互独立,微小的随机因素的总和构成的,且每一个随机因素对总和的影响是均匀微小的,即可认为此随机变量服从正态分布[3]。
(2)工程应用正态分布适用于有基本均匀的累积效应的情况。
也就是说, 由累积耗损所造成的故障,如腐蚀、磨损、表面破坏及器件老化等,一般认为其寿命服从正态分布。
正态分布广泛应用于各个领域,其中一个重要应用就是质量控制,即为了控制实验中的测量(或实验)误差,常以标准差的倍数作为上、下警戒值和控制值,其依据是:正常情况下测量(或实验)误差服从正态分布[4]。
在航空维修可靠性上,正态分布主要用于分析由于磨损而发生失效的附件,因为耗损失效分布往往接近正态分布。
另外,寿命数据符合正态分布的产品,通常时间特性比较明显,在使用到某个特定的时间后性能衰退较快,因而可以据此制定合理的维修计划。
正态分布的另一种重要作用是对制造的产品质量及其性能是否符合规范进行分析。
(三)、对数正态分布若一个随机变量的对数服从正态分布,则称其服从对数正态分布,它是一种偏正态分布,是正态分布的一种改进,在某些领域有重要应用价值。
1、定义:若t 的概率密度函数为f (t )=⎪⎩⎪⎨⎧≤+∞<<-∞>>⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛0x 0;0;0x -ln t 21-ex p 2t 12μσσμπσ (3.1)则称其服从对数正态分布。
式中μ称为对数均值;σ称为对数标准差。
2.对数正态分布的可靠度与不可靠度函数 不可靠度F (t )=dt -ln t 21-ex p 2t 1t2⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσ (3.2)可靠度R (t )=1-F (t )=dt -ln t 21-exp 2t 1t2⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσ (3.3) 3.对数正态分布失效率λ(t )=)()(t R t f =dt -ln t 21-exp 2t 1-ln t 21-exp 2t 1t 22⎰∞+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σμπσσμπσ (3.4)4.图像分析(1)下图为对数正态分布失效概率密度函数图像图3-1 对数正态分布失效概率密度函数从图3-1中可以看出函数图像呈现单峰性,且为偏锋,峰值向t较小一侧偏移。
