多元函数求导
多元函数的求导法则-精选

z z u z v y u y v y
x yx y
eusinvx eucovs1
e x y [x six n y ) (co x y s )( ]
山东农业大学
高等数学
主讲人: 苏本堂
例2. u f(x ,y ,z ) e x 2 y 2 z 2 ,z x 2 sy i,求nu , u x y
山东农业大学
高等数学
主讲人: 苏本堂
推广: 设下面所涉及的函数都可微 .
1) 中间变量多于两个的情形. 例如, zf(u,v,w ),
u ( t ) ,v ( t ) ,w ( t )
z
d z z du z dv z dw d t u d t v dt w dt
在点 t 可导, 且有链式法则 dzzduzdv dt u dt v dt
z
uv
证: 设 t 取增量△t , 则相应中间变量 t t
有增量△u ,△v ,
zzuzvo() (( u)2( v)2)
u vΒιβλιοθήκη 山东农业大学高等数学
主讲人: 苏本堂
zzuzv o ( ) (( u)2( v)2)
山东农业大学
高等数学
主讲人: 苏本堂
第四节多元复合函数的求导法则
一、多元复合函数求导的链式法则 二、多元复合函数的全微分
山东农业大学
高等数学
主讲人: 苏本堂
一、多元复合函数求导的链式法则
定理. 若函数 u (t),v (t)在 t可 点 ,z导 f(u,v) 在点 (u,v)处偏导连续, 则复合函数 zf((t) ,(t))
e xy[x six ny ) (co x y s )]d(y 所以 zexy[ysixn y()co x sy)(]
多元函数的隐函数与参数方程求导

多元函数的隐函数与参数方程求导隐函数求导是微积分中常用的求导方法之一,它用于求解含有多个未知变量的方程。
而参数方程则是将一个变量表示为另外两个变量的函数,通常用于描述曲线或曲面。
一、多元函数的隐函数求导对于一个含有多个未知变量的方程,如果我们无法将其中一个变量表达为其他变量的函数形式,就需要使用隐函数求导的方法。
以二维平面上的函数为例,假设有一个方程 f(x, y) = 0,我们想要求解关于y 的导数dy/dx。
首先,我们需要确保该方程存在一个解y=f(x)。
求解步骤如下:1. 对方程两边同时对 x 求导,得到:∂f/∂x + ∂f/∂y * dy/dx = 02. 将这个方程关于 dy/dx 进行变形,得到 dy/dx 的表达式:dy/dx = - (∂f/∂x) / (∂f/∂y)这样,我们就得到了多元函数隐函数的导数表达式。
二、多元函数的参数方程求导参数方程是将一个变量(通常为 t)表示为另外两个变量(通常为 x 和 y)的函数形式。
在参数方程中,我们可以通过对 t 的求导来求解 x和 y 的导数。
以二维平面上的函数为例,假设有一个由参数方程描述的曲线:x = f(t)y = g(t)我们要求解这条曲线上各个点的导数 dy/dx。
求解步骤如下:1. 先对 x 和 y 分别关于 t 求导,得到导数 dx/dt 和 dy/dt。
2. 计算 dy/dx:dy/dx = (dy/dt) / (dx/dt)这样,我们也可以得到多元函数参数方程的导数表达式。
综上所述,多元函数的隐函数和参数方程求导的步骤和原理是类似的,只是需要根据具体的函数形式进行求解。
总结:多元函数的隐函数求导和参数方程求导是微积分中常用的求导方法。
对于隐函数求导,需要通过对方程两边同时对某个变量求导,并变形后得到导数表达式。
而对于参数方程求导,需要分别对 x 和 y 关于参数求导,并计算 dy/dx 的表达式。
这两种方法在解决多元函数的导数问题时非常有用,能够帮助我们更好地理解函数的性质和变化趋势。
4多元函数求导法则

一、多元复合函数求导法则
二、小结 思考题
一、多元复合函数的求导法则
在一元函数微分学中,复合函数的求导法则 起着重要的作用.
现在我们把它推广到多元复合函数的情形.
下面按照多元复合函数不同的复合情形, 分三种情况进行讨论.
1.复合函数的中间变量均为一元函数的情形
定理 1 如果函数u (t ) 及 v (t ) 都在点 t 可 导,函数 z f ( u, v ) 在对应点( u, v ) 具有连续偏导 数, 则复合函数 z f [ ( t ), ( t )]在对应点 t 可导, 且其导数可用下列公式计算:
sin t 2 t 3
z z 二、设 z ue ,而u x y , v xy ,求 , . x y
v u
dz ,则 ________________. dt
2 2
三、设 z arctan( xy) ,而 y e
x
dz ,求 . dx
四、设 z f ( x 2 y 2 , e xy ), (其中f具 有一阶连续偏导
全微分形式不变性
z z dz du dv ;当 u ( x , y ) 、v ( x , y ) u v z z 时,有dz dx dy . x y
设函数 z f ( u, v )具有连续偏导数, 则有全微分
全微分形式不变性的实质:
无论 z是自变量 u、v的函数或中间变量 u、v 的函数,它的全微分形式是一样的.
z z du dv . u v
例 4 已知e
xy
z z 2 z e 0 ,求 和 . x y
z
解
d(e
xy
多元复合函数的求导法则

上式两端同时除以△t ,得到
.
3
z f u f v o( ) ( (u)2 (v)2 )
t u t v t t 令 t 0, 则有u 0, v 0,
z
u du , v dv
uv
t dt t dt
o ( ) o( ) (u)2 ( v)2 0 t t
t
t
u xyz xt
u f f f
z
dt u dt v dt t
v e t u sin t cos t
uvt
e t (cost sin t) cos t
tt
注意:多元抽象复合函数求导在偏微分方程变形与 验证解的问题中经常遇到, 下列几个例题有助于掌握 这方面问题的求导技巧与常用导数符号.
求导口诀 : 分段用乘, 分叉用加.
在对应点(u, v)可微, 则复合函数 z f ( (t), (t))
在点 t 可导, 且有链法则(见右边的树图)
dz f du f dv dt u dt v dt 证: 设 △t 为t 的增量, 则相应中间变量
z
uv
有增量△u ,△v , 由于 f 可微,所以
tt
z f u f v o ( ) ( (u)2 (v)2 )
d t 2 u dt v dt
.
5
定理2. 设 z f (u,v) 在对应点可微
u(x,y), v(x,y)偏导数都存在,
则
z z u z v
x u x v x
z
uv x yx y
z z u z v y u y v y 推广: 设下面所涉及的函数都可微 . 1) 中间变量多于两个的情形. 例如,
注意防止记号的混淆.
.
高等数学 第四节 多元复合函数的求导法则

11
例 4 . 已知 e
−xy
∂z ∂z − 2z + e = 0 , 求 . 和 ∂x ∂y
z
解 . Q d (e − x y − 2 z + e z ) = 0 , ∴ e − x y d (− x y ) − 2 d z + e z d z = 0 ,
− e − xy ( x d y + y d x) = ( 2 − e z ) dz
dz=
− y e−xy (2−e )
z
dx+
− x e−xy (2−e )
z
dy
∴
∂ z y e−xy = z , ∂x e −2
∂ z x e−xy = z . ∂y e −2
12
复合函数的高阶偏导数
∂2z 2 2 2 例5 . 设 z = f ( x y , x − y ) , f ∈ C , 求 . ∂x∂y
= f x ⋅ x ′( t ) + f y ⋅ y ′( t ) + 0 ⋅ x ′ 2 + y ′ 2
即
du = f x ⋅ x′(t ) + f y ⋅ y′(t ) . dt
2
x = x (t ) 推广 . 对于 u = f ( x , y , z ) , y = y ( t ) , z = z (t ) f 可微, x(t ) , y(t ) , z(t ) 可导.
∂z ∂z 求 , . ∂x ∂y ∂z ′ 解. = f1′ ⋅ u x + f 2 ∂x
9.4 多元复合函数求导法则(新)
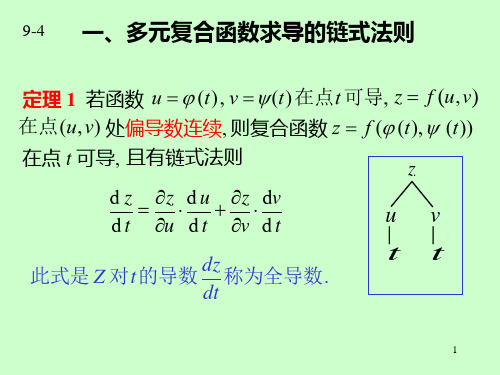
∂z 2 x = e cos y + ∂x x
∂z 1 x = −e sin y + ∂y y
18
z = f (u, v) =
u2v 2 2 , u +v ≠ 0 2 2 u +v
u =t , v =t
t 但,z = f (t, t ) = 2
dz 1 = dt 2
0,
u2 +v2 = 0
∂z du ∂z dv ≠ ∂u ⋅ dt + ∂v ⋅ dt = 0⋅1+ 0⋅1 = 0
2
常用导数符号
∂z = fv (u, v) = fv = f2′ ∂v ∂2 z ′′ = fvv (u, v) = fvv = f22 2 ∂v
称为混合偏导数
′′ ′′ ′′ ′′ 当 f12 和 f21 均连续时有 f12 = f21
3
推广: 推广 设下面所涉及的函数都可微 . 1、中间变量多于两个的情形 、中间变量多于两个的情形.
8
例 3.
u = f (x, y, z) = e
x2 + y2 +z2
, z = x sin y, 已知
2
∂u ∂u , . 可微,求 ∂x ∂ y
u
x y z
∂u ∂ f = 解: ∂x ∂x
x y
2 2 x2 + y2 +x4 sin 2 y
= 2 x (1+ 2 x sin y) e
∂u ∂ f ∂ f ∂z = + ⋅ ∂y ∂y ∂z ∂y
x
y x
y
5
z = eu sin v, u = xy , v = x + y , 求 例2. 设
多元复合函数求导法则和隐函数求导公式

z
= e [ y ⋅ sin( x + y ) + cos( x + y )]
xy
u x yx
v y
∂ z ∂ z ∂u ∂ z ∂v = ⋅ + ⋅ ∂ y ∂u ∂ y ∂v ∂ y = e u sin v ⋅ x + e u cos v ⋅1 = e [ x ⋅ sin( x + y ) + cos( x + y )]
4
x 2 + y 2 + x 4 sin 2 y
dz . 例3. 设 z = u v + sin t , u = e , v = cos t , 求全导数 dt d z ∂ z du ∂ z dv ∂ z + = ⋅ + ⋅ 解: z d t ∂u d t ∂v dt ∂t
t
= v e t− u sin t + cos t = e t (cos t − sin t ) + cos t
u
x y z
= 2 x (1 + 2 x sin y ) e
2
x 2 + y 2 + x 4 sin 2 y
∂u ∂ f ∂ f ∂ z + ⋅ = ∂ y ∂ y ∂z ∂ y
x
cos y
y
= 2 ye
x2 + y2 + z 2
+2 z e
x2 + y2 + z 2⋅ x 2
= 2 ( y + x sin y cos y ) e
多元复合函数的求导法则
一元复合函数
y = f (u ), u = ϕ ( x)
dy dy d u 求导法则 = ⋅ dx du dx 微分法则 d y = f ′(u ) d u= f ′(u ) ϕ ′ ( x) d x
多元函数 矩阵 求导

多元函数矩阵求导
多元函数的矩阵求导是微积分中的一个重要内容,它涉及到矩
阵的偏导数和梯度等概念。
首先,我们来看多元函数的梯度。
对于
一个多元函数,如果其自变量是一个n维向量,因变量是一个标量,那么这个函数的梯度就是一个n维向量,其中每个分量分别是函数
对自变量的偏导数。
假设有一个多元函数f(x1, x2, ..., xn),那
么它的梯度可以表示为∇f = [∂f/∂x1, ∂f/∂x2, ...,
∂f/∂xn]。
这里∂f/∂xi表示函数f对自变量xi的偏导数。
接下来我们来看矩阵的求导。
对于一个矩阵函数F(X),其中X
是一个矩阵,我们可以对其进行求导。
如果F(X)的每个元素都是关
于X的函数,那么F(X)的导数就是一个与X同型的矩阵,其中每个
元素是对应元素的偏导数。
具体来说,如果F(X)是一个m×n的矩
阵函数,那么它的导数就是一个m×n的矩阵,其中第i行第j列的
元素是∂Fij/∂Xkl,其中k是第i行,l是第j列。
在实际应用中,多元函数的矩阵求导常常用于优化问题、机器
学习和深度学习等领域。
通过对多元函数的梯度和矩阵的导数进行
求解和分析,可以帮助我们理解函数的变化规律,并且为优化算法
的设计提供重要的数学基础。
在深度学习中,梯度下降法等优化算
法的实现也离不开对多元函数的矩阵求导。
总之,多元函数的矩阵求导是一项重要且复杂的数学工作,它在实际问题中有着广泛的应用,并且对于理解和解决实际问题具有重要意义。
希望我的回答能够帮助你更好地理解这一内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z 求 y x
x 1 1 z 1 ′′ ′′ ′′ ′′ = f1′ + x[ y f11 + f12] 2 f2′ 2 [ yf 21 + f 22 ] y y y y yx 1 y 2 g′ 3 g′′ x x
2
1 y 1 x ′′ ′′ = f1′ + x y f11 2 f2′ 3 f22 2 g′ 3 g′′ x x y y
第三节 多元复合函数的求导法则
一元复合函数 y = f (u), u = (x) 求导法则 微分法则
d y d= f ′(u) du= f ′(u)′ (x) dx
推广
(1)多元复合函数求导的链式法则 ) (2)多元复合函数的全微分 )
1
可导, 可导 且有链式法则 z = f (φ (t), ψ (t)) 在点 t d z z du z d v = + dt u dt v dt
x2 + y2 +z2
x y
+2ze
x2 + y2 +z2 x2 cos y x2 + y2 +x4 sin2 y
7
= 2 ( y + x sin y cos y ) e
例 3. 设 z = u v + sin t , u = e ,
t
dz 求全导数 . dt
解:
z
t t
d z z du z d v z = + + dt u dt v dt t
2
x y z x y z f 2′ f 2′ u f 2′ v ′′ ′′ = f 21 + xyf 22 ; + = u z v z z 2w ′′ ′′ ′′ ′′ = f11 + xyf12 + yf 2′+ yz( f 21 + xyf 22 ) 于是 xz
′′ ′′ ′′ = f11 + y( x + z ) f12 + xy 2 zf 22 + yf 2′.
y = 2 xf + x f u′ ( 2 ) + x 2 f v′ y x
2
11
= 2 xf yf u′ + x yf v′
2
f u′ ( f v′)
u
v
x y x
z 2 = 2 x ( f ) ( yf u′ ) + x ( yf v′) y y y xy
2
y
f u f v f u′ u f u′ v = 2 x[ + ] f u′ y[ + ] u y v y u y v y
t
(t < 0 时,根式前加“–”号) 根式前加“ 号
d z z du z d v = + dt u dt v dt
( 全导数公式 )
3
推广: )中间变量多于两个的情形。 推广 1)中间变量多于两个的情形。例如 z = f (u, v, w) , u = φ (t) , v =ψ (t) , w = ω (t)
z = f (u, v) , u = φ (x, y) , v =ψ (x, y)
z
′ ′ f1′φ2 + f 2′ψ2
u v
x
y x 4
y
又如 z = f (x, v) , v =ψ (x, y) 当它们都具有可微条件时, 当它们都具有可微条件时,则有 z f f v ′ = = f1′ + f 2′ψ1 + x x v x z f v ′ = f 2′ψ2 = y v y z f 与 不同 注意: 注意 这里 x x z 表示固定 表示固定 y 对 x 求导
xy
+ e [xsin( x + y) + cos(x + y) ]d y
xy
16
习题8 3 P24
A : 1(5),2(6),4(3,4) B : 1(5,6),4
17
记
f ( u , v ) f1′ = , u ′′ f11 ,
2 f ( u, v ) ′′ f12 = , u v ′′ f 22 .
w
u v
同理有 f 2′,
w f u f v + = = f1′ + yzf 2′; x u x v x
x y z x y z
9
f1′ f 2′ w ( f1′ + yzf 2′) = ; + yf 2′ + yz = z z xz z ′ f1′ , f2 f1′ f1′ u f1′ v ′′ ′′ + = f11 + xyf12 ; = u v u z v z z
10
y 例5 设z = x f ( , xy ), 其中f具有二阶连续偏导 , x 2z f . 求 x y u v y 解 : 令u = , v = xy , x x yx y
2
∴ z = x f ( u, v )
2
z f u f v 2 = 2 xf + x [ + ] x u x v x
f v′ u f v′ v + x f v′ + x y[ + ] u y v y
2 2
y ′′ ′′ = f u′ + 3 x f v′ f uu + x 3 yf vv x
2
12
具有连续导数, 例6 设z = f ( xy ),y = g( x ),且f、g具有连续导数, dz 求 。 dx
f 表示固定 v 对 x 求导 x
z= f
x v
x y
x
连线相乘, 分线相加。 口诀 : 连线相乘 分线相加。
5
解:z = z u + z v
例1. 设 z = e sin v , u = x y , v = x + y z z , 求 . x y
u
z
u v
x
= e sin v y + e cos v 1
u
u
= e [sin( x + y)d(x y) + cos(x + y)d(x + y)]
= e [sin( x + y) ( ydx + xd y) + cos(x + y)(d x + d y)]
xy
xy
= e [ y sin( x + y) + cos(x + y)]dx
z = ex y[ y sin( x + y) + cos(x + y)] 所以 x z xy = e [x sin( x + y) + cos(x + y)] y
z z u z v o( ρ ) + = + t t u t v t
( ρ = (u) + (v) )
2 2
令 t → 0 ,则有 u →0, v →0,
z
v
u du → , dt t
o ( ρ ) o( ρ ) = t ρ
u v dv → t dt t u 2 v 2 ( ) + ( ) →0 t t
dz z z dy 解 = + dx x y dx
z
x
y
x
= f ′( xy ) y + f ′( xy ) x g ′( x )
= yf ′ + xf ′ g ′
13
x y 例7: 已知 Z = f ( x y, ) + g 其中 f , g 二阶连续可导 y x 2
解: z = x f ′ x f2 + 1 g′ ′ 1 2 y x y
x2 + y2 +z2
, z = x2sin y ,
u
x y z
x2 + y2 +z2 2 xsin y +2z e 2 x2 + y2 +x4 sin2 y
= 2 xe = 2 x (1+ 2 x2 sin y) e u f f z = + y y z y
= 2ye
x2 + y2 +z2 4
xy
u x u
v x u
x
y x
y
= e [ y sin( x + y) + cos(x + y)]
z z u z v + = y u y v y u = eu sin v
x + e cos v 1
6
= ex y[x sin( x + y) + cos(x + y)]
例2. u = f (x, y, z) = e u u , 求 x y u f f z = + 解: x x z x
则在它们都可微的条件下 d z z du z d v z d w = + + dt u dt v dt w dt
z
u v w
t t t
= f1′φ′ + f 2′ψ ′ + f3′ω′
2)中间变量是多元函数的情形。例如 )中间变量是多元函数的情形。 则在它们都可微的条件下 z z u z v = + x u x v x z z u z v = + = y u y v y
这说明,无论 u , v 是自变量还是中间变量, 其全微分表 15 达式一样, 这性质叫做全微分形式不变性 . 全微分形式不变性
z z , . 例8. z = e sin v , u = xy , v = x + y , 求 x y u 解: d z = d ( e sin v )
u
= e sin v du + e cos v dv
