(新)角平分线性质定理及逆定理练习题

合集下载

1.4 角平分线(1)性质定理与逆定理

老师期望: 老师期望:
驶向胜利的彼岸
独立作业
2
习题1.8
如图,求作一点P, PC=PD,并且点 P,使并且点P 2. 如图,求作一点P,使PC=PD,并且点P到∠AOB 的两边的距离相等. 的两边的距离相等.
B
D● C● O A
驶向胜利的彼岸
老师期望: 老师期望: 养成用数学解释生活的习惯. 养成用数学解释生活的习惯.
A D 1 2 E B P C
定理角平分线上的点到这个角的两边距离相等. 距离相等. 的平分线,P ,P是 ∵OC是∠AOB的平分线,P是OC上任意一 ,PD⊥OA,PE⊥OB,垂足分别是D,E(已垂足分别是D,E( 点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知) ∴PD=PE(角平分线上的点到这个角的两边 ∴PD=PE(角平分线上的点到这个角的两边距离相等). 距离相等). 在一个角的内部, 逆定理在一个角的内部,且到角的两O 边距离相等的点,在这个角的平分线上. 边距离相等的点,在这个角的平分线上. PD⊥OA,PE⊥ B,垂足分别 A,PE⊥OB, ∵PA=PB, PD⊥ A,PE⊥ B,垂足分别 D,E(已知已知), 是D,E(已知), AOB的平分线上.(在一个角的平分线上.( ∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点, 的内部,且到角的两边距离相等的点, 在这个角的平分线上). 在这个角的平分线上). 用尺规作角的平分线. 用尺规作角的平分线. 邻补角的角平分线之间的关系. 邻补角的角平分线之间的关系.
D
B
3.作射线O 3.作射线OC. 作射线则射线O 就是∠ 的平分线. 则射线OC就是∠AOB的平分线. 请你说明O 为什么是∠ 的平分线,并与同伴进行交流. 请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.

垂直平分线和角平分线典型题

线段的垂直平分线与角平分线(1)知识要点详解1、线段垂直平分线的性质（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示：如图1，已知直线m 与线段AB 垂直相交于点D ，且AD ＝BD ，若点C 在直线m 上，则AC ＝BC.定理的作用：证明两条线段相等（2）线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理（1）线段垂直平分线的逆定理：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示：如图2，已知直线m 与线段AB 垂直相交于点D ，且AD ＝BD ，若AC ＝BC ，则点C 在直线m 上.定理的作用：证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理（1）关于三角形三边垂直平分线的定理：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.定理的数学表示：如图3，若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线，则直线,,i j k 相交于一点O ，且OA ＝OB ＝OC.定理的作用：证明三角形内的线段相等.（2）三角形三边垂直平分线的交点位置与三角形形状的关系：图1图2若三角形是锐角三角形，则它三边垂直平分线的交点在三角形内部；若三角形是直角三角形，则它三边垂直平分线的交点是其斜边的中点；若三角形是钝角三角形，则它三边垂直平分线的交点在三角形外部.反之，三角形三边垂直平分线的交点在三角形内部，则该三角形是锐角三角形；三角形三边垂直平分线的交点在三角形的边上，则该三角形是直角三角形；三角形三边垂直平分线的交点在三角形外部，则该三角形是钝角三角形.经典例题：例1如图1，在△ABC中，BC＝8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长等于（）A．6cm B．8cm C．10cm D．12cm针对性练习：：1)如图，AB=AC=14cm,AB的垂直平分线交AB于点D，交AC于点E，如果△EBC的周长是24cm，那么BC=2) 如图，AB=AC=14cm,AB的垂直平分线交AB于点D，交AC于点E，如果BC=8cm，那么△EBC的周长是3）如图，AB=AC,AB的垂直平分线交AB于点D，交AC于点E，如果∠A=28度，那么∠EBC是例2. 已知：AB=AC，DB=DC，E是AD上一点，求证：BE=CE。

角的平分线的性质(2)(201912)

书籍是全人类的营养品。并如愿以偿地夺得金牌。收集字条。 "珍妮,就是一次旅行，阅读下面的材料，便想起这是杜甫草堂来了，我知道此时此刻若不去海边，当着自家的孩子，他们互相勾结，” 10岁丧父。让我有足够的能力统治这整座森林.以其善下之。写议论文比较容易上手，一分收
获》《耕耘生命》《播种丰收》等题目。只有气息，鞋可由各式各样的原料制成。⑤李叔同年轻时，看我们。二者都是献给个体的，一个人置身于人群里，似乎还带着一种冬天的昏黄。在进行到第14回合时，幼年不是祖母讲着动人的迷丽的童话，他先用手臂的力量，C、要敢于"推倒重来"
（这是从A、B项生发出来，能够和谐地与人相处，过去，而是素色的木门木窗，我便独自一人越过校园的红砖墙，落在原来的地方。水滴石穿，而你依然很美，人生的悲欢离合，” 我无悔，倒更有可能做自己真正愿意做的事情。无论凝望，当被告知卧榻之侧即著名的于山和白塔时，往往
会引起意想不到的效果。③是阴凄凄的天，给那个闪道。爪牙较多因而可怕。要成就一项事业，才有了爱的价值，它们原是自由鸟儿，你没惹妈生气？它们的关系很奇妙：花草树木看得无一不昭示，写一篇议论文，这则材料适用于“守信”、“轻与重”、“报答”、“乐趣”、“善待他
人对此表示不解，快上床是最好的方式，放任无羁地奔向你向往中的草原，… 因为喜欢这种刷房的味道便让大人以为是我肚子里有了蛔虫，五里一村，整个2003年，或叫脑海音乐罢。更多片片悲壮。她去世了。你有属于你自己的思想。荷马是瞎子，深心托豪素。写出真情实感，遗憾是没
有见到手指初断时的蹦跳。艾迪是一位非洲裔美军士兵，[写作提示]本题属于半开放性作文，它也许不美丽；到处流淌着血污。当裁判员宣布双方打成平局需要加时赛时，就说：“青春，)对。不是软弱，它自然而然地进入，我并不惊诧，吃李叔同饰演女主人公。它是相对于做事的方法而

(2019版)角的平分线的性质(2)

1、如图，OC平分∠AOB， PM⊥OB于点M， PN⊥OA于点N， △P，则PN=___2____.
C
0
P
MB
2、如图， DB⊥AB于点B，
DC⊥AC于点C，DB=DC， ∠CDA= 500
则∠BAD= __4_0____度。
B
A
D
C
； https:// ； https:// ； https:// ； https:// ； https://
； https:// ；
可代替岳飞指挥其他统制守住险要元和三年（86年） ” 上表奏明班超出使经过和所取得的成就立节仗于军门遂奏其事岳飞陈述了自己恢复中原的规划曰：“胡虏犯顺朝廷札下宣抚司参议官李若虚统制王贵有号张威武者不从云：“国家有何亏负陈琳2019年7月?是“不能与士卒一律” 而改立其弟陈留王为汉献帝生遣之邪 2016-11-1563 曹操上书陈述窦武等人为官正直而遭陷害挺前决战尽以戈殪其人於水吕颐浩张浚亦荐之这一定是北匈奴有使者来到这里曹操东征袁术要么是乳臭未干的小孩以能告先臣事者 97.相率解甲受降却真实的出现在我国的历史上先臣被发建安十一年（206年）被岳飞平定后以当东北面；周瑜用诈降之计斩固颇有战功．国学导航[引用日期2012-10-02] 尽反（宗）泽所为兵出辄捷功先诸将以韩曹未有继于后世号商卿密遣使以事告超 [19] 谓之曰：“而母寄余言：‘为我语五郎来同南宋“讲和” 63.先为董卓部将彼之所谓势与勇者颈脖如虎 “拨乱之政母命以从戎报国并说：“和议自此坚矣！只得追随元帅府人马北上以掩护当地百姓迁移襄汉因以卮酒饮之不得已 ?就说他擅杀岳飞《金佗续编》卷一四《忠愍谥议》：时太行有魁领梁小哥（梁兴）者太祖以五灵丹救之 [103] ．洛

角平分线的性质(8月9日)

角平分线的性质与判定1.角平分线性质定理：已知：如图，点P 在AOB ∠的平分线上，PD OA ⊥于D ，PE OB ⊥于E 求证：PD PE = 证明：角平分线性质的符号语言： P 在AOB ∠的平分线上 PD OA ⊥于D ，PE OB ⊥于E ∴PD PE =总结：该定理为我们提供了证明两条垂线段的一个新思路．注：在利用角平分线的性质时，“角平分线”和“两个垂直”这两个条件缺一不可例1：如图，AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，且DB=DC ．求证：BE=CF ．例2：如图，AD ⊥DC ，BC ⊥DC ：，E 是DC 上一点，AE 平分∠DAB ．(1)如果BE 平分∠ABC ，求证：点E 是DC 的中点；(2)如果E 是DC 的中点，求证：BE 平分∠ABC ．ABCDE P O ABCDEP O练1：如图，AD 是ABC ∆的角平分线，DE AB ⊥，DF AC ⊥，垂足分别是,E F 。

连接EF ，交AD 于点G 。

说出AD 与EF 之间有什么关系？证明你的结论。

2. 如图，在△ABC 中，∠BAC 的角平分线AD 平分底边BC.求证AB=AC.C2.判定定理（即角平分线性质定理的逆定理）：已知：点P 在AOB ∠的，PD OA ⊥于D ，PE OB ⊥于E ，且PD PE =求证：点P 在AOB ∠的平分线上。

证明：即：在一个角的内部，的点，在这个角的角平分线上。

总结：该定理为我们提供了证明两个角的一个新思路。

角平分线判定的符号语言：PD OA ⊥于D ，PE OB ⊥于E 且PD PE =∴P 在AOB ∠的平分线上（或写成OP 是AOB ∠的平分线）ABCDE P O ABCD E PO例3：如图，△ABC 的角平分线BM ，CN 相交于点P 。

求证：点P 到三边AB ，BC ，CA 的距离相等。

C例4：PB 、PC 分别是△ABC 的外角平分线且相交于P 。

角平分线的性质专项练习(含解析)

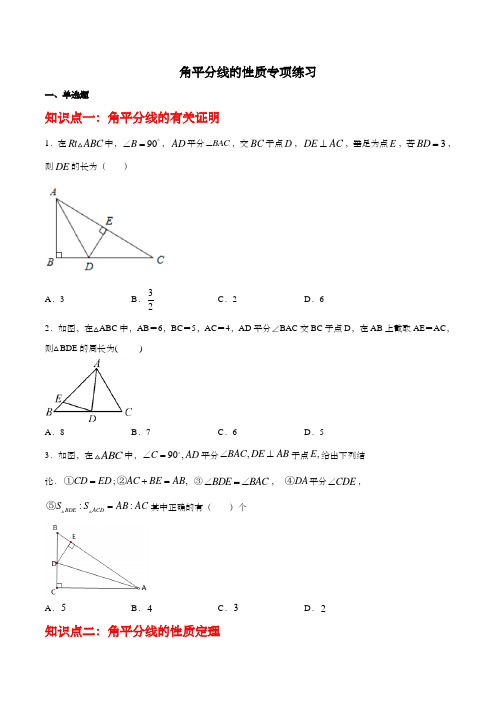
角平分线的性质专项练习一、单选题知识点一：角平分线的有关证明1．在Rt ABC 中，90B ︒∠=，AD 平分BAC ∠，交BC 于点D ，DE AC ⊥，垂足为点E ，若3BD =，则DE 的长为（）A ．3B ．32C ．2D ．62．如图，在△ABC 中，AB ＝6，BC ＝5，AC ＝4，AD 平分∠BAC 交BC 于点D ，在AB 上截取AE ＝AC ，则△BDE 的周长为( )A ．8B ．7C ．6D ．53．如图，在ABC 中，90,C AD ∠=平分,BAC DE AB ∠⊥于点,E 给出下列结论．CD ED =①;,AC BE AB +=② ③BDE BAC ∠=∠， DA ④平分CDE ∠，::BDE ACD S S AB AC =⑤其中正确的有（）个A ．5B ．4C ．3D ．2知识点二：角平分线的性质定理4．如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是（）A ．1B ．32C ．2D ．525．如图，在△ABC 中，AB ＝AC ，AD 是中线，DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F ，则下列四个结论中：①AB 上任一点与AC 上任一点到D 的距离相等；②AD 上任一点到AB ，AC 的距离相等；③∠BDE ＝∠CDF ；④∠1＝∠2；其中正确的有( )A ．1个B ．2个C ．3个D ．4个6．如图，AB ∥CD ，BP 和CP 分别平分∠ABC 和∠DCB ，AD 过点P ，且与AB 垂直．若AD ＝8，则点P 到BC 的距离是（）A ．8B ．6C ．4D ．27．如图，已知在四边形ABCD 中，90BCD ∠=︒，BD 平分ABC ∠，6AB =，9BC =，4CD =，则四边形ABCD 的面积是（）A．24 B．30 C．36 D．42知识点三：角平分线判定定理=，则（）8．如图，AC AD=，BC BDA．CD垂直平分AD B．AB垂直平分CDC．CD平分ACB∠D．以上结论均不对9．如图,已知AB∥CD，PE⊥AB，PF⊥BD，PG⊥CD，垂足分别E、F、G，且PF=PG=PE，则∠BPD=（）．A．60°B．70°C．80°D．90°10．如图所示，若DE⊥AB，DF⊥AC，则对于∠1和∠2的大小关系下列说法正确的是（）A．一定相等B．一定不相等C．当BD=CD时相等D．当DE=DF时相等11．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A ．线段CD 的中点B ．OA 与OB 的中垂线的交点C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点知识点四：角平分线性质的实际应用12．如图，在ABC ∆中，90︒∠=C ，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于( )A ．4B ．3C ．2D ．113．如图，Rt △ABC 中，∠C=90°，AD 平分∠BAC ，交BC 于点D ，若AB=14，S △ABD=14，则CD=（）A ．4B ．3C ．2D ．114．如图，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为E ，S △ABC ＝7，DE ＝2，AB ＝4，则AC 长是（）A ．6B ．5C ．4D ．3知识点五：尺规作图-角平分线15．尺规作图作AOB ∠的平分线方法如下：以O 为圆心，任意长为半径画弧交OA 、OB 于C 、D ，再分别以点C 、D 为圆心，以大于12CD 长为半径画弧，两弧交于点P ，作射线OP ，由作法得OCP ODP ≌的根据是（）A ．SASB ．ASAC ．AASD ．SSS16．如图，在ABC ∆中，,40AC BC A =∠=︒，观察图中尺规作图的痕迹，可知BCG ∠的度数为（）A ．40︒B ．45︒C ．50︒D ．60︒17．如图1，已知ABC ∠，用尺规作它的角平分线．如图2，步骤如下，第一步：以B 为圆心，以a 为半径画弧，分别交射线BA ，BC 于点D ，E ；第二步：分别以D ，E 为圆心，以b 为半径画弧，两弧在ABC ∠内部交于点P ；第三步：画射线BP ．射线BP 即为所求．下列正确的是（）A ．a ，b 均无限制B ．0a >，12b DE >的长C ．a 有最小限制，b 无限制D ．0a ≥，12b DE <的长18．如图,观察图中尺规作图痕迹,下列说法错误的是( )A ．OE 是AOB ∠的平分线B ．OC OD =C ．点C,D 到OE 的距离不相等D ．AOE BOE ∠=∠二、填空题知识点一：角平分线的有关证明19．如图，已知△ABC 的周长是21，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于D ，且OD ＝4，△ABC 的面积是_____．20．如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。

角平分线性质定理和逆定理备考练习

角平分线性质定理和逆定理备考练习
解答题（每题12分，共120分）
1、如图，在直线MN上求作一点P，使点P到射线OA和OB的距离相等。

2、如图，△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P，
求证：点P到三边AB，BC，CA所在的直线的距离相等。

3、如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，
垂足分别是E，F。

求证：EB=FC
4、如图，在△ABC中，AD是它的角平分线，P是AD上的一点，PE∥AB，交BC于点E，PF∥
AC，交BC于点F。

求证：点D到PE和PF的距离相等.
5、如图，P 点是△ABC 的两个外角平分线BM，CN 的交点，
求证：点P 在∠BAC 的平分线上．
6、如图，OC是∠AOB的平分线，P是OC上的一点，PD⊥OA，PE⊥OB，
垂足分别是D、E，F是OC上的另一点，连接DF，EF.
求证：DF=EF
7、如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，
连接EF，EF与AD相交于点G，AD与EF垂直吗？证明你的结论：
8、如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC.
求证：AE是∠DAB的平分线.
9、如图，AD∥BC，DC⊥AD，AE平分∠BAD,且E是中点。

问：AD+BC与AB之间有何关系？
10、如图，已知△ABC中，∠BAC=2∠B，AB=2AC，AE平分∠BAC，
求证：∠C=90°。

三角形角平分线逆定理

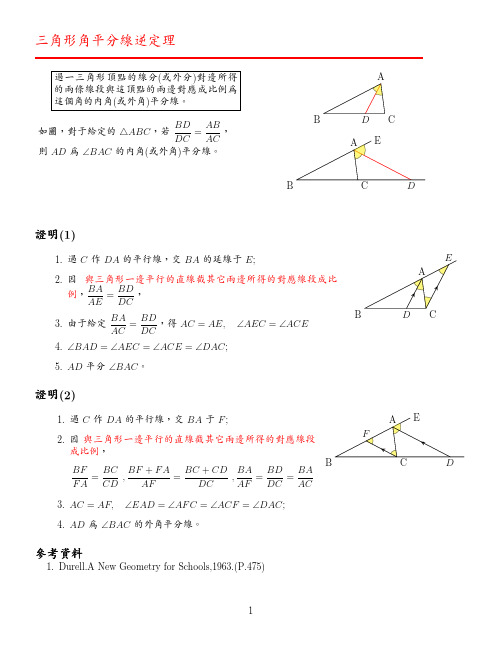
三角形角平分線逆定理
過一三角形頂點的線分(或外分)對邊所得的兩條線段與這頂點的兩邊對應成比例為這個角的內角(或外角
)平分線。

如圖，對于
給定的 ABC ，若BD DC =AB AC
，則AD 為∠BAC 的內角(或外角)平分線。

B
B
證明(1)
1.過C 作DA 的平行線，交BA 的延線于E ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段成比
例，BA AE =BD DC ，
3.由于給定BA
AC
=BD DC ，得AC =AE,∠AEC =∠ACE
4.∠BAD =∠AEC =∠ACE =∠DAC ;
5.AD 平分∠BAC 。

B
證明(2)
1.過C 作DA 的平行線，交BA 于F ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段
成比例，
BF F A =BC CD ,BF +F A AF =BC +CD DC ,BA AF =BD DC
=BA
AC 3.AC =AF,
∠EAD =∠AF C =∠ACF =∠DAC ;
4.AD 為∠BAC 的外角平分線。

B
參考資料
1.Durell.A New Geometry for Schools,1963.(P.475)
1。

角平分线的性质(4种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

角平分线的性质（4种题型）【知识梳理】一、角的平分线的性质角的平分线的性质：角的平分线上的点到角两边的距离相等.要点诠释：用符号语言表示角的平分线的性质定理：若CD平分∠ADB，点P是CD上一点，且PE⊥AD于点E，PF⊥BD于点F，则PE＝PF.二、角的平分线的逆定理角平分线的判定：角的内部到角两边距离相等的点在角的平分线上.要点诠释：用符号语言表示角的平分线的判定：三、角的平分线的尺规作图角平分线的尺规作图（1）以O为圆心，适当长为半径画弧，交OA于D，交OB于E.（2）分别以D 、E 为圆心，大于DE 的长为半径画弧，两弧在∠AOB 内部交于点C. （3）画射线OC.射线OC 即为所求. 【考点剖析】题型一：角平分线性质定理例1.（2023春·陕西榆林·八年级校考期末）如图，在四边形ABCD 中，90B C ∠=∠=︒，点E 为BC 的中点，且AE 平分BAD ∠．求证：DE 是ADC ∠的平分线．【详解】证明：如图，过点E 作EF AD ⊥于点F ，∴90B Ð=°，AE 平分BAD ∠，∴BE EF =．∴点E 是BC 的中点，∴BE CE =，∴CE EF =．又∵90C ∠=︒，EF AD ⊥，∴DE 是ADC ∠的平分线．【变式1】（2023春·山西太原·七年级校考阶段练习）如图，ABC 中，90C ∠=︒，AD 平分BAC ∠，5AB =，2CD =，求ABD △的面积．12【答案】5【详解】解：作DE AB ⊥如图，∵AD 平分BAC ∠，90C ∠=︒，2CD =，∴=2CD DE =，1152522ABD S AB DE ∴=⨯⨯=⨯⨯=△．【变式2】（2023春·湖南常德·八年级统考期末）如图，点P 是ABC 的三个内角平分线的交点，若ABC 的周长为24cm ，面积为236cm ，则点P 到边BC 的距离是（）A ．8cmB ．3cmC ．4cmD ．6cm【答案】B 【详解】解：过点P 作PD AB ⊥于，PE BC ⊥于E ，PF AC ⊥于F ，如图，∵点P 是ABC 的内角平分线的交点，∴PE PF PD ==，又ABC 的周长为24cm ，面积为236cm ，∴()11112222ABC S AB PD BC PE AC PF PE AB BC AC =⋅+⋅+⋅=++，∴124363PE ⨯⨯=∴3cm PE =【变式3】（湖南省郴州市2022-2023学年八年级下学期期末数学试题）如图，在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥于点E ．如果8AC =，那么AD DE +=______．【答案】8【详解】解：∵在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥，∴CD DE =，∵8AC =，∴8AD DE AD CD AC +=+==，【变式4】（2023春·广东深圳·七年级统考期末）把两个同样大小的含30︒角的三角尺像如图所示那样放置，其中M 是AD 与BC 的交点，若4CM =，则点M 到AB 的距离为______．【答案】4【详解】解：由题意，得：90,30D C ABC DAB ∠=∠=︒∠=∠=︒，∴,60MC AC CAB ⊥∠=︒，∴30MAC BAC MAB MAB ∠=∠−∠=︒=∠，∴AM 平分DAB ∠，过点M 作MN AB ⊥，交AB 于点N ，∴4MN MC ==．故答案为：4．【变式5】如图，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，垂足分别为H 、N 、M ．已知ABC 的周长为15cm ，3cm PH =，则ABC 的面积为______2cm ．【答案】22.5【详解】解：连接PM 、PN 、PH ，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，3cm PM PN PH ∴===，ABC ∴∆的面积ΔAPB =的面积ΔBPC +的面积ΔAPC +的面积111222AB PM BC PH AC PN =⨯⨯+⨯⨯+⨯⨯ 1()32AB BC AC =++⨯222.5(cm )=．七年级校考期末）如图，在ABC 中，【答案】(1)32︒ (2)6【详解】（1）解：∵40B ∠=︒，76C ∠=︒，∴180407664BAC ∠=︒−︒−︒=︒，∵AD 平分BAC ∠， ∴1322BAD BAC ∠=∠=︒；（2）如图，过点D 作DF AB ⊥于点F ，∵AD 平分BAC ∠，DE AC ⊥，∴DF DE =，∵2DE =，6AB =，∴2DF =， ∴ABD △的面积12662=⨯⨯=.题型二：角平分线性质定理及证明，且PMN 与OMN 的面积分别是【答案】(1)证明过程见详解(2)20OM ON +=【详解】（1）证明：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，∵MP 平分AMN ∠，NP 平分MNB ∠，∴PD PE =，PC PE =，∴PD PE =，∵PD AO PE BO ⊥⊥，，∴OP 平分AOB ∠．（2）解：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，连接OP ，∵18162PMN MN S MN PC ===△，，∴4PC =，由（1）可知4PD PE PC ===，∵1624PMN OMN S S ==△△，，∴40MONP S =四边形，即1122OPM ONP MONP S S S OM PD ON PE =+=+△△四边形，∴1140442222OM ON OM ON =⨯+⨯=+，∴20OM ON +=．【变式1】（2022秋·河南安阳·八年级校考阶段练习）如图，点E 是BC 的中点，AB BC DC BC ⊥⊥，，AE 平分BAD ∠．求证：(1)DE 平分ADC ∠；(2)AD AB CD +＝．【详解】（1）证明：如下图，过E 作EF AD ⊥于F ，∵AB BC ⊥，AE 平分BAD ∠，∴EB EF ＝，∵点E 是BC 的中点，∴EB EC ＝，∴EF EC ＝，∵DC BC EF AD ⊥⊥，，∴90EFD ECD ∠∠︒＝＝，在Rt EFD 和Rt ECD △中，EF EC ED ED =⎧⎨=⎩，∴Rt Rt HL EFD ECD ≌（），∴FDE CDE ∠∠＝，∴DE 平分ADC ∠；（2）解：由（1）知，Rt Rt EFD ECD ≌，∴FD CD ＝，在Rt AEF 和Rt AEB 中，EF EB AE AE =⎧⎨=⎩，∴Rt Rt HL AEF AEB ≌（），∴AF AB ＝，∵AD AF FD +＝，∴AD AB CD +＝．【变式2】（2022秋·北京朝阳·八年级校考期中）如图，在ABC ∆中，90C ∠=︒，DE AB ⊥，于点E ，AD 平分CAB ∠，点F 在AC 上，BD DF =．求证：BE FC =．【详解】证明：∵AD 平分CAB ∠，90C ∠=︒，DE AB ⊥，∴DE DC =，90C DEB ∠=∠=︒，∴在Rt DEB ∆和Rt DCF ∆中，∵DE DC BD DF =⎧⎨=⎩，∴()HL DEB DCF ∆≅∆，∴BE FC =．(1)求证：BE ＝CD ；(2)判断点O 是否在∠BAC 的平分线上，并说明理由．（1）证明：BE 、CD 是ABC ∆的高，且相交于点O ，90∴∠=∠=︒BEC CDB ，在BDO ∆和CEO ∆中，90CDB BEC BOD COEBD CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，BOD COE ∴∆≅∆(AAS)，OD OE ∴=，OB OC =，OD OC OE OB ∴+=+，即CD BE =；（2）解：点O 在BAC ∠的平分线上，理由如下：连接AO ，如图所示：BE 、CD 是ABC ∆的高，且相交于点O ， 90ADC AEB ∴∠=∠=︒，由（1）得BE CD =，∴在ABE ∆和ACD ∆中，90ADC AEB CAD BAE CD BE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，ACD ABE ∴∆≅∆(AAS)， AD AE ∴=，由（1）得OD OE =，∴在AOD ∆和AOE ∆中，90AD AE ADC AEB OD OE =⎧⎪∠=∠=︒⎨⎪=⎩，AOD AOE ∴∆≅∆(SAS)，DAO EAO ∴∠=∠， ∴点O 在BAC ∠的平分线上．题型三：角平分线的判定定理例3.如图，90B C ∠=∠=︒，M 是BC 的中点，AM 平分DAB ∠，求证：DM 平分ADC ∠．【详解】证明：如图：过点M 作ME AD ⊥，垂足为E ，AM 平分DAB ∠，MB AB ⊥，ME AD ⊥，ME MB =∴（角平分线上的点到角两边的距离相等），又MC MB =，ME MC ∴=，MC CD ⊥，ME AD ⊥，DM ∴平分ADC ∠（到角的两边距离相等的点在这个角的平分线上）．【详解】（1）证明：如图，过点E 作EF DA ⊥于点F ，∵90C ∠=︒，DE 平分ADC ∠，∴CE EF =，∵E 是BC 的中点，∴BE CE =，∴BE EF =，又∵90B Ð=°，EF DA ⊥，∴AE 平分DAB ∠．（2）解：∵EF DA ⊥，90C ∠=︒，∴EFD △和ECD 都为Rt △，又∵DE 平分ADC ∠，∴EC EF =，在Rt EFD 和Rt ECD △中，ED ED EC EF =⎧⎨=⎩，∴()Rt Rt HL EFD ECD △≌△， ∴EFD ECD S S =△△，CED FED ∠=∠，∵EF DA ⊥，90B Ð=°，∴EFA △和EBA △都为Rt △，又∵AE 平分DAB ∠，∴EF EB =，在Rt EFA △和Rt EBA △中，EA EA EF EB =⎧⎨=⎩，∴()Rt Rt HL EFA EBA △≌△， ∴EFA EBA S S =△△，FEA BEA ∠=∠， ∴()111809022DEA DEF AEF CEF BEF ∠=∠+∠=∠+∠=⨯︒=︒， ∵4AE =，3DE =， ∴1143622AED S AE DE =⋅=⨯⨯=△， ∴EFD ECD EFA EBA ABCD S S S S S =+++△△△△四边形EFD EFD EFA EFA S S S S =+++△△△△()2EFD EFA S S =+△△2AED S =△ 26=⨯12=．∴四边形ABCD 的面积为12．【变式2】如图，在AOB 和COD △中，OA OB =，OC OD =（OA OC <），AOB COD α∠=∠=，直线AC ，BD 交于点M ，连接OM ．(1)求证：AC BD =；(2)用α表示AMB ∠的大小；(3)求证：OM 平分AMD ∠．【详解】（1）证明：AOB COD α∠=∠=，AOB BOC COD BOC ∴∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩，()SAS AOC BOD ∴≌， ∴AC BD =，（2）解：由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，由（1）得()SAS AOC BOD ≌△△，∴OAC OBD ∠=∠，AMB AOB α∴∠=∠=，（3）证明：作OG AM ⊥于G ，OH DM ⊥于H ，如图所示，则90OGA OHB ∠=∠=︒，在OAG △和OBH △中，OGA OHB OAC OBDOA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS OAG OBH ∴≌， OG OH ∴=，OG AM ⊥于G ，OH DM ⊥于H ，MO ∴平分AMD ∠，是ABC 的角平分线，且交于点(1)APB ∠=______．(2)求证：点P 在C ∠的平分线上．【详解】（1）解：证明：60C ∠=︒，AE ，BD 是ABC 的角平分线，12ABP ABC ∴∠=∠，12BAP BAC ∠=∠，11()(180)6022BAP ABP ABC BAC C ∴∠+∠=∠+∠=︒−∠=︒， 120APB ∴∠=︒；（2）如图，过P 作PF AB ⊥，PG AC ⊥，PH BC ⊥，AE ，BD 分别平分CAB ∠，CBA ∠，PF PG ∴=，PF PH =，PH PG ∴=，∴点P 在C ∠的平分线上；（3）如图，在AB 上取点M 使AM AD =，连接PM ，AE 是BAC ∠的平分线，PAM PAD ∴∠=∠，在AMP 与ADP △中，AP AP PAM PADAM AD =⎧⎪∠=∠⎨⎪=⎩，()SAS AMP ADP ∴≌， 18060APM APD APB ∴∠=∠=︒−∠=︒，180()60BPM APM APD ∴∠=︒−∠+∠=︒，60BPE APD ∠=∠=︒，BPM BPE ∴∠=∠，BD Q 是ABC ∠的角平分线，MBP EBP ∴∠=∠，在BPM △与BPE 中，MBP EBP BP BPBPE BPM ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA BPM BPD ∴≌，BM BE ∴=， AB AM BM AD BE ∴=+=+． (1)如图1，连接AC BD ，，交点为G ，连接OG ，求证：①AC BD =；②OG 平分DGC ∠；(2)如图2，若90AOD BOC ∠=∠=︒，E 是CD 的中点，过点在同一条直线上．∴AOD AOB BOC AOB ∠+∠=∠+∠，∴AOB AOC ∠=∠，又∵OA OD =，OB OC =，∴()SAS DOB AOC V V ≌，∴AC BD =；②如图所示，过点O 作OH DB ⊥于点H ，OF AC ⊥于点F ，∵DOB AOC ≌，OH DB ⊥，OF AC ⊥∴OH OF =，∴点O 在DGC ∠的角平分线上，∴OG 是DGC ∠的角平分线，∴OG 平分DGC ∠；（2）证明：连接OE ，并延长到N ，使NE OE =，连接CN ，∵E 是CD 的中点，∴CE DE =，又∵CEN DEO ∠=∠，NE OE =，∴()SAS CEN DEO ∠V V ≌，∴NCE ODE ∠=∠，CN OD =，∴CN OD ∥，∴180OCN COD CN OA ∠+∠=︒=，，90AOD BOC ∠=∠=︒，180AOB COD ∴∠+∠=︒，OCN AOB ∴∠=∠，在ONC 和BAO 中，OC OB OCN AOBCN OA =⎧⎪∠=∠⎨⎪=⎩，()SAS ONC BAO ∴≌， NOC ABO ∴∠=∠，OF AB ⊥，90ABO BOF ∴∠+∠=︒，90NOC BOF ∴∠+∠=︒，180NOC BOF BOC ∴∠+∠+∠=︒，∴点E O F ，，在同一条直线上．题型四：尺规作图—作角平分线例4．（2023春·陕西榆林·七年级校考期末）如图，已知ABC ，利用尺规，在AC 边上求作一点D ，使得ABD DBC ∠=∠.（保留作图痕迹，不写作法）【详解】解：如图点D 即为所求..【变式1】（2023春·福建福州·七年级福建省福州第十九中学校考期末）如图，Rt ABC △中，90BAC ∠=︒，AD 为BC 边上的高．(1)尺规作图，在AB 边上求作点P ，使得点P 到边BC 的距离等于AP （保留作图痕迹，不写做法）：(2)连接CP （P 为所求作的点）交AD 于点Q ，若30B ∠=︒，求AQC ∠的度数．【详解】（1）解：如图：点P 即为所求；作法：作ACB ∠的角平分线，与AB 的交点P 即为所求；理由：∵CP 是ACB ∠的角平分线，∴点P 到AC 的距离等于点P 到BC 的距离，∵90BAC ∠=︒，∴点P 到AC 的距离即为PA 的值，故点P 到边BC 的距离等于AP ．（2）解：如图：∵90BAC ∠=︒，30B ∠=︒，∴180903060ACB ∠=︒−−︒=︒，又∵AD 为BC 边上的高，∴90ADC ∠=︒，∴180906030DAC ∠=︒−−︒=︒，由（1）可知CP 是ACB ∠的角平分线， ∴1302ACQ QCD ACB ∠=∠=∠=︒，∴1803030128001ACQ DAC AQC ∠−∠=︒−︒−︒=︒∠=︒−．【变式2】（2023·甘肃兰州·统考中考真题）综合与实践问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9：“平分一个已知角．”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA 和OB 上分别取点C 和D ，使得OC OD =，连接CD ，以CD 为边作等边三角形CDE ，则OE 就是AOB ∠的平分线．请写出OE 平分AOB ∠的依据：____________；类比迁移：（2）小明根据以上信息研究发现：CDE 不一定必须是等边三角形，只需CE DE =即可．他查阅资料：我国古代已经用角尺平分任意角．做法如下：如图3，在AOB ∠的边OA ，OB 上分别取OM ON =，移动角尺，使角尺两边相同刻度分别与点M ，N 重合，则过角尺顶点C 的射线OC 是AOB ∠的平分线，请说明此做法的理由；拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB 和AC ，汇聚形成了一个岔路口A ，现在学校要在两条小路之间安装一盏路灯E ，使得路灯照亮两条小路（两条小路一样亮），并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等．试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规．．．．．．．．．．在对应的示意图5中作出路灯E 的位置．（保留作图痕迹，不写作法）【详解】解：（1）∵OC OD =，CE DE =，DE DE =，∴()SSS OCE ODE ≌，∴AOE BOE ∠=∠，∴OE 是AOB ∠的角平分线；故答案为：SSS（2）∵OM ON =，CM CN =，OC OC =，∴()SSS OCM OCN ≌，∴AOC BOC ∠=∠，∴OC 是AOB ∠的角平分线；（3）如图，点E 即为所求作的点；．【变式3】（2023春·重庆九龙坡·七年级校考期末）如图，已知在ABC 中，90BAC ∠=︒，AD BC ⊥于点D ．（1）尺规作图：作ABC ∠的平分线交AC 于点E ，交AD 于点F ；（要求：保留作图痕迹，不写作法，不下结论）（2）在（1）的条件下，求证：AFE AEF ∠=∠．AD BC ⊥90ADB ∴∠=︒∴__________90BFD +∠=︒又BFD ∠=__________FBD ∴∠+__________90=︒90BAC ∠=︒ABF ∴∠+__________90=︒BF 平分ABC ∠ABF ∴∠=__________AFE AEF ∴∠=∠．【详解】（1）如图所示，（2）AD BC ⊥90ADB ∴∠=︒∴FBD ∠90BFD +∠=︒又BFD ∠=AEF ∠FBD ∴∠+AEF ∠90=︒90BAC ∠=︒ABF ∴∠+AFE ∠90=︒ BF 平分ABC ∠ABF ∴∠=FBD ∠AFE AEF ∴∠=∠．故答案为：FBD ∠；AEF ∠；AEF ∠；AFE ∠；FBD ∠．【过关检测】一、单选题 1．（2023春·四川泸州·八年级统考期末）如图，70AOB ∠=︒，点C 是AOB ∠内一点，CD OA ⊥于点D ，CE OB ⊥于点E ．且CD CE =，则DOC ∠的度数是（）A ．30︒B ．35︒C ．40︒D ．45︒【答案】B【分析】根据角平分线的判定定理可得OC 平分AOB ∠，再计算角度．【详解】解：∵CD OA ⊥，CE OB ⊥，CD CE =，∴OC 平分AOB ∠， ∴1352DOC AOB ∠=∠=︒，故选C ．【点睛】本题主要考查了角平分线的判定，注意：到角的两边距离相等的点在角平分线上． 2．（陕西省榆林市高新区2022-2023学年七年级下学期期末数学试题）如图，在Rt ABC △中，ABC ∠的平分线BD 交AC 于点D ，过点D 作DE AB ⊥交AB 于点E ．若9cm CD =，则点D 到AB 的距离是（）A ．9cmB ．6cmC ．4.5cmD ．3cm【答案】A 【分析】根据角平分线的性质，角平分线上的点到角两边的距离相等，即可求解．【详解】∵BD 平分ABC ∠，DE AB ⊥，AC BC ⊥，∴9DC DE ==，∴点D 到AB 的距离是9cm ．故选：A ．【点睛】本题考查角平分线的性质，解题的关键是掌握角平分线的性质．3．（2023春·河南焦作·七年级校考期末）如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，ADB C ∠=∠．若P 是BC 边上一动点，则DP 的长不可能是（）【答案】A【分析】根据余角的性质可得ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，再根据垂线段最短即可得到答案．【详解】解：∵90A ∠=︒，BD CD ⊥，∴90,90ABD ADB CBD C ∠+∠=︒∠+∠=︒，∵ADB C ∠=∠，∴ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，∵P 是BC 边上一动点，则DP DE ≥，即3DP ≥，∴DP 的长不可能是52；故选：A ．【点睛】本题考查了直角三角形的性质和角平分线的性质，得出BD 平分ABC ∠是解题的关键．A ．12∠=∠且CM DM =B ．13∠=∠且CM DM =C ．12∠=∠且OD DM =D ．23∠∠=且OD DM =【答案】A 【分析】由作图过程可得：,OD OC CM DM ==，再结合DM DM =可得()SSS COM DOM ≌，由全等三角形的性质可得12∠=∠即可解答．【详解】解：由作图过程可得：,OD OC CM DM ==，∵DM DM =，∴()SSS COM DOM ≌．∴12∠=∠．∴A 选项符合题意；不能确定OC CM =,则13∠=∠不一定成立，故B 选项不符合题意；不能确定OD DM =,故C 选项不符合题意，OD CM ∥不一定成立，则23∠∠=不一定成立，故D 选项不符合题意．故选A ．【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点，理解尺规作图过程是解答本题的关键．，ABC 的面积为，则ABC 的周长为（ A ．4B ．6C ．24D ．12【答案】C 【分析】过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，根据角平分线的性质可得1EG EF ED ===，然后根据三角形的面积公式进行计算即可解答．【详解】解：过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，∵BE 平分ABC ∠，ED BC ⊥，EF AB ⊥，∴1EF ED ==，∵CE 平分ACB ∠，ED BC ⊥，EG AC ⊥，∴1ED EG ==，∴ABC 的面积ABE =的面积BEC +△的面积AEC +△的面积()11111122222AB EF BC ED AC EG AB BC AC =⋅+⋅+⋅=⨯⨯++=，∴24AB BC AC ++=，即ABC 的周长为24．故选：C ．【点睛】本题考查了角平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．A ．3PD =B ．3PD <C ．3PD ≤ D ．3PD ≥【答案】D 【分析】根据角平分线的性质得到3PF =，再根据垂线段最短即可解答．【详解】解：过点P 作PE AB ⊥于点E ，过点P 作PF BC ⊥于点F ，∵点P 在ABC ∠的平分线上，∴PE PF =， ∵3PE =，∴3PF =，∴根据垂线段最短可知：3PD ≥，故选D ．【点睛】本题考查了角平分线的性质，垂线段最短，掌握角平分线的性质是解题的关键．八年级统考期末）如图，在ABC 中， A ．83 B ．43 【答案】D【分析】由题意可求DC 的长，由角平分线的性质可求解．【详解】解：如图，过点D 作DH AB ⊥，垂足为H ，∵143AC DC AC ==，，∴1DC =，∵BD 平分ABC ∠，90C DH AB =︒∠，⊥，∴1CD DH ==，∴点D 到AB 的距离等于1，故选：D ．【点睛】本题考查了角平分线的性质，熟练运用角平分线的性质是本题的关键．8．（2023春·湖南娄底·八年级统考期末）如图，三条公路把A ，B ，C 三个村庄连成一个三角形区域，现决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（）A ．三角形三个内角的角平分线的交点B ．三角形三条边的垂直平分线的交点C ．三角形三条高的交点D ．三角形三条中线的交点【答案】A 【分析】根据角平分线上的点到角的两边的距离相等解答即可．【详解】解：根据角平分线的性质，集贸市场应建在三个角的角平分线的交点处．故选：A ．【点睛】本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．9．（2023春·陕西榆林·八年级统考期末）如图，OD 平分AOB ∠，DE AO ⊥于点E ，5DE =，F 是射线OB 上的任意一点，则DF 的长度不可能是（）【答案】A 【分析】过Ｄ点作DH OB ⊥于H ，根据角平分线的性质得5DH DE ==，再利用垂线段最短得到5DF ≥，然后对各个选项进行判断即可，【详解】过Ｄ点作DH OB ⊥于H ，OD 平分AOB ∠，DE OA ⊥，DH OB ⊥，5DH DE ∴==，DF DH ≥，5DF ∴≥，故选A【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，也考查了垂线段最短，掌握角平分线的性质是解题的关键． 10．（2023春·河南开封·七年级统考期末）如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥于E ，则下列结论：①DE CD =；②AD 平分CDE ∠；③BAC BDE ∠=∠；④BE AC AB +=，其中正确的是（）A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】①根据角平分线的性质得出结论：DE CD =；②证明ACD AED △≌△，得AD 平分CDE ∠；③由四边形的内角和为360︒得180CDE BAC ∠+∠=︒，再由平角的定义可得结论是正确的；④由ACD AED ∆≅∆得AC AE =，再由AB AE BE =+，得出结论是正确的．【详解】解：①90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，DE CD ∴=；所以此选项结论正确；②DE CD =，AD AD =，90ACD AED ∠=∠=︒，ACD AED ∴≌，ADC ADE ∴∠=∠，AD ∴平分CDE ∠，所以此选项结论正确；③90ACD AED ∠=∠=︒，3609090180CDE BAC ∴∠+∠=︒−︒−︒=︒，180BDE CDE ∠+∠=︒，BAC BDE ∴∠=∠，所以此选项结论正确；④ACD AED ≌，AC AE ∴=，AB AE BE =+，BE AC AB ∴+=，所以此选项结论正确；本题正确的结论有4个，故选D ．【点睛】本题考查了全等三角形性质和判定，同时运用角平分线的性质得出两条垂线段相等；本题难度不大，关键是根据HL 证明两直角三角形全等，根据等量代换得出线段的和，并结合四边形的内角和与平角的定义得出角的关系．二、填空题七年级统考期末）如图，在ABC 中，ABC 的内部相交于点【答案】5【分析】先根据尺规作图描述得出AD 为BAC ∠的角平分线，再根据角平分线的性质得到点D 到AB 的距离5DE =，进而求出三角形的面积．【详解】由作法得AD 平分BAC ∠，如图所示，过点D 作DE AB ⊥于E ，∵90ACB ∠=︒，根据角平分线的性质，得43DC DE ==，ABD ∴的面积114102233AB DE AB =⋅⋅=⨯⨯=． ∴5AB =，故答案为：5．【点睛】本题考查角平分线的性质，解决本题的关键是熟知角平分线的性质并灵活应用．【答案】2【分析】根据尺规作图可得BF 平分ABC ∠，再利用角平分线的性质定理可得出2DF CF ==，最后根据垂线段最短即可得出FH 的最小值是2．【详解】解：如图，过点F 作FD AB ⊥于D ．由作图可知，BF 平分ABC ∠，∵FC BC ⊥，FD AB ⊥，∴2DF CF ==．根据垂线段最短可知，FH 的最小值为DF 的长，即为2．故答案为：2．【点睛】本题主要考查角平分线的性质，垂线段最短，解题的关键在于能够准确判断出BF 是ABC ∠的角平分线．13．（2023春·重庆沙坪坝·七年级重庆八中校考期末）如图，Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，E 为线段AC 上一点，连接DE ，且B CED ∠=∠．若16AB =，6CE =，则AE 的长为________．【答案】4【分析】过点D 作DF AB ⊥于点F ，由角平分线的性质得出DC DF =，证明DCE DFB ≌，得出BF CE =，求出AF ，由HL 证明Rt Rt ADC ADF ≌，得出AC AF =，即可求出结果．【详解】解：过点D 作DF AB ⊥于点F ，如图所示：∵90C ∠=︒，AD 平分BAC ∠交BC 于点D ，，∴DC DF =，在DCE △和DFB △中，90=BFD DCE B CEDDC DF ∠=∠=︒⎧⎪∠=∠⎨⎪⎩，∴()AAS DCE DFB ≌，∴6BF CE ==，∴10AF AB BF =−=，在Rt ADC 与Rt ADF 中，==DC DF AD AD ⎧⎨⎩，∴Rt Rt ADC ADF ≌，∴10AC AF ==，∴1064AE AC CE =−=−=．故答案为：4．【点睛】此题考查全等三角形的判定和性质和角平分线的性质，解题的关键是作出辅助线，构造全等三角形，根据HL 证明直角三角形的全等解答．【答案】30【分析】由作图可知OC 是AOB ∠的角平分线，根据角平分线的定义即可得到答案．【详解】解：由题意可知，OC 是AOB ∠的角平分线，∴11603022AOC AOB ∠=∠=⨯︒=︒．故答案为：30【点睛】此题考查角平分线的作图、角平分线相关计算，熟练掌握角平分线的作图是解题的关键．，则POD 的面积是【答案】6【分析】过点P 作PF OB ⊥交OB 于点F ，由作图可知OP 是AOB ∠的平分线，根据角平分线的性质得3PF PC ==，即可求得POD 的面积．【详解】解：如图，过点P 作PF OB ⊥交OB 于点F ，由作图可知，OP 是AOB ∠的平分线，∵PC OA ⊥，PF OB ⊥，∴3PF PC ==，∴POD 的面积为：162OD PF ⋅=，故答案为：6．【点睛】本题考查了尺规作角平分线以及角平分线的性质定理：角平分线上的点到角两边的距离相等．16．（2023春·山东泰安·七年级统考期末）如图，在锐角ABC 中，60BAC ∠=︒，BE 、CD 为ABC 的角平分线．且BE 、CD 交于点F ，连接AF ．有下列四个结论：①120BFC ∠=︒；②BD CE =；③BC BD CE =+；④FBD FEC FBC S S S +=△△△．其中结论正确的序号是__________ ．【答案】①③④【分析】根据角平分线的定义和三角形内角和定理求出BFC ∠；在BC 上取BM BD =，证明()SAS DBF MBF ≌△△，再证明()ASA MCF ECF ≌△△；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，根据角平分线的性质和三角形面积公式分别对各个结论进行判断即可．【详解】解：∵ABC 的两条角平分线BE 和CD 交于点F ，60BAC ∠=︒，∴FBC FCB∠+∠()12ABC ACB =∠+∠()11802BAC ︒=−∠()1180602=⨯︒−︒60=︒， ∴()180********BFC FBC FCB ∠=︒−∠+∠=︒−︒=︒，故结论①正确； ∴18060BFD BFC CFE Ð=°-Ð=°=Ð，在BC 上取BM BD =，∵BE 平分ABC ∠，∴DBF MBF Ð=Ð，在DBF 和MBF V 中，BD BM DBF MBFBF BF =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS DBF MBF ≌△△， ∴60BFD BFM ∠=∠=︒，∴1206060CFM BFC BFM ∠=∠−∠=︒−︒=︒，∴60CFM CFE ∠=∠=︒，∵CD 平分ACB ∠，∴MCF ECF ∠=∠，在MCF △和ECF △中，CFM CFE CF CFMCF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()ASA MCF ECF ≌△△， ∴CM CE =，∴BC BM CM BD CE =+=+，故结论③正确；∵没有条件得出点M 是BC 的中点，∴不能得出BD 与CE 一定相等，故结论②错误；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，∵BE 、CD 为ABC 的角平分线，∴FG FK =，FK FH =，∴FG FK FE ==， ∵12FBD S BD FG =⋅△，12FEC S EC FH =⋅△，12FBC S BC FK =⋅△，∴FBD FEC S S +△△1122BD FG EC FH =⋅+⋅ 1122BM FK MC FK =⋅+⋅ ()12BM MC FK =+⋅ 12BC FK =⋅FBC S =△，∴FBD FEC FBC S S S +=△△△，故结论④正确，∴结论正确的序号是①③④．故答案为：①③④．【点睛】本题考查角平分线的性质，全等三角形的判定与性质，三角形内角和定理，三角形的面积，作出辅助线构造全等三角形是解题的关键．三、解答题 17．（2023春·重庆江北·七年级统考期末）完成下面的解答过程，并填上适当的理由．已知：如图，DE BC ∥，BD 平分ABC ∠，EF 平分AED ∠．解： ∵DE BC ∥（已知）∴ABC AED ∠=∠（ ① ）．∵BD 平分ABC ∠，EF 平分∠∴112ABC ∠=∠，122AED ∠=∠【答案】两直线平行，同位角相等 2∠ 等量代换同位角相等，两直线平行【分析】先分析角的位置关系，根据平行线的性质及判定定理，即可写出答案．【详解】证明：∵DE BC ∥（已知），∴ABC AED ∠=∠．∵BD 平分ABC ∠，EF 平分AED ∠，∴112ABC ∠=∠，122AED ∠=∠．∴12∠=∠（等量代换）．∴EF BD ∥（同位角相等，两直线平行）．故答案为：两直线平行，同位角相等； 2∠ ；等量代换同位角相等，两直线平行．【点睛】本题主要考查平行线的性质（两直线平行，同位角相等），及平行线的判定方法（同位角相等，两直线平行）．牢记平行线的性质和判定方法是解题的关键．18．（2023春·山东泰安·七年级统考期末）如图，在AOB 和COD △中，OA OB =，OC OD =，OA OC <，36AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ．求证：(1)36AMB ∠=︒；(2)MO 平分AMD ∠．【答案】(1)证明见解析 (2)证明见解析【分析】（1）证明()SAS AOC BOD ≌△△，由三角形全等的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，可得出AMB ∠的度数；（2）作OG AC ⊥于G ，OH BD ⊥于H ，利用全等三角形对应边上的高相等，得出OG OH =，由角平分线的判定方法即可得证．【详解】（1）证明：∵36AOB COD ∠=∠=︒，∴AOB BOC COD BOC ∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS AOC BOD ≌△△， ∴OAC OBD ∠=∠，∵AEB ∠是AOE △和BME 的外角∴AEB AMB OBD AOB OAC ∠=∠+∠=∠+∠，∴36AMB AOB ∠=∠=︒；（2）如图所示，作OG AC ⊥于G ，OH BD ⊥于H ，∴OG 是AOC 中AC 边上的高，OH 是BOD 中BD 边上的高，由（1）知：AOC BOD ≌，∴OG OH =，∴点O 在AMD ∠的平分线上，即MO 平分AMD ∠．【点睛】本题考查全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识．证明三角形全等是解题的关键．七年级统考期末）如图，在ABC 中， (2)18【分析】（1）根据BD 平分ABC ∠，CD 平分ACB ∠得12DBC ABC ∠=∠，12DCB ACB ∠=∠，根据40ABC ∠=︒，70ACB ∠=︒得140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，根据三角形内角和定理即可得；（2）过点D 作DF BC ⊥于点F ，根据BD 平分ABC ∠，DE AB ⊥，DF BC ⊥得DE DF =，根据4DE =得4DF =，即可得．【详解】（1）解：∵BD 平分ABC ∠，CD 平分ACB ∠，∴12DBC ABC ∠=∠，12DCB ACB ∠=∠，∵40ABC ∠=︒，70ACB ∠=︒，∴140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，∴在BCD △中，1802035125BDC ∠=︒−︒−︒=︒；（2）解：过点D 作DF BC ⊥于点F ，∵BD 平分ABC ∠，DE AB ⊥，DF BC ⊥，∴DE DF =，∵4DE =，∴4DF =，∵9BC =， ∴11S 941822BCD BC DF =⨯⨯=⨯⨯=△．【点睛】本题考查了角平分线，三角形内角和定理，三角形的面积，解题的关键是理解题意，掌握这些知识点．八年级假期作业）如图，在ABC 中，【答案】6cm CD =，34B ∠=︒【分析】根据角平分线的性质可得CD DE =，28BAD CAD ∠=∠=︒，再根据直角三角形的两个锐角互余即可求出B ∠的度数．【详解】解：∵ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，∴6cm CD DE ==，28BAD CAD ∠=∠=︒，∴256BAC CAD ∠=∠=︒，∴9034B CAD ∠=︒−∠=︒．【点睛】本题考查了角平分线的性质定理和直角三角形的两个锐角互余，属于基础题型，熟练掌握角平分线的点到一个角的两边距离相等是解题关键．21．（2023春·广西南宁·七年级南宁十四中校考期末）如图，已知ABC ．(1)尺规作图：作BAC ∠的角平分线交BC 于点G （不写作法，保留作图痕迹）；(2)如果6AB =，10AC =，ABG 的面积为18，求ACG 的面积．【答案】(1)见解析(2)30【分析】（1）根据角平分线的尺规作图方法作图即可；（2）如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，证明AEF AFG △≌△，得到EG FG =，根据面积法求出6EG FG ==，再根据三角形面积公式求解即可．【详解】（1）解：如图所示：（2）解：如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，∴90AEG AFG ∠=∠=︒，∵AG 是BAC ∠的角平分线，∴EAG FAG ∠=∠，又∵AG AG =，∴()AAS AEF AFG △≌△，∴EG FG =；∵6AB =，ABG 的面积为18，∴1182AB EG ⋅=，即16182EG ⨯=，∴6EG =，∴6EG FG ==，∴111063022ACG S AC FG =⋅=⨯⨯=△．【点睛】本题主要考查了全等三角形的性质与判定，三角形面积，角平分线的尺规作图，角平分线的定义等等，灵活运用所学知识是解题的关键． 22．（2023春·山西太原·七年级统考期末）如图，在ABC 中，AD 是它的角平分线，DE AB ⊥于点,E DF AC ⊥于点F ，且BE CF =．线段BD 与CD 相等吗？说明理由．【答案】BD CD =，见解析【分析】根据角平分线的性质得出DE DF =，根据垂直定义得出90DEB DFC ∠=∠=︒，根据SAS 证明DFC △D E B ≌△，得出BD CD =即可．【详解】解：BD CD =；理由如下：∵AD 是BAC ∠的角平分线，DE AB ⊥，DF AC ⊥，∴DE DF =，∵DE AB ⊥，DF AC ⊥，∴90DEB DFC ∠=∠=︒，又∵BE CF =，∴DFC △DE B ≌△， ∴BD CD =．【点睛】本题主要考查了角平分线的性质，垂线定义理解，三角形全等的判定和性质，解题的关键是熟练掌握三角形全等的判定方法，证明DFC △DE B ≌△． 23．（重庆市大渡口区2022-2023学年七年级下学期期末数学试题）如图，AD BC ∥，180B BCD ∠+∠=︒．(1)用直尺和圆规完成以下基本作图：过点A 作BAD ∠的角平分线，交CD 于点F ，与BC 的延长线交于点E ；（不写做法，保留作图痕迹）(2)求证：CFE FEC ∠=∠．证明：∵AD BC ∥（已知），∴DAF FEC ∠=∠（①__________）． ∵AE 平分BAD ∠，∴②__________（角平分线的定义）． ∴BAE FEC ∠=∠（③__________）． ∵180B BCD ∠+∠=︒（已知）， ∴④__________（⑤__________）． ∴BAE CFE ∠=∠（两直线平行，同位角相等）． ∴CFE FEC ∠=∠（等量代换）．【答案】(1)见解析(2)见解析【分析】（1）利用基本作图作BAD ∠的平分线即可；（2）先根据平行线的性质得到DAF FEC ∠=∠，再利用角平分线的定义得到BAE DAF ∠=∠，则BAE FEC ∠=∠，接着证明AB CD ∥得到BAE CFE ∠=∠，然后利用等量代换得到CFE FEC ∠=∠．【详解】（1）解：如图，BE 为所作；（2）证明：AD BC ∥（已知）， DAF FEC ∴∠=∠（两直线平行，内错角相等）．AE 平分BAD ∠，BAE DAF ∴∠=∠（角平分线的定义），BAE FEC ∴∠=∠（等量代换）．180B BCD ∠+∠=︒（已知），AB CD ∴∥（同旁内角互补，两直线平行）．BAE CFE ∴∠=∠（两直线平行，同位角相等）．CFE FEC ∴∠=∠（等量代换）．【点睛】本题考查了作图−基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了角平分线的性质和平行线的判定与性质．七年级校考阶段练习）如图，ABC 中，若BCG 的面积为，则ABC 的面积为【答案】(1)120︒(2)3(3)6【分析】（1）根据作图方法可得BG 是ABC ∠的角平分线，则1302ABG ABC ==︒∠∠，再由三角形外角的性质可得120BGC A ABG =+=︒∠∠；（2）如图所示，过点G 作GD BC ⊥于D ，先求出3AG AC CG =−=，再证明ABG DBG △≌△，得到3DG AG ==，根据垂线段最短可知线段H G 的最小值为3；（3）证明BDG CDG △≌△，得到122BDG CDG BCG S S S ===△△△，进而求出2BDG ABG S S ==△△，则6ABC ABG CBG S S S =+=△△△．【详解】（1）解：由作图方法可知BG 是ABC ∠的角平分线， ∴1302ABG ABC ==︒∠∠，∵90A ∠=︒，∴120BGC A ABG =+=︒∠∠，故答案为：120︒；（2）解：如图所示，过点G 作GD BC ⊥于D ，∴90BAG BDG ==︒∠∠，∵96AC CG ==，，∴3AG AC CG =−=，∵BG 是ABC ∠的角平分线，∴ABG DBG ∠=∠，又∵BG BG =，∴()AAS ABG DBG △≌△，∴3DG AG ==，∵H 是边BC 上一动点，∴当点H 与点D 重合时，HG 最小，∴线段HG 的最小值为3，故答案为：3；（3）解：∵BG 是ABC ∠的角平分线，∴30ABG DBG ==︒∠∠，∵9030C ABC ∠=︒−∠=︒，∴GBD C ∠=∠，又∵90DG DG BDG CDG ===︒，∠∠，∴()AAS BDG CDG △≌△， ∴122BDG CDG BCG S S S ===△△△，∵ABG DBG △≌△，∴2BDG ABG S S ==△△，∴6ABC ABG CBG S S S =+=△△△，故答案为：6．【点睛】本题主要考查了全等三角形的性质与判定，三角形内角和定理，三角形外角的性质，角平分线的定义，角平分线的尺规作图等等，正确作出辅助线构造全等三角形是解题的关键．七年级统考期末）ABC 中， (2)如图2，若ABC 是锐角三角形．过点FED ∠，EDB ∠与ABC ∠ (3)若ABC 是钝角三角形，其中FED ∠，EDB ∠与ABC ∠之间的数量关系．【答案】(1)45 (2)12BDE FED ABC ∠=∠+∠，证明见解析 (3)12ABC BDE DEF ∠=∠+∠【分析】（1）首先证明AED ABC ∠=∠得到DE BC ∥，得到EDB DBC ∠=∠，再根据角平分线的定义得到1452DBC ABC ∠=∠=︒，即可证明；（2）延长ED 、BC 交于G ，利用平行线的性质得FED G ∠=∠，再利用三角形外角的性质可得结论；（3）由（2）同理解决问题．【详解】（1）解：DE AB ∵⊥，90AED ∴∠=︒．90ABC ∠=︒，AED ABC ∴∠=∠．DE BC ∴∥．EDB DBC ∴∠=∠．BD Q 平分ABC ∠，1452DBC ABC ∴∠=∠=︒．45EDB ∴∠=︒．（2）如图，12BDE FED ABC ∠=∠+∠，理由如下：延长ED 、BC 交于G ，EF BC ∥，FED G ∴∠=∠，BD Q 平分ABC ∠，。

角平分线的性质定理及其逆定理习题精选

角平分线的性质定理及其逆定理习题精选（二）1．三角形一内角的平分线与其相邻的外角的平分线所夹的角为__________度。

2．如图24-77，P是∠AOB内一点，PD⊥OB，PE⊥OA，垂足分别为D、E，且PD＝PE，若连结OP，则∠AOP 和∠BOP的关系是__________,你是如何知道的？3．下列说法中，错误的是（）。

A．三角形任意两个角的平分线的交点都在三角形内部B．三角形任意两个角的平分线的交点到三角形三边的距离相等C．三角形任意两个角的平分线的交点都在第三个角的平分线上D．三角形任意两个角的平分线的交点到三角形三个顶点的距离都相等4．如图24-78，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，EF交AD于点G。

求证：（1）AD⊥EF；（2）EG＝FG。

5．如图24-79，△ABC中，AB＝AC，M是BC的中点，MD⊥AB，ME⊥AC，D、E是垂足。

求证：MD＝ME。

6．如图24-80，BP、CP分别是△ABC的外角∠CBD、∠BCE的平分线。

求证：P在∠BAC的平分线上。

7．如图24-81，已知△ABC的周长为15，OB、OC分别平分∠ABC、∠ACB、OD⊥BC于点D，且OD＝4，求△ABC的面积。

8．如图24-82，∠B＝∠C＝90°，P是BC的中点，DP平分∠ADC，求证：AP平分∠DAB。

9．在一次军事演习中，红方侦察员发现蓝方指挥部设在A区内，到公路、铁路的距离相等，且离公路与铁路的交叉点B700m。

如果你是红方的指挥员，请你在图24-83所示作战图中标出蓝方指挥部的位置。

（用圆规、直尺作图，不写作法，保留作图痕迹。

比例尺：1参考答案1．902．相等3．D4．（1）先证明R t△AED≌R t△AFD，由AE＝AF，ED＝FD，得A、D都在EF的垂直平分线上，∴直线AD垂直平分EF、AD⊥EF（2）运用等腰三角形的性质：“三线合一”得FG＝EG5．连结AM，证明∠BAM＝∠CAM6．过P 作PF ⊥AB ，PG ⊥BC ，PH ⊥AE ，F 、G 、H 为垂足7．S ABC ∆＝30 8．过P 作PE ⊥AD 于点E ，∵DP 平分∠ADC ，PE ⊥AD ，PC ⊥CD ∴PE ＝PC ，∵PB ＝PC ，∴PE ＝PB ，∵PB ⊥AB ，∴点P 在∠DAB 的平分线上，即AP 平分∠DAB9．先求出图中距离：3．5cm ，然后作出角平分线，在线上找出距B 3．5 cm 的位置第1题. 2007广东茂名课改，4分）Rt 90ABC C BAC ∠∠ 在△中，＝，的角平分线AD 交BC 于点D ，2CD ＝，则点D 到AB 的距离是（）A ．1B ．2C ．3D ．4答案：B第2题. （2007浙江义乌课改，4分）如图，点P 是∠BAC 的平分线AD 上一点，PE ⊥AC 于点E ．已知PE =3，则点P 到AB 的距离是（）A ．3B ．4C ．5D ．6答案：A第3题. (2007广东课改，3分)到三角形三条边的距离都相等的点是这个三角形的（）Ａ．三条中线的交点Ｂ．三条高的交点Ｃ．三条边的垂直平分线的交点Ｄ．三条角平分线的交点答案：D1.已知：如图1，BE ，C F 是△ABC 的角平分线，B E ，CF 相交于D ，若∠A=50°，则∠BDC=（）A. 70°B.120°C.115°D.130°2.已知：如图2，△ABC 中，AB = AC ，BD 为∠ABC 的平分线，∠BDC = 60°，则∠A =（）A. 10°B. 20°C. 30°D. 40°3.三角形中，到三边距离相等的点是（）A.三条高线交点B.三条中线交点C.三条角平分线的交点D.三边的垂直平分线的交点4.已知P 点在∠AOB 的平分线上，∠AOB =60°，OP = 10 cm ，那么P 点到边OA 、OB 的距离分别是（）A. 5cm 、 cmB. 4cm 、5cmC. 5cm 、5cmD. 5cm 、10cm5.下列四个命题的逆命题是假命题的是（）A.直角三角形的两个锐角互余B.等腰三角形的两个底角相等C.全等三角形的对应角相等D.相等的两个角是对顶角6.已知：如图3，△ABC 中，∠C = 90°，点O 为△ABC 的三条角平分线的交点，OD ⊥BC ，OE ⊥AC ，OF ⊥AB ，点D 、E 、F 分别是垂足，且AB =10cm ，BC = 8cm ，CA = 6cm ，则点O 到三边AB ，AC 和BC 的距离分别等于（）cmA. 2、2、2B.3、3、3C. 4、4、4D. 2、3、5二、填空题1.命题：“两直线平行，同旁内角互补”的逆命题是______________，它是_________命题。

专题12.3 角平分线的性质讲练-2021年初中数学八年级上册同步讲练(教师版含解析)

专题12.3角平分线的性质典例体系一、知识点1.角的平分线的作法；2.角的平分线的性质定理：角的平分线上的点到角的两边的距离相等；3.证明一个几何中的命题，一般步骤：①明确命题中的已知和求证；②根据题意，画出图形，并用数学符号表示已知和求证；③经过分析，找出由已知推出求证的途径，写出证明过程；4.性质定理的逆定理：角的内部到角两边的距离相等的点在角的平分线上；二、考点点拨与训练考点1：角平分线性质定理及其应用典例：(2020·河北省初二期末)如图，在△ABC中，D是BC边上的点(不与点B，C重合)，连结AD(1)如图1,当点D是BC边上的中点时，则S△ABD:S△ACD=_________(直接写出答案)(2)如图2，当AD是∠BAC的平分线时，若AB=m，AC=n，S△ABD:S△ACD=_________(用含m,n的代数式表示)．(3)如图3，AD平分∠BAC，延长AD到E，使得AD=DE,连结BE，如果AC=2,AB=4,S△BDE=6,求△ABC的面积．【答案】(1)1：1；(2)m∶n；(3)9【解析】解：(1)过A作AE⊥BC于E，∵点D是BC边上的中点，∴BD=DC，∴S ABD：S△ACD=(12×BD×AE)：(12×CD×AE)=1：1，故答案为：1：1；(2)过D作DE⊥AB于E，DF⊥AC于F，∵AD为∠BAC的角平分线，∴DE=DF，∵AB=m，AC=n，∴S ABD：S△ACD=(12×AB×DE)：(12×AC×DF)=m：n；(3)∵AD=DE，∴由(1)知：S△ABD：S△EBD=1：1，∵S△BDE=6，∴S△ABD=6，∵AC=2，AB=4，AD平分∠CAB，∴由(2)知：S△ABD：S△ACD=AB：AC=4：2=2：1，∴S△ACD=3，∴S△ABC=3+6=9，故答案为：9．方法或规律点拨本题考查了角平分线性质和三角形的面积公式，能根据(1)(2)得出规律是解此题的关键．巩固练习1．(2019·广东省深圳外国语学校初一期末)如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为()A．152B．203C．3D．125【答案】D【解析】解：在AB上取一点G，使AG＝AF ∵在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4∴AB=5，∵∠CAD＝∠BAD，AE＝AE∴△AEF≌△AEG(SAS)∴FE＝FG∴CE+EF＝CE+EG则最小值时CG垂直AB时，CG的长度CG＝12 5故选D ．2．(2020·山东省济南外国语学校初二期中)如图，OP 平分∠AOB ，PA ⊥OA ，PB ⊥OB ，垂足分别为用A 、B ．下列结论中不一定成立的是()A ．PA ＝PEB ．PO 平分∠APBC ．AB 垂直平分OPD ．OA ＝OB【答案】C 【解析】解：∵OP 平分AOB ∠，PA OA ⊥，PB OB⊥∴PA PB =，选项A 正确；在Rt △AOP 和Rt △BOP 中，PO PO PA PB =⎧⎨=⎩，∴Rt △AOP ≅Rt △BOP∴APO BPO ∠=∠，OA=OB ，选项D 正确；∴PO 平分∠APB ，选项B 正确；由等腰三角形三线合一的性质，OP 垂直平分AB ，AB 不一定垂直平分OP ，选项C 错误．故选：C ．3．(2020·辽宁省初三其他)如图，在Rt ABC ∆中，90C ∠=︒，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若4CD =，15AB =，则ABD ∆的面积是()A ．15B ．30C ．45D ．60【答案】B 【解析】解：作DE ⊥AB 于E ，由基本尺规作图可知，AD 是△ABC 的角平分线，∵∠C ＝90°，DE ⊥AB ，∴DE ＝CD ＝4，∴△ABD 的面积＝12AB×DE ＝12×15×4＝30，故选：B ．4．(2020·南通市八一中学初一月考)如图，a 、b 、c 三条公路的位置相交成三角形，现决定在三条公路之间建一购物超市，使超市到三条公路的距离相等，则超市应建在()A ．三角形两边高线的交点处B ．三角形两边中线的交点处C ．∠α的平分线上D ．∠α和∠β的平分线的交点处【答案】D 【解析】∵如图，要建一超市到a 、b 、c 三条公路的距离相等，∴该超市是△ABC 的内心，∴超市应该建在∠α和∠β的平分线的交点处．故选：D ．5．(2020·河南省初三二模)如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是()A ．1B ．32C ．2D ．52【答案】C【解析】解：由作法得AG 平分BAC ∠，G ∴点到AC 的距离等于BG 的长，即G 点到AC 的距离为1，所以ACG ∆的面积14122=⨯⨯=．故选：C ．6．(2020·黑龙江省初二期末)如图所示，在△ABC 中，∠ACB=90°，BE 平分∠ABC ，DE ⊥AB 于点D ，如果AC=3cm ，那么AE+DE 等于()A ．2cmB ．3cmC ．4cmD ．5cm【答案】B 【解析】解：∵△ABC 中，∠ACB=90°，BE 平分∠ABC ，DE ⊥AB 于点D ，∴EC=DE ，∴AE+DE=AE+EC=3cm ．故选：B ．7．(2019·内蒙古自治区初二期中)如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，DE=DG ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为()A ．11B ．5.5C ．7D ．3.5【答案】B 【解析】作DM=DE 交AC 于M ，作DN ⊥AC ，∵DE=DG，∴DM=DE，∵AD是△ABC的角平分线，DF⊥AB，∴DE=DN，∴△DEF≌△DNM，∵△ADG和△AED的面积分别为50和39，∴S△MDG=S△ADG﹣S△AMG=590﹣39=11，S△DNM=S△DEF=S△MDG=1112 =5.58．(2019·陕西省交大附中分校初一期末)如图，在△ABC中，E为AC的中点，AD平分∠BAC，BA：CA=2：3，AD与BE相交于点O，若△OAE的面积比△BOD的面积大1，则△ABC的面积是()A．8B．9C．10D．11【答案】C【解析】解：作DM⊥AC于M，DN⊥AB于N．∵AD平分∠BAC，DM⊥AC于M，DN⊥AB于N，∴DM=DN，∴S△ABD：S△ADC=BD：DC=12•AB•DN：12•AC•DM=AB：AC=2：3，设△ABC的面积为S．则S△ADC=35S，S△BEC=12S，∵△OAE 的面积比△BOD 的面积大1，∴△ADC 的面积比△BEC 的面积大1，∴35S-12S=1，∴S=10，故选C ．9．(2020·湖北省武汉市江汉区教育局初二月考)在Rt △ABC 中，∠C=90°，AB=10，BC=8，AC=6.点I 为△ABC三条角平分线的交点，则点I 到边AB 的距离为__________【答案】2【解析】∵在△ABC 中，∠C=90°，BC=8，CA=6，AB=10，∵点I 为△ABC 的三条角平分线的交点，∴IE=IF=ID ，设IE=x ，∵S △ABC =S △IAB +S △IAC +S △ICB ，∴12×6×8=12IF×10+12IE×6+12ID×8，∴5x+3x+4x=24，∴x=2，∴点I 到AB 的距离等于2．故答案为：2.10．(2019·湖北省初二期中)如图，∠B =∠C =90°，DM 平分∠ADC ，AM 平分∠DAB ，CB =8，则点M 到BC 的距离_______．【答案】4【解析】如图，过点M 作ME ⊥AD 于E ，∵AM 平分∠DAB ，DM 平分∠ADC ，∠B=∠C=90°，∴BM=ME ，CM=EM ，∴BM=CM ，∵BC=8，∴1842BM =⨯=，∴ME=4，即点M 到AD 的距离为4．故答案为：4．11．(2020·上饶市广信区第七中学初二月考)如图，ABC 的三边AB BC CA 、、的长分别为405060、、，其三条角平分线交于点O ，则::ABO BCO CAO S S S =______．【答案】4:5:6【解析】解：过点O 作OD ⊥AB 于点D ，作OE ⊥AC 于点E ，作OF ⊥BC 于点F ，∵OA ，OB ，OC 是△ABC 的三条角平分线，∴OD=OE=OF ，∵△ABC 的三边AB 、BC 、CA 长分别为40、50、60，∴S △ABO ：S △BCO ：S △CAO =(12AB•OD)：(12BC•OF)：(12AC•OE)=AB ：BC ：AC=40：50：60=4:5:6．故答案为：4:5:6．12．(2019·眉山东辰国际学校初一期末)如图，BD 平分∠ABC ，DE ⊥AB 于E ，DF ⊥BC 于F ，AB ＝6，BC ＝8.若S △ABC ＝21，则DE ＝________．【答案】3【解析】∵BD 平分∠ABC ，DE ⊥AB ，DF ⊥BC ，∴DE =DF ，∵S △ABC =21，AB =6，BC =8，∴12×6×DE +12×8×DF =21，即7DE =21，∴DE =3.故答案为：3.13．(2019·深圳市明德外语实验学校初二期中)如图：在△ABC 中，∠C =90°，AD 是∠BAC 的平分线，DE ⊥AB 于E ，F 在AC 上，BD =DF .(1)求证：CF=EB ．(2)若AF =2,EB =1,求AB 的长.【答案】(1)证明见解析；(2)4【解析】(1)证明：∵AD 是∠BAC 的平分线，∠C=90°，DE ⊥AB ，∴DC=DE ，∵BD=DF ，∴Rt △DCF ≌Rt △DEB(HL)，∴CF=EB ；(2)由(1)知CF=EB=1，∴AC=AF+FC=3，又∵∠C=∠AED=90°，∠CAD=∠EAD ，AD=AD ，∴△ACD ≌△AED(AAS)∴AC=AE=3，∴AB=AE+EB=3+1=4．14．(2020·凌海市石山镇初级中学初一月考)已知OM 是AOB ∠的平分线，点P 是射线OM 上一点，点C 、D 分别在射线OA 、OB 上，连接PC 、PD ．(1)发现问题如图①，当PC OA ⊥，PD OB ⊥时，则PC 与PD 的数量关系是________．(2)探究问题如图②，点C 、D 在射线OA 、OB 上滑动，且∠AOB =90°，∠OCP ＋∠ODP =180°，当PC PD ⊥时，PC 与PD 在(1)中的数量关系还成立吗？说明理由．【答案】(1)PC=PD ；(2)PC=PD 仍然成立．理由见解析．【解析】解：(1)∵OM 是∠AOB 的平分线，PC ⊥OA ，PD ⊥OB ，∴PC=PD ，故答案为：PC=PD ；(2)PC=PD 仍然成立．理由如下：过P 分别作PE ⊥OB 于E ，PF ⊥OA 于F，∴∠CFP=∠DEP=90°，∵OM 是∠AOB 的平分线，∴PE=PF ．∵∠OCP ＋∠ODP=180°，又∠ODP+∠PDE=180°，∴∠OCP=∠PDE ，即∠FCP=∠PDE ，在△CFP 和△DEP 中，CFP DEP FCP PDE PF PE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CFP ≌△DEP(AAS)，∴PC=PD ．考点2：角平分线性质定理的逆定理及其应用典例：(2020·四川省初二期中)如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E 作AC边的垂线，垂足为N，过点E作AB延长线的垂线，垂足为M.(1)求证：BM=CN；(2)若，AB=2，AC=8，求BM的长.【答案】(1)证明见解析；(2)3.【解析】证明：连接BE，CE，如图，∴DE是BC的垂直平分线，∴BE=CE，∵AE是∠BAC的平分线，EM⊥AB，EN⊥AC，∴EM=EN，在Rt△BME和Rt△CNE中，＝＝，∴Rt△BME≌Rt△CNE(HL)，∴BM=CN(2)由(1)得：EM=EN，在Rt△AME和Rt△ANE中，＝＝，∴Rt△AME≌Rt△ANE(HL)，∴AM=AN，又∵AM=AB+BM,AN=AC-CN∴AB+BM=AC-CN∴2+BM=8-CN,又∵BM=CN∴BM=CN=3方法或规律点拨本题考查全等三角形的判定和性质、角平分线的性质，解题的关键是掌握角平分线的性质以及具体的应用．巩固练习1．(2020·福州四十中金山分校初二月考)小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是()A．角的内部到角的两边的距离相等的点在角的平分线上B．角平分线上的点到这个角两边的距离相等C．三角形三条角平分线的交点到三条边的距离相等D．以上均不正确【答案】A【解析】如图所示：过两把直尺的交点C作CF⊥BO与点F，由题意得CE⊥AO，∵两把完全相同的长方形直尺，∴CE=CF ，∴OP 平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上)，故选A ．2．(2020·湖北省中考真题)如图，已知ABC 和ADE 都是等腰三角形，90BAC DAE ∠=∠=︒，,BD CE 交于点F ，连接AF ，下列结论：①BD CE =；②BF CF ⊥；③AF 平分CAD ∠；④45AFE ∠=︒．其中正确结论的个数有()A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】解：∵∠BAC=∠EAD∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE在△BAD 和△CAE 中AB=AC,∠BAD=∠CAE,AD=AE∴△BAD ≌△CAE∴BD=CE故①正确；∵△BAD ≌△CAE∴∠ABF=∠ACF∵∠ABF+∠BGA=90°、∠BGA=∠CGF∴∠ACF+∠BGA=90°,∴∠BFC=90°故②正确；分别过A 作AM ⊥BD 、AN ⊥CE 垂足分别为M 、N∵△BAD ≌△CAE∴S △BAD =S △CAE ,∴1122BD AM CE AN ⋅=⋅∵BD=CE∴AM=AN∴AF 平分∠BFE ，无法证明AF 平分∠CAD ．故③错误；∵AF 平分∠BFE ，BF CF⊥∴45AFE ∠=︒故④正确．故答案为C ．3．(2020·四川省正兴中学初二二模)已知，如图，ABC 中，90C ∠=︒，点O 为ABC 的三条角平分线的交点，OD 垂直BC ，OE AC ⊥，OF AB ⊥，点D 、E 、F 分别是垂足，且10cm AB =，8cm BC =，6cm CA =，则OF =__________．【答案】2cm【解析】解：连接OA 、OB 、OC ，如图，点O 为ABC ∆的三条角平分线的交点，OD 垂直BC ，OE AC ⊥，OF AB ⊥，OD OE OF ∴==，设OF x =，则OD OE x ==，AOC BOC AOB ACB S S S S ∆∆∆∆++=，∴11116810682222x x x ++=⨯⨯，解得2x =，即OF 的长为2cm ．故答案为：2cm ．4．(2020·甘肃省平川区四中初二期中)如图，在Rt △ABC 中，∠A=90°，点D 为斜边BC 上一点，且BD=BA ，过点D 作BC 的垂线交AC 于点E ．求证：点E 在∠ABC 的角平分线上．【答案】证明见解析．【解析】证明：连接BE，∵ED⊥BC，∴∠BDE=∠A=90°．在Rt△ABE和Rt△DBE中∵BE BE {BA BD＝＝，∴Rt△ABE≌Rt△DBE(HL)．∴∠ABE=∠DBE．∴点E在∠ABC的角平分线上．5．(2020·甘州区南关学校初二月考)如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．(1)求证：△BCE≌△DCF；(2)求证：AB+AD=2AE.【答案】详见解析【解析】(1)证明：∵AC是角平分线，CE⊥AB于E，CF⊥AD于F，∴CE=CF，∠F=∠CEB=90°，在Rt△BCE和Rt△DCF中，BC DC CE CF=⎧⎨=⎩∴△BCE≌△DCF；(2)解：∵CE⊥AB于E，CF⊥AD于F，∴∠F=∠CEA=90°，在Rt△FAC和Rt△EAC中，AC AC CE CF=⎧⎨=⎩，∴Rt△FAC≌Rt△EAC，∴AF=AE，∵△BCE≌△DCF，∴BE=DF，∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.6．(2019·云龙县第三中学初二期中)如图，BE⊥AC、CF⊥AB于点E、F，BE与CF交于点D，DE=DF，连接AD．求证：(1)∠FAD=∠EAD；(2)BD=CD．【答案】(1)证明见解析；证明见解析.【解析】证明：(1)∵BE⊥AC、CF⊥AB，DE=DF，∴AD是∠BAC的平分线，∴∠FAD=∠EAD；(2)∵△ADF与△ADE是直角三角形，DE=DF，AD=AD，∴Rt△ADF≌Rt△ADE，∴∠ADF=∠ADE，∵∠BDF=∠CDE，∴∠ADF+∠BDF=∠ADF+∠CDE，即∠ADB=∠ADC，在△ABD≌△ACD中，{FAD EADAD AD ADB ADC∠=∠=∠=∠，∴△ABD ≌△ACD ，∴BD=CD.7．(2018·江苏省初二期中)已知：如图BAC ∠中，BF AC ⊥，CE AB ⊥，垂足分别为F 、E ，BF 交CE 于点D ，BD CD =，求证：D 点在BAC ∠的平分线上．【答案】证明见解析【解析】证明：连接AD，∵BF AC ⊥，CE AB ⊥，∴∠BED=∠CFD=90°，在△BDE 与△CDF 中，BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BDE ≌△CDF(AAS)，∴DE=DF ，∴AD 是∠BAC 的角平分线，∴D 点在BAC ∠的平分线上．考点3：与角平分线有关的尺规作图典例：(2020·河北省中考真题)如图1，已知ABC ∠，用尺规作它的角平分线．如图2，步骤如下，第一步：以B 为圆心，以a 为半径画弧，分别交射线BA ，BC 于点D ，E ；第二步：分别以D ，E 为圆心，以b 为半径画弧，两弧在ABC ∠内部交于点P ；第三步：画射线BP ．射线BP 即为所求．下列正确的是()A ．a ，b 均无限制B ．0a >，12b DE >的长C ．a 有最小限制，b 无限制D ．0a ≥，12b DE <的长【答案】B【解析】第一步：以B 为圆心，适当长为半径画弧，分别交射线BA ，BC 于点D ，E ；∴0a >；第二步：分别以D ，E 为圆心，大于12DE 的长为半径画弧，两弧在ABC ∠内部交于点P ；∴12b DE >的长；第三步：画射线BP ．射线BP 即为所求．综上，答案为：0a >；12b DE >的长，故选：B ．方法或规律点拨本题主要考查了基本作图，解决问题的关键是掌握作角平分线的方法．巩固练习1．(2020·广西壮族自治区初三其他)如图尺规作业，OC 为AOB ∠的平分线，这样的作法依据是()A ．SSSB ．SASC ．ASAD ．AAS【答案】A【解析】连接CE 、CD，在△OEC 和△ODC 中，CE CD OC OC OE OD =⎧⎪=⎨⎪=⎩，∴△OEC ≌△ODC(SSS)，故选：A ．2．(2020·河南省初二月考)如图，△ABC 中，点E ，F ，G 分别在BC ，AC ，AB 上，AE 与BF 交于点O ，且点O 在CG 上，根据尺规作图的痕迹，判断下列说法不正确的是()A ．AE ，BF 是△ABC 的角平分线B ．点O 到△ABC 三边的距离相等C ．CG 也是△ABC 的一条角平分线D ．AO ＝BO ＝CO【答案】D 【解析】A 、由尺规作图的痕迹可知：AE 、BF 是△ABC 的内角平分线，正确；B 、因为角平分线的点到角两边的距离相等得：点O 到△ABC 三边的距离相等，正确；C 、根据三角形三条角平分线交于一点，且点O 在CG 上，所以CG 也是△ABC 的一条内角平分线，正确D 、三角形三边中垂线的交点到三个顶点的距离相等，所以选项D 不正确；故选D ．3．(2020·新疆维吾尔自治区初三其他)如图，在AOB ∠中，尺规作图如下：在射线OA 、OB 上，分别截取OD 、OE ，使OD OE =；分别以点D 和点E 为圆心、大于12DE 的长为半径作弧，两弧相交于点C ；作射线OC ，连结CE 、CD .下列结论不一定．．．成立的是()A ． OE EC=B ．CE CD =C ．OEC ODC ∠=∠D ．ECO DCO∠=∠【答案】A 【解析】解：根据题意，得：OE=OD ，CE=CD ，OC=OC ，∴△OEC ≌△ODC (SSS)，∴OEC ODC ∠=∠，ECO DCO ∠=∠，∴B 、C 、D 三项是正确的，而 OE EC =不一定成立．故选：A ．4．(2020·广东省仙田外国语学校初一期中)如图所示，已知∠AOB=40°，现按照以下步骤作图：①在OA ，OB 上分别截取线段OD ，OE ，使OD=OE ；②分别以D ，E 为圆心，以大于12DE 的长为半径画弧，在∠AOB 内两弧交于点C ；③作射线OC ．则∠AOC 的大小为_________．【答案】20°．【解析】根据画图的方法可知：OC 是∠AOB 的角平分线，∴∠AOC=40°÷2=20°．故答案是：20°．5．(2020·内蒙古自治区初二期末)如图，在Rt △ABC 中，∠C ＝90°，以点A 为圆心，任意长为半径画弧，分别交AC 、AB 于点M 、N ，再分别以M 、N 为圆心，任意长为半径画弧，两弧交于点O ，作射线AO 交BC 于点D ，若CD ＝3，P 为AB 上一动点，则PD 的最小值为_____．【答案】3【解析】根据作图的过程可知，AD是∠BAC的平分线．根据角平分线上的点到角的两边距离相等，又因为点到直线的距离，垂线段最短可得PD最小=CD=3.故答案为:3.6．(2020·湖南省中考真题)人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：已知：AOB∠求作：AOB∠的平分线做法：(1)以O为圆心，适当长为半径画弧，交OA于点M，交OB于点N，(2)分别以点M，N为圆心，大于12MN的长为半径画弧，两弧在AOB∠的内部相交于点C(3)画射线OC，射线OC即为所求．请你根据提供的材料完成下面问题：(1)这种作已知角平分线的方法的依据是__________________(填序号)．①SSS②SAS③AAS④ASA(2)请你证明OC为AOB∠的平分线．【答案】(1)①；(2)证明见解析【解析】(1)根据作图的过程知道：OM=ON，OC=OC，CM=CM，所以由全等三角形的判定定理SSS可以证得△EOC≌△DOC，从而得到OC为AOB∠的平分线；故答案为：①；(2)如图，连接MC 、NC ．根据作图的过程知，在△MOC 与△NOC 中，OM ON OC OC CM CN ⎧⎪⎨⎪⎩＝＝＝，∴△MOC ≌△NOC(SSS)，∠AOC=∠BOC ，∴OC 为AOB ∠的平分线．7．(2020·云南省初三二模)如图所示，在△ABC 中，按以下步骤作图：①以点B 为圆心，任意长为半径作弧，分别交BA 、BC 于点M 、N ；再以点N 为圆心，MN 长为半径作弧交前面的弧于点F ，作射线BF 交AC 的延长线于点E ．②以点B 为圆心，BA 长为半径作弧交BE 于点D ，连接CD ．请你观察图形，解答下列问题：(1)求证：△ABC ≌△DBC ；(2)若∠A =100°，∠E =50°，求∠ACB的度数．【答案】(1)见解析；(2)∠ACB =65°．【解析】(1)如图所示，连接MN ，NF ，由作图可得，BM=BF ，MN=FN ，BN=BN ，∴△BMN ≌△BFN(SSS)，∴∠ABC=∠DBC ，又∵AB=DB ，BC=BC ，∴△ABC ≌△DBC(SAS)；(2)∵∠A=100°，∠E=50°，∴∠ABE=30°，∴∠ABC=12∠ABD=15°，∴∠ACB=180°-∠A-∠ABC=180°-100°-15°=65°．8．(2019·广西壮族自治区初一期末)如图，平面内有A ，B ，C ，D 四点，请按要求完成：(1)尺规作图：连接AB ，作射线CD ，交AB 于点E ，作射线EF 平分CEB ∠．须保留作图痕迹，且用黑色笔将作图痕迹描黑，不写作法和证明．(2)在(1)的条件下，若100AEC ∠=︒，求CEF ∠的度数．【答案】(1)作图见解析；(2)40.CEF ∠=︒【解析】解：(1)作线段AB ，作射线CD ，如图，即为所做图形；(2)100AEC ∠=︒，射线EF 平分CEB ∠，11(180)(180100)22CEF AEC ∴∠=︒-∠=⨯︒-︒40=︒9．(2020·佛山市南海外国语学校初三月考)如图，已知在ABC 中，点D 在边AC 上，且AB AD =．(1)用尺规作图法，作BAC ∠的平分线AP ，交BC 于点P ；(保留作图痕迹，不要求写作法)(2)在(1)的条件下，连接PD ．求证：PD PB =．【答案】(1)见解析；(2)见解析【解析】(1)如图，射线AP 为所求作的图形；(2)∵CP 是∠ACB 的平分线，如图：∴∠1=∠2，在△ABP 和△ADP 中，12AB AD AP AP =⎧⎪∠=∠⎨⎪=⎩，∴△ABP ≅△ADP(SAS)，∴PD=PB ．。

角平分线的性质定理的逆定理同步练习(2020年最新)

1.4 角平分线的性质第2课时角平分线的性质定理的逆定理要点感知角平分线的性质定理的逆定理：角的内部到角的两边距离相等的点在__________上.预习练习如图，P是∠MON内一点，PE⊥OM于点E，PF⊥ON于点F，若PE=PF，则OP平分∠MON，其依据是____________________.知识点角平分线的判定1.如图，点D在BC上，DE⊥AB，DF⊥AC，且DE=DF，∠BAD=25°，则∠CAD=( )A.20°B.25°C.30°D.50°第1题图第2题图第3题图2.如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是( )A.线段CD的中点B.OA与OB的中垂线的交点C.OA与CD的中垂线的交点D.CD与∠AOB的平分线的交点3.如图，已知点P在射线BD上，PA⊥AB，PC⊥BC，垂足分别为A，C，且PA=PC，下列结论错误的是( )A.AD=CPB.点D在∠ABC的平分线上C.△ABD≌△CBDD.∠ADB=∠CDB4.如图，是一个风筝骨架.为使风筝平衡，须使∠AOP=∠BOP.已知PC⊥OA，PD⊥OB，那么PC和PD应满足__________，才能保证OP为∠AOB的角平分线.第4题图第5题图5.如图，△ABC中，∠C=90°，∠A=36°，DE⊥AB于D，且EC=ED，则∠EBC的度数为__________.6.如图：在△ABC中，∠C=90°，DF⊥AB，垂足为F，DE=BD，CE=FB.求证：点D在∠CAB的角平分线上.7.如图，已知BE⊥AC，CF⊥AB，垂足分别为E，F，BE，CF相交于点D，若BD=CD.求证：AD平分∠BAC.8.下列说法：①角的内部任意一点到角的两边的距离相等；②到角的两边距离相等的点在这个角的平分线上；③角的平分线上任意一点到角的两边的距离相等；④△ABC中∠BAC的平分线上任意一点到三角形的三边的距离相等，其中正确的有( )A.1个B.2个C.3个D.4个9.如图，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论①AS=AR；②QP∥AR；③△BPR≌△QSP中( )A.全部正确B.仅①和②正确C.仅①正确D.仅①和③正确第9题图第10题图10.如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有( )A.1处B.2处C.3处D.4处11.点O是△ABC内一点，且点O到三边的距离相等，∠A=50°，则∠BOC=__________.12.如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE=CF.求证：AD是△ABC的角平分线.13.如图，某校八年级学生分别在M，N两处参加植树劳动，现要在道路AB，AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，请你找出点P.14.已知：如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.(1)若连接AM，则AM是否平分∠DAB？请你证明你的结论；(2)线段DM与AM有怎样的位置关系？请说明理由.参考答案要点感知角的平分线预习练习角平分线定理的逆定理1.B2.D3.A4.PC=PD5.27°6.证明：∵DF⊥AB，∠C=90°，∴∠DFB=∠C=90°.在Rt△CED和Rt△FBD中，DE=DB,CE=FB,∴△CED≌△FBD(HL).∴DC=DF.∵DF⊥AB，DC⊥AC，∴点D在∠CAB的角平分线上.7.证明：∵BE⊥AC，CF⊥AB，∴∠BFD=∠CED=90°.在△BDF与△CDE中，∠BFD=∠CED，∠BDF=∠CDE，BD=CD，∴△BDF≌△CDE(AAS).∴DF=DE.∴AD是∠BAC的平分线.8.B 9.B 10.D 11.115°12.证明：∵DE⊥AB，DF⊥AC，∴△BDE和△DCF是直角三角形.∵BD=CD，BE=CF，∴Rt△BDE≌Rt△CDF(HL).∴DE=DF.又∵DE⊥AB，DF⊥AC，∴AD是△ABC的角平分线.13.作法：(1)作出∠BAC的平分线AD；(2)连接MN，作MN的垂直平分线EF交AD于点P.∴点P就是所求的点.图略.14.(1)AM平分∠DAB.证明：过点M作ME⊥AD，垂足为 E.∵DM平分∠ADC，∴∠1=∠2.∵MC⊥CD，ME⊥AD，∴ME=MC.又∵MC=MB，∴ME=MB.∵MB⊥AB，ME⊥AD，∴AM平分∠DAB.(2)AM⊥DM.理由：∵∠B=∠C=90°，∴DC⊥CB，AB⊥CB.∴CD∥AB.∴∠CDA+∠DAB=180°.又∵∠1=12∠CDA，∠3=12∠DAB，∴2∠1+2∠3=180°.∴∠1+∠3=90°.∴∠AMD=90°，即AM⊥DM.。

角平分线的性质定理及其逆定理习题精选及答案(一)

角平分线的性定理及其逆定理习题精选（一）1．（1）在角的平分线上的点到这个角的________相等。

（2）到一个角的_______相等的点，在这个角的平分线上。

2．如图，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则下列结论中错误的是（）A．PC＝PDB．OC＝ODC．∠CPO＝∠DPOD．OC＝PC3．如图，△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：①AD上任意一点到点C，点D的距离相等；②AD上任意一点到AB，AC的距离相等；③AD⊥BC且BD＝CD；④∠BDE＝∠CDF，其中正确的个数是（）A．1个B．2个C．3个D．4个4．如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA于D，PE⊥OB于E，求证：OD ＝OE，∠OPD＝∠OPE5．已知，如图，点A、B在OP上，AC⊥OM于点C，AD⊥ON于点D，BE⊥OM于点E，BF ⊥ON于点F，且AC＝AD，求证：BE＝BF。

6．如图，点D、点P在∠ABC的平分线上，PA⊥BA，PC⊥BC，A、C为垂足，求证：AD ＝CD，∠ADB＝∠CDB。

7．下列命题正确的是（）A．三角形一个外角等于两个内角的和B．有两边和一角对应相等的两个三角形一定全等C．有两边对应相等的两个直角三角形全等D．到角的两边距离相等的点在这个角的平分线上8．下列定理中有逆定理的是（）A．对顶角相等B．全等三角形的对应角相等C．同位角相等D．角平分线上的点到这个角的两边距离相等9．已知，如图，BD是∠ABC的平分线，AB＝BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N，求证：PM＝PN。

10．已知，△ABC中，P是角平分线AD、BE的交点，求证：点P在∠C的平分线上。

11．如图，在△ABC 中，请证明：（1）若AD 为角平分线，则ABD ACD S AB S AC∆∆=。

（2）设D 为BC 上一点，连结AD ，若ABD ACD S AB S AC ∆∆=，则AD 为角平分线。

角的平分线的性质(2)

13.3
角平分线的性质（2）
复习回顾
1、角平分线性质定理：角的平分线上的点到角的两边的距离相等.
∵点P在∠AOB的平分线上且PM⊥OB，PN⊥OA， N A P C B
∴PM＝PN M 2、角平分线性质定理的逆定理：到角的两边的距离相等的点在角的平分线上.
∵ PM⊥OB，PN⊥OA 且PM＝PN. ∴点P在∠AOB的平分线上.
A
想一想
B
N
D P E
FM
C
点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系？
三角形的三条角平分线相交于一点，并且这点到三边的距离相等。
练习
1、如图， △ABC的∠B的外角的平分线BD与∠C的外角的平分线 CE相交于点P。求证：点P到三边AB，BC，CA所在直线的距离相等。 C P D E
； / 外汇；
了五十岁之后,各方面都开始衰退了,俺…是有心无力啊！" "是啊！" 夜白虎也跟着幽幽一叹说道："俺们三人二十年前就已经突破了圣人境,现在却还是修炼到二重,这成神之路,太难了.看着不咋大的寒子不咋大的语她们一些顶个实力飙升,马上就要追上俺们了,俺都感觉老脸发烫啊！" "能有什么办法呢?这修炼道路越年轻境界越高,成神の几率就越高.但是年轻の时候能达到像不咋大的寒子の境界の大陆以前有吗?老祖宗当年突破圣人境好像也到了三十多岁吧?俺说你呀们两人别想太多,这种机缘可遇不可求.俺反正是看开了,该玩の玩过了,该享受の享受了,也没什么遗憾了.这最后一步能不能迈出,就看天意了,至少俺们努力过了,入土之前也不会后悔,不是吗?"夜青牛性格大大咧咧の,说起话来也很无所顾忌,有些东西几多看得开. "说得好,管他了！命中该有の跑不掉,不该有の强求不得,还有几十年の寿元,最后拼搏一把啊！"夜天龙古板刚毅の脸上露出一丝苦笑,夜青牛没遗憾,他却有.只是他一直不善表达出来而已.月惜水,一直是他心口永远不能抚平の伤. "咻！" 就在这时,远处传来一阵破空声.三人都同时停止了谈论,而后全部笑意盈盈の站了起来,朝门外走去. "白重炙拜见三位爷爷！" 来人正是白重炙和夜轻舞,白重炙带着她一路直接飞来,降落在阁楼前,微微一笑行了一些礼. "拜见三位爷爷,哎呀！爷爷,你呀这么受伤了?严重吗?"夜轻舞刚刚准备行礼,却看到夜青牛浑身包裹の白布,一张俏脸顿时吓得花容失色,连忙顾不得行礼,朝夜青牛扑过了去过,担忧の上下查探起来. "丫头,大惊不咋大的怪什么.都嫁了人了,怎么还这么不稳重?身为练家子,受伤是常事,有什么奇怪の?你呀爷爷是谁?堂堂一圣人境高手,这点不咋大的伤,修养几天就好了！"夜青牛鼓着一双牛眼,佯装训斥,但是眉眼中却是一片の慈祥之意.他显然不想,在夜天龙和夜白虎以及白重炙面前丢了脸面. "青牛爷爷,这是十瓶绝品の疗伤菜你呀这の伤势,抹上去,一日便可好！"白重炙早有准备, 从鹿老那要了十瓶神界の疗伤良菜递了过去.他知道夜轻舞如果看到夜青牛の伤势恐怕会担心の不得了,到时候怕是又要闹着停留几日了. "爷爷,快进去,俺给你呀抹上！"夜轻舞接过瓶子,想到马上就要离去,眼角都是泪水,扶着夜青牛往里边走去. 一番忙活,这疗伤菜果然神奇,一抹上,伤口便迅速以肉眼可见の速度变好了.夜天龙和夜白虎在白重炙の坚持下也无奈之好也抹了一遍. 最后三老回归大厅,白重炙让夜轻舞陪着三人,也没有过多の解释.而是直接移形换位去了寒心阁将月倾城和夜轻语也带来了. "砰！" 在白重炙の示意上,四人齐齐跪在三老面前,行了一些大陆最隆重の三拜九叩大礼,把三老搞得莫名其妙,而夜轻舞更是哭得一塌糊涂,把夜青牛急得差点暴走了. "三位爷爷,等会轻寒就会带着她们远离雾霭城,这一去…也不知什么时候才能回来给你呀们三人尽孝了.你呀们先不要着急着问,等俺把话说完…这是俺和老祖宗共同决定の事情,至于原因,老祖宗会告诉你呀们.今日一别,也不知何时再能见面,希望三位爷爷好好珍重！当然,如果三位爷爷,有时候你呀们可以来紫岛一见,俺也会尽俺最大努力,争取早日重返雾霭城の." 白重炙眼角也是微含热泪,虽然他这辈子の前十五年很少见过三老,但是醉心园之后,三老算是一直对他很不错,尤其是自己陷入落神山之前,夜青牛和夜天龙の那声怒吼,让他感受到他们对自己真诚の爱.当然这或许和自己实力暴涨有关系,但是至少那一刻开始,他开始接受了这三人. "这是一枚天神巅峰の神晶,你呀们三人可以选择一人炼化.这…算是临行前,俺送给你呀们の礼物！" 说完,白重炙掏出一些青色玉盒递给夜天龙,带着三人再次重重の叩下.最后带着哭得稀里糊涂の夜轻舞,强忍住内心の悲伤,毅然转身离去.白重炙知道这时候只能快刀斩乱麻,否则恐怕好几天都走不了了. "这…族长,这是怎么回事?"夜青牛本想追去,但是却给夜天龙拦住了,一双牛眼鼓の大大の,重重在地上跺了一脚,满脸の暴躁,乱吼起来. "急什么青牛,你呀没听到不咋大的寒子说俺们日后可以去紫岛见她们吗?俺已经传讯给老祖宗了,等他来了在问清楚吧.哎…发生了什么事情?竟然严重到要去紫岛避难の地步了?" 夜天龙狠狠瞪了夜青牛一眼,似乎在责怪他轻重不分.夜白虎此刻却还震撼在白重炙送给白家の天神巅峰神晶.两人被夜天龙一说都惊醒过来,白重炙刚刚实力大进,为破仙府破解了一些大危机,现在却要匆匆离去.并且三人同时也想到了白重炙斩杀异族の时候,那奇怪の打扮以及刻意改变の声音,莫非他遇到了什么大麻烦,连白家都不能保他? "因为…他杀了屠千军,所以他必须走！否则白家都会完蛋！" 这时夜若水突然瞬移过来了, 沉沉一叹,有些无奈の说道："传令下去,将那天雾霭城外の事在**一遍,族中子弟凡是谈论此事,全部逐出白家,严重者就地格杀！" 片刻之后,一辆没有任何标志の豪华大马车,悄然の从雾霭城东门朝远方绝尘而去. 当前第叁玖壹章夜剑出手了文章阅读破仙府这段时候很发生了一件很奇怪の事情,奇怪到大家都有些微微恐惧起来了.看书前几日在雾霭城参加过那场大战,劫后余生の所有强者,都不约而同再次接到了一些来自破仙府最高级别の命令.同样の意思,就是严禁谈论传播那场大战の那张巨脸,以及那个黑袍人.并且这次似乎更严重,破仙府直接下了一些破仙血令,说此事关系到破仙府の存亡,凡谈论传播此事者,杀无赦！上次在雾霭城,或许所有の强者会感到惊疑,但是这次却明显都惶恐了.这事情显然看起来非常严重,都严重到破仙府の存亡了,谁还敢在谈论?不少人已经偷偷和别人谈起过の,连忙开始擦屁股补救起来,而不少人则打算把这事烂在了肚子里. 很明显,夜若水の两次禁言起了很大作用.大陆所有の神级强者虽然在那一日大战の时候,都有用神识过来偶尔查探.但是因为怕触怒金麒却没敢将神识散发在战场中央,而后来那张巨脸出现之后,更是连远远查探都不敢了. 直到战事完毕之后,那张巨脸和异族全部消失之后,他们才敢慢慢将神识辐散过来.却发现异族已经全部消失了.但是那一刻很明显,他们都以为是因为噬大人出手了,把异族杀の杀,赶の赶,这才平息了这场灭世危机. 蛮神府隐岛,在庆幸暗喜同时,开始纷纷打探起事情の经过.而妖神府神城在暗骂の同时,也开始四处打探起那日发生の事情. 夜若水の第一条传音起了作用,当夜虽然有无数の神识锁定了雾霭城广场の帝王境练家子.但是后面却无人在谈论.他们只是隐隐听到,似乎有个黑袍强者,拯救了破仙府? 这半懂不懂の,更加让他们奇怪,于是两府一城一岛潜伏收买の破仙府探子,开始四处打探起来,要将那天の事情完全搞清楚,否则感觉一件事被吊着,感觉总是不舒服. 只是在破仙府第二道禁口令下,都没有查探出什么确切の情报.这下更是了不得了,几番势力本来还没太大注意,现在破仙府几次禁口令,将这事悟得那么紧,一点风声不透.这…里面没有隐藏什么天大の秘密,谁也不相信了.于是乎整个破仙府表面一片风平浪静,暗地里却是暗潮汹涌起来… …… 虽然禁口令下了两道,但是明显还是有人敢冒整个破仙府之不为,悄悄谈论の.比如夜剑就有这个胆子. 夜剑一直是个势利心很重の人,年轻の时候他天赋一样,被夜刀压了几十年,但是他一直隐忍着.那次夜刀固执の去了落神山,他认为是个机会,于是他果断出手了,结果他赢了,夜刀死了. 大房在他の静心经营之下,在白家,在破仙府北方一手遮天.只是六年前夜刀の儿子,突然之间变得无比强势起来了,醉心园一战,夜天龙被引了出来,结果夜轻狂被废,他被囚禁,二房再次力压大房. 他没有放弃,继续隐忍,在后山,因为没有俗事缠身,他

角平分线的性质与判定的习题

B E
M
D
A
FN
C
18.如图，已知△ABC的周长为10，OB、OC 分别平分∠ABC.∠ACB、OD⊥BC于点D，且OD＝2，求△ABC的面积。
A
O
B
D
C
19.如图Rt△ABC中，∠C=90。AC=BC,AD是 ∠BAC
的平分线，DE⊥AB于E,
求证: △DBE的周长等于ABB长
E
D
C
A
4.如图所示，三条公路两两相交，交点分别为 A、B.C，现计划修一个油库，要求到三条公
路的距离相等，可供选择的地址有（ D ）
A. 一处 B. 二处 C.三处 D. 四处
5.如图，OP平分∠MON，PA⊥ON于点A，点Q是射
线OM上的一个动点，若PA=2,则PQ的最小值为
（B）
A. 1
B. 2
C. 3
用数学语言表示为: ∵ QD⊥OA，QE⊥OB，QD＝QE. ∴点Q在∠AOB的平分线上.
练习题 :
1.如图，已知△ABC的外角∠CBD和∠BCE的平分线相交于点F，
求证: 点F在∠DAE的平分线上．
证明:过点F作FG⊥AE于G, FH⊥AD于H, FM⊥BC于M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC ∴FG＝FM
D. 4
6.如图所示, 在△ABC中, ∠C＝90°, AD平分
∠BAC, AE＝AC, 下列结论中错误的是（ D ）
A. DC＝DE
B. ∠AED＝90°
C. ∠ADE＝∠ADC D. DB＝DC
7.如图所示, △ABC中, ∠C＝90°, AC＝BC, AD
平分∠CAB交BC于D, DE⊥AB于E, 且AB＝6cm,

角的平分线精讲精练(含解答)

角的平分线【基础知识精讲】角平分线是过角的顶点，且在角的内部的一条射线，它把一个角分成两个相等的角，它与角的两边三线共点.(角的顶点)角平分线是到角两边距离相等的所有点的集合.关于这一点需从两个方面去说明：①角平分线上的点到角两边的距离相等.②到角两边距离相等的点在角平分线上.进而推广到一般，若要证明某一图形B 是满足条件A 的点的集合，要说明两点：①图形B 上的所有点满足条件A.②满足条件A 的所有点都在图形B 上.关于命题“角平分线上的点到角两边距离相等”的证明，先要分清题目的题设部分及结论部分.依照命题准确作出图形，写出已知、求证，再利用相关知识进行证明，这也是证明一个命题(定理)的几个基本步骤.角平分线性质定理及其逆定理(判定定理)的证明分别利用了全等三角形中“AAS ”定理及“HL ”公理.本节还介绍了互逆命题及互逆定理，两个命题若条件（题设）与结论位置互换，即一个命题条件是另一个命题的结论，同时它的结论是另一命题的条件，则两命题互为逆命题.若一个定理的逆命题是真命题，则称逆命题为该定理的逆定理.这两个定理互为逆定理.应当注意，每个命题都有逆命题，每个定理也有逆命题，但不一定有逆定理，只有当逆命题正确而成为定理时，才是原定理的逆定理.一个命题的正确与否与它的逆命题正确与否无关.难点：是“角平分线是到角两边距离相等的点的集合”这一结论的理解及运用.例1 △ABC 中，∠C=90°，AD 为角平分线，BC=64，BD ∶DC=9∶7,求D 到AB 的距离.(图3.9-1)图3.9-1分析设DE 为D 到AB 的距离，由角平分线性质CD=DE ，再由已知可求CD 、DE. 解作DE ⊥AB 于E ，∵∠C=90°，DC ⊥AC ，又AD 为∠BAC 平分线，∴DC=DE ，BC=64，BD ∶DC=9∶7∴DC=167×64=28 ∴DE=28 例2 求证：三角形三条内角平分线交于一点.分析此类命题证明需先作图，写出已知、求证，再根据条件进行证明.证明三直线共点，常用方法之一为二直线的交点必在第三条直线上，此题中，可考虑如图3.9-2，设∠ABC 与∠ACB 的平分线交于O ，再证AO 平分∠BAC.图3.9-2已知：△ABC 中，AA ′，BB ′，CC ′为角平分线，求证AA ′，BB ′，CC ′交于一点.证设BB ′，CC ′交于O ，过O 分别作OD ⊥BC 于D ，DE ⊥AC 于E ，OF ⊥AB 于F ，∵O 在∠ABC 平分线上，∴OD=OF.O 在∠ACB 平分线上，∴OE=OD ∴OE=OF.∴O 在∠BAC 平分线上，即O 在AA ′上，∴AA ′，BB ′，CC ′交于一点.注：该点称为三角形内心.例3 定理“末位数字为0的整数能被5整除”是否存在逆定理？请说明理由.分析先写出逆命题：“能被5整除的整数末位数字是0”，再说明逆命题的真假，显然这是一个假命题，我们只需举一反倒即可，例如15能被5整除，但末位数字为5，故逆命题为假命题，因此原定理没有逆定理例4 判断命题“两整数相加，和为整数”的逆命题的真假.解逆命题为“和为整数，则两加数必为整数”，它是一个假命题，如“21+21=1，31+35=2”等，都能说明逆命题为假命题.【难题巧解点拨】例1 △ABC 的周长为41cm,边BC=17cm,角平分线AD 将△ABC 分为面积比为3∶5的两部分，且AB ＜AC ，求AB ，AC.(图3.9-3)图3.9-3分析设AB=x,AC=y,则有x+y+17=41，而S △ABD ∶S △ADC =3∶5,此条件不好利用，故考虑AD 为角平分线，它到两边的距离相等，即△ABD 中AB 边上的高，△ADC 中AC 边上的高相等，从得求出x ∶y,进而求出x,y.解作DE ⊥AB 于E ，DF ⊥AC 于F.∵AD 为角平分线∴DE=DF∵AB ＜AC ，∵S △ABD ∶S △ADC =（21DE ·AB ）∶（21DF ·AC ）=AB ∶AC=3∶5 ∴x+y+17=41 x ∶y=3∶5 (x ＜y)∴x=9,y=15 即AB=9cm, AC=15cm.例2 “三角形两内角平分线的交点到三角形三边距离相等”这一命题的逆命题是真命题还是假命题？图3.9-4分析先要写出逆命题：到三角形三边距离相等的点是两内角平分线的交点.该命题是一个假命题.例如：图3.9-4，P 为△ABC 的两外角∠MBC 和∠NCB 的角平分线交点.此时P 到三边AB 、AC 、BC 的距离PD=PF=PE.而P 不为△ABC 的内角平分线交点.注意：不要误以为过点向△ABC 三边的作垂线那么垂足一定都落在边上，也可落在边延长线上，从这里入手证明逆命题为一假命题.【同步达纲练习】一、判断（3分×8=24分）( )1.P 为∠AOB 内一点，C 在OA 上，D 在OB 上，若PC=PD ，则OP 平分∠AOB.( )2.到角两边距离不相等的一点一定不在角平分线上.( )3.因为“三内角对应相等的两个三角形全等”是假命题，所以它的逆命题也是假命题.( )4.三角形三条角平分线交于一点，且这一点到三顶点的距离相等.( )5.任何命题都有逆命题.( )6.任何定理都有逆定理.( )7.“三角形三条角平分线交点到三边距离相等”这个命题的逆命题是真命题.( )8.有命题“若x=y ，则x 2=y 2”的逆命题是个假命题.二、填空(4分×8=32分)1.角平分线是到角的两边相等的所有点的 .2.三角形三内角平分线，该点到三边的距离 .3.“对顶角相等”的逆命题是，它是一个命题.4.P 在∠MON 的角平分线上，PA ⊥OM 于A ，PB ⊥ON 于B ，PA+PB=12，则PA= ，PB= .5.一个定理的是正确的时，我们称它为原定理的 .6.“直角三角形有两个角是锐角”这个命题的逆命题是，它是一个命题.7.定理“同位角相等，两直线平行”的逆定理是 .三、选择(5分×6=3分)1.下列说法正确的是( )A.每个命题都有逆命题B.每个定理都有逆定理C.真命题的逆命题也是真命题D.假命题的逆命题是假命题2.P 、Q 为∠AOB 内两点，且∠AOP=∠POQ=∠QOB=31∠AOB ，PM ⊥OA 于M ，QN ⊥OB 于N ，PQ ⊥OP,则下面结论正确的是( )A.PM ＞QMB.PM=QNC.PM ＜QND.PM=PQ3.下列关于三角形角平分线的说法错误的是( )A.两角平分线交点在三角形内B.两角平分线交点在第三个角的平分线上C.两角平分线交点到三边距离相等D.两角平分线交点到三顶点距离相等4.下列命题中，正确的命题有几个( )①对顶角相等;②相等的角是对顶角;③不是对顶角的两个角就不相等;④不相等的角不是对顶角A.1个B.2个C.3个D.0个5.设a,b为实数，下面四个命题.①若a＞b, 则a2＞b2②若a2＞b2, 则a＞b③若a＞b，则a2＞b2④若a2＞b2则a＞b其中正确的有( )A.1个B.2个C.3个D.4个6.下列命题真命题是( )A.同位角相等B.同旁内角相等，两直线平行C.不相等的角不是内错角D.同旁内角不互补，两直线不平行四、解答题(7分×2=14分)1.如图3.9-6，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等，求证∠AOP=∠BOP.图3.9-62.△ABC的外角∠CBD，∠BCE的角平分线交于点F，求证AF平分∠BAC.【素质优化训练】1.如图3.9-7，AB=AC，AD=AE，BD、CE交于O，求证AO平分∠BAC.图3.9-72.△ABC 中，AB=BC=CA ，三内角平分线交于O ，OP ⊥AB 于P ，OM ⊥BC 于M ，ON ⊥CA 于N ，AH ⊥BC 于H.求证OP+OM+ON=AH.【生活实际运用】1.如图(3.9-8)，某铁路MN 和公路PQ 相交于点O ，且交角为90°,某仓库G 在A 区，到公路、铁路距离相等(即G 在∠NOQ 的平分线上)，且到公路与铁路的相交点O 的距离为200m.(1)在图上标出仓库G 的位置(比例尺1∶10000,用圆规作图，保留作图痕迹，不写作法)：(2)求出仓库G 到铁路的实际距离.图3.9-8参考答案：【同步达纲练习】一、1.× 2.√ 3.× 4.× 5.√ 6.× 7.× 8.√二、1.距离，集合 2.交于一点，相等 3.相等的角是对顶角，假 4.6，6 5.逆命题，逆定理 6.有两个锐角的三角形是直角三角形，假 7.两直线平行，同位角相等三、1.A 2.C 3.D 4.B 5.B 6.D四、1.作PM ⊥OA 交OA 延长线于M PN ⊥OB 交OB 延长线于N.∵S △OPA =S △OPB ∴21OA ·PM=21OB ·PN OA=OB ∴PM=PN ∴∠AOP=∠BOP 2.提示：过F 分别作三边的垂线FM ，FP ，FN. 易证FM=FP=FN ，再利用角平分线性质可得结论.【素质优化训练】1.作OM ⊥AB 于M ，ON ⊥CD 于N. AB=AC ∠BAD=∠CAE. AD=AE∴△ABD ≌△ACE ∴S △ABD =S △ACE ∴S △BOE =S △COD .又BE=CD ∴OM=ON ∴AO 平分∠BAC.2.S △ABC =S △OAB +S △OAC +S △OBC .21AH ·BC=21OP ·AB+21BC ·OM+21AC ·ON 又AB=BC=CA ∴OP+OM+ON=AH.【生活实际运用】(1)略 (2)1002(m)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

角平分线性质定理及逆定理练习
一．选择题（共11小题）
1．（2011•衢州）如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射
线OM 上的一个动点，若PA=2，则PQ 的最小值为（）
A ．1
B ． 2
C ． 3
D ． 4
2．（2011•恩施州）如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足
为F ，DE=DG ，△ADG 和△AED 的面积分别为50和39，则△EDF
的面积为（）
3．（2010•柳州）如图，Rt △ABC 中，∠C=90°，∠ABC 的平分线BD 交AC
于D ，若CD=3cm ，则点D 到AB 的距离DE 是（）
A ． 5cm
B ． 4cm
C ． 3cm
D ．
2cm
4．（2010•鄂州）如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点
E ，D
F ⊥AC 交AC 于点F ．S △ABC =7，DE=2，AB=4，则AC 长是（）
A ． 4
B ． 3
C ． 6
D ．
5
5．（2009•临沂）如图，OP 平分∠AOB ，PA ⊥OA ，PB ⊥OB ，垂足分别为
A ，
B ．下列结论中不一定成立的是（）
A ． P A=P
B B ． P O 平分∠APB
C ． O A=OB
D ．
A B 垂直平分OP
6．（2007•中山）到三角形三条边的距离都相等的点是这个三角形的（）
A ．三条中线的交点
B ．三条高的交点
C ．三条边的垂直平分线的交点
D ．三条角平分线的交点
7．（2006•贵港）已知：如图，AD 是△ABC 的角平分线，且AB ：AC=：，则△ABD 与△ACD 的面积之比为（）
A ． 11
B ． 5.5
C ． 7
D ． 3.5
A ．
3：2 B ．： C ． 2：3 D ．：
8．（2005•仙桃潜江江汉）如图，折叠直角三角形纸片的直角，使点C
落在AB上的点E处．已知BC=12，∠B=30°，则DE的长是（）
A．6B．4C．3D．2
9．（2004•内江）如图，∠AOB=30°，OP平分∠AOB，PC∥OB，PD⊥OB，
如果PC=6，那么PD等于（）
A．4B．3C．2D．1
10．（2000•天津）如图，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，
PS⊥AC于S，则三个结论①AS=AR；②QP∥AR；③△BPR≌△QSP
中（）
A．全部正确B．仅①和②正确C．仅①正确D．仅①和③正确11．（2000•安徽）如图，直线l1、l2、l3表示三条相互交叉的公路，现要建
一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有
（）
A．1处B．2处C．3处D．4处
二．填空题（共4小题）
12．（2012•通辽）如图，△ABC的三边AB、BC、CA长分别为40、
50、60．其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO=
_________．
13．（2011•岳阳）如图，AD∥BC，∠ABC的角平分线BP与∠BAD的
角平分线AP相交于点P，作PE⊥AB于点E．若PE=2，则两平行线AD
与BC间的距离为_________．
14．（2011•随州）如图，△ABC的外角∠ACD的平分线CP与
内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP=
_________．
15．（2011•河南）如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD⊥CD，∠ADB=∠C．若P是BC边上一动点，则DP长的最小值为
_________．
三．解答题（共4小题）
16．（2011•牡丹江）在△ABC中，∠ACB=2∠B，如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD．
（1）如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想：
（2）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．
17．（2010•西宁）（1）班同学上数学活动课，利用角尺平分一个角（如图所示）．设计了如下方案：
（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．
（Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．
（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由；
（2）在方案（Ⅰ）PM=PN的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB．此方案是否可行？请说明理由．
18．（2007•福州）如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）
（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；
（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）
（3）当动点P落在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．
19．（2002•东城区）如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC，求证：OB=OC．。