工程流体力学(第二版)习题答案2010.
工程流体力学课后习题答案

工程流体力学(第二版)习题与解答1 2p p 2 1 V 第 1 章 流体的力学性质1-1 用压缩机压缩初始温度为 20℃的空气,绝对压力从 1 个标准大气压升高到 6 个标准大气压。
试计算等温压缩、绝热压缩、以及压缩终温为 78℃这三种情况下,空气的体积 减小率∆V = (V 1 - V 2 )/V 1 各为多少?解:根据气体压缩过程方程: pV k = const ,有(V /V ) = ( p / p )1/ k ,所以2112(V -V ) V ⎛ p ⎫1/ k ∆ = 1 2 = 1 - 2= 1 - 1 ⎪VV V p 1 1 ⎝ 2 ⎭ 等温过程 k =1,所以∆V = 1 - p 1 / p 2 = 1 -1/ 6 =83.33%绝热过程 k =1.4,所以 ∆ = 1 - ( p / p )1/1.4= 1 - (1/ 6)1/1.4 =72.19% 压缩终温为 78℃时,利用理想气体状态方程可得∆ = 1 - V 2 = 1 - p 1T 2 = 1 - 1⨯ 78=80.03% V 1 p 2T 1 6 ⨯ 201-2 图 1-12 所示为压力表校验器,器内充满体积压缩系数 β = 4.75 ⨯10-10 m 2/N 的油, 用手轮旋进活塞达到设定压力。
已知活塞直径 D =10mm ,活塞杆螺距 t =2mm ,在 1 标准大气压时的充油体积为 V 0=200cm 3。
设活塞周边密封良好,问手轮转动多少转,才能达到 200 标准大气压的油压(1 标准大气压=101330Pa )。
解:根据体积压缩系数定义积分可得:β = - 1 d V → V = V exp[-β ( p - p )]pV d pp因为 ntπ D 24 = V 0 - V = V 0 ⎩⎣1 - e x p - β p ( p - p 0 ) ⎤⎦所以n = 4 V ⎡1 - e - β ( p - p )⎤ = 12.14 rpmπ D 2t 0 ⎣⎦0.05mm1kN20°图 1-12 习题 1-2 附图图 1-13 习题 1-3 附图1-3 如图 1-13 所示,一个底边为200mm ⨯ 200mm 、重量为 1kN 的滑块在 20°斜面的油膜上滑动,油膜厚度 0.05mm ,油的粘度μ= 7 ⨯10-2 Pa·s 。
流体力学第二版课后习题答案

答案 :第一章习题答案选择题(单选题)1.1 按连续介质的概念,流体质点是指:(d)(a )流体的分子;(b)流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
1.2 作用于流体的质量力包括:(c)(a )压力;(b)摩擦阻力;(c )重力;(d)表面张力。
1.3 单位质量力的国际单位是:(d )(a )N ;(b )Pa ;(c)kg N /;(d )2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是:(b )(a)剪应力和压强;(b )剪应力和剪应变率;(c)剪应力和剪应变;(d )剪应力和流速。
1.5 水的动力黏度μ随温度的升高:(b )(a )增大;(b )减小;(c )不变;(d )不定。
1.6 流体运动黏度ν的国际单位是:(a )(a )2/s m ;(b )2/m N ;(c )m kg /;(d )2/m s N ⋅。
1.7 无黏性流体的特征是:(c )(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RT p=ρ。
1.8 当水的压强增加1个大气压时,水的密度增大约为:(a )(a )1/20000;(b)1/10000;(c)1/4000;(d)1/2000. 1.9 水的密度为10003kg/m ,2L 水的质量和重量是多少? 解:10000.0022m V ρ==⨯=(kg )29.80719.614G mg ==⨯=(N )答:2L 水的质量是2kg ,重量是19.614N 。
1.10 体积为0.53m 的油料,重量为4410N ,试求该油料的密度是多少? 解:44109.807899.3580.5m G g V V ρ====(kg/m 3) 答:该油料的密度是899.358kg/m 3。
1.11 某液体的动力黏度为0.005Pa s ⋅,其密度为8503/kg m ,试求其运动黏度。
解:60.005 5.88210850μνρ-===⨯(m 2/s )答:其运动黏度为65.88210-⨯m 2/s 。
《工程流体力学》习题参考答案

闻建龙主编的《工程流体力学》习题参考答案第一章 绪论1-1 物质是按什么原则分为固体和液体两大类的?解:从物质受力和运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。
如空气、水等。
而在同等条件下,固体则产生有限的变形。
因此,可以说:流体不管是液体还是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。
与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。
1-2 何谓连续介质假设?引入连续介质模型的目的是什么?在解决流动问题时,应用连续介质模型的条件是什么?解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。
流体连续性假设是流体力学中第一个根本性假设,将真实流体看成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可看成时间和空间位置的连续函数,使我们有可能用数学分析来讨论和解决流体力学问题。
在一些特定情况下,连续介质假设是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm )内的流动。
1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水和C 020时密度为3856m kg 的原油时,移动平板所需的力各为多大?题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水: 233/410416101m N u=⨯⨯=⋅=--δμτN A F 65.14=⨯=⋅=τ油: 233/8.2810416102.7m N u=⨯⨯=⋅'=--δμτ N A F 2.435.18.28=⨯=⋅=τ1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律是直线。
(完整版)工程流体力学课后习题(第二版)答案

第一章绪论31-1. 20C的水2.5m,当温度升至80C时,其体积增加多少?[解]温度变化前后质量守恒,即V 2V3又20C时,水的密度i 998.23kg /m380C 时,水的密度 2 971.83kg/m3V2— 2.5679m323则增加的体积为V V V i 0.0679m1-2.当空气温度从0C增加至20C时,运动粘度增加15%,重度减少10%,问此时动力粘度增加多少(百分数)?[解](1 0.15)原(1 0.1)原1.035原原1.035原原 1.035原原0.035原原此时动力粘度增加了 3.5%1-3•有一矩形断面的宽渠道,其水流速度分布为u 0.002 g(hy 0.5y2)/ ,式中、分别为水的密度和动力粘度,h为水深。
试求h 0.5m时渠底(y=0)处的切应力。
[解]——0.002 g(h y)/dy0.002 g(h y) dy当h =0.5m , y=0 时0.002 1000 9.807(0.5 0)9.807Pa1-4.一底面积为45 x 50cm2,高为1cm的木块,质量为5kg,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s,油层厚1cm,斜坡角22.620(见图示),求油的粘度。
[解]木块重量沿斜坡分力F与切力T平衡时,等速下滑mg sindu T Adymg sin A U 5 9.8 sin 22.621 0.4 0.45 -0.0010.1047 Pa s1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律沿y方向的分布图。
3 3 5 2 [解] A dl 3.14 0.8 10 20 10 5.024 10 m 石,定性绘出切应力1-6 •为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径的粘度=0.02Pa. s。
若导线以速率50m/s拉过模具,试求所需牵拉力。
0.9mm,长度20mm,涂料(1.O1N)yU 50 5F R A 0.02 3 5.024 10 1.01Nh 0.05 10 31-7.两平行平板相距0.5mm,其间充满流体,下板固定,上板在2Pa的压强作用下以0.25m/s匀速移动,求该流体的动力粘度。
工程流体力学第二版习题答案解析-[杜广生]
![工程流体力学第二版习题答案解析-[杜广生]](https://img.taocdn.com/s3/m/69030e8165ce0508763213b5.png)
《工程流体力学》习题答案(杜广生主编)第一章 习题1. 解:依据相对密度的定义:1360013.61000f w d ρρ===。
式中,w ρ 表示4摄氏度时水的密度。
2. 解:查表可知,标准状态下:231.976/CO kg m ρ=,232.927/SO kg m ρ=,231.429/O kg m ρ=,231.251/N kg m ρ=,230.804/H O kg m ρ= ,因此烟气在标准状态下的密度为:112231.9760.1352.9270.003 1.4290.052 1.2510.760.8040.051.341/n nkg m ρραραρα=++=⨯+⨯+⨯+⨯+⨯=3. 解:(1)气体等温压缩时,气体的体积弹性模量等于作用在气体上的压强,因此,绝对压强为4atm的空气的等温体积模量:34101325405.310T K Pa =⨯=⨯ ;(2)气体等熵压缩时,其体积弹性模量等于等熵指数和压强的乘积,因此,绝对压强为4atm 的空气的等熵体积模量:31.44101325567.410S K p Pa κ==⨯⨯=⨯式中,对于空气,其等熵指数为1.4。
4. 解:根据流体膨胀系数表达式可知:30.0058502V dV V dT m α=⋅⋅=⨯⨯=因此,膨胀水箱至少应有的体积为2立方米。
5. 解:由流体压缩系数计算公式可知:392511050.5110/(4.90.98)10dV V k m N dp -⨯÷=-=-=⨯-⨯ 6. 解:根据动力粘度计算关系式:74678 4.2810 2.910Pa S μρν--==⨯⨯=⨯⋅7. 解:根据运动粘度计算公式:3621.310 1.310/999.4m s μνρ--⨯===⨯8. 解:查表可知,15摄氏度时空气的动力粘度617.8310Pa s μ-=⨯⋅,因此,由牛顿内摩擦定律可知:630.317.83100.2 3.36100.001U F AN h μπ--==⨯⨯⨯⨯=⨯ 9. 解:如图所示,高度为h 处的圆锥半径:tan r h α=,则在微元高度dh 范围内的圆锥表面积:2=2=tan cos cos dh h dA rdh παπαα由于间隙很小,所以间隙内润滑油的流速分布可看作线性分布,则有:===tan d r h υυωωαυδδδ则在微元dh 高度内的力矩为:332===2tan tan tan tan cos cos h h dM dA r dh h h dh ωαπαωατμαπμδαδα⋅⋅因此,圆锥旋转所需的总力矩为:33430==2=24tan tan cos cos H H M dM h dh ωαωαπμπμδαδα⎰⎰10. 解:润滑油与轴承接触处的速度为0,与轴接触处的速度为轴的旋转周速度,即:=60n Dπυ 由于间隙很小,所以油层在间隙中沿着径向的速度分布可看作线性分布,即:=d dy υυδ则轴与轴承之间的总切应力为:==T A Db υτμπδ克服轴承摩擦所消耗的功率为:2==P T Db υυμπδ因此,轴的转速可以计算得到:60=r/min n D υπ11.解:根据转速n 可以求得圆盘的旋转角速度:2290===36060n ππωπ⨯ 如图所示,圆盘上半径为r 处的速度:=r υω,由于间隙很小,所以油层在间隙中沿着轴向的速度分布可看作线性分布,即:=d dy υυδ则微元宽度dr 上的微元力矩:3233==2=2=6r dM dA r rdr r r dr r dr ωπμτμππμπδδδ⋅⋅ 因此,转动圆盘所需力矩为:4422322-30(2)0.40.23==6=6=6 3.14=71.98N m 40.23104DD M dM r dr μμππδδ⨯⨯⨯⋅⨯⎰⎰12. 解:摩擦应力即为单位面积上的牛顿内摩擦力。
工程流体力学第二版答案
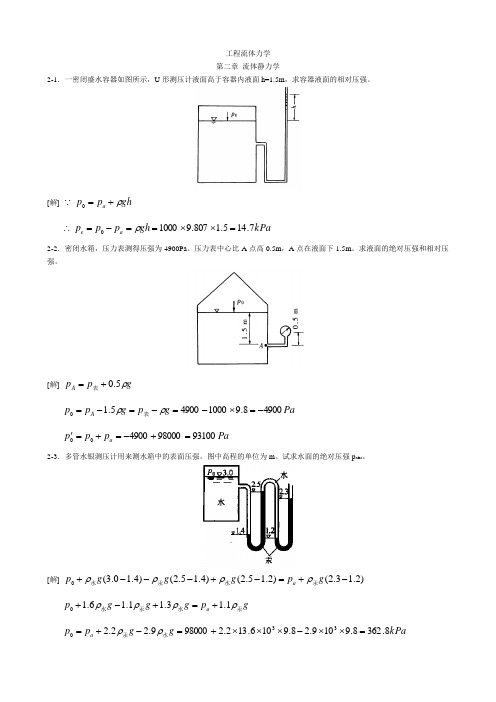
工程流体力学 第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
[解] gh p p a ρ+=0kPa gh p p p a e 7.145.1807.910000=⨯⨯==-=∴ρ2-2.密闭水箱,压力表测得压强为4900Pa 。
压力表中心比A 点高0.5m ,A 点在液面下1.5m 。
求液面的绝对压强和相对压强。
[解]g p p A ρ5.0+=表Pa g p g p p A 49008.9100049005.10-=⨯-=-=-=ρρ表 Pa p p p a 9310098000490000=+-=+=' 2-3.多管水银测压计用来测水箱中的表面压强。
图中高程的单位为m 。
试求水面的绝对压强p abs 。
[解])2.13.2()2.15.2()4.15.2()4.10.3(0-+=-+---+g p g g g p a 汞水汞水ρρρρ g p g g g p a 汞水汞水ρρρρ1.13.11.16.10+=+-+kPa g g p p a 8.3628.9109.28.9106.132.2980009.22.2330=⨯⨯-⨯⨯⨯+=-+=水汞ρρ2-4. 水管A 、B 两点高差h 1=0.2m ,U 形压差计中水银液面高差h 2=0.2m 。
试求A 、B 两点的压强差。
(22.736N /m 2)[解] 221)(gh p h h g p B A 水银水ρρ+=++Pa h h g gh p p B A 22736)2.02.0(8.9102.08.9106.13)(33212=+⨯⨯-⨯⨯⨯=+-=-∴水水银ρρ2-5.水车的水箱长3m,高1.8m ,盛水深1.2m ,以等加速度向前平驶,为使水不溢出,加速度a 的允许值是多少?[解] 坐标原点取在液面中心,则自由液面方程为:x gaz -=0 当m lx5.12-=-=时,m z 6.02.18.10=-=,此时水不溢出 20/92.35.16.08.9s m x gz a =-⨯-=-=∴2-6.矩形平板闸门AB 一侧挡水。
工程流体力学课后习题答案解析(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τ Pa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
工程流体力学课后习题答案(第二版)【范本模板】

第一章 绪论1-1.20℃的水2。
5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1—2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1—3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力. [解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1—4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s,油层厚1cm ,斜坡角22。
620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yuATmgddsinμθ==001.0145.04.062.22sin8.95sin⨯⨯⨯⨯==δθμuAmgsPa1047.0⋅=μ1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律yuddμτ=,定性绘出切应力沿y方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过.已知导线直径0.9mm,长度20mm,涂料的粘度μ=0.02Pa.s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 分别表示加入的盐溶液和流出的盐溶液的质量流量, 分别表示加入的盐溶液和流出的盐溶液中盐的质量分数; 分别为搅拌槽内流体的瞬时总质量和初始质量。
由质量守恒方程,得水和盐的总质量平衡关系为
由质量守恒方程,得食盐组分的质量平衡关系为
由牛顿剪切定律可得,轴表面处在转速为U时,流体所受的剪切力为:
由功率消耗公式得,消耗的功率为:
W
1-3解:由公式 得:
m
所以:高度差d=-h=11.81mm
1-4
解:对液面上任一点A,设液面内侧压力为 ,外侧压力为 ,由拉普拉斯表面张力公式,得:
(1)(R为液面所在圆的半径,趋于∞)
由已知得:
(2)
又因为: (3)
由(1)、(2)、(3)三式联立,得:
(4)
其特征方程为:
解之得:
所以:方程(4)的通解为:
所以:
当x趋向于∞时, =0故 =0
当x=0时,
故
所以:
当x=0时,
第二章流体运动学基本概念
2-1解:由拉格朗日流场:
判断是否稳态流动
则
此流场非稳态流动
判断是否不可压流场
不可压缩流场
判断是否是有旋流动
则有:
即大于r的地方才会流动,则产生相对运动满足:
若设:
即若ΔP*足够小以至于r0>R则,非牛顿流体不流动
5-5解:
设左侧液面到正上方管中线的垂直距离为s
则:
第六章流体流动微分方程
6-1证明:
该流体的流动满足连续性方程
6-4(1)证明: 质量通量为流体密度与流体在该表面上的法向速度的乘积
法向速度为
流体流过 单位面积的质量流量,即质量通量为
设作用点在距离液面y处
则:
得:y=55.74m
可计算出作用点距离液面55.74m
3-4解:
取水平向右为x方向,垂直纸面向外为y方向,竖直向上为z方向,则可得:
各方向重力加速度为:
液体由于旋转受到的离心惯性力的分量为:
容器中液体受到的单位质量力为:
可得:
对等压面dp=0,即
积分可得: (c为常数)
即
表明等压面为圆柱面,且等压面的中心轴线比容器的转动轴线高 。
7-4解:(1)
此速度场满足连续方程
(2)
为有旋流动
(3)
流函数为 +c
(4)因该流场有旋,则不存在势函数。
(5)将 , 代入流线微分方程得
,即
积分上式得
流线方程为 即 ( 均为常数)
由
即
由x方向上动量守恒
即
由上面两式得
由y方向上动量守恒:
②
设Fy的作用点距离射流中心的距离为 。
由动量矩守恒,可得:
代入数据,可得:
则:
4-5 解:(1)
由题意知,叶轮转动不影响进入控制体的流量,仅影响相对速度,则:
(2)
4-6解:
4-7 解:
当用 代替时,其误差较小。故可行。
4-8解:有伯努利方程知
解得:
t=0且过点(0,0)时,得到:
综上,给定条件下流线方程为:
迹线方程为:
若 时,则两曲线趋于重合
2-7解:
则,由
第三章流体静力学
3-1解:(1)由两边压强相等得
代入相应数据得
(2)由阿基米德原理知,物体所受浮力
即:
得到: ,
即:浸入液体中的物体体积是
左侧油上升
设右侧水上升 ,在体积不变的条件下,由两侧截面积不同可知,左侧水位下降 。
3-5解:
由角速度相等,则中心圆筒转动的角速度为w。
中心圆筒中液体所受的单位质量力为
将质量力代入压力全微分公式有
积分得
自由表面压力为大气压力 , 时,令 ,则 ,得
,
(1)
有机玻璃管自身旋转角速度为0,同理,得
(2)
由连通器压强平衡原理,得 (3)
由(1)、(2)、(3)三式得
第四章 流体流动基本原理
0
无旋流动
2-2解:
代入数值x=3,y=1,z=o,得:
2-3解:
代入x=3 y=0 z=2,得:
2-4解:
已知 ,
代入流体流线方程: ,解得:
t=0时 上式即为t=0时流体的流线方程
2-5解:由题意知:
通过点(a,b,c)时的流线方程带入即:
带入x=a,y=b
2-6解:已知:
则可解出流线方程为:
已知:
容器左侧底部压强
右侧底部压强 ,
将以上各式代入即
求得:
3-2解:
船加上货物的总质量为207360kg.
3-3解:以水平向右为x轴,以竖直向下为y轴,则单位宽度上作用力为:
则在单位宽度上合力:
F的大小为
作用点位置: 的作用位置距液面为2/3×41=27.33m
的作用位置为距底面为1/3×37=12.33m
4-9解:(1)取图示控制体,由动量方程可知
(2)由伯努利引申方程,对如题所示的控制体,得
第五章不可压缩流体的一维层流流动
5-1 解:
5-2 解:由环形截面管流量公式
其中:
带入上式,得到:
5-3解:将 代入:
得:
代入边界条件:
即:
解得:
整理即:
体积流量:
5-4解:由
积分得:
由中心到两边,u减小,则du/dr随r增大而减小
,其中
代入相关数据得:
当
代入整理得:
(2)搅拌槽中盐含量为
解得:
搅拌槽中溶液的盐含量达到200kg时所需的时间为36.6min。
4-2解:设射流的质量流量和体积流量分别为 ,流速为v。
由 ,
4-3 证明:设水平向右为正方向
(2)叶片以速度 运动,即相对速度减小
此时,
4-4 证明:由质量守恒知,
①
由质量守恒方程:
第一章流体的力学性质
1-1解:既然油膜内速度为线性分布,则速度满足下列等式:
由牛顿剪切定律可得滑块表面处流体所受切应力为:
Pa
则滑块所受切应力与 大小相等,方向相反,而滑块所受摩擦力为 ,设达到平衡时,滑块速度为 ,由平衡得:
所以:
1-2解:因润滑油膜内速度为线性分布,轴转速为U,轴承则一直处于静止状态。
(2)证明:流体流过 单位面积的质量流量为
则,流体流过 单位面积的动量流量为
流体x、y、z方向动量的输入通量分别为
(3)简化后,流体质量的输入通量为
即,流体x、y、z方向质量的输入通量分别为
流体x、y、z方向动量的输入通量分别为
即Hale Waihona Puke 流体x、y、z方向动量的输入通量分别为
第七章不可压缩理想流体的平面运动
