八年级数学培优竞赛专题20 正方形
八年级数学培优——正方形

第22讲正方形考点•方法•破译1.有一组邻边相等且有一个角是直角的平行四边形叫正方形,即邻边相等的矩形或有一个角为直角的菱形叫正方形.2.熟练掌握正方形的性质,并能在解决问题时将正方形与等腰直角三角形进行替换思考.3.掌握正方形的判断方法,并应用它的对称性质解决问题.经典•考题•赏析【例1】如图,已知平行四边形ABCD中,对角线AC、BD交于点O, E是BD延长线上的点,且“CE是等边三角形.⑴求证:四边形ABCD是菱形;⑵若/AED=2Z EAD,求证:四边形ABCD是正方形.【变式题组】01.如图,已知正方形ABCD的对角线AC和BD相交于O,点M、N分别在OA、OD上, 且MN〃AD.探究:线段DM和CN之间的数童关系,写出结论并给出证明.A02.如图,点P是正方形ABCD对角线AC上的点,PE±AB, PF±BC, E、F是垂足,问PD与EF有怎样的关系?请说明理由.03 .如图,将正方形ABCD中的△ ABD绕对称中心O旋转至△ GEF的位置,EF交AB于M, GF交BD于N.请猜想BM与FN有怎样的数量关系?并证明你的结论.04.把一个正方形分成面积相等的四个三角形的方法有很多,除了可以分成相互全等的四个三角形外,你还能用三种不同的方法将正方形分成面积相等的四个三角形吗?请分别画出示意图.【例2】如图,正方形ABCD绕点A逆时针旋转废后得到正方形AEFG,边EF与CD交于点O.⑴以图中已标有字母的点为端点连接两条线段(正方形的对角线除外),要求所连接的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;⑵若正方形的边长为2cm,重叠部分(四边形AEOD)的面积为“ cm2,求旋转的角度.3【变式题组】01.如图,边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕点A顺时针旋转45°,则这两个正方形重叠部分的面积是_________ .02.我们给定两个全等的正方形ABCD、AEFG它们共顶点A(如图1),可以绕顶点A旋转,CD、EF相交于点P.⑴连接BE、DG(如图2),求证:BE=DG, BE±DG⑵连接BG、CF(如图),求证:BG//CF.【例3】数学课上,张老师提出了问题:如图1,四边形ABCD是正方形,点E是BC 边的中点.Z AEF = 90°,且EF交正方形外角N DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则似AM=EC, 易证△ AME/△ ECF,所以AE=EF.在此基础上,同学们进一步的研究:⑴小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B、C外)的任意一点”,其他条件不变,那么结论"AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是边BC的延长线上(除C点外)的任意一点,其他条件不变,结论" AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.图】图2 图3【变式题组】01.如图,已知正方形ABCD在直线MN上方,BC在直线MN上;E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.⑴连接GD,求证:△ ADG/△ ABE;⑵连接FC,观察并猜测Z FCN的度数,并说明理由.02.如图,在正方形ABCD中,点E、F分别是BC、DC边上的点,且AE± EF.⑴延长EF交正方形外角平分线CP于点P,试判断AE与EP的大小关系,并说明理由;⑵在AB边上是否存在一点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.【例4】已知:正方形ABCD中,N MAN=45°,N MAN绕点A顺时针旋转,它的两边分别CB、DC(或它们的延长线)点M、N.当N MAN绕点A旋转至U BM=DN时(如图1), 易证BM+DN=MN.⑴当N MAN绕点A旋转至U BN W DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;⑵当N MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间有怎样的数量关系?写出猜想并明.【变式题组】01.如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:⑴N EAF的大小是否有变化?请说明理由;⑵^ECF的周长是否有变化?请说明理由.02.如图,有四个动点P、Q、E、F分别从边长为1的正方形ABCD的四个顶点出发,沿AB、BC、CD、DA以同样的速度向B、C、D、A各点移动⑴试判断四边形PQEF的形状,并证明;⑵PE是否总过某一定点,并说明理由;⑶四边形PQEF的顶点位于何处时,其面积最小和最大?各是多少?03.在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、%轴的正半轴上,点O在原点.现将正方形OABC绕点O顺时针旋转,当A点第一次落在直线y=%上时停止旋转,旋转过程中,AB边交直线y=%于点M,BC边交%轴于点N(如图).⑴旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;⑵设△ MBN的周长为p,在正方形OABC旋转的过程中,p值是否有变化?请证明你的结论.【例5】小杰和他的同学组成了“爱琢磨”学习小组,有一次,他们碰到了这样一道题:“已知正方形ABCD,点E、F、G、H只分别在AB、BC、CD、DA上,若EG± FH ,则GE=FH”经过思考,大家给出了以下两个方案:(甲)过点A做AM〃HF交BC于点M,过点B作BN〃EG交CD于点N;(乙)过点A做AM〃HF交BC于点M,作AN〃EG交CD的延长线于点N;小杰和他的同学顺利的解决了该题后,人家琢磨着想改变问题的条件,作更多的探索.⑴对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1);⑵如果把条件中的“EG± HF"改为“EG与HF的夹角为45°”,并假设正方形ABCD的边长为1, FH的长为至(如图2),试求EG的长度.2【变式题组】01.若正方形ABCD的边长为4, E为BC边上一点,BE =3, M为线段AE上一点,射线BM交正方形的一边于点F,且BF = AE,则BM的长为.02.如图,已知正方形ABCD的边长为3, E为BC边上一点,BE=1.以点A为中心,把△ADE顺时针旋转90°,得4ADE',连接EE,,则EE'的长等于.03.已知正方形ABCD中,点E在边DC上,DE=2, EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为.04.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M 点正好在N NDG的平分线上,矩形ABCD长与宽的比值为.E B (! B C /? C B E C H E① ②③第之题图第W题掰第4噩图05.平面内有一等腰直角三角板(N ACB=90°)和一直线MN.过点C作以CE± MN于点E,过点B作BF± MN于点F.当点E与A重合时(如图1),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图2、图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,清直接写出你的猜想,并证明.演练巩固•反馈提高01.顺次连接菱形各边中点所得的四边形一定是()A .等腰梯形反 正方形C 平行四边形。
初二数学知识点专题讲解与练习20---正方形(培优版)

F
A
D
M
B
C
A
D
F
EB
M C
E
G
图1
图G2
【例 3】如图,正方形 ABCD 中,E ,F 是 AB ,BC 边上两点,且 EF = AE + FC , DG ⊥ EF 于 G ,求证: DG = DA .
(重庆市竞
2 / 17
解题思路:构造 AE + FC 的线段是解本例的关键.
赛试题)
A
D
E
G
B
延长线上 (CG > BC) ,取线段 AE 的中点 M .连 MD , MF . (1)探究线段 MD , MF 的关系,并加以证明. (2)将正方形 CGEF 绕点 C 旋转任意角后(如图 2),其他条件不变. 探究线段 MD , MF 的关系,并加以证明.
(大
连市中考题改编) 解题思路:由 M 为 AE 中点,想到“中线倍长法”再证三角形全等.
(黑龙江省中考 试题)
解题思路:对于(2),构造 DN − BM 是解题的关键.
4 / 17
A
D
N
BM
C
图1
A
D
C MB
A
D
N
BM
C
图2
浙教版数学八年级下册5.3正方形培优练习(含解析)

浙教版数学八年级下册5.3正方形培优练习一、选择题1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )A.当AC=BD时,四边形ABCD是矩形B.当AB=BC时,四边形ABCD是菱形C.当AC平分∠BAD时,四边形ABCD是菱形D.当∠DAB= 90°时,四边形ABCD是正方形2.如图,在正方形ABCD中,E是AC 上的一点,且AB=AE,则∠EBC的度数为( )A.37.5°B.30°C.22.5°D.12.5°3.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于( )A.1B.12C.13D.144.如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是( )A.16B.25C.144D.1695.如图,在正方形ABCD中,E为CD边上一点,将△AED沿着AE翻折得到△AEF,点D的对应点F恰好落在对角线AC上,连接BF.若EF=2,则BF2=( )A.42+4B.6+42C.12D.8+426.将四个全等的三角形按如图所示的方式围成一个正方形ABCD,记△AED的面积为S1,四边形EFCG的面积为S2.若EG∥CF,EG=3,S1S2=16,则图中阴影部分的面积为( )A.23B.94C.32D.92二、填空题7.如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件: ,使得四边形ABCD 是正方形.8.如图,A(0,2),D(1,0),以AD为边作正方形ABCD,则点B的坐标为 .9.勾股定理被合为“几何明珠”,在数学的发展历程中占有举足轻重的地位.中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵夹弦图”(如图①所示).图②由弦图变化得到,它是由八个全等的直角三角形拼接而成的.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=129,则S2的值是 .10.如图,在Rt△ABC中,∠BAC=90°,以BC为边向上作正方形BCDE,以AC为边作正方形ACFG,点D落在GF上,连接AE,EG.若AB=9,BC+GD=9,则△AEG的面积为 .2三、解答题11.如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.12.如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.(1)求证:四边形AEDF是菱形;(2)若∠B=35°,当∠C=▲度时,四边形AEDF为正方形并证明.13.如图,点E为正方形ABCD内一点,∠BEC=90°,将△BEC绕点B逆时针方向旋转90°得到△BFA (点E的对应点为点F),延长CE交AF于点G。
八年级竞赛辅导之正方形
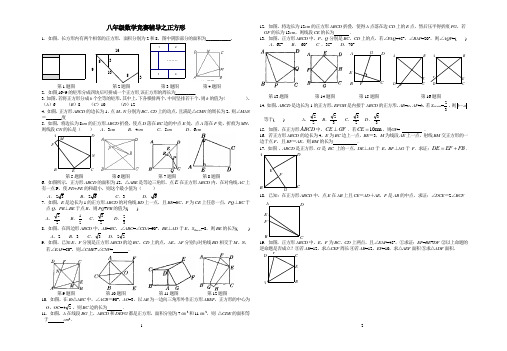
八年级数学竞赛辅导之正方形1.如图,长方形内有两个相邻的正方形,面积分别为2和8,图中阴影部分的面积为___________。
953351016第7题 ⋅⋅⋅⋅⋅⋅⋅4321第1题图 第2题图 第3题图 第4题图2.如图,16×9的矩形分成四块后可拼成一个正方形,该正方形的周长为_________.3.如图,若将正方形分成k 个全等的矩形,其中上、下各横排两个,中间坚排若干个,则k 的值为( )。
(A )6 (B )8 (C )10 (D )12 4.如图,正方形ABCD 的边长为1,点M 、N 分别为BC 、CD 上的动点,且满足△CMN 的周长为2,则∠MAN=_______度. 5.如图,将边长为8cm 的正方形ABCD 折叠,使点D 落在BC 边的中点E 处,点A 落在F 处,折痕为MN ,则线段CN 的长是( ) A .3cm B .4cm C .5cm D .6cmN MFED C BA第5题图 第6题图 第7题图 第8题图6.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD+PE 的和最小,则这个最小值为( )A. B. C .3 D7.如图,E 是边长为1的正方形ABCD 的对角线BD 上一点,且BE =BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ +PR 的值为( )A .22B .21C .23D .328.如图,在四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°,BE ⊥AD 于E ,S ABCD =8,则BE 的长为( ) A .2 B .3 C .3 D .229.如图,已知E 、F 分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于M 、N ,若∠EAF =50°,则∠CME +∠CNF = .第9题图 第10题图 第11题图 第12题图 10.如图,在Rt △ABC 中,∠ACB =90°,AC =3,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,OC =24,则BC 边的长为 .11.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7㎝2和11㎝2,则 △CDE 的面积等于 cm 2.12.如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,则线段CE 的长为 .13.如图,正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠P AQ =45°,∠BAP =20°,则∠AQP =( )A .65°B . 60°C .35°D .70°A B C DEF G FED CBAABCD EF 第13题图 第14题图 第15题图 第16题图14.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE =a ,AF =b ,若S EFGH =32,则ab -等于( ) A .22 B .32 C .23 D .3315.如图,在正方形ABCD 中,CE GF ⊥.若10cm CE =,则GF = . 16.若正方形ABCD 的边长为4,E 为BC 边上一点,BE =3,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF =AE ,则BM 的长为 .17.如图 ,ABCD 是正方形.G 是 BC 上的一点,DE ⊥AG 于 E ,BF ⊥AG 于 F .求证:DE EF FB =+.18.已知:在正方形ABCD 中,点E 在AB 上且CE =AD +AE ,F 是AB 的中点,求证:∠DCE =2∠BCF .FE DC B A19.如图,正方形ABCD 中,E 、F 为BC 、CD 上两点,且∠EAF =45°,①求证:EF =BE +DF . ②以上命题的逆命题是否成立?③若AB =12,求△CEF 周长.④若AB =12,EF =10,求△AEF 面积.⑤求△ADF 面积.DC B AFEA D E FC B20.如图,BF平行于正方形ADCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.A CDEF21.如图,ABCD是正方形,AB=1,∠AOx=30°,求点B坐标.22.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.90AEF∠= ,且EF交正方形外角∠DCG的平行线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证AME ECF△≌△,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.23.如图,分别以△ABC的三边向形外作正方形ABDE、BCFG、ACMN,直线OP⊥AB,①求证:OP平分FM;②以上命题的逆命题成立吗?为什么?PONMGFE DCBA24.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)25.如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.A DFG B图1 A DFGB图2A DFEB图3DE图②图③D图①。
正方形培优试题及答案【范本模板】
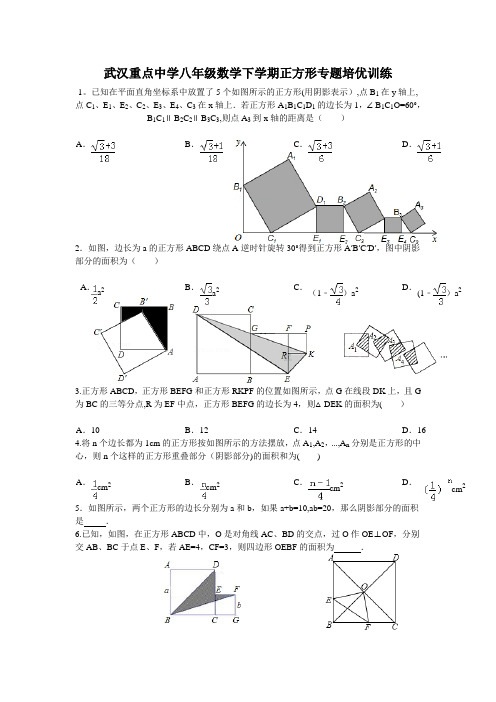
武汉重点中学八年级数学下学期正方形专题培优训练1。
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是()A.B.C.D.2.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为()A.a2B.a2C.(1﹣)a2D.(1﹣)a23.正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G 为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为()A.10 B.12 C.14 D.16 4.将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,A n分别是正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积和为()A.cm2B.cm2C.cm2D.cm25.如图所示,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么阴影部分的面积是.6.已知,如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于点E、F,若AE=4,CF=3,则四边形OEBF的面积为.7。
如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,四边形ADEF是菱形?(4)当△ABC满足什么条件时,四边形ADEF是正方形?(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?(第(2)(3)(4)(5)题不必说明理由)8。
在平面直角坐标系xOy中,OEFG为正方形,点F的坐标为(1,1).将一个最短边长大于的直角三角形纸片的直角顶点放在对角线FO上.(1)如图,当三角形纸片的直角顶点与点F重合,一条直角边落在直线FO上时,这个三角形纸片与正方形OEFG重叠部分(即阴影部分)的面积为;(2)若三角形纸片的直角顶点不与点O,F重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形OEFG重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不写求解过程),并画出此时的图形.9。
人教版数学八年级培优竞赛 正方形 专题课件

CD 于 F.
A
D
E
A
D
E
P
F
P
F
B
图⑴
C
B
C
图⑵
(1)求证:PC=PE; (2)求 CPE 的度数; (3)如图②,把正方形 ABCD 改为菱形 ABCD,其他条件不变,若 ABC 65 ,则 CPE =__________.
(1)提示:证△ABP≌△CBP(SAS); (2)由(1)知,AABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA =PE, ∴∠DAP=∠E,.∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等), ∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,即∠CPF=∠EDF=90°; (3)115.
B A
图1
B A
图2
10.如图,在由边长为 1 的小正方形组成的网格图中有两个格点 A、B.(注: 网格线交点称为格点)
(1)请在图 1 中确定格点 C,使得△ABC 的面积为 12.如果符合题意的格点 C 不止一个,请分别用 C1 、 C2 、 C3 …表示;
(2)请用无刻度的直尺在图 2 中以 AB 为一边画一个面积为 18 的矩形 ABMN.
(第 3 题)
H
A
D
F
E
G
B
C
(第4题)
4.如图,正方形 ABCD 的边长为 1,AC,BD 是对角线,将△DCB 绕着点 D 顺时针旋转 45 得到△DGH,
HG 交 AB 于点 E,连接 DE 交 AC 于点 F,连接 FG.则下列结论:
① 四边形 AEGF 是菱形; ②△AED≌△GED; ③ DFG 112.5 ;④ BC+FG=1.5
八年级数学竞赛题:正方形

八年级数学竞赛题:正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形,或有一组邻边相等的矩形是正方形,也即有一角是直角的菱形是正方形,正方形具有矩形、菱形的一切性质,主要体现在:正方形的四条边相等;正方形的四个角是直角;正方形的对角线互相垂直平分,且每条对角线平分一组对角.由于正方形往往与直角三角形联系在一起,所以在解与正方形相关问题时,常用到勾股定理,具有代数风格,体现数形结合思想.熟悉以下基本图形、基本结论:例1 如图,四边形ABCD为正方形,以AB为边向正方形外作等边三角形ABE,CE与DB 相交于点F,则∠AFD=____________度.例2 如图,正方形ABCD的面积为256,点E在AD上,点F在AB的延长线上EC⊥FC 在AB的延长线上,EC⊥FC,△CEF的面积是200,则BF的长是().A.15 B.12 C.11 D.10例3 (1)如图1,已知正方形ABCD和正方形CGEF(CG>BC),B、C、G在同一直线上,M为线段AE的中点M.探究:线段MD、MF的关系.(2)若将正方形CGEF绕点C逆时针旋转45°,使得正方形CGEF对角线CE在正方形ABCD的边BC的延长线上,M为AE的中点.试问:(1)中探究的结论是否成立?若成立,请证明,若不成立,请说明理由.例4 如图,将正方形ABCD折叠,使顶点A与CD边上的M点重合折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.(1)如果M为CD边的中点,求证DE:DM:EM=3:4:5;(2)如果M为CD边上的任意一点,设AB=2a,△CMG的周长是否与点M的位置有关?若有关,请把△CMG的周长用含DM的长x的代数式表示;若无关,请说明理由.例5 在边长为6cm的正方形ABCD中,点E、F、G、H分别按A→B、B→C、C→D、D→A的方向同时出发,以1cm/S的速度匀速运动.(1)在运动中,点E、F、G、H所形成的四边形EFGH为().A.平行四边形B.矩形C.菱形D.正方形(2)四边形EFGH的面积S(cm2)随运动时间t(s)变化的图象大致是().(3)写出四边形EFGH的面积S(cm2)关于运动时间t(s)变化的函数关系式,并求运动几秒钟时,面积最小?最小值是多少?1.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF 交AD于点H,那么DH的长为______________.2.如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为_____________.3.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则正方形的边长是_____________.4.若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM 交正方形的一边于点F,且BF=AE,则BM的长为_______________.5.将n个边长都为1cm的正方形按如图所示摆放,点A1、A2,…,A n分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为().A.14cm2B.4ncm2C.14ncm2D.(14)n cm26.如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F 处,折痕为MN,则线段CN的长是().A.3cm B.4cm C.5cm D.6cm7.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有().A.1个B.2个C.3个D.4个‘8.如图,正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为().A.7 8.5 C.4 ·D.39.如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC、BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H.(1)图中有若干对三角形是全等的,请你任选一对进行证明(不添加任何辅助线);.(2)证明四边形AHBG是菱形;(3)若使四边形AHBG是正方形,还需在Rt△ABC的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)10.如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E ,交∠BCA 的外角平分线于点F .(1)探究:线段OE 与OF 的数量关系,并加以证明;(2)当点O 在边AC 上运动时,四边形BCFE 会是菱形吗?若是,请证明;若不是,请说明理由;(3)当点O 运动到何处,且△ABC 满足什么条件时,四边形AECF 是正方形?11.在正方形ABCD 中,点P 是CD 上一动点,连结P A ,分别过点B 、D 作BE ⊥P A 、DF ⊥P A ,垂足为E 、F ,如图1. 。
奥数培优超常思维竞赛 数学 初二年级试卷及答案

初二年级超常思维竞赛数学试卷考试时间:100分钟满分150分1.如图所示,左侧有一组排列好的方格,经过空间平面的顺时针或逆时针方向旋转之后,成为五个选项中的一组,那么正确的一组方格为( ).2.若一切非零实数x和y满足x=1y ,则(x−1x)(y+1y)=().A.2x2B.2y2C.x2+y2D.x2−y2E.y2−x23.正方形ABCD的边长为36,点E在AB边上且到B的距离为12,点F为BC边的中点,点G在CD边上且到C的距离为12. 则在△EFG之内且在△AFD之外区域的面积为( ).A.133B.144C.155D.166E.1774.如果4(√x+√y−1+√z−2)=x+y+z+9,那么xyz的值是().A.0B.2C.15D.120E.1505.在20182+2016×2017×2019×2020;20192+2017×2018×2020×2021;20202+2018×2019×2021×2022;20212+2019×2020×2022×2023这四个数中共有( )个是完全平方数.A.0B.1C.2D.3E.46.若√a+√b=1,又√a=m+a−b2,√b=n−a−b2,其中m,n均为有理数,则有( ).A.mn=12B.m2+n2=12C.m+n=12D.m−n=12E.m2−n2=147.把一个矩形剪去一个正方形,所剩矩形与原矩形相似,则原矩形长边与短边之比为( ).A.(1+√5):2B.3:2C.(1+√3):2D.(1+√6):2E.(1+√5):(1−√3)8.设x>0,y>0,√x(√x+2√y)=√y(6√x+5√y),则x+xy−y2x+√xy+3y的值为( ). A.14 B.13C.12D.1E.29.根式√810+41084+411的值等于( ). A.√2B.16C.32D.12E.512. 510.如图所示,已知菱形ABCD 的两条对角线长分别为a ,b ,分别以每条边为直径向菱形内作半圆,则四条半圆弧围成的花瓣形面积(阴影部分的面积)为( ).A.π(a 2+b 2)B.18π(a 2+b 2)−ab 2C.12π(a 2+b 2)−ab 2D.18π(a 2+b 2)+ab 2E.12π(a 2+b 2)+ab11.两个相同的瓶子装满酒精溶液,在一个瓶子中酒精与水的体积之比是p :1,而在另一个瓶子中是q :1.若把两瓶溶液混合在一起,则混合溶液中的酒精与水的体积之比是( ).A.p+q 2B.p 2+q 2p+qC.2pq p+qD.2(p 2+pq+q 2)3(p+q)E.p+q+2pq p+q+212.小明将一块正方形的钟面画成一块投镖的靶板,利用“钟点位置”作为边界线(如图). 如果t 是8个三角形之一(例如,12点与1点间的区域)的面积,q 是4个角上的四边形之一(例如,1点与2点间的区域)的面积,那么qt =( ).A.2√3−2B.32C.√5+12D.√3E.213.一矩形R 的边长为a 和b ,其中a <b ,要得到边长为x ,y (x <a ,y <a )的矩形,使其周长为R 的周长的13,面积为R 的面积的13,这样的不同矩形的个数为( ).A.0B.1C.2D.4E.无限多14.已知周长为28cm 的长方形ABCD ,如图所示,以A 为圆心,AD 为半径画弧交AB 于A 1,以B 为圆心,BA 1为半径画弧交BC 于A 2,依此类推,即依次以C ,D ,A ,B 为圆心,用同样方法画弧,分别得交点A 3,A 4,A 5,A 6,若点A 6与点C 重合,则长方形的长和宽分别为( ) cm .A.12,2B.11,3C.10,4D.9,5E.8,615.如图所示,两面墙间的距离为w ,它们之间的P 点处有一个梯子,梯子的长度为a ,梯子向一侧墙靠去,上端触墙于Q 点,Q 到地面的距离为k ,此时梯子与地面成45°角,梯子向另一侧墙靠去,上端触墙于R 点,R 到地面的距离为ℎ,此时梯子与地面成75°角,那么两墙间的距离w 为( ).A.aB.RQC.kD.ℎ+k 2E.ℎ16.P 是高为ℎ的等边三角形内部一点,设P 到各边的距离分别为x ,y ,z ,若以x ,y ,z 为长度的三条线段可以构成一个三角形,则x ,y ,z 各自所应满足的条件是( ). A.x <ℎ,y <ℎ,z <ℎ B.x <ℎ2,y <ℎ2,z <ℎ2C.x ≤ℎ2,y ≤ℎ2,z ≤ℎ2 D.x <ℎ3,y <ℎ3,z <ℎ3E.x ≤ℎ3,y ≤ℎ3,z ≤ℎ317.如图所示,把正方形ABCD的对角线AC分成n段,以每一段为对角线作正方形,设这n个小正方形的周长为p,正方形ABCD的周长为l,则p与l的关系是( ).A.p>lB.p≥lC.p=lD.p≤lE.p<l18.若x+y+z=30,3x+y−z=50,其中x,y,z皆为非负数,则M=5x+4y+2z的取值范围是( ).A.100≤M≤110B.110≤M≤120C.120≤M≤130D.130≤M≤140E.M的范围无法确定19.如图所示,展示了12个排成一圈的30°−60°−90°三角形,并使每个三角形的斜边恰好为相邻下一个,其中m和n 大三角形的较长直角边. 图中第4个和最后一个三角形以阴影标记,其周长之比可以表示为mn为互素正整数. 则m+n的值为().A.333B.334C.335D.336E.33720.已知存在正整数m和n,使得x=m+√n是等式x2−10x+1=√x(x+1)的一个解,则m+n的值为().A.11B.22C.33D.44E.5521.如图所示,ABCD是正方形,BF//AC,AEFC是菱形,则∠ACF与∠F的度数之比是().A.7:1B.6:1C.5:1D.4:1E.3:122.已知a =√43+√23+1,那么,3a +3a 2+1a 3的值是( ).A.√23B.13C.14D.15E.123.正方形A 与正方形B 毗邻,正方形B 又与正方形C 毗邻. 如图所示,这3个正方形的底边都在同一条直线上,其左上角的顶点共线. 若A 的面积为24,B 的面积为36,则C 的面积为( ).A.48B.50C.52D.54E.以上都不对24.各边不相等的△ABC 的两条高的长度分别是4和12,若第三条高的长度也是整数,则它的最大值是( ).A.4 B.5 C.6 D.7 E.以上都不对25.如图中的(1)(2)(3)(4)是同样的小等边三角形,(5)(6)也是等边三角形且边长为(1)的2倍,(7)(8)(9)(10)是同样的等腰直角三角形,(11)是正方形. 那么,以(5)(6)(7)(8)(9)(10)(11)为平面展开图的立体图形的体积是以(1)(2)(3)(4)为平面展开图的立体图形体积的( )倍.A.2B.4C.8D.16E.以上都不对26.n 为正整数,若2n 有28个正因子,3n 有30个正因子,则6n 的正因子的个数为( ).A.32 B.33 C.34 D.35E.3627.矩形ABCD 的尺寸为70×40,对角线AC 上标记的18个点(包括A 和C )将对角线分成17等份,AB 边上标记的22个点(包括A 和B )将该边分成21等份. 我们进而构建如图所示的17个无交叠的三角形,每个三角形的2个顶点即为矩形边上相邻的2点,而另一顶点则是矩形对角线上的一点. 如此,在矩形边的21等份中,只有左侧17等份被用来作为这些三角形的底. 则这17个三角形的面积之和为( ).A.600B.700C.800D.900E.100028.小明的父亲在小明过生日时送给小明一个L形的生日蛋糕. 小明的父亲让小明只用一刀将蛋糕切为三块,以便将蛋糕分给小明的弟弟及妹妹. 因此,小明可以如图(a)(b)的方式切,但不可以如图(c)的方式切.但小明的父亲说切完后,必须让弟弟和妹妹先挑选,他们一定是挑比较大块的,而小明只能挑选最后剩下的那块. 所以小明要设法使切完后的三块蛋糕中,最小的那块要越大越好. 若小明达成了目标,则小明能分到的那块蛋糕的面积为()cm2.A.60B.70C.80D.90E.400329.环形跑道周长为400米,甲、乙两人同时同地顺时针沿环形跑道跑,甲每分钟跑52米,乙每分钟跑46米,甲、乙两人每跑100米休息1分钟. 问:甲需()分钟追上乙.A.14713B.145213C.142313D.139413E.以上都不对30.一间4m×4m房间的地板可以被8块1m×2m的地毯以不同形式覆盖,如图所示的三种不同的形式如下:则共有()种不同的覆盖形式.A.28B.32C.36D.40E.以上都不对初二年级超常思维竞赛数学试卷答案考试时间:100分钟满分150分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AD专题20 正方形阅读与思考矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的菱形,因此,我们可以利用矩形、菱形的性质来研究正方形的有关问题.正方形问题常常转化为三角形问题解决,在正方形中,我们最容易得到特殊三角形、全等三角形,熟悉以下基本图形.例题与求解【例l 】 如图,在正方形纸片ABCD 中,对角线AC ,BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后,折痕DE 分别交AB ,AC 于点E ,G .下列结论:①05.112=∠AGD ;②2=AEAD;③OGD AGD S S ∆∆=;④四边形AEFG 是菱形;⑤OG BE 2=. 其中,正确结论的序号是______________. (重庆市中考试题)解题思路:本题需综合运用轴对称、菱形判定、数形结合等知识方法.【例2】如图1,操作:把正方形CGEF 的对角线CE 放在正方形ABCD 的边BC 的延长线上)(BC CG >,取线段AE 的中点M .连MD ,MF .(1)探究线段MD ,MF 的关系,并加以证明. (2)将正方形CGEF 绕点C 旋转任意角后(如图2),其他条件不变. 探究线段MD ,MF 的关系,并加以证明.(大连市中考题改编) 解题思路:由M 为AE 中点,想到“中线倍长法”再证三角形全等.图2图1EABEBA【例3】如图,正方形ABCD 中,E ,F 是AB ,BC 边上两点,且FC AE EF +=,EF DG ⊥于G ,求证:DA DG =.(重庆市竞赛试题)解题思路:构造FC AE +的线段是解本例的关键.B A E【例4】 如图,正方形ABCD 被两条与边平行的线段EF 、GH 分割成四个小矩形,P 是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定HAF ∠的大小,并证明你的结论.(北京市竞赛试题) 解题思路:先猜测HAF ∠的大小,再作出证明,解题的关键是由条件及图形推出隐含的线段间的关系.【例5】 如图,在正方形ABCD 中,E ,F 分别是边BC ,CD 上的点,满足DF BE EF +=,AF AE ,分别与对角线BD 交于点N M ,.求证:(1)045=∠EAF ;(2)222DN BM MN +=. (四川省竞赛试题)解题思路:对于(1),可作辅助线,创造条件,再通过三角形全等,即可解答;对于(2),很容易联想到直角三角形三边关系.A B CD E F GHPBAF【例6】已知 :正方形ABCD 中,045=∠MAN ,MAN ∠绕点A 顺时针旋转,它的两边分别交CB ,DC (或它们的延长线)于点N M ,.当MAN ∠绕点A 旋转到DN BM =时(如图1),易证MN DN BM =+.(1)当MAN ∠绕点A 旋转到DN BM ≠时(如图2),线段DN BM ,和MN 之间有怎样的数量关系?写出猜想,并加以证明;(2)当M AN ∠绕点A 旋转到如图3的位置时,线段DN BM ,和MN 之间又有怎样的数量关系?请直接写出你的猜想.(黑龙江省中考试题)解题思路:对于(2),构造BM DN -是解题的关键.能力训练A 级ABCDMN图3ABCDMN图2ABCDMN图11. 如图,若四边形ABCD 是正方形,CDE ∆是等边三角形,则EAB ∠的度数为__________.(北京市竞赛试题)2. 四边形ABCD 的对角线BD AC 、相交于点O ,给出以下题设条件: ①DA CD BC AB ===;②BD AC DO CO BO AO ⊥===,; ③BD AC DO BO CO AO ⊥==,,; ④DA CD BC AB ==,.其中,能判定它是正方形的题设条件是______________. (把你认为正确的序号都填在横线上)(浙江省中考试题)3.如图,边长为1的两个正方形互相重合,按住一个不动,将另一个绕顶点A 顺时针旋转030,则这两个正方形重叠部分的面积是__________.(青岛市中考试题)BA E第1题图 第3题图 第4题图4.如图,P 是正方形ABCD 内一点,将ABP ∆绕点B 顺时针方向旋转至能与'CBP ∆重合,若3=PB ,则'PP =__________. (河南省中考试题)5.将n 个边长都为cm 1的正方形按如图所示摆放,点n A A A ,,21分别是正方形的中心,则n 个正方形重叠形成的重叠部分的面积和为( )A .241cm B .24cm n C. 241cm n - D. 2)41(cm n(晋江市中考试题)ABCDPP ''B'D 'B F第5题图 第6题图6. 如图,以BCA Rt ∆的斜边BC 为一边在BCA ∆的同侧作正方形BCEF ,设正方形的中心为O ,连接AO ,如果26,4==AO AB ,则AC 的长为( )A . 12B .8 C.34 D. 28(浙江省竞赛试题)7.如图,正方形ABCD 中,035,=∠=MCE MN CE ,那么ANM ∠是( ) A .045 B .055 C. 065 D. 0758.如图,正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,CEF Rt ∆的面积为200,则BE 的值是( )A .15B .12C .11D .10第8题图第7题图ABAD E F9.如图,在正方形ABCD 中,E 是AD 边的中点,BD 与CE 交于F 点,求证:BE AF ⊥.B A10. 如图,在正方形ABCD 中,E 是AB 边的中点,F 是AD 上的一点,且AD AF 41= . 求证:CE 平分BCF ∠.BAE11. 如图,已知P 是正方形ABCD 对角线BD 上一点,F E BC PF DC PE ,,,⊥⊥分别是垂足. 求证:EF AP =.(扬州市中考试题)EBA12.(1)如图1,已知正方形ABCD 和正方形)(BC CG CGEF >,G C B ,,在同一条直线上,M 为线段AE 的中点.探究:线段MF MD ,的关系.(2)如图2,若将正方形CGEF 绕点C 顺时针旋转045,使得正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上,M 为AE 的中点.试问:(1)中探究的结论是否成立?若成立,请证明;若不成立,请说明理由.(大连市中考试题)ABCDEFGMABCDEFGM图1 图2B 级1. 如图,在四边形ABCD 中,090,=∠=∠=ABC ADC DC AD ,AB DE ⊥于E ,若四边形ABCD 的面积为8,则DE 的长为__________.2.如图,M 是边长为1的正方形ABCD 内一点,若02290,21=∠=-CMD MB MA ,则=∠MC D __________.(北京市竞赛试题)第3题图第1题图第2题图CBAAAC3.如图,在ABC Rt ∆中,3,900==∠AC C ,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,且24=OC ,则BC 的长为__________.(“希望杯”邀请赛试题)4.如图:边长一定的正方形ABCD ,Q 是CD 上一动点,AQ 交BD 于M ,过M 作AQ MN ⊥交BC 于N 点,作BD NP ⊥于点P ,连接NQ ,下列结论:①MN AM =;②BD MP 21=; ③NQ DQ BN =+;④BMBNAB +为定值,其中一定成立的是( )A . ①②③B .①②④ C. ②③④ D. ①②③④ 5.如图,ABCD 是正方形,AC BF //,AEFC 是菱形,则ACF ∠与F ∠度数的比值是( ) A . 3 B .4 C. 5 D. 不是整数6.一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )A .58 B .527C. 8D. 65E.35(美国高中考试题)第7题图第5题图第4题图第6题图Q BABADA QP7.如图,正方形ABCD 中,8=AB ,Q 是CD 的中点,设α=∠DAQ ,在CD 上取一点P ,使α2=∠BAP ,则CP 的长度等于 ( )A . 1B .2 C. 3 D.3(“希望杯”邀请赛试题)8.已知正方形ABCD 中,M 是AB 中点,E 是AB 延长线上一点,DM MN ⊥且交CBE ∠平分线于N (如图1)(1)求证:MN MD =;(2)若将上述条件中的“M 是AB 中点”改为“M 是AB 上任意一点”其余条件不变(如图2),(1)中结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)如图2,点M 是AB 的延长线上(除B 点外)的任意一点,其他条件不变,则(1)中结论是否成立?如果成立,请证明;如果不成立,请说明理由;(临汾市中考试题)图3图2图1AAA DDDE `9.已知,10,10<<<<b a 求证:22)1()1()1()1(22222222≥-+-+-+++-++b a b a b a b a .10.如果,点N M ,分别在正方形ABCD 的边CD BC ,上,已知MCN ∆的周长等于正方形ABCD 周长的一半,求MAN ∠的度数. (“祖冲之杯”邀请赛试题)ADM11.如图,两张大小适当的正方形纸片,重叠地放在一起,重叠部分是一个凸八边形ABCDEFGH ,对角线CG AE ,分这个八边形为四个小的凸四边形,请你证明:CG AE ⊥,且CG AE =.(北京市竞赛试题)12.如图,正方形MNBC 内有一点A ,以AC AB ,为边向ABC ∆外作正方形ABRT 和正方形ACPQ ,连接BP RM ,.求证:RM BP //.(武汉市竞赛试题)PR。
