SPSS均值比较
第6章 SPSS参数检验——均值比较
总体2
抽取简单随机样均值之差的检验 (s12、 s22 已知)
• 1.假定条件
两个样本是独立的随机样本 两个总体都是正态分布 若不是正态分布, 可以用正态分布来近似(n130和
n230) 2.检验统计量为
Z ( X1 - X 2 ) - (m1 - m2 ) ~ N (0,1)
6.2 MEANS 过程
• 功能：分组计算、比较指定变量的描述统计量。包括均值、 标准差、总和、观测数、方差等等，还可以给出方差分析表 和线性检验结果。
• Analyze-> Compare Means->Means
n Dependent List：用于选入需要分析的变量，如果选入两 个以上变量，系统会在同一张输出表中依次给出分析结果 。
)
1. 检验具有不等方差的两个总体 的均值
2. 假定条件
两个样本是独立的随机样本
两个总体都是正态分布
两个总体方差未知且不相等 s12 s22
3. 检验统计量
( S12 S22 )2
t
(
X1
-
X2) S12 n1
- (m1 S22
n2
-
m2
)
~
t(
(
S12 n1
)2
/(
n1
n1 -1)
s
2 1
s
2 2
n1 n2
两个总体均值之差的检验 (s12、 s22 未知，大样本)
• 检验统计量为
Z (X1 - X 2 ) - (m1 - m2 ) ~ N (0,1)
s12 s22 n1 n2
两个总体均值之差的检验 (s12、 s22 未知但相等,小样本)
平均值的多重比较SPSS操作
平均值的多重比较SPSS操作一、简介多重比较是一个非常重要的统计方法。
在采集大量数据后，通常会对某个变量进行平均值的比较。
但是，如果对数据进行简单的比较可能会存在问题：假设有10个不同的样本，进行10次比较，这将导致多达45个比较(10C2)，这个时候难免会出现误差。
多重比较是一种用于调整显著性水平和减少误差的方法，可以在比较中减少错误的拒绝。
二、SPSS操作1、单因素方差分析打开SPSS软件，加载数据并选择“Analyze”菜单，选择“Compare Means”选项，进入子菜单，选择“One-Way ANOVA”，进入单因素方差分析子菜单，如下图所示。
2、设置分析变量在“One-Way ANOVA”对话框中，选择需要分析的变量，并将其添加到右侧区域，如下图所示。
3、添加编辑标签在“Options”标签页中，选择“Descriptive”。
在描述性统计选项卡中，选择“Mean”、“Std. Deviation”和“N”三个选项，并单击“Continue”按钮。
现在我们将为分组变量添加标签。
4、分组变量标签点击“Post Hoc...”按钮进入“Post Hoc Tests”对话框，并选择一个或多个比较类型进行比较，如下图所示。
5、设置显著性水平在“Options”标签页中，将显著性水平设置为0.05，如下图所示。
6、执行分析完成设置后，单击“OK”按钮开始分析过程。
SPSS运行程序并输出结果，如下图所示。
分析结果可以得出：1）整体效应不显著，F（2,54）=2.49,P=0.09。
2）当α = 0.05 时，相应的 Bonferroni 校正后置Hoc比较表明，组1、2和组1、3之间差异不显著，但组2和组3之间差异显著。
3）平均得分方面，在平均得分方面，组1的平均得分小于2和组三的平均得分；组2的平均得分高于组一和组三的平均得分；组三的平均得分最高。
四、总结平均值的多重比较SPSS操作是非常重要的，该方法让我们能够在更复杂的数据集中得出显著的结论。
spss 均值的比较与检验
输出结果：
结果分析：
1、两种样本的均数分别为3318.75, 2506.25, 样本个数均为8。
2、相关系数r=0.584, p=0.129>0.05 ， 认为两配对变量无相关关 系。
3、t=4.207，自由度df=7, p=0.004<0.05, 故可认为两组样本的均 值差异显著。
4、配对数差的均数为812.50, 标准差为546.25 ，标准误为193.13， 95％的可信区间为355.82～1269.18。 结论：两配对变量无相关关系，且两组样本的均值差异显著。
结论：
处理前后两组样本方差相等，均值有明显差异。
例5-5-3 以银行男女职工的现工资为例，数据e5-5-4.sav, 检验男女职 工现工资是否有显著性差异。执行结果如下：
结果分析：
1、各组观测数目，男258人，女216人。
2、男性平均工资：41441.8, 女性工资为： 26031.9. 3、方差齐次性检验结果（levene检验)，F值为119.669, 显著性 概率为P=0.000<0.05.因此，两组方差差异显著。在下面的t 检验结 果中应该选择Equal variances not assumed (假设方差不相等）一行的 数据作为本例t检验的结果数据。
z ~ t (n 1) sz / n
在显著水平α下， 双侧检验的H0拒绝区域为： | t | t (n 1)
2
二、配对样本T检验功能与应用
配对样本T检验是进行配对样本均数的比较。执行该过程， SPSS显示：
每个变量的均数、标准差、标准误和样本含量；
每对变量的相关系数；
每对变量的均数的差值、差值的标准误和可信区间； 检验每对变量均数的差值是否来自总体均数为0 的t检验结果。 三、应用举例 例5-5-4 ：(e5-5-5.sav)
SPSS统计分析第四章均值比较与T检验
N 258 216
Mean $41441.8 $26031.9
Std. Dev iation $19,499.214 $7,558.021
Std. Error Mean $1213.97
$514.258
左第一栏为分析变量标签和分类变量标签 N观测量数目 Mean均值 Std. Deviation标准差 Std. Error Mean标准误
三、配对样本T检验
配对样本T检验（Paired Sample T test）用 于检验两个相关的样本是否来自具有相同均 值的总体。这种相关的或配对的样本常常来 自这样的实验结果，在实验中被观测对象在 实验前后均被观测。两个变量可以是before after，配对分析的测度也不是必须来自同一 个观测对象。一对可以两者组合而成。
练习题
已知某水样中含CaCO3的真值为20.7mg/L， 现用某方法重复测定该水样11次CaCO3的含 量（mg/L）为：20.99，20.41，20.10， 20.00，20.91，22.60，20.99，20.41， 20.00，23.00，22.00。问该方法测得的均值 是否偏高？
2、Independent Sample T test（独立样本T检验）
例题一
现有银行雇员工资为例，检验男女雇员现工 资是否有显著差异。一个是要比较salary变量 的均值，另一个是gender变量作为分水平变 量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
如果你试图比较的变量明显不是正态分布的，则应该 考虑使用一种非参数检验过程（Nonparametric test）。 如果想比较的变量是分类变量，应该使用Crosstabs 功能。
SPSS实验报告——均值比较
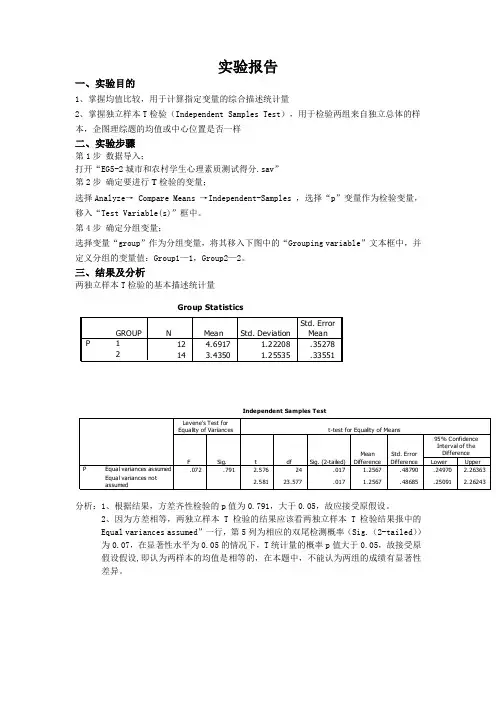
实验报告一、实验目的1、掌握均值比较，用于计算指定变量的综合描述统计量2、掌握独立样本T 检验（Independent Samples Test ），用于检验两组来自独立总体的样本，企图理综题的均值或中心位置是否一样二、实验步骤第1步 数据导入；打开“EG5-2城市和农村学生心理素质测试得分.sav ” 第2步 确定要进行T 检验的变量；选择Analyze → Compare Means →Independent-Samples ，选择“p ”变量作为检验变量，移入“Test Variable(s)”框中。
第4步 确定分组变量；选择变量“group ”作为分组变量，将其移入下图中的“Grouping variable ”文本框中，并定义分组的变量值：Group1—1，Group2—2。
三、结果及分析两独立样本T 检验的基本描述统计量Group Statistics12 4.6917 1.22208.35278143.43501.25535.33551GROUP12PNMean Std. DeviationStd. Error MeanIndependent Samples Test.072.791 2.57624.0171.2567.48790.24970 2.263632.58123.577.0171.2567.48685.250912.26243Equal variances assumedEqual variances not assumedPFSig.Levene's Test for Equality of VariancestdfSig. (2-tailed)Mean DifferenceStd. Error DifferenceLower Upper 95% Confidence Interval of the Difference t-test for Equality of Means分析：1、根据结果，方差齐性检验的p 值为0.791，大于0.05，故应接受原假设。
SPSS均值比较与T检验
.
7
H 西0 南财经大学出版社
5.1 统计推断与假设检验
2、假设检验的几个概念 (4) 概率p值
SPSS16.0与统计数据分析
p值是当零假设正确时，观测到的样本信息出现的概率。 如果这个概率很小，以至于几乎不可能在零假设正确时出现 目前的观测数据时，我们就拒绝零假设。p值越小，拒绝零假 设的理由就越充分。但怎样的p值才算“小”呢？通常是与预 先设定的显著性水平 值比较，若 值为0.05，p值小于0.05则 认为该概率值足够小，应拒绝零假设。
.
8
H 西0 南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
3、假设检验的基本步骤
➢第1步 给出检验问题的原假设；
根据检验问题的要求，将需要检验的最终结果作为零假 设。例如，需要检验某学校的高考数学平均成绩是否同往年 的平均成绩一样，都为75,由此可做出零假设，H0 :75
④配对样本T检验（Paired-Sample T Test），用于检 验两个相关的样本是否来自具有相同均值的总体。
.
4
H 西0 南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
2、假设检验的几个概念
(1)统计假设
➢ 原假设：在很多情况下，我们给出一个统计假设仅仅是
为了拒绝它。例如，如果我们要判断给定的一枚硬币是
.
3
西南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
1、参数检验
①均值比较（Means），用于计算指定变量的 综合描述统计量；
Compare Means子菜单
②单样本T检验（One-Sample T Test），检验单个 变量的均值与假设检验值之间是否存在差异；
SPSS软件的操作与应用第3讲均值比较
均值比较结果解读方法
解读均值差异检验结果
根据T值和自由度等指标，判断均值差异是否显著，并给出相应的 结论。
解读置信区间
根据置信区间的范围和上下限，判断样本均值的稳定性，并据此作 出决策。
综合分析
结合样本描述性统计和检验结果，对数据进行分析和解释，得出科 学合理的结论。
均值比较结果的应用
差异显著性判断
记录处理过程
在分析过程中记录异常值的处理方式，以便于后 续的审查和验证。
比较标准的设定
确定比较对象
明确需要比较的变量、组别或时间点。
选择比较方法
根据数据类型和比较目的选择适当的比较方法，如独立样本T检验、 配对样本T检验、单因素方差分析等。
设定比较标准
根据研究目的和实际情况设定合理的比较标准，如差异的显著性水 平、效应量等。
04 均值比较结果解读
均值比较结果的构成
样本描述性统计
包括样本数量、均值、标准差、最小值、最大值等统计指标，用 于描述样本数据的集中趋势和离散程度。
均值差异检验
通过独立样本T检验或配对样本T检验等方法，比较两组或多组 数据的均值是否存在显著差异。
置信区间
表示样本均值的可靠程度，通常以95%或99%的置信水平表示。
THANKS FOR WATCHING
感谢您的观看
差异。
均值比较的原理
T检验是通过比较两组数据的平 均值和标准差来判断它们是否显
著不同。
方差分析是通过比较不同组之间 的变异和误差变异来确定组间差
异是否显著。
在进行均值比较时，需要满足一 定的假设条件，如正态分布、方 差齐性等，以确保统计结果的准
确性。
03 SPSS软件操作流程
第5章SPSS均值比较T检验和方差分析
第5章SPSS均值比较T检验和方差分析第5章主要介绍了SPSS软件中进行均值比较的方法，包括t检验和方差分析。
本文将详细介绍SPSS中进行均值比较的步骤，以及如何解读结果。
5.1t检验t检验是一种用于比较两个样本均值差异的统计方法。
在SPSS中，进行t检验的步骤如下：1.打开SPSS软件，并导入需要进行t检验的数据集。
2.选择“分析”菜单，在下拉菜单中选择“比较均值”选项，再选择“独立样本t检验”选项。
3.在弹出的对话框中，将需要比较的变量移动到“因子”框中，将“分组变量”移动到“因子”框中，并选择需要进行的假设检验类型。
4.点击“确定”按钮，等待计算结果。
5.在输出窗口中，可以查看计算结果，包括均值、标准差、样本量、t值和p值等。
通常，我们关注的是p值，如果p值小于0.05，则认为差异显著。
例如，我们想比较男性和女性的体重是否有显著差异。
我们将体重作为因变量，性别作为自变量，进行t检验。
在计算结果中，如果p值小于0.05，则可以认为男女性别对体重有显著影响。
5.2方差分析方差分析是一种用于比较三个或更多个样本均值是否存在差异的统计方法。
在SPSS中，进行方差分析的步骤如下：1.打开SPSS软件，并导入需要进行方差分析的数据集。
2.选择“分析”菜单，在下拉菜单中选择“比较均值”选项，再选择“单因素方差分析”选项。
3.在弹出的对话框中，将需要比较的变量移动到“因子”框中，将“分组变量”移动到“因子”框中，并选择需要进行的假设检验类型。
4.点击“确定”按钮，等待计算结果。
5.在输出窗口中，可以查看计算结果，包括均值、标准差、样本量、F值和p值等。
通常，我们关注的是p值，如果p值小于0.05，则认为差异显著。
例如，我们想比较不同药物对治疗效果的影响。
我们将药物作为因变量，治疗效果作为自变量，进行方差分析。
在计算结果中，如果p值小于0.05，则可以认为不同药物对治疗效果有显著影响。
通过以上步骤，我们可以在SPSS中进行均值比较、t检验和方差分析。
SPSS的均值比较过程
一、相关分析1、参数相关分析Pearson相关系数，又称积矩相关系数，适用于连续分布或正态分布变量，是最常用的参数相关分析。
2、非参数相关分析当资料不服从双变量正态分布或总体分布未知，或原始数据用等级表示时，宜用spearman 或kendall相关。
Spearman，等级相关，适合定序变量或不满足正态分布假设的等间隔数据，适用于连续等级资料；Kendall，等级相关，适合定序变量或不满足正态分布假设的等间隔数据，适用于合并等级资料；（1）Spearman相关分析Spearman相关系数又称秩相关系数，是根据等级资料研究两个变量间相关关系的方法。
它是依据两列成对等级的各对等级数之差来进行计算的，所以又称为“等级差数法”。
它对数据条件的要求没有积差相关系数严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关来进行研究。
它是利用两变量的秩次大小作线性相关分析，对原始变量的分布不作要求，属于非参数统计方法，适用范围要广些。
对于服从Pearson相关系数的数据亦可计算Spearman相关系数，但统计效能要低一些。
Pearson相关系数的计算公式可以完全套用Spearman相关系数计算公式，但公式中的x和y用相应的秩次代替即可。
（2）Kendall相关分析肯德尔(Kendall)系数又称和谐系数，是表示多列等级变量相关程度的一种方法。
适用这种方法的数据资料一般是采用等级评定的方法收集的，即让K个评委（被试）评定N件事物，或1个评委（被试）先后K次评定N件事物。
等级评定法每个评价者对N件事物排出一个等级顺序，最小的等级序数为1 ，最大的为N，若并列等级时，则平分共同应该占据的等级，如，平时所说的两个并列第一名，他们应该占据1，2名，所以它们的等级应是1.5,又如一个第一名，两个并列第二名，三个并列第三名，则它们对应的等级应该是1,2.5,2.5,5,5,5,这里2.5是2,3的平均，5是4,5,6的平均。
SPSS第5章 平均数比较
5.3.2 单一样本T检验过程选择
• 顺序单击“Analyze”→“Compare Means”→“One Sample T test”命令，可打开图5.3的对话框。“Test Variable”框中的变量是需要作检验的变量，要从源变 量框中选取某个变量进入该框，然后单击向右的箭头， 再在“Test Value”参数框中输入一个定值作为假设检 验值（总体参数）。 • “Options”对话框将给出置信水平“Confidence Interval”和缺失值“Missing Value”处置方式。置信水 平必须在1-99之间，如90、95，99等（一般取95）。 缺失值的处置方式一般有两种（图5.4）：一种是只 要变量中含有缺失值，该组样本都被剔除（Exclude cases Listwise）；另一种是尽可能保留样本，仅剔除 被分析变量的那个变量中含有缺失值的Cases。
•1、统计检验中的假设条件
•假设是进行检验的前提，是有待确认的一种事实。例 如，某样本是否满足正态分布，两样本平均数是否源 于同一总体等等。
•假设检验中，首先要建立一个关于总体参数的假设（原 假设），然后抽取样本，检验所做假设正确与否。在进行 研究时，往往需要根据已有的理论和经验，事先对研究结 果作出一种预想希望能证实的一种假设。这种假使叫科学 假设或被择假设，记为H1；而要对总体的某种假设（论断） 作出判断时，常要对相反的假设进行统计检验，称这个假 设为零假设（或虚无假设、无偏假设），记作H0。进行假 设检验的目的是为了推翻假设，主要是推翻假设时的犯错 误概率容易把握，而承认假设正确的概率不容易把握。 •假设建立得合适与否是决定检验成败的关键，统计中的 假设检验有两个基本要求。第一，建立假设的目的是为了 推翻原假设，因为推翻假设远远比承认原假设容易，因此， 真正需要证明的往往作为备择假设，即使不能推翻原假设， 也只能说，没有足够的证据推翻原假设。第二，原假设必 须是虚无（无显著性差异）假设，即必须包括等号，因为 所有的统计分析、统计计算都建立在这个基础之上；而备 择假设一定不能包含等号。
spss教程第二章--均值比较检验与方差分析
第二章均值比较检验与方差分析在经济社会问题的研究过程中，常常需要比较现象之间的某些指标有无显著差异，特别当考察的样本容量n比较大时，由随机变量的中心极限定理知，样本均值近似地服从正态分布。
所以，均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。
◆本章主要内容：1、单个总体均值的 t 检验（One-Sample T Test）；2、两个独立总体样本均值的 t 检验（Independent-Sample T Test）；3、两个有联系总体均值均值的 t 检验（Paired-Sample T Test）；4、单因素方差分析（One-Way ANOVA）；5、双因素方差分析（General Linear Model Univariate）。
◆假设条件：研究的数据服从正态分布或近似地服从正态分布。
在Analyze菜单中，均值比较检验可以从菜单Compare Means，和General Linear Model得出。
如图2.1所示。
图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验（One-Sample T Test）分析单个总体的 t 检验分析也称为单一样本的 t 检验分析，也就是检验单个变量的均值是否与假定的均数之间存在差异。
如将单个变量的样本均值与假定的常数相比较，通过检验得出预先的假设是否正确的结论。
例1：根据2002年我国不同行业的工资水平（数据库SY-2），检验国有企业的职工平均年工资收入是否等于10000元，假设数据近似地服从正态分布。
首先建立假设：H0：国有企业工资为10000元；H1：国有企业职工工资不等于10000元打开数据库SY-2，检验过程的操作按照下列步骤：1、单击Analyze →Compare Means →One-Sample T Test，打开One-Sample T Test 主对话框，如图2.2所示。
图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量（国有单位）进入检验框中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
独立与相关总体
独立的 不同的数据来源
不相关的 Unrelated 独立的 Independent
相关的 同一数据来源
成对的或对应的 Paired or Matched 如：重复测量（前/后） (Before/After)
两个样本平均数的
差异 Difference between sample means
24
秩和检验--例题
您是一名生产计划者，您想了解两个工厂生
产率的中位数是否相同。工厂1，生产率为 (百分比值): 71, 82, 77, 92, 88; 工厂2, 生产率 为: 85, 82, 94, 97. 在0.01水平上两个工厂的 生产率中位数是否相同？
25
秩和检验—计算表
工厂1 生产率 71 82 77 92 秩 1 4 3.5 2 7 85 82 94 97 工厂2 生产率 秩 5 4 3.5 8 9
可用于定序、定距或定比数据 总体近乎对称
如：钟形、矩形等
4. 如果 ni > 10可以用正态分布近似计算
23
秩和检验--步骤
1. 令 Ri 表示排序结果,样本观测值从第1 排到第 n1 + n2如果样本容量不同，令样本容量较小 者为n1
最小值 = 第1 如有并列，则取排序的平均值
2. 计算等级之和，以Ti 表示每个样本的等级之 和 3. 检验统计量是 T1 (较小的样本)
10
不同方差均值的t 检验
t (X1 X 2 ) (μ1 μ 2 )
2 S1 S2 2 n1 n 2 2 1 2 2 2
S S n n 2 1 其中 df 2 2 2 2 S1 S2 n n 1 2 (n 1 1) (n 2 1)
假设
H0 H1
有差别
P1P2 0 P 1P 2 0
P 1P 2
0
P 1P 2
0
P 1P 2 0
P 1P 2 0
31
两个比率差异的Z检验
1. 假设
总体相互独立 总体服从二项分布 可以用正态分布近似计算 每个总体满足：n· p 5 & n· (1 - p) 5
2. 两个比率的Z检验统计量
27
SPSS中两个独立样本的非参数检验
独立样本的检验过程的步骤： 打开数据文件，执行analyze nonparametric 2 independent-sample test,打开对话框。 选择一个或几个数值变量； 选择分组变量 在test type子栏里提供了4种检验方法 如果需要输出统计量，单击option按钮
拒绝H0 拒绝H0
/2
不拒绝H0 0
/2
F
F
α L( ;df1 ,df 2 ) 2
1 F
α U( ;df 2 ,df1 ) 2
F
α U( ;df1 ,df 2 ) 2
注意区别！
20
方差的F 检验--示例
作为Charles Schwab的金融分析员, 您想知道分别在
NYSE和NASDAQ市场上市的股票在利息收益上有 没有差异。您收集到以下数据:
向下 取整 的自 由度
11
不同方差均值的t 检验：实例
作为Charles Schwab的金融分析员, 您想知道分别在
NYSE和NASDAQ市场上市的股票在利息收益上有 没有差异。您收集到以下数据:
样本容量 均值
标准差
NYSE 21 3.27 1.30
NASDAQ 25 2.53 1.16
假定总体方差不同, 试检验平均 利息收益有没有差异(= 0.05)？
α 0.05 df1 20； df 2 24
拒绝H0
决定： 在 0.05水平上不拒绝H 0 结论： 没有足够证据表明两总体 方差有差异。
拒绝H0
/2
不拒绝H0
0 0.415 2.33
/2
F
临界值
22
两个中位数的秩和检验
1. 检验两个独立总体的中位数 2. 适用于任意总体分布的检验过程 3. 假定
13
不同方差均值的t 检验：题解
检验统计量： H1 : μ1 μ 2 0 (μ1 μ 2 ) (3.27 2.53) (μ1 μ 2 ) t 2.01 0.05 1.698 1.353 21 25 df 40.58 44(向下取整) 决定：
1. 假设
2 H 0 : σ1 σ2 2 2 或 H 0 : σ1 σ2 2（or ）
H1 : σ σ
2 1
2 2
H1 : σ σ （or ）
2 1 2 2
2. 检验统计量
2 S1 F 2 S2
df1 n1 - 1； df 2 n 2 - 1 统计量服从F分布
19
方差的F检验--临界值
试，成绩见数据文件。假定两个年级成绩均 服从正态分布。设显著性水平为0.05，问两 个年级的英语成绩有无显著性差异？
具体步骤见课堂演示。
17
两个总体方差差异的F检验
1. 两个独立总体方差差异的检验
2. 为参数检验过程 3. 假定 两个总体都服从正ቤተ መጻሕፍቲ ባይዱ分布
这一检验对正态假定较为敏感
18
方差的F检验
12
自由度和检验统计量的计算
t (X1 X 2 ) (μ1 μ 2 )
2 S1 S2 2 n1 n 2 2 1 2 2 2
(3.27 2.53) (μ1 μ 2 ) 2.01 1.698 1.353 21 25
2 S S 1.698 1.353 n n 21 25 1 2 df 40.58 2 2 2 2 2 S1 S2 1.698 1.353 2 n n 21 25 1 2 (21 1) (25 1) (n 1 1) (n 2 1)
7
检验统计量的计算
t (X1 X 2 ) (μ1 μ 2 ) 1 1 S n1 n 2
2 P
(3.27 - 2.53) (0) 1 1 1.51 21 25
2.03
2 2 (n 1) S (n 1) S 1 1 2 2 S2 P (n 1 1) (n 2 1)
0.05 df 21 25 - 2 44
拒绝H0 拒绝H0
决定： 在 0.05水平上拒绝H 0 结论：
t
0.025
0.025
-2.0154 0 2.0154
有证据表明存在均值差异。
临界值
9
两样本不同方差均值的t 检验
1.检验两个有不相同方差的独立总体的均值 2.属于参数检验过程 H 0 : μ1 μ 2 0 (μ1 μ 2 ) H1 : μ1 μ 2 0 (μ1 μ 2 ) 3.假定：两个总体都是正态分布 如果不是正态分布，当n1 30 & n 2 30 可以用正态分布近似 总体方差未知，但可以假定两个方差不同
均值比较
（双样本检验）
1
学习目标
1. 2. 3. 4. 5. 6. 7. 8.
区分独立总体与相关总体的概念 混合方差时两独立总体均值差异的t检验 不同方差时两独立总体均值差异的t检验 两总体方差差异的F检验 两个独立总体的中位数差异的秩和检验 两个独立总体比率差异的Z检验 两个相关总体(成对样本)均值差异的t检验 两个相关总体中位数差异的符号秩检验
样本容量 均值
标准差
NYSE 21 3.27 1.30
NASDAQ 25 2.53 1.16
在0.05水平上, NYSE和NASDAQ 市场的方差是否有差异?
21
方差的F检验--方法
H0 : σ σ
2 1 2 2 2 H1 : σ1 σ2 2
检验统计量：
2 S12 (1.30) F 2 1.25 2 S 2 (1.16)
88 秩和
6 19.5 25.5
26
秩和检验--方法
H0: M1 = M2 H1: M1 M2 =0.10 n1 = 4 n 2 = 5 临界值:
拒绝 不拒绝 12 28 拒绝 T1 检验统计量: T1 = 5 + 3.5 + 8+ 9 = 25.5 (较小的样本) 查秩和检验表得到临界值 决定: 在 = 0.10 水平上不拒绝 结论: 证据不能表明中位数不同
(21 1) 1.30 2 (25 1) 1.16 2 (21 1) (25 1)
1.51
8
混合方差的t 检验方法：题解
H 0 : μ1 μ 2 0 (μ1 μ 2 ) H1 : μ1 μ 2 0 (μ1 μ 2 )
t (3.27 - 2.53) (0) 1 1 1.51 21 25 2.03
5
混合方差均值的t检验
t (X1 X 2 ) (μ1 μ 2 ) 1 1 S n1 n 2
2 P
假设的差异
2 2 (n 1) S (n 1) S 2 1 2 2 其中 SP 1 (n 1 1) (n 2 1)
df n1 n 2 2
28
SPSS中四种检验方法
1. Mann-Whitney U：即为Wilcoxon秩和检验
法，用于检验两个独立样本是否来自于同 一总体。这种检验需用ORDINAL测度水平 的数据。当数据按升序排列后，U等于第一 组中的一个值优先于第二组中的一个值出 现的次数。 2. Moses extreme reactions:（略） 3. Kolmogorov-Smirnov（略） 4. Wald-Wolfowitz runs（略）