中考复习相似三角形基础复习(一)
中考复习专题1:相似三角形中的旋转问题配有辅导训练资料含试题解析与参考答案教师版

中考专题:相似三角形与旋转1. 已知,如图1,已知Rt △ABC 中,∠ACB =90°,D 、E 分别是AC 、BC 上的点,连DE ,且3AC BCDC EC==,2tan 2B =; (1)如图2,将△CDE 绕C 点旋转,连AD 、BE 交于H ,求证:AD ⊥BE ;(2)如图3,当△CDE 绕C 点旋转过程中,当5CH =时,求2A H ﹣BH 的值;(3)若CD =1,当△CDE 绕C 点旋转过程中,直接写出AH 的最大值是 .2. 在△ABC 中,CA =CB ,∠ACB =α(0°<α<180°).点P 是平面内不与A ,C 重合的任意一点,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,CP .点M 是AB 的中点,点N 是AD 的中点.(1)如图1,当α=60°时,PCMN的值是 ,直线MN 与直线PC 相交所成的较小角的度数是 .(2)如图2,当α=120°时,请写出的PCMN 值及直线MN 与直线PC 相交所成的较小角的度数,并就图2的情形说明理由. (3)如图3,当α=90°时,若点E 是CB 的中点,点P 在直线ME 上,请直接写出点B ,P ,D 在同一条直线上时MN PD的值.3. 在△ABC 中,∠ABC =120°,线段AC 绕点C 顺时针旋转60°得到线段CD ,连接BD .(1)如图1,若AB =BC ,求证:BD 平分∠ABC ;(2)如图2,若AB =2BC ,①求ACBD 的值;②连接AD ,当S △ABC =23时,直接写出四边形ABCD 的面积为 .4. (1)如图1,在Rt △ABC 中,∠C =90°,AC =BC ,AP 、BP 分别平分∠CAB 、∠CBA ,过点P作DE ∥AB 交AC 于点D ,交BC 于点E .①求证:点P 是线段DE 的中点; ②求证:BP 2=BE •BA .(2)如图2,在Rt △ABC 中,∠C =90°,AB =13,BC =12,BP 平分∠ABC ,过点P 作DE ∥AB 交AC 于点D ,交BC 于点E ,若点P 为线段DE 的中点,求AD 的长度.5.在△ABC中,AB=AC,点D在底边BC上,∠EDF的两边分别交AB、AC所在直线于E,F两点,∠EDF=2∠ABC,BD=nCD.(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;(2)如图2,求DEDF的值(含n的式子表示):(3)如图3,连接EF,若tan∠B=1,EF∥BC,且58EFBC=,直接写出n的值为.6.已知:在▱ABCD中,点E,F分别在AB,AD边上,且∠ECF=∠B=α(0°<α<90°)(1)如图1,若CF⊥AD,求证:CE CB CF CD=;(2)如图2,若α=60°,∠AEF=∠ECB,求证:四边形ABCD是菱形;(3)如图3,若α=45°,AC⊥EF,EH⊥BC于点H,34CEAD=,直接写出AECH的值.中考专题:相似(一)1. 已知,如图1,已知Rt △ABC 中,∠ACB =90°,D 、E 分别是AC 、BC 上的点,连DE ,且3AC BCDC EC==,2tan 2B =; (1)如图2,将△CDE 绕C 点旋转,连AD 、BE 交于H ,求证:AD ⊥BE ;(2)如图3,当△CDE 绕C 点旋转过程中,当5CH =时,求2A H ﹣BH 的值; (3)若CD =1,当△CDE 绕C 点旋转过程中,直接写出AH 的最大值是 .【解答】(1)证明:如图2中,设BE 交AC 于O .∵∠ACB =∠DCE =90°,∴∠ACD =∠ECB , AC BCDC EC =,∴AC CDBC CE =,∴△ACD ∽△BCE , ∴∠DAC =∠EBC ,∵∠AOH =∠BOC ,∴∠AHO =∠BCO =90°,∴AD ⊥BE . (2)解:如图2中,在HB 上取一点T ,使得HT =AH ,连接AT .在Rt △AHT 中,2tan AH ATH HT ∠==, 2tan ABC ∠=,∴∠ATH =∠ABC , ∵∠ATH +∠HAT =90°,∠ABC +∠CAB =90°,∴∠HAT =∠CAB ,∴∠CAH =∠BAT ,∴△AHT ∽△ACB ,∴AT AH AB AC =,∴AH AC AT AB =,∴△CAH ∽△BAT ,∴CH AHBT AT=,2HT AH =,设AH m =,则2HT m =,3AT m , ∴53m =15BT ∴ (3)解:如图3中,在Rt △AHB 中,∵AH =AB •sin ∠ABH ,∴当∠ABH 最大时,AH 的值最大,此时CE ⊥BE , ∵∠DCE =∠CEH =∠EHD =90°, ∴此时四边形ECDH 是矩形,∴DH =EC ,∠ADC =∠CDH =90°, 由题意CD =1,,2EC 3AC =, 2DH CE ∴==在Rt ACD ∆中,22312AD AC CD =-=-= 2222AH AD DH ∴=+= 的最大值为2. 在△ABC 中,CA =CB ,∠ACB =α(0°<α<180°).点P 是平面内不与A ,C 重合的任意一点,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,CP .点M 是AB 的中点,点N 是AD 的中点.(1)如图1,当α=60°时,PCMN的值是 ,直线MN 与直线PC 相交所成的较小角的度数是 .(2)如图2,当α=120°时,请写出的PCMN 值及直线MN 与直线PC 相交所成的较小角的度数,并就图2的情形说明理由. (3)如图3,当α=90°时,若点E 是CB 的中点,点P 在直线ME 上,请直接写出点B ,P ,D 在同一条直线上时MN PD的值.【解答】(1)如图1中,连接PC ,BD ,延长BD 交PC 于K ,交AC 于G . ∵CA =CB ,∠ACB =60°,∴△ABC 是等边三角形,∴∠CAB =∠PAD =60°,AC =AB ,∴∠PAC =∠DAB ,∵AP =AD ,∴△PAC ≌△DAB (SAS ),∴PC =BD ,∠ACP =∠ABD , ∵AN =ND ,AM =BM ,∴BD =2MN ,∴PCMN=21.∵∠CGK =∠BGA ,∠GCK =∠GBA ,∴∠CKG =∠BAG =60°,∴BK 与PC 的较小的夹角为60°, ∵MN ∥BK ,∴MN 与PC 较小的夹角为60°. (2)如图设MN 交AC 于F ,延长MN 交PC 于E .∵CA =CB ,PA =PD ,∠APD =∠ACB =120°,∴△PAD ∽△CAB ,∴ABADAC AP =,∵AM =MB ,AN =ND ,∴AMANAC AP =,∴△ACP ∽△AMN ,∴∠ACP =∠AMN ,PCMN =23=AC AM∵∠CFE =∠AFM ,∴∠FEC =∠FAM =30°. (3)设MN =a ,∵PCMN=22=AC AM ,∴PC =2a ,∵ME 是△ABC 的中位线,∠ACB =90°,∴ME 是线段BC 的中垂线, ∴PB =PC =2a ,∵MN 是△ADB 的中位线,∴DB =2MN =2a ,如图3﹣1中,当点P 在线段BD 上时,PD =DB ﹣PB =(2﹣2)a ,∴MN PD=2﹣2.如图3﹣2中,PD =DB +PB =(2+2)a ,∴MN PD=2+2.3. 在△ABC 中,∠ABC =120°,线段AC 绕点C 顺时针旋转60°得到线段CD ,连接BD .(1)如图1,若AB =BC ,求证:BD 平分∠ABC ;(2)如图2,若AB =2BC ,①求ACBD 的值;②连接AD ,当S △ABC =23时,直接写出四边形ABCD 的面积为 .【解答】(1)证明:连接AD ,由题意知,∠ACD =60°,CA =CD ,∴△ACD 是等边三角形,∴CD =AD ,又∵AB =CB ,BD =BD ,∴△ABD ≌△CBD (SSS ),∴∠CBD =∠ABD ,∴BD 平分∠ABC ; (2)解:①连接AD ,作等边三角形ACD 的外接圆⊙O , ∵∠ADC =60°,∠ABC =120°,∴∠ADC +∠ABC =180°,∴点B 在⊙O 上,∵AD =CD ,∴⁔AB =⁔CD ,∴∠CBD =∠CAD =60°, 在BD 上截取BM ,使BM =BC ,则△BCM 为等边三角形,∴∠CMB =60°,∴∠CMD =120°=∠CBA ,又∵CB =CM ,∠BAC =∠BDC ,∴△CBA ≌△CMD (AAS ),∴MD =AB ,设BC =BM =1,则AB =MD =2,∴BD =3,过点C 作CN ⊥BD 于N , 在Rt △BCN 中,∠CBN =60°,∴∠BCN =30°, ∴BN =21BC =21,CN =23BC =23,∴ND =BD ﹣BN =25, 在Rt △CND 中,CD =722=+DN CD ,∴AC =7,∴773=ACBD ;②如图3,分别过点B ,D 作AC 的垂线,垂足分别为H ,Q , 设CB =1,AB =2,CH =x ,则由①知,AC =7,AH =7﹣x , 在Rt △BCH 与Rt △BAH 中,BC 2﹣CH 2=AB 2﹣AH 2,即1﹣x 2=22﹣(7﹣x )2,解得,x =772,∴BH =721,在Rt △ADQ 中,DQ =23AD =23×7=221,∴72=DQ BH∵AC 为△ABC 与△ACD 的公共底,∴72==∆∆DQ BH S SACDABC ,∵S △ABC =23,∴S △ACD =437,∴S 四边形ABCD =23+437=439,4. (1)如图1,在Rt △ABC 中,∠C =90°,AC =BC ,AP 、BP 分别平分∠CAB 、∠CBA ,过点P 作DE ∥AB 交AC 于点D ,交BC 于点E .①求证:点P 是线段DE 的中点; ②求证:BP 2=BE •BA .(2)如图2,在Rt △ABC 中,∠C =90°,AB =13,BC =12,BP 平分∠ABC ,过点P 作DE ∥AB 交AC 于点D ,交BC 于点E ,若点P 为线段DE 的中点,求AD 的长度.【解答】(1)①证明:∵BP 平分∠ABC ,∴∠ABP =∠CBP ,∵DE ∥AB ,∴∠ABP =∠EPB ,∴∠CBP =∠EPB ,∴BE =PE , 同理可证:DP =DA ,∵DE ∥AB ,∴CE CDCB CA=, ∵CA =CB ,∴CE =CD ,∴BE =AD ,∴PE =PD ,∴点P 是DE 的中点. ②证明:由①得∠ABP =∠EBP =∠EPB =21∠CBA , ∵AP 平分∠CAB ,∴∠P AB =21∠CAB , ∵CA =CB ,∴∠CBA =∠CAB ,∴∠ABP =∠EBP =∠EPB =∠P AB ,∴△ABP ∽△PBE ,∴BP BEBA BP=,∴BP 2=BA •BE . (2)过点P 作FG ∥AC 交BC 于F ,交AB 于G .在Rt △ACB 中,222213125AC AB BC =-=-=,∵FG ∥AC ,∴∠PFE =∠C =90°,∵PD ∥AG ,∴四边形AGPD 是平行四边形,∴PG =AD , ∵PE =PD ,PF ∥CD ,∴EF =FC ,∴PF =21CD ,由(1)可知BE =EP ,设AD =PG =x ,则CD =5﹣x ,PF =21(5﹣x ),∵DE ∥AB ,∴CD CE CA CB =,∴512CD CA CE CB ==, 125CE CD ∴=,12(5)5x =-,则6(5)5EF x =-,1212120(5)55BE EP x x ∴==-=,在Rt EFP ∆中,6(5)125sin sin sin 1213(5)5x EF EPF EDC BAC EP x -∠===∠=∠=-,解得6537x =,6537AD ∴=.5.在△ABC中,AB=AC,点D在底边BC上,∠EDF的两边分别交AB、AC所在直线于E,F两点,∠EDF =2∠ABC,BD=nCD.(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;(2)如图2,求DEDF的值(含n的式子表示):(3)如图3,连接EF,若tan∠B=1,EF∥BC,且58EFBC=,直接写出n的值为.【解答】(1)证明:如图1中,连接AD.∵AB=AC,∴∠ABC=∠C=45°,∵BD=nCD,n=1,∴BD=CD,∴AD⊥BC,∠DAC=∠DAB=45°,AD=DB=DC,∵∠EDF=2∠ABC=90°,∴∠BDA=∠EDF=90°,∴∠BDE=∠ADF,∵∠B=∠DAF,BD=AD,∴△BDE≌△ADF(SAS),∴DE=DF.(2)解:在射线B上取一点T,使得DB=DT.∵DB=DT,∴∠B=∠T,∴∠TDC=∠B+∠T=2∠B,∵∠EDF=2∠B,∴∠EDF=∠TDC,∴∠EDT=∠DFC,∵∠BAC+2∠B=180°,∴∠BAC+∠DEF=180°,∴∠TED+∠AFD=180°,∵∠DFC+∠AFD=180°,∴∠TED=∠DFC,∴△TED∽△FDC,∴DE DT DBn DF DC CD===.(3)如图3中,作ET⊥BC于E,FH⊥BC于H.∵EF∥BC,ET∥FH,∴四边形EFHT是平行四边形,∵∠ETH=90°,∴四边形EFHT是矩形,∴ET=FH,EF=TH,∵EF:BC=5:8,设EF=5k,BC=8k,则TH=5k,∵tan B=1,∴∠B=∠C=45°,∵∠ETB=∠FHC=90°,∴ET=BT=FH=CH=1.5k,设DT=x,则DH=5K﹣x,∵∠EDF=2∠B=90°,∠ETD=∠FHD=90°,∴∠EDT+∠FDH=90°,∠TED+∠EDT=90°,∴∠TED=∠FDH,∴△ETD∽△DHF,∴ET DTDH FH=,∴1.55 1.5k xk x k=-,∴x2﹣5kx+2.25k2,解得x=0.5k或4.5k,∴BD=2k或6k,∴BD:DC=2k:6k=1:3或BD:DC=6k:2k=3:1.∴n=3或.6. 已知:在▱ABCD 中,点E ,F 分别在AB ,AD 边上,且∠ECF =∠B =α(0°<α<90°)(1)如图1,若CF ⊥AD ,求证:CE CBCF CD=; (2)如图2,若α=60°,∠AEF =∠ECB ,求证:四边形ABCD 是菱形;(3)如图3,若α=45°,AC ⊥EF ,EH ⊥BC 于点H ,34CE AD =,直接写出AECH 的值. 【解答】(1)证明:如图1中,∵在▱ABCD 中,∠B =∠D ,∵∠ECF =∠B =α,∴∠D =∠ECF =α,∵CF ⊥AD ,∴∠D +∠DCF =90°,∴∠ECF +∠DCF =90°,∴EC ⊥CD , ∵AB ∥CD ,∴CE ⊥AB ,∴∠BEC =∠CFD =90°,∴∠BCE ∽△DCF ,∴CE CBCF CD=; (2)证明:如图2中,连接AC ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,∠B =60°,∴∠BAC =120°,∵∠ECF =60°,∴∠EAF +∠ECF =180°,∴A ,E ,C ,F 四点共圆,∴∠AEF =∠ACF , ∵∠AEF =∠BCE ,∴∠ACF =∠BCE ,∴∠ACB =∠ECF =60°,∴△ABC 是等边三角形, ∴AB =BC ,∴四边形ABCD 是菱形;(3)解:∵∠ECF =∠B =45°,∵34CE AD =,∴设CE =3m ,BC =AD =4m , 过C 作CI ⊥BC 交BA 的延长线于I ,交AD 于K ,交EF 于J ,延长HE 交DA 的延长线于L , 则CI =BC =4m ,作JM ⊥LH 于M ,交BI 于R ,连接AJ ,∵∠ECF =∠B =45°,∴∠EAF =135°,∴C ,E ,A ,F 四点共圆,∴∠CEF =∠F AC , ∵AC ⊥EF ,∴∠EJC =∠CAF ,∴∠CEJ =∠EJC ,∴CE =CJ ,∴AC 垂直平分EJ ,∴AE =AJ , 设BH =EH =n ,CH =4m ﹣n ,在Rt △CHE 中,EH 2+CH 2=CE 2, ∴n 2+(4m ﹣n )2=(3m )2,解得42n ±=,(取42n -=时,结论一样), 424KL CH m n -∴==-=,42223ME MH HE CJ EH m +-=-=-=-=,2LE LA =,2222KJ LM ME -===,422AK LK AL -=-=-, 2222224222(()22AE AJ AK JK --∴==+=+, 解得:3(21)32AE -=-,∴3(21)3322742AE CH --==-。
2024年中考数学一轮复习基础训练:相似三角形(无答案)
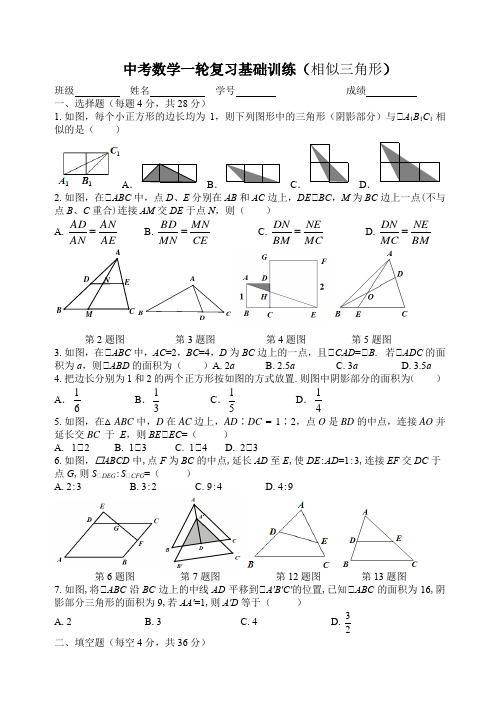
中考数学一轮复习基础训练(相似三角形)班级 姓名 学号 成绩一、选择题(每题4分,共28分)1.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A 1B 1C 1相似的是( )A .BC .D .2.如图,在△ABC 中,点D 、E 分别在AB 和AC 边上,DE △BC ,M 为BC 边上一点(不与点B 、C 重合)连接AM 交DE 于点N ,则 ( ) A .AE AN AN AD = B .CEMNMN BD = C .MC NE BM DN = D .BMNE MC DN =第2题图 第3题图 第4题图 第5题图3.如图,在△ABC 中,AC =2,BC =4,D 为BC 边上的一点,且△CAD =△B . 若△ADC 的面积为a ,则△ABD 的面积为( )A .2a B .2.5a C .3a D .3.5a4.把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为( )A .61B .31C .51D .41 5.如图,在△ABC 中,D 在AC 边上,AD ∶DC = 1∶2,点O 是BD 的中点,连接AO 并延长交BC 于 E ,则BE △EC =( )A . 1△2B . 1△3C . 1△4D . 2△36.如图, ABCD 中,点F 为BC 的中点,延长AD 至E ,使DE :AD =1:3,连接EF 交DC 于点G ,则S △DEG :S △CFG =( )A .2:3B .3:2C .9:4D .4:9第6题图 第7题图 第12题图 第13题图7.如图,将△ABC 沿BC 边上的中线AD 平移到△A'B'C'的位置,已知△ABC 的面积为16,阴影部分三角形的面积为9,若AA'=1,则A'D 等于( )A .2B .3C .4D .32 二、填空题(每空4分,共36分) N EAB C D M B A CD8.若23=+x y x ,则xy = . 9.在某一时刻,侧的一根高为1.8m 的竹竿的影长为3m ,同时同地测得一栋楼的影长为90m ,则这栋楼的高度为 m .10.在平面直角坐标系中,点A (4,2),B (5,0),以点O 为位似中心,相似比为1:2,把△ABO 缩小,得到△A 1B 1O ,则点A 的对应点A 1的坐标为 .11.若△ABC ∽△A B C ''',相似比为1﹕2,则△ABC 与△A B C '''的周长的比为 .12.如图,D 、E 分别是△ABC 边AB 、AC 上的点,∠ADE =∠ACB ,若AD =2,AB =6,AC =4,则AE 的长是 .13.如图,在△ABC 中,D 、E 分别是AB 、AC 边上的点,DE ∥BC ,若AD =2,AB =3,DE =4,则BC 等于 .14.如图,在Rt △ABC 中,∠ACB =90°,AB =10,BC =6,CD ∥AB ,∠ABC 的平分线BD 交AC 于点E ,DE = .第14题图 第15题图 第16题图15.如图,在一斜边长30cm 的直角三角形木板(即Rt △ACB )中截取一个正方形CDEF ,点D 在边BC 上,点E 在斜边AB 上,点F 在边AC 上,若AF :AC =1:3,则这块木板截取正方形CDEF 后,剩余部分的面积为 .16.如图,在△ABC 中,点D 为BC 边上的一点,AD △AB 且AD =AB =2,过点D 作DE △AD ,DE 交AC 于点E .若DE =1,则△ABC 的面积为 .三、解答题(17至19题每题8分,20题12分,共36分)17.如图,为了测量一栋楼的高度OE ,小明同学先在操场上A 处放一面镜子,向后退到B 处,恰好在镜子中看到楼的顶部E ;再将镜子放到C 处,然后后退到D 处,恰好再次在镜子中看到楼的顶部E (O 、A 、B 、C 、D 在同一条直线上),测得AC =2m ,BD =2.1m ,如果小明眼睛距地面髙度BF ,DG 为1.6m ,试确定楼的高度OE .第17题图18.如图,△ABD =△BCD =90°,DB 平分△ADC ,过点B 作BM △CD 交AD 于M .连接CM 交DB 于N .(1)求证:BD 2 =AD ·CD ;(2)若CD =6,AD =8,求MN 的长.第18题图19.如图,Rt△ABC 中,△ACB =90°,以AC 为直径的△O 交AB 于点D 过点D 作△O 的切线交BC 于点E ,连接OE .(1)求证:△DBE 是等腰三角形;(2)求证:△COE △△CA B.第19题图 20.如图,在等腰Rt △ABC 中,∠ACB =90°,ABD ,E 分别在边AB ,BC 上,将线段ED 绕点E 按逆时针方向旋转90°得到EF .(1)如图1,若AD =BD ,点E 与点C 重合,AF 与DC 相交于点O ,求证:BD =2DO .(2)已知点G 为AF 的中点.如图2,若AD =BD ,CE =2,求DG 的长.第20题图E B 图图2图1G F AB (E)CD E。
初中数学精品试卷:相似三角形基础复习

一、平行线分线段成比例(一)、比例式比例式:1、设2y -3x =0(y ≠0),则yyx += . 比例中项:1、已知线段a=2,b=8,若线段c 是线段a 与b 的比例中项,则c = .(二)、A 字型1、在△ABC 中,已知点D 、E 分别在边AB 、AC 上,DE ∥BC .如果AD =1cm ,AB =3cm ,DE =4cm ,那么BC = cm .2、已知:在△ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC .如果AD =4cm ,AB =6cm ,DE =3cm ,那么BC = cm .3、如图,在△ABC 中,DE ∥B C ,DB AD =21, 则BCDE= . 4、已知:如图,在△ABC 中,BD 是∠ABC 的平分线,过点D 作DE ∥CB ,交AB 于点E ,DC AD =31,DE =6,则AB = .(三)、X 型1、如图,AB//CD ,AD 与BC 交于点O , 若35=OD OC ,则BO AO= .2、如图,E 是平行四边形ABCD 边AD 上一点,且AE ∶ED=1∶2,CE 与BD 交于点O ,则BO :OD= .3、已知:如图,在梯形ABCD 中,AB ∥CD .且AB =2CD ,点E 、F 分别是AB 和BC 的中点,EF 与BD 相交于点M .求证:DM =2BM .(四)、中间比1、如图,在△ABC 中,DE ∥BC ,DF ∥AB ,那么下列比例式中正确的是( ) (A )EB AE =FC BF ; (B )EB AE =FBCF;A D CEBDBCAE FE DAB CODACB OB CD AE FMBCADE(C )BC DE =DC AD ; (D )BC DE =ABDF. 2、已知:如图,在△ABC 中,DE ∥BC ,点F 为AD 上的一点,且AD 2=AB ·AF . 求证:EF ∥CD .3、已知:如图,AB ∥PD ,BC ∥PE . 求证:AC ∥DE . 1、判定三角形相似1、已知:如图,在△ABC 中,∠ACB =90°,CM 是斜边AB 上的中线.过点M 作CM 的垂线与AC 和CB 的延长线分别交于点D 和点E ,求证:△CDM ∽△ABC ;2、已知:如图七,△ABC 为等腰直角三角形,∠ACB =90°,点E 、F 是AB 边所在直线上的两点, 且∠EC F =135°.(1)求证:△ECA ∽△CFB ;(2)若AE =3,设AB =x ,BF =y ,求 y 与x 之间的函数关系式,并写出定义域.针对训练:1、已知矩形ABCD ,长BC=12cm ,宽AB=8cm ,P 、Q 分别是AB 、BC 上运动的两点。
相似三角形判定复习(一)

A E
C
二、证明题: 证明题: 1.D为 ABC中AB边上一点 边上一点, 1.D为△ABC中AB边上一点, ∠ACD= ∠ ABC. A 2=AD AB. 求证: 求证:AC =AD·AB. 2.△ABC中 BAC是直角 是直角, 2.△ABC中,∠ BAC是直角,过斜 边中点M而垂直于斜边BC BC的直线 边中点M而垂直于斜边BC的直线 CA的延长线于 的延长线于E AB于D,连 交CA的延长线于E,交AB于D,连AM. 求证: 求证:① △ MAD ∽△ MEA B ② AM2=MD · ME D 如图,AB∥CD,AO=OB, 3. 如图,AB∥CD,AO=OB, E DF=FB,DF交AC于 DF=FB,DF交AC于E, 求证: 求证:ED2=EO · EC. A
复习( 复习(一)
一、相似三角形的判定定理: 相似三角形的判定定理:
A'
定理1 两角对应相等,两三角形相似。 定理1:两角对应相等,两三角形相似。 ∠A' ∠A= ∠A ⇒△ABC∽△A'B'C' B' ABC∽△ B C C' ∠B' ∠B= ∠B A 定理2 两组边的比相等且夹角相等, 定理2:两组边的比相等且夹角相等, 两三角形相似。 两三角形相似。 AB BC = ABC∽△ B C A 'B ' B ' C ' ⇒ △ABC∽△A'B'C' ∠B' ∠B= ∠B B C 定理3 三组边的比相等,两三角形相似。 定理3:三组边的比相等,两三角形相似。
解: ∵ DE∥BC ∴∠ADE= ∠B, ∠EDC=∠DCB=∠A ① ∵ DE∥BC ∴△ADE ∽ △ABC D ② ∵ ∠A= ∠DCB, ∠ADE= ∠B ∴△ADE∽ △CBD ③ ∵ △ADE ∽ △ABC B △ADE ∽ △CBD ∴ △ABC ∽ △CBD ④ ∵ ∠DCA= ∠DCE, ∠A= ∠EDC ∴ △ADC ∽ △DEC
《相似三角形》中考复习题专题及答案

《相似三角形》复习题及答案一.选择题(1)△ABC 中,D 、E 、F 分别是在AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,那么下列各式正确的是( ) A.DB AD =EC BF B.AC AB =FCEF C.DB AD =FC BF D.EC AE =BF AD (2)在△ABC 中,BC=5,CA=45,AB=46,另一个与它相似的三角形的最短边是15,则最长边是( ) A.138 B.346 C.135 D.不确定(3)在△ABC 中,AB=AC,∠A=36°,∠ABC 的平分线交AC 于D ,则构成的三个三角形中,相似的是( )A.△ABD ∽△BCDB.△ABC ∽△BDCC.△ABC ∽△ABDD.不存在(4)将三角形高分为四等分,过每个分点作底边的平行线,将三角形分四个部分,则四个部分面积之比是( )A.1∶3∶5∶7B.1∶2∶3∶4C.1∶2∶4∶5D.1∶2∶3∶5(5)下列命题中,真命题是( )A.有一个角为30°的两个等腰三角形相似B.邻边之比都等于2的两个平行四边形相似C.底角为40°的两个等腰梯形相似D.有一个角为120°的两个等腰三角形相似(6)直角梯形ABCD 中,AD 为上底,∠D=Rt ∠,AC ⊥AB ,AD=4,BC=9,则AC 等于( )A.5B.6C.7D.8 (7)已知CD 为Rt △ABC 斜边上的中线,E 、F 分别是AC 、BC 中点,则CD 与EF 关系是( )A.EF >CDB.EF=CDC.EF <CDD.不能确定(8)下列命题①相似三角形一定不是全等三角形 ②相似三角形对应中线的比等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O 是△ABC 内任意一点.OA 、OB 、OC 的中点连成的三角形△A′B′C′∽△ABC 。
其中正确的个数是( )A.0个B.1个C.2个D.3个(9)D 为△ABC 的AB 边上一点,若△ACD ∽△ABC ,应满足条件有下列三种可能①∠ACD=∠B ②∠ADC=∠ACB ③AC 2=AB·AD ,其中正确的个数是( )A.0个B.1个C.2个D.3个(10)下列命题错误的是( )A.如果一个菱形的一个角等于另一个菱形的一个角,则它们相似B.如果一个矩形的两邻边之比等于另一个矩形的两邻边之比,则它们相似C.如果两个平行四边形相似,则它们对应高的比等于相似比D.对应角相等,对应边成比例的两个多边形相似二、填空题(1)比例的基本性质是________________________________________(2)若线段a=3cm,b=12cm,a、b的比例中项c=________,a、b、c的第四比例线段d=________(3)如下图,EF∥BC,若AE∶EB=2∶1,EM=1,MF=2,则AM∶AN=________,BN∶NC=________(4)有同一三角形地块的甲乙两地图,比例尺分别为1∶200和1∶500,则甲地图与乙地图的相似比为________,面积比为________(5)若两个相似三角形的面积之比为1∶2,则它们对应边上的高之比为________(6)已知CD是Rt△ABC斜边AB上的高,则CD2=________(7)把一个三角形改成和它相似的三角形,如果边长扩大为原来的10倍,那么面积扩大为原来的____倍,周长扩大为原来的______倍.(8)Rt△ABC中,∠C=90°,CD为斜边上的高。
《相似三角形》全章复习与巩固(基础)-知识讲解

《相似三角形》全章复习与巩固(基础)知识讲解【学习目标】(1)了解比例的基本性质,了解线段的比、成比例线段的概念;(2)通过具体实例认识图形的相似,探索相似图形的性质,知道相似多边形的对应角相等,对应边成比例,周长的比等于对应边的比,面积的比等于对应边比的平方;(3)了解两个三角形相似的概念,探索两个三角形相似的条件;(4)通过典型实例观察和认识现实生活中物体的相似,利用图形的相似解决一些实际问题( 如利用相似测量旗杆的高度);(5)理解实数与向量相乘的定义及向量数乘的运算律。
【知识网络】【要点梳理】要点一、比例线段及比例的性质1。
比例线段:(1)线段的比:如果选用同一长度单位量得两条线段a,b的长度分别是m,n,那么就说这两条线段的比是a:b=m:n,或写成,其中a叫做比的前项;b叫做比的后项.(2)成比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(3)比例的项:已知四条线段a,b,c,d,如果,那么a,b,c,d,叫做组成比例的项,线段a,d叫做比例外项,线段b,c叫做比例内项,线段d还叫做a,b,c的第四比例项.(4)比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c或,那么线段b叫做线段a和c的比例中项.要点诠释:通常四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b的单位一致,c,d的单位一2。
比例的性质(1)比例的基本性质:(2)反比性质:(3)更比性质: 或(4)合比性质:(5)等比性质: 且3。
平行线分线段成比例定理(1)三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
(2)三角形一边的平行线性质定理推论:平行于三角形一边并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边的对应成比例.(3)三角形一边的平行线判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边。
相似三角形复习1

A D B M C
D
C O
2. 如图,AB∥CD,AO=OB, DF=FB,DF交AC于E, 求证:ED2=EO ·EC.
E A B
F
△ABC中,∠ BAC是直角,过斜边中点M而垂直于 斜边BC的直线交CA的延长线于E, 交AB于D,连AM. 求证:① △ MAD ~△ MEA
E
② AM2=MD ·ME
证明:①∵∠BAC=90°
M为斜边BC中点 ∴AM=BM=BC/2 ∴ ∠B= ∠MAD A D 又 ∵ ∠B+ ∠BDM=90° B C ∠E+ ∠ADE= 90° M ∠BDM= ∠ADE ② ∵ △MAD∽ △MEA ∴∠B=∠E AM ME ∴∠MAD= ∠E ∴ MD AM 又 ∵ ∠DMA= ∠AME 2 即AM =MD· ME ∴△MAD∽ △MEA
AC BC BC BD
b 时,即当
BD
1 时, B
D
a 2 b2 BD
2 2
时,
△ABC∽ △BDC, ∴ BD b a b
答:略.
a
将两块完全相同的等腰直角三角板摆成如图的样子,假 设图形中的所有点、线都在同一平面内,则图中有相似 (不包括全等)三角形吗?如有,把它们一 一写出来. A 解:有相似三角形,它们是: △ADE∽ △BAE, △BAE ∽ △CDA ,△ADE∽ △CDA 1 2 E C ( △ADE∽ △BAE ∽ △CDA ) B D G
1.平行线分线段成比例定理及推论 对应高,中线,角平分线 的比等于相似比 对应周长的比等于相似比
相 似 三 角 形
2.性质
面积比等于相似比的平方
1.平行
3.判定
2.AA 3.SAS 4.SSS
相似三角形复习(较全)

相似三角形知识点汇总【知识要点】1. 比例线段的有关概念: 在比例式::中,、叫外项,、叫内项,、叫前项,a b cda b c d a d b c a c ==()b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线段AC 和BC ,使AC 2=AB ²BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质: ①基本性质:a b c dad bc =⇔= ②合比性质:±±a b c d a b b c dd =⇒= ③等比性质:……≠……a b c d m n b d n a c m b d n ab===+++⇒++++++=()03. 平行线分线段成比例定理:①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。
则,,,…AB BC DE EF AB AC DE DF BC AC EFDF=== ②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
二、有关知识点:1.相似三角形定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比:相似三角形的对应边的比叫做相似比。
4.相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
5.相似三角形的判定定理:(1)三角形相似的判定方法与全等的判定方法的联系列表如下:从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理,这就是我们数学中的用类比的方法,在旧知识的基础上找出新知识并从中探究新知识掌握的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形基础复习(一)
1、如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEFG,使得点F在CD边上,连接DG。
若AB=3,BE=2,求tan∠GFD的值。
知识点相似三角形的性质与判定
【知识梳理】
1、相似三角形的概念
对应角相等,对应边成比例的三角形叫做相似三角形。
相似用符号“∽”来表示,读作“相似于”。
相似三角形对应边的比叫做相似比。
2、相似三角形的判定方法
(1)常规方法
①定义法:对应角相等,对应边成比例的两个三角形相似。
②平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
用数学语言表述如下:∵DE∥BC,∴△ADE∽△ABC
③判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
④判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
⑤判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
(2)直角三角形相似的判定方法
①以上各种判定方法均适用
②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
3、相似三角形的性质
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方。
4、位似图形
(1)位似图形的概念:如果一个图形的点与另一个图形上的点分别对应,并且它们的连线都经过同一个点,那么这两个图形叫做位似图形,这个点是位似中心。
由一个图形得到它的位似图形的变换叫做位似变换。
利用位似变换可以把一个图形放大或缩小。
(示例1)(示例2)
(2)位似图形的性质
①每一组对应点和位似中心在同一直线上,它们到位似中心的距离之比都等于位似比;
②位似图形的对应边互相平行。
【例题精讲】直击中考
例1. 1、已知:线段OA OB,点C为OB中点,D为线段OA上一点。
连结AC,BD交于点P。
若OA=OB,且
D为OA中点,则AP
PC
=。
2、已知四边形ABCD的一组对边AD、BC的延长线交于点E。
如图,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB。
3、在△ABC中,P为边AB上一点。
如图,若∠ACP=∠B,求证:AC2=AP•AB。
4、已知四边形ABCD 中,E 、F 分别是AB 、AD 边上的点,DE 与CF 交于点G 。
如图,若四边形ABCD 是矩形,且DE ⊥CF ,求证。
【课堂练习】
1、已知锐角△ABC 中,边BC 长为12,高AD 长为8。
如图,矩形EFGH 的边GH 在BC 边上,其余两个顶点E 、F 分别在AB 、AC 边上,EF 交AD 于点K 。
求
AK
EF
的值。
CD
AD
CF DE
2、如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q.记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3。
求证:EF+PQ=BC;
3、如图,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接P Q。
若△BPQ与△ABC相似,求t的值。
4、如图,在△ABC 中,点D ,E ,Q 分别在AB ,AC ,BC 上,且DE ∥BC ,AQ 交DE 于点P 。
求证:
DP PE
BQ QC。
1、如图,在直角坐标系中,有两点A (6,3)、B (6,0)。
以原点O 为位似中心,相似比为3
1,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( ) A .(2,1)
B .(2,0)
C .(3,3)
D .(3,1)
(第1题) (第2题)
2、等边△ABC 的边长为6,在AC ,BC 边上各取一点E ,F ,连接AF ,BE 相交于点P ,AE =2,BF =4,则BP ·BE 等于 。
3、如图1,在平行四边形ABCD 中,对角线AC 、BD 交于点O ,E 为AD 上一点,连接CE 交BD 于F 。
如图,若E 为AD 中点,则
DF
OF
的值为 。
(第3题)(第4题)
4、在△ABC中,点D为BC上一点。
如图,若∠BAD=∠CAD,求证:BD AB CD AC
=。
5、如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,点O是AC边上一点,连接BO交AD于F,OE⊥BC交BC边于点E。
求证:△ABF∽△COE。
CE DF 的值。
6、如图,四边形ABCD是正方形,E边BC的中点,F是边CD上一点,且∠AEF=90°,求。
