有限单元法原理与应用(第三版)
有限元法基本原理及应用第3章重庆大学龙雪峰
有限元原理及应用
第三章 弹性力学有限元法
• 4．整体分析和有限元方程求解 • 由已知的单元刚度矩阵和等效节点载荷列阵组装成整个结 构的整体刚度矩阵和载荷列阵，得到一个由总体刚度矩阵 [K]、总载荷向量{F}和整体节点位移向量{δ}表示的平衡方 程式：[K] {δ}＝{F}。引进位移边界条件后求解得到整体节 点位移向量。 • 有限元离散方程是一个代数方程组，代入边界条件处理以 后的刚度矩阵是一个正定的对称稀疏方阵，这样一个代数 方程组可以用高斯消元法、三角分解法、波前法和雅可比 迭代法等多种方法求解。
a) 四边形薄板单元 b) 三角形薄板单元 图3.5 薄板单元
有限元原理及应用
第三章 弹性力学有限元法
• 3.2.4 多面体单元 • 对于实体结构就要用三维多面体单元进行分析，如机 床工作台、机械基础件等等。常用的三维多面体单元 有四节点四面体单元和八节点六面体单元，六面体单 元有规则六面体和不规则六面体， 如图3.6 所示。为 了提高精度也有八节点四面体单元和二十节点六面体 单元。
有限元原理及应用
第三章 弹性力学有限元法
• 在有限元分析中一般都采用多项式作为插值函数，多项式 的项数由所选取的单元和单元的节点数决定，如对于平面 三节点三角形单元有如下插值函数
3.1
• 式中的上标e 表示单元，而对 于图3.10 所示六节点三角形单 元则有如下插值函数
3.2
有限元原理及应用
第三章 弹性力学有限元法
有限元原理及应用
第三章 弹性力学有限元法
• 3.2.3 薄板弯曲单元和薄板单元 • 板壳结构是工程上经常采用的一类结构形式，其特点是在 一个方向上的尺度远小于另外两个方向的，通过一定的弹 性力学假设，简化为特殊的二维结构，即便于解析方法求 解也给有限元分析带来了很大的方便。这类结构通常有压 力容器、舰船外壳，体育馆屋顶，建筑物楼板等等。 • 薄板弯曲单元通常也有三角形单元和四边形单元两种，矩 形单元为后者的特殊形式，通常三角形单元有三个节点， 四边形单元有四个节点。主要承受横向载荷和绕水平轴的 弯矩。 • 如果挠度与板厚相比是小量时，板的中面应变可以忽略不 及，如图3.4 所示单元的每个节点有三个自由度，这样的 单元一般称为薄板弯曲单元。
有限单元法
•
u ( x) N j
Ni
—i点单位位移对内位移所做的贡献
性质：本质上与位移函数有相同的形式
性质1：本端为1，他端为0 性质2：任意一点的总和为1
k i , j
N
k
( x) N i ( x) N j ( x) 1
•
数学意义 若结构被自然结点离散化为有限元的集合，实现了结构模型的离 散化，而形状函数完成了数学模型的离散化，这两个离散化的步骤构 成了有限元法的理论基础。
① 平面桁架单元（只有一个沿轴向位移）
λ [l11 l12 ] cos
l11 l12 λ l21 l22 0 0 0 cos sin 0 1 0
sin
sin cos 0 0 0 1
② 平面自由式单元（轴向位移、横向位移及转角）
1 l Q Fp , 2 8 ,
e
1 l , 2 8
T
T
xi Qe M x ( 1 ) l
e
xi l
T
1 Q M x 2
e
2 2 6 xi 6 xi 2 xi 3 xi 3 , 2 l2 l l l
Qe mz
0 mz
0
T
6x 6x N v 2 3 l l
2
, 1
4 x 3x 2 2 , l l
6x 6x2 2 x 3x 2 , 2 l2 l3 l l
E-mail: wh@
LOGO
集中载荷
Q
e
N x
E-mail: wh@
LOGO
第二章 杆件结构有限元分析
“有限元法原理及应用”讲义-2012
二、最小总势能原理
一个“系统”是一个结构加上作用与其上的力。 对于保守系统，系统总势能定义为： 总势能 = 应变能 － 已知外力所作的功 为什么是减去“已知外力所作的功”？一种理解就是，把外力在结构变形前构形上的势 能定义为 0，则在任何可能的构形上任何一部分外力的势能就是“0 － 外力所作的功” 。 如何对系统总势能进一步理解？ 系统总势能用符号 p 表示， 它是系统位移的泛函， 对于系统每一个 “可能位移” （场） ， 系统有一个总势能与之对应。它是系统的一个状态函数。 “可能位移”—— 满足内部连续性和位移边界条件的位移场。 举例：对于一个图 1-1 所示，一端受集中力 P，具有刚度 k 的单自由度线性弹簧。
d p kDeq dD PdD 0
2
所以： Deq
P k
该结果与静力学求出的结果相同！ 2、多自由度系统、矩阵形式 如果决定一个系统的构形需要 n 个独立的量， 那么这个系统就具有 n 个自由度， 称为广 义坐标。 对于有限自由度（离散系统）问题，势能 p 是广义坐标的函数。广义坐标记为 Di 。 势能表达式为： p p ( D1 , D2, ..., Dn ) 它的全微分为：
位移是可能的待定参数必须满足一定约束关系因此该问题的独立参量广义坐标只里兹解往往是过刚的除非假定场包含了精确由于前面两点经典里兹法在解决实际问题时尤其是几何形状复杂的二三维问题解决的办法下面以一维直杆的分析为例子研究基于里兹法考虑图21a所示的结构长度改为3l把杆分为三个部分
“有限元法原理及应用”讲义
对于图 1-3 所示的多自由度弹簧系统，其总势能为：
p
1 1 1 2 k 1 D1 k 2 ( D 2 D1 ) 2 k 3 ( D 3 D 2 ) 2 P1 D1 P2 D 2 P3 D 3 2 2 2
有限单元法原理与应用
有限单元法原理与应用有限单元法（Finite Element Method，简称FEM）是一种数值计算方法，广泛应用于工程领域的结构分析、流体力学、热传导等问题的求解。
它将复杂的结构或物理现象分割成有限数量的简单单元，通过对每个单元进行数学建模和分析，最终得出整个系统的行为。
本文将介绍有限单元法的基本原理和其在工程领域中的应用。
有限单元法的基本原理是将连续的物理现象离散化为有限数量的单元，每个单元都可以通过简单的数学方程来描述。
这些单元相互连接，形成一个整体的系统，通过对每个单元的行为进行分析，最终得出整个系统的行为。
有限单元法的核心思想是将复杂的问题简化为简单的数学模型，通过数值计算方法求解这些模型，从而得到系统的行为。
有限单元法在工程领域有着广泛的应用。
在结构分析中，可以用有限单元法来模拟各种复杂的结构，如桥梁、建筑、飞机机翼等，通过对结构的受力、变形等进行分析，来评估结构的安全性和稳定性。
在流体力学中，有限单元法可以用来模拟流体的流动行为，如水流、气流等，通过对流体的速度、压力等进行分析，来优化流体系统的设计。
在热传导问题中，有限单元法可以用来模拟物体的温度分布和传热行为，如热传导、对流、辐射等，通过对热场的分析，来优化热传导系统的设计。
有限单元法的应用还不仅限于工程领域，它也被广泛应用于地质勘探、医学图像处理、材料科学等领域。
在地质勘探中，有限单元法可以用来模拟地下岩层的力学行为，来评估地下资源的分布和开采方案。
在医学图像处理中，有限单元法可以用来模拟人体组织的力学行为，来辅助医学诊断和手术设计。
在材料科学中，有限单元法可以用来模拟材料的力学性能和热物理性能，来指导新材料的设计和制备。
总的来说，有限单元法作为一种数值计算方法，具有广泛的应用前景和重要的理论意义。
通过对有限单元法的深入理解和应用，可以更好地解决工程领域中的复杂问题，推动工程技术的发展和进步。
希望本文对有限单元法的原理和应用有所帮助，也希望读者能够进一步深入研究和应用有限单元法，为工程领域的发展做出更大的贡献。
有限单元法原理与应用
yi yj ym
ai x j ym xm y j , bi y j ym , ci xm x j a j x m y i xi y m , b j y m y i , c j xi x m am xi y j x j yi , bm yi y j , cm x j xi
v 4 5 x 6 y
因此可以得到:
ui 1 2X i 3Yi ui 1 2X j 3Yj ui 1 2X m 3Y m v i 4 5X i 6Yi v i 4 5X j 6Yj v i 4 5X m 6Y m
2.3单元应变
•单元内的应变分量可用矩阵表示为：
u x x y v y xy u v y x
应变分 量是常 量
其子矩阵：
bi 1 Bi 0 2A c i
在（x，y）中，
， D , ,
,
,
D
,
,
T
,
D
,
T
整体坐标 系的弹性 矩阵
0 ci bi
bj 0 cj
0 cj bj
bm 0 cm
0 e e c m B bm
应力矩阵
S D 0
e
S D B S i
Sj
Sm
有限单元法
F2
x
1
2
e T
EP 0 eT e EP B T EAl B l e eT (F q( x)N dx) 0 0
单元是平衡的
eT T eT l e 0
eT T
k B
其中
EAl B
1 / l EAl 1 / l 1 / l 1/ l EA 1 1 l 1 1 --局部坐标系下的单元刚度矩阵
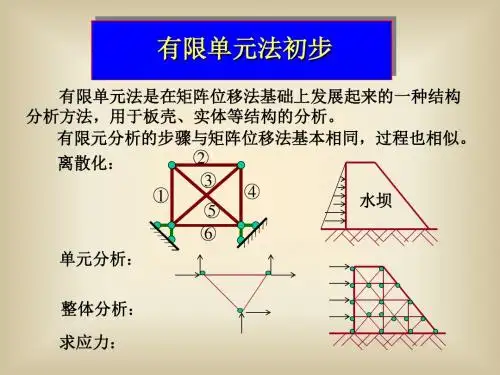
有限单元法初步
有限单元法是在矩阵位移法基础上发展起来的一种结构 分析方法，用于板壳、实体等结构的分析。 有限元分析的步骤与矩阵位移法基本相同，过程也相似。 2 离散化： 3 4 1 水坝 5 6
单元分析：
整体分析： 求应力：
§1 杆系结构的有限单元法
§1.1 泛函与变分
“最速落径问题”---质量为m的小环从A处自由滑下， 试选择一条曲线使所需时间最短。（不计摩擦）
§1.1 泛函与变分
y* ( x) y( x) y( x)
称 y ( x ) 为y（x）的变分，它是一个无穷小的任意函数。 变分运算在形式上与微分运算相同。
y 2 ( x) 2 y( x)y( x)
微分与变分运算次序可以交换。 d dy (y ) ( ) dx dx 积分与变分运算次序也可以交换。
杆中任一点应变
三、应力分析 ---用杆端位移表示杆中内力
杆中任一点应力
du dx d N e dx dN2 e dN 1 dx dx
E
EB
e
杆中任一截面的轴力
N A
B
B2
e
EAB
有限单元法ppt课件
06
有限单元法的发展趋势和展 望
发展趋势
工程应用领域拓展
随着科技的发展，有限单元法在解决 复杂工程问题上的应用越来越广泛， 不仅局限于结构分析，还涉及到流体 动力学、热传导等领域。
与其他方法的结合
有限单元法正与其他数值方法（如有 限差分法、边界元法等）进行交叉融 合，形成更为强大的数值分析工具。
05
有限单元法的优缺点
优点
灵活性
有限单元法允许对复杂的几何形状进 行离散化，适用于解决各种形状和大 小的问题。
高效性
有限单元法能够处理大规模问题，通 过使用计算机技术，可以快速求解。
广泛的应用领域
有限单元法被广泛应用于工程、物理 、生物等领域，是一种通用的数值分 析方法。
易于理解和实现
有限单元法的基本概念直观易懂，且 实现起来相对简单。
01
利用线性代数方法，将 各个单元的数学模型和 节点信息组合成整体方
程组。
03
将节点的未知量返回到 原问题中，得到问题的
解。
05
根据问题的物理性质和 边界条件，建立单元的 数学模型和节点信息。
02
解整体方程组，得到节 点的未知量。
04
有限单元法的特点
适用范围广
可以用于解决各种类型的问题，如弹性力学 、流体力学、传热学等。
高精度与高效率
研究者们致力于开发更高效、精确的 算法，以解决大规模、非线性、动态 等复杂问题。
并行化与云计算应用
随着计算资源的丰富，有限单元法的 计算过程正逐步实现并行化，利用云 计算平台进行大规模计算已成为趋势 。
展望
理论完善与创新
随着工程实践的深入，有限单元法的理论体系将进一步完善，同时会 有更多创新性的算法和模型出现。
第一章概述 有限元法基本原理及应用课件
1.3.2 有限元法的应用领域
线性静力分析
静力分析
非线性静力分析
数控立式加工中心床身位移云图
1.3.2 有限元法的应用领域
动力分析
模态分析。 瞬态响应分析。 谐响应分析。 频谱响应分析和随机振动分析。 屈曲和失稳分析。 自动接触分析。
美国的Daniel S Pipkinsay & Satya N Atlurib提出了 FEAM。
西班牙的Onate E和波兰的Rojek J将DEM 和FEM结 合解决地质力学中的动态分析问题；
瑞典的Birgersson F和英国的Finnveden S针对FEM 在频域中的应用提出了SFEM 。
1.3.1 有限元法的发展
整机模态分析
反挤压成型过程
1.3.2 有限元法的应用领域
失效和破坏分析
框架 结构 地震 倒塌 模拟
框架 结构 地震 倒塌 模拟
汽 车 正 撞 刚 性 墙
New Structural system and design method
1.3.2 有限元法的应用领域
热传导分析
发动机进排气流场温度
铸造成型：温度变化和气泡
20世纪90年代以来，大批FEA系统纷纷向微机移植， 出现了基于各种微机版FEA系统。有限元法向流体力学、 温度场、电传导、磁场、渗流和声场等问题的求解计算 方面发展，并发展到求解一些交叉学科的问题。
1.3.1 有限元法的发展
3．有限元法的研究现状பைடு நூலகம்
美国的HeoFanis Strouboulis等人提出用GFEM 解决 分析域内含有大量孔洞特征的问题；比利时的Nguyen Dang Hung 和越南的Tran Thanh Ngoc 提出用HSM解 决实际开裂问题
有限元分析与应用 第3讲、杆梁问题的有限单元法
计算简图:
在结构分析当中用来代替实际结构的计算模型(图形)
确定计算简图的原则： 简化内容:
1.能反映实际结构的主要力学特性; 2.分析计算尽可能简便 杆件 杆件的轴线 刚结点 铰结点 半铰结点(组合结点) 固定铰支座 可动较支座 固定端支座 滑动支座(定向支座) 空间结构 平面结构 集中力、集中力偶、分布荷载
6 EI y l
2
单元刚度矩阵第三列的其他元素为0。
⑷ xi 1 ，其他结点位移为0（图3-5），生成第四列 元素。
图3-5
为杆件的扭转基本变形情况，由材料力学公式有
k 4, 4 GJ M xi l k10, 4 GJ M xj l
单元刚度矩阵第四列的其他元素为0。
⑸ yi 1 ，其他结点位移为0（图3-6），生成第五列 元素。
j结点各自由度分别出现单位位移而生成的单元刚度矩阵元素 的分析类似，最后得至空间梁单元的单元刚度矩阵为
EA l 0 0 0 0 0 EA l 0 0 0 0 0 12EI z l3 0 0 0 6 EI z l2 0 12EI z l3 0 0 0 6 EI z l2 12EI y l3 0 6 EI y l2 0 0 0 12EI y l3 0 6 EI y l2 0 GJ l 0 0 0 0 0 GJ l 0 0 4 EI y l 0 0 0 6 EI y l2 0 2 EI y l 0 4 EI z l 0 6 EI z l2 0 0 0 2 EI z l EA l 0 0 0 0 0 12EI z l3 0 0 0 6 EI 2z l 12EI y l3 0 6 EI y l2 0 GJ l 0 0 4 EI y l 0 称 对
有限单元法原理及应用
有限单元法原理及应用有限单元法（Finite Element Method, FEM）是一种数值分析方法，广泛应用于工程结构、材料力学、流体力学等领域。
它通过将复杂的结构或系统分割成有限数量的小单元，然后建立数学模型，最终求解得到整体系统的行为。
本文将介绍有限单元法的基本原理和在工程实践中的应用。
首先，有限单元法的基本原理是将一个连续的结构或系统离散化为有限数量的单元，每个单元都可以用简单的数学方程描述。
这些单元之间通过节点连接在一起，形成整体系统。
然后，通过施加外部载荷或边界条件，可以得到每个单元的位移、应力等信息。
最终，将所有单元的信息组合起来，就可以得到整个系统的行为。
在工程实践中，有限单元法被广泛应用于结构分析、热传导、流体力学等领域。
在结构分析中，可以通过有限单元法来模拟各种复杂的结构，如桥梁、建筑、飞机等，从而预测其受力情况和变形情况。
在热传导领域，有限单元法可以用来分析材料的温度分布、热传导性能等。
在流体力学中，有限单元法可以模拟流体的流动情况、压力分布等。
此外，有限单元法还可以与优化算法相结合，用于优化设计。
通过改变单元的尺寸、形状或材料性质，可以得到最优的结构设计。
这在工程实践中具有重要意义，可以降低结构的重量、提高结构的强度和刚度。
总之，有限单元法作为一种数值分析方法，具有广泛的应用前景。
它不仅可以用于工程结构的分析和设计，还可以用于材料力学、流体力学等领域。
随着计算机技术的不断发展，有限单元法将会变得更加高效、精确，为工程实践提供更多的支持和帮助。
以上就是有限单元法的基本原理及在工程实践中的应用，希望对读者有所帮助。
有限单元法作为一种强大的分析工具，将继续在工程领域发挥重要作用。
有限单元法原理及应用
有限单元法原理及应用有限单元法（Finite Element Method，简称FEM）是一种用于求解工程问题的数值方法。
它将一个连续问题分割成一系列离散的有限单元，通过对每个单元进行局部的数值近似，再将它们组合起来得到全局解。
有限单元法的基本原理是根据假设的位移关系和应变能量原理，将连续介质离散为有限个单元，然后通过数学方法对每个单元进行近似。
在每个单元内，假设解的形式，并通过插值方法得到每个节点的未知位移。
根据边界条件的限制，将每个单元的刚度矩阵组装成整个结构的刚度矩阵。
最后，通过求解线性方程组，得到整个结构的位移和应力分布。
有限单元法广泛应用于求解各种工程领域的问题，如结构力学、电磁场、流体力学等。
它的应用范围包括但不限于以下几个方面：1. 结构分析：有限单元法可用于结构强度分析、振动分析、热传导分析等。
通过对结构进行离散，可以计算结构的应力、应变分布，以及结构的固有频率和模态形式。
2. 热传导分析：有限单元法可以用于求解具有复杂边界条件的热传导问题。
通过离散化连续介质，可以计算温度分布和热流量分布，进而获取材料的热传导性能。
3. 流体力学：有限单元法可用于求解流体动力学问题，如流体的流动、传热、传质等。
通过将流体域离散化为网格，在每个单元上建立基本流动方程的数值近似，可以计算流体的速度、压力分布，以及各种力学量和热力学量。
4. 电磁场分析：有限单元法可以用于求解电磁场分布及其对物体的影响。
通过离散化电磁场区域，可以计算电场、磁场和电流分布，以及物体的电磁参数。
5. 地下水流动：有限单元法可用于模拟地下水流动和污染传输。
通过离散化地下水流动域，并运用流体力学的基本方程，可以计算地下水的流动速度、压力分布，以及污染物的传输路径和浓度分布。
总之，有限单元法在工程领域有广泛的应用，可以用于求解各种复杂的力学、热学和流体学问题，并为工程设计和分析提供重要的数值仿真工具。
第三章 有限单元法
第3章有限单元法在工程技术领域内，工程师常常运用数学和力学的知识将实际问题抽象成它们应遵循的基本方程（常微分方程或偏微分方程）和相应的边界条件。
对于大多数的工程技术问题，由于物体的几何形状和载荷作用方式是很复杂的，除了方程性质比较简单且几何边界相当规则的少数问题之外，试图按经典的弹性力学和塑性力学方法获得解析解是十分困难的，甚至是不可能的。
为了克服这种困难，有两条解决途径：一是引入简化假设，将方程和边界条件简化为能够处理的问题，从而得到它在简化状态下的解答。
这种方法只在有限的情况下可行，因为过多的简化将可能导致不正确的甚至错误的答案。
另一条解决途径就是数值解法，如有限差分法、边界元法、有限单元法和离散元法等。
对于非线性问题，有限单元法更为有效，且已经出现了许多通用程序。
有限单元法的主要优点是：①建立于严格理论基础上的可靠性。
因为用于建立有限元方程的变分原理或加权余量法在数学上已被证明是微分方程和边界条件的等效积分形式。
只要原问题的数学模型是正确的，同时用来求解有限元方程的算法是稳定、可靠的，如果单元满足收敛准则，则近似解最后收敛于原数学模型的精确解；②适应性强，应用范围广，不仅能成功地分析具有复杂边界条件、非线性、非均质材料、动力学等难题，而且还可以推广到解答数学方程中的其它边值问题，如热传导、电磁场、流体力学等问题；③适合计算机实现的高效性。
由于有限元分析的各个步骤可以表达成规范化的矩阵形式，最后导致求解方程可以统一为标准的矩阵代数问题，特别适合计算机的编程和执行。
已经出现了许多大型结构分析通用程序，如：NASTRAN、ASKA、ADINA、ANSYS、ABAQUS等，可以直接应用。
这些优点使有限单元法得到了广泛的应用和发展。
3.1有限单元法分析的基本步骤在工程或物理问题的数学模型（基本变量、基本方程、求解域和边界条件等）确定以后，有限单元法作为对其进行分析的数值计算方法的基本步骤如下：(1) 离散化一个复杂的弹性体可以看成是由无限个质点组成的连续体，它具有无限个自由度。
有限单元法第一章
1.13.如何利用最小位能原理建立数值解的求解方程？方程有何特点？解的收敛性和极值性的条件是什么? 建立系统总位能，1()()()()2P ij i i ijkl ij kl i i iV S V S U u dV u dS D fu dV Tu dS σσεφψεε⎡⎤∏=++=--⎣⎦⎰⎰⎰⎰真实位移使系统总位能取最小值，0P δ∏=0ia ∂∏=∂,其中i a 为位置参数。
方程系数对称正定。
解的收敛性和极值性的条件：一阶变分为0，二阶变分大于0。
1.14.什么是最小余能原理?它是如何导出的?场函数是什么? 它事先应满足什么条件? 对场函数的试探函数有什么要求? 最小余能原理：在所有在弹性体内满足平衡方程，在边界上满足力的边界条件的可能应力中，真实的应力使系统的总余能取驻值。
推导过程：由几何方程和位移边界条件的等效积分“弱”形式，即虚应力原理，0ui ij iji VsdV T u dS δσεδ-=⎰⎰ij ijkl kl C εσ=代入得0ui ij ijkl kl i V s C dV T u dS δσσδ-=⎰⎰1()()2ij ijkl kl ijkl ij kl mn C C V δσσδσσδσ==0c δ∴∏=其中12ui c ijkl ij kl i V S C dV T u dS σσ∏=-⎰⎰由泛函知场函数为应力。
事先满足应力边界条件。
场函数的试探函数的要求：完备性和协调性。
练习题1.3某问题的微分方程是22220c Q x xφφφ∂∂+++=∂∂ 在Ω内边界条件是=φφ（在1Γ上）q nφ∂=∂（在2Γ上）其中c 和Q 仅是坐标的函数，试证明此方程的微分算子是自伴随的，并建立相应的自然变分原理。
解：由x y n n n x yφφφ∂∂∂=+∂∂∂（x n ，y n 为边界外法线的方向余弦）有： 222222222222()()()()()(x y x x y y x x vL d v d x y v v v n d d v n d d x x x y y y v vv n d n d d x x x v vv n d n d d y y yv d v n n v x y x x φφφφφφφφφφφφφφφφφφφΩΩΓΩΓΩΓΓΩΓΓΩΩ∂∂Ω=+Ω∂∂∂∂∂∂∂∂=Γ-Ω+Γ-Ω∂∂∂∂∂∂∂∂∂=Γ-Γ-Ω∂∂∂∂∂∂+Γ-Γ-Ω∂∂∂∂∂∂∂∂=+Ω+-+∂∂∂∂⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰)()..(,)y y v n n d y y L v d b t v φφφΓΩ∂-Γ∂∂=Ω+⎰⎰假设φ已事先满足1Γ强制边界条件，则问题的迦辽金提法如下：22222()()0c Q d q d x y n φφφδφφδφΩΓ∂∂∂+++Ω--Γ=∂∂∂⎰⎰由上述有2221()2x d n d d x x x φφφδφδφδΩΓΩ∂∂∂Ω=Γ-Ω∂∂∂⎰⎰⎰2221()2y d n d d yyyφφφδφδφδΩΓΩ∂∂∂Ω=Γ-Ω∂∂∂⎰⎰⎰带入化简得：()0δφ∏=，其中222111()()()222c Q d q d x y φφφφφφΩΓ⎡⎤∂∂∏=+--Ω-Γ⎢⎥∂∂⎣⎦⎰⎰1.4在习题1.3给出的微分方程中，如令c=0，Q=2，并令在全部边界上0φ=，则表示求解杆件自由扭转的应力函数问题，截面的扭矩=2T dxdy φ⎰⎰。
有限元法及应用课件解读
了今天人们熟知的确定单元特性的直接刚度法，
其研究工作随同当时出现的数值计算机一起打开
了求解复杂平面弹性问题的新局面。
21
1960年美国的克劳夫(W.Clough)采用此方法进行 飞机结构分析时首次将这种方法起名为“有限单 元法”，简称“有限元法”。此后有限元法在工 程界获得了广泛的应用。到20世纪70年代以后，
8
其中最主要的是离散化方法，把问题归结为 只求有限个离散点的数值，把无限自由度问题变 成有限个自由度。 把一个连续体分割成有限个单元，即把一个
复杂的结构看成由有限个通过节点相连的单元组
成的整体，先进行单元分析，然后再把这些单元
组合起来代表原来的结构，以得到复杂问题的近
似数值解。这种方法称为有限元法（The Finite Element Method ）。
25
热分析
热分析用于确定物体中的温度分布。 可模拟三种热传递方式：热传导、热 对流、热辐射。 稳态分析 忽略时间效应 瞬态分析 确定以时间为函数的温度值等。 可模拟相变（熔化及凝固）
26
电磁分析
电磁分析用于计算电磁装置中的磁场 静态磁场及低频电磁场分析 模拟由直流电源，低频交流电或低频瞬时 信号引起的磁场。 例如：螺线管制动器、电动机、变压器 磁场分析中考虑的物理量是：磁通量密度、 磁场密度、磁力和磁力矩、阻抗、电感、 涡流、能耗及磁通量泄漏等。
5
传统方法在处理载荷场、温度场、电磁场等这类 问题时，往往要对一个实际的物理系统作出多种假设，
比如形状假设、连续性假设、物体的各项同性假设，然
后通过经典理论方法得出问题的解析解，这种解析解从 形式上看，可以得出关于实际问题的连续解，比如用方 程描述某一点的位移和应变，但这样的解析解往往和实 际情况有比较大的偏差。这对于精度要求不高的领域是
有限单元法原理及应用简明教程ppt课件
(a) 瞬变结构
(b) 分离体分析
(c) 平衡状态分析
图2-32 瞬变结构
24
第二章 结构几何构造分析
(2) 两刚片规则 两刚片用三根既不完全平行也不交于同一点的链杆 相联，所得结构是几何不变结构。
(a) 铰与链杆连接两刚片 (b) 三链杆连接两刚片 图2-33 两刚片连接规则
25
第二章 结构几何构造分析
章
生刚体位移时，称之为几何不变结构或几何稳定结构，
节
反之则称为几何可变结构或几何不稳定结构。几何可
目 录
变结构不能承受和传递载荷。对结构进行几何构造分
析也是能够对工程结构作有限单元法分析的必要条件。
11
第二章 结构几何构造分析
(a) 结构本身可变 (b) 缺少必要的约束条件 (c) 约束汇交于一点 图2-1 几何可变结构
节
何不变结构上，由增加二元体而发展的结构，是一个
目
几何不变结构。铰接三角形是最简单的几何不变结构。
录
图2-31 铰接三角形
23
第二章 结构几何构造分析
结构的特征是：当它受载荷作用时会产生微小的 位移， 但位移一旦发生后， 即转变成一几何不变结 构，但结构的内力可能为无限大值或不定值，这样的 结构称为瞬变结构。显然，瞬变结构在工程结构设计 中应尽量避免。
(5) 约束处理，求解系统方程
(6) 其它参数计算
4
第一章 概述
图1-2 工程问题有限单元法分析流程
5
第一章 概述
1.3 工程实例
返 回 章 节 目 录
(a) 铲运机举升工况测试
(b) 铲运机工作装置插入工况有限元分析
图1-3 WJD-1.5型电动铲运机
有限单元法简介课案课件
06
结论与展望
总结有限单元法的主要内容与特点
总结内容
有限单元法是一种广泛应用于工程和科 学计算中的数值分析方法，其主要思想 是将连续的求解域离散化为一组单元的 组合体，并在每个单元内假设一个近似 函数，然后通过单元组合体的方式求解 整个域的解。其主要特点包括离散化、 单元划分、近似函数和整体组装四个方 面。
有限单元法的物理原理
物理问题的离散化
将连续的物理问题离散化为有限个离 散的单元，每个单元内的物理量（例 如，位移、温度等）可以近似为常数 。
单元之间的相互作用
考虑单元之间的相互作用和边界条件 （例如，位移边界条件、温度边界条 件等），将各个单元连接起来形成一 个整体的求解对象。
有限单元法的应用范围与限制
求解方程
1 2
选择求解器
根据方程的特点和需要，选择合适的求解器进行 求解。
导入求解器
将方程导入到求解器中，进行求解。
3
分析求解结果
根据求解结果，分析方程的解是否符合要求，如 果不符合要求，需要重新进行求解。
结果分析
结果可视化
将求解结果进行可视化处理，生成模型在不同时刻的 状态图。
结果评估
对求解结果进行评估，分析模型的位移、应力、应变 等参数是否符合实际情况。
结果优化
根据结果评估的结果，对模型进行优化设计，提高模 型的性能和稳定性。
04
有限单元法的应用实例
结构分析
总结词
有限单元法在结构分析中得到广泛应用，能够解决各种复杂结构问题。
详细描述
通过将结构离散化为有限个单元，并对每个单元进行受力分析，可以得出结构的整体受力情况和变形，广泛应用 于桥梁、建筑、机械等领域。
分。
第3章：有限单元法的一般原理
第3章 有限单元法的一般原理 3.1.3 单元特性分析
第01篇 有限单元法基本理论
在位移法有限元中，首先要针对所选定的单元类型选择一简 单多项式函数近似表达单元内各位移分量的分布规律，并把单 元内任意点的位移分量写成统一形式的结点位移插值函数形式， 从而通过单元结点位移，表达出单元内任意点的位移、应变和 应力。其次，利用虚功原理或变分原理建立单元结点力与结点 位移之间的特性关系，称为单元有限元方程。该方程可用矩阵形 式表示为： [F]e=[K]e[]e
第3章 有限单元法的一般原理
第01篇 有限单元法基本理论
单元中的位移模式一般采用以广义坐标为待定系数的有限项 多项式作为近似函数。因为多项式的数学处理比较容易，尤其便于 微分与积分运算。另外任意阶次的多项式可以近似地表示真实解。 当然，只有无限次的多项式才与真实解相对应。但为了实用，通常 只取有限次多项式来近似。如3结点三角形单元位移函数的广义坐 标表示为：
（1）自然离散问题单元；
自然离散问题单元有杆单元、梁单元。对于杆系结构（二力杆）的 离散化，通常采用自然离散的形式，即把结构的杆作为单元，称为 杆单元。有限个杆单元之间，利用有限个结点相互铰接（桁架情 况），以传递负荷。 x
第3章 有限单元法的一般原理
第01篇 有限单元法基本理论
备注：桁架问题（杆单元问题）需要两个坐标系来描述。固定的整体坐标系XY或 XYZ： （1）描述每个节点的位置，使用角度记录每个杆件（单元）的方向；施 加约束及载荷；（3）表示问题的解。单元坐标系用来描述杆件的轴向效应。杆 单元LINK每个节点只有平动自由度。
第3章 有限单元法的一般原理
第01篇 有限单元法基本理论
(c)位移函数在单元内部必须是连续函数，即单元内部的连续性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
122123
60
组建
周年60组建
周年
主要完成人：朱伯芳
受奖单位：水电中心/结构材料所
【创新性】
全面系统地阐述了有限单元法的基本原理及其在土木、水利工程问题中的应用，包括弹性力学平面问题和空间问题、薄板、薄壳、厚板、厚壳、弹性稳定、塑性力学、大位移、断裂、动力反应、徐变、岩土力学、极限分析、混凝土和钢筋混凝土、流体力学、渗流分析、热传导、工程反分析、仿真分析、网格自动生成、误差估计及自适应技术等。
本书取材实用、由浅入深、先易后难，便于自学；对于实际工程中有用的计算方法力求讲述清楚并给出具体计算公式，便于应用；对有限元法的工程应用，注意工程的物理特性，要求采用的概化假定、计算参数和计算荷载等尽量接近实际，注重计算方法精度的适应性等，并重视有限元计算结果与实际观测资料相验证。
【影响力】
我国最早的有限元专著之一，为在我国推广有限元法发挥了重要作用；本书共出版三版，第一版于1976年8月，第二版于1998年10月，第三版于2009
年6月；曾作为多所高校的有限元课程教材使
用；英文版已由清华大学出版社和美国Wiley 出版社联合出版；中国科学技术信息研究所编著的《中国高被引指数分析》（2011版）中，本书列为国内水利工程领域高被引图书第2名。
有限单元法原理与应用（第三版）
著作类成果
【Innovation】
This book expounds, in an all-round and systematic manner, the basic theory of the finite element method and its application to civil engineering and hydraulic engineering , including plane and space problems of elasticity, thin plate, thin shell, thick plate, thick shell, elastic stability, plasticity, large displacement, fracture, dynamic response, creep, rock and soil mechanics, limit analysis, concrete and reinforced concrete, fluid mechanics, seepage analysis, heat conduction, back analysis in engineering, simulated analysis, automatic generation of meshes, error estimation and adaptive technique. This book is learner-friendly because it contains practical content and expounds knowledge step by step and from easy to difficult; and is also easy to use because it strives to clarify the computing methods usable in actual engineering and gives corresponding formulas. Regarding the engineering application of the finite element method, it pays attention to the physical characteristics of projects, requires adopted conceptualized assumption, calculation parameter and calculation load be close enough to reality and accuracy of calculation methods be adaptive, and stresses the verification between the calculation result of the finite element method and actual observational data.
【Influence】
Amongst the earliest finite element books in China, this
book plays an important role in generalizing the finite element method in China. It has registered three editions, with the first edition published in August, 1976, the second edition in October, 1998 and the third edition in June, 2009. It served as a finite element textbook of many colleges and universities; and its English version has been published jointly by Tsinghua University Press and the U.S.-based Wiley & Sons, Inc. This
book ranks second amongst the highly-cited books of hydraulic engineering in China, according to the Analysis Report of Chinese Highly Cited Paper 2011 of the Institute of Scientific and Technical Information of China (ISTIC)
Main Contributor : Zhu Bofang
Award-winning Unit : Research Center for Sustainable Hydropower/Department of Structures and Materials
THE FINITE ELEMENT METHOD THEORY AND APPLICATIONS(EDITION III)。