第章主成分分析和因子分析习题答案
主成分分析和因子分析习题答案
81
98
94
95
29
79
95
83
89
89
79
30
81
90
79
73
85
80
31
85
77
75
52
73
59
32
68
85
70
84
89
86
33
85
91
95
63
76
66
34
91
85
100
70
65
76
35
74
74
84
61
80
69
36
88
100
85
49
71
66
37
63
82
66
89
78
80
38
87
84
100
74
81
.554
Bartlett's Test of Sphericity
Approx. Chi-Square
df
28
Sig.
.000
从检验表中可见,Bartlett球度检验统计量为。检验的值接近0。表明8个变量之间有较强的相关关系。而KMO统计量为,小于。进行因子分析的效果不一定很好。
(2)旋转后的因子载荷矩阵如下:
Cumulative %
1
2
3
4
.843
5
.754
6
.337
7
.249
8
.163
Extraction Method: Principal Component Analysis.
spss第8章主成分分析与因子分析

, yn ) 是 n 维随机向量. 若对任
⎛ Cov(x1, y1) Cov(x1, y2 )
⎜ ⎜
Cov(
x2
,
y1
)
Cov(x2 , y2 )
⎜
⎜ ⎝ Cov(xm , y1) Cov( xm , y2 )
⎟ ⎟
⎟
xpn ⎟⎟⎠
(σ ij ) p× p
, F = AX
Cov(F) = Cov(AX, AX) = ACov(X)A′ V (F)
由于 Cov(X) 是非负定对称矩阵,所以存在正交矩阵 U ,使得
⎡λ1 0
0⎤
U−1Cov(X)U
=
⎢ ⎢ ⎢
0
λ2
0
⎥ ⎥
⎥
⎢ ⎣
0
0
λ
p
⎥ ⎦
其中 λ1, λ2, ,λp 为 Cov(X) 的特征根,不妨假设 λ1 ≥ λ2 ≥
(5)若 X 是随机向量, Cov(X) 存在,则 Cov(X) 是非负定矩阵.
后面的推导过程中用到两个线性代数中的 2 个重要结论. 定理 7-2 (1)若 A 是 p 阶实对称阵,则一定可以找到正交阵 U ,使
⎡λ1 0
0⎤
U−1AU
=
⎢ ⎢ ⎢
0
λ2
0
⎥ ⎥
⎥
⎢ ⎣
0
0
λp
⎥ ⎦
其中 λi ,i = 1.2. p 是 A 的特征根.
(3)对任何向量 a = (a1, a2 , , am )′ , b = (b1,b2 , , bn )′ ,有 Cov(a′X, b′Y) = a′Cov(X, Y)b . (4)对任何 p × m 阶矩阵 A , q × n 阶矩阵 B ,有 Cov(AX, BY) = ACov(X, Y)B′
第13章主成分分析与因子分析

洛衫矶对12个人口调查区的数据
编号 总人口 中等学校平均
no
pop
校龄School
1
5700 12.8
2
1000 10.9
3
3400
8.8
4
3800 13.6
5
4000 12.8
6
8200
8.3
7
1200 11.4
8
9100 11.5
9
ห้องสมุดไป่ตู้
9900 12.5
10
9600 13.7
11
9600
9.6
12
第13章 主成分分析与因子分析
介绍: 1、主成分分析与因子分析的概念 2、主成分分析与因子分析的过程
主成分分析与因子分析的概念
需要与可能:在各个领域的科学研究中,往往需要对反映事物的 多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。 多变量大样本无疑会为科学研究提供丰富的信息,但也在一定程 度上增加了数据采集的工作量,更重要的是在大多数情况下,许 多变量之间可能存在相关性而增加了问题分析的复杂性,同时对 分析带来不便。如果分别分析每个指标,分析又可能是孤立的, 而不是综合的。盲目减少指标会损失很多信息,容易产生错误的 结论。因此需要找到一个合理的方法,减少分析指标的同时,尽 量减少原指标包含信息的损失,对所收集的资料作全面的分析。 由于各变量间存在一定的相关关系,因此有可能用较少的综合指 标分别综合存在于各变量中的各类信息。主成分分析与因子分析 就是这样一种降维的方法。
Pop 0.01602 f1 + 0.9946f2 School 0 .941f1 - 0.00882f2 employ 0.137f1 + 0.98f2 Services 0.825f1 +0.447f2 house 0.968f1 - 0.00605f2 第一主因子对中等学校平均校龄,专业服务项目,中等房价有绝对值较大的载荷(代 表一般社会福利-福利条件因子); 而第二主因子对总人口和总雇员数有较大的载荷 (代表人口-人口因子). P326 比较有用的结果:因子得分fac1_1, fac2_1。其计算公式:因子得分系数和原始 变量的标准化值的乘积之和(P326)。然后可以利用因子得分进行聚类p327 (Analyze->Classify->Hierarchical Cluster)。
多元分析:主成分分析与因子分析

第十一章 多元分析:主成分分析与因子分析引言主成分分析和因子分析在多元分析框架内是数据结构分析技术,与第六章的多元回归、第七章的多变量协整一起是多变量分析中广泛使用的技术。
它们不同于多元回归。
回归的目标是识别外生变量与内生变量的关系,而在主成分分析和因子分析情形下,仅确定内生变量间的结构关系。
它们也不像协整,变量间不需要平稳性。
在金融、社会科学或其它领域,通常需要识别多变量结构的特征,其有两个特征是被子广泛关心的:1. 多变量结构中的波动性。
2. 变量间的相关或共线性。
在结构的整体变化中,通常是一些变量起产生主要的影响,而其它变量仅有次要的或不显著的影响。
困难的是要了解哪些变量能被确定在这个结构中和它在结构中应怎样度量。
例如,如果两个变量是完全相关的,则不需要第二个变量,它不会带来进一步的信息。
这类似多元回归的共线问题。
在一般情况下,包含哪个变量,剔除哪个变量并不是很清楚的,我们需要有能够程序化的有效方法来识别带有最可用信息的变量或变量组合。
主成分分析(PCA )是分析多变量结构波动时有用的技术。
因子分析(F A )在分析多变量结构变量的相关时很有用。
两者都依赖于方差/协方差矩阵,因为这个矩阵在一定范围内包含了变量间有用的全部信息。
因此在一定范围内,两者是重复的或相互补充的。
在这章,我们将方差/协方差矩阵记为C 。
尽管PCA 和F A 都利用方差/协方差矩阵,但它们不同于第四章和第九章中的均值—方差分析。
均值—方差分析度量了一组变量的总体变异性,而没有特别指明一部分变量对总变异性的贡献。
PCA 识别和排序了部分变量在总变异性中的贡献,每个部分变量称为“主成分”。
它识别了部分变量间组成的协方差的强度,每个主成分对总的变异性的贡献,并根据部分变量组的方差进行排序。
使用PCA ,数据内的总体变异性由特征值之和(它等于C矩阵主对角线上元素之和,也称为迹)度量,成分(变量的线性组合)的选择是依次序减少特征值,直到满足总变异性的一个足够大的比例。
SPSS统计分析 第10章 主成分分析和因子分析

x3 28.53 0.279 0.653 1.011 3.572 3.682 0.898 1.584 1.657 0.497 1.84 2.252 0.321 1.533 0.502
x4 0.878 0.339 10.254
1.6 27.841 6.429 8.276 2.327 2.837 26.151 9.242 9.558 8.153 1.499 5.773
过综合得分的高低可 知各国参与国际化水 平的高低,其中美国 最高,印度最低。
a
19
主要内容
10.1 主成分分析和因子分析简介 10.2 主成分分析 10.3 因子分析
a
20
10.3 因子分析
10.3.1 统计原理与分析步骤
(1)统计原理
x1 a11F1 a12F2
x2
a21F1
a22F2
y3 3.01 -0.46 -0.27 -0.27 1.19 1.46 -0.31 -0.43 0.03 -1.75 -0.52 -0.26 -0.54 -0.30 -0.30 -0.28
-0.63 -1.11 0.88 -0.88 -0.20 3.80 -0.38 -0.83 -0.94 2.05 0.49 1.06 -0.25 -1.05 -0.93 -1.09
y1 -2.19 -2.56 0.45 -1.69 5.28 3.30 -0.43 -1.91 -1.68 4.46 0.87 1.40 -0.61 -2.35 -1.36 -0.99
y2 0.07 -0.11 1.85 -0.46 -6.26 6.07 -0.47 -0.06 -0.68 0.98 0.46 1.34 0.10 -0.20 -0.92 -1.73
提取方法:主成分分析。
主成分分析和因子分析习题答案

主成分分析和因子分析
习题答案
SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
第11章主成分分析和因子分析
司盈利能力有关,因此可命名为“盈利能力”。
因子2 与X5(资产负债率)、X6(流动比率)X8(资本积累率)这3个变量的载荷系数较大,这三个变量主要涉及企业的偿债能力,因此可命为“偿债能力因子”。
因子3与X1(主营业务利润)、 X4(总资产周转率)、X7(主营业务收增长率)这三个变量的载荷系数较大,这三个变量分别涉及了盈利能力、资产管理水平、企业成能力等,因此,这个因子的命名比较困难。
各公所的因子综合得分和排名如下:
对下表中的50名学生成绩进行主成分分析,可以选择几个综合变量来代表这些学生的六门课程绩
学生代码数学物理化学语文历史英语
1716494526152
2789681808976
3695667759480
4779080686660
5846775607063
6626783718577。
第六单元 主成分分析与因子分析
统计软件实习
三、主成分分析/因子分析的用途 主成分分析/
综合评价:在进行多指标综合评价时,需要从各方面 用多个指标进行测量,这样指标存在信息重叠、量纲、 权重等问题,此时用因子分析,可进行信息浓缩,并 解决权重的确定等问题。 共线性问题:解决共线性问题:利用主成分提取出主 要信息,然后使用提取出的主成分代替原变量进行分 析,可避免原变量的共线性问题。 寻找变量间潜在结构:许多变量是无法直接观测到, 往往需要用一系列可直接观测的相关变量来间接反映。 通过因子分析就可将这些变量间潜在的结构推导出来。
第六单元
主成分分析与因子分析
统计软件实习
主成分/因子数量的确定一般遵循以下原则: 主成分的累积贡献率:80~85%以上; 特征根:大于1 ; 综合判断 :如果根据累积贡献率确定因子数 量较多,用特征根确定又往往偏少,许多时候将 两者结合起来综合判断; 因子分析时更重要的是因子的可解释性 。
第六单元
第六单元
主成分分析与因子分析
统计软件实习
九、综合实例
例:现搜集了甘肃省2005年14个市(州)经济 运行状况的有关数据,并通过计算得出12项人均指 标,请对甘肃省这14个市(州)的经济运行状况进 行分析。(数据见14个市经济发展水平.sav)
第六单元
主成分分析与因子分析
统计软件实习
Any Question?
第六单元 主成分分析与因子分析
统计软件实习
一、主成分分析
第六单元
主成分分析与因子分析
统计软件实习
一、主成分分析 Y1=X1cosθ+X2sinθ Y2=-X1sinθ+X2cosθ
第六单元
主成分分析与因子分析
应用多元统计分析习题解答_因子分析
第七章 因子分析7.1 试述因子分析与主成分分析的联系与区别。
答:因子分析与主成分分析的联系是:①两种分析方法都是一种降维、简化数据的技术。
②两种分析的求解过程是类似的,都是从一个协方差阵出发,利用特征值、特征向量求解。
因子分析可以说是主成分分析的姐妹篇,将主成分分析向前推进一步便导致因子分析。
因子分析也可以说成是主成分分析的逆问题。
如果说主成分分析是将原指标综合、归纳,那么因子分析可以说是将原指标给予分解、演绎。
因子分析与主成分分析的主要区别是:主成分分析本质上是一种线性变换,将原始坐标变换到变异程度大的方向上为止,突出数据变异的方向,归纳重要信息。
而因子分析是从显在变量去提炼潜在因子的过程。
此外,主成分分析不需要构造分析模型而因子分析要构造因子模型。
7.2 因子分析主要可应用于哪些方面?答:因子分析是一种通过显在变量测评潜在变量,通过具体指标测评抽象因子的统计分析方法。
目前因子分析在心理学、社会学、经济学等学科中都有重要的应用。
具体来说,①因子分析可以用于分类。
如用考试分数将学生的学习状况予以分类;用空气中各种成分的比例对空气的优劣予以分类等等②因子分析可以用于探索潜在因素。
即是探索未能观察的或不能观测的的潜在因素是什么,起的作用如何等。
对我们进一步研究与探讨指示方向。
在社会调查分析中十分常用。
③因子分析的另一个作用是用于时空分解。
如研究几个不同地点的不同日期的气象状况,就用因子分析将时间因素引起的变化和空间因素引起的变化分离开来从而判断各自的影响和变化规律。
7.3 简述因子模型中载荷矩阵A 的统计意义。
答:对于因子模型1122i i i ij j im m i X a F a F a F a F ε=++++++ 1,2,,i p =因子载荷阵为11121212221212(,,,)m m m p p pm a a a a a a A A A a a a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦Ai X 与j F 的协方差为:1Cov(,)Cov(,)mi j ik k i j k X F a F F ε==+∑=1Cov(,)Cov(,)mikk j i j k aF F F ε=+∑=ij a若对i X 作标准化处理,=ij a ,因此 ij a 一方面表示i X 对j F 的依赖程度;另一方面也反映了变量iX对公共因子jF的相对重要性。
第章主成分分析和因子分析习题答案
.707
X8
-.066
.575
.090
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
a Rotation converged in 5 iterations.
28
61
65
81
98
94
95
29
79
95
83
89
89
79
30
81
90
79
73
85
80
31
85
77
75
52
73
59
32
68
85
70
84
89
86
33
85
91
95
63
76
66
34
91
85
100
70
65
76
35
74
74
84
61
80
69
36
88
100
85
49
71
66
37
63
82
66
89
78
80
38
87
84
100
55.043
43.677
中国石油
33.441
19.900
0.735
0.923
28.068
1.043
42.682
45.593
广聚能源
6.790
15.650
0.441
应用多元统计分析习题解答_因子分析
第七章 因子分析7.1 试述因子分析与主成分分析的联系与区别。
答:因子分析与主成分分析的联系是:①两种分析方法都是一种降维、简化数据的技术。
②两种分析的求解过程是类似的,都是从一个协方差阵出发,利用特征值、特征向量求解。
因子分析可以说是主成分分析的姐妹篇,将主成分分析向前推进一步便导致因子分析。
因子分析也可以说成是主成分分析的逆问题。
如果说主成分分析是将原指标综合、归纳,那么因子分析可以说是将原指标给予分解、演绎。
因子分析与主成分分析的主要区别是:主成分分析本质上是一种线性变换,将原始坐标变换到变异程度大的方向上为止,突出数据变异的方向,归纳重要信息。
而因子分析是从显在变量去提炼潜在因子的过程。
此外,主成分分析不需要构造分析模型而因子分析要构造因子模型。
7.2 因子分析主要可应用于哪些方面? 答:因子分析是一种通过显在变量测评潜在变量,通过具体指标测评抽象因子的统计分析方法。
目前因子分析在心理学、社会学、经济学等学科中都有重要的应用。
具体来说,①因子分析可以用于分类。
如用考试分数将学生的学习状况予以分类;用空气中各种成分的比例对空气的优劣予以分类等等②因子分析可以用于探索潜在因素。
即是探索未能观察的或不能观测的的潜在因素是什么,起的作用如何等。
对我们进一步研究与探讨指示方向。
在社会调查分析中十分常用。
③因子分析的另一个作用是用于时空分解。
如研究几个不同地点的不同日期的气象状况,就用因子分析将时间因素引起的变化和空间因素引起的变化分离开来从而判断各自的影响和变化规律。
7.3 简述因子模型中载荷矩阵A 的统计意义。
答:对于因子模型1122i i i ij j im m i X a F a F a F a F ε=++++++ 1,2,,i p =因子载荷阵为11121212221212(,,,)m m m p p pm a a a a a a A A A a a a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦Ai X 与j F 的协方差为:1Cov(,)Cov(,)mi j ik k i j k X F a F F ε==+∑=1Cov(,)Cov(,)mikk j i j k aF F F ε=+∑=ij a若对i X 作标准化处理,=ij a ,因此 ij a 一方面表示i X 对j F 的依赖程度;另一方面也反映了变量iX 对公共因子jF 的相对重要性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Kaiser-Meyer-Olkin Measure of Sampling Adequacy.
29.321
2
2.059
25.732
55.053
2.059
25.732
55.053
3
1.249
15.614
70.667
1.249
15.614
70.667
4
.843
10.539
81.206
5
.754
9.421
90.628
6
.337
4.215
94.843
7
.249
3.114
97.957
8
.163
2.043
0.688
22.350
2.158
21.199
21.953
国阳新能
16.061
14.920
1.030
1.623
48.386
0.973
15.342
20.860
盘江股份
11.003
6.660
0.260
1.187
30.201
1.682
41.657
75.804
上海能源
24.876
17.950
0.709
0.968
78
59
72
66
19
80
100
83
53
73
70
20
58
51
67
79
91
85
21
72
89
88
77
80
83
22
64
55
50
68
68
65
23
77
89
80
73
75
70
24
72
68
77
83
92
79
25
72
67
61
92
92
88
26
73
72
70
88
86
79
27
77
81
62
85
90
87
28
61
65
81
98
94
95
29
.554
Bartlett's Test of Sphericity
Approx. Chi-Square
75.082
df
28
Sig.
.000
从检验表中可见,Bartlett球度检验统计量为75.082。检验的值接近0。表明8个变量之间有较强的相关关系。而KMO统计量为0.554,小于0.7。进行因子分析的效果不一定很好。(2)旋转后的因子载荷矩阵如下:Rotated Component Matrix(a)
11.3对下表中的50名学生成绩进行主成分分析,可以选择几个综合变量来代表这些学生的六门课程成绩?
学生代码
数学
物理
化学
语文
历史
英语
1
71
64
94
52
61
52
2
78
96
81
80
89
76
3
69
56
67
75
94
80
4
77
90
80
68
66
60
5
84
67
75
60
70
63
6
62
67
83
71
85
77
7
74
65
75
第11章 主成分分析和因子分析
教材习题答案
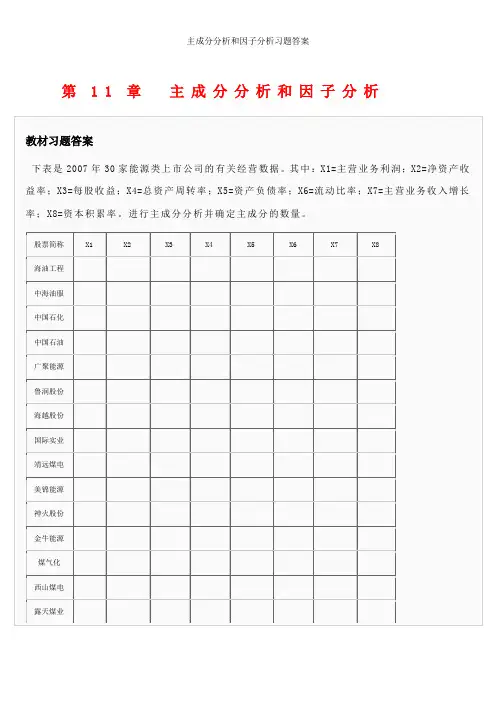
11.1下表是2007年30家能源类上市公司的有关经营数据。其中:X1=主营业务利润;X2=净资产收益率;X3=每股收益;X4=总资产周转率;X5=资产负债率;X6=流动比率;X7=主营业务收入增长率;X8=资本积累率。进行主成分分析并确定主成分的数量。
股票简称
72
90
73
8
91
74
97
62
71
66
9
72
87
72
79
83
76
10
82
70
83
68
77
85
11
63
70
60
91
85
82
12
74
79
95
59
74
59
13
66
61
77
62
73
64
14
90
82
98
47
71
60
15
77
90
85
68
73
76
16
91
82
84
54
62
60
17
78
84
100
51
60
60
18
90
78
Component
Initial Eigenvalues
Extraction Sums of Squared Loadings
Total
% of Variance
Cumulative %
Total
% of Variance
Cumulative %
1
2.346
29.321
29.321
2.346
29.321
Cumulative %
Total
% of Variance
Cumulative %
1
3.729
62.146
62.146
3.729
62.146
62.146
2
1.206
20.096
82.242
1.206
20.096
82.242
3
.403
6.724
88.966
4
.325
5.414
94.380
5
.204
3.395
美锦能源
23.342
18.580
0.497
0.923
60.963
0.992
1.271
12.128
神火股份
26.042
42.500
1.640
0.990
69.776
0.510
50.138
52.066
金牛能源
35.022
15.730
0.725
0.944
39.267
0.953
9.002
-3.877
煤气化
25.809
.498
X5
.573
.643
-.219
X6
-.434
-.672
.332
X7
-.329
.248
.610
X8
.147
.524
-.219
Extraction Method: Principal Component Analysis.a 3 components extracted.主成分方差贡献率表中前3个主成分的累计方差贡献率为70.667%,虽然没有达到80%以上,但第四个主成分的特征根小于1。因此,按着主成分的选择要求,选择3个主成分比较合适。从因子载荷矩阵看,第一主成分主要解释了X2(净资产收益率)和X3(每股收益)两个变量;第二个主成分主要解释了X1(主营业务利润)、X4(总资产周转率)、X5(资产负债率)、X6(流动比率)和X8(资本积累率)这5个变量;而第三个主成分只解释了X7(主营业务收入增长率)一个变量。
14.980
0.677
0.928
45.768
0.949
-3.851
24.881
西山煤电
39.506
17.820
0.868
0.703
45.450
1.525
9.162
-85.430
露天煤业
29.895
22.450
0.709
0.800
40.977
1.321
3.310
4.369
郑州煤电
18.160
12.740
33.721
海越股份
3.357
15.480
0.538
0.626
48.830
0.807
33.438
54.972
国际实业
29.332
10.340
0.299
0.662
53.140
1.218
16.579
7.622
靖远煤电
29.961
16.040
0.255
0.662
36.596
0.700
20.902
-3.682
79
95
83
89
89
79
30
81
9079Βιβλιοθήκη 738580
31
85
77
75
52
73
59
32
68
85
70
84
89
86
33
85
91
95
63
76
66
34
91
85
100
70
65
