第4章 斯特瓦尔特定理及应用(含答案)
初中数学奥林匹克中的几何问题:第4章斯特瓦尔特定理及应用附答案

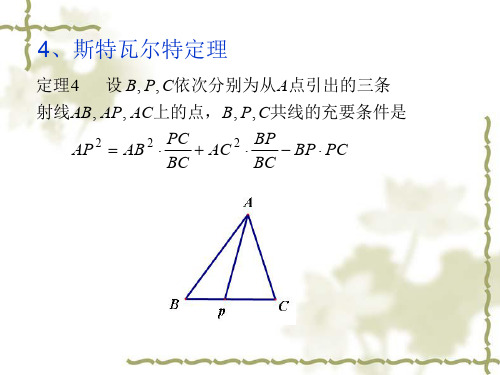
第四章 特瓦尔特定理及应用【基础知识】斯特瓦尔特定理 设P 为ABC △的BC 边上任一点(P B ≠,P C ≠),则有 222AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅①或 2222P C B P B P P C A P A B A C B C B C B C B C B C=⋅+⋅-⋅⋅.② 证明 如图4-1,不失一般性,不妨设90APC <︒∠,则由余弦定理,有图4-1PCB A2222cos AC AP PC AP PC APC =+-⋅⋅∠, 2222cos(180)AB AP BP AP BP APC =+-⋅⋅︒-∠ 222cos AP BP AP BP APC =++⋅⋅∠.对上述两式分别乘以BP ,PC 后相加整理,得①式或②式.斯特瓦尔特定理的逆定理 设B ,P ,C 依次分别为从A 点引出的三条射线AB ,AP ,AC 上的点,若22AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅,或 2222P C B P B P P C A P A B A C B C B C B C B C B C=⋅+⋅-⋅⋅, 则B ,P ,C 三点共线.证明 令1BPA θ=∠,2APC θ=∠,对△ABP 和△APC 分别应用余弦定理,有 22212cos AB AP PB AP PB θ=+-⋅⋅,22222cos AC AP PC AP PC θ=+-⋅⋅.将上述两式分别乘以PC ,BP 后相加,再与已知条件式相比较得 ()122cos cos 0AP BP PC θθ-⋅⋅⋅+=,由此推出12180θθ=︒-,即证.斯特瓦尔特定理的推广 (1)设P 为ABC △的BC 边延长线上任一点,则2222PC BP PC BPAP AB AC BC BC BC BC BC=-⋅+⋅+⋅⋅. ③ (2)设P 为ABC △的BC 边反向延长线上任一点,则 2222PC BP PC BPAP AB AC BC BC BC BC BC=⋅-⋅+⋅⋅.④注 若用有向线段表示,则②,③,④式是一致的.推论1 设P 为等腰ABC △的底边BC 上任一点,则22AP AB BP PC =-⋅. 注 此推论也可视为以A 为圆心,AB 为半径的圆中的圆幂定理. 推论2 设AP 为ABC △的BC 边上的中线,则2222111224AP AB AC BC =+-. 推论3 设AP 为ABC △的A 的内角平分线,则2AP AB AC BP PC =⋅-⋅. 推论4 设AP 为ABC △的A 的外角平分线,则2AP AB AC BP PC =-⋅+⋅. 推论5 在ABC △中,若P 分线段BC 满足BPBCλ=,则 2222(1)(1)AP BC AB AC λλλλ=-+-+⋅.注 若BPk PC =,则()222221111k k AP AB AC BC k k k =⋅+-⋅+++. 【典型例题与基本方法】1.选择恰当的三角形及一边上的一点,是应用斯特瓦尔特定理的关键.例1 如图4-2,凸四边形ABCD 中,60ABC =︒∠,90BAD BCD ==︒∠∠,2AB =,1CD =,对角线AC ,BD 交于点O .求sin AOB ∠. (1996年北京中学生竞赛题)DC BAPO图4-2解 延长BA ,CD 相交于P ,设BC x =,则2PB x =,PC =,对△PBC 及PB 边上的点A ,应用斯特瓦尔特定理,有222AB PACA PC BC AB PA PB PB=⋅+⋅-⋅)()2222222222x x x x x-=⋅+⋅-- 224x x =-+.由Rt Rt ADP CBP △∽△,有PD P C P A P B ⋅=⋅,即)()1222x x-⋅-⋅,求得4BC x ==于是,2153CA =-.又在Rt BCD △中,22120BD x =+=-,从而B DA C ⋅=12.而()(1242ABCD ABD BCD S S S =+=+=△△, 故()1112s i n 2AOB ⋅=∠,即sin AOB =∠ 例2 如图4-3,在ABC △中,60A =︒∠,AB AC >,点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM CN =,求MH NHOH+的值.(2002年全国高中联赛题)L ST图4-3解 延长BE 交O 于L ,由三角形垂心性质,知L 为H 关于AC 的对称点,则LC CH =.设O 的半径为R ,OH d =,CH x =,BH y =,由60CLB A =︒∠=∠,知LH LC CH x ===.延长OH 两端交O 于T ,S ,如图4-3,由相交弦寇理有TH HS BH HL ⋅=⋅,即()()R d R d x y +-=⋅,即22R d xy =+.在△BCL 及边BL 上的点H ,应用斯特瓦尔特定理,并注意到2sin BC R A =⋅∠ ,可得 222BC LH LC BH LH BH BL CH BL ⋅+⋅=⋅⋅+⋅,即)()()222x x y x y x y x x y ⋅+⋅=⋅⋅++⋅+,亦即 ()22213R x x y y =++. 于是,有()22213x xy y d xy ++=+. 亦即()223x y d -=,即x y d-=而当AB AC >时,MH NH BH BM CN CH BH CH y x x y +=-+-=-=-=-, 故x y MH NH OH d-+==2.注意斯特瓦尔特定理的推论的应用例3 如图4-4,自O 外一点引圆的两条切线PE ,PF ,E ,F 为切点,过P 点任意引圆的割线交O 于A ,B ,交EF 于C .证明:211PC PA PB=+. (2001年湖南中学生夏令营试题)CBAEFP图4-4证明 由相交弦定理,有EC CF AC CB ⋅=⋅.由于PE PF =,对等腰△PEF 及底边EF 上的点C ,应用斯特瓦尔特定理的推论1,有22PC PE =- EC CF ⋅,即有222PE PC EC CF PC AC CB =+⋅=+⋅()()2PC PC PA PB PC =+-⋅-22PC PC PA PB PC PB PC PA =--⋅+⋅+⋅ PA PC PB PC PA PB =⋅+⋅-⋅.而2PE PA PB =⋅,从而2PA PB PA PC PB PC ⋅=⋅+⋅.故211P C P A P B=+. 注 此例结论表示线段PC 是线段PA ,PB 的调和平均.这个结论亦即为点P 、C 调和分割弦AB . 例 4 如图4-5,设在ABC △中,AB AC >,AE 平分A ∠,且交BC 于E ,在BC 上有一点S ,使BS EC =.求证:()222AS AE AB AC -=-.(1979年江苏省竞赛题)CB ASE 图4-5证明 对ABC △及边BC 上的点S ,应用斯特瓦尔特定理,有222SC BSAS AB AC BS SC BC BC=⋅+⋅-⋅. 由AE 平分A ∠,对ABC △及边BC 上的点F ,应用斯特瓦尔特定理的推论3,有2AE AB AC =⋅- BE EC ⋅,从而2222SC BSAS AE AB AC AB AC BE EC BS SC BC BC-=⋅+⋅-⋅+⋅-⋅. ①因BS EC =,有BE SC =,即BE EC BS SC ⋅=⋅. 由角平分线的性质,有 ,B E A B E C A CB C A B A C B C A B A C==++, 即,S C B EA B B S E C A CB C B C A B A C B C B C A B A C====++. 从而,由①式,有()222AS AE AB AC -=-.例5 凸多边形ABCD 外切于O ,两组对边所在的直线分别交于点E 、F ,对角线交于点G .求证:DG EF ⊥. (《中等数学》奥林匹克题高中251题) 证明 如图4-6,设O 与边AB 、BC 、CD 、DA 分别切于点M 、N 、R 、S ,则由牛顿定理知,AC 、BD 、MR 、NS 四线共点于G .由切线长定理,知EM ER =.G SOM NRFEDC BA图4-6由推论1,有22EG FS MG GR =-⋅. ① 同理,22FG FS SG GN =-⋅.②联结MO 、EO 、SO ,令O 的半径为r ,则 22222EM OE r FS OF r =-=-,. ③ 又由相交弦定理,有MG GR SG GN ⋅=⋅.④于是,由①、②、③、④有2222EG ED FG FO -=-. 由定差幂线定理,知OG EF ⊥.注 (1)牛顿定理 圆外切四边形的两条对角线、两对边切点的连线,这4条直线共点.(2)定差幂线定理 设MN 、PQ 是两条线段,则MN PQ ⊥的充要条件为2222PM PN QM QN -=-. 此定理可用勾股定理及逆定理证明.这个定理放到空间也是成立的.运用向量法可给出平面、空间的统一证明如下:由22222222PM QN PN QM PM QN PN QM +--=+-- ()()2222PM PN PQPN PM PQ =+----22222222PM PN PQ PN PQ PM PQ PM PQ PN =++-⋅--+⋅-()2222PM PQ PN PQ PM PN PQ NM PQ =⋅-⋅=-⋅=⋅ .知 0N M P Q N M P Q ⇔⋅=⊥ . 故 2222M N P Q P M P N O M QN ⇔-=-⊥. 例6 已知E 、F 分剔是ABC △的边AB 、AC 的中点,CM 、BN 是边AB 、AC 上的高,联结EF 、MN 交于点P .又设Q 、H 分别是ABC △的外心、垂心,联结AP 、OH .求证:AP OH ⊥.(2005年国家队集训题)证明 如图4-7,联结AO 、AH .设1O 、1H 分别为AO 、AH 的中点,则112H N AH =,112H M AM =,即知点1H 在线段MN 的中重线上,应用推论1,有B图4-72211H P H M MP PN =-⋅.注意到EF 为ABC △中位线,O 在BC 的中垂线上,由此知1O 也在EF 的中垂线上,应用推论1,有 2211O P O E EP PF =-⋅.再注意到ANM ABC AEF ==∠∠∠,知M 、E 、N 、F 四点共圆,并由直角三角形性质,有 MP PF EP PF ⋅=⋅. ③ 及11O E O A =、11H M H A =.④由①、②、③、④得22221111H A H P O A O P -=-.由定差幂线定理,11O H AP ⊥. 而1O H OH ∥,故AP OH ⊥.注 此例的其他证法可参见第九章例16、第十章例15. 例7 设D 是ABC △的边BC 上一点,满足CDA CAB △∽△,O 经过B 、D 两点,并分别与AB 、AD 交于E 、F 两点,BF 、DE 交于点G ,联结AO 、AG ,取AG 的中点M .求证:CM AO ⊥. 证明 如图4-8,在AG 的延长线上取点P ,使得AG AP AF AD ⋅=⋅(即G 、P 、D 、F 四点共圆),则由AE AB AF AD ⋅=⋅知E 、B 、P 、G 也四点共圆.于是180180BPA BED BFD =︒-=︒-=∠∠∠BFA ∠,知B 、P 、F 、A 四点共圆,即有2FG GB AG GP AF AD AG ⋅=⋅=⋅-.C图4-8联结OD 、OF 、OE ,并令O 半径为R ,则对ODE △、ODF △分别应用推论1,有 222OG OD EG GD R FG GB =-⋅=-⋅.① 2222OA OD AF AD R FG GB AG =+⋅=+⋅+.②联结OM ,由三角形中线长公式,并注意①、②,有222222211(22)44MO MA OA OG AG AG R -=+--=.③联结OB 、OC ,对OBD △应用推论1,有222CO OB CD CB R CD CB =+⋅=+⋅. 又由CDA CAB △∽△,有2CA CD CB =⋅,即有222CO CA R -=.④注 P 即为完全四边形的密克尔点,由③、④有2222MO MA CO CA -=-.由定差幂线定理,知CM ⊥AO .3.注意斯特瓦尔特定理等价于托勒密定理 斯特瓦尔特定理可推导出托勒密定理.证明 如图4-9,在ABC △中,点P 在BC 上,由斯特瓦尔特定理,有CBAEP图4-9222AP BC AB PC AC BP BP PC BC ⋅=⋅+⋅-⋅⋅.延长AP 交ABC △的外接圆于E ,连BE ,EC ,由ABP CEP △∽△和ACP BEP △∽△,有AB AP ⋅= CE AP ⋅,AC BP AP BE ⋅=⋅.又由相交弦定理,有BP PC AP PE ⋅=⋅.于是,得2AP BC AB CE AP AC AP BE AP PE BC ⋅=⋅⋅+⋅⋅-⋅⋅, 即 ()B C A P P EA B C EA CB E +=⋅+⋅, 亦即 A B C E A C B E B C ⋅+⋅=⋅.即为托勒密定理.由托勒密定理也可推导斯特瓦尔特定理.证明 如图4-10,设圆内接四边形ABEC 的对角线AE ,BC 交于P .由托勒密定理,有CBAEP 图4-10AB EC AC BE BC AE ⋅+⋅=⋅.即 ()A B E C A C B E B P P C A E⋅+⋅=+⋅. 由△ABP ∽△CEP 和△ACP ∽△BEP ,有AB PC EC AP ⋅=,AC BPBE AP⋅=.由相交弦定理,有BP PCPE AP⋅=.将这些式子代入前述式子即得斯特瓦尔特定理. 因此,在应用中,两个定理的应用范围相同,所显示的功能也一样,即凡能用托勒密定理处理的问题也能用斯特瓦尔特定理处理.反之亦然.例8 若ABC △的三边为连续整数,且最大角B ∠是最小角A ∠的两倍,求三角形的三边长.(IMO -10试题)解法1 作ABC ∠的平分线BD (图略),则BD AD =,令AD y =,AB x =,则 1AC x =+,1BC x =-,1CD x y =+-. 由斯特瓦尔特定理的推论3,有()()211y x x y x y =--+-,即()11x x y x -=+,又AB AD BC CD =,即1xx =-1yx y +-,有()121x x y x +=-.故由22121x x x xx x -+=+-,求得5x =(舍去0x =),即5AB =,4BC =,6AC =. 解法2 作ABC △的外接圆O ,取 AC 的中点D ,连AD ,BD ,CD ,则A B C D 为梯形,其中CD BA ∥.令AB x =,则1AC x =+,1BC x =-,且1CD BC x ==-,1BD AC x ==+.对四边形ABCD 应用托勒密定理,有()()()22111x x x x +=-+-,求得5x =.(下略) 【解题思维策略分析】1.获得线段倍分关系的一条途径例9 如图4-11,已知ABC △的外接圆k 的圆心为O ,半径为R ,内切圆的圆心为I ,半径为r ,另一个圆0k 与边CA ,CB 分别切于点D ,E ,且与圆k 内切.求证:内心I 是线段DE 的中点.(IMO -34预选题)A图4-11证明 设圆0k 的圆心为1O ,半径为ρ,于是1O ,I ,C 三点共线,且1sin 2r CI C =∠,11sin 2CO C ρ=∠,则11sin 2rIO C ρ-=∠,且1O E ρ=.于是,111IO r rCO ρρρ-==-. 连OC ,OI ,1O O ,对△1COO ,及边1O C 上的点I ,应用斯特瓦尔特定理,有 22211111OO CI OC IO OI CO CI IO CO ⋅+⋅=⋅+⋅⋅①注意到欧拉公式,222OI R Rr =-,及1OO R ρ=-,OC R =,并将其代入①式,得到()2211sin sin 22r rR R C C ρρ--⋅+⋅∠∠ ()221111sin sin sin sin 2222r r R Rr C C C C ρρρ-=-⋅+⋅⋅∠∠∠∠, 化简得 21s i n12r r C ρρρ-==-∠. 从而 221111sin 2IO C CO CO ρ⎛⎫== ⎪ ⎪⎝⎭∠, 即 22111IO CO O E ρ⋅==.②因为1O E CE ⊥,1CO DE ⊥且平分DE ,令DE 的中点为I ',由射影定理,有 2111I O CO O E '⋅=.③比较③式和②式,知I '与I 重合,即得I 为DE 的中点.例10 如图4-12,两个大圆A ,B 相等且相交;两个小圆C ,D 不相等但相交,且交点为P ,Q .若C ,D 既同时与A 内切,又同时与B 外切.试证:直线PQ 平分线段AB .(《中等数学》奥林匹克问题高中58题)图4-12证明 由于C ,D 半径不相等,此两圆交点所在直线PQ 必与线段AB 相交,设交点为M .连AC ,MC ,BC ,AD ,MD ,BD ,PC ,PD ,CD ,显然PQ CD ⊥,设垂足为N ,又设A ,B 的半径均是ρ,C ,D 的半径分别为R ,()r R r ≠,则易得AC R ρ=-,BC R ρ=+,AD r ρ=-,BD r ρ=+,因为PQ CD ⊥,或MP CD ⊥,垂足为N ,则 ()()2222222MC MD CN NM MN ND -+-+=22CN ND =-2222()()PC PN PD PN =---2222PC PD R r =-=-.设AM x =,MB y =,对△CAB 及边AB 上的点M ,应用斯特瓦尔特定理,有()()22x BC y AC x y MC x y x y ⋅+⋅=+⋅++⋅ ()222x y MC x MB y AM =+⋅+⋅+⋅.①对△DAB 及边AB 上的点M ,应用斯特瓦尔特定理,有()22222x BD y AD x y MD x MB y AM ⋅+⋅=+⋅+⋅+⋅. ②①-②,得()()()()()()22222222x BC BD y AC AD x y MC MD x y R r ⋅-+-=+-=+-,即 ()()()()()()222222[][]x R r y R r x y R r ρρρρ⋅+-++⋅---=+-, 亦即 ()()20x y R r ρ⋅-⋅-=.因0ρ≠,R r ≠,从而0x y -=,即x y =. 故AM M B =,即直线PQ 平分线段AB .2.求解三角形问题的一种工具斯特瓦尔特定理在求解三角形中有关线段的问题有着重要作用,这可从习题A 中的第6题,习题B 中的第7题等可以看出.在求解三角形的其他问题中,它也有着重要作用.例11 设ABC △的三边为a ,b ,c ,其面积为S,则222a b c ++≥,当且仅当ABC △为正三角形时,等式成立. (IMO -3试题) 证明 取BC 的中点D ,对ABC △及BC 边上的点D ,应用斯特瓦尔特定理的推论2,有 2222222111111224224A D A C AB BC b c a =+-=+-.从而有22222322a b c AD a AD a ++=+⋅≥.设ABC △的BC 边上的高为h ,则AD h ≥,于是122AD a a h ⋅⋅⋅=≥.故222a b c ++≥,其中等号当且仅当22322AD a =且AD h =时成立,也即AD BC ⊥且AD =,此时ABC △恰为正三角形.例12 如图4-13,在ABC △中,D ,E 分别为AC 和AB 同方向延长线上的点,BD 与CE 相交于P ,且BD CE =.当P 在BC 边的中线上时,则AB AC =.EDC B APQ图4-13证明 设AP 交BC 于Q .分别对△BPQ 及点A 和△CPQ 及点A 应用斯特瓦尔特定理的推广结论,有222AQ APBA BP BQ AP AQ PQ PQ =-⋅+⋅+⋅, 222AQ APCA CP CQ AP AQ PQ PQ=-⋅+⋅+⋅. 于是()()222222AQ APBA CA CP BP BQ CQ PQ PQ-=-⋅+-⋅. 由于BD CE =,对△PBC 及点A 应用塞瓦定理,有1QB EC DP QC EP DB⋅⋅=,即PD QCPE QB =.当P 点在BC 边上的中线上时,有BQ QC =.从而PD PE =,由此知PC PB =,故AB AC =.例13 如图4-14,若D 是ABC △的边BC 延长线上一点,则AD 平分A ∠的外角的充分必要条件是2AD BD CD AB AC =⋅-⋅.DCBAF图4-14证明 必要性:若AD 平分A ∠的外角,则由推论4即有 2AD BD CD AB AC =⋅-⋅.或者按证明斯特瓦尔特定理的方法来推导.充分性:设直线AD 交ABC △的外接圆于E ,连BE 、CE .由割线定理有BD CD AD ED ⋅=⋅,并将其代入条件式2AD BD CD AB AC =⋅-⋅可得 ()AD ED AD AB AC -=⋅.由此可知E 必在DA 的延长线上(因0ED AD ->). 于是AD AE AB AC ⋅=⋅. ① 由△ACD ∽△BCD ,有AC BD AD BE ⋅=⋅.② 由①⨯②得 A E B D A B B E ⋅=⋅.③ 又由△ECD ∽△BAD ,有EC AD CD AB ⋅=⋅. ④ 由①÷④得,AE CD AC CE ⋅=⋅. ⑤由③-⑤得,AE BC AB BE AC CE ⋅=⋅-⋅. 对四边形EBCA 应用托勒密定理,有 AE BC AB CE AC BE ⋅=⋅-⋅.于是AB CE AC BE AB BE AC CE ⋅-⋅=⋅-⋅. 即()()0AB AC CE BE +-=,从而CE BE =.因此CAD EBC ECB EAB ===∠∠∠∠. 故AD 平分A ∠的外角.例14 如图4-15,设正ABC △的内切圆圆心为I ,半径为r ,在I 内任取一点P ,设点P 到BC ,CA ,AB 的距离分别为1d ,2d ,3d,(《数学通报》问题1356题)I d 3d 2d 1D CBAP图4-15证明 设正三角形ABC 的边长为1,则123d d d ++=2IA IB IC r ==== 连AP 并延长交BC 于D ,则由题设知 32APB APC S d BD DC S d ==△△, ()1123131BPC BAC BPC S d d DPPA S S d d d d d d ===-+++-△△△. 由于BI IC =,BA AC =,对△BIC 及边BC 上的点D ,对ABC △及边BC 上的点D ,均应用斯特瓦尔特定理的推论1,有2222ID IB BD DC AD AB BD DC =-⋅=-⋅,.又由32d BD DC d =,知332323d d BD BC d d d d =⋅=++,223d DC d d =+. 于是()22322313d d ID d d =-+,()2232231d d AD d d =-+. ①又对△AID 及边AD 上的点P 应用斯特瓦尔特定理,有 222PA DPIP ID IA DP PA AD AD=⋅+⋅-⋅.由123d DP PA d d =+,知23123d d PA AD d d d +=++,1123d DPAD d d d =++.将上述各式及①式代入②式,并注意IA =,123d d d ++=123444d d d =+,有222DP PAIP IA ID DP PA AD AD=⋅+⋅-⋅ ()2232312133123231133d d d d d DP PAAD d d d d d d AD ADd d ⎡⎤+⎢⎥=⋅+-⋅-⋅⋅+++++⎢⎥⎣⎦()()()12312323232212323122123231113d d d d d d d d d d d d d d d d d d d d d d d ⎡⎤+++⎢⎥=⋅-⋅-⋅-++++++++⎢⎥⎣⎦()()2312312323414333d d d d d d d d d -=-+-+ ()()()23112323414333d d d d d d d d =-+-+ ()1213231433d d d d d d =-++. 即 ()21213231143IP d d d d d d ⎡⎤=-++⎣⎦. 于是,()2221231213232d d d d d d d d d ---+++()()21231213234d d d d d d d d d =-+++++()()22231334IP r IP =-+-=-.此式可写成为=()223r IP -. ③由于P 点在I 内部,则220r IP ->,从而,必有0>0>0.如若不然,,0<,则0+<,即0与已知矛盾,则知可见,以,,积为 【模拟实战】习题A1.在ABC △中,2AB AC ==,BC 边有100个不同的点1P ,2P ,…,100P ,记22i i im A P B P P C =+⋅(i =1,2,…,100),求12100m m m +++…的值.2.在ABC △中,C ∠的平分线交AB 于D.证明:CD <(匈牙利中学生数学竞赛题) 3.在ABC △中,D 是BC 边上的点,已知13AB =,12AD =,15AC =,5BD =,求DC . 4.在ABC △中,AB =AC 2BC =,设P 为BC 边上任一点,则( ) A .2PA PB PC <⋅B .2PA PB PC =⋅C .2PA PB PC >⋅D .2PA 与PB PC ⋅的大小关系不确定5.D 是ABC △的边AC 上的一点,且21AD DC =∶∶,45C =︒∠,60ADB =︒∠,求证:AB 是△BCD的外接圆的切线.6.设ABC △的三边BC a =,CA b =,AB c =,()12p a b c =++.设a m ,a h 分别为BC 边上的中线长和高线长;a t ,at '分别为BC 边所对的角的内、外角平分线长.求证下列各式:(Ⅰ)a m ;(Ⅱ)a t =(Ⅲ)at '=(Ⅳ)a h . 7.在ABC △中,2AB BC =,2B A =∠∠,求证:ABC △是直角三角形. 8.证明:到三角形三顶点的距离的平方和最小的点是重心.习题B1.设,,分别是共线的三点A ,B ,C 对于O 所作切线的长.求证:a BC ⋅+ c AB b AC BC AC AB ⋅-⋅=⋅⋅.2.锐角ABC △的外接圆过B ,C 的切线相交于N ,点M 是BC 的中点.求证:BAM =∠ CAN ∠.(IMO -26预选题) 3.1PT 和2PT 是O 的割线,分别交O 于1S ,2S ,且12PT PT =,过P 的直线交O 于Q ,R (Q 在R 与P 之间),交12T T ,12S S 于T ,S .求证1111PQ PR PS PT+=+. 4.A ,B ,C ,D 四点在同一圆周上,且4BC DC ==,6AE =,线段BE 和DE 的长都是整数,求BD 的长.5.在正方形ABCD 中,E 在BC 上,2BE =,1CE =,P 点在BD 上,则PE 和PC 的长度之和最小可达到多少?6.设凸四边形的边长是a ,b ,c ,d ,对角线长是e 和f .求证:2min{,,,}a b c d 当且仅当这个凸四边形是菱形时等号成立.7.设I ,O ,G ,H 分别为ABC △的内心,外心,重心,垂心,令BC a =,CA b =,AB c =,()12p a b c =++,R ,r 分别为外接圆和内切圆的半径.求证下列各式: (Ⅰ)222a IA b IB c IC abc ⋅+⋅+⋅=; (Ⅱ)2222abcIO R R Rr a b c=-=-++;(Ⅲ)()()()()22222222221222918IG a b c b c a c a b a b c abc p ⎡⎤=+++++-++-⎣⎦()2222254318p a b c Rr =-++-;(Ⅳ)()22222142IH R a b c abc p=-+++. 8.已知ABC △满足2ACB ABC =∠∠,设D 是BC 边上一点,且2CD BD =.延长线段AD 至E ,使AD DE =.证明:1802ECB EBC +︒=∠∠.(IMO -39预选题)第四章 斯特瓦尔特定理应用习题A1.因A B A C =,由斯特瓦特定理推论1,有22i i i AP AB BP PC =-⋅,则22i i iAP BP PC AB +⋅=,即224i i i im AP BP PC AB =+⋅==,即121004100400m m m ++=⋅=….2.由CD 平分ACB ∠,由斯特瓦特定理推论3,知2C D C A C B A D D B C A C B =⋅-⋅<⋅,故C D <3.由斯特瓦尔特定理,有222CD BD AD AB AC BD DC BC BC=⋅+⋅-⋅.设D C x =,则5BC x =+,则2225121315555x x x x=⋅+⋅-++,解得19x =(舍去29x =-).4.由斯特瓦尔特定理,有222222PC PB PC PBPA AB AC PB BC PB BC BC =⋅+⋅-⋅=⋅+⋅-⋅4PC PC PB PB PC =+-⋅,242PA PB PC PC PB PB PC ∴-⋅=+-⋅,又2PB PC =-,则2PA PB -⋅22115422(2)222(2)2()048PC PC PC PC PC PC PC PC PC =+---⋅=-+=+=-+>,故选(C ). 5.由21AD DC =∶∶,由斯特瓦尔特定理推论5,有2222122359BD AB BC AC =+-. 由45C ∠=︒,60ADB ∠=︒,及sin sin BD BCC BDC =∠∠,有2232BD BC =. 又由21AD DC =∶∶,有232AC AD AC =⋅. 于是有2AB AD AC =⋅,由切割线定理即证.6.设P 为ABC △的BC 所在直线上任一点,且1BPBC λ=∶∶,有斯特瓦尔特定理推论5,有2222(1)(1)AP λλa λb λc =-++-. 12λ=时,a AP m =即得(Ⅰ); 当cλb c =+时,a AP t =,即得(Ⅱ)当1λb c=-时,a AP t '=,即得(Ⅲ);当22222a b c λa -+=时,a AP h =,即得(Ⅳ).7.作B ∠的平分线交AC 于D ,则2A D A BD C B C==,对ABC 及AC 边上点D 应用斯特瓦尔特定理推论3,有2BD AB BC AD DC =⋅-⋅,即222(2)22DC BC DC =-,即2213DC BC =,又2222()93AC AD DC DC BD =+==,从而22224AC BC BC AB +==,故ABC △为直角三角形.8.设G 为三条中线AD ,BE ,CF 的交点,P 为ABC △所在平面上任一点.不妨设P 在ABC △内,连PA ,PB ,PC ,PD ,PG ,对APD △及点G 应用斯特瓦尔特定理,有 222PA DG PD AG PG AD AG GD AD ⋅+⋅=⋅+⋅⋅.由12DG AG =,32AD AG =,则22223322PG PA PD AG =+=. ①在PBC △和GBC △中,D 为BC 中点,应用斯特瓦尔特定理推论2,则2222111224PD PB PC BC =+-,2222111224GD GB GC BC =+-,此两式相减,并注意12GD AG =,222222111()()224PD PB PC GB GC AG =+-++,代入①式,得2222223()()PG PA PB PC GA GB GC =++-++.显然,当P 异于G 时,横有222222PA PB PC GA GB GC ++>++.故到三角形三顶点距离的平方和为最小的点是三角形的重心. 习题B1.设O ⊙的半径为r ,连OA ,OB ,OC ,对OAC △及AC 边上的点B ,应用斯特瓦尔特定理,有222OA BC OC AB OB AC AB BC AC ⋅+⋅=⋅+⋅⋅,而22OA r α=+,22OB r b =+,22OC r c =+,于是 222()()()r a BC r c AB r b AC AB BC AC +⋅++⋅=+⋅+⋅⋅,化简即得结论.2.对ABC △及BC 边上的点M ,应用斯特瓦尔定理推论1,有22221(22)4AM AB AC BC =+-,cos 2cos BM BC BN A A ==∠∠.又2222222cos 4cos BC AN AB BN AB BN ABN AB A=+-⋅⋅∠=+∠ cos (cos cos )cos C AB BC ABN C A ∠+⋅⋅∠=-∠∠,于是222221cos cos 4AN A AB A BC ⋅∠=⋅∠++cos cos AB BC C A ⋅⋅∠⋅∠而cos cos cos()sin sin sin sin sin A C A C A C A C B ∠⋅∠=∠+∠+∠⋅∠=∠⋅∠-∠,则222222221cos cos sin sin cos (cos sin )4AN A AB A BC AB BC A C AB BC A AB A A ⋅∠=⋅∠++⋅⋅∠⋅∠-⋅⋅∠=⋅∠+∠22222222111()(22)424BC AB BC AC AB AC BC AM +-⋅+-=+-⋅(其中s i n s i n B C C A B A⋅∠=⋅∠),即cos AM CM A AN CN =∠=,sin(180)sin AN A C CN CAN ︒-∠-∠=∠,又B M C M =,且s i n s i n A M BB M B A M ∠=∠,故s i n s i n B A M C A N ∠=∠,即证.另证:设AN 交圆于D ,连BD ,CD ,对四边形ABCD 应用托勒密定理,有AD BC AC BD AB CD ⋅=⋅+⋅,由ACN CDN △∽△,ABN BDM △∽△,有AC AN CD CN =,AB ANBD BN=,而BN CN =,则AC BD AB ⋅=⋅ CD .注意到2BD BM =,有22AD BM AB CD ⋅=⋅,即A D A BC D B M=,又A B M A D C ∠=∠,从而A D C A B M △∽△,故NAC BAM ∠=∠.3.由12PT PT =及1122PT PS PT PS ⋅=⋅,有12PS PS =,从而1212TT S S ∥,即11PS PT PS PT=,而 11PT PS PQ PQ ⋅=⋅3,则21PSPS PQ PR PT=⋅⋅,对12S PS △及12S S 边上的点S 应用斯特瓦尔特定理推论1,有22112PS PS S S SS =-⋅,又在O ⊙中12()()S S SS RS SQ PR PS PS PQ ⋅=⋅=--,故2()()PSPS PQ PR PR PS PS PQ PT=⋅⋅---,故1111PQ PR PS PT +=+. 4.对ABCD △及BD 边上的点E ,应用斯特瓦尔特定理或其推论1,有22244BE DECE BD BD=⋅+⋅-161616166BE DEBE DE BE DE BE DE AE CE CE BD+⋅=⋅-⋅=-⋅=-⋅=-.解得2CE =(负值舍去). 于是12BE DE CE AE ⋅=⋅=,而8B D B C C D <+=,即3BE =,4DE =或4BE =,3DE =,故7BD =.5.由2BE CE =∶,对BCP △及BC 边上的点E ,应用斯特瓦尔特定理的推论5,有22212233PE PB PC =+-.对BCD △及BD 边上点P 应用推论1,有2229PC BC BP PD PB =-⋅=+-,于是224PE PB =-+,故PE PC +=令PB x =,上式表示x 轴上动点(,0)Q x 到两定点A ,,B 的距离之和,当Q 为线段AB 与x 轴交点0)时,即PB 时,PE PC + 6.设凸四边形ABCD 的对角线交点为E .令AB a =,BC b =,CE c =DA d =,AC e =,BD f =,AE g =,BE h =,CE k =,DE l =.不妨设h l ≤,则在ABC △中,有{}2222min ,a k bga b kg h k g+≤=++(斯特瓦尔特定理)22221()()()2k g h l e f ++≤+=+,于是{}{}2min ,,,2min ,a b c d a b ≤=a b =,g k =,h l =,{}{}min ,min ,a b c d ≤时等号成立,即ABCD 为菱形.7.由于四个结论都与内心I 有关,不妨设AD 平分A ∠交BC 于D ,显然I 在AD 上.设P 为ABC △所在平面内任一点,连PB ,PD ,PC ,PI ,注意到ac BD b c =+,abCD b c =+,对PBC △及边上点D 应用斯特瓦尔特定理,有22222()b c a bc PD PB PC b c b c b c =⋅+⋅-+++. 又AI c b b cID BD CD a+===,有2b c AI AD p +=,2a ID AD p =,而224()()bcp AD p a b c =-+,对PAD △及AD 边上点I 应用斯特瓦尔特定理,有222()22()b c a abc p a PI PD PA p p p b c +-=⋅+⋅-+.将2PD 表达式代入上式,得2222a PAb PBc PC abcPI a b c⋅+⋅+⋅-=++.(Ⅰ)当P 与I 重合时,由①式即证(Ⅱ)当P 为外心O 时,PA PB PC R ==+,由①式即证.(Ⅲ)当P 为中心G 时,2222241(22)99a PA GA mbc a ===+-,等等.由①式即证、(Ⅳ)当P 为垂心H 时,22222222cot (csc 1)4PA HA a A a A R a ==⋅∠=∠-=-,等等.由①式即证.8.设CD 的中点为H ,则ABEH 是平行四边形,延长BC 至G ,使CG CA =.设3aBD DH HC ===,CA b =,AB c =,BE AH x ==,AD DE y ==,CE z =.由2ABC ACB CGA ∠=∠=∠+22CAG CGA CAG ∠=∠=∠,则ABG CAG △∽△.于是有AB CABG AG=或2()c b a b =+. ① 在ACD △,ABH △,CDE △中分别应用斯特瓦尔特定理推论2,得2222229b y x a +=+,2222229x c y a +=+,2222229y z c a +=+.从前两式中消去y ,有222222243x c b x a ++=+,将①式代入得22()()33a x b a b =+-.再求得23z b a =+,故有2()x z z a =-或2()BE CE CE BC CE EP =-=⋅.这里P 是CE 上一点,且满足CP BC =.故BE EPCE BE=,又BEP CEB ∠=∠,知BEP CEB △∽△,从而 1(180)2ECB EBP EBC ECB ∠=∠=∠-︒-∠.故1802ECB EBC ∠+︒=∠.。
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
解三角形三大定理——倍角定理,中线长定理,斯特瓦而特定理(三)

,A B ++22A π<54512π⎛∈ ⎝()sin 45A ⎛+∈ ⎝)(453∈2,13+为BC 的中线,则中线定理:虽说网络上的老师都讲烂了这个定理,但是我还要说一下,基于证明方法是:在ABD ∆和ADC ∆中,用余弦定理有:)(20222222222222DC AD AC AB DC BD DC AD AC DC AD BD AD AB BD AD +=+⇒⎪⎩⎪⎨⎧==⋅-++⋅-+ 希望老师们引导学生遇到中线,就要往这个定理上面去想。
AD ()22222DC AD AC AB +=+由阿罗波尼斯圆可知:例2.(2020年广州六十五中高三11月月考)设的内角的对边分别为,已知边上的中线,则 .解析:由中线长定理:得 ,再由余弦定理:综上解之得:.例2.(2020年广州六十五中高三11月月考)设的内角的对边分别为,已知面积为,,若为中点,且,则的最大值为( )解析:,由余弦定理和中线长定理:例2.(2020年广州六十五中高三11月月考)已知中,,为中点,,则的取值范围为 .解析:由中线长定理:又因为不妨令:此处的方法,利用了∆判别式法,具体研究在公共号文章解三角形的第一篇文章。
32211222121222=⋅-⋅⋅=⋅=⋅⋅≤=∆∆r BD r BD S S ABD ABC ABC ∆C B A ,,c b a ,,,6,60==c ABC19=AD =B sin 2224b a =+2222366123621cos a b b ba b A -+=⇒-+==721sin 72,4=⇒==B a b ABC ∆C B A ,,c b a ,,ABC ∆S )sin sin sin (21C c B b A a c S -+=D AB 2=C CD 3π=C 3max =CD ABC ∆060A ∠=M BC 3AM =2AB AC +)(22222BM AM c b +=+1222=++ac c b 0123322222=-+-⇒-=⇒+=+=t tc c c t b b c AC AB t 3432003120)12(129222<<⇒⎪⎪⎩⎪⎪⎨⎧>>->--=∆t t t t t三.斯特瓦尔特定理例1.(马鞍山2020届二模理)在中,,点在线段上,且,则面积的最大值( ) 解析: 设,由斯特瓦尔特定理和余弦定理:① ②由 ①②得: ③ 取等条件: 所以:面积最大值为:例2.(东北三省三校2020届高三二模文16)设的内角所对的边分别为,且,边上的点满足,则的面积( )解析:由由斯特瓦尔特定理得:,再由余弦定理得:,下面我来解出:,之后得:ABC ∆ 60=∠BAC D BC 2,3==AD BD BC ABC ∆bc BAC bc S ABC 43sin 21=∠=x DC x BD 2,==122321226222222-+=⇒-+=b c a b c x bc c b a -+=2226≤bc b c =2ABC S 233ABC ∆C B A ,,c b a ,,ac c b a c b a 3))((=+-++AC D 22===AD CD BD ABC ∆=S ac c b a c b a 3))((=+-++33)(22π=⇒=-+∴B ac b c a 18222=+c a ac c a =-+922c a ,c a ca ac c a 2222222=⇒+=-+3,32==b a 三角形斯特瓦尔特定理: 在ABD ∆和ADC ∆中,用余弦定理有:022222222=⋅-++⋅-+DCAD AC DC AD BD AD AB BD AD ⇒ DC BD BCDBAC DC AB AD ⋅-⋅+⋅=222DC BD BC DB AC DC AB AD ⋅-⋅+⋅=222所以:例3.(2020信阳市高三二模16)在中,角所对的边为,满足且,则的最小值为( )解析:如图由斯特瓦尔特定理: ,当且仅当:时取等。
《第4章 光及其应用》试卷及答案_高中物理选择性必修第一册_沪教版_2024-2025学年

《第4章光及其应用》试卷(答案在后面)一、单项选择题(本大题有7小题,每小题4分,共28分)1、某单色光从空气斜射入水中时,折射光线向法线【】,折射角小于入射角【】,该单色光的波长在水中【】。
A. 折向法线,是,变短B. 折向法线,否,不变C. 离开法线,是,变短D. 离开法线,否,不变2、在全反射现象中,下列说法正确的是【】。
A. 一定发生在光从光密介质射向光疏介质时B. 折射光线与界面垂直,入射光线与界面成45°角C. 光线会在界面上发生全反射而不进入第二介质D. 界面一侧的总反射光强等于入射光强3、下列关于光现象的说法中,正确的是()A. 光的干涉现象只有在相干光源的照射下才能产生B. 光的衍射现象只能在光遇到障碍物或通过狭缝时才能产生C. 光的折射现象只能在光从一种介质进入另一种介质时才能产生D. 光的反射现象只能在光遇到平面镜时才能产生4、一束单色光从空气射入水中,已知光在水中的折射率为1.33,求该单色光在水中的传播速度与在空气中的传播速度之比()A. 3/4B. 4/3C. 3/2D. 2/35、一束单色光从水中射向空气,当入射角为30°时,折射角恰好为45°。
若将这束单色光的入射角增大,折射角将如何变化?A、增大B、不变C、减小D、可能增大也可能减小6、一个肥皂膜在阳光下展露呈现出彩虹色,这一现象是由于光的:A、折射B、反射C、干涉D、散射7、一束单色光从空气进入水中,其速度减小,根据光的折射定律,下列说法正确的是:A、光的波长将增大,频率将减小B、光的波长将减小,频率将增大C、光的频率将不变,波长将增大D、光的频率将不变,波长将减小二、多项选择题(本大题有3小题,每小题6分,共18分)1、题干:下列关于光的现象及其应用的描述中,正确的是:A、全息照片利用了光的干涉现象B、光纤通信利用了光的折射原理C、液晶显示器利用了光的衍射现象D、雷达探测利用了光的反射原理2、题干:关于光的波动性和粒子性的描述,以下正确的是:A、光的干涉和衍射现象说明光具有波动性B、光电效应说明光具有粒子性C、光的反射和折射现象只能说明光具有波动性D、光的偏振现象说明光具有波动性3、下列关于光的波粒二象性的描述,正确的是()。
《第4章 原子结构》试卷及答案_高中物理选择性必修 第三册_鲁科版_2024-2025学年

《第4章原子结构》试卷(答案在后面)一、单项选择题(本大题有7小题,每小题4分,共28分)1、下列关于原子结构的叙述中,正确的是()A.α粒子散射实验揭示了原子中存在带正电的原子核B.汤姆孙提出了“行星模型”,认为电子像行星环绕太阳一样在原子内运动C.波尔理论完美地解释了各种原子光谱线的实验结果D.玻尔理论彻底否定了经典电磁理论中关于电子的轨道半径和能量只能取某些特殊值的观点2、最早提出电子存在的是下列哪位科学家?()A.普朗克B.爱因斯坦C.汤姆孙D.居里夫妇3、γ射线穿透物质的穿透能力最强,这种射线属于()A. α粒子B. β粒子C. γ射线D.闪烁射线4、在卢瑟福α粒子散射实验中,绝大多数α粒子都穿过金箔后仍沿着原来的直线前进,这是因为()A. 原子质量和电荷集中在核上B. 电子所带电荷AMY大,对α粒子的作用力很大C. 原子的质量主要分布在电子上D. 核与电子的距离相对较远5、下列关于原子结构的描述中,正确的是:A、原子的质量主要集中在原子核上,电子的质量可以忽略不计。
B、原子核是由质子和中子组成的,电子围绕原子核旋转。
C、原子的核电荷数等于其质子数,但不一定等于其电子数。
D、原子中的电子总是按照能量最低的原则分布在原子核外的各个能级上。
6、根据波尔理论,氢原子的电子在特定的能级上运动时,其轨道半径与能量的关系是:A、轨道半径随能量的增加而增加,能量随轨道半径的增加而增加。
B、轨道半径随能量的增加而增加,能量随轨道半径的增加而减少。
C、轨道半径随能量的增加而减少,能量随轨道半径的增加而增加。
D、轨道半径随能量的增加而减少,能量随轨道半径的增加而减少。
7、下列关于原子结构的说法中,正确的是()A. 阿斯顿的质谱仪(1909年)发现了原子核。
B. 汤姆孙通过α粒子散射实验提出电子云模型。
C. 卢瑟福通过α粒子散射实验提出了原子的核式模型。
D. 玻尔的原子模型放弃了经典电磁理论中的能量连续性概念,提出了量子化的能级模型。
斯特瓦尔特定理的应用

斯特瓦尔特定理的应用1. 斯特瓦尔特定理简介哎,大家好!今天咱们来聊聊一个有趣又实用的数学概念——斯特瓦尔特定理。
这名字听着就有点高大上,对吧?其实,它的意思挺简单的,就是在某些情况下,我们可以把一个复杂的数学问题变得轻松又简单。
想象一下,就像把一块大蛋糕切成好几块,吃起来可方便多了!斯特瓦尔特定理主要用来处理一些极限、级数和连续性的问题,听上去有点深奥,但我保证,越往下看,越简单。
斯特瓦尔特定理的核心思想,就是通过某种方式把复杂的数学关系转化为简单的形式。
说白了,就是让那些看起来很难的公式,变得像吃糖一样简单。
就像我小时候玩拼图一样,把那些零散的小块拼成一幅美丽的画,关键是找到合适的方法!所以,今天咱们就来看看这定理是怎么用的。
2. 斯特瓦尔特定理的基本应用2.1. 极限的计算好啦,先来看看斯特瓦尔特定理在极限计算中的应用吧。
想象一下,有一天你在海边晒太阳,突然想到一个问题:当我让某个数越来越大时,它的极限到底是什么?这是个棘手的问题,但别担心!斯特瓦尔特定理就像你身边的救生圈,帮你轻松找到答案。
假设我们要计算 (lim_{x to 0 frac{sin x{x)。
这个极限看上去让人摸不着头脑,但根据斯特瓦尔特定理,我们可以找到一个很好的替代函数。
我们知道,当 (x) 趋近于0时,(sin x) 的值也会趋近于 (x)。
于是,我们就可以把问题化简为 (lim_{x to 0 frac{sin x{x = 1)。
哎,真是轻松搞定呀,犹如一口气喝完了一瓶可乐,爽快!2.2. 级数的收敛性接下来,咱们再来聊聊级数的收敛性。
你知道吗?有些数学级数就像一把双刃剑,收敛时美妙无比,但一旦不收敛,那简直就是噩梦!这时候,斯特瓦尔特定理再次闪亮登场。
它帮助我们判断级数是否收敛,简直就是数学界的“神探”!举个例子,假设你在研究级数 (sum_{n=1^{infty frac{1{n^2)。
看似复杂,但借助斯特瓦尔特定理,我们可以用一个简单的函数来替代它。
初几2-斯特瓦尔特定理
证明 设 AD, BE, CF为ABC的高,垂心为H,L、M、N 分别是BC、CA、AB的中点,P、Q、R分别为AH、BH、 CH的中点。
9、四心共线定理: 三角形的外心、垂心、 重心、九点圆圆心共 线;且九点圆圆心在 外心与垂心连线的中 点,重心在外心与垂 心的三分点处。
9、四心共线定理: 三角形的外心、垂 心、重心、九点圆圆 心共线;且九点圆圆 心在外心与垂心连线 的中点,重心在外心 与垂心的三分点处。
定理7 设 AB, CD, EF是交于 ⊙ O内一点M的三条 不同的弦,CF , DE交AB于P, Q两点,则M平分AB 的充要条件是M平分PQ。
8、九点圆定理
定理8
任意三角形三条高的垂 足、三边的中点以及垂 心与 顶点的三条连线的中点 ,这九点共圆。
证明 设 AD, BE, CF为ABC的高,垂心为H,L、M、N 分别是BC、CA、AB的中点,P、Q、R分别为AH、BH、 CH的中点。
6、西姆松定理
定理6 三角形 外一点在三角形外接圆上的充要条 件是该点在三角形三边所在直线上的射影共线。
设ABC外一点P在其三边BC, CA, AB上的射影 分别为L, M , N , 则P, A, B, C四点共圆的充要条 件是L, M , N共线.
设ABC外一点P在其三边BC, CA, AB上的射影 分别为L, M , N, 则P, A, B, C四点共圆的充要条 件是L, M , N共线.
MH NH 3 OH
的充要条件是A 60.
5、张角定理
定理5 设 B, P, C依次分别为从A点引出的三条
射线AB, AP, AC上的点,线段BP, PC对点A的张
角分别为 , ,且 180,则B, P, C共线的
充要条件是
电路分析习题解答(第四章)
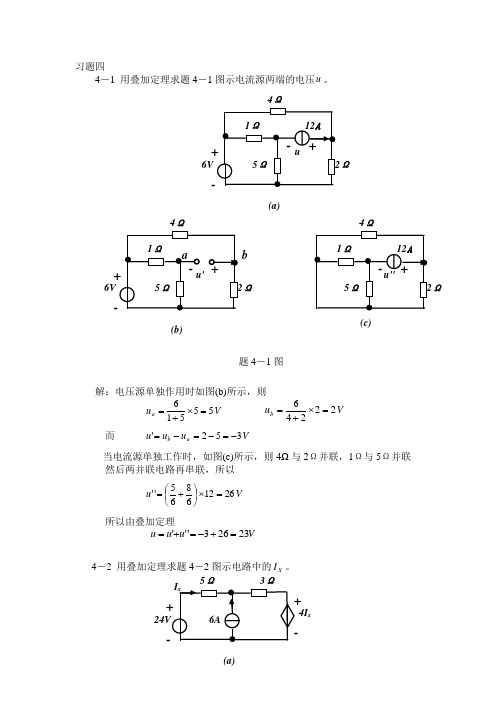
习题四4-1 用叠加定理求题4-1图示电流源两端的电压u 。
解:电压源单独作用时如图(b)所示,则V u a 55516=⨯+= V u b 22246=⨯+=而 V u u u a b 352'-=-=-=当电流源单独工作时,如图(c)所示,则4Ω与2Ω并联,1Ω与5Ω并联然后两并联电路再串联,所以V u 26126865''=⨯⎪⎭⎫⎝⎛+=所以由叠加定理V u u u 23263'''=+-=+=4-2 用叠加定理求题4-2图示电路中的X I 。
题4-1图 6V 4Ω Ω (b)b (c) 4Ω Ω5Ω 3Ω (a)4I x6V 4Ω Ω (a)解:电压源单独作用时的电路如图(b) 所示,则()24435''=++x x I I 解得 A I x 2'=电流源单独作用时的电路如图(c)所示,图中虚线为网孔电流,则 ()0''4''63''5=+++x x x I I I 解得 A I x 5.1''-= 所以 A I I I x x x 5.05.12'''=-=+=4-3 用叠加定理求题4-3图示电路中的独立电压源和独立电流源发出的功率。
5Ω 3Ω '(b) 4I 'x 4I ''x5Ω 3Ω I ''x(c) 题4-2图 题4-3图 2A 4Ω (a) 2V2A 4Ω 2i'(b) + - i''14Ω (c) u''1 2V解:电流源单独作用时的电路如图(b) 所示,则A i 2'1= 0'=i则 V i i u 824''1'1=-=电压源单独作用时的电路如图(b) 所示,则A i 5.042''1-=-= A i i 5.0''1''=-=则 V i u 122''''1=-=所以由叠加定理 A i i i 5.15.02''1'11=-=+=V u u u 918''1'11=+=+=可得电压源和电流源的功率分别为W i P V 3212-=-= W u P A 18212==4-4 题4-4图示电路中,R N 为电阻网络,由两个电流源供电。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 特瓦尔特定理及应用【基础知识】斯特瓦尔特定理 设P 为ABC △的BC 边上任一点(P B ≠,P C ≠),则有 222AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅①或 2222PC BP BP PCAP AB AC BC BC BC BC BC=⋅+⋅-⋅⋅. ② 证明 如图4-1,不失一般性,不妨设90APC <︒∠,则由余弦定理,有 图4-1PCB A2222cos AC AP PC AP PC APC =+-⋅⋅∠, 2222cos(180)AB AP BP AP BP APC =+-⋅⋅︒-∠ 222cos AP BP AP BP APC =++⋅⋅∠.对上述两式分别乘以BP ,PC 后相加整理,得①式或②式.斯特瓦尔特定理的逆定理 设B ,P ,C 依次分别为从A 点引出的三条射线AB ,AP ,AC 上的点,若22AB PC AC BP AP BC BP PC BC ⋅+⋅=⋅+⋅⋅,或 2222PC BP BP PCAP AB AC BC BC BC BC BC=⋅+⋅-⋅⋅, 则B ,P ,C 三点共线. 证明 令1BPA θ=∠,2APC θ=∠,对△ABP 和△APC 分别应用余弦定理,有 22212cos AB AP PB AP PB θ=+-⋅⋅,22222cos AC AP PC AP PC θ=+-⋅⋅.将上述两式分别乘以PC ,BP 后相加,再与已知条件式相比较得 ()122cos cos 0AP BP PC θθ-⋅⋅⋅+=,由此推出12180θθ=︒-,即证.斯特瓦尔特定理的推广 (1)设P 为ABC △的BC 边延长线上任一点,则2222PC BP PC BPAP AB AC BC BC BC BC BC=-⋅+⋅+⋅⋅. ③ (2)设P 为ABC △的BC 边反向延长线上任一点,则 2222PC BP PC BPAP AB AC BC BC BC BC BC=⋅-⋅+⋅⋅.④注 若用有向线段表示,则②,③,④式是一致的.推论1 设P 为等腰ABC △的底边BC 上任一点,则22AP AB BP PC =-⋅. 注 此推论也可视为以A 为圆心,AB 为半径的圆中的圆幂定理. 推论2 设AP 为ABC △的BC 边上的中线,则2222111224AP AB AC BC =+-. 推论3 设AP 为ABC △的A 的内角平分线,则2AP AB AC BP PC =⋅-⋅. 推论4 设AP 为ABC △的A 的外角平分线,则2AP AB AC BP PC =-⋅+⋅. 推论5 在ABC △中,若P 分线段BC 满足BPBCλ=,则 2222(1)(1)AP BC AB AC λλλλ=-+-+⋅.注 若BPk PC =,则()222221111k k AP AB AC BC k k k =⋅+-⋅+++. 【典型例题与基本方法】1.选择恰当的三角形及一边上的一点,是应用斯特瓦尔特定理的关键.例1 如图4-2,凸四边形ABCD 中,60ABC =︒∠,90BAD BCD ==︒∠∠,2AB =,1CD =,对角线AC ,BD 交于点O .求sin AOB ∠. (1996年北京中学生竞赛题)DC BAPO图4-2解 延长BA ,CD 相交于P ,设BC x =,则2PB x =,PC =,对△PBC 及PB 边上的点A ,应用斯特瓦尔特定理,有222AB PACA PC BC AB PA PB PB=⋅+⋅-⋅)()2222222222x x x x x-=⋅+⋅-- 224x x =-+.由Rt Rt ADP CBP △∽△,有PD PC PA PB ⋅=⋅,即)()1222x x -=-⋅,求得4BC x == 于是,215CA =-.又在Rt BCD △中,22120BD x =+=-,从而BD AC ⋅=12=.而()(1242ABCD ABD BCD S S S =+=+△△ 故()112sin 2AOB ⋅∠,即sin AOB =∠为所求. 例2 如图4-3,在ABC △中,60A =︒∠,AB AC >,点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM CN =,求MH NHOH+的值.(2002年全国高中联赛题)L ST图4-3解 延长BE 交O 于L ,由三角形垂心性质,知L 为H 关于AC 的对称点,则LC CH =.设O 的半径为R ,OH d =,CH x =,BH y =,由60CLB A =︒∠=∠,知LH LC CH x ===.延长OH 两端交O 于T ,S ,如图4-3,由相交弦寇理有TH HS BH HL ⋅=⋅,即()()R d R d x y +-=⋅,即22R d xy=+.在△BCL 及边BL 上的点H ,应用斯特瓦尔特定理,并注意到2sin BC R A =⋅=∠ ,可得 222BC LH LC BH LH BH BL CH BL ⋅+⋅=⋅⋅+⋅,即)()()222x x y x y x y x x y ⋅+⋅=⋅⋅++⋅+,亦即 ()22213R x xy y =++. 于是,有()22213x xy y d xy ++=+. 亦即()223x y d -=,即x y d-=而当AB AC >时,MH NH BH BM CN CH BH CH y x x y +=-+-=-=-=-,故x y MH NH OH d-+=2.注意斯特瓦尔特定理的推论的应用 例3 如图4-4,自O 外一点引圆的两条切线PE ,PF ,E ,F 为切点,过P 点任意引圆的割线交O于A ,B ,交EF 于C .证明:211PC PA PB=+. (2001年湖南中学生夏令营试题)CBAEFP图4-4证明 由相交弦定理,有EC CF AC CB ⋅=⋅.由于PE PF =,对等腰△PEF 及底边EF 上的点C ,应用斯特瓦尔特定理的推论1,有22PC PE =- EC CF ⋅,即有222PE PC EC CF PC AC CB =+⋅=+⋅ ()()2PC PC PA PB PC =+-⋅-22PC PC PA PB PC PB PC PA =--⋅+⋅+⋅PA PC PB PC PA PB =⋅+⋅-⋅.而2PE PA PB =⋅,从而2PA PB PA PC PB PC ⋅=⋅+⋅.故211PC PA PB=+. 注 此例结论表示线段PC 是线段PA ,PB 的调和平均.这个结论亦即为点P 、C 调和分割弦AB . 例 4 如图4-5,设在ABC △中,AB AC >,AE 平分A ∠,且交BC 于E ,在BC 上有一点S ,使BS EC =.求证:()222AS AE AB AC -=-.(1979年江苏省竞赛题)CB ASE 图4-5证明 对ABC △及边BC 上的点S ,应用斯特瓦尔特定理,有222SC BSAS AB AC BS SC BC BC=⋅+⋅-⋅. 由AE 平分A ∠,对ABC △及边BC 上的点F ,应用斯特瓦尔特定理的推论3,有2AE AB AC =⋅- BE EC ⋅,从而2222SC BSAS AE AB AC AB AC BE EC BS SC BC BC-=⋅+⋅-⋅+⋅-⋅. ①因BS EC =,有BE SC =,即BE EC BS SC ⋅=⋅. 由角平分线的性质,有 ,BE AB EC ACBC AB AC BC AB AC==++, 即,SC BE AB BS EC ACBC BC AB AC BC BC AB AC====++. 从而,由①式,有()222AS AE AB AC -=-.例5 凸多边形ABCD 外切于O ,两组对边所在的直线分别交于点E 、F ,对角线交于点G .求证:DG EF ⊥.(《中等数学》奥林匹克题高中251题) 证明 如图4-6,设O 与边AB 、BC 、CD 、DA 分别切于点M 、N 、R 、S ,则由牛顿定理知,AC 、BD 、MR 、NS 四线共点于G .由切线长定理,知EM ER =.G SOM NRFEDC BA图4-6由推论1,有22EG FS MG GR =-⋅. ① 同理,22FG FS SG GN =-⋅.②联结MO 、EO 、SO ,令O 的半径为r ,则 22222EM OE r FS OF r =-=-,.③ 又由相交弦定理,有MG GR SG GN ⋅=⋅.④于是,由①、②、③、④有2222EG ED FG FO -=-. 由定差幂线定理,知OG EF ⊥.注 (1)牛顿定理 圆外切四边形的两条对角线、两对边切点的连线,这4条直线共点.(2)定差幂线定理 设MN 、PQ 是两条线段,则MN PQ ⊥的充要条件为2222PM PN QM QN -=-. 此定理可用勾股定理及逆定理证明.这个定理放到空间也是成立的.运用向量法可给出平面、空间的统一证明如下:由22222222PM QN PN QM PM QN PN QM +--=+-- ()()2222PM PN PQPN PM PQ =+----22222222PM PN PQ PN PQ PM PQ PM PQ PN =++-⋅--+⋅-()2222PM PQ PN PQ PM PN PQ NM PQ =⋅-⋅=-⋅=⋅. 知 0NM PQ NM PQ ⇔⋅=⊥.故 2222MN PQ PM PN OM QN ⇔-=-⊥.例6 已知E 、F 分剔是ABC △的边AB 、AC 的中点,CM 、BN 是边AB 、AC 上的高,联结EF 、MN 交于点P .又设Q 、H 分别是ABC △的外心、垂心,联结AP 、OH .求证:AP OH ⊥.(2005年国家队集训题)证明 如图4-7,联结AO 、AH .设1O 、1H 分别为AO 、AH 的中点,则112H N AH =,112H M AM =,即知点1H 在线段MN 的中重线上,应用推论1,有B图4-72211H P H M MP PN =-⋅.注意到EF 为ABC △中位线,O 在BC 的中垂线上,由此知1O 也在EF 的中垂线上,应用推论1,有 2211O P O E EP PF =-⋅.再注意到ANM ABC AEF ==∠∠∠,知M 、E 、N 、F 四点共圆,并由直角三角形性质,有MP PF EP PF ⋅=⋅. ③ 及11O E O A =、11H M H A =.④由①、②、③、④得22221111H A H P O A O P -=-.由定差幂线定理,11O H AP ⊥. 而1O H OH ∥,故AP OH ⊥.注 此例的其他证法可参见第九章例16、第十章例15.例7 设D 是ABC △的边BC 上一点,满足CDA CAB △∽△,O 经过B 、D 两点,并分别与AB 、AD 交于E 、F 两点,BF 、DE 交于点G ,联结AO 、AG ,取AG 的中点M .求证:CM AO ⊥. 证明 如图4-8,在AG 的延长线上取点P ,使得AG AP AF AD ⋅=⋅(即G 、P 、D 、F 四点共圆),则由AE AB AF AD ⋅=⋅知E 、B 、P 、G 也四点共圆.于是180180BPA BED BFD =︒-=︒-=∠∠∠BFA ∠,知B 、P 、F 、A 四点共圆,即有2FG GB AG GP AF AD AG ⋅=⋅=⋅-.C图4-8联结OD 、OF 、OE ,并令O 半径为R ,则对ODE △、ODF △分别应用推论1,有 222OG OD EG GD R FG GB =-⋅=-⋅.① 2222OA OD AF AD R FG GB AG =+⋅=+⋅+.②联结OM ,由三角形中线长公式,并注意①、②,有222222211(22)44MO MA OA OG AG AG R -=+--=.③联结OB 、OC ,对OBD △应用推论1,有222CO OB CD CB R CD CB =+⋅=+⋅. 又由CDA CAB △∽△,有2CA CD CB =⋅,即有222CO CA R -=.④注 P 即为完全四边形的密克尔点,由③、④有2222MO MA CO CA -=-.由定差幂线定理,知CM ⊥AO .3.注意斯特瓦尔特定理等价于托勒密定理 斯特瓦尔特定理可推导出托勒密定理.证明 如图4-9,在ABC △中,点P 在BC 上,由斯特瓦尔特定理,有CBAEP图4-9222AP BC AB PC AC BP BP PC BC ⋅=⋅+⋅-⋅⋅.延长AP 交ABC △的外接圆于E ,连BE ,EC ,由ABP CEP △∽△和ACP BEP △∽△,有AB AP ⋅= CE AP ⋅,AC BP AP BE ⋅=⋅.又由相交弦定理,有BP PC AP PE ⋅=⋅.于是,得2AP BC AB CE AP AC AP BE AP PE BC ⋅=⋅⋅+⋅⋅-⋅⋅, 即 ()BC AP PE AB CE AC BE +=⋅+⋅,亦即 AB CE AC BE BC AE ⋅+⋅=⋅.即为托勒密定理.由托勒密定理也可推导斯特瓦尔特定理.证明 如图4-10,设圆内接四边形ABEC 的对角线AE ,BC 交于P .由托勒密定理,有CBAEP 图4-10AB EC AC BE BC AE ⋅+⋅=⋅.即 ()AB EC AC BE BP PC AE ⋅+⋅=+⋅.由△ABP ∽△CEP 和△ACP ∽△BEP ,有AB PC EC AP ⋅=,AC BPBE AP⋅=.由相交弦定理,有BP PCPE AP⋅=.将这些式子代入前述式子即得斯特瓦尔特定理. 因此,在应用中,两个定理的应用范围相同,所显示的功能也一样,即凡能用托勒密定理处理的问题也能用斯特瓦尔特定理处理.反之亦然.例8 若ABC △的三边为连续整数,且最大角B ∠是最小角A ∠的两倍,求三角形的三边长.(IMO -10试题)解法1 作ABC ∠的平分线BD (图略),则BD AD =,令AD y =,AB x =,则 1AC x =+,1BC x =-,1CD x y =+-. 由斯特瓦尔特定理的推论3,有()()211y x x y x y =--+-,即()11x x y x -=+,又AB AD BC CD =,即1xx =-1yx y +-,有()121x x y x +=-.故由22121x x x xx x -+=+-,求得5x =(舍去0x =),即5AB =,4BC =,6AC =. 解法2 作ABC △的外接圆O ,取AC 的中点D ,连AD ,BD ,CD ,则ABCD 为梯形,其中CD BA ∥.令AB x =,则1AC x =+,1BC x =-,且1CD BC x ==-,1BD AC x ==+.对四边形ABCD 应用托勒密定理,有()()()22111x x x x +=-+-,求得5x =.(下略) 【解题思维策略分析】1.获得线段倍分关系的一条途径例9 如图4-11,已知ABC △的外接圆k 的圆心为O ,半径为R ,内切圆的圆心为I ,半径为r ,另一个圆0k 与边CA ,CB 分别切于点D ,E ,且与圆k 内切.求证:内心I 是线段DE 的中点.(IMO -34预选题)A图4-11证明 设圆0k 的圆心为1O ,半径为ρ,于是1O ,I ,C 三点共线,且1sin 2r CI C =∠,11sin 2CO C ρ=∠,则11sin 2rIO C ρ-=∠,且1O E ρ=.于是,111IO r rCO ρρρ-==-. 连OC ,OI ,1O O ,对△1COO ,及边1O C 上的点I ,应用斯特瓦尔特定理,有 22211111OO CI OC IO OI CO CI IO CO ⋅+⋅=⋅+⋅⋅①注意到欧拉公式,222OI R Rr =-,及1OO R ρ=-,OC R =,并将其代入①式,得到()2211sin sin 22r rR R C C ρρ--⋅+⋅∠∠ ()221111sin sin sin sin 2222r r R Rr C C C C ρρρ-=-⋅+⋅⋅∠∠∠∠, 化简得 21sin 12r rC ρρρ-==-∠.从而 221111sin 2IO C CO CO ρ⎛⎫== ⎪ ⎪⎝⎭∠, 即 22111IO CO O E ρ⋅==.②因为1O E CE ⊥,1CO DE ⊥且平分DE ,令DE 的中点为I ',由射影定理,有 2111I O CO O E '⋅=.③比较③式和②式,知I '与I 重合,即得I 为DE 的中点.例10 如图4-12,两个大圆A ,B 相等且相交;两个小圆C ,D 不相等但相交,且交点为P ,Q .若C ,D 既同时与A 内切,又同时与B 外切.试证:直线PQ 平分线段AB .(《中等数学》奥林匹克问题高中58题)图4-12证明 由于C ,D 半径不相等,此两圆交点所在直线PQ 必与线段AB 相交,设交点为M .连AC ,MC ,BC ,AD ,MD ,BD ,PC ,PD ,CD ,显然PQ CD ⊥,设垂足为N ,又设A ,B 的半径均是ρ,C ,D 的半径分别为R ,()r R r ≠,则易得AC R ρ=-,BC R ρ=+,AD r ρ=-,BD r ρ=+,因为PQ CD ⊥,或MP CD ⊥,垂足为N ,则 ()()2222222MC MD CN NM MN ND -+-+=22CN ND =-2222()()PC PN PD PN =---2222PC PD R r =-=-.设AM x =,MB y =,对△CAB 及边AB 上的点M ,应用斯特瓦尔特定理,有 ()()22x BC y AC x y MC x y x y ⋅+⋅=+⋅++⋅ ()222x y MC x MB y AM =+⋅+⋅+⋅.①对△DAB 及边AB 上的点M ,应用斯特瓦尔特定理,有 ()22222x BD y AD x y MD x MB y AM ⋅+⋅=+⋅+⋅+⋅.②①-②,得()()()()()()22222222x BC BD y AC AD x y MC MD x y R r ⋅-+-=+-=+-,即 ()()()()()()222222[][]x R r y R r x y R r ρρρρ⋅+-++⋅---=+-, 亦即 ()()20x y R r ρ⋅-⋅-=.因0ρ≠,R r ≠,从而0x y -=,即x y =. 故AM MB =,即直线PQ 平分线段AB .2.求解三角形问题的一种工具斯特瓦尔特定理在求解三角形中有关线段的问题有着重要作用,这可从习题A 中的第6题,习题B 中的第7题等可以看出.在求解三角形的其他问题中,它也有着重要作用.例11 设ABC △的三边为a ,b ,c ,其面积为S,则222a b c ++≥,当且仅当ABC △为正三角形时,等式成立. (IMO -3试题) 证明 取BC 的中点D ,对ABC △及BC 边上的点D ,应用斯特瓦尔特定理的推论2, 有 2222222111111224224AD AC AB BC b c a =+-=+-.从而有22222322a b c AD a AD a ++=+=⋅≥.设ABC △的BC 边上的高为h ,则AD h ≥,于是122AD a a h ⋅⋅⋅=≥.故222a b c ++≥,其中等号当且仅当22322AD a =且AD h =时成立,也即AD BC ⊥且AD =,此时ABC △恰为正三角形.例12 如图4-13,在ABC △中,D ,E 分别为AC 和AB 同方向延长线上的点,BD 与CE 相交于P ,且BD CE =.当P 在BC 边的中线上时,则AB AC =.EDC B APQ图4-13证明 设AP 交BC 于Q .分别对△BPQ 及点A 和△CPQ 及点A 应用斯特瓦尔特定理的推广结论,有222AQ APBA BP BQ AP AQ PQ PQ =-⋅+⋅+⋅, 222AQ APCA CP CQ AP AQ PQ PQ=-⋅+⋅+⋅. 于是()()222222AQ APBA CA CP BP BQ CQ PQ PQ-=-⋅+-⋅. 由于BD CE =,对△PBC 及点A 应用塞瓦定理,有1QB EC DP QC EP DB ⋅⋅=,即PD QCPE QB=. 当P 点在BC 边上的中线上时,有BQ QC =.从而PD PE =,由此知PC PB =,故AB AC =.例13 如图4-14,若D 是ABC △的边BC 延长线上一点,则AD 平分A ∠的外角的充分必要条件是2AD BD CD AB AC =⋅-⋅.DCBAF图4-14证明 必要性:若AD 平分A ∠的外角,则由推论4即有 2AD BD CD AB AC =⋅-⋅.或者按证明斯特瓦尔特定理的方法来推导.充分性:设直线AD 交ABC △的外接圆于E ,连BE 、CE .由割线定理有BD CD AD ED ⋅=⋅,并将其代入条件式2AD BD CD AB AC =⋅-⋅可得 ()AD ED AD AB AC -=⋅.由此可知E 必在DA 的延长线上(因0ED AD ->). 于是AD AE AB AC ⋅=⋅. ① 由△ACD ∽△BCD ,有AC BD AD BE ⋅=⋅. ② 由①⨯②得 AE BD AB BE ⋅=⋅. ③ 又由△ECD ∽△BAD ,有EC AD CD AB ⋅=⋅. ④ 由①÷④得,AE CD AC CE ⋅=⋅. ⑤由③-⑤得,AE BC AB BE AC CE ⋅=⋅-⋅. 对四边形EBCA 应用托勒密定理,有 AE BC AB CE AC BE ⋅=⋅-⋅.于是AB CE AC BE AB BE AC CE ⋅-⋅=⋅-⋅. 即()()0AB AC CE BE +-=,从而CE BE =.因此CAD EBC ECB EAB ===∠∠∠∠. 故AD 平分A ∠的外角. 例14 如图4-15,设正ABC △的内切圆圆心为I ,半径为r ,在I 内任取一点P ,设点P 到BC ,CA ,AB 的距离分别为1d ,2d ,3d(《数学通报》问题1356题)I d 3d 2d 1D CBAP图4-15证明 设正三角形ABC 的边长为1,则123d d d ++2IA IB IC r ====. 连AP 并延长交BC 于D ,则由题设知 32APB APC S d BD DC S d ==△△, ()1123131BPC BAC BPC S d d DP PA S S d d d d d d ===-+++-△△△. 由于BI IC =,BA AC =,对△BIC 及边BC 上的点D ,对ABC △及边BC 上的点D ,均应用斯特瓦尔特定理的推论1,有2222ID IB BD DC AD AB BD DC =-⋅=-⋅,.又由32d BD DC d =,知332323d d BD BC d d d d =⋅=++,223d DC d d =+. 于是()22322313d d ID d d =-+,()2232231d d AD d d =-+. ①又对△AID 及边AD 上的点P 应用斯特瓦尔特定理,有 222PA DPIP ID IA DP PA AD AD=⋅+⋅-⋅.由123d DP PA d d =+,知23123d d PA AD d d d +=++,1123d DPAD d d d =++.将上述各式及①式代入②式,并注意IA,123d d d ++=123444d d d =+,有 222DP PAIP IA ID DP PA AD AD=⋅+⋅-⋅ ()2232312133123231133d d d d d DP PAAD d d d d d d AD ADd d ⎡⎤+⎢⎥=⋅+-⋅-⋅⋅+++++⎢⎥⎣⎦ ()()()12312323232212323122123231113d d d d d d d d d d d d d d d d d d d d d d d ⎡⎤+++⎢⎥=⋅-⋅-⋅-++++++++⎢⎥⎣⎦()()2312312323414333d d d d d d d d d -=-+-+ ()()()23112323414333d d d d d d d d =-+-+ ()1213231433d d d d d d =-++. 即 ()21213231143IP d d d d d d ⎡⎤=-++⎣⎦. 于是,()2221231213232d d d d d d d d d ---+++ ()()21231213234d d d d d d d d d =-+++++()()22231334IP r IP =-+-=-.此式可写成为=()223r IP -. ③由于P 点在I 内部,则220r IP ->,从而,必有0-0>0>.如若不然,0<,0,则0+<,即0<与已知矛盾,则知>++可见,以,,为边可以构成三角形,且由海伦—秦九韶公式及③式知其面积为 【模拟实战】习题A1.在ABC △中,2AB AC ==,BC 边有100个不同的点1P ,2P ,…,100P ,记22i i i m AP BP PC =+⋅(i =1,2,…,100),求12100m m m +++…的值.2.在ABC △中,C ∠的平分线交AB 于D.证明:CD <.(匈牙利中学生数学竞赛题) 3.在ABC △中,D 是BC 边上的点,已知13AB =,12AD =,15AC =,5BD =,求DC . 4.在ABC △中,AB =AC 2BC =,设P 为BC 边上任一点,则( ) A .2PA PB PC <⋅B .2PA PB PC =⋅C .2PA PB PC >⋅D .2PA 与PB PC ⋅的大小关系不确定5.D 是ABC △的边AC 上的一点,且21AD DC =∶∶,45C =︒∠,60ADB =︒∠,求证:AB 是△BCD 的外接圆的切线.6.设ABC △的三边BC a =,CA b =,AB c =,()12p a b c =++.设a m ,a h 分别为BC 边上的中线长和高线长;a t ,at '分别为BC 边所对的角的内、外角平分线长.求证下列各式:(Ⅰ)a m(Ⅱ)a t(Ⅲ)a t '=(Ⅳ)a h 7.在ABC △中,2AB BC =,2B A =∠∠,求证:ABC △是直角三角形. 8.证明:到三角形三顶点的距离的平方和最小的点是重心.习题B1.设,,分别是共线的三点A ,B ,C 对于O 所作切线的长.求证:a BC ⋅+c AB b AC BC AC AB ⋅-⋅=⋅⋅.2.锐角ABC △的外接圆过B ,C 的切线相交于N ,点M 是BC 的中点.求证:BAM =∠ CAN ∠.(IMO -26预选题) 3.1PT 和2PT 是O 的割线,分别交O 于1S ,2S ,且12PT PT =,过P 的直线交O 于Q ,R (Q 在R 与P 之间),交12TT ,12S S 于T ,S .求证1111PQ PR PS PT+=+. 4.A ,B ,C ,D 四点在同一圆周上,且4BC DC ==,6AE =,线段BE 和DE 的长都是整数,求BD 的长.5.在正方形ABCD 中,E 在BC 上,2BE =,1CE =,P 点在BD 上,则PE 和PC 的长度之和最小可达到多少?6.设凸四边形的边长是a ,b ,c ,d ,对角线长是e 和f .求证:2min{,,,}a b c d 当且仅当这个凸四边形是菱形时等号成立.7.设I ,O ,G ,H 分别为ABC △的内心,外心,重心,垂心,令BC a =,CA b =,AB c =,()12p a b c =++,R ,r 分别为外接圆和内切圆的半径.求证下列各式: (Ⅰ)222a IA b IB c IC abc ⋅+⋅+⋅=; (Ⅱ)2222abcIO R R Rr a b c=-=-++;(Ⅲ)()()()()22222222221222918IG a b c b c a c a b a b c abc p ⎡⎤=+++++-++-⎣⎦()2222254318p a b c Rr =-++-;(Ⅳ)()22222142IH R a b c abc p=-+++. 8.已知ABC △满足2ACB ABC =∠∠,设D 是BC 边上一点,且2CD BD =.延长线段AD 至E ,使AD DE =.证明:1802ECB EBC +︒=∠∠.(IMO -39预选题) 第四章 斯特瓦尔特定理应用答案习题A1.因AB AC =,由斯特瓦特定理推论1,有22i i i AP AB BP PC =-⋅,则22i i i AP BP PC AB +⋅=,即224i i i im AP BP PC AB =+⋅==,即121004100400m m m ++=⋅=….2.由CD 平分ACB ∠,由斯特瓦特定理推论3,知2CD CA CB AD DB CA CB =⋅-⋅<⋅,故CD <3.由斯特瓦尔特定理,有222CD BDAD AB AC BD DC BC BC=⋅+⋅-⋅.设DC x =,则5BC x =+,则2225121315555x x x x=⋅+⋅-++,解得19x =(舍去29x =-).4.由斯特瓦尔特定理,有222222PC PB PC PBPA AB AC PB BC PB BC BC =⋅+⋅-⋅=⋅+⋅-⋅4PC PC PB PB PC =+-⋅,242PA PB PC PC PB PB PC ∴-⋅=+-⋅,又2PB PC =-,则2PA PB -⋅22115422(2)222(2)2()048PC PC PC PC PC PC PC PC PC =+---⋅=-+=+=-+>,故选(C ). 5.由21AD DC =∶∶,由斯特瓦尔特定理推论5,有2222122359BD AB BC AC =+-.由45C ∠=︒,60ADB ∠=︒,及sin sin BD BCC BDC =∠∠,有2232BD BC =. 又由21AD DC =∶∶,有232AC AD AC =⋅.于是有2AB AD AC =⋅,由切割线定理即证.6.设P 为ABC △的BC 所在直线上任一点,且1BP BC λ=∶∶,有斯特瓦尔特定理推论5,有2222(1)(1)AP λλa λb λc =-++-. 12λ=时,a AP m =即得(Ⅰ); 当cλb c =+时,a AP t =,即得(Ⅱ)当1λb c =-时,a AP t '=,即得(Ⅲ);当22222a b c λa-+=时,a AP h =,即得(Ⅳ). 7.作B ∠的平分线交AC 于D ,则2AD ABDC BC==,对ABC 及AC 边上点D 应用斯特瓦尔特定理推论3,有2BD AB BC AD DC =⋅-⋅,即222(2)22DC BC DC =-,即2213DC BC =,又2222()93AC AD DC DC BD =+==,从而22224AC BC BC AB +==,故ABC △为直角三角形.8.设G 为三条中线AD ,BE ,CF 的交点,P 为ABC △所在平面上任一点.不妨设P 在ABC △内,连PA ,PB ,PC ,PD ,PG ,对APD △及点G 应用斯特瓦尔特定理,有 222PA DG PD AG PG AD AG GD AD ⋅+⋅=⋅+⋅⋅.由12DG AG =,32AD AG =,则22223322PG PA PD AG =+=. ①在PBC △和GBC △中,D 为BC 中点,应用斯特瓦尔特定理推论2,则2222111224PD PB PC BC =+-,2222111224GD GB GC BC =+-,此两式相减,并注意12GD AG =,222222111()()224PD PB PC GB GC AG =+-++,代入①式,得2222223()()PG PA PB PC GA GB GC =++-++.显然,当P 异于G 时,横有222222PA PB PC GA GB GC ++>++.故到三角形三顶点距离的平方和为最小的点是三角形的重心. 习题B1.设O ⊙的半径为r ,连OA ,OB ,OC ,对OAC △及AC 边上的点B ,应用斯特瓦尔特定理,有222OA BC OC AB OB AC AB BC AC ⋅+⋅=⋅+⋅⋅,而22OA r α=+,22OB r b =+,22OC r c =+,于是 222()()()r a BC r c AB r b AC AB BC AC +⋅++⋅=+⋅+⋅⋅,化简即得结论.2.对ABC △及BC 边上的点M ,应用斯特瓦尔定理推论1,有22221(22)4AM AB AC BC =+-,cos 2cos BM BC BN A A==∠∠.又2222222cos 4cos BC AN AB BN AB BN ABN AB A =+-⋅⋅∠=+∠ cos (cos cos )cos C AB BC ABN C A ∠+⋅⋅∠=-∠∠,于是222221cos cos 4AN A AB A BC ⋅∠=⋅∠++cos cos AB BC C A ⋅⋅∠⋅∠而cos cos cos()sin sin sin sin sin A C A C A C A C B ∠⋅∠=∠+∠+∠⋅∠=∠⋅∠-∠,则222222221cos cos sin sin cos (cos sin )4AN A AB A BC AB BC A C AB BC A AB A A ⋅∠=⋅∠++⋅⋅∠⋅∠-⋅⋅∠=⋅∠+∠22222222111()(22)424BC AB BC AC AB AC BC AM +-⋅+-=+-⋅(其中sin sin BC C AB A ⋅∠=⋅∠),即cos AM CM A AN CN =∠=,sin(180)sin AN A C CN CAN ︒-∠-∠=∠,又BM CM =,且sin sin AM BBM BAM ∠=∠,故sin sin BAM CAN ∠=∠,即证. 另证:设AN 交圆于D ,连BD ,CD ,对四边形ABCD 应用托勒密定理,有AD BC AC BD AB CD ⋅=⋅+⋅,由ACN CDN △∽△,ABN BDM △∽△,有AC AN CD CN =,AB ANBD BN=,而BN CN =,则AC BD AB ⋅=⋅ CD .注意到2BD BM =,有22AD BM AB CD ⋅=⋅,即AD ABCD BM=,又ABM ADC ∠=∠,从而ADC ABM △∽△,故NAC BAM ∠=∠.3.由12PT PT =及1122PT PS PT PS ⋅=⋅,有12PS PS =,从而1212TT S S ∥,即11PS PT PS PT=,而 11PT PS PQ PQ ⋅=⋅3,则21PSPS PQ PR PT=⋅⋅,对12S PS △及12S S 边上的点S 应用斯特瓦尔特定理推论1,有22112PS PS S S SS =-⋅,又在O ⊙中12()()S S SS RS SQ PR PS PS PQ ⋅=⋅=--,故2()()PSPS PQ PR PR PS PS PQ PT=⋅⋅---,故1111PQ PR PS PT +=+. 4.对ABCD △及BD 边上的点E ,应用斯特瓦尔特定理或其推论1,有22244BE DECE BD BD=⋅+⋅-161616166BE DEBE DE BE DE BE DE AE CE CE BD+⋅=⋅-⋅=-⋅=-⋅=-.解得2CE =(负值舍去). 于是12BE DE CE AE ⋅=⋅=,而8BD BC CD <+=,即3BE =,4DE =或4BE =,3DE =,故7BD =. 5.由2BE CE =∶,对BCP △及BC 边上的点E ,应用斯特瓦尔特定理的推论5,有22212233PE PB PC =+-.对BCD △及BD 边上点P 应用推论1,有2229PC BC BP PD PB =-⋅=+-,于是224PE PB =-+,故PE PC +.令PB x =,上式表示x 轴上动点(,0)Q x 到两定点A ,,B 的距离之和,当Q 为线段AB 与x 轴交点,0)时,即PB 时,PE PC + 6.设凸四边形ABCD 的对角线交点为E .令AB a =,BC b =,CE c =DA d =,AC e =,BD f =,AE g =,BE h =,CE k =,DE l =.不妨设h l ≤,则在ABC △中,有{}2222min ,a k bga b kg h k g+≤=++(斯特瓦尔特定理)22221()()()224k g h l e f ++≤+=+,于是{}{}2min ,,,2min ,a b c d a b ≤=,当且仅当a b =,g k =,h l =, {}{}min ,min ,a b c d ≤时等号成立,即ABCD 为菱形.7.由于四个结论都与内心I 有关,不妨设AD 平分A ∠交BC 于D ,显然I 在AD 上.设P 为ABC △所在平面内任一点,连PB ,PD ,PC ,PI ,注意到ac BD b c =+,abCD b c =+,对PBC △及边上点D 应用斯特瓦尔特定理,有22222()b c a bc PD PB PC b c b c b c =⋅+⋅-+++. 又AI c b b cID BD CD a+===,有2b c AI AD p +=,2a ID AD p =,而224()()bcp AD p a b c =-+,对PAD △及AD 边上点I 应用斯特瓦尔特定理,有222()22()b c a abc p a PI PD PA p p p b c +-=⋅+⋅-+.将2PD 表达式代入上式,得2222a PAb PBc PC abcPI a b c⋅+⋅+⋅-=++.(Ⅰ)当P 与I 重合时,由①式即证(Ⅱ)当P 为外心O 时,PA PB PC R ==+,由①式即证.(Ⅲ)当P 为中心G 时,2222241(22)99a PA GA mbc a ===+-,等等.由①式即证、(Ⅳ)当P 为垂心H 时,22222222cot (csc 1)4PA HA a A a A R a ==⋅∠=∠-=-,等等.由①式即证.8.设CD 的中点为H ,则ABEH 是平行四边形,延长BC 至G ,使CG CA =.设3aBD DH HC ===,CA b =,AB c =,BE AH x ==,AD DE y ==,CE z =.由2ABC ACB CGA ∠=∠=∠+22CAG CGA CAG ∠=∠=∠,则ABG CAG △∽△.于是有AB CABG AG=或2()c b a b =+. ① 在ACD △,ABH △,CDE △中分别应用斯特瓦尔特定理推论2,得2222229b y x a +=+,2222229x c y a +=+,2222229y z c a +=+.从前两式中消去y ,有222222243x c b x a ++=+,将①式代入得22()()33a x b a b =+-.再求得23z b a =+,故有2()x z z a =-或2()BE CE CE BC CE EP =-=⋅.这里P 是CE 上一点,且满足CP BC =.故BE EPCE BE=,又BEP CEB ∠=∠,知BEP CEB △∽△,从而 1(180)2ECB EBP EBC ECB ∠=∠=∠-︒-∠.故1802ECB EBC ∠+︒=∠.。
