苏教版七年级上册数学期末提优训练
苏教版七年级上册数学 期末试卷培优测试卷
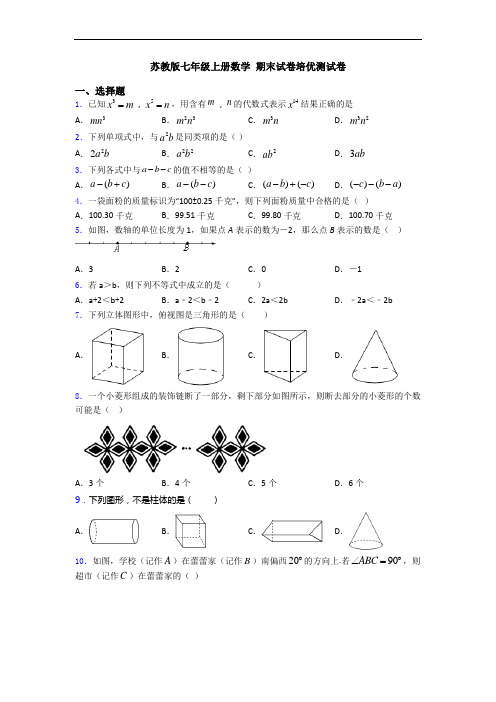
苏教版七年级上册数学 期末试卷培优测试卷一、选择题1.已知3x m =,5x n =,用含有m ,n 的代数式表示14x 结果正确的是A .3mnB .23m nC .3m nD .32m n 2.下列单项式中,与2a b 是同类项的是( ) A .22a b B .22a b C .2abD .3ab 3.下列各式中与a b c --的值不相等的是( )A .()a b c -+B .()a b c --C .()()a b c -+-D .()()c b a --- 4.一袋面粉的质量标识为“100±0.25千克”,则下列面粉质量中合格的是( ) A .100.30千克B .99.51千克C .99.80千克D .100.70千克5.如图,数轴的单位长度为1,如果点A 表示的数为-2,那么点B 表示的数是( )A .3B .2C .0D .-1 6.若a >b ,则下列不等式中成立的是( ) A .a +2<b +2B .a ﹣2<b ﹣2C .2a <2bD .﹣2a <﹣2b7.下列立体图形中,俯视图是三角形的是( )A .B .C .D .8.一个小菱形组成的装饰链断了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )A .3个B .4个C .5个D .6个9.下列图形,不是柱体的是( ) A .B .C .D .10.如图,学校(记作A )在蕾蕾家(记作B )南偏西20︒的方向上.若90ABC ∠=︒,则超市(记作C )在蕾蕾家的( )A .北偏东20︒的方向上B .北偏东70︒的方向上C .南偏东20︒的方向上D .南偏东70︒的方向上11.我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x 人,依题意列方程得( ) A .()31003xx +-=100 B .10033xx -+ =100 C .()31001003xx --= D .10031003xx --= 12.若x ,y 满足等式x 2﹣2x =2y ﹣y 2,且xy =12,则式子x 2+2xy +y 2﹣2(x +y )+2019的值为( ) A .2018B .2019C .2020D .202113.3-的倒数是( ) A .3 B .13C .13-D .3-14.将方程21101136x x ++-=去分母,得( ) A .2(2x +1)﹣10x +1=6 B .2(2x +1)﹣10x ﹣1=1 C .2(2x +1)﹣(10x +1)=6D .2(2x +1)﹣10x +1=115.如图,是一个正方体的展开图则“数”字的对面的字是( )A .核B .心C .素D .养二、填空题16.比较大小:π1-+ _________3-(填“<”或“=”或“>”).17.要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是_____. 18.单项式213-xy 的次数是_______________. 19.如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ;OF 平分∠COE ,若∠AOC =82°,则∠BOF =______°.20.如图,直线//,1125∠=︒a b ,则2∠=_____________度21.用一副三角尺可以直接得到或可以拼出的锐角的个数总共有___________个.22.单项式23x y-的系数是____.23.科学家们测得光在水中的速度约为225000000米/秒,数字225000000用科学计数法表示为___________.24.点A 、B 、C 在直线l 上,若3BC AC =,则ACAB=__________. 25.若关于x 的方程1322020x x b +=+的解是2x =,则关于y 的方程1(1)32(1)2020y y b -+=-+的解是__________. 三、解答题26.如图,已知BD 平分∠ABC ,点F 在AB 上,点G 在AC 上,连接FG 、FC ,FC 与BD 相交于点H ,如果∠GFH 与∠BHC 互补,那么∠1=∠2吗?请说明理由.27.如图,OC 是AOB ∠内的一条射线,OD 、OE 分别平分AOB ∠、AOC ∠.(1)若80BOC ∠=︒,40AOC ∠=︒,求DOE ∠的度数;(2)若BOC α∠=,50AOC ∠=︒,求DOE ∠的度数;(3)若BOC α∠=,AOC β∠=,试猜想DOE ∠与α、β的数量关系并说明理由. 28.在如图所示的方格纸上作图并标上相应的字母.(1)过点P 画线段AB 的平行线a ; (2)过点P 画线段AB 的垂线,垂足为H ; (3)点A 到线段PH 的距离即线段 的长.29.如图,已知点A 、B 、C 是数轴上三点,O 为原点,点A 表示的数为-12,点B 表示的数为8,点C 为线段AB 的中点.(1)数轴上点C 表示的数是 ;(2)点P 从点A 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时,点Q 从点B 出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当P 、Q 相遇时,两点都停止运动,设运动时间为t (t >0)秒. ①当t 为何值时,点O 恰好是PQ 的中点;②当t 为何值时,点P 、Q 、C 三个点中恰好有一个点是以另外两个点为端点的线段的三等分点(三等分点是把一条线段平均分成三等分的点).(直接写出结果) 30.如图,点P 是∠AOB 的边OB 上的一点 (1)过点P 画OA 的平行线PQ (2)过点P 画OA 的垂线,垂足为H (3)过点P 画OB 的垂线,交OA 于点C(4)线段PH 的长度是点P 到______的距离,______是点C 到直线OB 的距离. (5)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC .PH 、OC 这三条线段大小关系是______(用“<“号连接).31.一项工程由甲单独做需12天完成,由乙单独做需8天完成,若两人合作3天后,剩下部分由乙单独完成,乙还需做多少天? 32.解方程; (1)3(x +1)﹣6=0(2)1132x x +-= 33.解方程:(1)523(2)x x -=--(2)321143x x ---= 四、压轴题34.(阅读理解)如果点M ,N 在数轴上分别表示实数m ,n ,在数轴上M ,N 两点之间的距离表示为MN m n(m n)=->或MN n m(n m)=->或m n -.利用数形结合思想解决下列问题:已知数轴上点A 与点B 的距离为12个单位长度,点A 在原点的左侧,到原点的距离为24个单位长度,点B 在点A 的右侧,点C 表示的数与点B 表示的数互为相反数,动点P 从A 出发,以每秒2个单位的速度向终点C 移动,设移动时间为t 秒.()1点A 表示的数为______,点B 表示的数为______.()2用含t 的代数式表示P 到点A 和点C 的距离:PA =______,PC =______.()3当点P 运动到B 点时,点Q 从A 点出发,以每秒4个单位的速度向C 点运动,Q 点到达C 点后,立即以同样的速度返回,运动到终点A ,在点Q 开始运动后,P 、Q 两点之间的距离能否为2个单位?如果能,请求出此时点P 表示的数;如果不能,请说明理由.35.如图,数轴上点A ,B 表示的有理数分别为6-,3,点P 是射线AB 上的一个动点(不与点A ,B 重合),M 是线段AP 靠近点A 的三等分点,N 是线段BP 靠近点B 的三等分点.(1)若点P 表示的有理数是0,那么MN 的长为________;若点P 表示的有理数是6,那么MN 的长为________;(2)点P 在射线AB 上运动(不与点A ,B 重合)的过程中,MN 的长是否发生改变?若不改变,请写出求MN 的长的过程;若改变,请说明理由.36.点O 在直线AD 上,在直线AD 的同侧,作射线OB OC OM ,,平分AOC ∠. (1)如图1,若40AOB ∠=,60COD ∠=,直接写出BOC ∠的度数为 ,BOM ∠的度数为 ;(2)如图2,若12BOM COD ∠=∠,求BOC ∠的度数; (3)若AOC ∠和AOB ∠互为余角且304560AOC ∠≠,,,ON 平分BOD ∠,试画出图形探究BOM ∠与CON ∠之间的数量关系,并说明理由.37.定义:若90αβ-=,且90180α<<,则我们称β是α的差余角.例如:若110α=,则α的差余角20β=.(1)如图1,点O 在直线AB 上,射线OE 是BOC ∠的角平分线,若COE ∠是AOC ∠的差余角,求∠BOE 的度数.(2)如图2,点O 在直线AB 上,若BOC ∠是AOE ∠的差余角,那么BOC ∠与∠BOE 有什么数量关系.(3)如图3,点O 在直线AB 上,若COE ∠是AOC ∠的差余角,且OE 与OC 在直线AB 的同侧,请你探究AOC BOCCOE∠-∠∠是否为定值?若是,请求出定值;若不是,请说明理由.38.如图,已知150AOB ∠=,将一个直角三角形纸片(90D ∠=)的一个顶点放在点O 处,现将三角形纸片绕点O 任意转动,OM 平分斜边OC 与OA 的夹角,ON 平分BOD ∠. (1)将三角形纸片绕点O 转动(三角形纸片始终保持在AOB ∠的内部),若30COD ∠=,则MON ∠=_______;(2)将三角形纸片绕点O 转动(三角形纸片始终保持在AOB ∠的内部),若射线OD 恰好平分MON ∠,若8MON COD ∠=∠,求COD ∠的度数;(3)将三角形纸片绕点O 从OC 与OA 重合位置逆时针转到OD 与OA 重合的位置,猜想在转动过程中COD ∠和MON ∠的数量关系?并说明理由.39.已知线段AD=80,点B、点C都是线段AD上的点.(1)如图1,若点M为AB的中点,点N为BD的中点,求线段MN的长;(2)如图2,若BC=10,点E是线段AC的中点,点F是线段BD的中点,求EF的长;(3)如图3,若AB=5,BC=10,点P、Q分别从B、C出发向点D运动,运动速度分别为每秒移动1个单位和每秒移动4个单位,运动时间为t秒,点E为AQ的中点,点F为PD的中点,若PE=QF,求t的值.40.如图,两条直线AB,CD相交于点O,且90∠=,射线OM从OB开始绕O点逆AOC时针方向旋转,速度为15/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12/s.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)(1)当012t <<时,若369AOM AON ∠=∠-.试求出的值; (2)当06t <<时,探究BON COM AOCMON∠-∠+∠∠的值,问:t 满足怎样的条件是定值;满足怎样的条件不是定值?41.对于数轴上的,,A B C 三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点,,A B C 所表示的数分别为1,3,4,满足2AB BC =,此时点B 是点,A C 的“倍联点”.若数轴上点M 表示3-,点N 表示6,回答下列问题:(1)数轴上点123,,D D D 分別对应0,3. 5和11,则点_________是点,M N 的“倍联点”,点N 是________这两点的“倍联点”;(2)已知动点P 在点N 的右侧,若点N 是点,P M 的倍联点,求此时点P 表示的数. 42.点O 为直线AB 上一点,在直线AB 同侧任作射线OC 、OD ,使得∠COD=90°(1)如图1,过点O 作射线OE ,当OE 恰好为∠AOC 的角平分线时,另作射线OF ,使得OF 平分∠BOD ,则∠EOF 的度数是__________度;(2)如图2,过点O 作射线OE ,当OE 恰好为∠AOD 的角平分线时,求出∠BOD 与∠COE 的数量关系;(3)过点O 作射线OE ,当OC 恰好为∠AOE 的角平分线时,另作射线OF ,使得OF 平分∠COD ,若∠EOC=3∠EOF ,直接写出∠AOE 的度数43.一般地,n 个相同的因数a 相乘......a a a ⋅,记为n a , 如322228⨯⨯==,此时,3叫做以2为底8的对数,记为2log 8 (即2log 83=) .一般地,若(0na b a =>且1,0)a b ≠>, 则n 叫做以a 为底b 的对数, 记为log a b (即log a b n =) .如4381=, 则4叫做以3为底81的对数, 记为3log 81 (即3log 814=) .(1)计算下列各对数的值:2log 4= ;2log 16= ;2log 64= . (2)观察(1)中三数4、16、64之间满足怎样的关系式,222log 4,log 16,log 64之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?(4) 根据幂的运算法则:n m n m a a a +=以及对数的含义说明上述结论.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】根据同底数幂的乘法法则可得:14333533 x x x x x m m m n m n m n =⨯⨯⨯=⨯⨯⨯=⨯=,故选C.2.A解析:A 【解析】试题分析:含有相同字母,并且相同字母的指数相同的单项式为同类项,故选A . 考点:同类项的概念.3.B解析:B 【解析】 【分析】根据去括号法逐一计算即可. 【详解】A. a b +c a b c -=--(),正确;B. ()a b c a b c --=-+,错误;C. ()()a b c a b c -+-=--,正确;D. ()()c b a a b c ---=--,正确; 故答案为:B . 【点睛】本题考查了去括号法的应用,掌握去括号法逐一计算是解题的关键.4.C解析:C 【解析】 【分析】根据题意,明确“正”和“负”所表示的意义求出合格产品的范围,再求解即可. 【详解】依题意,合格面粉的质量应大于等于97.75千克, 小于等于100.25千克 选项中只有99.75<99.8<100.25故答案选C【点睛】本题考查了正负数的意义,本题难度较小,解决本题的关键是理解正负数的意义.5.A解析:A【解析】【分析】根据数轴的单位长度为1,点B在点A的右侧距离A点5个单位长度,直接计算即可.【详解】解:点B在点A的右侧距离A点5个单位长度,∴点B 表示的数为:-2+5=3,故选:A.【点睛】本题主要考查数轴,解决此题时,明确数轴上右边的数总是比左边的数大是解题的关键.6.D解析:D【解析】A. ∵a>b,a+2>b+2 ,故不正确;B. ∵a>b,a﹣2>b﹣2 ,故不正确;C. ∵a>b, 2a>2b,故不正确;D. ∵a>b,﹣2a<﹣2b,故正确;故选D.点睛:本题考查了不等式的基本性质,①把不等式的两边都加(或减去)同一个整式,不等号的方向不变;②不等式两边都乘(或除以)同一个正数,不等号的方向不变;③不等式两边都乘(或除以)同一个负数,不等号的方向改变.7.C解析:C【解析】【分析】俯视图是从物体上面看所得到的图形,据此判断得出物体的俯视图.【详解】解:A、立方体的俯视图是正方形,故此选项错误;B、圆柱体的俯视图是圆,故此选项错误;C、三棱柱的俯视图是三角形,故此选项正确;D、圆锥体的俯视图是圆,故此选项错误;故选:C.【点睛】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.解析:C【解析】【分析】答案中断去的菱形个数均为较小的正整数,由所示的图形规律画出完整的装饰链,可得断去部分的小萎形的个数.【详解】解:如图:断去部分的小菱形的个数最小为5.故选: C.【点睛】本题考查了图形的变化规律.注意按照图形的变化规律得到完整的装饰链是解决本题的关键. 9.D解析:D【解析】锥体必有一个顶点和一个底面,一个曲面;柱体必有两个底面(上底和下底),其他部分可能是平面,也可能是曲面,有两个面互相平行且大小相同,余下的每个相邻两个面的交线互相平行.故选D.10.D解析:D【解析】【分析】直接利用方向角的定义得出∠2的度数.【详解】如图所示:由题意可得:∠1=20°,∠ABC=90°,则∠2=90°-20°=70°,故超市(记作C)在蕾蕾家的南偏东70°的方向上.故选:D.【点睛】本题考查了方向角的定义,正确根据图形得出∠2的度数是解答本题的关键.解析:B【解析】【分析】设大和尚有x人,则小和尚有(100﹣x)人,根据3×大和尚人数+小和尚人数÷3=100,即可得出关于x的一元一次方程,此题得解.【详解】设大和尚有x人,则小和尚有(100﹣x)人,根据题意得:3x1003x-+=100.故选B.【点睛】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.12.C解析:C【解析】【分析】由已知条件得到x2﹣2x+y2﹣2y=0,2xy=1,化简x2+2xy+y2﹣2(x+y)+2019为x2﹣2x+y2﹣2y+2xy+2019,然后整体代入即可得到结论.【详解】解:∵x2﹣2x=2y﹣y2,xy=12,∴x2﹣2x+y2﹣2y=0,2xy=1,∴x2+2xy+y2﹣2(x+y)+2019=x2﹣2x+y2﹣2y+2xy+2019=0+1+2019=2020,故选:C.【点睛】本题考查代数式求值,掌握整体代入法是解题的关键.13.C解析:C【解析】【分析】由互为倒数的两数之积为1,即可求解.【详解】∵1313⎛⎫-⨯-=⎪⎝⎭,∴3-的倒数是13-.故选C 14.C 解析:C【分析】方程的分母最小公倍数是6,方程两边都乘以6即可.【详解】方程两边都乘以6得:2(2x+1)﹣(10x+1)=6.故选:C.【点睛】去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.15.D解析:D【解析】【分析】根据正方体的展开图即可得出答案.【详解】根据正方体的展开图可知:“数”的对面的字是“养”“学”的对面的字是“核”“心”的对面的字是“素”故选:D.【点睛】本题主要考查正方体的展开图,掌握正方体展开图的特点是解题的关键.二、填空题16.>【解析】【分析】根据两个负数比较大小,绝对值大的反而小,即可得到答案.【详解】解:∵,且,∴,故答案为:.【点睛】本题考查了实数的大小比较,解题的关键是掌握实数比较大小的法则.解析:>【解析】根据两个负数比较大小,绝对值大的反而小,即可得到答案.【详解】解:∵1(1)ππ-+=--,且13π-<,∴13π-+>-,故答案为:>.【点睛】本题考查了实数的大小比较,解题的关键是掌握实数比较大小的法则.17.两点确定一条直线【解析】【分析】根据两点确定一条直线解答.【详解】解:要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是:两点确定一条直线,故答案为两点确定一条直线.【点睛】本解析:两点确定一条直线【解析】【分析】根据两点确定一条直线解答.【详解】解:要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是:两点确定一条直线,故答案为两点确定一条直线.【点睛】本题考查了直线的性质,熟记两点确定一条直线是解题的关键.18.【解析】【分析】根据单项式的定义即可解题.【详解】解:的次数是指其所有字母的指数之和,故的次数是3,故答案是:3.【点睛】本题考查了单项式的知识,熟悉单项式的定义是解题关键.解析:3【解析】【分析】根据单项式的定义即可解题.【详解】 解:213-xy 的次数是指其所有字母的指数之和, 故213-xy 的次数是3, 故答案是:3.【点睛】本题考查了单项式的知识,熟悉单项式的定义是解题关键.19.5°【解析】【分析】根据对顶角相等求得∠BOD 的度数,然后根据角的平分线的定义求得∠EOD 的度数,则∠COE 即可求得,再根据角平分线的定义求得∠EOF,最后根据∠BOF=∠EOF-∠BOF 求解解析:5°【解析】【分析】根据对顶角相等求得∠BOD 的度数,然后根据角的平分线的定义求得∠EOD 的度数,则∠COE 即可求得,再根据角平分线的定义求得∠EOF,最后根据∠BOF=∠EOF-∠BOF 求解.【详解】解:82BOD AOC ︒∠=∠=,又∵OE 平分∠BOD ,11824122DOE BOD ︒︒∴∠=∠=⨯=, 180********COE DOE ︒︒︒︒∴∠=-∠=-=,OF 平分∠COE ,1113969.522EOF COE ︒︒∴∠=∠=⨯=, 69.54128.5BOF EOF BOF ︒︒︒∴∠=∠-∠=-=故答案是28.5°.【点睛】本题考查了对顶角和角平分线的性质,解决本题的关键是熟练掌握两者性质,根据未知角和已知角的关系,推断出未知角的度数.20.55【解析】【分析】根据对顶角相等的性质可知∠1的对顶角的度数,再根据平行线的性质可知同旁内角互补,从而可求答案.【详解】∵∴∠2+∠3=180°又∵∠1=∠3=125°∴∠2=1解析:55【解析】【分析】根据对顶角相等的性质可知∠1的对顶角的度数,再根据平行线的性质可知同旁内角互补,从而可求答案.【详解】a b∵//∴∠2+∠3=180°又∵∠1=∠3=125°∴∠2=180°-∠3=180°-125°=55°故答案为55.【点睛】本题考查的是对顶角的性质和平行线的性质,知道两直线平行同旁内角互补是解题的关键. 21.【解析】【分析】用三角板画出角,是用角度加减法.比如:画个75°的角,先将30°角在纸上画出来,再将45°角叠加就画出了75°角.【详解】用一副三角板可以画出:15°、30°、45°、60解析:5【解析】【分析】用三角板画出角,是用角度加减法.比如:画个75°的角,先将30°角在纸上画出来,再将45°角叠加就画出了75°角.【详解】用一副三角板可以画出:15°、30°、45°、60°、75°五个锐角.故填:5.【点睛】用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数.22.-【解析】【分析】单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数; 单项式的系数:单项式中的数字因数.【详解】单项式-的系数是: -.故答案为-【点睛】本题考核知解析:-1 3【解析】【分析】单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数;单项式的系数:单项式中的数字因数.【详解】单项式-2x y3的系数是: -13.故答案为-1 3【点睛】本题考核知识点:单项式的系数.解题关键点:理解单项式的系数的意义.23.25×108【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原解析:25×108【解析】【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:根据科学记数法的定义:225000000=82.2510⨯故答案为:82.2510⨯.【点睛】此题考查的是科学记数法,掌握科学记数法的定义是解决此题的关键.24.或【解析】【分析】分两种情况求解,当B 在点A 的左侧时可得出AB=2AC ,当点B 在点C 的右侧时可得出AB=4AC ,即可得解.【详解】解:B 在点A 的左侧时,画图如下,可得,;点B 在点C 的解析:14或12【解析】【分析】 分两种情况求解,当B 在点A 的左侧时可得出AB=2AC ,当点B 在点C 的右侧时可得出AB=4AC ,即可得解.【详解】解:B 在点A 的左侧时,画图如下,可得,12AC AB =; 点B 在点C 的右侧时,画图如下:可得,14 ACAB=故答案为:14或12.【点睛】本题考查的知识点是线段的和与差,通过画图可以更好的读懂题意,得出答案.25.【解析】【分析】将方程看成关于(y+1)的方程即可进行计算即可.【详解】解:∵关于的方程的解是∴关于的方程的解∴故答案为:【点睛】本题考查了方程的解的概念,准确理解方程的解是解题解析:3y=【解析】【分析】将方程1(1)32(1)2020y y b-+=-+看成关于(y+1)的方程即可进行计算即可.【详解】解:∵关于x的方程1322020x x b+=+的解是2x=∴关于()-1y的方程1(1)32(1)2020y y b-+=-+的解12y-=∴3y=故答案为:3y=【点睛】本题考查了方程的解的概念,准确理解方程的解是解题的关键.三、解答题26.∠1=∠2;见解析.【解析】【分析】根据题意算出∠GFH +∠FHD =180°,利用同旁内角互补两直线平行,证明FG ∥BD,再由角平分线性质判断即可.【详解】解:12∠=∠,理由如下:∵∠BHC =∠FHD ,∠GFH +∠BHC =180°,∴∠GFH +∠FHD =180°,∴FG ∥BD ,∴∠1=∠ABD ,∵BD 平分∠ABC ,∴∠2=∠ABD ,∴∠1=∠2;【点睛】本题考查了平行线的判定与性质和角平分线的有关计算,关键在于掌握相关基础知识.27.(1)40︒;(2)2α;(3)2DOE α∠=,与β无关 【解析】【分析】(1)由角平分线的定义可得,AOD AOE ∠∠的度数,相减即得DOE ∠的度数;(2)由角平分线的定义可用含α的代数式表示AOD ∠的度数,求出AOE ∠相减即得DOE ∠的度数;(3)由角平分线的定义可分别用含α、β的代数式表示,AOD AOE ∠∠,相减即得DOE ∠与α、β的数量关系.【详解】解:(1)80BOC ∠=︒,40AOC ∠=︒120AOB BOC AOC ︒∴∠=∠+∠= OD 、OE 分别平分AOB ∠、AOC ∠1160,2022AOD AOB AOE AOC ︒︒∴∠=∠=∠=∠= 40DOE AOD AOE ︒∴∠=∠-∠=所以DOE ∠的度数40︒.(2)BOC α∠=,50AOC ∠=︒50AOB BOC AOC α︒∴∠=∠+∠=+ OD 、OE 分别平分AOB ∠、AOC ∠150125,252222AOD AOB AOE AOC αα︒︒︒+∴∠=∠==+∠=∠= 2DOE AOD AOE α∴∠=∠-∠=所以DOE ∠的度数2α. (3)BOC α∠=,AOC β∠=AOB BOC AOC αβ∴∠=∠+∠=+OD 、OE 分别平分AOB ∠、AOC ∠11,222222AOD AOB AOE AOC αβαββ+∴∠=∠==+∠=∠= 2DOE AOD AOE α∴∠=∠-∠= 所以2DOE α∠=,与β无关. 【点睛】本题考查了角平分线,灵活利用角平分线的定义是解题的关键.28.(1)见解析;(2)见解析;(3)AH【解析】【分析】(1)根据平行线的性质与网格结构的特点作出即可;(2)根据网格结构作出垂线与AB 相交于点D 即可;(3)根据点到直线的距离的定义解答;【详解】(1)如图所示:(2)如图所示:(3)如图所示:【点睛】本题考查了网格结构中平行线与垂线的作法,熟练掌握网格结构是解题的关键.29.(1)-2 ;(2)当t 为4秒时,点O 恰好是PQ 的中点;(3)104025,,374【解析】【分析】(1)利用中点公式计算即可;(2)①用t 表示OP ,OQ ,根据OP=OQ 列方程求解;②分别以P 、Q 、C 为三等分点,分类讨论.【详解】解:(1)∵点A表示的数为-12,点B表示的数为8,点C为线段AB的中点.∴点C表示的数为:-12+8=-2 2故答案为:-2(2)①设t秒后点O恰好是PQ的中点.根据题意t秒后,点由题意,得-12+2t=-(8-t)解得,t=4;即4秒时,点O恰好是PQ的中点.②当点C为PQ的三等分点时PC=2QC或QC=2PC,∵PC=10-2t,QC=10-t,所以10-2t=2(10-t)或10-t=2(10-2t)解得t=103;当点P为CQ的三等分点时(t>4)PC=2QP或QP=2PC ∵PC=-10+2t,PQ=20-3t∴-10+2t=2(20-3t)或20-3t=2(-10+2t)解得t=254或t=407;当点Q为CP的三等分点时PQ=2CQ或QC=2PQ ∵当P、Q相遇时,两点都停止运动∴此情况不成立.综上,t=104025,,374秒时,三个点中恰好有一个点是以另外两个点为端点的线段的三等分点.【点睛】本题考查一元一次方程应用,利用数形结合思想分类讨论是解答的关键.30.(1)作图见解析;(2)作图见解析;(3)直线OA(或点H);线段CP的长度;PH<PC<OC【解析】【分析】按照要求作图即可,利用两个方格组成的矩形的对角线可作出与OB的平行线MN和垂线PC,沿方格线可作出OA的垂线;再由垂线段最短即可解答.【详解】解:(1)(2)(3)按要求作图即可,如下图,(4) 由图可知,PH是点P到直线OA(或点H)的距离,点到直线的垂线段长度即为该点到直线的距离,故CP的长度为点C到直线OB的距离;故答案为:直线OA(或点H);线段CP的长度(5)故PH<PC;CP是C到OB的距离,故CP<CO,故答案为:PH<PC<OC.【点睛】本题考查了与线相关的作图以及点到直线的距离.31.乙还需做3天.【解析】试题分析:等量关系为:甲的工作量+乙的工作量=1,列出方程,再求解即可.试题解析:设乙还需做x天.由题意得:331 1288x++=,解之得:x=3.答:乙还需做3天.考点:一元一次方程的应用.32.(1)x=1;(2)x=﹣0.25.【解析】【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【详解】(1)去括号得:3x+3﹣6=0,移项合并得:3x=3,解得:x=1;(2)去分母得:2(x+1)﹣6x=3,去括号得:2x+2﹣6x=3,移项合并得:﹣4x=1,解得:x=﹣0.25.【点睛】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.33.(1)1x =;(2)75x =【解析】【分析】 (1)根据解一元一次方程的步骤依次去括号、移项、合并同类项、系数化为1,据此计算可得;(2)根据解一元一次方程的步骤依次去分母、去括号、移项、合并同类项、系数化为1,据此计算可得.【详解】解:(1)523(2)x x -=--去括号得:523+6x x -=-移项得:5+36+2x x =合并同类项得:88x =系数化为1得:1x =(2)321143x x ---= 去分母得:()()1233421x x --=-去括号得: 129+384x x -=-移项得: 3-84-12+9x x =-合并同类项得: -57x =-系数化为1得: 75x =【点睛】本题主要考查解一元一次方程,解一元一次方程的一般步骤:分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a 形式转化. 四、压轴题34.(1)2412--;;(2)2t ;362t -;(3)P 、Q 两点之间的距离能为2,此时点P 点Q 表示的数分别是2-,2,2226,33. 【解析】【分析】 ()1因为点A 在原点左侧且到原点的距离为24个单位长度,所以点A 表示数24-;点B 在点A 右侧且与点A 的距离为12个单位长度,故点B 表示:241212-+=-;()2因为点P 从点A 出发,以每秒运动2两个单位长度的速度向终点C 运动,则t 秒后点P 表示数242t(0t 18-+≤≤,令242t 12-+=,则t 18=时点P 运动到点C),而点A 表示数24-,点C 表示数12,所以()PA 242t 242t =-+--=,PC 242t 12362t =-+-=-;()3以点Q 作为参考,则点P 可理解为从点B 出发,设点Q 运动了m 秒,那么m 秒后点Q 表示的数是244m -+,点P 表示的数是122m -+,再分两种情况讨论:①点Q 运动到点C 之前;②点Q 运动到点C 之后.【详解】()1设A 表示的数为x ,设B 表示的数是y . x 24=,x 0<∴x 24=-又y x 12-=y 241212.∴=-+=-故答案为24-;12-.()2由题意可知:t 秒后点P 表示的数是()242t 0t 18-+≤≤,点A 表示数24-,点C表示数12 ()PA 242t 242t ∴=-+--=,PC 242t 12362t =-+-=-.故答案为2t ;362t -.()3设点Q 运动了m 秒,则m 秒后点P 表示的数是122m -+.①当m 9≤,m 秒后点Q 表示的数是244m -+,则()PQ 24m 4m 122m 2=-+--+=,解得m 5=或7,当m=5时,-12+2m=-2,当m=7时,-12+2m=2,∴此时P 表示的是2-或2;②当m 9>时,m 秒后点Q 表示的数是()124m 9--,则()()PQ 124m 9122m 2=----+=,解得2931m 33或=, 当m=293时,-12+2m=223, 当m=313时,-12+2m=263, 此时点P 表示的数是222633或. 答:P 、Q 两点之间的距离能为2,此时点P 点Q 表示的数分别是2-,2,2226,33. 【点睛】本题考查了数轴上两点间的距离公式以及实数与数轴的相关概念,解题时同时注意数形结合数学思想的应用,解题关键是要读懂题目的意思,根据题目给出的条件,用代数式表示出数轴上的动点代表的数,找出合适的等量关系列出方程,再求解.35.(1)6;6;(2)不发生改变,MN为定值6,过程见解析【解析】【分析】(1)由点P表示的有理数可得出AP、BP的长度,根据三等分点的定义可得出MP、NP的长度,再由MN=MP+NP(或MN=MP-NP),即可求出MN的长度;(2)分-6<a<3及a>3两种情况考虑,由点P表示的有理数可得出AP、BP的长度(用含字母a的代数式表示),根据三等分点的定义可得出MP、NP的长度(用含字母a的代数式表示),再由MN=MP+NP(或MN=MP-NP),即可求出MN=6为固定值.【详解】解:(1)若点P表示的有理数是0(如图1),则AP=6,BP=3.∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.∴MP=23AP=4,NP=23BP=2,∴MN=MP+NP=6;若点P表示的有理数是6(如图2),则AP=12,BP=3.∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.∴MP=23AP=8,NP=23BP=2,∴MN=MP-NP=6.故答案为:6;6.(2)MN的长不会发生改变,理由如下:设点P表示的有理数是a(a>-6且a≠3).当-6<a<3时(如图1),AP=a+6,BP=3-a.∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.∴MP=23AP=23(a+6),NP=23BP=23(3-a),∴MN=MP+NP=6;当a>3时(如图2),AP=a+6,BP=a-3.∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.∴MP=23AP=23(a+6),NP=23BP=23(a-3),∴MN=MP-NP=6.。
苏教版 七年级上册期末提优复习
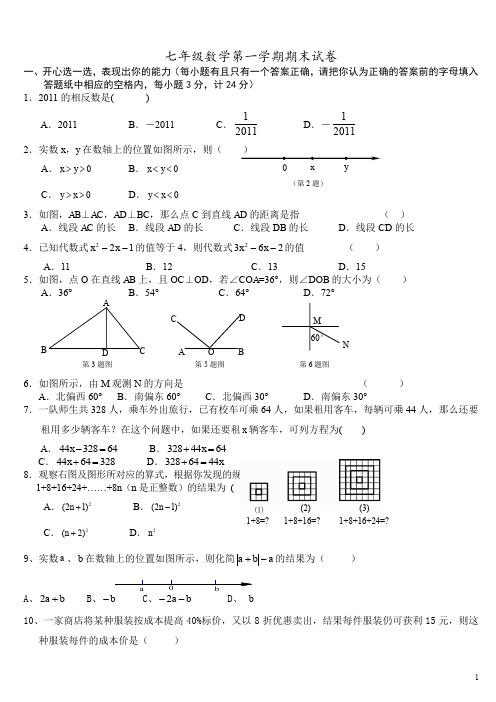
ba七年级数学第一学期期末试卷一、开心选一选,表现出你的能力(每小题有且只有一个答案正确,请把你认为正确的答案前的字母填入答题纸中相应的空格内,每小题3分,计24分) 1.2011的相反数是( )A .2011B .-2011C .12011D .-120112.实数x ,y 在数轴上的位置如图所示,则( )A .0>>y xB .0<<y xC .0>>x yD .0<<x y3.如图,AB ⊥AC ,AD ⊥BC ,那么点C 到直线AD 的距离是指 ( )A .线段AC 的长B .线段AD 的长C .线段DB 的长D .线段CD 的长 4.已知代数式122--x x 的值等于4,则代数式2632--x x 的值 ( )A .11B .12C .13D .15 5.如图,点O 在直线AB 上,且OC ⊥OD ,若∠COA =36°,则∠DOB 的大小为( ) A .36° B .54° C .64° D .72°6.如图所示,由M 观测N 的方向是 ( ) A .北偏西60° B .南偏东60° C .北偏西30° D .南偏东30°7.一队师生共328人,乘车外出旅行,已有校车可乘64人,如果租用客车,每辆可乘44人,那么还要租用多少辆客车?在这个问题中,如果还要租x 辆客车,可列方程为( ) A .4432864x -= B .3284464x += C .4464328x += D .3286444x +=8.观察右图及图形所对应的算式,根据你发现的规律计算 1+8+16+24+……+8n (n 是正整数)的结果为 ( )A .2(21)n +B .2(21)n -C .2(2)n +D .2n9、实数a 、b 在数轴上的位置如图所示,则化简a b a -+的结果为( )A 、b a +2B 、b -C 、b a --2D 、 b10、一家商店将某种服装按成本提高40%标价,又以8折优惠卖出,结果每件服装仍可获利15元,则这种服装每件的成本价是( )xy(第2题)A C D OB 第5题图 60°N M第6题图A CB D 第3题图 1+8+16+24=?(3)(2) ⑴ 1+8=?1+8+16=?A 、120元;B 、125元;C 、135元;D 、140元.二、静心填一填,你一定能行(每题3分,共30分)11、一个角的补角是它的余角的3倍,则这个角是 。
期末综合提优测试卷2021-2022学年苏科版七年级上册数学

2021-2022学年苏科版七年级上册数学期末综合提优测试卷(时间60分钟 满分100分)一、选择题(每题2分,共20分)1.在有理数(3)-- ,2(2)-,0,23-,3-,13-中,负数的个数是 ( ) A .0个 B .1个 C .2个 D .3个2.有理数a 、b 、c 在数轴上的对应点如图,下列结论中,正确的是 ( )A .a >c >bB .a >b >cC .a <c <bD .a <b <c3.已知a -b =1,则代数式2a -2b -3的值是( )A .-1B .1C .-5D .54.a 是一个三位数,b 是—个两位数,若把b 放在a 的左边,组成—个五位数,则这个五位数为 ( )A .b +aB .10b +aC .100b +aD .1000b +a5.某道路一侧原有路灯106盏,相邻两盏灯的距离为36米,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70米,则需更换的新型节能灯有( )A .54盏B .55盏C .56盏D .57盏6.下面四个平面图形中,沿虚线折叠后不能围成一个三棱锥的有 ( )A .1个B .2个C .3个D .4个7.某项工程由甲队单独做需18天完成,由乙队单独做只需甲队的一半时间完成,设两队合作需x 天完成,则可得方程 ( )A .11189x += B .11()1189x += C .111836x += D .11()11836x +=8.如图,是由8相同的小立方块搭成的几何体的左视图,它的三个视图是2×2的正方形.若拿掉若干个小立方块后(几何体不倒掉...),其三个仍都为2×2的正方形,则最多能小立方块的个数为A .1B .2C .3D .49.4张扑克牌如图⑴所示放在桌上,小敏把其中一张旋转180°后得到如图⑵所示,那么她所旋转的牌从左数起是()A.第一张B.第二张C.第三张D.第四张10.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC等于( )A.120°B.120°或60°C.30°D.30°或90°二、填空题(每题3分,共30分)11.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOD=104°,则∠BOM=_______.12.若代数式-4x6y与x2n y是同类项,则常数n的值为_______13.已知2a-+(b+3)2=0,则b a的值等于_______14.已知222211⨯=+,333322⨯=+,444433⨯=+,…,若ab×10=ab+10(a、b都是正整数),则a+b=___________.15.把一张长方形纸条按如图的方式折叠后,量得∠AOB'=110°,则∠B'OC=_______.16.已知a:b:c=2:3:4,a+b+c=27,则a-2b-3c=______17.随着电子技术的发展,手机价格不断降低,某品牌手机按原价降低m元后,又降低20%.此时的售价为n元,则该手机原价为_______元.18.平面内不同的两点确定一条直线,不同的三点最多确定三条直线,若平面内不同的n 个点最多可确定15条直线,则n 的值为_______.19.如图是一个长方体的表面展开图,将它沿虚线折叠后棱AB 与棱 重合,棱AC与棱 重合,棱EF 与棱 重合.20.如图是由大小相同的小立方块组成的简单几何体的主视图和左视图,那么组成这个几何体的小立方块的个数最多为_______.三、解答题(共50分)21.计算: (1) 2(2)2(2)--+--- (2) 22312()(0.8)2-⨯-÷(3) 42110016(2)(5)1005+÷--⨯---(4) 22112(10.5)3(2)3⎡⎤⎡⎤----⨯⨯--⎣⎦⎢⎥⎣⎦22.化简求值:(1)3x 2+2xy -4y 2-2(3xy -y 2-2x 2),其中x =1,y =-2;(2)4(x2-3x)-5(2x2-5x),其中x=-1.23.如图,点P是∠AOB的边OB上的一点.(1)过点P画OB的垂线,交OA于点C;(2)过点P画OA的垂线,垂足为H;(3)线段PH的长度是点P到_______的距离,_______是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是_______(用“<”号连接),其根据是___________.24.某公司在甲、乙两仓库分别有农用车12辆和6辆,现需要调往A县10辆,调往B县8辆.已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元,从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元,设从甲仓库调往A县农用车x辆.(1)甲仓库调往B县农用车_______辆,乙仓库调往A县农用车_______辆.(用含x的代数式表示)(2)写出公司从甲、乙两仓库调往农用车到A,B两县所需要的总运费.(用含x的代数式表示)(3)在(2)的基础上,求当从甲仓库调往A县农用车4辆时,总运费是多少.25.王老师家装修需要买灯,他亲自去市场调查,得到的数据如下表:如果这两种灯的照明亮度一样,且用电度数计算公式是:用电度数=功率(瓦)×时间(小时)÷1000,费用=灯的售价+电费,其中电费为0.6元/度.(1)两种灯都需要使用5000小时,请你通过计算建议王老师购买哪一种灯合算?(2)在普通白炽灯的使用寿命内,设照明时间为x 小时.①用含x 的式子分别表示使用一盏普通白炽灯的费用y 1和使用一盏优质节能灯的费用y 2;②当照明时间为多少时,使用优质节能灯合算?(精确到1小时)26.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察如图中的几种简单多面体模型,解答下列问题:(1)根据如图所示的多面体模型,完成表格中的空格:你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______;(2)一个多面体的面数比顶点数多8,且有30条棱,则这个多面体的面数是_______;(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表面三角形的个数为x ,八边形的个数为y ,求x +y 的值.27.同学们都知道,()52--表示5与-2的差的绝对值,实际上也可理解为5与 -2两数在数轴上所对应的两点之间的距离.试探索:(1) ()52--=___________.(2)找出所有符合条件的整数x ,使527x x ++-=成立. (3)由以上探索猜想,对于任何有理数x ,36x x -+-是否有最小值?如果有,写出最小值;如果没有,说明理由.。
苏科版数学七年级上提优练习与答案(垂直)

苏科版数学七年级上提优练习内容:垂直1.下列说法中正确的个数为( )①两条直线相交所成的四个角中,如果有两个角相等,那么这两条直线垂直:②两条直线相交所成的四个角中,如果有一个角是直角.那么这两条直线垂直:③一条直线的垂线可以画无数条:④在同一平面内,经过一个已知点能画一条且只能面一条直线与已知直线垂直.A.1 B,2 C.3 D.42.如图6—5—1,直线BC、DE相交于点O,OA、OF为射线,O A⊥OB,OF平分∠COE,∠COF+∠BOD=510,求∠AOD的度数.3.已知:如图6—5—2①,点0在直线AB上,C0⊥AB于点O.OD平分∠AOC.OE平分∠BOC.(1)∠DOE= ,OD 与OE的位置关系是:(2)若C0与AB不垂直,如图6—5—2②,其他条件不变,(1)中的结论还成立吗?若成立,请说明理由:若不成立,请直接写出正确的结论:(3)若∠AOD=400,请你利用(2)中得到的结论求出∠BOE的度数.4.(1)如图6—5—3①,过P点画AB的垂线:(2)如图6—5—3②,过P点分别画0A、OB的垂线;(3)如图6—5—3③,过点A画BC的垂线.5.如图6—5—4,在方格纸中,直线AC与CD相交于点C. (1)过点E画直线EF,使EF⊥AC;(2)分别写出AC,CD,EF之间的位置关系;(3)根据你观察到的EF与CD之间的位置关系,用一句话来表达你的结论.6.(2019贵州毕节中考改编)如图6—5—5,点C到直线AB的距离是 ( )A.线段CA的长度 B.线段CM的长度C.线段CD的长度 D.线段CB的长度7.如果CO⊥AB手点0,自0C上任意一点向AB画垂线.那么所画垂线与OC ( )A.垂直 B.相交 C.重合 D.无法确定8.(2020独家原创试题)如图6—5—6,AB⊥BC,垂足为B, AB=4.5,P是射线BC 上的动点.则线段AP的长不可能是 ( )A.6 B.5, C.4.5 D.4.49.如图6—5—7①,L是一条笔直的公路,A、B是刚建成的两个生活小区,为了出行方便.小区本着最经济(最省钱)的原则,准备修建公交站点及站点到小区的道路.(1)若要修两个站点,则站点及道路建在何处最合适?请在图6—5—7①中画出所修建的道路,并用字母标出两个站点的位置:(2)若只修一个站点,则此时站点及道路建在何处最合适?请在图6—5—7②中厕出所修建的道路.并用字母标出站点的位置.10.(2020江苏南京雨花台期末,6,★☆☆)如F--1 6—5—8,∠ACB=900,CD⊥AB,垂足为D,则下面的结论中正确的是 ( )①BC与AC互相垂直;②AC与CD互相垂直:③点A 到BC的垂线段是线段BC:④点C到AB的垂线段是线段CD;⑤线段BC的长度是点B到AC的距离:⑥线段AC的长度是点A到BC的距离.A.①④⑤⑥ B.①④⑥C.②③⑤ D.①④11.(2019江苏扬州邗江期末,4,★☆☆)如图6-5-9,已知ON⊥L,OW⊥L,所以OM 与ON重合,其理由是 ( )A.两点确定一条直线.B.在同一平面内,过一点有且只有一条直线与已知直线垂直C.在同一平面内,过一点只能作一条垂线D.垂线段最短12.(2020江苏南京秦淮期末,15,★☆☆) 在同一平面内,∠BOC=500,0A⊥OB,OD平分∠AOC,则∠BOD的度数是______________ .13.(2019广东广州广稚中学期末,24,★☆☆)如图6—5一l0,直线AB、CD相交于点0,∠DOE=∠BOD,OF平分∠AOE.(1)判断0F与OD的位置关系,并说明理由:(2)若∠AOC:∠AOD=1:5.求∠EOF的度数.14.(2019江苏常州中考,4,★☆☆)如图6-5—11,在线段PA、PB、PC、PD中,长度最小的是 ( )A.线段PA B.线段PBC.线段PC D.线段PD15.(2018湖南益阳中考,5,★☆☆)如图6—5一l2,直线AB、CD相交于点0,E0⊥CD.下列说法错误的是( )A.∠AOD=∠BOCB.∠AOE+∠BOD=900C.∠ADC=∠A4DED.∠A0D+∠BO D=180016.(2019广东广州中考,11,★☆☆)如图 6—5—13,点A,B,C在直线L上,PB⊥L,PA=6cm,PB=5 cm,PC=7 cm,则点P到直线L的距离是 cm .17.(2018河南中考,12,★☆☆)如图6—5—14,直线AB,CD相交于点0,EO ⊥AB 于点0,∠EOD=500,则∠BOC的度数为.18.将两个相同三角板的直角顶点重合在一起,按如图6—5一l5①②所示的方式放置.(1)若∠BOC=600,如图6—5—15①,求∠AOD的度数:_______________________(2)若∠BOC=700,如图6—5一l5②,求∠AOD的度数:_______________________(3)猜想∠AOD和∠BOC的关系,并说明理由.19.噪音对环境的影响与距离有关,距离越小,噪音越大.如图6—5—16,一辆汽车在笔直的公路上由点A向点B 行驶,M、N分别是位于公路AB两侧的两所学校,通过画图,完成下列各题,并说明理由.(1)找出学校M受噪音影响最严重的P点;(2)找出学校Ⅳ受噪音影响最严重的Q点;(3)汽车在公路上的哪一段行驶时,学校M受噪音影响越来越小,而学校N受噪音影响越来越大?20.(1)在图6—5—17①中以P为顶点画∠2,使∠2 的两边分别和∠1的两边垂直:(2)量一量∠2和∠1的度数,它们之间的数量关系______________;(3)同样在图6-5—17②和图6—5—17③中以P为顶点画∠2.使∠2的两边分别和∠1的两边垂直,分别写出图6—5一l7②和图6—5一l7③中∠2和∠l之问的数量关系(不要求写出理由):图6—5—17②:_____________ ,图6—5—17③:_________________;(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).。
苏教版七年级数学上册 期末试卷培优测试卷
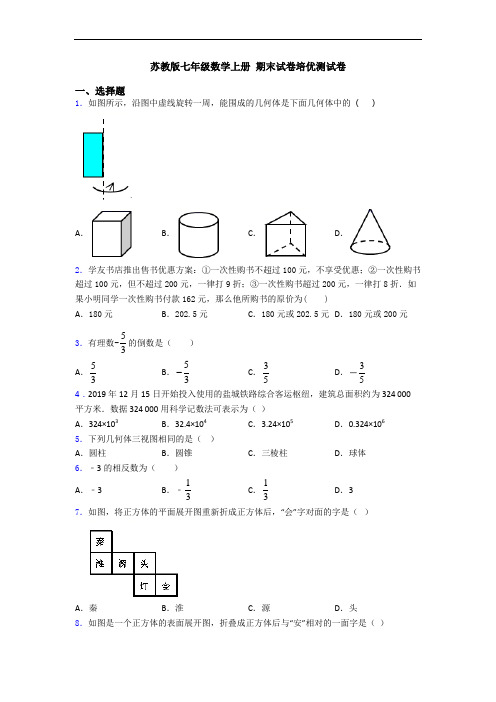
苏教版七年级数学上册期末试卷培优测试卷一、选择题1.如图所示,沿图中虚线旋转一周,能围成的几何体是下面几何体中的()A.B.C.D.2.学友书店推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元,但不超过200元,一律打9折;③一次性购书超过200元,一律打8折.如果小明同学一次性购书付款162元,那么他所购书的原价为( )A.180元B.202.5元C.180元或202.5元D.180元或200元3.有理数-53的倒数是()A.53B.53C.35D.354.2019年12月15日开始投入使用的盐城铁路综合客运枢纽,建筑总面积约为324 000平方米.数据324 000用科学记数法可表示为()A.324×103B.32.4×104C.3.24×105D.0.324×1065.下列几何体三视图相同的是()A.圆柱B.圆锥C.三棱柱D.球体6.﹣3的相反数为()A.﹣3 B.﹣13C.13D.37.如图,将正方体的平面展开图重新折成正方体后,“会”字对面的字是()A.秦B.淮C.源D.头8.如图是一个正方体的表面展开图,折叠成正方体后与“安”相对的一面字是()A.高B.铁C.开D.通9.一个几何体的侧面展开图如图所示,则该几何体的底面是()A.B.C.D.10.甲、乙两人在长为25米泳池内始终以匀速游泳,两人同时从起点出发,触壁后原路返回,如是往返;甲的速度是1米/秒,乙的速度是0.6米/秒,那么第十次迎面相遇时他们离起点()A.7.5米B.10米C.12米D.12.5米11.一个几何体的侧面展开图如图所示,则该几何体的底面是()A.B.C.D.12.小红在计算23202011114444⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭时,拿出 1 张等边三角形纸片按如图所示方式进行操作.①如图1,把 1 个等边三角形等分成 4 个完全相同的等边三角形,完成第 1 次操作;②如图 2,再把①中最上面的三角形等分成 4 个完全相同的等边三角形,完成第 2 次操作;③如图 3,再把②中最上面的三角形等分成 4 个完全相同的等边三角形,······依次重复上述操作.可得23202011114444⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值最接近的数是()A .13B .12C .23D .113.如图,数轴的单位长度为1,如果点表示的数为-2,那么点表示的数是( ).A .-1B .0C .3D .414.下列四个图中的1∠也可以用AOB ∠,O ∠表示的是( )A .B .C .D .15.下列计算中正确的是( )A .()33a a -=B .235a b ab +=C .22243a a a -=D .332a a a +=二、填空题16.若60A ∠=︒,且A ∠与B 互补,则B ∠=_______________度.17.计算:82-+-=___________.18.把一张长方形纸条ABCD 沿EF 折叠,若∠AEG =62°,则∠DEF =_____°.19.一个数的平方为16,这个数是 .20.请写出一个系数是-2,次数是3的单项式:________________.21.已知220x y +-=,则124x y --的值等于______.22.如图,一根绳子对折以后用线段AB 表示,在线段AB 的三等分点处将绳子剪短,若所得三段绳长的 最大长度为 8cm ,则这根绳子原长为________cm .23.点A 、B 、C 在直线l 上,若3BC AC =,则AC AB =__________. 24.若132=∠,则1∠的余角为__________.25.如图,直线AB ,CD 相交于点O ,若∠AOC +∠BOD =100°,则∠AOD 等于__________度.三、解答题26.如图所示,O 为一个模拟钟面圆心,M 、O 、N 在一条直线上,指针 OA 、OB 分别从 OM 、ON 出发绕点 O 转动,OA 运动速度为每秒 30°,OB 运动速度为每秒10°,当一根指针与起始位置重合时,运动停止,设转动的时间为 t 秒,试解决下列问题:(1)如图①,若OA 顺时针转动,OB 逆时针转动,t = 秒时,OA 与OB 第一次重合;(2)如图②,若OA 、OB 同时顺时针转动,①当t =3秒时,∠AOB = °;②当t 为何值时,三条射线OA 、OB 、ON 其中一条射线是另两条射线夹角的角平分线?27.如图,COD ∠为平角,,2AO OE AOC DOE ⊥∠=∠,求AOC ∠的度数.28.某校办工厂生产一批新产品,现有两种销售方案。
2020-2021学年苏教版七年级数学上册期末提优冲刺卷(word版含答案解析)

2020-2021学年苏教版七年级数学上册期末提优冲刺卷一、选择题(共10小题;共40分)1. 下列实数中最大的是( )A. 1B. −√2C. 3D. ∣∣−12∣∣2. 2020年5月,中科院沈阳自动化所主持研制的“海斗一号”万米海试成功,下潜深度超10900米,刷新我国潜水器最大下潜深度记录.将数据10900用科学记数法表示为( )A. 1.09×103B. 1.09×104C. 10.9×103D. 0.109×1053. 下列各方程中,解为x=2的是( )A. 2x+4=0B. 2(x+1)=5C. x3−12=16D. −2x=−14. −4的相反数是( )A. 4B. −4C. −14D. 145. 如图,在数轴上表示−1,−√2的对应点为A,B,若点A是线段BC的中点,则点C表示的数为( )A. 1−√2B. 2−√2C. √2−1D. √2−26. 射线OA位于北偏东25∘方向,射线OB位于南偏东20∘方向,则∠AOB的度数是( )A. 135∘B. 95∘C. 45∘D. 25∘7. 王先生到银行存了一笔三年期的定期存款,年利率是 4.25%.到期后取出,得到本息(本金+利息)33825元.设王先生存入的本金为x元,则下面所列方程正确的是( )A. x+3×4.25%x=33825B. x+4.25%x=33825C. 3×4.25%x=33825D. 3(x+4.25x)=338258. 若单项式a m−1b2与12a2b n的和仍是单项式,则2m−n的值是( )A. 3B. 4C. 6D. 89. 当1<a<2时,代数式∣a−2∣+∣1−a∣的值是( )A. −1B. 1C. 3D. −310. 若∠α+∠θ=90∘,∠β=∠θ,则∠α与∠β的关系是( )A. ∠α 与 ∠β 互余B. ∠α 与 ∠β 互补C. ∠α 与 ∠β 相等D. ∠α 大于 ∠β二、填空题(共8小题;共40分)11. 计算:(−23)2= .12. 判断以下合并是否正确:(1)−2x −3x =−5;( )(2)2x +3y =5xy ;( )(3)3x 2−2x 2=x ;( )(4)−5xy +2xy =7xy .( )13. 已知 a <1,化简 ∣3−a ∣−∣a −1∣= . 14. 已知关于 x 的方程 mx 2+3=x 与方程 3−2x =1 的解相同,则 m = .15. 已知 4a +3b =1,则整式 8a +6b −3 的值为 .16. 如图,C ,D ,E 是线段 AB 上三点,各线段长如图所示,使用 a ,b ,c 的式子表示 x = .17. 如图,OC 是 ∠AOB 的平分线,如果 ∠AOB =130∘,∠BOD =24∘48ʹ,那么∠COD = .18. 某班 5 名学生在一次数学测验中的成绩以 90 分为标准,超过的分数记为正数,不足的分数记为负数,记录如下:−4,+9,0,−1,+6,则他们的平均成绩是 分.三、解答题(共7小题;共70分)。
苏教版七年级数学上册 期末试卷培优测试卷
苏教版七年级数学上册 期末试卷培优测试卷一、选择题1.学友书店推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元,但不超过200元,一律打9折;③一次性购书超过200元,一律打8折.如果小明同学一次性购书付款162元,那么他所购书的原价为( ) A .180元 B .202.5元 C .180元或202.5元 D .180元或200元 2.下列单项式中,与2a b 是同类项的是( )A .22a bB .22a bC .2abD .3ab 3.在钟表上,下列时刻的时针和分针所成的角为90°的是( ) A .2点25分 B .3点30分 C .6点45分 D .9点 4.下列几何体三视图相同的是( )A .圆柱B .圆锥C .三棱柱D .球体5.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A 、B 、C 三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )A .20B .25C .30D .356.已知点A 、B 、C 、D 在同一条直线上,线段8AB =,C 是AB 的中点, 1.5DB =.则线段CD 的长为( ) A .2.5B .3.5C .2.5或5.5D .3.5或5.57.已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为( )A .B .4C .或4D .2或48.-5的倒数是 A .15B .5C .-15D .-59.小红在计算23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭时,拿出 1 张等边三角形纸片按如图所示方式进行操作.①如图1,把 1 个等边三角形等分成 4 个完全相同的等边三角形,完成第 1 次操作;②如图 2,再把①中最上面的三角形等分成 4 个完全相同的等边三角形,完成第 2 次操作;③如图 3,再把②中最上面的三角形等分成 4 个完全相同的等边三角形,······依次重复上述操作.可得23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值最接近的数是( )A .13B .12C .23D .110.某商品原价为m 元,由于供不应求,先提价30%进行销售,后因供应逐步充足,价格又一次性降价30%,售价为n 元,则m ,n 的大小关系为( ) A .m n = B .0.91n m =C .30%n m =-D .30%n m =-11.单项式24x y 3-的次数是( ) A .43-B .1C .2D .312.某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个,如果每人做4个,那么比计划少7个,设计划做x 个“中国结”,可列方程( ) A .9764x x --= B .96x -=74x +C .x 9x+764+= D .x 9x 764+-= 13.如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的主视图为( )A .B .C .D .14.如图,左面的平面图形绕轴旋转一周,可以得到的立体图形是( )A .B .C .D .15.下列说法中正确的有( ) ①经过两点有且只有一条直线; ②连接两点的线段叫两点的距离; ③两点之间的所有连线中,垂线段最短; ④过直线外一点有且只有一条直线与已知直线平行. A .0个B .1个C .2个D .3个二、填空题16.若关于x 的方程5x ﹣1=2x +a 的解与方程4x +3=7的解互为相反数,则a =________. 17.计算:3-|-5|=____________.18.据统计,我市常住人口56.3万人,数据563000用科学计数法表示为__________. 19.比较大小:π1-+ _________3-(填“<”或“=”或“>”). 20.单项式-4x 2y 的次数是__.21.在2π,3.14,0,0.1010010001(每两个1之间依次增加1个0),23中,无理数有_________个.22.已知1x =是方程253ax a -=+的解,则a =__.23.实验室里,水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5cm 高度处连接(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm ,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位高度为56cm ,则开始注入________分钟的水量后,甲与乙的水位高度之差是16cm.24.单项式23x y-的系数是____.25.若单项式64x y -与2n x y 的和仍为单项式,则21n 的值为________.三、解答题26.解下列方程:(1)3(1)4(21)8x x --+= (2)12123x x-+-= 27.如图,过直线AB 上点O 作AB 的垂线OE ,三角尺的一条直角边OD 从与OB 重合的位置开始,绕点O 按逆时针方向旋转至与OA 重合时停止,在旋转过程中,设BOD ∠的度数为α,作DOE ∠的平分线OF .(1)当OD 在∠BOE 的内部时,BOD ∠的余角是___________;(填写所有符合条件的角)(2)在旋转过程中,若14EOF BOF ∠=∠,求α的值; (3)在旋转过程中,作AOD ∠的平分线,OG FOG ∠的度数是否会随着α的变化而变化?若不变,直接写出FOG ∠的度数;若变化,试用含有α的式子表示FOG ∠的度数.28.已知线段AB =12cm ,C 为线段AB 上一点,BC =5cm ,点D 为AC 的中点,求DB 的长度.29.解方程:(1)5(x ﹣1)+2=3﹣x (2)2121136x x -+=- 30.先化简,再求值.22225(3)4(31)a b ab ab a b ---+-,其中2(2)10a b ++-=.31.计算:(1)25)(277+-()-(-)-;(2)315(2)()3-⨯÷-.32.如图,已知所有小正方形的边长都为1,点A 、B 、C 都在格点上,借助网格完成下列各题.(1)过点A 画直线BC 的垂线,并标出垂足D ; (2)线段______的长度是点C 到直线AD 的距离;(3)过点C 画直线AB 的平行线交于格点E ,求出四边形ABEC 的面积.33.画图题:已知平面上点A B C D 、、、,用刻度尺按下列要求画出图形:(保留画图痕迹,不要求写画法)(1)画直线BD ,射线 C B(2)连结AD 并延长线段AD 至点 F ,使得DF AD =.四、压轴题34.探索、研究:仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数a n 与层数n 之间满足关系式a n =n²−32n+247,1⩽n<16,n 为整数。
苏教版数学七年级上册 期末试卷培优测试卷
苏教版数学七年级上册 期末试卷培优测试卷一、选择题1.下列运算中,结果正确的是( )A .3a 2+4a 2=7a 4B .4m 2n+2mn 2=6m 2nC .2x ﹣12x =32x D .2a 2﹣a 2=2 2.若x 3=是方程3x a 0-=的解,则a 的值是( ) A .9 B .6C .9-D .6- 3.下列各式中与a b c --的值不相等的是( )A .()a b c -+B .()a b c --C .()()a b c -+-D .()()c b a --- 4.如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A .63B .70C .92D .105 5.下列各组代数式中,不是同类项的是( ) A .2与-5B .-0.5xy 2与3x 2yC .-3t 与200tD .ab 2与-8b 2a 6.已知:如图,AB ⊥CD ,垂足为O ,EF 为过点O 的一条直线,则∠1与∠2的关系一定成立的是( )A .相等B .互余C .互补D .不确定7.将一副直角三角尺按如图所示摆放,图中锐角∠1的度数为( )A .58°B .59°C .60°D .61°8.如图,点C 是AB 的中点,点D 是BC 的中点,则下列等式中正确的有( )①CD AC DB =-②CD AD BC =-③2BD AD AB =- ④13CD AB = A .4个 B .3个 C .2个 D .1个9.完全相同的6个小矩形如图所示放置,形成了一个长、宽分别为n 、m 的大矩形,则图中阴影部分的周长是( )A .6(m ﹣n )B .3(m +n )C .4nD .4m10.如图正方体纸盒,展开后可以得到( )A .B .C .D .11.小明同学用手中一副三角尺想摆成α∠与β∠互余,下面摆放方式中符合要求的是( ).A .B .C .D .12.下列说法错误的是( )A .对顶角相等B .两点之间所有连线中,线段最短C .等角的补角相等D .不相交的两条直线叫做平行线 13.据统计,2020年元旦到高邮市旅游的旅客约为15000人,数据15000用科学计数法可表示为( )A .50.1510⨯B .51.510⨯C ..41510⨯D .31510⨯ 14.如图,已知正方形2134A A A A 的边长为1,若从某一点开始沿逆时针方向走点的下标数字的路程,则把这种走法成为一次“逆移”,如:在点3A 开始经过3412A A A A →→→为第一次“逆移”, 在点2A 开始经过2341A A A A →→→为第二次“逆移”.若从点1A 开始,经过2020次“逆移”,最终到达的位置是( )A .1AB .2AC .3AD .4A15.如图,是一个正方体的展开图则“数”字的对面的字是( )A .核B .心C .素D .养二、填空题16.一个两位数,个位数字比十位数字大4,且个位数字与十位数字的和为10,则这个两位数为_______.17.动点,A B 分别从数轴上表示10和2-的两点同时出发,以7个单位长度/秒和4个单位长度/秒的速度沿数轴向负方向匀速运动,__________秒后,点,A B 间的距离为3个单位长度.18.要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是_____.19.如果20a b --=,那么代数式122a b +-的值是_____.20.如图是一把剪刀,若∠AOB+∠COD =60°,则∠BOD =____°.21.线段AB=10cm ,BC=5cm ,A 、B 、C 三点在同一条直线上,则AC=______.22.如图,三个一样大小的小长方形沿“竖-横-竖”排列在一个长为10,宽为8的大长方形中,则图中一个小长方形的宽为______.23.如图,135AOD ∠=︒,75COD ∠=︒,OB 平分AOC ∠,则BOC ∠=________度.24.若代数式2434x x +-的值为 1,则代数式2314x x --的值为_________. 25.甲数x 的23与乙数y 的14差可以表示为_________ 三、解答题 26.解方程(1)2-3(x+1)=8 (2)531243x x +--=- 27.先化简,再求值:22223(2)(54)a b ab a b ab ---,其中21a b ==-、28.化简:(1)()632m m n --+ (2)()()22835232ab a ab ab a ---- 29.如图所示,O 为一个模拟钟面圆心,M 、O 、N 在一条直线上,指针 OA 、OB 分别从 OM 、ON 出发绕点 O 转动,OA 运动速度为每秒 30°,OB 运动速度为每秒10°,当一根指针与起始位置重合时,运动停止,设转动的时间为 t 秒,试解决下列问题:(1)如图①,若OA 顺时针转动,OB 逆时针转动,t = 秒时,OA 与OB 第一次重合;(2)如图②,若OA 、OB 同时顺时针转动, ①当t =3秒时,∠AOB = °;②当t 为何值时,三条射线OA 、OB 、ON 其中一条射线是另两条射线夹角的角平分线?30.如图,所有小正方形的边长都为1,点O 、P 均在格点上,点P 是∠AOB 的边 OB 上一点,直线PC ⊥OA ,垂足为点C .(1)过点 P 画 OB 的垂线,交OA 于点D ;(2)线段 的长度是点O 到直线PD 的距离;(3)根据所画图形,判断∠OPC ∠PDC (填“>”,“<”或“=”),理由是 .31.计算题(1)(3)78--+--(2)2211-3--6-3()(2)32⨯-+-÷. 32.把边长为1的10个相同正方体摆成如图的形式.(1)画出该几何体的主视图、左视图、俯视图;(2)试求出其表面积(包括向下的面);(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多..可以再添加 个小正方体. 33.如图,点O 在直线AB 上,OC 、OD 是两条射线,OC ⊥OD ,射线OE 平分∠BOC .(1)若∠DOE =150°,求∠AOC 的度数.(2)若∠DOE =α,则∠AOC = .(请用含α的代数式表示)四、压轴题34.在有些情况下,不需要计算出结果也能把绝对值符号去掉,例如:|6+7|=6+7;|7﹣6|=7﹣6;|6﹣7|=7﹣6;|﹣6﹣7|=6+7.(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:①|7+21|=______;②|﹣12+0.8|=______;③23.2 2.83--=______; (2)用合理的方法进行简便计算:1111924233202033⎛⎫-++---+ ⎪⎝⎭ (3)用简单的方法计算:|13﹣12|+|14﹣13|+|15﹣14|+…+|12004﹣12003|. 35.点O 在直线AD 上,在直线AD 的同侧,作射线OB OC OM ,,平分AOC ∠. (1)如图1,若40AOB ∠=,60COD ∠=,直接写出BOC ∠的度数为 ,BOM ∠的度数为 ;(2)如图2,若12BOM COD ∠=∠,求BOC ∠的度数; (3)若AOC ∠和AOB ∠互为余角且304560AOC ∠≠,,,ON 平分BOD ∠,试画出图形探究BOM ∠与CON ∠之间的数量关系,并说明理由.36.如图,OC 是AOB ∠的角平分线,OD OB ⊥,OE 是BOD ∠的角平分线,85AOE ∠=(1)求COE ∠;(2)COE ∠绕O 点以每秒5的速度逆时针方向旋转t 秒(013t <<),t 为何值时AOC DOE ∠=∠;(3)射线OC 绕O 点以每秒10的速度逆时针方向旋转,射线OE 绕O 点以每秒5的速度顺时针方向旋转,若射线OC OE 、同时开始旋转m 秒(024.5m <<)后得到45AOC EOB ∠=∠,求m 的值. 37.已知:点O 为直线AB 上一点,90COD ∠=︒ ,射线OE 平分AOD ∠,设COE α∠=.(1)如图①所示,若25α=︒,则BOD ∠= .(2)若将COD ∠绕点O 旋转至图②的位置,试用含α的代数式表示BOD ∠的大小,并说明理由;(3)若将COD ∠绕点O 旋转至图③的位置,则用含α的代数式表示BOD ∠的大小,即BOD ∠= .(4)若将COD ∠绕点O 旋转至图④的位置,继续探究BOD ∠和COE ∠的数量关系,则用含α的代数式表示BOD ∠的大小,即BOD ∠= .38.如图1,点A ,B ,C ,D 为直线l 上从左到右顺次的4个点.(1) ①直线l 上以A ,B ,C ,D 为端点的线段共有 条;②若AC =5cm ,BD =6cm ,BC =1cm ,点P 为直线l 上一点,则PA +PD 的最小值为 cm ;(2)若点A 在直线l 上向左运动,线段BD 在直线l 上向右运动,M ,N 分别为AC ,BD 的中点(如图2),请指出在此过程中线段AD ,BC ,MN 有何数量关系并说明理由;(3)若C 是AD 的一个三等分点,DC >AC ,且AD=9cm ,E ,F 两点同时从C ,D 出发,分别以2cm/s ,1cm/s 的速度沿直线l 向左运动,Q 为EF 的中点,设运动时间为t ,当AQ+AE+AF=32AD 时,请直接写出t 的值. 39.如图①,已知线段30cm AB =,4cm CD =,线段CD 在线段AB 上运动,E 、F 分别是AC 、BD 的中点.(1)若8cm AC ,则EF =______cm ;(2)当线段CD 在线段AB 上运动时,试判断EF 的长度是否发生变化?如果不变请求出EF 的长度,如果变化,请说明理由;(3)我们发现角的很多规律和线段一样,如图②已知COD ∠在AOB ∠内部转动,OE 、OF 分别平分AOC ∠和BOD ∠,则EOF ∠、AOB ∠和COD ∠有何数量关系,请直接写出结果不需证明.40.点O 为直线AB 上一点,在直线AB 同侧任作射线OC 、OD ,使得∠COD=90°(1)如图1,过点O 作射线OE ,当OE 恰好为∠AOC 的角平分线时,另作射线OF ,使得OF 平分∠BOD ,则∠EOF 的度数是__________度;(2)如图2,过点O 作射线OE ,当OE 恰好为∠AOD 的角平分线时,求出∠BOD 与∠COE 的数量关系;(3)过点O 作射线OE ,当OC 恰好为∠AOE 的角平分线时,另作射线OF ,使得OF 平分∠COD ,若∠EOC=3∠EOF ,直接写出∠AOE 的度数41.已知120AOB ∠︒= (本题中的角均大于0︒且小于180︒)(1)如图1,在AOB ∠内部作COD ∠,若160AOD BOC ∠∠︒+=,求COD 的度数;(2)如图2,在AOB ∠内部作COD ∠,OE 在AOD ∠内,OF 在BOC ∠内,且3DOE AOE ∠∠=,3COF BOF ∠=∠,72EOF COD ∠=∠,求EOF ∠的度数;(3)射线OI 从OA 的位置出发绕点O 顺时针以每秒6︒的速度旋转,时间为t 秒(050t <<且30t ≠).射线OM 平分AOI ∠,射线ON 平分BOI ∠,射线OP 平分MON ∠.若3MOI POI ∠=∠,则t = 秒.42.如图1,射线OC 在∠AOB 的内部,图中共有3个角:∠AOB 、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的三倍,则称射线OC 是∠AOB 的“奇分线”,如图2,∠MPN=42°:(1)过点P 作射线PQ,若射线PQ 是∠MPN 的“奇分线”,求∠MPQ ;(2)若射线PE 绕点P 从PN 位置开始,以每秒8°的速度顺时针旋转,当∠EPN 首次等于180°时停止旋转,设旋转的时间为t (秒).当t 为何值时,射线PN 是∠EPM 的“奇分线”?43.(1)探究:哪些特殊的角可以用一副三角板画出?在①135︒,②120︒,③75︒,④25︒中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线EF ,然后将一副三角板拼接在一起,其中45角(AOB ∠)的顶点与60角(COD ∠)的顶点互相重合,且边OA 、OC 都在直线EF 上.固定三角板COD 不动,将三角板AOB 绕点O 按顺时针方向旋转一个角度α,当边OB 与射线OF 第一次重合时停止.①当OB 平分EOD ∠时,求旋转角度α;②是否存在2BOC AOD ∠=∠?若存在,求旋转角度α;若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】将选项A ,C ,D 合并同类项,判断出选项B 中左边两项不是同类项,不能合并,即可得出结论,【详解】解:A 、3a 2+4a 2=7a 2,故选项A 不符合题意;B 、4m 2n 与2mn 2不是同类项,不能合并,故选项B 不符合题意;C.、2x -12x =32x ,故选项C 符合题意; D 、2a 2-a 2=a 2,故选项D 不符合题意;故选C .【点睛】 本题考查同类项的意义,合并同类项的法则,解题关键是掌握合并同类项法则.2.A解析:A【解析】【分析】把x =3代入方程3x ﹣a =0得到关于a 的一元一次方程,解之即可.【详解】把x =3代入方程3x ﹣a =0得:9﹣a =0,解得:a =9.故选A .【点睛】本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键.3.B解析:B【解析】【分析】根据去括号法逐一计算即可.【详解】A. a b +c a b c -=--(),正确;B. ()a b c a b c --=-+,错误;C. ()()a b c a b c -+-=--,正确;D. ()()c b a a b c ---=--,正确;故答案为:B .【点睛】本题考查了去括号法的应用,掌握去括号法逐一计算是解题的关键.4.C解析:C【解析】【分析】设“H”型框中的正中间的数为x ,则其他6个数分别为x-8,x-6,x+-1,x+1,x+6,x+8,表示出这7个数之和,然后分别列出方程解答即可.【详解】解:设“H”型框中的正中间的数为x ,则其他6个数分别为x-8,x-6,x-1,x+1,x+6,x+8,这7个数之和为:x-8+x-6+x-1+x+1+x+x+6+x+8=7x.由题意得A、7x=63,解得:x=9,能求得这7个数;B、7x=70,解得:x=10,能求得这7个数;C、7x=92,解得:x=927,x须为正整数,∴不能求得这7个数;D、7x=105,解得:x=15,能求得这7个数.故选:C【点睛】此题考查一元一次方程的实际运用,掌握“H”型框中的7个数的数字的排列规律是解决问题的关键.5.B解析:B【解析】【分析】同类项定义:单项式所含字母及字母指数相同的是同类项,单个数也是同类项.根据定义即可判断选择项.【详解】A是两个常数,是同类项;B中两项所含字母相同但相同字母的指数不同,不是同类项;C和D所含字母相同且相同字母的指数也相同的项,是同类项.故选:B.【点睛】本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项.注意同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同.6.B解析:B【解析】【分析】根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.【详解】解:图中,∠2=∠COE(对顶角相等),又∵AB⊥CD,∴∠1+∠COE=90°,∴∠1+∠2=90°,∴两角互余.故选:B.【点睛】本题考查了余角和垂线的定义以及对顶角相等的性质.解析:C【解析】【分析】根据特殊直角三角形的角度即可解题.【详解】解:由特殊直角三角形可知,∠1=90°-30°=60°,故选C.【点睛】本题考查了特殊直角三角形的认识,属于简单题,熟悉特殊三角形的角度是解题关键. 8.C解析:C【解析】【分析】根据线段的中点,即可找到线段之间的数量关系.【详解】∵点C是AB的中点,点D是BC的中点,∴AC=BC,CD=BD,∵CD=CB-BD=AC-BD,∴①正确,∵AD-BC=AC+CD-BC=CD,∴②正确,∵2AD-AB=2AC+2CD-AB=2CD=2BD BD,∴③错误,∵CD=12BC, BC=12AB,即CD=14AB,∴④错误,综上只有两个是正确的,故选C.【点睛】本题考查了线段中点的性质,属于简单题,灵活利用相等的线段等量代换是解题关键. 9.D解析:D【解析】【分析】【详解】解:设小长方形的宽为a,长为b,则有b=n-3a,阴影部分的周长:2(m-b)+2(m-3a)+2n=2m-2b+2m-6a+2n=4m-2(n-3a)-6a+2n=4m-2n+6a-6a+2n=4m.故选D.解析:D【解析】【分析】根据折叠后白色圆与蓝色圆所在的面的位置进行判断即可.【详解】解:A.两个蓝色圆所在的面折叠后是对面,不合题意;B.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;C.白色圆与一个蓝色圆所在的面折叠后是对面,不合题意;D.白色圆与两个蓝色圆所在的面折叠后是相邻的面,符合题意;故选:D.【点睛】本题主要考查正方体的展开图,掌握正方体的展开图各个面的相对位置是解题的关键.11.A解析:A【解析】试题解析:A、∠α+∠β=180°-90°=90°,则∠α与∠β互余,选项正确;B、∠α与∠β不互余,故本选项错误;C、∠α与∠β不互余,故本选项错误;D、∠α和∠β互补,故本选项错误.故选A.12.D解析:D【解析】【分析】根据各项定义性质判断即可.【详解】D选项应该为:同一平面内不相交的两条直线叫平行线.故选D.【点睛】本题考查基础的定义性质,关键在于熟记定义与性质.13.C解析:C【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】15000用科学计数法可表示为:.41510⨯故选:C【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.14.A解析:A【解析】【分析】利用“逆移”的定义,找到循环规律,进行比较即可.【详解】解:∵在点1A 开始经过1234A A A A →→→为第一次“逆移”在点4A 开始经过4123A A A A →→→为第二次“逆移”在点3A 开始经过3412A A A A →→→为第三次“逆移”在点2A 开始经过2341A A A A →→→为第四次“逆移”∴每四次“逆移”为一次循环∵20204=505÷∴第2020次“逆移”为:2341A A A A →→→∴经过2020次“逆移”,最终到达的位置是1A故选:A【点睛】本题考查了规律的寻找,正确找出循环规律是解题的关键.15.D解析:D【解析】【分析】根据正方体的展开图即可得出答案.【详解】根据正方体的展开图可知:“数”的对面的字是“养”“学”的对面的字是“核”“心”的对面的字是“素”故选:D .【点睛】本题主要考查正方体的展开图,掌握正方体展开图的特点是解题的关键.二、填空题16.37【解析】【分析】根据题意列出一元一次方程即可求解.【详解】解:设十位上的数字为a,则个位上的数为(a+4),依题意得:a+a+4=10,解得:a=3,∴这个两位数为:37【点睛解析:37【解析】【分析】根据题意列出一元一次方程即可求解.【详解】解:设十位上的数字为a,则个位上的数为(a+4),依题意得:a+a+4=10,解得:a=3,∴这个两位数为:37【点睛】本题考查了一元一次方程的实际应用,属于简单题,找到等量关系是解题关键.17.或【解析】【分析】设经过t秒时间A、B间的距离为个单位长度,分两种情况:①B在A的右边;②B在A的左边.由BA=3分别列出方程,解方程即可;【详解】解:设经过t秒时间A、B间的距离为个单位解析:3或5【解析】【分析】设经过t秒时间A、B间的距离为3个单位长度,分两种情况:①B在A的右边;②B在A 的左边.由BA=3分别列出方程,解方程即可;【详解】解:设经过t秒时间A、B间的距离为3个单位长度,此时点A表示的数是:10-7t,点B 表示的数是:-2-4t.①当B在A的右边时:(10-7t)-(-2-4t.)=3,解得:t=3;②当B在A的左边时:(-2-4t.)-(10-7t)=3,解得:t=5;故答案为:3或5【点睛】本题考查一元一次方程的应用和数轴,解题关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出等量关系列出方程,再求解.18.两点确定一条直线【解析】【分析】根据两点确定一条直线解答.【详解】解:要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是:两点确定一条直线,故答案为两点确定一条直线.【点睛】本解析:两点确定一条直线【解析】【分析】根据两点确定一条直线解答.【详解】解:要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是:两点确定一条直线,故答案为两点确定一条直线.【点睛】本题考查了直线的性质,熟记两点确定一条直线是解题的关键.19.【解析】【分析】将所求式子化简后再将已知条件中整体代入即可求值;【详解】,,;故答案为.【点睛】本题考查代数式求值;熟练掌握整体代入法求代数式的值是解题的关键. 解析:5【解析】【分析】将所求式子化简后再将已知条件中2a b -=整体代入即可求值;【详解】20a b --=,∴2a b -=,∴()12212145a b a b +-=+-=+=;故答案为5.【点睛】本题考查代数式求值;熟练掌握整体代入法求代数式的值是解题的关键.20.150【解析】【分析】根据对顶角相等得到∠AOB 的度数,再根据邻补角的定义即可得出结论.【详解】∵∠AOB=∠COD,∠AOB+∠COD=60°,∴∠AOB=∠COD=30°,∴∠BOD= 解析:150【解析】【分析】根据对顶角相等得到∠AOB 的度数,再根据邻补角的定义即可得出结论.【详解】∵∠AOB =∠COD ,∠AOB +∠COD =60°,∴∠AOB =∠COD =30°,∴∠BOD =180°-∠AOB =180°-30°=150°.故答案为150°.【点睛】本题考查了对顶角相等和邻补角的定义.求出∠AOB 的度数是解题的关键.21.cm 或15 cm【解析】【分析】【详解】解:根据题意画出图形:①当点C 在线段AB 上时,如图1,=②当点C 在线段AB 的延长线上时,如图2,=故答案为:5 cm或15 cm【点睛】解析:cm或15 cm【解析】【分析】【详解】解:根据题意画出图形:①当点C在线段AB上时,如图1,AC AB BC=-=1055;cm-=②当点C在线段AB的延长线上时,如图2,AC AB BC=+=10515.cm+=故答案为:5 cm或15 cm【点睛】本题考查线段的和与差,注意分类讨论是本题的解题关键.22.2【解析】【分析】设小长方形的长为x,宽为y,根据大长方形的长及宽,可得出关于x、y的二元一次方程组,解之即可得出结论.【详解】设小长方形的长为x,宽为y,根据题意得:,解得:,∴解析:2【解析】【分析】设小长方形的长为x,宽为y,根据大长方形的长及宽,可得出关于x、y的二元一次方程组,解之即可得出结论.【详解】设小长方形的长为x,宽为y,根据题意得:21028x yx y⎧⎨⎩+=+=,解得:42x y ⎧⎨⎩==, ∴宽为2.故答案为:2.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.23.【解析】【分析】先根据题意算出∠AOC,再由平分的条件算出∠BOC.【详解】∵,,∴∠AOC=∠AOD -∠COD=135°-75°=60°,∵OB 平分∠AOC,∴∠BOC=.故答案解析:【解析】【分析】先根据题意算出∠AOC,再由平分的条件算出∠BOC.【详解】∵135AOD ∠=︒,75COD ∠=︒,∴∠AOC=∠AOD-∠COD=135°-75°=60°,∵OB 平分∠AOC,∴∠BOC=1302AOC ∠=︒.故答案为:30.【点睛】本题考查角度的计算,关键在于结合图形进行计算. 24.【解析】【分析】根据题意表达出,将其代入计算即可.【详解】解:∵代数式的值为 1∴∴∴∴故答案为:【点睛】本题考查了代数式的求值,掌握整体思想求代数式的值是解题的关键. 解析:1-4【解析】【分析】 根据题意表达出235=44x x +,将其代入2314x x --计算即可. 【详解】解:∵代数式2434x x +-的值为 1∴2434=1x x +-∴243=5x x + ∴235=44x x + ∴23511=1-=-444x x -- 故答案为:1-4 【点睛】本题考查了代数式的求值,掌握整体思想求代数式的值是解题的关键.25.【解析】【分析】【详解】被减式为x 的,减式为y 的,让它们相减即可.解:所求的关系式为:.求两个式子的差的关键是找到被减式和减式. 解析:2134x y - 【解析】【分析】【详解】被减式为x 的23,减式为y 的14,让它们相减即可. 解:所求的关系式为:2134x y -. 求两个式子的差的关键是找到被减式和减式.三、解答题26.(1)x=-3;(2)x=3711-. 【解析】【分析】(1)直接去括号,然后移项合并,系数化为1,即可得到答案;(2)先去分母,然后去括号,移项合并,系数化为1,即可得到答案.【详解】解:(1)23(1)8x -+=,∴2338x --=,∴39x -=,∴3x =-;(2)531243x x +--=-, ∴3(53)4(1)24x x +--=-,∴1594424x x +-+=-,∴1137x =-, ∴3711x =-. 【点睛】 本题考查了解一元一次方程,解题的关键是掌握解一元一次方程的方法和步骤.27.-2【解析】【分析】先根据整式的乘法去括号,再合并同类项,进行化简,再代入已知数求值即可.【详解】解:原式22226354a b ab a b ab =--+22a b ab =+()ab a b =+当a=2,b=-1时,原式21=-⨯2=-【点睛】本题考核知识点:整式化简求值. 解题关键点:掌握整式的基本运算法则.28.(1)96m n -;(2)23ab a -+【解析】【分析】(1)先去括号再合并同类项即可;(2)去括号再合并同类项即可.解:(1)原式636m m n =+-96m n =-(2)原式2283564ab a ab ab a =---+23ab a =-+【点睛】本题考查了整式的加减,熟练掌握合并同类项的方法是解题的关键,易错点在于括号前是负号时去括号要变号.29.(1)4.5;(2)① 120°;②经过4.5,7.2秒时,其中一条射线是另外两条射线夹角的平分线.【解析】【分析】(1)设t 秒后第一次重合.根据题意,列出方程,解方程即可;(2)①利用180°减去OA 转动的角度,加上OB 转动的角度,即可得到答案;②先用t 的代数式表示∠BON 和∠AON ,然后分为三种情况进行讨论:当ON 、OA 、OB 为角平分线时,分别求出t 的值,即可得到答案.【详解】解:(1)若OA 顺时针转动,OB 逆时针转动,∴∠AOM+∠BON=180°,∴3010180t t +=,解得: 4.5t =;∴ 4.5t =秒,OA 与OB 第一次重合;故答案为:4.5;(2)①若OA 、OB 同时顺时针转动,∴30390AOM ∠=︒⨯=︒,10330BON ∠=︒⨯=︒,∴1809030120AOB ∠=︒-︒+︒=︒;故答案为:120;② 由题意知012t ≤≤,∴∠BON =10t ,∠AON =180-30t (0≤t ≤6),∠AON =30t -180(6<t ≤12).当ON 为∠AOB 的角平分线时,有180-30t =10t ,解得:t =4.5;当OA 为∠BON 的角平分线时,10t =2(30t -180),解得:t =7.2;当OB 为∠AON 的角平分线时,30t -180=2×10t ,解得:t =18(舍去);∴经过4.5,7.2秒时,射线OA 、OB 、ON 其中一条射线是另外两条射线夹角的平分线.本题考查一元一次方程的应用,解题的关键是理解题意,学会设未知数列方程解决问题,注意利用分类讨论的思想进行解题,属于中考常考题型.30.(1)详见解析;(2)OP;(3)=,同角的余角相等【解析】【分析】(1)过点P作PD⊥OB,交OA于点D即可;(2)根据点到直线距离的定义即可得出结论;(3)根据同角的余角相等即可得出结论.【详解】解:(1)如图即为所求:(2)∵PD⊥OB∴线段OP的长度是点O到直线PD 的距离故答案为:OP(3)∵PC⊥OA∴∠PDC+∠CPD=90°∵PD⊥OB∴∠OPC+∠CPD=90°∴∠OPC=∠PDC故答案为:=,同角的余角相等【点睛】本题考查网格线内基本作图、点到直线的距离的定义及同角的余角相等,熟知相关知识点灵活应用是解答此题的关键.31.(1)2;(2)-6.【解析】【分析】(1)先括号、去绝对值,再根据有理数加减混合运算法则计算即可;(2)先计算绝对值和平方,再根据有理数混合运算法则计算即可.【详解】(1)原式=3+7-8=2.(2)原式=-9-6+1+4×2=-15+1+8=-6.【点睛】本题考查有理数混合运算,熟练掌握运算法则是解题关键.32.(1)见解析;(2)38;(3)4.【解析】【分析】(1)根据三视图的画法画出三视图即可;(2)分别求出前后左右上下一共有几个面,再计算它们的和即可;(3)保持这个几何体的左视图和俯视图不变,可以在第二层第二排(从左向右数)的小正方体上放置1个小正方体,第三排小正方体上放2个小正方体,在第三层第三排的小正方体上放1个小正方体,再计算放置小正方体的和即可.【详解】(1)该几何体的主视图、左视图、俯视图如图所示:(2)该几何体表面积为6+6+6+6+7+7=38;(3)要保持这个几何体的左视图和俯视图不变,可以在第二层第二排(从左向右数)的小正方体上放置1个小正方体,第三排小正方体上放2个小正方体,在第三层第三排的小正方体上放1个小正方体,所以可放置小正方体的个数为1+2+1=4.【点睛】本题考查组合体的三视图,解题的关键是计算出当左视图和俯视图不变时,可以在每一层上放置的小正方体数.33.(1)∠AOC=60°,(2)360°﹣2α.【解析】【分析】(1)利用垂直的定义和角的和差关系可得∠COE,由角平分线的性质可得∠BOE,然后根据平角的定义解答即可;(2)根据垂直的定义和角的和差关系可得∠COE,由角平分线的性质可得∠BOE,然后利用平角的定义求解即可.【详解】解:(1)∵OC⊥OD,∴∠DOC=90°,∵∠DOE=150°,∴∠COE=∠DOE﹣∠COD=150°﹣90°=60°,∵射线OE平分∠BOC,∴∠COE=∠BOE=60°,∴∠AOC=180°﹣∠COE﹣∠BOE=180°﹣60°﹣60°=60°,(2)∵OC⊥OD,∴∠DOC=90°,∵∠DOE=α,∴∠COE=∠DOE﹣∠COD=α﹣90°,∵射线OE平分∠BOC,∴∠COE=∠BOE=α﹣90°,∴∠AOC=180°﹣∠COE﹣∠BOE=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,故答案为:360°﹣2α.【点睛】本题考查了垂直的定义、角平分线的性质、平角的定义和角的和差关系,属于基本题型,熟练掌握基本知识是解题关键.四、压轴题34.(1)①7+21;②10.82-;③22.83.23+-;(2)9;(3)10012004.【解析】【分析】(1)根据绝对值的性质:正数的绝对值等于它本身;负数的绝对值等于它的相反数;0的绝对值是0即可得出结论;(2)首先根据有理数的运算法则判断式子的符号,再根据绝对值的性质正确化简即可;(3)首先根据有理数的运算法则判断式子的符号,再根据绝对值的性质正确化简即可.【详解】解:(1)①|7+21|=21+7;故答案为:21+7;②110.80.822 -+=-;故答案为:1 0.82-;③23.2 2.83--=22.83.23+-故答案为:22.83.23+-;(2)原式=1111 9242 33202033 -++-=9(3)原式 =11111111... 23344520032004 -+-+-++-=1122004- =10012004【点睛】 此题考查了有理数的加减混合运算,此题的难点把互为相反的两个数相加,使运算简便.做题时,要注意多观察各项之间的关系.35.(1)80°,20°;(2)90°;(3)当030AOB <∠<时,45BOM CON ∠+∠=;当3090AOB <∠<,45CON BOM ∠-∠=,理由见解析【解析】【分析】 (1)利用平角的定义、角平分线的定义和角的和差即可得出结论(2)设AOM COM x ∠=∠=,再根据已知12BOM COD ∠=∠得出∠BOM=90°-x , 再利用BOC BOM COM ∠=∠+∠即可得出结论(3)分030AOB <∠<,3090AOB <∠<两种情况加以讨论【详解】解:(1)∵∠AOB=40°,∠COD=60°∴∠BOC=180°-∠AOB -∠COD=80°,∠AOC=180°-∠COD =120°∵OM 平分∠AOC∴∠AOM=60°∴∠BOM=∠AOM-∠AOB =20°故答案为:80°,20°(2)∵OM 平分∠AOC∴设AOM COM x ∠=∠=,则1802COD x ∠=-∵12BOM COD ∠=∠ ∴()11802902BOM x x ∠=-=- ∴9090BOC BOM COM x x ∠=∠+∠=-+=(3)当030AOB <∠<时,即OB 在OM 下方时设AOB x ∠=∴90AOC x ∠=- ∴1452AOM x ∠=-∴13454522BOM x x x ∠=--=- ∴119022DOA DOB x ∠==-. ∴13909022CON DOC DON x x x ∠=∠-∠=+-+= ∴45BOM CON ∠+∠=②当3090AOB <∠<,即OB 在OM 上方时设AOB x ∠=∴90AOC x ∠=-∴1452AOM x ∠=-∴3452BOM x ∠=- ∴1809090DOC x x ∠=-+=+,∵ON 平分BOD ∠,∴119022DON BOD x ∠=∠=- ∴32CON x ∠= ∴45CON BOM ∠-∠=【点睛】本题考查角的相关计算,难度适中,涉及角平分线的定义和邻补角相加等于180°的知识点;同时,里面的小题从易到难,体现了分类讨论的数学思想.36.(1)∠COE =20°;(2)当t =11时,AOC DOE ∠=∠;(3)m=296或10114【解析】【分析】 (1)根据角平分线的定义和垂直定义即可求出∠BOD=90°,∠BOE=∠DOE =45°,即可求出∠AOB ,再根据角平分线的定义即可求出∠BOC ,从而求出∠COE ;(2)先分别求出OC 与OD 重合时、OE 与OD 重合时和OC 与OA 重合时运动时间,再根据t 的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出t 即可; (3)先分别求出OE 与OB 重合时、OC 与OA 重合时、OC 为OA 的反向延长线时运动时、OE 为OB 的反向延长线时运动时间,再根据m 的取值范围分类讨论,分别画出对应的图形,根据等量关系列出方程求出m 即可;【详解】解:(1)∵OD OB ⊥,OE 是BOD ∠的角平分线,∴∠BOD=90°,∠BOE=∠DOE=12∠BOD =45° ∵85AOE ∠=∴∠AOB=∠AOE +∠BOE=130°∵OC 是AOB ∠的角平分线,∴∠AOC=∠BOC=12AOB ∠=65° ∴∠COE=∠BOC -∠BOE=20°(2)由原图可知:∠COD=∠DOE -∠COE=25°,故OC 与OD 重合时运动时间为25°÷5°=5s ;OE 与OD 重合时运动时间为45°÷5°=9s ;OC 与OA 重合时运动时间为65°÷5°=13s ;①当05t <<时,如下图所示∵∠AOD=∠AOB -∠BOD=40°,∠COE=20°∴∠AOD ≠∠COE∴∠AOD +∠COD ≠∠COE +∠COD∴此时AOC DOE ∠≠∠;②当59t <<时,如下图所示。
苏教版七年级上册数学 期末试卷培优测试卷
苏教版七年级上册数学 期末试卷培优测试卷一、选择题1.有理数-53的倒数是( ) A .53 B .53-C .35D .352.钟面上8:45时,时针与分针形成的角度为( ) A .7.5°B .15°C .30°D .45°3.下列各组中的两个单项式,属于同类项的一组是( ) A .23x y 与23xyB .3x 与3xC .22与2aD .5与-34.已知点C 在线段AB 上,则下列条件中,不能确定点C 是线段AB 中点的是( ) A .AC =BCB .AB =2ACC .AC +BC =ABD .12BC AB =5.有理数 a 在数轴上的位置如图所示,下列各数中,可能在 1 到 2 之间的是( )A .-aB .aC .a -1D .1 -a6.某商品在进价的基础上提价 70 元后出售,之后打七五折促销,获利 30 元,则商品进价为 ( )元. A .100B .140C .90D .1207.-8的绝对值是( ) A .8B .18C .-18D .-88.一个几何体的侧面展开图如图所示,则该几何体的底面是( )A .B .C .D .9.下列平面图形不能够围成正方体的是( ) A .B .C .D .10.13-的倒数是( )A .3B .13C .13-D .3-11.下列图形,不是柱体的是( ) A .B .C .D .12.若,,则多项式与的值分别为( ) A .6,26 B .-6,26 C .-6,-26 D .6,-26 13.若1x =是方程260x m +-=的解,则m 的值是( )A .﹣4B .4C .﹣8D .814.让人欲罢不能的主题曲,让人潸然泪下的小故事,让人惊叹不已的演出阵容《我和我的祖国》首日票房超过285000000元,数字285000000科学记数法可表示为( ) A .2.85×109B .2.85×108C .28.5×108D .2.85×10615.小红在计算23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭时,拿出 1 张等边三角形纸片按如图所示方式进行操作.①如图1,把 1 个等边三角形等分成 4 个完全相同的等边三角形,完成第 1 次操作;②如图 2,再把①中最上面的三角形等分成 4 个完全相同的等边三角形,完成第 2 次操作;③如图 3,再把②中最上面的三角形等分成 4 个完全相同的等边三角形,······依次重复上述操作.可得23202011114444⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值最接近的数是( )A .13B .12C .23D .1二、填空题16.在-4,0,π,1.010010001,-227,1.3•这6个数中,无理数有______个. 17.若∠1= 42°36’,则∠1 的余角等于___________°.18.已知∠α=28°,则∠α的补角为_______°. 19.﹣|﹣2|=____.20.请写出一个系数是-2,次数是3的单项式:________________.21.一件衬衫先按成本提高50%标价,再以8折出售,获利20元,则这件衬衫的成本是__22.如图,已知直线AB 和CD 相交于点O ,射线OE 在COB ∠内部,OE OC ⊥,OF 平分AOE ∠,若40BOD ∠=,则COF ∠=__________度.23.己知:如图,直线,AB CD 相交于点O ,90COE ∠=︒,:1BOD BOC ∠∠=:5,过点O 作OF AB ⊥,则∠EOF 的度数为_______.24.如图,直线AB ,CD 相交于点O ,若∠AOC +∠BOD =100°,则∠AOD 等于__________度.25.计算:32--=________.三、解答题26.解方程:(1)()()210521x x x x -+=+- (2)1.7210.70.3x x --= 27.如图,在数轴上,点A 表示10-,点B 表示11,点C 表示18.动点P 从点A 出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q 从点C 出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t 秒.(1)当t 为何值时,P 、Q 两点相遇?相遇点M 所对应的数是多少?(2)在点Q 出发后到达点B 之前,求t 为何值时,点P 到点O 的距离与点Q 到点B 的距离相等;(3)在点P 向右运动的过程中,N 是AP 的中点,在点P 到达点C 之前,求2CN PC -的28.先化简,再求值:()()22224333a b ab aba b ---+.其中 1a =-、 2b =-.29.已知同一平面内,∠AOB=90°,∠AOC=30°, (1)画出图形并求∠COB 的度数;(2)若OD 平分∠BOC ,OE 平分∠AOC ,求∠DOE 的度数.30.在如图所示的方格纸中,每个小正方形的顶点称为格点,每个小正方形的边长为1,已知四边形的四个顶点在格点上,利用格点和直尺按下列要求画图:(1)过点O 画AD 的平行线CE ,过点B 画CD 的垂线,垂足为F ; (2)四边形ABCD 的面积为____________31.有三条长度均为a 的线段,分别按以下要求画圆.(1)如图①,以该线段为直径画一个圆,记该圆的周长为C 1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C 2,请指出C 1和C 2的数量关系,并说明理由;(2)如图③,当a =11时,以该线段为直径画一个大圆,再在大圆内画若千小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为 .(直接填写答案,结果保留π)32.已知:如图,点P 是数轴上表示-2与-1两数的点为端点的线段的中点.(1)数轴上点P 表示的数为 ;(2)在数轴上距离点P 为2.5个单位长度的点表示的数为 ;(3)如图,若点P 是线段AB (点A 在点B 的左侧)的中点,且点A 表示的数为m ,那么点B 表示的数是 .(用含m 的代数式表示)33.已知A 、B 在直线l 上,28AB =,点C 线段AB 的中点,点P 是直线l 上的一个动点.(1)若5BP =,求CP 的长;(2)若M 是线段AP 的中点,N 是BP 的中点,求MN 的长.四、压轴题34.点A 、B 在数轴上分别表示数,a b ,A 、B 两点之间的距离记为AB .我们可以得到AB a b =-:(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5两点之间的距离是 ;数轴上表示1和a 的两点之间的距离是 .(2)若点A 、B 在数轴上分别表示数-1和5,有一只电子蚂蚁在数轴上从左向右运动,设电子蚂蚁在数轴上的点C 对应的数为c .①求电子蚂蚁在点A 的左侧运动时AC BC +的值,请用含c 的代数式表示; ②求电子蚂蚁在运动的过程中恰好使得1511c c ,c 表示的数是多少? ③在电子蚂蚁在运动的过程中,探索15c c 的最小值是 .35.某市两超市在元旦节期间分别推出如下促销方式: 甲超市:全场均按八八折优惠;乙超市:购物不超过200元,不给于优惠;超过了200元而不超过500元一律打九折;超过500元时,其中的500元优惠10%,超过500元的部分打八折; 已知两家超市相同商品的标价都一样.(1)当一次性购物总额是400元时,甲、乙两家超市实付款分别是多少? (2)当购物总额是多少时,甲、乙两家超市实付款相同?(3)某顾客在乙超市购物实际付款482元,试问该顾客的选择划算吗?试说明理由. 36.如图,数轴上A ,B 两点对应的数分别为4-,-1 (1)求线段AB 长度(2)若点D 在数轴上,且3DA DB =,求点D 对应的数(3)若点A 的速度为7个单位长度/秒,点B 的速度为2个单位长度/秒,点O 的速度为1个单位长度/秒,点A ,B ,O 同时向右运动,几秒后,3?OA OB =37.已知:点O 为直线AB 上一点,90COD ∠=︒ ,射线OE 平分AOD ∠,设COE α∠=.(1)如图①所示,若25α=︒,则BOD ∠= .(2)若将COD ∠绕点O 旋转至图②的位置,试用含α的代数式表示BOD ∠的大小,并说明理由;(3)若将COD ∠绕点O 旋转至图③的位置,则用含α的代数式表示BOD ∠的大小,即BOD ∠= .(4)若将COD ∠绕点O 旋转至图④的位置,继续探究BOD ∠和COE ∠的数量关系,则用含α的代数式表示BOD ∠的大小,即BOD ∠= .38.尺规作图是指用无刻度的直尺和圆规作图。
苏科版数学七年级上提优练习与答案(期末综合练习一)
苏科版数学七年级上提优练习内容:期末综合练习一一.选择题(每小题3分,共30分)1.(2019吉林中考)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图l,A、B两地问修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )A.两点之间线段最短B.平行于同一条直线的两条直线平行C.垂线段最短D.两点确定一条直线2.下列几何体中,是圆锥的为 ( )3.(2019湖南益阳中考)下列几何体中,其侧面展开图为扇形的是 ( )4.(2019江苏淮安中考)如图2是由4个相同的小正方体搭成的几何体,则该几何体的主视图是 ( ) 5.下列各式中,正确的是 ( )A.3a+2b=5ab B.一3ab一2ab=一abC.-5(a一3)=一5a+3 D.2a一3=一(3—2n)6.图3是一个正方体纸盒的表面展开图,折成正方体后,相对面上的两个数互为相反数,则A,B,C表示的数分别为 ( )A.0,一5,3B.0,3,一5C.3,0,一5D.一5,3,07.计算机按如图4所示的程序工作,若输入的数是l,则输出的数是 ( )A.一63 B.63 C.-639 D.6398.(2020独家原创试题)当x=一1时,代数式ax3+bx+1的值为一2019,则当x=1时,代数式ax3+bx+1的值为( )A.一2018 B .2019 C.一2020 D.202l9.(20t9福建中考)《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问君每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34685个字,设他第一天读x个字,则下面所列方程正确的是 ( )A.x+2x+4x=34685 B.x+2x+3x=34685C.x+2x+2x=34685 D.x+21x+41x=3468510.如图5,数轴上,点A的初始位置表示的数为l,现点A做如下移动:第1次点A向左移动3个单位长度至点A1.,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3…一,按照这种移动方式进行下去.如果点An与原点的距离不小于20,那么n的最小值是 ( )A .12B .13C .14D .15二填空题 (每小题3分,共24分)11.用科学记数法写出的数为7.04×104.则原来的数是 . 12.一252的倒数是 , 一252-的相反数是 . 13.若一3x a y 3与-y b x 5是同类项,则血a-b 2=____________.14.如图6,直线AB 、CD 相交于点0,∠1=∠2,若∠AOD=680,则∠l 的度数为______. 15.有六个数:0.123,0.1020020002,(一1.5)3,3.1416,711,一2π,若其中无理数的个数为x ,正数的个数为y,则x+y=____________ .16.在一项居民住房节能改造工程中,某社区计划用a 天完成建筑面积为l000平方米的居民住房节能改造任务,若实际比计划提前b 天完成改造任务.则代数式-ba -1000表示 .17.(2019四川宜宾中考改编)已知一个组合体是由几个相同的正方体叠合在一起组成的.该组合体的主视图与俯视图如图7所示,则该组合体中正方体的个数最多是 .18.(2020独家原创试题)如图8.观察每个图形构成的规律,第n 个图中小圆点的个数为 .三解答题 (共66分)19.(6分)如图9,所有小正方形的边长都为l .A 、B 、C 都在格点上(小正方形的顶点叫做格点).请仅用没有刻度的直尺完成画图(不要求写湎法)及解答:(1)过点C 画直线AB 的平行线CD : (2)过点A 画直线BC 的垂线,并注明垂足为G ,过点A 画直线AB 的垂线,交BC 于点H : (3)线段______的长度是点A 到逝线BC 的距离;(4) ∠B 与∠HAG 的大小关系为________,理由是 .20.(2020江苏南京江-7期中)(7分)计算:一l 2+|一2—1|÷6×(31一21)21.(7分)解方程:22+x -632-x =l22.(8分)先化简,再求值:4x 2一[3x 2一(5xy 一2x 2)+3xy],其中x=10,y=5.23.(8分)如图l0,C、D两点将线段AB分成2:3:4的三部分,E为线段AB的中点,AD=6cm.(1)求线段AB的长:(2)求线段DE的长.24.(10分)如图l1,点0在直线AD上,∠EOC=900,∠DOB=900.已知∠EOD=500.(1)求∠AOC的度数;(2)若OM平分∠AOC,ON平分∠BOC,求∠MON的度数.25.(10分)平价商场经销甲、乙两种商品,甲种商品每件售价为60元,利润率为50%;乙种商品每件进价为50元,售价为80元.(1)甲种商品每件进价为元,每件乙种商品的利润率为;(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件;打折前一次性购物总金额优惠措施少于或等于450元不优惠超过450元.但不超过600元按售价打九折超过600元600元部分打八点二折,超过600元部分打i折乙种商品多少件.26.(10分)如图l2①,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC.若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.(1)一个角的平分线这个角的奇妙线(填“是”或“不是”):(2)如图l2②,若∠MPN=600,射线PO绕点P从PN的位置开始,以每秒l00的速度逆时针旋转,当∠QPN首次等于1800时停止旋转,设旋转的时间为t S.①当t为何值时,射线PM是∠QPN的奇妙线?②若射线PM同时绕点P以每秒60的速度逆时针旋转,并与PQ同时停止旋转.当射线PQ是∠MPN的奇妙线时.求出t的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教案(数学)
1、如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中和∠DFM相等的角(不含它本身)的个数为()
A.5 B.6 C.7 D.8
2、珠江流域某江段江水流向经过B、C、D三点拐弯后和原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= .
3、下列说法:①两条直线被第三条直线所截,内错角相等;②同角或等角的余角相等;③相等的角是对顶角;④三角形的三条高交于一点.其中正确的有()
A.1个B.2个C.3个D.4个
4、△ABC中,∠B的外角平分线的和∠C外角平分线相交于点P,且∠BPC=80°,则∠A的度数为.
4、给出以下判断:
(1)线段的中点是线段的重心
(2)三角形的三条中线交于一点,这一点就是三角形的重心
(3)平行四边形的重心是它的两条对角线的交点
(4)三角形的重心是它的中线的一个三等分点
那么以上判断中正确的有()
A.一个B.两个C.三个D.四个
5、两本书按如图所示方式叠放在一起,则图中相等的角是()
A、∠1和∠2 B.∠2和∠3 C.∠1和∠3 D.三个角都相等
6、如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分
别延长AB、BC、CA至点A
1、B
1
、C
1
,使得A
1
B=2AB,B
1
C=2BC,C
1
A=2CA,
顺次连接A
1、B
1
、C
1
,得到△A
1
B
1
C
1
,记其面积为S
1
;第二次操作,分
别延长A
1B
1
、B
1
C
1
、C
1
A
1
至点A
2
、B
2
、C
2
,使得A
2
B
1
=2A
1
B
1
,B
2
C
1
=2B
1
C
1
,
C
2A
1
=2C
1
A
1
,顺次连接A
2
、B
2
、C
2
,得到△A
2
B
2
C
2
,记其面积为S
2
;…;
按此规律继续下去,可得到△A
5B
5
C
5
,则其面积S
5
= .
7、边长为2的等边△ABC和等边△DEF互相重合,将△ABC沿直线L 向左平移m个单位长度,将△DEF向右也平移m个单位长度,如图,当C、E是线段BF的三等分点时,m的值为.
8、如图,已知△ABC的面积是2平方厘米,△BCD的面积是3平方厘米,△CDE的面积是3平方厘米,△DEF的面积是4平方厘米,△EFG 的面积是3平方厘米,△FGH的面积是5平方厘米,那么,△EFH的面积是平方厘米.
9、(1)已知:如图1,在四边形ABCD中,BC⊥CD,∠ACD=∠ADC.
求证:AB+AC>
BC2+CD2
;
(2)已知:如图2,在△ABC中,AB上的高为CD,试判断(AC+BC)2和AB2+4CD2
之间的大小关系,并证明你的结论.
10、平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.将点P移到AB、CD 内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
圆的面积公式:
11、如图,长方形内的阴影部分是由四个半圆围成的图形,则阴影部分的面积是()
B.C.D.
A.
12、观察下列运算过程:S=1+3+32+33+…+32012+32013①,
①×3得3S=3+32+33+…+32013+32014②,
②﹣①得2S=32014﹣1,S=.
运用上面计算方法计算:1+5+52+53+…+52013= .
13、观察下列各式:
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(1)根据上面各式的规律可得(x n+1﹣1)÷(x﹣1)= ;
(2)利用(1)的结论求22015+22014+…+2+1的值;
(3)若1+x+x2+…+x2015=0,求x2016的值.
14、一批志愿者组成了一个“爱心团队”,专门到全国各地巡回演出,以募集爱心基金.第一个月他们就募集到资金1万元.随着影响的扩大,第n(n≥2)个月他们募集到的资金都将会比上个月增加20%,则当该月所募集到的资金首次完成突破10万元时,相应的n的值为.(参考数据:1.25≈2.5,1.26≈3.0,1.27≈3.6)
15、多项式x2+mx+5因式分解得(x+5)(x+n),则m= ,n= .
16、已知a﹣b=4,ab+c2+4=0,则a+b+c的值为()
17、计算﹣的值是()
A.B.
C.D.
18、已知a是大于1的实数,且有a3+a﹣3=p,a3﹣a﹣3=q成立.
(1)若p+q=4,求p﹣q的值;
(2)当q2=22n+﹣2(n≥1,且n是整数)时,比较p和(a3+)的大小,
19、王芳同学到文具店购买中性笔和笔记本,中性笔每支0.8元,笔记本每本1.2元,王芳同学花了10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于0.8元)()
A.6 B.7 C.8 D.9
21、在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由
于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每
班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1
幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
22、某单位欲购买A、B两种电器.根据预算,共需资金15750元.购买一件
A种电器和两件B种电器共需资金2300元;购买两件A种电器和一件B种电器
共需资金2050元.
(1)购买一件A种电器和一件B种电器所需的资金分别是多少元?
(2)若该单位购买A种电器不超过5件,则可购买B种电器至少有多少件?
(3)为节省开支,该单位只购买A、B两种电器共6件,并知道获政府补贴资
金不少于700元;自己出资金不超过4000元;其中政府对A、B两种电器补贴
资金分别为每件100元和150元.请你通过计算求出有几种购买方案?
八上第一章全等三角形
一.知识框架
20、为了参加 2011 年威海国际铁人三项(游泳、自行车、长跑)系列赛业余组的比赛,李明针自行车和长跑项目进行专项训练. 某次训练中,李明骑白行车的平均速度为每分钟 600米. 跑步的平均速度为每分钟200米,自行车路段和长跑路段共 5 千米.用时 15 分钟.求自行车路段和长跑路段的长度.
二.知识概念
1.全等三角形:两个三角形的形状、大小、都一样时,其中一个可以经过平移、旋转、对称等运动(或称变换)使之和另一个重合,这两个三角形称为全等三角形。
2.全等三角形的性质:全等三角形的对应角相等、对应边相等。
3.三角形全等的判定公理及推论有:
(1)“边角边”简称“SAS”
(2)“角边角”简称“ASA”
(3)“边边边”简称“SSS”
(4)“角角边”简称“AAS”
(5)斜边和直角边相等的两直角三角形(HL)。
4.角平分线推论:角的内部到角的两边的距离相等的点在叫的平分线上。
5.证明两三角形全等或利用它证明线段或角的相等的基本方法步骤:①、确定已知条件(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系),②、回顾三角形判定,搞清我们还需要什么,③、正确地书写证明格式(顺序和对应关系从已知推导出要证明的问题).。
