光学谐振腔与引力波探测(方洪烈著)思维导图
光学物理思维导图PPT讲稿思维导图知识点归纳总结[PPT白板课件]
![光学物理思维导图PPT讲稿思维导图知识点归纳总结[PPT白板课件]](https://img.taocdn.com/s3/m/5fbf49e4a1c7aa00b52acbee.png)
光速:3.0x108m/s(真空、空气中)
光的反射
条件:不同介质的分界面
三线共面
反射规律 法线居中
反射角等于入射角
分类:镜面反射和漫反射
应用(例子):潜望镜、后视镜等
原理:光的反射
凸
透
镜
平面镜成像
成
像
规
律
物距(u) 像距(v) 正倒 u>2f 2f>v>f 倒立 u=2f v=2f 倒立
光的反射大小虚实应用特点的位置关系u2f2fvf倒立缩小实像照相机摄像机u2fv2f倒立实像测焦距成像大2fufv2f倒立放大实像幻灯机电影放不成像强光聚焦手电放大虚像放大镜虚像在物体同侧虚像在物体之后物像同条件
总有一款PPT 适合您
【最新出品\精心整理\倾情奉献\敬请珍惜】
光源
光的 直线 传播
条件:透明均匀物质中
2f>u>f v>2f 倒立
u=f -
-
f>u v>u 正立
大小 缩小 等大 放大 -
放大
物,像
虚实 应用 特点 的位置
关系
实像 照摄相像机机、-
物像异 侧
实像
测焦距
成像大 小的分 界点
物像异 侧
幻灯机、
实像电影放 映机、- Nhomakorabea物像异 侧
投影仪
不成像
强光聚 焦手电
成像虚 实的分
-
筒 界点
虚像在
虚像
放大镜
物体同 侧虚像 在物体
物像同 侧
之后
条件:不均匀物质或不同种介质
光 的 折射规律 折射
三线共面
法线居中
华中科技大学-夏珉【激光原理与技术】03光学谐振腔-PPT文档资料116页

– 驻波频率为平面波频率,而且可以为任意值。
3.2.1平平腔的驻波
• 平行平面腔中的驻波
– 当光波在腔镜上反射时,入射波与反射波发生干涉,而多次往复 反射形成的多光束干涉,稳定的振荡要求干涉加强,发生相长干 涉的条件为:波从某一点出发,经腔内往返一次再回到原位时,
– 相以Δ位φ应表与示初往始返出一发周时后相的差相2π位的差整:数 倍。2 2L'4 Lq2
时,称为稳定腔;
• 当 g1g20或 g1g21时,称为非稳腔; • 当 g1g20或 g1g21时,称为临界腔;
ቤተ መጻሕፍቲ ባይዱ
3.1.1光学谐振腔的构成与分类
• 常见开腔的构成及分类:
– 1、平行平面腔: R1,R2
g11R d11,g21R d21
平行平面腔属于临界腔。
g1g2 1
L
R 1 R2
RR
R1 R2
共焦腔 共心腔
3.1.1光学谐振腔的构成与分类
– 平面、凹面反射镜腔
• 由一个平面反射镜和一个凹面反射镜构成 的光腔,
R1 ,R2>0; • 当R2>d时,求得0<g1g2<1,构成稳定腔; • 当R2=d时,构成半共焦腔,g1g2=0,构成 临界腔;
• 当R2<d时,g1g2<0,构成非稳腔;
T
q 1
q 2
t1
t
3.4开腔模式的物理概念和衍射理论分析方法
• 我们关心的问题:在由无侧面的共轴反射 镜构成的开放光学谐振腔区域中,是否存 在不随时间变化的稳定的电磁场分布?
• 如何求出这个分布的具体形式? • 在考察光学谐振腔中电磁场的分布时,我
们首先关心的是镜面上的分布,因为镜面 一般作为激光输出窗口,而输出激光的场 分布就直接与镜面上的场分布有关。
【电动力学课件】4-4-5 谐振腔-波导

n × ( E 2 − E1 ) = 0
n × ( H 2 − H1 ) = α
3
式中n为由介质1指向介质2的法线。这两等式成立后,另外 两个关于法向分量的关系:
n ⋅ ( D2 − D1 ) = σ
自然能够满足。 导体表面边界条件:
n ⋅ ( B2 − B1 ) = 0
取角标 1代表理想导体,角标 2 代表真空或绝缘介质。取法 线由导体指向介质中。在理想导体情况下,导体内部没有 电磁场,因此,E1=H1=0。 略去角标2,以E和H表示介质一侧的场强,有边界条件:
k x A1 + k y A2 + k z A3 = 0
因此A1 , A2 和A3中只有两个是独立的。通常使A1和A2独立 变化,A3由A1和A2表示。例如三个振幅分别为:
k y A2 k x A1 ) ( A1 ,0,− ) 或 (0, A2 ,− kz kz
14
由数学知识可知,这两个向量线性无关。所以任何电场的 三个分量的振幅组成的向量,均可由以上两个向量的线性 组合来表示。
∇2 E + k 2 E = 0 ∇⋅ E = 0
n× E = 0
理想导体界面边界条件可以形象地表述为,在导体表面上, 电场线与界面正交,磁感应线与界面相切。
5
实际求解时,先看方程 ∇·E=0对边界电场的限制往往能 够带来方便。 在边界面上,若取x,y轴在切面上,z轴沿法线方向,由 于该处Ex=Ey=0,因此方程∇·E=0在靠近边界上为 ∂Ez/∂z =0,即
(C3 cos k z z + D3 sin k z z )
E x = A1 cos k x x sin k y y sin k z z , E y = A2 sin k x x cos k y y sin k z z , E z = A3 sin k x x sin k y y cos k z z.
《光学谐振腔理论》PPT课件

规定:光线出射方向在腔轴线的上方时, 为正;反之,为负。
当凹面镜向着腔内时,R取正值;
当凸面镜向着腔内时,R取负值。
精选ppt
18
2.2 开放光学球面谐振腔的稳定性
用一个二阶方阵描述入射光线和出射光线的坐标变换。该 矩阵称为光学系统对光线的变换矩阵T。
r2
2
A
C
B D
r1
1
近轴光线通过焦距为f的薄透镜的变换矩阵
r2 2
r1
1 f
r1 1
r2
2
1
1
f
0
1
r1
1
1
2
r1
r2
P1 P2
精选ppt
22
2.2 开放光学球面谐振腔的稳定性
精选ppt
23
2.2 开放光学球面谐振腔的稳定性
精选ppt
24
2.2 开放光学球面谐振腔的稳定性
2)光线在谐振腔中往返一周变换矩阵
y
sin
p
l
z e im ,n, pt
k k xex k ye y kzez ,k x m / a,k y n / b,kz p / l
m,n,p c / k
c
m / a 2 n / b2 p / l 2
精选ppt
6
2.1
光学谐振腔概论
相邻两个模式波矢之间的间距
精选ppt
8
2.1 光学谐振腔概论
谐振腔内只能存在满足以下条件的光场:经腔内往返一周再回 到原来位置时,与初始出发波同相(即相差是2的整数倍—— 相长干涉
q
q 2cLq
c 2L
2 2L q2L q q
q
大学物理4-2速记思维导图 脑图
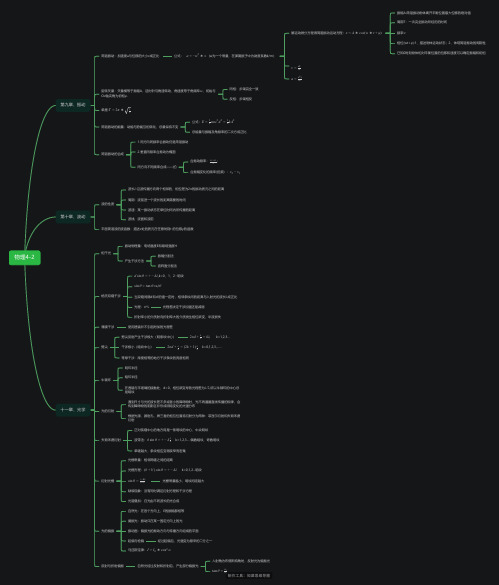
物理4-2第九章、振动简谐振动:加速度a与位移的大小x成正比 公式: (w为一个常量,在弹簧振子中为劲度系数k/m)a=−w∗2x解运动微分方程得简谐振动运动方程:x=A∗cos(w∗t+φ)振幅A:简谐振动物体离开平衡位置最大位移的绝对值周期T:一次完全振动所经历的时间频率:ν相位(wt+):1、描述物体运动状态;2、体现简谐振动的周期性φ已知0时刻物体相对平衡位置的位移和速度可以确定振幅和初相v=dtdxa=dt2d x2旋转矢量:矢量模等于振幅A,逆时针匀角速转动,角速度等于角频率,初始与Ox轴夹角为初相.ωφ同相:步调完全一致反相:步调相反单摆:T=2π∗g l简谐振动的能量:动能与势能互相转化,总量保持不变公式:E=mωA=2122kA212总能量与振幅及角频率的二次方成正比简谐振动的合成1.同方向同频率合振动仍是简谐振动2.垂直同频率合振动为椭圆同方向不同频率合成——拍合振动频率:;2v+v12合振幅变化的频率(拍频):v−2v1第十章、波动波的性质波长:沿波传播方向两个相邻的、相位差为2的振动质元之间的距离λπ周期:波前进一个波长的距离需要的时间波速:某一振动状态在单位时间内所传播的距离波线、波面和波前平面简谐波的波函数:描述x处的质元在任意时刻t 的位移y的函数十一章、光学相干光振动物理量:电场强度E和磁场强度H产生干涉方法振幅分割法波阵面分割法杨氏双缝干涉,k=0、1、2···明纹d sinθ=+−kλ=x/d'sinθ≈tanθ当双缝间隔d和d'的值一定时,相邻条纹间的距离与入射光的波长成正比λ光程:n*L光程差决定干涉加强还是减弱折射率小的介质射向折射率大的介质发生相位跃变,半波损失薄膜干涉使用透镜并不引起附加的光程差劈尖劈尖反射产生干涉极大(明条纹中心), k=1,2,3...2nd+=2λkλ干涉极小(暗纹中心) k=0,1,2,3,......2nd+=2λ(2k+1)2λ等厚干涉:厚度相等的地方干涉条纹的亮度相同牛顿环明环半径暗环半径在透镜与平玻璃的接触处,d=0,相位跃变导致光程差为,所以牛顿环的中心总是暗纹λ/2光的衍射遇到尺寸与光的波长差不多或者小的障碍物时,光不再遵循直线传播的规律,会传到障碍物的阴影区并形成明暗变化的光强分布根据光源,颜射孔,屏三者的相互位置将衍射分为两种:菲涅尔衍射和夫琅禾费衍射夫琅禾费衍射正对狭缝中心的地方将是一条明纹的中心,中央明纹波带法: k=1,2,3.....偶数暗纹,奇数明纹b sinθ=+−k2λ单缝越大,条纹相应变得狭窄而密集衍射光栅光栅常量:相邻两缝之间的距离光栅方程: k=0,1,2...明纹(b+b)sinθ=′+−kλsinθ=b+b′+−kλ光栅常量越小,明纹间距越大缺级现象:没有同时满足衍射方程和干涉方程光谱叠加:白光由不同波长的光合成光的偏振自然光:在各个方向上,E的振幅都相等偏振光:振动只在某一固定方向上的光振动面:偏振光的振动方向与传播方向组成的平面起偏与检偏经过起偏后,光强变为原来的二分之一马吕斯定律:I=I∗cosα2反射与折射偏振自然光经过反射和折射后,产生部分偏振光入射角为布儒斯特角时,反射光为偏振光tanθ=n1n2。
3.1光学谐振腔的衍射理论——激光原理课件PPT

每一个模的激光束的发散角
四 开放式光腔 • 激光器中使用的谐振腔通常是开放式的,即侧面
没有光学边界(理想化的处理方法),称为开放 式光学谐振腔,简称开腔。 开腔模的一般物理概念
• 为突出特征、简化分析,提出理想的开腔模型:两块反射镜 片沉浸在均匀的、无限的、各向同性的介质中,没有侧壁的 不连续性。
3.1.2 光学谐振腔的自再现模积分方程
1.决定腔模的形成:
(1)反射镜的有限大小会引起衍射损耗,而且在决定开腔 中激光振荡能量的空间分布方面,衍射将起主要作用
(2)非选择性损耗将使横截面内各点的场按同样的比例衰 减,对场的空间分布不会发生重要影响
(3)衍射主要发生在镜的边缘上,将对场的空间分布发生 重要影响;而且,只要镜的横向尺寸是有限的,这种影响 将永远存在。
的激光模式的良好近似 • 激活介质的作用主要是补充腔内电磁场在振荡过
程中的能量损耗,使之满足阈值条件;激活介质 对场的空间分布和振荡频率的影响是次要的,不 会使模式发生本质的变化
三 采用的理论
• 衍射光学理论(标量衍射理论) --深入了解模式特 性
模的概念——腔与模的一般
• 在激光技术术语中,通常将光学谐振腔内可能存在 的电磁波的本征态称为腔的模式。(每种本征态将 具有一定的振荡频率和空间分布)。
本章讨论:由两个球面镜构成的开放式光学谐振腔
我们更关心镜面上的场
激光输出直接与镜面上的场相。镜面上稳态场分 布的形成可以看成是光在两个镜面间往返传播的 结果。因此,两个镜面上的场必然是互相关联的: 一个镜面上的场可以视为另一个镜面上的场所产 生,反之亦然。
新激光ppt课件第二章 光学谐振腔理论02-精选文档32页

图3-1 惠更斯-菲涅耳原理
式中 源点
为源点 P'与观察点
P'处的波面法线 n与
P之间的距离; 为
P'P 的夹角;k2/
为光波矢的大小,为光波长; ds'为源点 P'
处的面元。
二、衍射积分公式在谐振腔中的应用
(3)等相位面的分布 共焦腔行波场相位分布决定于
m(x n ,y,z)k[fz2 z((x f2 2 y z2 2))](m n 1 ) 4 (arz fc)tg
与腔的轴线相交于z0点的等相位面的方程为
φ (x,y,z)= φ (0,0,z)
zz0
x2 y2 2R(z0)
迭代法
所谓迭代法,就是利用迭代公式
uj1(x,y) Kju(x',y')d's
M'
直接进行数值计算。 首先,假设在某一镜面上存在一个初始场分布u1,将它代 人上式,计算在腔内经第一次渡越而在第二个镜面上生成 的场u2,然后再用所得到的场代入,计算在腔内经第二次 渡越而在第一镜上生成的场u3。如此反复运算,在对称 开腔的情况下,当j足够大时,数值计算得出的uj uj+1uj+2满 足
m nar1 m g n k L (m n 1 ) 2
为单程附加相移Δ φ mn
谐振频率: νmnq2cL[q1 2(mn1)]
讨论 共焦腔模在频率上是高度简并的
频率间隔
同横邻纵
qm(n q1)mnq2cL
同纵邻横
m(m1)nqm
uj1(x,y)iL uj(x',y')eikd's M'
新激光ppt课件第二章 光学谐振腔理论01

将光学谐振腔内可能存在的电磁场的本征态称 为腔的模式。从光子的观点来看,激光模式也就是 腔内可能区分的光子的状态。
2.腔与模的一般联系
腔内电磁场的本征态应由麦克斯韦方程组及腔的边界 条件决定。不同谐振腔的模式各不相同。对闭腔一般可
以通过直接求解麦克斯韦方程组来决定其模 式,而寻求开腔模式的问题通常归结为求解 一定类型的积分方程。
2.要制作一个腔长L=60cm的对称稳定腔,反射镜的曲 率半径取值范围如何?设稳定腔的一块反射镜的曲 率半径R1=4L,求另一面镜的曲率半径取值范围。
波的波节数由q决定.
➢ 腔的纵模:
由整数q所表征的腔内纵向场分布称为腔的纵模。
q为纵模序数.
➢ 纵模间隔:
腔的相邻两个纵模的频率之差Δvq称为纵模间隔。
q
q1q
C 2L
Δvq与q无关,对一定的光腔为一常数,因而腔的纵
模在频率尺度上是等距离排列的,
频率梳
例:对L=10cm的气体激光器(设η=1), Δvq=1.5×109Hz
TEMmnq 三个独立的模序数,mn横模序数;q纵模序数
方形镜 m:水平轴光场节线数;n:垂直轴光场节线数
圆形镜 m:角向光场节线数;n:径向光场节线园数
➢ 基模与高阶模: m=0,n=0的横模为基模;其他横模为高阶模。
不同的纵模从频率的差异来区分,光场分布的差异极小; 不同的横模从强度花样来区分,但频率的差异也是存在的
A C
B D
就为光学系统的光线变换矩阵
自由空间的光线变换矩阵:
r2
r1 L1 2 1
TL 12
z
L
球面反射镜的光线变换矩阵:
2
r2 r1
