信号与线性系统-第13周综合练习答案
信号与线性系统分析试题及答案(10套)

信号与线性系统分析试题及答案(10套)标准答案(⼀)⼀、填空题(每空1分,共30分)1、⽆线电通信中,信号是以电磁波形式发射出去的。
它的调制⽅式有调幅、调频、调相。
2、针对不同的调制⽅式有三种解调⽅式,分别是检波、鉴频、和鉴相。
3、在单调谐放⼤器中,矩形系数越接近于1、其选择性越好;在单调谐的多级放⼤器中,级数越多,通频带越窄、(宽或窄),其矩形系数越(⼤或⼩)⼩。
4、调幅波的表达式为:uAM(t)= 20(1 +0.2COS100πt)COS107πt(V);调幅波的振幅最⼤值为24V,调幅度Ma为20℅,带宽fBW为100Hz,载波fc为5*106Hz。
5、在⽆线电技术中,⼀个信号的表⽰⽅法有三种,分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种⽅式。
7、检波有同步、和⾮同步检波两种形式。
8、反馈式正弦波振荡器按照选频⽹络的不同,可分为LC、RC、⽯英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、⽤模拟乘法器⾮线性器件实现调幅最为理想。
⼆、选择题(每⼩题2分、共20分)将⼀个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息(C )A、载波信号B、本振信号C、已调波信号2、⼩信号谐振放⼤器的主要技术指标不包含(B )A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于( A )分量A、基波B、⼆次谐波C、其它⾼次谐波D、直流分量4、并联型⽯英晶振中,⽯英谐振器相当于(C )元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为( B )A、|AF|=1,φA+φF= 2nπB、|AF| >1,φA+φF = 2nπC、|AF|>1,φA+φF ≠2nπD、|AF| =1,φA+φF ≠2nπ6、要实现集电极调制特性应使功放⼯作在(B )状态A、⽋压状态B、过压状态C、临界状态D、任意状态7、⾃动增益控制可简称为( B )A、MGCB、AGCC、AFCD、PLL8、利⽤⾮线性器件相乘作⽤来实现频率变换其有⽤项为( B )A、⼀次⽅项B、⼆次⽅项C、⾼次⽅项D、全部项9、如右图所⽰的电路是(D )A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在⼤信号包络检波器中,由于检波电容放电时间过长⽽引起的失真是(B)A、频率失真B、惰性失真C、负峰切割失真D、截⽌失真三、判断题,对的打“√”,错的打“×”(每空1分,共10分)1、谐振放⼤器是采⽤谐振回路作负载的放⼤器。
信号与系统课后答案

信号与系统课后答案1-1 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-31-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=:1-9 已知信号的波形如图1-11所示,分别画出)(tf和dttdf)(的波形。
解:由图1-11知,)3(tf-的波形如图1-12(a)所示()3(tf-波形是由对)23(tf-的波形展宽为原来的两倍而得)。
将)3(tf-的波形反转而得到)3(+tf的波形,如图1-12(b)所示。
再将)3(+tf的波形右移3个单位,就得到了)(tf,如图1-12(c)所示。
dttdf)(的波形如图1-12(d)所示。
1-23 设系统的初始状态为)0(x,激励为)(⋅f,各系统的全响应)(⋅y与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-tt dxxxfxety)(sin)0()((2)⎰+=t dxxfxtfty)()0()()((3)⎰+=t dxxftxty)(])0(sin[)((4))2()()0()5.0()(-+=kfkfxky k(5)∑=+=kj j f kx k y 0)()0()(2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++-- (4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
信号与线性系统分析知到章节答案智慧树2023年潍坊学院

信号与线性系统分析知到章节测试答案智慧树2023年最新潍坊学院第一章测试1.时域上离散,值域上连续的信号为()。
参考答案:抽样信号2.下列选项关于Sa(t)信号的描述,错误的是()。
参考答案:3.已知信号,可由下列哪种运算过程得到()参考答案:向左移动个单位4.下列各表达式中正确的是()。
参考答案:5.。
()参考答案:1006.()。
参考答案:7.积分等于()。
参考答案:8.已知信号的波形如图所示,则的表达式为()。
参考答案:9.下列关于系统的描述不正确的是()。
参考答案:包含记忆元件的系统称为即时系统10.已知系统激励信号与响应之间满足,则该系统是()。
参考答案:线性时变系统第二章测试1.下列说法错误的是()。
参考答案:若系统初始状态为零,则系统的零状态响应就是系统的强迫响应;2.零输入响应是 ( )。
参考答案:部分自由响应3.设某系统全响应为,则系统的暂态响应为()。
参考答案:4.已知系统的冲激响应为,加入系统的激励信号为,则系统的零状态响应为()。
参考答案:5.卷积的结果为( )。
参考答案:6.已知两个系统的冲激响应分别为和,则两个系统级联组成的新系统的冲激响应为()。
参考答案:7.系统的完全响应可以分解为自由响应和强迫响应。
()参考答案:对8.自由响应和零输入响应解的形式相同。
()参考答案:对9.利用卷积运算可以求解系统的零输入响应。
()参考答案:错10.系统没有输入激励信号时不会发生跳变。
()参考答案:对第三章测试1.积分等于()。
参考答案:2.从信号频谱的特点来考虑,周期信号的频谱是()。
参考答案:离散的3.符合奇谐函数的条件为()。
参考答案:4.如是实信号,下列说法不正确的是()。
参考答案:该信号的频谱是实偶函数5.已知,则所对应的原函数为()。
参考答案:6.已知的频谱密度函数为,则的频谱密度函数为()。
参考答案:7.周期信号的频谱满足谐波性。
()参考答案:对8.非周期信号既可以进行傅里叶级数分析,又可以进行傅里叶变换分析。
信号与系统课后习题答案(金波 华中科技大学出版社)

基本练习题
题 一
1-1 判断下列信号是否是周期的,如果是周期的,求出它的基频和公共周期。 (a) f (t ) 4 3 sin(12 t ) sin(30 t ) ; (b) f (t ) cos(10 t ) cos(20 t ) ; (c) f (t ) cos(10 t ) cos(20t ) ; (d) f (t ) cos(2t ) 2 cos(2t
1 1 s。 f0 3
(c) 由于两个分量的频率 1 =10 rad/s、 1 =20 rad/s的比值是无理数,因此无法找出公共 周期。所以是非周期的。 1 (d) 两个分量是同频率的,基频 f 0 1/ Hz。因此,公共周期 T s。 f0 1-2 解 (a) 波形如图1-2(a)所示。显然是功率信号。
0
f (t )
2
3
题图 1-8
t
1-9 在以下每个系统中, f (t ) 是输入, y (t ) 是输出。将每个系统按线性、时变和因果性 进行分类。 (a) y (t ) 3 y (t ) 2 f (t ) f (t ) ; (b) y (t ) 3 y(t ) y (t ) 2 f (t ) f (t ) ; (c) y (t ) 3tf (t ) y (t ) 2 f (t ) ; (d) y (t ) 3 y (t ) 2 f (t ) f (t 2) 。
(6 t 2 )[ (t 4) 2 (2t 4)] dt ;
4
10
(t )
sin 3t dt 。 t
1-7 画出题图1.7中的信号的一阶导数波形。
f1 (t )
4
2
0
f 2 (t )
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与线性系统 白恩健书答案

第1章基本概念K第1章习题k1.1解:(1)x(t)为周期信号,周期为T=10。
(2)x(t)为非周期信号。
(3)x[n]为非周期信号。
(4)x[n]为周期信号,周期为N=2。
(5)x(t)为非周期信号。
(6)x[n]为周期信号,周期为N=2。
1.2解:(1)x(t)为功率信号。
(2)x(t)既不是能量信号也不是功率信号。
(3)x[n]为能量信号。
(4)x(t)为能量信号。
(5)x(t)为能量信号。
(6)x[n]为能量信号。
1.3略。
1.4略。
1.5(原题有误)一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统,即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解:提示:可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解:(1)因果、无记忆、非线性、时不变、BIBO稳定系统。
(2)因果、无记忆、线性、时变和BIBO稳定系统。
(3)因果、无记忆、线性、时变和非稳定系统。
(4)因果、记忆、线性、时不变和BIBO稳定系统。
(5)因果、无记忆、线性、时变和BIBO稳定系统。
(6)因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念(7)因果、无记忆、线性、时不变和BIBO稳定系统。
(8)非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解:(1)x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
(2)x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
(3)x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示:根据微积分的极限定义证明。
1.10解:(1)x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
(2)x(t)的响应为[2(t+e−t)−2]u(t)。
信号与线性系统分析课后答案_吴大正
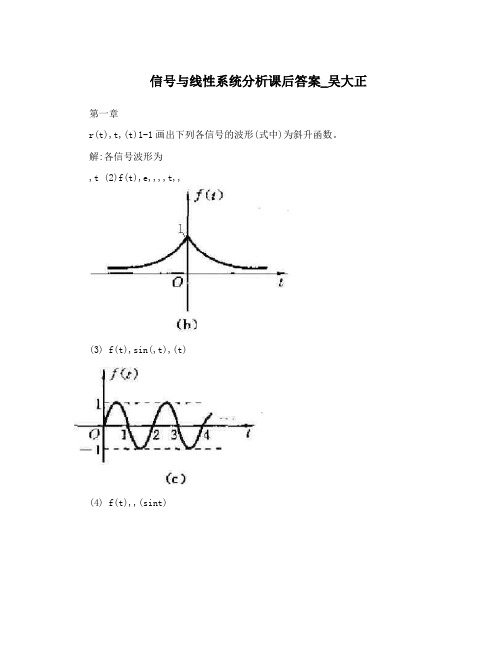
信号与线性系统分析课后答案_吴大正第一章r(t),t,(t)1-1画出下列各信号的波形(式中)为斜升函数。
解:各信号波形为,t (2)f(t),e,,,,t,,(3) f(t),sin(,t),(t)(4) f(t),,(sint)(5) f(t),r(sint)k(7) f(t),2,(k)k(10) f(k),[1,(,1)],(k)r(t),t,(t)1-2 画出下列各信号的波形[为斜升函数]。
f(t),r(t),2r(t,1),r(t,2)f(t),2,(t,1),3,(t,1),,(t,2) (1) (2) f(k),k[,(k),,(k,5)]f(t),r(2t),(2,t) (5) (8),kkf(k),sin()[,(k),,(k,7)]f(k),2[,(3,k),,(,k)](11) (12) 6解:各信号波形为f(t),2,(t,1),3,(t,1),,(t,2) (1)f(t),r(t),2r(t,1),r(t,2) (2)f(t),r(2t),(2,t) (5)f(k),k[,(k),,(k,5)] (8),kf(k),sin()[,(k),,(k,7)](11) 6kf(k),2[,(3,k),,(,k)](12)1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
3,,,,f(t),3cost,2sin(,t)f(k),cos(k,),cos(k,) (2) (5) 524436 解:f(t)1-6 已知信号的波形如图1-5所示,画出下列各函数的波形。
f(0.5t,2)f(1,2t)f(t,1),(t)f(t,1),(t,1) (1) (2) (5) (6) tdf(t)f(x)dx (7) (8) ,,,dt解:各信号波形为f(t,1),(t) (1)f(t,1),(t,1) (2)f(1,2t) (5) f(0.5t,2) (6)df(t)(7) dttf(x)dx (8) ,,,f(k)1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统考试题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与线性系统-第13周综合练习答案
1、请判断下面描述的系统是否为线性时不变系统;
1)()()(+=+t e t tr t r dt
d
2、判断如下周期信号(T=2)的三角函数形式的傅里叶级数所包含的分量;
21
-1
t
f (t )0
3、已知某系统在输入信号为()t ε时全响应为()2()t t e e t ε--+,输入信号为2()t ε时全响应为()242()t t e e t ε--+。
求该系统的冲激响应()h t 。
4、求门信号()22G t t t τττεε⎛⎫⎛⎫
=+-- ⎪ ⎪⎝⎭⎝⎭
的单边拉普拉斯变换及其收敛区间。
5、已知某因果系统的系统函数为1
()1
H s s =
+,求其对信号()()cos e t t =
[]t -∞<<+∞的响应。
6、已知()f t 的波形如下图所示。
请画出f(-2t+1)的图形
2
1
-1
t
f (t )0
1
7、已知某信号()f t 的拉普拉斯变换为1
()(3)(5)
F s s s =
++,收敛区间为
5Re()3s -<<-。
求()f t
8、已知1()f t 和2()f t 的波形如下图所示,画出)()()(21t f t f t f *=的的波形图
t
)
(1t f 0
1
t
)
(2t f 01
1
9、已知系统的框图如下图所示,
设子系统的冲激响应分别为)1()(1-=t t h δ,)()(22t e t h t ε-=。
求整个系统的冲激响应h (t )。
解:
)1()1()1()()1()()()()(22121-+-=-*+-=*+=--t e t t t e t t h t h t h t h t δδδεδ
10、若已知)()]([ωj F t f F =,利用傅里叶变换的性质求)24(t f -的傅里叶变换。
解:
)2
(21)]42([)()]4([)()]([44ω
ωωωωj F e t f F j F e t f F j F t f F j j -=
+-↔=+↔=
11、已知系统转移算子2
31
)(2
+++=p p p p H ,初始条件为:(0)1(0)2r r '==,。
求其零输入响应。
解:
)
()34()(34221)(2
;1221212122111t e e t r C C C C C C e C e C t r t t t
t ελλ-----=⎩⎨
⎧-==⇒⎩⎨⎧=--=++=-=-=
12、一系统如下图,信号e(t )=ε(t +1)-ε(t -1),滤波器的频率响应
⎩
⎨
⎧><=πωπ
ωω||,0||,1)(j H 。
试画出A 、B 、C 、D 、E 五点处信号的频谱图。
h 1(t
h 2(t
h 1(t
e(t
r(t
H(j
ω)
A
B
C
2e (t)
D
2
H(j ω)
E
答: A 点
B 点
F(jw)
w
π
2
C 点
F(jw)w
π
21
π
2-
D 点
F(jw)w
π
41
π
4-1/2
E 点
F(jw)w
1
π
13、求激励e (t )=e -2t ε(t -1)+δ(t -2)通过系统H (j ω)=2e -3j ω 的响应。
r (t )=2e -2(t-3)ε(t -4)+2δ(t -5)
14、求下图信号的傅里叶变换
2
1
-1
t
f (t )0
1
其中f(t)可分解为直流1和f 1(t), f 1(t)的微分如下图所示
1
-1
t
1
)('1t f 0.5
)()]('[ωωSa e t f F j -=
根据积分性质,其中F (0)=0;
)
(2)
()]([)
()]([1ωπδω
ωωωω
ω+-=
-=
j Sa e
t f F j Sa e t f F j j
此系统为线性非失真系统,因此只是增益为2,并延时3
15、已知LTI 因果系统函数2
31
)(2
+++=
s s s s H ,激励 )()(t t e ε= ,求系统的
零状态响应,并指出响应中的自然响应与受迫响应。
=
)(s R 2
5.05.0121+-=•+s s s s
)()5.05.0()(2t e t r t ε-+=
自由
受迫分。
