天津大学生数学竞赛
天津普通高校大学数学竞赛结果

赵鸿雁
13
天津科技大学
互联网+移动污水处理
郭亚男,杨婷婷,刘晓慧,邓妍,赵雅静,刘莹,林诚乔,郑云飞,张洁
杨宗政,尹钧惠,曹井国
14
天津工业大学
超声波精准定标衣物清洗机
李发贵,孙可亮,张子龙,闫庆鹏,刘本一,张厚鑫
逯力红,高慧
15
天津工业大学
功夫汉字
刘姝君,李文凯,李端阳,王常维,田然,刘月,刘博文,孟祥至,许雷
姬生振,麻妙玲,孟丹阳,王雨,赵梦帆,王映丽
郑刚,秦勤
24
天津理工大学
Life designer
王立歆,李冉,罗慧芳,王旭,王能,刘中毅
吴娜
25
天津农学院
智能育苗机器人
王铠,王建跃,丁允贺
杨磊
26
天津农学院
多肉植物的组织培养、快繁和销售
姚雨欣,霍少洁,付雨婷,周敏,孟洁,马昕
杨静慧
27
天津农学院
智能折叠婴儿摇床
明东
7
天津科技大学
果蔬拮抗菌紫外介导微管高产溶菌酶防腐技术
李丽梅,庞玲玲,赵亚婷,杨鸿远,杨帅
李喜宏,刘霞,冯明智
8
天津科技大学
基于深度人工智能技术的视频监控系统
锁雪萍,陈幻杰,尹成娟,韩佳林
王以忠,王琦琦
9
天津科技大学
互联网+生鲜食品全程冷链物流品控系统
张新,张瑞,张博,唐先谱,庞玲玲,李丽梅,杨莉杰,张苹苹,闫珍
8
天津渤海职业技术学院
互联网+多样食材便民配送O2O模式的应用
朱乐天,岳钲淇,何佳俊,刘玉茜,何荣贵,高阳,王树鲲
张子文,张蕊,佟超
2014年全国大学生数学建模竞赛天津赛区竞赛结果公示
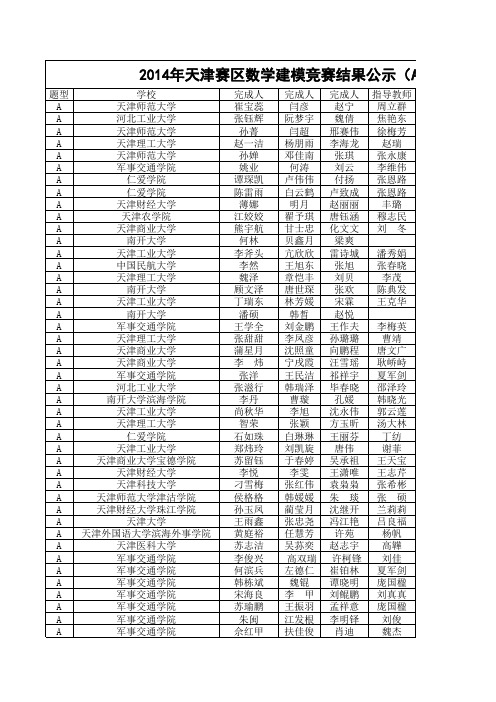
A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A
中国民航大学 中国民航大学 中国民航大学 河北工业大学城市学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 军事交通学院 南开大学 南开大学 南开大学 南开大学 南开大学 南开大学 南开大学 南开大学 南开大学滨海学院 南开大学滨海学院 南开大学滨海学院 南开大学滨海学院 南开大学滨海学院 南开大学滨海学院 天津财经大学 天津财经大学 天津财经大学 天津财经大学 天津财经大学珠江学院 天津财经大学珠江学院 天津城建大学 天津城建大学 天津大学 天津大学 天津大学 天津大学 天津大学 天津工业大学 天津工业大学 天津工业大学 天津工业大学 天津工业大学 天津工业大学 天津工业大学
石洛宜 陈科 白志惠 赵军健 潘秀娟 尹逊武 陈科 夏国坤 王冬梅 刘素娟 程树林 贾学龙 冯晶 鲁礼勇 吴利萍 曹靖 王雷 汤大林 刘蓓 常之艳 王武 韩亮 刘琦 陈雁东 刘琦 穆志民 房宏 朱文新 朱文新 赵俊英 孟丽丽 王全文 李秀仙 李美凤 刘 杨 王玉津 李 天 王天宝 李海霞 弋生辉 王洁 高韡 高韡 袁程 曹瑾 曹瑾
王恒 刘用策 陈克俭 何强 吴庆国 郝安东 周凯强 崔亚明 陆峰 张志祥 金碧辉 朱文平 吴旭东 燕刚 丁震 王一鸣 施呈优 于闯 黄敬尧 李炼炫 曾顺杨 王涵 黄毅 凌文杰 胡钱琪 郭钦贝 段昊昱 杨铭格 郑菲菲 姚舜达 张晨 金瑾 刘学青 文俊方 孙冉 张资殷 张寒 冯伟 杨若岚 吴海成 王媛媛 梁莹 张欢 李前辉 肖鹏飞 程书芝 张懿
天津市教育委员会关于表彰2012年天津市普通高校大学数学竞赛组织工作先进单位(个人)及获奖学生的通知

天津市教育委员会关于表彰2012年天津市普通高校大学数学竞赛组织工作先进单位(个人)及获奖学生的通知文章属性•【制定机关】天津市教育委员会•【公布日期】2012.07.05•【字号】津教委办[2012]49号•【施行日期】2012.07.05•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】高等教育正文天津市教育委员会关于表彰2012年天津市普通高校大学数学竞赛组织工作先进单位(个人)及获奖学生的通知(津教委办〔2012〕49号)各普通高等学校、独立学院、驻津院校:为进一步推进我市普通高校大学数学课程建设与改革,不断提高大学生的数学素质和综合能力,由天津市教育委员会主办的2012年天津市普通高校大学数学竞赛于5月26日在天津理工大学、天津科技大学、天津商业大学举行。
现将获奖结果公布如下:经过学校初赛、市级竞赛,天津市普通高等学校大学数学竞赛组委会对全体参赛学生成绩排序进行核准,共有26所学校的445名学生获得大学数学竞赛奖项。
其中,53名学生获得特等奖,160名学生获得一等奖,220名学生获得二等奖,12名学生获得优秀奖。
同时,经学校申请,天津市高等学校大学数学竞赛组委会核准,天津理工大学等10所高校获得组织工作先进单位奖,薛锋等26名同志获得组织工作先进个人奖,郭飞等12名同志获得优秀指导教师奖。
市教委决定对以上获奖结果予以确认并表彰。
附件:1.2012年天津市普通高校大学数学竞赛组织工作先进单位和先进个人名单2.2012年天津市普通高校大学数学竞赛获奖学生名单3.2012年天津市普通高校大学数学竞赛优秀指导教师名单二○一二年七月五日附件1:2012年天津市普通高校大学数学竞赛组织工作先进单位和先进个人名单组织工作先进单位:天津理工大学天津科技大学天津商业大学天津财经大学天津工业大学天津大学南开大学河北工业大学军事交通学院天津商业大学宝德学院组织工作先进个人:薛锋南开大学于倩天津大学陈彦婷王春雨天津理工大学梁楠梁邦助天津商业大学邱强刘凤林天津科技大学樊岩天津工业大学何要武河北工业大学王友雨天津财经大学张双德武警后勤学院胡宝安军事交通学院孙雨霞天津医科大学许虎男天津外国语大学巩长忠中国民航大学任丽丽天津师范大学郭阁阳天津职业技术师范大学黄淑云天津中医药大学李禾嘉南开大学滨海学院宋一杰天津大学仁爱学院贾丽天津财经大学珠江学院李振华天津商业大学宝德学院马松青天津理工大学中环信息学院杨策天津外国语大学滨海外事学院宋爱荣北京科技大学天津学院附件2:2012年天津市普通高校大学数学竞赛获奖学生名单本科理工类特等奖(29人)一等奖(86人)二等奖(111人)优秀奖(7人)2012年天津市普通高校大学数学竞赛获奖学生名单本科经管类特等奖(20人)一等奖(63人)二等奖(92人)优秀奖(4人)2012年天津市普通高校大学数学竞赛获奖学生名单本科人文及医学类特等奖(4人)一等奖(11人)二等奖(17人)优秀奖(1人)附件3:2012年天津市普通高校大学数学竞赛优秀指导教师名单郭飞天津大学郭强辉南开大学苟长义天津理工大学陈雅颂天津工业大学马薇天津财经大学唐文广天津商业大学崔然武警后勤学院王瑞军事交通学院张翠杰中国民航大学郭献洲河北工业大学尹立群天津中医药大学刘晓杰天津财经大学珠江学院。
2016天津市大学数学竞赛经管类获奖名单

2016年天津市大学生数学竞赛(经管类)获奖名单序号准考证号姓名学号性别所学专业所属院校获奖等级12016210327朱彤1512368女物流管理南开大学特等奖22016222004丁悦成1513337男金融学类南开大学特等奖32016222229曾馨1513399女金融学类南开大学特等奖42016222327冯译萱1513505女保险学南开大学特等奖52016222228刘杰03022015044男2015汽车分队指挥军事交通学院特等奖62016210920赵田田1510610127女会计学天津工业大学特等奖72016221403叶登焕1513383男金融学类南开大学特等奖82016221616魏文石2015110594男金融工程天津财经大学特等奖92016222024孙畅1513517女保险学南开大学特等奖102016222019戚飞成1513490男保险学南开大学特等奖112016210817孙淼珍1511130105男金融学天津工业大学特等奖122016211222王志宽1512300男国际会计南开大学特等奖132016210104张慧丽1512012女经济学院国际商务南开大学特等奖142016210410曹娜1512163女工商管理类南开大学特等奖152016210722金鹏1512344男商学院物流管理南开大学特等奖162016210210罗天奇1512129男工商管理类南开大学特等奖172016210220梁健健1512207女工商管理类南开大学特等奖182016210813易铭昕1512153男工商管理类南开大学特等奖192016210205刘瑞明20153424男工商管理 天津理工大学特等奖202016210313郑文韬1512304男国际会计南开大学特等奖212016210412赵佳悦1511130328女金融学天津工业大学特等奖222016221824旷美琦1513419女金融学类南开大学特等奖232016222722李婕1513509女保险学南开大学特等奖242016210707单有1512105男工商管理类南开大学一等奖252016210405黄惊金1510630215女工商管理天津工业大学一等奖262016210618张梦琳1512336女国际会计南开大学一等奖272016211026范家玮1512975男经管法南开大学一等奖282016210408王亚苹1510620224女财务管理天津工业大学一等奖292016210613王筱薇1511931女经济学类南开大学一等奖302016221413冯赫03482015006男2015铁路运输指挥军事交通学院一等奖312016221711赵子昂2015110597男金融工程天津财经大学一等奖322016222301谢志伟1513494男保险学南开大学一等奖332016222402苏若严1513491男保险学南开大学一等奖342016210703张秀怡1512096女管理科学与工程类南开大学一等奖352016210709王福祥1512062男管理科学与工程类南开大学一等奖362016222317董宗霖1513479男保险学南开大学一等奖372016232813贺杰20152233男金融学天津商业大学一等奖382016210711秦阳1512226女工商管理类南开大学一等奖392016210712汪佳敏20153514女保险学天津理工大学一等奖402016211108张文进1510660230女工业工程 天津工业大学一等奖412016211219齐竹君1512225女工商管理类南开大学一等奖422016222226沈忠华2015113014女教改实验班天津财经大学一等奖432016211231潜宣谕1512133男工商管理类南开大学一等奖442016221308马锦霄2015110803女国际金融天津财经大学一等奖452016221324张尉峰1513388男金融学类南开大学一等奖462016232816王冰20152145女金融学天津商业大学一等奖472016221422杨兴源2015110690男金融学天津财经大学一等奖482016221609张骏2015110260男公共事业管理天津财经大学一等奖492016222105陈竹君2015110818女国际金融天津财经大学一等奖502016222530朱彦齐03632015010男2015军事装卸指挥工程军事交通学院一等奖512016221708余舒婷1513462女金融学类南开大学一等奖522016233103曾兆芳20152394女经济学天津商业大学一等奖532016233127蔡凯浩20151719男经济学天津商业大学一等奖542016222714上官森1513367男金融学类南开大学一等奖552016233118张小莹20153411女工商类天津商业大学一等奖562016211224刘星1510650220女 信息管理与信息系统 天津工业大学一等奖572016222016吴雨航1513376男金融学类南开大学一等奖582016222309吴晓楠1513375男金融学类南开大学一等奖592016222629龚蓉2015112450女物流管理天津财经大学一等奖602016233307牛旭20153037女工商类天津商业大学一等奖612016221807李佳怡1513421女金融学类南开大学一等奖622016222011董春奇2015111673男财务会计天津财经大学一等奖632016222717张金星2015113035男教改实验班天津财经大学一等奖642016232810陈丽星20152399女经济学天津商业大学一等奖652016221517邸艺翀03392015007男2015管理工程军事交通学院一等奖662016221625李季旺2015111481男工程管理天津财经大学一等奖672016221702安笑含1513333男金融学类南开大学一等奖682016222006冯兴阳03632015007男2015军事装卸指挥工程军事交通学院一等奖692016222313戴锋902031501004男营房管理中国人民武装警察部队后勤学院一等奖702016232808康漫20153300女工商类天津商业大学一等奖712016210816胡成均15721905男会计学北京科技大学天津学院一等奖722016222524郑亦清1513536女保险学南开大学一等奖732016232811张文琴20152439女经济学天津商业大学一等奖742016232828常梦珂20152180女金融学天津商业大学一等奖752016233016刘琳20153089女工商类天津商业大学一等奖762016233018张帅鹏20152283男金融学天津商业大学一等奖772016233213李月20152961女工程管理天津商业大学一等奖782016210502张沁萱1511961女经济学类南开大学一等奖792016221605成思睿1513403女金融学类南开大学一等奖802016221915刘翔03422015020男2015铁路运输指挥军事交通学院一等奖812016222526田宇03412015003男2015国防交通指挥工程军事交通学院一等奖822016222601方一清2015111853男注册会计师天津财经大学一等奖832016222622刘乃溶2015110649女金融学天津财经大学一等奖842016233220刘丽晨20152323男金融学天津商业大学一等奖852*********孟玉1513432女金融学类南开大学二等奖862016210107赵晓晨1510610229女会计学天津工业大学二等奖872016210529周俊超1510660420男工业工程 天津工业大学二等奖882016211130练换楠1510680116女土地资源管理 天津工业大学二等奖892016221813马丽飞151242123女公共事业管理中国民航大学二等奖902016221926高雄2015111927男财务管理天津财经大学二等奖912016222626连艳帅03022015183男2015汽车分队指挥军事交通学院二等奖922016222725李吉03022015047男2015汽车分队指挥军事交通学院二等奖932016222732方冰15081115女国际经济与贸易天津科技大学二等奖942016233205赵文玲20153367女工商类天津商业大学二等奖952016233317张玥20153493女工商类天津商业大学二等奖962016211125尹雪辉1510620124女财务管理天津工业大学二等奖972016221827张港2015110601男金融工程天津财经大学二等奖982016221923李京鸿1513227女会展经济与管理南开大学二等奖992016222605童淑文151242128女公共事业管理中国民航大学二等奖1002016222708王宁902031501077男营房管理中国人民武装警察部队后勤学院二等奖1012016233120杨婷20153102女工商类天津商业大学二等奖1022016233211王贺佳20153299女工商类天津商业大学二等奖1032016233331李佳潞20153123女工商类天津商业大学二等奖1042016210116余良伟1510660117男工业工程 天津工业大学二等奖1052016221603纪明晖2015110564女保险学天津财经大学二等奖1062016222022郭晋江03022015050男2015汽车分队指挥军事交通学院二等奖1072016222320章楷文1513474女金融学类南开大学二等奖1082016222428吴可心1513455女金融学类南开大学二等奖1092016222514韩冬临150546111女经济与金融中国民航大学二等奖1102016210323盛松1510660317男工业工程 天津工业大学二等奖1112016210421宋俊佑20154049男工业工程天津理工大学二等奖1122016210510武晓聪20153516女保险学天津理工大学二等奖1132016211007孙冲1511809男经济学类南开大学二等奖1142016221619张怡然2015113049女教改实验班天津财经大学二等奖1152016221901徐余阳03022015197男2015汽车分队指挥军事交通学院二等奖1162016232825程小丽20152497女经济学天津商业大学二等奖1172016233008彭燕20152128女金融学天津商业大学二等奖1182016233306宫迪雅20153287女工商类天津商业大学二等奖1192016210924赵京阳20153393男信息管理与信息系统 天津理工大学二等奖1202016211105江薇羽1512074女管理科学与工程类南开大学二等奖1212016221316刘港03322015007男2015军事物流军事交通学院二等奖1222016221424高岩1513411女金融学类南开大学二等奖1232016221601马力03422015005男2015铁路运输指挥军事交通学院二等奖1242016221614杨凡佳150441231男工商管理中国民航大学二等奖1252016221629方芳2015111503女管理科学天津财经大学二等奖1262016221707唐家兴902031501075男营房管理中国人民武装警察部队后勤学院二等奖1272016221903郑伟2015162301男实验班天津财经大学珠江学院二等奖1282016221919孟庆雷03022015157男2015汽车分队指挥军事交通学院二等奖1292016222114吴明博03022015174男2015汽车分队指挥军事交通学院二等奖1302016222123谭奥凡1513443女金融学类南开大学二等奖1312016222126马璎新2015111909女注册会计师天津财经大学二等奖1322016222407蒿敏2015111805女国际会计天津财经大学二等奖1332016222617刘英杰2015113109女教改实验班天津财经大学二等奖1342016232815吴煜20153336女工商类天津商业大学二等奖1352016233329张克燕20152412女经济学天津商业大学二等奖1362016210114张和平1510660118男工业工程 天津工业大学二等奖1372016210430钟荣盛1511834男经济学类南开大学二等奖1382016221527蔡奇宏2015111920男注册会计师天津财经大学二等奖1392016221615王翼1513451女金融学类南开大学二等奖1402016221709王梓旭2015113090男教改实验班天津财经大学二等奖1412016222710武滨榕1513524女保险学南开大学二等奖1422016232821彭利文20152218男金融学天津商业大学二等奖1432016233218张娇娇20152129女金融学天津商业大学二等奖1442016233223任雅锐20153331女工商类天津商业大学二等奖1452016233229刘盼盼20153505女工商类天津商业大学二等奖1462016233315李汉乔20153293男工商类天津商业大学二等奖1472016210427曹效喜1511110301男国际经济与贸易天津工业大学二等奖1482016210907李小磊1510660309男工业工程 天津工业大学二等奖1492016221401吴会娟150541234女工商管理中国民航大学二等奖1502016221512王菲151242129女公共事业管理中国民航大学二等奖1512016221713高旭2015111886女注册会计师天津财经大学二等奖1522016221829魏晓枫2015112470男信息管理天津财经大学二等奖1532016222113何思雅2015110682女金融学天津财经大学二等奖1542016222217杜晨光1508s201男工商管理类(卓越人才实验班)天津科技大学二等奖1552016222316文灿兵03422015016男2015铁路运输指挥军事交通学院二等奖1562016222406徐旭03022015217男2015汽车分队指挥军事交通学院二等奖1572016222608高婧2015113036女教改实验班天津财经大学二等奖1582016222615裴婕妤151242224女公共事业管理中国民航大学二等奖1592016232911马越 152094女会计学河北工业大学二等奖1602016232926张柳玥20152917女工程管理天津商业大学二等奖1612016233216姚巧玲20153211女工商类天津商业大学二等奖1622016233314王慧敏20152307女金融学天津商业大学二等奖1632016210810张晓宁1530130191女物流管理天津师范大学优秀奖1642016210723谢晶晶15991036女物流管理南开大学滨海学院优秀奖1652016210506陈万双15298241女会计学(注册会计师方向)天津商业大学宝德学院优秀奖1662016211229马炳旭 2.01514E+11男市场营销天津中医药大学优秀奖1672016232925盛梦寒15103258女金融学类天津天狮学院优秀奖。
天津市教委组织和认定竞赛一览表

全国大学生数学建模竞赛天津赛区

温佰培
王文才
陈成钢
杨威
韩超
梁睿
王丽霞
王雪琦
李蕴辉
王玥娜
宋庆凤
15
天津商业大学宝德学院
1队
晏国柱
张东华
和志茹
王天宝
16
天津大学仁爱学院
2队
付磊
高康
杨钊
刘元
卢建宏
苏华
夏欢
李海龙
17
南开大学滨海学院
1队
柯佩佩
王宇
杨喆
孔玲军
18
中国人民武装警察部队后勤学院
1队
唐家兴
陈潇雅
柳青河
杜勇
19
天津市职业大学
2队
李佳蓉
曹雅昕
王琪
李秀仙
刘晟伟
袁晓晖
常娥
徐立
于宁
陈舒贺
张克
李美凤
李玥
田洪琴
宁欣荣
耿峤峙
孔佳佳
乔昕
巩木
王玉津
9
天津医科大学
2队
杨子珍
姜文蓁
杨小桐
高韡
吴鸿丽
吴承蔚
廖蓉
高韡
10
中国民航大学
15队
侯娇
姜景浩
元国强
赵静
葛献何
李根茂
梁峰海
关静
华慧
李振昊
王仕成
张连顺
徐亚鹏
杨天瑜
熊国虹
张宇翔
方舒悦
李君富
岳梦莉
刘广瑄
黄思雨
陈鑫
刘琦
12
天津职业技术师范大学
8队
李亚欣
谢孟岑
李智强
陈珂
高玉芹
刘华月
2018年 天津市普通高校大学生数学竞赛(经管类)试卷

x 1,
1
,
x 1 1, x 1 1,
则
3
f
(x)
g(x)
dx
请
__________
3
将
最
Page 1
得分 评卷人
复核人
二. 选择题(本题 15 分,每小题 3 分. 每个小题的四个选 项中仅有一个是正确的,把你认为“正确选项”前的字母填在 括号内. 选对得分;选错、不选或选出的答案多于一个,不得分)
津 2018. 06.
考试时间: 150 分钟
姓名
装
类别
订
线 准考证号
内
不
准
答
题
经管类
2018 年天津市大学数学竞赛试题 (经管类)
本试卷共 12 页,十二大题,考试时间为 150 分钟,满分 100 分.
总分
题号 一
二
三
四
五
核分人 复查人
题 分 15
15
6
6
Hale Waihona Puke 6得分题号 六
七
八
九
十 十一 十二
题分 7
经管类
Page 3
得分 评卷人 复核人
四.(本题6分)
证明不等式
63
1
1
0 1+x2 8x4 1 x4
dx 4
经管类
Page 4
得分 评卷人 复核人
五.(本题 6 分)
计算
1
k2 k !(k 2)
装 订 线 内 不 准 答 题
经管类
Page 5
得分 评卷人 复核人
六.(本题 7 分)
3.
当x 0时, x (x t)sin t2dt 与 c4x4 c3x3 c2x2 c1x
2017年全国大学生数学建模竞赛天津赛区竞赛获奖名单

方宇
袁诚锋
李旭东
21
中国人民武装警察部队后勤学院
1队
王世杰
李辰旭
余恋雨
杜勇
22
天津市职业大学
6队
赵林源
李泽宇
卫晨辉
张立圃
张莉娜
丁旭
刘志坚
李艳梅
刘菊
韦应隆
杨森
周爱丽
廖睿鑫
罗彦明
马晓宝
刘振云
张钟文
贾健楠
易忠新
张立圃
韩影影
支繁茂
晏宁瑞
王鲁静
23
天津城市职业学院
1队
张磊
严中奇
吕思同
张沛宇
24
天津机电职业技术学院
2队
霍冬冬
苗宏
刘杉杉
王钦烈
段敏
魏雅萍
焦文清
高建云
20
天津机电职业技术学院
1队
苗鹏
秦士杰
雒江波
肖满红
21
天津中德应用技术大学
2队
曾鑫
冯欣怡
李尚
王翠芳
齐奇
张健
赵磊
孙健
22
北京科技大学天津学院
1队
王超
赵振
胡浩聪
鲍勇
23
天津理工大学中环信息学院
1队
韩管中
邱双双
张壹鼎
王颖
24
中国人民解放军海军勤务学院院
3队
李进伟
王然江
张世瑜
刘明佳
赵瑞
刘金鑫
王宇
朱亚鹏
周庆霞
赵亮玉
孙浩然
李瑞
郭宏博
6
天津师范大学
3队
晏兵川
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年天津市大学数学竞赛试题 (理工类)一. 填空题(本题15分,每小题3分): 1. 设()f x 是连续函数, 且0()lim41cos x f x x →=-, 则01()lim 1x f x x →⎛⎫+= ⎪⎝⎭2e .2. 设223()2x f x ax b x +=++- , 若lim ()0,x f x →∞=则a =2,-4.- 3. 1e ln d x x x x ⎛⎫+= ⎪⎝⎭⎰e ln .x x C +4. 设(,)f x y 是连续函数, 且(,)(,)d d ,Df x y xy f x y x y =+⎰⎰其中由x 轴、y 轴以及直线1x y +=围成, 则(,)f x y =1.12xy +5. 椭球面22221x y z ++=平行于平面20x y z -+=的切平面方程为20x y z -++=和20.x y z -+= 二. 选择题(本题15分,每小题3分):1. 设()(2)ln(1),f x x x =+-则()f x 在0x =处(A) (0)2f '=-, (B) (0)0f '=, (C) (0)2f '=, (D) 不可导. 答: (A)2. 设函数()y f x =具有二阶导数, 且满足方程sin e 0.x y y '''+-=已知0()0,f x '=则 (A) ()f x 在的某个邻域中单调增加, (B)()f x 在的某个邻域中单调增少,(C)()f x 在处取得极小值, (D) ()f x 在处取得极大值. 答: ( C)3. 图中曲线段的方程为()y f x =, 函数()f x 在区间[0,]a 上有连续的导数, 则积分()d a x f x x '表示(A)直角三角形AOB 的面积, (B) 直角三角形AOC 的面积, (C) 曲边三角形AOB 的面积, (D) 曲边三角形AOC 的面积答: (D)4. 设在区间[,]a b 上的函数()0,f x >且()0,f x '<()0.f x ''>令1()d ,ba S f x x =⎰2()(),S fb b a =-31[()()](),2S f a f b b a =+-则 (A) 123,S S S << (B) 312,S S S << (C) 213,S S S << (D) 231.S S S <<答: (C )5. 设曲面22{(,,)|,01},x y z z x y z ∑==+≤≤取上侧为正,是在0x ≥的部分, 则曲面积分(A)d d 0,x y z ∑=⎰⎰ (B) 1d d 2d d .z x y z x y ∑∑=⎰⎰⎰⎰ (C) 122d d 2d d ,y y z y y z ∑∑=⎰⎰⎰⎰ (D) 122d d 2d d ,x y z x y z ∑∑=⎰⎰⎰⎰答: (B)三. (6分) 设函数()202[(1)()d ]d 0sin 00xt t u u t ,x ,f x x,x .ϕ⎧-⎪≠=⎨⎪=⎩⎰⎰其中函数处处连续. 讨论()f x 在0x =处的连续性及可导性.解222[(1)()d ]d (1)()d lim ()limlim2x x x x t x t u u tx u uf x xxϕϕ→→→--==⎰⎰⎰x220()d ()d limlim22x x x x x u uu ux xϕϕ→→=-⎰⎰202()0lim 0(0)2x x x f ϕ→⋅=-==因此, ()f x 在0x =处连续. 200300[(1)()d ]d ()(0)lim lim xx x t t u u t f x f x x ϕ→→--=⎰⎰220(1)()d lim 3x x x u u xϕ→-=⎰ 22002200()d ()d 11lim lim 33x x x x x u u u u x xϕϕ→→=-⎰⎰1(0)3ϕ=- 因此, ()f x 在0x =处可导, 且1(0)(0).3f ϕ'=-四. (6分) 设函数()x x t =由方程cos 0t x x +=确定, 又函数()y y x =由方程2e 1y xy --=确定, 求复合函数(())y y x t =的导数0d d .t yt =解方程cos 0t x x +=两边对求导d d cos sin 0.d d x xx t x t t -⋅+=当t=0时, x=0, 故00d cos 1.d sin 1t t x x xt t x ====--= 方程2e 1y xy --=两边对x 求导2d d e 0.d d y y y y x x x -⋅--⋅= 当0x =时,2,y =故 022d 2.d ex y y x y y xx==-==-=因此,00d d d .d d d 2t x t y yxt xt ====⋅=- 五. (6分) 设函数()f x 在(,)-∞+∞上二阶可导,且0()lim0x f x x→=,记10()()x f xt dt ϕ'=⎰,求)(x ϕ的导数,并讨论)(x ϕ'在0x =处的连续性.解由已知的极限知(0)0,(0)0,f f '==从而有1(0)(0)d 0.f t ϕ'==⎰当0x ≠时, 1100011()()()()d()()d ,x f x x f x t dt f x t x t f u u x x xϕ'''====⎰⎰⎰从而有 (),0()0,0.f x x x xx ϕ⎧≠⎪=⎨⎪=⎩因为00()lim ()lim0(0),x x f x x xϕϕ→→===所以, ()x ϕ在0x =处连续. 当0x ≠时,2()()(),xf x f x x xϕ'-'=在0x =处, 由(0)0,ϕ=有2000()(0)()()1(0)lim lim lim (0)22x x x x f x f x f x x x ϕϕϕ→→→'-'''====所以,2()(),0()1(0),0.2xf x f x x xx f x ϕ'-⎧≠⎪⎪'=⎨⎪''=⎪⎩而200000()()()()lim ()limlim lim lim 2x x x x x f x f x f x f x x x x x x ϕ→→→→→''''=-=-001()1()(0)1lim lim (0)(0),222x x f x f x f f x x ϕ→→'''-'''====故()x ϕ'在0x =处连续. 六. (7分) 设函数()y y x =在(,)-∞+∞上可导, 且满足: 22,(0)0.y x y y '=+=(Ⅰ) 研究()y x 在区间(0,)+∞的单调性和曲线()y y x =的凹凸性.(Ⅱ) 求极限3()lim.x y x x →解(Ⅰ) 当0x >时, 有220,y x y '=+> 故()y x 在区间(0,)+∞单调增加. 从而当0x >时, 22y x y '=+也单调增加. 可见, 曲线()y y x =在区间(0,)+∞向下凸. (或当0x >时, 可得222222()0.y x y y x y x y '''=+⋅=++> 可见, 曲线()y y x =在区间(0,)+∞向下凸. )(Ⅱ) 由题设知, (0)(0)0.y y '==应用洛必达法则22322000()()lim lim lim 33x x x y x y x x y x x x→→→'+== []22011111lim (0).33333x y y x →⎛⎫'=+=+= ⎪⎝⎭ 七. (7分) 设()f x 在[0,1]上具有连续导数, 且0()1,(0)0.f x f '<≤=试证211300()d ][()]d .f x x f x x ⎡⎤≥⎢⎥⎣⎦⎰⎰证令2300()()d [()]d ,x xF x f t t f t t ⎡⎤=-⎢⎥⎣⎦⎰⎰则()F x 在[0,1]连续, 且对(0,1)x ∈,30()2()()d [()]xF x f x f t t f x '=-⎰20()2()d ().xf x f t t f x ⎡⎤=-⎢⎥⎣⎦⎰又由题设知, 当(0,1)x ∈时, ()0.f x >令20()2()d (),x g x f t t f x =-⎰则()g x 在[0,1]上连续, 且()2()[1()]0,(0,1),g x f x f x x ''=-≥∈故有()(0)0(0,1).g x g x ≥=∈因此()0,(0,1),F x x '≥∈于是()F x 在[0,1]上单调增加, ()(0)0,[0,1].F x F x ≥=∈取1x =, 即得211300(1)()d [()]d 0.F f t t f t t ⎡⎤=-≥⎢⎥⎣⎦⎰⎰ 所证结论成立.八. (7分) 设函数()y f x =具有二阶导数, 且()0.f x ''>直线是曲线()y f x =上任意一点(,())a f a 处的切线, 其中[0,1].a ∈记直线与曲线()y f x =以及直线0,1x x ==所围成的图形绕轴旋转一周所得旋转体的体积为().V a 试问为何值时()V a 取得最小值.解切线的方程为()()(),y f a f a x a '-=-即()()().y f a x af a f a ''=-+于是1()2[()()()()]d V a x f x f a x af a f a x π''=-+-⎰10112()d ()()().322a xf x x f a f a f a π⎡⎤''=-+-⎢⎥⎣⎦⎰可见, ()V a 在[0,1]连续, 在(0,1)可导. 令1()2[()()]()(32)0323a V a f a f a f a a ππ'''''''=-+=-=,由于()0,f a ''>()V a 在(0,1)内有唯一的驻点2.3a =并且, 当2(0,)3a ∈时, ()0V a '<; 当2(,1)3a ∈时, ()0,V a '>因此, ()V a 在23a =处取得最小值.九. (7分) 计算(sin )d (cos 1)d ,Ly y x x y y -+-⎰其中为从点(0,0)O 沿圆周222x y x +=在第一象限部分到点(1,1)A 的路径.解令sin ,cos 1,P y y Q x y =-=-则 cos (cos 1) 1.Q Py y x y∂∂-=--=∂∂ 取点(1,0).B 作有向直线段,OB 其方程为0(y x =从0变到1).作有向直线段,BA 其方程为1(x y =从0变到1). 由曲线、有向直线段AB 和BO 形成的闭曲线记为(沿顺时针方向), 所围成的区域记为, 则(sin )d (cos 1)d Ly y x x y y -+-⎰()((sin )d (cos 1)d )AB BOLy y x x y y =---+-⎰⎰⎰d (sin )d (cos 1)d D BAy y x x y y σ=-+-+-⎰⎰⎰ (sin )d (cos 1)d OBy y x x y y +-+-⎰101(cos 1)d 04y y π=-+-+⎰1sin1 1.4π=-+-十. (8分) 设(1)有向闭曲线是由圆锥螺线:θθθθθ===z y x ,sin ,cos ,(从0变到)和有向直线段AO构成,其中()0,0,0O ,()2,0,2A ππ; (2)闭曲线将其所在的圆锥面z =.(Ⅰ)如果()x z F -=,1,表示一力场,求沿所做的功;(Ⅱ)如果()x z F -=,1,表示流体的流速,求流体通过流向上侧的流量. (单位从略)解(Ⅰ)作有向直线段,AO 其方程为⎩⎨⎧==x z y 0从变到0).所求沿所做的功为d d d W z x y x z Γ=+-⎰()(d d d )OAAOz x y x z =++-⎰⎰()20cos sin sin cos cos d πθθθθθθθθθθ=-++-⎡⎤⎣⎦⎰()2d x x x π+-⎰a220(cos sin )d 0πθθθθθ=-+⎰24π=.(Ⅱ)所在的圆锥面方程为z =(,,1)x y n z z =--=在xOy 面上的投影区域为, 在极坐标系下表示为: 0,02.r θθπ≤≤≤≤故所求流体通过流向上侧的流量为d d d d d d ()()x y z y z z x x x y z z z x ∑∑⎡⎤Φ=+-=⋅-+--⎣⎦⎰⎰⎰⎰d d x x x y ∑⎛⎫=--- ⎪ ⎪⎝⎭⎰⎰()200d 2cos sin d r r r πθθθθ=-+⎰⎰22302cos sin d 32πθθθθθ⎛⎫=-+ ⎪⎝⎭⎰26π-=.注: (Ⅰ)的另一解法应用Stokes 公式,可得2d d 2d d y z x z x y ∑∑==-⎰⎰⎰⎰2d x y∑=⎰⎰222000sin 2d d sin d r r r rπθπθθθθθ=-⋅=-⎰⎰⎰24π=.十一. (8分) 设函数(,)u u x y =在心形线:1cos L r θ=+所围闭区域上具有二阶连续偏导数, 是在曲线上的点处指向曲线外侧的法向量(简称外法向), un∂∂是(,)u x y 沿的外法向的方向导数, 取逆时针方向.(Ⅰ) 证明: d d d .L L u u u s x y n y x∂∂∂=-+∂∂∂⎰⎰ (Ⅱ) 若222221,u ux y y x y∂∂+=-+∂∂求d L u s n ∂∂⎰的值. (Ⅰ) 证由方向导数的定义d (cos sin )d .LLuu us s nx y αα∂∂∂=+∂∂∂⎰⎰其中, 是相对于x 轴正向的转角.设是L 的切向量相对于x 轴正向的转角, 则1,2παα=+或1.2παα=-故11d (sin cos )d .L L u u us s n x y αα∂∂∂=-∂∂∂⎰⎰ d d .L u u x y y x ∂∂=-+∂∂⎰(Ⅱ) 解应用格林公式22222d ()d d (1)d d D D Lu u us x y x y y x yn x y ∂∂∂=+=-+∂∂∂⎰⎰⎰⎰⎰由对称性1cos 00d 1d d 2d d D L u s x y x r rn πθ+∂==∂⎰⎰⎰⎰⎰203(1cos )d .2πθθπ=+=⎰十二.(8分) 设圆222x y y +=含于椭圆22221x y a b+=的内部, 且圆与椭圆相切于两点(即在这两点处圆与椭圆都有公共切线).(Ⅰ) 求与满足的等式; (Ⅱ) 求与的值, 使椭圆的面积最小.x解 (Ⅰ) 根据条件可知, 切点不在轴上. 否则圆与椭圆只可能相切于一点. 设圆与椭圆相切于点00(,)x y , 则00(,)x y 既满足椭圆方程又满足圆方程, 且在00(,)x y 处椭圆的切线斜率等于圆的切线斜率, 即2002001b x xa y y -=--. 注意到00,x ≠因此, 点00(,)x y 应满足 2200222200022001(1)2(2)1(3)1x y a b x y y b a y y ⎧+=⎪⎪⎪+=⎨⎪⎪=-⎪⎩由(1)和(2)式, 得222200220.b a y y a b--+=(4) 由 (3) 式得2022.b y b a =-代入(4) 式 2242222222220.()b a b b a b b a b a-⋅-+=-- 化简得2222,b a b a=-或22420.a b a b --= (5) (Ⅱ) 按题意, 需求椭圆面积S ab π=在约束条件 (5) 下的最小值.。
