2018-2019学年度第一学期期末教学质量检测附参考答案 (2).docx
2018-2019学年度第一学期期末教学质量参考答案(高三理科数学1.2)_最新修正版
2018—2019学年度第一学期期末教学质量检查高三数学（理科）参考答案及评分标准一、选择题二、填空题 13.31011- 16. -1三、解答题17.解：(1)设等差数列{}n a 的首项为1a ,公差为d ,由已知条件可知11851060a d a d +=⎧⎨+=⎩， ……… 2分解得：14,4a d ==.……… 4分所以4n a n =…………..6分 (2).因为2(44)S 222n n n n n +==+ ……… 7分 2111111()S 222(1)21n n n n n n n ===-+++……… 9分所以1231111111111=[(1)()++)]22231n S S S S n n ++++-+--+（11=(1)=2122nn n -++ ……… 12分18. 解：（1）由正弦定理可得 ,……… 2分 ， ， ,……… 4分 ，.……… 6分 （2）在 中，， ……… 8分 ∵ 为 的中点，∴ ，……… 9分 在 中，,……… 11分……… 12分19. 证明：(1)因为PA ⊥底面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥ ……… 1分 又ABCD 为菱形，连接AC 交BD 于O ,所以.……… 2分 又因为，平面PAC ，PA ⊂平面PAC ，所以BD ⊥平面PAC……… 4分又因为PC ⊂平面PAC ，所以BD⊥PC ，又因为DM PC ⊥， DM BD D =，DM ⊂平面BDM ，DB ⊂平面BDM ,所以PC ⊥平面BDM ，又因为BM ⊂平面BDM……… 5分 所以PC ⊥BM . ……… 6分 (2)法一：因为PA ∥平面 ， 平面 平面PAC平面BDM =MO ，从而PA ∥MO ，……… 7分MO ⊥平面ABCD ,又因为BD ⊥AC .以O 为原点，分别以OB ，OC ，OM 为x 轴，y 轴，z 轴建立空间直角坐标系. ……… 8分设2PA =，(0,0,1)M ,(1,0,0)B ,(1,0,0)D -,(0,2)P设平面PBD 的法向量为1111=(,,)n x y z 因为 ， ，（ ， ）， 由1=0n BP ，1=0n DP，得1111112020x z x z ⎧-+=⎪⎨+=⎪⎩ ，令11y =,则110,2x z ==.1=(0,1,n ……… 10分设平面MBD 的法向量为2222=(,,)n x y z ,因为OC ⊥平面MBD ，可设2222=(,,n x y z ，……… 11分设二面角P BD M --的平面角为θ，由图可知θ为锐角，从而1212|00+1||cos =7||||n n n n θ⨯==……… 12分法二：因为在平面PBD 中PO BD ⊥，在平面MBD 中，MO BD ⊥，从而POM ∠为二面角P BD M--的平面角， ……… 8分cos cos()=sin =2PA POM POA POA PO π∠=-∠∠==……… 12分20解：（1）根据所给表格数据计算得2345645x ++++==，1 2.534 4.535y ++++==，………4分5521127.512202768.5,4916253690i ii i i x yx ===++++==++++=∑∑，AC ^BD AC ∩PA =A AC Ì515221568.560ˆˆˆ0.85,0.490805i ii ii x yx yba y bx xx ==-⋅-∴====-=---∑∑， ………8分 所以，y 关于x 的线性回归方程为ˆ0.850.4yx =-. ………9分 （2）由（1）得，当10x =时，ˆ0.85100.48.1y=⨯-=， 即技术改造后的10年的维修费用为8.1万元，相比技术改造前，该型号的设备维修费降低了0.9万元. ………12分 21解：(1).由题意知,()f x 的定义域为(0)+∞. ………1分()'0f x <时，解得x e >；当()'0f x >时，0x e <<. ………3分 所以函数()f x 的增区间为(0,)e ；()f x 的减区间为(,)e +∞ ………4分 (2).因为22()()2ln 2g x xf x x x x bx =+++=,从而2141'()4+x bx g x x b x x++=+=令 '()0g x =，得2410x bx ++=，由于设方程两根分别为由韦达定理可知，12121,44b x x x x +=-=………6分2212111222()()=(ln 2)(ln 2)g x g x x x bx x x bx -++-++22112122ln2()+()x x x b x x x =+-- 2211212122ln2()4()()x x x x x x x x =+--+- 2211211221222111ln ln 22x x x x x x x x x x x x ⎛⎫-=-=-- ⎪⎝⎭设12x t x =，则 ………8分因为120x x <<，所以12(0,1)x t x =∈，又b ≤12=4b x x +-≥，所以()()2212121211169(2)4448x x x x t x x t ++==++≥整理得212145120t t -+≥，解得112t ≤或12t ≥. 所以10,12t ⎛⎤∈ ⎥⎝⎦………10分222111(1)'()1022t h t t t t -⎛⎫=-+=-< ⎪⎝⎭，所以()h t 在10,12⎛⎤⎥⎝⎦单调递减，g (x 1)-g (x 2)=h (t )=ln t -12(t -1t)()1143ln121224h t h ⎛⎫≥=- ⎪⎝⎭………11分故………12分22.解:（1）曲线的的普通方程为()2211x y -+=，直线l 的普通方程为y x = ………3分联立方程()2211x y y x⎧-+=⎪⎨=⎪⎩，解得00x y =⎧⎨=⎩或11x y =⎧⎨=⎩所以，直线l 与曲线1C 公共点的极坐标为()π0, 0, 4⎫⎪⎭ ………5分（2）依题意，设直线的参数方程为3cos 21sin 2x t y t αα⎧=+⎪⎪⎨⎪=+⎪⎩（α为倾斜角,为参数）,代入()2211x y -+=,整理得：()21cos sin 02t t αα++-=. ………8分因为AB 的中点为P ，则， 所以，cos sin 0αα+=即tan 1α=-.直线'l 的斜率为1- ………10分 23.解:（1）当1=a 时,2|2||1|)(---+=x x x f ,令0)(≥x f ,………1分 ①当1-<x 时,02)2()1(≥--++-x x ,05≥-,矛盾.………2分 ②当21<≤-x 时,02)2()1(≥--++x x ,23≥x ,所以,223<≤x . ………3分 ③当2≥x 时,02)2()1(≥---+x x ,01≥,所以,2≥x . ………4分 综上所述,不等式()0f x ≥的解集为}23|{≥x x .………5分 （2）由题意得:02|2|||≥---+x a x ,2|2|||≥--+x a x , ………6分 因为,|2||)2()(||2|||+=--+≤--+a x a x x a x ,………8分 所以,2|2|≥+a ,于是,22-≤+a ,或22≥+a ,所以,4-≤a ,或0≥a .………10分g (x 1)-g (x 2)1C 'l t 021=+t t。
【优质文档】2018–2019学年度高一数学上学期期末质量检测试卷一含答案
3. 下列各组函数中表示同一函数的是（
）
A. y
x2 和 y （ x）2
B.
y x 和 y 3 x3
C. y log a x2 和 y 2log a x
D. y x 和 y alog a x ( a 0, a 1)
4. sin15 cos 45 sin 75 sin135 的值为（ ）
A. 3 2
1
B.
2
1
C.
D.
3
2
2
5. 如果点 P(sin , cos ) 位于第四象限，那么角 所在的象限是（ ）
A. 第一象限 B. 第二象限 C 第三象限 D. 第四象限
第 1页共6 页
1
6. 函数 f ( x )
1 2x
-x 2 的零点一定位于下列哪个区间（
）
A. (0,1) B. (1, 2) C. (2, 3) D. (3, 4)
）
A.0
B.1
C.2
D.3
8. 已知 a 0 且 a 1 ，f ( x) x 2 a x ，当 x ( 1,1) 时恒有 f ( x )
取值范围是（
1 A. (0, ] [3,
3
)
B.
[1 ，1）（1,3] C.
1 [ ，1） [3,
3
3
) D.
1 (0, ]
（1，3]
3
2 ，则实数 a 的
3
二、填空题
（ I ）若 A B A ，求实数 m 的取值范围；
（ II ）若 A B
，求实数 m 的取值范围 .
1
16. （本小题 13 分）计算： l o g 2 32 lg 4 lg 25 5log5 2 2(16) 2
2018-2019 学年度第一学期七年级期末质量检测数学试卷参考答案
CED BCM 90 （已知） ∴ CED ACN （同角的余角相等）-----------8 分
∴AC∥DE（内错角相等，两直线平行）-----------9 分 ∵AC⊥BF（已知）
A
B
M
C
E
N
∴∠ACB=90°（垂直定义）---------------------10 分 又∵AC∥DE（已证）
解得：x=4，-----------------------------------------------------------------------------------------12 分
∴点 P 运动 4 秒时，追上点 Q．------------------------------------------------------------ 13 分
三、解答题
17. 解：原式= 4 1 ( 3) --------------------------------------4 分（绝对值计算 2 分，其他 1 分） 6
=2
------------------------------------------6 分
18. 解法一：原式= 2x 2 y 3x 3y 3x 3y 2x 2 y ---4 分（评分点：每去一个括号正确得 1 分）
2018-2019 学年第一学期七年级期末质量检测 数学试卷参考答案与评分说明
一．选择题（每小题 4 分，共 40 分）
题号
1
2
3
4
5
6
部编版2018—2019学年度第一学期期末质量检测八年级语文(含答案)
2018-2019学年度第一学期期末质量检测八年级语文试卷注意事：1.本试卷共8页,总分100分,考试时间90分钟。
2.答卷前将密封线左侧的项目填写清楚。
3.答案须用蓝色、黑色字迹的笔书写。
第一部分(1-5题21分)1.给下列加点的字注音。
(2分)佃．农( ) 黝．黑( ) 轩．榭( ) 洗涤．( )2.根据拼音写出汉字。
(3分)(1)他们有的坐火车旅行漫长的路程,有的从图拉驾车赶来,在客厅里 zhèng jīn wēi zuò( )地等待这位大师的接见。
(2)情郁于中,自然要发之于外;家庭 suǒ xiè( )便往往触他之怒。
(3)苏州园林栽种和修剪树木也着眼在画意。
高树与低树 fǚ yǎng shēng zī( )3.填写诗文原句。
(每句1分,共9分)(1)它没有婆娑的姿态，。
也许你要说它不美。
(茅盾《白杨礼赞》)(2)白头搔更短，。
(杜甫《春望》 )(3) ,学诗谩有惊人句。
(李清照《渔家傲》)(4)居天下之广居, ,行天下之大道。
(《富贵不能淫》(5) ,自将磨洗认前朝。
(杜牧《赤壁》)(6)守住心中风景,尽享世间美好。
在喧嚣闹市,陶渊明守住那份淡泊,享受“ , ”的宁静(用《饮酒》中的句子回答)；在茫茫边塞,王维守住那份超然,享受“，”的壮美 (用《使至塞上》中的句子回答)。
(10分)4.学校“经典诵读,感悟人生”演讲比赛组委会已邀请到资深记者吕女士担任评委,现请你将本次大赛的相关事宜电话告知她。
选出表述最准确、语言最得体的一项(2分)A.7月3日下午两点,在我校礼堂举行经典诵读,感悟人生”演讲比赛,请您按时参加。
B.吕女士,您好!请您来我校参加“经典诵读,感悟人生”演讲比赛。
C.吕女士,您好!7月3日下午两点,“经典诵读,感悟人生”演讲比赛将在我校礼堂举行,届时请您光临指导。
D.吕女士,您好17月3日下午两点,“经典诵读,感悟人生”演讲比赛将在我校礼堂举行,请您必须准时到达现场!5.阅读下面的文字,回答问题。
2018~~2019学年度第一学期期末教学质量检查
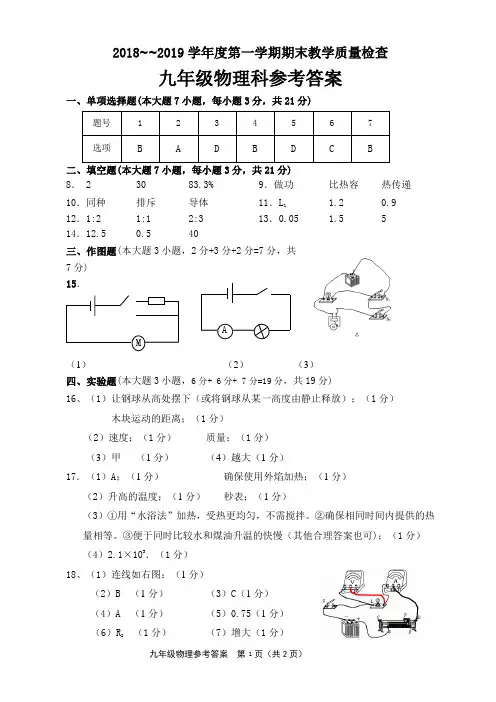
2018~~2019学年度第一学期期末教学质量检查九年级物理科参考答案一、单项选择题(本大题7小题，每小题3分，共21分)二、填空题(本大题7小题，每小题3分，共21分) 8． 2 30 83.3% 9．做功 比热容 热传递 10．同种 排斥 导体11．L 1 1.2 0.912．1:2 1:12:3 13．0.051.5514．12.5 0.540三、作图题(本大题3小题，2分+3分+2分=7分，共7分) 15．（1）（2）（3）四、实验题(本大题3小题，6分+ 6分+ 7分=19分，共19分)16、（1）让钢球从高处摆下（或将钢球从某一高度由静止释放）；（1分）木块运动的距离；（1分） （2）速度；（1分） 质量；（1分）（3）甲（1分）（4）越大（1分） 17．（1）A ；（1分）确保使用外焰加热；（1分） （2）升高的温度；（1分）秒表；（1分）（3）①用“水浴法”加热，受热更均匀，不需搅拌。
②确保相同时间内提供的热量相等。
③便于同时比较水和煤油升温的快慢（其他合理答案也可)；（1分） （4）2.1×103．（1分） 18、（1）连线如右图：（1分）（2）B （1分） （3）C （1分） （4）A （1分） （5）0.75（1分） （6）R 2 （1分）（7）增大（1分）五、计算题(本大题2小题，6分+7分=13分，共13分)19.（6分）解：（1）满载时的总重G=mg=150×1000kg×10N/kg=1.5×106N-------------（2分）（2）抬高一次需要克服气垫船重力所做的功：W=Gh=1.5×106N × 1.72 m =2.58×106 J-------------------------（1分）所需要的汽油的质量：m = Q/q= W/q =2.58×106 J /4.3×107J/kg =0.06kg--------------------（1分）（3）推力的功率：P= Fv=fv=7×104N×30m/s =2.1×106W -------------（2分）答：略。
2018—2019学年度第一学期期末教学质量检查
...3 分 1 / 52018—2019学年度第一学期期末教学质量检查参考答案:•选择题：填空题：解答题:=1,二 t 2-5t +4 <0,解得：(1,4 ) ........⑵ p :由 t 2 -5at +4a 2 < 0 得(t —a)(t —4a) v 0由 a >0且(t-a)(t-4a) <0得，a v t c4a设 A ={t I a c t <4a }, B ={t | 2 <t , 因为q 是p 的充分不必要条件, 所以集合B 是集合A 的真子集a >0 I 3 故有{a <2得一<a <2I 2 I 4a >618.(本小题满分12分)••• sinC用2••• C 是锐角三角形的内角1-5 : A C B A B 6-1011-1213.14. 115. 216.25 1617. (本小题满分10分)解: (1)「P 为假，••• p 为真 ..q:由实数t 满足曲线+亠=1为双曲线.得2-t 6-t(2-t)(6-t)c0 解之 2vtv6 ........ 6 分...7 分...10 分解：(1)由题意知一b—sin B2c根据正弦定理得：泌 sin B2sinC...2 分....4 分・・.5分20.二 PD 丄 BC...1 分2 / 5• a +b =4^32 2 2由余弦定理c =a +b -2ab cosCc 2 =(a +b 2 -3ab=48-12=36(1)由s n+—3S n=1(n 亡 N )得：S n-3S n』=1(n>Zn 亡 N )又 S 2 -3S^ =1，即 Q + a 2 -3& = 1，可得数列 a 2 =3 ./. {a n }是以1为首项3为公比的等比数列,二 a n =3n」(2)①由(1)知，b n =log 3an+ = n ,1 1 1 1+ 1 +川+亠T1001X 22X 3 f = 211 _I 2丿l 2 3丿 200 101（本小题满分12分）解：（1）证明：PD 丄平面ABCD •••C =- 3（2）因为S 涉BC— 1=J 3 =—abs inC2••• ab =4ab19. ...12 分（本小题满分12分） ....9 分...11 分 解: 相减得旦^兰=3, （n >2,n 亡N *）,a nn (n +1) 贝y T n =1 +2 +川 +n =2+ 2仏-1〕+川 +2...12 分T i T 2・・.5分BC匸平面ABCD又•••PD丄平面ABCD，直线PA与底面ABCD所成的角为4520.二PD 丄BC ...1 分3 / 5...11 分4 / 5••• N PAD =45"，二 AD = PD = 2 在 RUBAD 中，BD 2 = BA 2 + AD 2= 8过B 作CD 的垂线BF ，则在RtABFC 中BC 2 =BF 2 +CF 2=82 2 2在也BCD 中，BD +BC =CD/. BD 丄 BCBD,PD u 平面 PBD/. BC 丄平面PBDT BC u 平面 PBC所以平面PBC 丄平面PBD(2)打PD 丄平面ABCD 且AD 丄DC 二以D 为原点，DA,DC, DP 为x,y,z 轴建立空间直角坐标系。
清远市2018—2019学年度第一学期期末教学质量检测高三语文试题含答案
清远市2018—2019学年度第一学期期末教学质量检测高三语文试卷注意事项：1．本试卷共4道大题22小题，满分为150分，考试时间150分钟。
2．答卷时，将答案填写在答题卡对应位置上；答在本试卷上无效。
3．考试结束后，将答题卡交回。
第Ⅰ卷阅读题一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。
中华民族的文化传统源远流长，这不仅培养了中国人民高尚文雅、彬彬有礼的精神风貌，而且使中国赢得了“礼仪之邦”的美称。
在中国古代社会里，上自朝廷的军国大政，下至民间的日常饮食，无不是在礼的规范下进行，礼是人们日常生活中最有权威的制约因素。
《礼记·礼运》中说：“夫礼之初，始诸饮食。
其燔黍捭豚，污尊而抔饮，蒉桴而土鼓，犹若可以致其敬于鬼神。
”这就是说，礼，最初产生于人们的饮食活动。
中国先民把黍米放在火上烧熟，把小猪放在火上烤熟，在地上挖个坑当作酒壶，用双手当酒杯捧着水来喝，用草扎成的槌子敲打地面当作鼓乐，好像用这种简陋的生活方式便可以向鬼神表示敬意，从而得到神的庇护和赐福。
这样，最原始的祭礼也就由此产生了。
《礼记》中认为原始的礼仪行为就是从人们的饮食活动中产生的，这便是所谓的“夫礼之初，始诸饮食”。
人要吃喝，以为神也离不开食物，所以要将自己的食物也毫无保留地奉献出来。
中国的先民们想通过这种简单的仪式向神灵表达虔诚的崇拜心情，而这种纪念仪式逐渐定型化，并取得较为固定的社会意义时，原始的礼便有了自己的雏形。
这里，我们将“污尊而抔饮”之类的仪式称之为“原始的礼”，主要是肯定了一种客观存在的事实。
这种源于饮食的祭礼，是中国先民顺应自然生活的文化创造，中国先民是按照人要吃饭穿衣的观念来构想诸神灵界生活的，以为祭祀就是让神吃喝，神吃好以后才能保证大家平安。
所以，“礼”与解为甜酒的“醴”字，音既相同，意义也有相通之处，亦非巧合。
人们通过饮食来祭祀神，表现了中国先民重视现实和生命的原初心理。
2018-2019第一学期八年级语文期末考试试卷(有答案)
2018—2019学年度第一学期期末教学质量检测试卷八年级语文参考答案1.B2.C3.B4.A （各2分）5（4分）红军战士埃德加·斯诺昆虫的史诗清道夫6.（6分）（1）长河落日圆（2）似曾相识燕归来（3）最爱湖东行不足绿杨阴里白沙堤（4）采菊东篱下悠然见南山7.（4分）（1）就是而是（2） C A B8.（2分）歌颂了守边将士浴血奋战，誓死报国的英雄气概和爱国主义情感。
9.（3分）“压”写出了敌军人马众多，来势凶猛，交战双方力量悬殊、守军将士处境的艰难。
运用比喻和夸张手法，渲染了敌军兵临城下的紧张气氛和危急情势；“开”写出了守军披坚执锐，严阵以待，雄姿英发，士气高昂，和敌军形成鲜明对比。
（意对即可）10.（4分）（1）阙同“缺”空隙、缺口（2）逆流而上（3）从（4）飞奔的马11.（4分）（1）水清，树荣，山高，草盛，确实有很多乐趣。
（2）山凭借（高峻的）地势，争着向上，仿佛都在争着往高处和远处伸展，形成无数的山峰。
12.（3分）《三峡》通过描写三峡的美丽景色，表达了作者对祖国大好河山的热爱之情。
《与朱元思书》反映出作者热爱自然，寄情山水的感情，也可以看出作者对追求功名利禄的鄙弃，对官场政务的厌倦。
13.（2分）“我”是一个爱岗敬业、尊重学生，能公平地对待学生，受学生爱戴、看重师生间的情意的师德高尚的人。
14.（2分）比喻、排比，生动形象地表现出了“我”对小岩那份别样的礼物的赞赏以及它带给“我”的惊喜与感动。
15.（3分）交代了小岩家境和他平日里不参加班级活动的情况，解释了“我”对小岩能来看望“我”感到意外的原因，表现了小岩对老师的真挚情感，为下文写小岩送“我”一句祝福当礼物做铺垫。
16.（3分）示例：亲爱的小岩：感谢你在我生病时送给我一份独特的礼物，你是一个纯真的孩子，老师希望你在今后的日子里能够继续保持这份纯真。
祝你学业有成，前途似锦。
（结合文章表达感谢之意，有祝福，表述符合老师身份。
20182019学年度第一学期期末教学质量检测附参考包括答案
2018-2019 学年度第一学期期末教课质量检测七年级数学试卷一、选择题（本大题共10 小题，每题 3 分，共 30 分）以下各题中均有四个备选答案，此中有且只有一个正确，请在答题卡大将正确答案的代号涂黑．1．（3分）四个有理数﹣ 1，2，0，﹣ 3，此中最小的是（）A．﹣ 1B．2C．0D．﹣ 32．（3分）以下是﹣ 3 的相反数是（）A． 3B．﹣C．D．﹣ 33．（3分）我国南海某海疆探明可燃冰储量约为19 400 000 000 立方米， 19 400 000 000 用科学记数法表示为（）A．×109B．×1010C．×1010D．× 1094．（3分）将以下平面图形绕轴旋转一周，可获得图中所示的立体图形的是（）A．B．C．D．5．（3分）若代数式﹣ 5x6y3与 2x2n y3是同类项，则常数n 的值（）A． 2B．3C．4D．66．（3分）若 x=﹣1是对于 x 的方程2x 5a=3的解，则 a 的值为（）+A．B．4C．1D．﹣ 17．（3分）以下运算中，正确的选项是（）A． 3a+2b=5ab B．3a2b﹣ 3ba2=0C． 2a3+3a2=5a5D．5b2﹣4b2=18．（3 分）程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100 个和尚分 100 个馒头，假如大和尚 1 人分 3 个，小和尚 3 人分 1 个，正好分完．大、小和尚各多少人？大和另有x 人，依意列方程得（）A．+ 3（100 x）=100C． 3x+=100 9．（3 分）在数上表示有理数B．3（100 x）=100D．3x=100a， a， b 1 的点如所示，（）A． b＜ a B．| b+1| ＜| a|C．| a| ＞| b|D．b 1＜a10．（ 3分）一列数，按必定律摆列成1，3， 9，27， 81，⋯，从中拿出三个相的数，若三个数的和a，三个数中最大的数与最小的数的差（）A．a B．| a|C．| a|D．a二、填空（本大共 6 小，每小 3 分，共 18 分）以下各不需要写出解答程，将果直接填写在答卡指定地点．11．（ 3分）某市 2018 年元旦的最低气温 1℃，最高气温 7℃，一天的最高气温比最低气温高℃．12．（ 3 分） 30° 30′=度．13．（ 3 分）式 2x2y 的次数是：．14．（ 3分）若一个角比它的角大36°，个角°．15．（ 3分）已知点 A、B、C 在直 l 上，若 BC= AC，=．16．（ 3分）如所示的运算程序中，若开始入的x100，我第 1 次出的果50，第 2 次出的果 25，⋯，第 2018 次出的果．三、解答（共 8 小，共 72 分）17．（ 8 分）算：（1）（ 3）+7+8+（ 9）．（2）（﹣ 1）10×2+（﹣ 2）3÷4．18．（ 8 分）解方程：（1）3x+2=7﹣2x．（2）x﹣=3﹣．19．（ 8 分）先化简，再求值：x﹣22）（﹣x y2），此中 x=﹣2，y=﹣1．（x﹣ y ++20．（8 分）笔录本的单价是 x 元，圆珠笔的单价是y 元．小红买 3 本笔录本， 6 支圆珠笔；小明买 6 本笔录本， 3 支圆珠笔．（1）买这些笔录本和圆珠笔小红和小明一共花销多少元钱？（2）若每本笔录本比每支圆珠笔贵 2 元，求小明比小红多花销了多少元钱？21．（ 8 分）如图，∠ AOC与∠ BOC互余， OD 均分∠ BOC，∠ EOC=2∠AOE．（1）若∠ AOD=75°，求∠ AOE的度数．（2）若∠ DOE=54°，求∠ EOC的度数．22．（ 10 分）2018 年元旦，某商场将甲种商品降价40%，乙种商品降价 20%展开优惠促销活动．已知甲、乙两种商品的原销售单价之和为 1400 元，某顾客参加活动购置甲、乙各一件，共付1000 元．（1）甲、乙两种商品原销售单价各是多少元？（2）若商场在此次促销活动中甲种商品损失25%，乙种商品盈余 25%，那么商场在此次促销活动中是盈余仍是损失了？假如是盈余，求商场销售甲、乙两种商品各一件盈余了多少元？假如是损失，求销售甲、乙两种商品各一件损失了多少元？23．（ 10 分）如图，点 B、C 在线段 AD 上， CD=2AB+3．（1）若点 C 是线段 AD 的中点，求 BC﹣AB 的值；（2）若 BC= AD，求 BC﹣AB 的值；（3）若线段 AC上有一点 P（不与点 B 重合）， AP+AC=DP，求 BP 的长．24．（12 分）如图 1，已知∠ AOB=120°，∠ COD=60°，OM 在∠ AOC内，ON 在∠ BOD内，∠ AOM=∠AOC，∠BON=O 逆时针旋转到OC与 OB 重合时，如图 2，∠MON=°；∠BOD．（1）∠COD从图 1 中的地点绕点（2）∠ COD从图 2 中的地点绕点 O 逆时针旋转 n°（ 0＜ n＜ 120 且 n≠ 60），求∠ MON 的度数；（3）∠ COD 从图 2 中的地点绕点O 顺时针旋转n°（0＜n＜120），则 n=时，∠ MON=2∠BOC．参照答案与试题分析一、选择题（本大题共10 小题，每题 3 分，共 30 分）以下各题中均有四个备选答案，此中有且只有一个正确，请在答题卡大将正确答案的代号涂黑．1．（3 分）四个有理数﹣1，2，0，﹣ 3，此中最小的是（）A．﹣ 1B．2C．0D．﹣ 3【剖析】有理数大小比较的法例：①正数都大于0；②负数都小于0；③正数大于全部负数；④两个负数，绝对值大的其值反而小，据此判断即可．【解答】解：依占有理数比较大小的方法，可得﹣3＜﹣ 1＜0＜2，∴四个有理数﹣ 1，2，0，﹣ 3，此中最小的是﹣ 3．应选： D．【评论】本题主要考察了有理数大小比较的方法，要娴熟掌握，解答本题的重点是要明确：①正数都大于 0；②负数都小于 0；③正数大于全部负数；④两个负数，绝对值大的其值反而小．2．（3 分）以下是﹣ 3 的相反数是（）A． 3B．﹣C．D．﹣ 3【剖析】依据相反数的定义，即可解答．【解答】解：﹣ 3 的相反数是 3．应选： A．【评论】本题考察了相反数的定义，解决本题的重点是熟记相反数的定义．3．（3 分）我国南海某海疆探明可燃冰储量约为19 400 000 000 立方米， 19 400 000 000 用科学记数法表示为（）A．×109B．×1010C．×1010D．× 109【剖析】科学记数法的表示形式为a×10n的形式，此中 1≤| a| ＜ 10，n 为整数．确立 n 的值时，要看把原数变为 a 时，小数点挪动了多少位，n 的绝对值与小数点挪动的位数同样．当原数绝对值＞ 1 时， n 是正数；当原数的绝对值＜ 1 时， n 是负数．【解答】解： 19 400 000 000用科学记数法表示为×1010，应选： B．【评论】本题考察科学记数法的表示方法．科学记数法的表示形式为a× 10n的形式，此中1≤| a| ＜ 10，n 为整数，表示时重点要正确确立 a 的值以及 n 的值．4．（3 分）将以下平面图形绕轴旋转一周，可获得图中所示的立体图形的是（）A．B．C．D．【剖析】面动成体．由题目中的图示可知：此圆台是直角梯形转成圆台的条件是：绕垂直于底的腰旋转．【解答】解： A、是两个圆台，故A 错误；B、上边小下边大，侧面是曲面，故 B 正确；C、是一个圆台，故 C 错误；D、下边小上边大侧面是曲面，故 D 错误；应选： B．【评论】本题考察直角梯形转成圆台的条件：应绕垂直于底的腰旋转．．（分）若代数式﹣ 6 3与 2x2n 3是同类项，则常数 n 的值（）5 35x y yA． 2B．3C．4D．6【剖析】依据同类项是字母同样且同样字母的指数也同样，可得答案．【解答】解：由﹣ 5x6y3与 2x2n y3是同类项，得2n=6，解得 n=3．应选： B．【评论】本题考察了同类项，同类项定义中的两个“同样”：同样字母的指数同样，是易混点，因此成了中考的常考点．6．（3 分）若x=﹣1 是对于x 的方程2x+5a=3的解，则 a 的值为（）A．B．4C．1D．﹣ 1【剖析】把x 的值代入方程计算即可求出 a 的值．【解答】解：把 x=1 代入方程得：﹣ 2+5a=3，解得： a=1，应选： C．【评论】本题考察了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．7．（3 分）以下运算中，正确的选项是（）A． 3a+2b=5ab B．3a2b﹣ 3ba2=0C． 2a3+3a2=5a5D．5b2﹣4b2=1【剖析】直接利用归并同类项法例分别化简得出答案．【解答】解： A、 3a+2b 没法计算，故此选项错误；B、3a2b﹣ 3ba2=0，正确；C、2a3+3a2，没法计算，故此选项错；D、5b2﹣4b2=b2，故此选项错误；应选： B．【评论】本题主要考察了归并同类项，正确掌握运算法例是解题重点．8．（3 分）程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100 个和尚分 100 个馒头，假如大和尚 1 人分 3 个，小和尚 3 人分 1 个，正好分完．试问大、小和尚各多少人？设大和另有x 人，依题意列方程得（）A．+ 3（100﹣x）=100B．﹣3（100﹣x）=100C． 3x+=100D．3x﹣=100【剖析】依据100 个和尚分100 个馒头，正好分完．大和尚一人分 3 个，小和尚 3 人分一个得到等量关系为：大和尚的人数+小和尚的人数 =100，大和尚分得的馒头数+小和尚分得的馒头数=100，依此列出方程即可．【解答】解：设大和另有x 人，则小和另有（ 100﹣ x）人，依据题意得： 3x+=100；应选： C．【评论】本题考察了由实质问题抽象出一元一次方程，重点以和尚数和馒头数作为等量关系列出方程．9．（3 分）在数轴上表示有理数a，﹣ a，﹣ b﹣ 1 的点如下图，则（）A．﹣ b＜﹣ a B．| b+1| ＜| a|C．| a| ＞| b|D．b﹣1＜a【剖析】由于 a 与﹣ a 互为相反数，因此依据图告知，a＜0＜﹣ a＜﹣ b﹣ 1，由此对选项进行一一剖析．【解答】解：∵ a 与﹣ a 互为相反数，∴依据图告知， a＜0＜﹣ a＜﹣ b﹣1，∴|﹣a| =| a| ＜| ﹣b﹣1| =| b+1| ，则 | b+1| ＞ | a| ，故 B 选项错误；∴﹣ b＞﹣ a，故 A 选项错误；∴| a| ＞| b| ，故 C 选项错误；∴b﹣1＜a，故 D 选项正确．应选： D．【点】此合考了数、的相关内容，用几何方法借助数来求解，特别直，体了数形合的点．10．（ 3 分）一列数，按必定律摆列成1，3， 9，27， 81，⋯，从中拿出三个相的数，若三个数的和 a，三个数中最大的数与最小的数的差（）A．a B．| a|C．| a|D．a【剖析】三个数中第一个数x，另两个数分3x、9x，依据三个数的和a，即可得出对于 x 的一元一次方程，解之即可得出 x 的，再依据 3x 与 9x 异号、 x 与 9x 同号，即可求出三个数中最大的数与最小的数的差．【解答】解：三个数中第一个数x，另两个数分 3x、 9x，依据意得： x 3x+9x=a，解得： x= a．∵ 3x 与 9x 异号， x 与 9x 同号，∴ 三个数中最大的数与最小的数的差| 9x（ 3x） | =12| x| = | a| ．故： C．【点】本考了一元一次方程的用，找准等量关系，正确列出一元一次方程是解的关．二、填空（本大共6 小，每小 3 分，共 18 分）以下各不需要写出解答程，将果直接填写在答卡指定地点．11．（ 3 分）某市 2018 年元旦的最低气温 1℃，最高气温7℃，一天的最高气温比最低气温高 8 ℃．【剖析】直接利用有理数的加减运算法算得出答案．【解答】解：由意可得：一天的最高气温比最低气温高7（ 1） =8（℃）．故答案： 8．【点】此主要考了有理数的加减运算，正确掌握运算法是解关．12．（ 3 分） 30° 30′=度．【剖析】依据 1 度等于60 分， 1分等于60 秒，由大位成小位乘以60，小位成大位除以60，按此化即可．【解答】解：（1）∵ 30′= °=0.5 °，∴30°30′=30°.5 °=30.5 °．+故答案为．【评论】本题主要考察的是度、分、秒的加法计算，相对照较简单，注意以60 为进制即可．13．（ 3 分）单项式 2x2y 的次数是： 3 ．【剖析】依据单项式次数的定义来确立．单项式中全部字母的指数和叫做这个单项式的次数．【解答】解：依据单项式次数的定义，字母x、y 的次数分别是 2、1，和为 3，即单项式的次数为3．故答案为 3．【评论】本题考察单项式次数的定义，要记清，单项式中全部字母的指数和叫做这个单项式的次数．14．（ 3 分）若一个角比它的补角大 36°，则这个角为108°．【剖析】设这个角为 x°，则这个角的补角为（ 180﹣ x）°，依据题意可得方程x﹣（180﹣x）=36，再解方程即可求解．【解答】解：设这个角为x°，则这个角的补角为（ 180﹣x）°，x﹣（ 180﹣x）=36，解得： x=108．故答案为： 108．【评论】本题主要考察了余角和补角，重点是掌握余角：假如两个角的和等于90°（直角），就说这两个角互为余角．即此中一个角是另一个角的余角．补角：假如两个角的和等于180°（平角），就说这两个角互为补角．即此中一个角是另一个角的补角．15．（ 3 分）已知点 A、B、C 在直线 l 上，若 BC= AC，则=或．【剖析】分类议论： C 点在线段 AB 上，则 AB=AC+BC；当 C 点在线段 AB 的反向延伸线上，则AB=BC﹣AC，而后把 BC= AC代入计算．【解答】解：当 C 点在线段 AB 上，如图 1，∵AB=AC+BC， BC= AC，∴==；当C 点在线段 AB 的反向延伸线上，如图 2，∵AB=BC﹣AC， BC= AC，∴==．故答案：或．【点】本考了两点的距离：两点之的段叫两点的距离．也考了分思想的运用．1 次出的果16．（ 3 分）如所示的运算程序中，若开始入的x100，我第50，第 2 次出的果 25，⋯，第 2018 次出的果4．【剖析】依据的程序行算，找到循的律，依据律推算．【解答】解：由的程序，知挨次出的果是50，25，32，16，8，4，2，1，8，4，2，1⋯，从 8 开始循．2018 4=2014， 2014÷ 4=503⋯2，故第 2018 次出的果是 4．故答案： 4．【点】此主要考了代数式求，正确循的律，依据循的律行推行．中除前 4 次不循外，后是 4 个一循．三、解答（共 8 小，共 72 分）17．（ 8 分）算：（1）（ 3）+7+8+（ 9）．（2）（ 1）10×2+（ 2）3÷4．【剖析】（ 1）原式合后，相加即可求出；（2）原式先算乘方运算，再算乘除运算，最后算加减运算即可求出．【解答】解：（1）原式 = 12+15=3；（2）原式 =2 2=0．【点】此考了有理数的混淆运算，熟掌握运算法是解本的关．18．（ 8 分）解方程：（1）3x+2=7﹣2x．（2）x﹣=3﹣．【剖析】（ 1）方程移项归并，把x 系数化为 1，即可求出解；（2）方程去分母，去括号，移项归并，把x 系数化为 1，即可求出解．【解答】解：（1）移项归并得： 5x=5，解得： x=1；（2）去分母得： 4x﹣2x﹣ 4=12﹣ x﹣ 1，移项归并得： 3x=15，解得： x=5．【评论】本题考察认识一元一次方程，解方程去分母时注意各项都乘以各分母的最小公倍数．19．（ 8 分）先化简，再求值：x﹣2（x﹣y2）+（﹣x+ y2），此中 x=﹣2，y=﹣1．【剖析】先去括号，而后归并同类项即可化简题目中的式子，而后将x、y 的值代入化简后的式子即可解答本题．【解答】解：x﹣2（x﹣y2） +（﹣ x+y2）==﹣ 3x+y2，当x=﹣2，y=﹣ 1 时，原式 =﹣ 3×（﹣ 2）+（﹣ 1）2=6+1=7．【评论】本题考察整式的加减﹣化简求值，解答本题的重点是明确整式化简求值的方法．20．（8 分）笔录本的单价是 x 元，圆珠笔的单价是y 元．小红买 3 本笔录本， 6 支圆珠笔；小明买 6 本笔录本， 3 支圆珠笔．（1）买这些笔录本和圆珠笔小红和小明一共花销多少元钱？（2）若每本笔录本比每支圆珠笔贵 2 元，求小明比小红多花销了多少元钱？【剖析】（ 1）分别用含 x、y 的代数式表示出小红、小明的花销，归并它们花销的代数式；（2）用含 x、y 的代数式表示出小明比小红多花销的钱数，把每本笔录本比每支圆珠笔贵 2 元朝入化简后的代数式．【解答】（ 1）由题意，得3x+6y+6x+3y=9x+9y答：买这些笔录本和圆珠笔小红和小明一共花销了（9x+9y）元；（2）由题意，的（ 6x+3y）﹣（ 3x+6y）=3x﹣3y由于每本笔录本比每支圆珠笔贵 2 元，即 x﹣ y=2因此小明比小红多花销：3x﹣ 3y=3（x﹣y）=6（元）答：小明比小红多花销了 6 元钱．【评论】本题考察了列代数式及代数式的化简求值．理解题意是解决本题的重点21．（ 8 分）如图，∠ AOC与∠ BOC互余， OD 均分∠ BOC，∠ EOC=2∠AOE．（1）若∠ AOD=75°，求∠ AOE的度数．（2）若∠ DOE=54°，求∠ EOC的度数．【剖析】设∠ AOE=x，表示出∠ EOC，进而获得∠ AOC 和∠ BOC，再依据角均分线的定义表示出∠COD，（1）依据∠ AOD=∠AOC+∠ COD列方程求解即可；（2）依据∠ DOE=∠EOC+∠COD列方程求出 x 的值，再求解即可．【解答】解：设∠ AOE=x，∵∠ EOC=2∠AOE，∴∠ EOC=2x，∴∠ AOC=∠ AOE+∠COE=3x，∵∠ AOC与∠ BOC互余，∴∠ BOC=90°﹣3x，∵OD 均分∠ BOC，∴∠ COD= ∠BOC=45°﹣x，（1）若∠ AOD=75°，则∠ AOD=∠AOC+∠COD=75°，即3x+45°﹣ x=75°，解得 x=20°，即∠ AOE的度数为 20°；（2）若∠ DOE=54°，则∠ DOE=∠ EOC+∠COD=54°，即2x+45°﹣ x=54°，解得 x=18°，2x=36°，即∠ EOC的度数是 36°．【评论】本题考察了余角和补角，角均分线的定义，正确识图是解题的重点，难点在于表示出∠COD．22．（ 10 分）2018 年元旦，某商场将甲种商品降价40%，乙种商品降价 20%展开优惠促销活动．已知甲、乙两种商品的原销售单价之和为 1400 元，某顾客参加活动购置甲、乙各一件，共付1000 元．（1）甲、乙两种商品原销售单价各是多少元？（2）若商场在此次促销活动中甲种商品损失25%，乙种商品盈余 25%，那么商场在此次促销活动中是盈余仍是损失了？假如是盈余，求商场销售甲、乙两种商品各一件盈余了多少元？如果是损失，求销售甲、乙两种商品各一件损失了多少元？【剖析】（ 1）设甲商品原销售单价为x 元，则乙商品的原销售单价为（1400﹣x）元，依据优惠后购置甲、乙各一件共需1000 元，即可得出对于x 的一元一次方程，解之即可得出结论；（2）设甲商品的进价为 a 元/ 件，乙商品的进价为 b 元/ 件，依据甲、乙商品的盈亏状况，即可分别得出对于 a、b 的一元一次方程，解之即可求出a、b 的值，再代入 1000﹣a﹣b 中即可找出结论．【解答】解：（1）设甲商品原销售单价为x 元，则乙商品的原销售单价为（1400﹣x）元，依据题意得：（1﹣40%）x+（1﹣20%）（ 1400﹣ x）=1000，解得： x=600，∴1400﹣x=800．答：甲商品原销售单价为600 元，乙商品的原销售单价为800 元．（2）设甲商品的进价为 a 元/ 件，乙商品的进价为 b 元/ 件，依据题意得：（1﹣25%）a=（1﹣40%）× 600，（1+25%）b=（1﹣20%）× 800，解得： a=480，b=512，∴1000﹣a﹣b=1000﹣480﹣ 512=8．答：商场在此次促销活动中盈余，盈余了8 元．【评论】本题考察了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．23．（ 10 分）如图，点 B、C 在线段 AD 上， CD=2AB+3．（1）若点 C 是线段 AD 的中点，求 BC﹣AB 的值；（2）若 BC= AD，求 BC﹣AB 的值；（3）若线段 AC上有一点 P（不与点 B 重合）， AP+AC=DP，求 BP 的长．【剖析】设 AB=x， BC=y，则 CD=2x+3．（1）依据 AC=CD建立方程即可解决问题；（2）依据 AB+CD=3BC，建立方程即可解决问题；（3）设 BP=m，依据 AP+AC=DP，建立方程即可解决问题；【解答】解：设 AB=x，BC=y，则 CD=2x+3．（1）∵ C 是 AD 中点，∴AC=CD，∴x+y=2x+3∴y﹣x=3，即 BC﹣ AB=3．（2）∵ BC= AD，即 AB+CD=3BC，∴x+2x+3=3y，∴y﹣x=1，即 BC﹣ AB=1．（3）设 AP=m，∵ AP+AC=DP，∴m+x+y=2x+3+x+y﹣ m，∴m﹣ x=，即BP=m﹣x=．【评论】本题考察两点间距离，线段的中点、线段的和差定义等知识，熟知各线段之间的和、差关系是解答本题的重点，学会利用参数建立方程解决问题．24．（12 分）如图 1，已知∠ AOB=120°，∠ COD=60°，OM 在∠ AOC内，ON 在∠ BOD内，∠ AOM=∠AOC，∠ BON= ∠BOD．（1）∠COD从图 1 中的地点绕点 O 逆时针旋转到 OC与 OB 重合时，如图 2，∠MON= 100°；（2）∠ COD从2 中的地点绕点O 逆时针旋转n°（ 0＜ n＜ 120 且n≠ 60），求∠ MON 的度数；图（3）∠COD从2 中的地点绕点O 顺时针旋转n（°0＜ n＜ 120），则n=50°或70°时，∠MON=2图∠BOC．【剖析】（ 1）依据∠ MON=∠BOM+∠BON 计算即可；（2）分两种情况分别计算即可；（3）分两种情况分别计算即可；【解答】解：（1）由题意；∠ MON= ∠AOB+∠COD=80°+20°=100°，故答案为 100；（2）①当 0＜n＜60°时，如图 1 中，∠AOC=120°﹣n°，∠ BOD=60°﹣ n°，∴∠ MON=∠MOC+∠COB+∠BON= （ 120°﹣n°）+n°+（60°﹣n°）=100°，②当 60°＜n＜120°时，如图 2 中，∠AOC=120°﹣n°，∠ COD=60°，∠ BOD=n°﹣60°M∴∠ MON∠ MOC+∠COD+∠ DON= （120°﹣n°）+60°+（n°﹣60°）=100°．综上所述，∠ MON=100°（3）① 0°＜n＜60°时，∠ BOC=n°，∠ MON=2n°，∠MON=（120°+n°）+60°﹣（60°+n°）=100°，∴n=50°．②当 60°＜n＜120°时，∠ AOC=360°﹣（ 120°+n°） =240°﹣n°，∠ BOD=60°+n°，∴∠ MON=360° ﹣∠ AOM﹣∠ AOB﹣∠ BON=360°﹣（ 240°﹣n°）﹣ 120°﹣（60°+n°）=140°∴n=70°．综上所述， n 的值为 50°或 70°．故答案为 50°或 70°．【评论】本题考察角的和差定义，解题的重点是学会用分类议论的思想思虑问题，学会利用参数解决问题．。
2018—2019学年度第一学期小学四年级语文期末教学质量检测试卷及参考答案
2018—2019学年度第一学期小学四年级语文期末教学质量检测试卷及参考答案2018—2019学年度第一学期小学期末教学质量检测四年级语文考试时间：90分钟满分：100分题号一二三四五六七总分得分一、拼音乐园(13分)（一）看拼音，写词语。
（10分）guīlǜfèng xìhén jìfùgài qīwǔzhìhuìlǎn duóróng qiàmǐn jiétáo tài(二)多音字组词。
（3分）piāo（）zhāo（）sh ě（）漂朝舍piào（）cháo（）shè（）二、字词积累(18分)(一)先在横线上写出所给字的形近字，再分别组词。
（6分）幻（）腊（）魂（）崭（）（）（）（）（）（二）写出下列词语的反义词。
（3分）责备——（）凶恶——（）暖和——（）短暂——（）复杂——（）狭窄——（）（三）将下列词语补充完整，并按要求完成练习。
（9分）（）天（）地（）逾（）稀慢（）斯（）（）（）绰绰恍然（）（）（）风（）雨1．仿照画“——”的词语再写两个“ABCC”式的词语：2．听了老师的讲解后，我，原来这道题还可以这样解。
（选词填空）三、句子天地(14分)(一)选择合适的关联词填在括号里。
（4分）虽然……但是因为……所以即使……也不但……而且1.（）我努力了，（）能在期末考试中取得优异的成绩。
2.（）再冷的天，我（）会坚持晨跑。
3.（）我们努力了不一定会成功，（）不努力就会失败。
4.我（）喜欢阅读，（）喜欢写作。
(二)按要求改写句子。
（10分）1.狡猾的狐狸一直盯着乌鸦嘴里的肉。
（缩写句子）2.我的脑海中浮现了两年前刚刚发生的事情。
（修改病句）3.诸葛亮精通兵法。
诸葛亮熟知天文地理。
（用关联词语连城一句话）4.不好好学习，怎么能取得好成绩呢？（改为陈述句）5.院子里那一墙的爬山虎，如同一片浓浓的湖水。
2018——2019学年度人教部编版第一学期期末八年级语文试卷(含答案及解析)(二)
2018——2019学年度第一学期期末八年级语文试卷一．积累和运用（15分）1.下列词语中加点字注音完全正确的一项是（2分）（）A．要塞．（sài）翘．首（qiào）殚．精竭虑（dān）B．窒．息（zhì）踌躇．（chú）坦荡如砥．（dì）C．濒．临（bīn）嶙．峋（lín）重峦叠嶂．（zhàng）D．喧嚣．（xiāo）遒劲．（jìn）络绎．不绝（yì）2.下面各项中表述正确的一项是 (2分) ( )A.《藤野先生》作者鲁迅，原名周树人，代表作有小说《朝花夕拾》等。
B.《饮酒》是一组七言古诗，共20首。
作者陶渊明，东晋诗人。
C.《记承天寺夜游》作者苏轼，字子瞻，号东坡居士，唐代文学家。
D.《白杨礼赞》的作者是茅盾，作家、社会活动家，代表作有小说《蚀》三部曲等。
4.李清照的《渔家傲》中①“闻天语，殷勤问我归何处”一句用了哪种修辞手法？在结构上有什么作用？②词中的“谩”有多层含义，请结合全词加以分析。
（3分）5.无可奈何花落去，似曾相识燕归来。
□□□□□□□。
(1分)6.《三峡》中最后一句故渔者歌曰：“□□□□□□□，□□□□□□□。
”（27.孟子认为真的大丈夫应该做到:□□□□□，□□□□□，□□□□□。
（3二、阅读（一）文言文阅读（15分）（甲）阅读《生于忧患，死于安乐》，回答问题。
（10分）8.本文的作者孟轲，战国时期，家学派代表人物之一。
（1分）9.解释下面加点词语在文中的意思。
（2分）①舜发．于畎亩之中（）②空乏．．其身（）③人恒．过（）④而后喻．（）10.开篇列举六位历史人物有什么共同的特点？列举他们的事例有什么作用？（2分）11.本文的中心论点是什么？（用文中句子回答）（2分）12.《朱子语类》中说：“人须从贫困艰苦中做来，方坚牢。
”结合文章内容，用自己的话说说此句所蕴含的道理是什么？（3分）（乙）阅读《孙叔敖为楚令尹》一文，回答问题。
2018-2019学年第一学期期末教学质量检测八年级语文试题及答案
能被打败。”下列对这句话的理解，不．正．确．的一项是（ A.生活中难兔遭遇各种各样的困难，甚至失敗。
）（2 分）
B.人生的价值却在于不断地克服各科困难，战胜磨难。
C.在奋斗的过程中人的生命可以被各种困苦磨难夺去。
D.一往无前拼的人是不会有失败的命运的。
6. 为下面一则新闻拟定一个单行标题。（要求不多于 20 字）（2 分）
B.归咎
荒谬
金銮殿
重峦迭嶂
C.簌簌
轩榭
文诌诌
转弯抹角
D. 缕空
绮丽
绿茵茵
气息奄奄
3.下列各句中，加点的成语使用正确的一项是（
）（2 分）
A.活动场所要选择平滑的广场，避开水坑、砂子、沙砾、铁栅栏和锐．不．可．当．的物体等。 B.首艘国产航母曝光，相比辽宁舰细节上差别很大，可以说失．之．毫．厘．，．差．之．千．里．。 C.工人的命价低是矿难屡发的一个重要原因，只有当生命高于一切，矿难才会销．声．匿．迹．。 D.惟．妙．惟．肖．的珍稀动植物标本，如同一座自然宝库，令参观者如同置身山林。 4.下列句子中，没．有．语病的一项是（ ）《2 分） A.一名普通的教师撰写了一份近 30 多页的《教材质量分析报告》并直呈教育部。
④____________________，万里送行舟。（李白《渡荆门送别》）
⑤相顾无相识，_____________________。（王绩《野望》）
⑥_______________________，铁马冰河入梦来。（陆游《十一月四日风雨大作》）
（3）根据语境，在横线上填入最恰当的古诗词名句。（2 分，本题有 2 分为附加分。第 7 题分数累加不超
①他近来一次次徘徊在夜间的街道，对一切都感到厌倦，就像重病缠身一样，懒得说话、懒得写作、 懒得弹奏和思考。 ②一七四一年八月二十一日，他像喝醉了酒似的沿街走回家，只有一个渴望的念头在驱使他：睡觉、睡觉， 最好是永远安息。但是，桌子上的一件四方形纸包让人眼前一亮。詹宁斯给他来信，信中说，他给他寄上 一部新的脚本，并希望他——伟大的音乐天才能对他的拙劣脚本多加包涵，希望能仰仗他的音乐翅膀是这 个脚本飞向永恒的苍天。 ③亨德尔霍得站起身来，好像被什么讨厌的东西触动了似的，难道这个詹宁斯还要讥诮他——一个麻木不 仁，已经死了的人吗？亨德尔气呼呼地吹灭了蜡烛，迷迷糊糊地摸索着走进自己的卧室，和衣躺在床上，
【精编】人教版2018--2019学年度第一学期期末教学质量检测.doc
12018～2019学年度第一学期期末教学质量检测小学二年级数学试题一、直接写出得数（每题1分，共24分）7×2＝ 8×8＝42÷7＝ 24÷6＝10÷5＝ 56÷8= 9×8＝ 40－8＝ 20÷4＝ 28÷7= 25÷5＝ 4×7＝ 4×4＝ 45÷9= 63÷9＝ 15÷3＝ 1×5＝ 64÷8＝ 6×3＋4＝ 9×6＋6＝ 6×4÷8＝ 3×3×9＝ 18÷2÷9＝32÷4×5＝二、用竖式计算（每题2分，共8分）3×7＝ 35÷5＝ 56＋7＝ 45－38=三、填空（第5题2分，第7题3分，其余每空1分，共26分）1. 5个8相加，用加法算式表示： ；用乘法算式表示： 或 。
2.18个正方体，每 个一堆，摆了 堆。
18÷□=□（堆）18个正方体摆成 堆，平均每堆 个。
18÷□=□（个）3. 在□里填数，（ ）里填单位名称。
这条线段的长是□（ ）。
学校______________ 班级___________ 姓名_______________ 号码______________……………………………………………装…………………………………………订…………………………………………线……………………………………………答 案 不 得 超 过 此 线24．把上面的绳子对折，再对折，每段刚好1米，这根绳全长 米；教室里黑板的长比这根绳稍短一些，黑板的长是 米多。
5. 在□里填上合适的数，组成和等号左边不同的算式。
6×6 =□×□ 3×8 =□×□6. 在○里填上“＞”“＜”或“＝”。
2018-2019学年度第一学期期末教学质量检测含答案
2018-2019学年度第一学期期末教学质量检测七年级数学试卷一、选择题：每小题只有一个选项符合题意，本大题共6小题，每小题3分，满分18分．1．（3分）|﹣3|的相反数是（）A．B．﹣C．3D．﹣32．（3分）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105B．3.12×106C．31.2×105D．0.312×1073．（3分）下列说法中，正确的是（）A．若AP=PB，则点P是线段AB的中点B．射线比直线短C．连接两点的线段叫做两点间的距离D．过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形4．（3分）如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M=mn B．M=m（n+1）C．M=mn+1D．M=n（m+1）5．（3分）如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=∠MFE．则∠MFB=（）A．30°B．36°C．45°D．72°6．（3分）过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（）A．B．C．D．二、填空题，本大题共6小题，每小题3分，共18分．7．（3分）一天早晨的气温是﹣2℃，半夜又下降了1℃，则半夜的气温是℃．8．（3分）请你写出一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式．9．（3分）已知∠α的补角是它的3倍，则∠α=．10．（3分）已知x2+3x=1，则多项式3x2+9x﹣1的值是．11．（3分）如图所示，点A、点B、点C分别表示有理数a、b、c，O为原点，化简：|a﹣c|﹣|b﹣c|=．12．（3分）用小立方块搭成的几何体从正面和上面看的视图如图，这个几何体中小立方块的个数可以是．三、解答题（本大题共5小题，每小题6分，共30分）13．（6分）计算：（1）点A、B、C在同一条直线上，点C在线段AB上，若AB=4，BC=1，求AC；（2）已知|x|=3，y2=4，且x＜y＜0，那么求x+y的值．14．（6分）计算．﹣14﹣（1﹣0.5）× [3﹣（﹣3）2]．15．（6分）根据下列语句，画出图形．如图：已知：四点A、B、C、D．①画直线AB；②画射线AC、BD，相交于点O．16．（6分）根据下面给出的数轴，解答下面的问题：（1）请你根据图中A、B两点的位置，分别写出它们所表示的有理数A：B：；（2）观察数轴，与点A的距离为4的点表示的数是：；（3）若将数轴折叠，使得A点与﹣3表示的点重合，则B点与数表示的点重合．17．（6分）先化简，再求值：﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中a=﹣1，b=﹣2．四、解答题（本大题共3小题，每小题8分，共24分）18．（8分）为了了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少”，共有4个选项：A、1.5小时以上；B、1～1.5小时；C、0.5～1小时；D、0.5小时以下．图1、2是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息，解答以下问题：（1）本次一共调查了多少名学生？（2）在图1中将选项B的部分补充完整；（3）若该校有3000名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下？19．（8分）已知关于x的方程2（x+1）﹣m=﹣的解比方程5（x﹣1）﹣1=4（x﹣1）+1的解大2．（1）求第二个方程的解；（2）求m的值．20．（8分）“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．（1）用含有x、y的代数式表示图中“囧”的面积；（2）若|x﹣6|+（y﹣3）2=0时，求此时“囧”的面积．五、解答题（本大题共2小题，每小题9分，共18分）21．（9分）一个车队共有n（n为正整数）辆小轿车，正以每小时36千米的速度在一条笔直的街道上匀速行驶，行驶时车与车的间隔均为5.4米，甲停在路边等人，他发现该车队从第一辆车的车头到最后一辆的车尾经过自己身边共用了20秒的时间，假设每辆车的车长均为4.87米．（1）求n的值；（2）若乙在街道一侧的人行道上与车队同向而行，速度为v米/秒，当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒，求v的值．22．（9分）已知数轴上两点A、B对应的数分别是6，﹣8，M、N、P为数轴上三个动点，点M 从A点出发速度为每秒2个单位，点N从点B出发速度为M点的3倍，点P从原点出发速度为每秒1个单位．（1）若点M向右运动，同时点N向左运动，求多长时间点M与点N相距54个单位？（2）若点M、N、P同时都向右运动，求多长时间点P到点M，N的距离相等？六、解答题（本大题共1小题，共12分）23．（12分）【问题提出】已知∠AOB=70°，∠AOD=∠AOC，∠BOD=3∠BOC（∠BOC＜45°），求∠BOC的度数．【问题思考】聪明的小明用分类讨论的方法解决．（1）当射线OC在∠AOB的内部时，①若射线OD在∠AOC内部，如图1，可求∠BOC的度数，解答过程如下：设∠BOC=α，∴∠BOD=3∠BOC=3α，∴∠COD=∠BOD﹣∠BOC=2α，∴∠AOD=∠AOC，∴∠AOD=∠COD=2α，∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°，∴α=14°，∴∠BOC=14°问：当射线OC在∠AOB的内部时，②若射线OD在∠AOB外部，如图2，请你求出∠BOC的度数；【问题延伸】（2）当射线OC在∠AOB的外部时，请你画出图形，并求∠BOC的度数．【问题解决】综上所述：∠BOC的度数分别是．参考答案与试题解析一、选择题：每小题只有一个选项符合题意，本大题共6小题，每小题3分，满分18分．1．（3分）|﹣3|的相反数是（）A．B．﹣C．3D．﹣3【分析】先根据绝对值的意义得到|﹣3|=3，然后根据相反数的定义求解．【解答】解：|﹣3|=3，3的相反数为﹣3，所以|﹣3|的相反数为﹣3．故选：D．【点评】本题考查了绝对值：当a＞0时，|a|=a；当a=0，|a|=0；当a＜0时，|a|=﹣a．也考查了相反数．2．（3分）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105B．3.12×106C．31.2×105D．0.312×107【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将3120000用科学记数法表示为：3.12×106．故选：B．【点评】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．（3分）下列说法中，正确的是（）A．若AP=PB，则点P是线段AB的中点B．射线比直线短C．连接两点的线段叫做两点间的距离D．过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形【分析】根据线段中点的性质可得AP=PB=AB，根据射线和直线的性质可得B错误；根据两点之间的距离定义可得C错误；n边形从一个顶点出发可引出（n﹣3）条对角线，分成（n﹣2）个三角形．【解答】解：A、若AP=PB=AB，则点P是线段AB的中点，故原题说法错误；B、射线比直线短，说法错误；C、连接两点的线段长度叫做两点间的距离，故原题说法错误；D、过六边形的一个顶点作对角线，可以将这个六边形分成4个三角形说法正确；故选：D．【点评】此题主要考查了直线、射线、多边形、以及两点之间的距离，关键是注意连接两点的线段长度叫做两点间的距离．4．（3分）如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m、n的关系是（）A．M=mn B．M=m（n+1）C．M=mn+1D．M=n（m+1）【分析】根据给定图形中三个数之间的关系找出规律“右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1）”，由此即可得出结论．【解答】解：∵1×（2+1）=3，3×（4+1）=15，5×（6+1）=35，∴右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1），∴M=m（n+1）．故选：B．【点评】本题考查了规律型中数字的变化类，根据给定图形中三个数之间的关系找出变化规律“右下圆圈内的数=上方圆圈内的数×（左下圆圈内的数+1）”是解题的关键．5．（3分）如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB=∠MFE．则∠MFB=（）A．30°B．36°C．45°D．72°【分析】由折叠的性质可得：∠MFE=∠EFC，又由∠MFB=∠MFE，可设∠MFB=x°，然后根据平角的定义，即可得方程：x+2x+2x=180，解此方程即可求得答案．【解答】解：由折叠的性质可得：∠MFE=∠EFC，∵∠MFB=∠MFE，设∠MFB=x°，则∠MFE=∠EFC=2x°，∵∠MFB+∠MFE+∠EFC=180°，∴x+2x+2x=180，解得：x=36°，∴∠MFB=36°．故选：B．【点评】此题考查了折叠的性质与平角的定义．此题比较简单，解题的关键是注意方程思想与数形结合思想的应用．6．（3分）过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（）A．B．C．D．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．【解答】解：选项A、C、D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，•与正方体三个剪去三角形交于一个顶点符合．故选：B．【点评】考查了截一个几何体和几何体的展开图．解决此类问题，要充分考虑带有各种符号的面的特点及位置．二、填空题，本大题共6小题，每小题3分，共18分．7．（3分）一天早晨的气温是﹣2℃，半夜又下降了1℃，则半夜的气温是﹣3℃．【分析】直接利用有理数的加减运算法则计算得出答案．【解答】解：由题意可得：半夜的气温是：﹣2﹣1=﹣3（℃）．故答案为：﹣3．【点评】此题主要考查了有理数的加减运算，正确掌握运算法则是解题关键．8．（3分）请你写出一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式﹣2m2n（答案不唯一）．【分析】直接利用单项式的定义分析得出答案．【解答】解：∵写一个只含有字母m、n，且它的系数为﹣2、次数为3的单项式，∴可以为：﹣2m2n（答案不唯一）．故答案为：﹣2m2n（答案不唯一）．【点评】此题主要考查了单项式，正确把握单项式的次数与系数是解题关键．9．（3分）已知∠α的补角是它的3倍，则∠α=45°．【分析】先表示出这个角的补角，然后再依据∠α的补角是它的3倍列出方程，从而可求得∠α的度数．【解答】解：∠α的补角是180°﹣α．根据题意得：180°﹣∠α=3∠α．解得：∠α=45°．故答案为：45°．【点评】本题主要考查的是余角和补角的定义，依据题意列出方程是解题的关键．10．（3分）已知x2+3x=1，则多项式3x2+9x﹣1的值是2．【分析】原式前两项提取3变形后，将已知等式代入计算即可求出值．【解答】解：∵x2+3x=1，∴原式=3（x2+3x）﹣1=3﹣1=2，故答案为：2【点评】此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．11．（3分）如图所示，点A、点B、点C分别表示有理数a、b、c，O为原点，化简：|a﹣c|﹣|b﹣c|=2c﹣a﹣b．【分析】根据各点在数轴上的位置判断出a、b、c的符号及绝对值的大小，再去绝对值符号，合并同类项即可．【解答】解：∵由图可知，a＜c＜0＜b， ∴a﹣c＜0，b﹣c＞0， ∴原式=c﹣a﹣（b﹣c）=c﹣a﹣b+c=2c﹣a﹣b． 故答案为：2c﹣a﹣b． 【点评】 本题考查的是整式的加减， 熟知整式的加减实质上就是合并同类项是解答此题的关键． 12． （3 分）用小立方块搭成的几何体从正面和上面看的视图如图，这个几何体中小立方块的个 数可以是 8、9、10 ．【分析】从俯视图中可以看出最底层小正方体的个数及形状，从主视图和左视图可以看出每一 层小正方体的层数和个数，从而算出总的个数． 【解答】解：从俯视图可以看出，下面的一层有 6 个，由主视图可以知道在中间一列的一个正 方体上面可以放 2 个或在一个上放 2 个，另一个上放 1 或 2 个； 所以小立方块的个数可以是 6+2=8 个，6+2+1=9 个，6+2+2=10 个． 故答案为：8、9、10． 【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考 查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．三、解答题（本大题共 5 小题，每小题 6 分，共 30 分） 13． （6 分）计算： （1）点 A、B、C 在同一条直线上，点 C 在线段 AB 上，若 AB=4，BC=1，求 AC； （2）已知|x|=3，y2=4，且 x＜y＜0，那么求 x+y 的值． 【分析】 （1）根据线段的和差，可得答案； （2）根据非负数的性质，可得 x，y，根据有理数的加法，可得答案． 【解答】解： （1）如图 由线段的和差，得 AC=AB﹣BC=4﹣1=3； （2）由|x|=3，y2=4，且 x＜y＜0，得 x=﹣3，y=﹣2． ，x+y=（﹣3）+（﹣2）=﹣5． 【点评】本题考查了两点间的距离，利用线段的和差是解题关键． 14． （6 分）计算． ﹣14﹣（1﹣0.5）× [3﹣（﹣3）2]．【分析】先乘方，再乘除，最后算加减即可． 【解答】解：﹣14﹣（1﹣0.5）× =﹣1﹣ × ×（﹣6） =﹣1+1 =0 【点评】此题考查了有理数的混合运算，有理数的混合运算首先弄清运算顺序，先乘方，再乘 除，最后算加减，有括号先算括号里边的，同级运算从左到右依次进行计算，然后利用各种 运算法则进行计算，有时可以利用运算律来简化运算． 15． （6 分）根据下列语句，画出图形．如图：已知：四点 A、B、C、D． ①画直线 AB； ②画射线 AC、BD，相交于点 O． [3﹣（﹣3）2]【分析】根据直线、射线的定义画图即可． 【解答】解：如图所示【点评】此题主要考查了简单作图，解答此题需要熟练掌握直线、射线、线段的性质，认真作 图解答即可． 16． （6 分）根据下面给出的数轴，解答下面的问题：（1）请你根据图中 A、B 两点的位置，分别写出它们所表示的有理数 A： 1 （2）观察数轴，与点 A 的距离为 4 的点表示的数是： 5 或﹣3 ； 0.5B： ﹣2.5；（3）若将数轴折叠，使得 A 点与﹣3 表示的点重合，则 B 点与数 【分析】 （1）直接根据数轴上 AB 两点的位置即可得出结论； （2）根据 A 点所表示的数即可得出结论； （3）根据中点坐标公式即可得出结论．表示的点重合．【解答】解： （1）由数轴上 AB 两点的位置可知，A 点表示 1，B 点表示﹣2.5． 故答案为：1，﹣2.5；（2）∵A 点表示 1， ∴与点 A 的距离为 4 的点表示的数是 5 或﹣3． 故答案为：5 或﹣3；（3）∵A 点与﹣3 表示的点重合， ∴其中点= =﹣1，∵点 B 表示﹣2.5， ∴与 B 点重合的数=﹣2+2.5=0.5． 故答案为：0.5． 【点评】本题考查的是数轴，熟知数轴上各点与实数是一一对应关系是解答此题的关键． 17． （6 分）先化简，再求值：﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b） ，其中 a=﹣1，b=﹣2． 【分析】先去括号、合并同类项将原式化简，再将 a、b 的值代入计算可得． 【解答】解：原式=﹣a2b+3ab2﹣a2b﹣4ab2+2a2b =﹣ab2， 当 a=﹣1、b=﹣2 时， 原式=﹣（﹣1）×（﹣2）2 =1×4 =4． 【点评】本题主要考查整式的化简求值，解题的关键是熟练掌握整式的混合运算顺序和法则．四、解答题（本大题共 3 小题，每小题 8 分，共 24 分）18． （8 分）为了了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题 是“你平均每天参加体育活动的时间是多少”，共有 4 个选项：A、1.5 小时以上；B、1～1.5 小 时；C、0.5～1 小时；D、0.5 小时以下．图 1、2 是根据调查结果绘制的两幅不完整的统计图， 请你根据统计图提供的信息，解答以下问题： （1）本次一共调查了多少名学生？ （2）在图 1 中将选项 B 的部分补充完整； （3）若该校有 3000 名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在 0.5小时以下？【分析】 （1）读图可得：A 类有 60 人，占 30%即可求得总人数； （2）计算可得：“B”是 100 人，据此补全条形图； （3）用样本估计总体，若该校有 3000 名学生，则学校有 3000×5%=150 人平均每天参加体育锻 炼在 0.5 小时以下． 【解答】解： （1）读图可得：A 类有 60 人，占 30%；则本次一共调查了 60÷30%=200 人；本次 一共调查了 200 位学生；（2）“B”有 200﹣60﹣30﹣10=100 人，画图正确；（3）用样本估计总体，每天参加体育锻炼在 0.5 小时以下占 5%；则 3000×5%=150， 学校有 150 人平均每天参加体育锻炼在 0.5 小时以下．【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中 得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计 图直接反映部分占总体的百分比大小． 19． （8 分）已知关于 x 的方程 2（x+1）﹣m=﹣ 解大 2． （1）求第二个方程的解； （2）求 m 的值． 【分析】 （1）首先去括号，移项、合并同类项可得 x 的值； （2）根据（1）中 x 的值可得方程 2（x+1）﹣m=﹣ 得关于 m 的方程，再解即可． 【解答】解： （1）5（x﹣1）﹣1=4（x﹣1）+1， 5x﹣5﹣1=4x﹣4+1， 5x﹣4x=﹣4+1+1+5， x=3； （2）由题意得：方程 2（x+1）﹣m=﹣ 把 x=5 代入方程 2（x+1）﹣m=﹣ 2（5+1）﹣m=﹣ 12﹣m=﹣ m=22． 【点评】此题主要考查了一元一次方程的解，关键是掌握使一元一次方程左右两边相等的未知 数的值叫做一元一次方程的解．把方程的解代入原方程，等式左右两边相等． 20． （8 分）“囧”（jiong）是最近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边 长为 20 的正方形的纸片， 剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案 （阴 ， ， 得： 的解为 x=3+2=5， 的解为 x=3+2=5，然后把 x 的值代入可 的解比方程 5（x﹣1）﹣1=4（x﹣1）+1 的影部分） ．设剪去的小长方形长和宽分别为 x、y，剪去的两个小直角三角形的两直角边长也 分别为 x、y． （1）用含有 x、y 的代数式表示图中“囧”的面积； （2）若|x﹣6|+（y﹣3）2=0 时，求此时“囧”的面积．【分析】 （1）根据图形和题意可以用代数式表示出图中“囧”的面积； （2）根据|x﹣6|+（y﹣3）2=0，可以求得 x、y 的值，然后代入（1）中的代数式即可解答本题． 【解答】解： （1）由图可得， 图中“囧”的面积是：20×20﹣ 即图中“囧”的面积是 400﹣2xy； （2）∵|x﹣6|+（y﹣3）2=0 ∴x﹣6=0，y﹣3=0， 解得，x=6，y=3， ∴400﹣2xy=400﹣2×6×3=400﹣36=364， 即|x﹣6|+（y﹣3）2=0 时，此时“囧”的面积是 364． 【点评】本题考查列代数式、非负数的性质，解答本题的关键是明确题意，写出相应的代数式， 求出相应的代数式的值． ﹣xy=400﹣xy﹣xy=400﹣2xy，五、解答题（本大题共 2 小题，每小题 9 分，共 18 分） 21． （9 分）一个车队共有 n（n 为正整数）辆小轿车，正以每小时 36 千米的速度在一条笔直的 街道上匀速行驶，行驶时车与车的间隔均为 5.4 米，甲停在路边等人，他发现该车队从第一 辆车的车头到最后一辆的车尾经过自己身边共用了 20 秒的时间， 假设每辆车的车长均为 4.87 米． （1）求 n 的值； （2）若乙在街道一侧的人行道上与车队同向而行，速度为 v 米/秒，当第一辆车的车头到最后一 辆车的车尾经过他身边共用了 40 秒，求 v 的值． 【分析】 （1）首先统一单位，由题意得等量关系：n（n 为正整数）辆小轿车的总长+（n﹣1）个每辆车之间的车距=20 秒×车的行驶速度，根据等量关系列出方程，再解即可； （2）计算出车对的总长度，再利用总路程为 200m 得出等式求出答案． 【解答】解：36 千米/小时=10 米/秒， 根据题意得，4.87n+5.4（n﹣1）=20×10， 解得，n=20；（2）车队总长度为：20×4.87+5.4×19=200（米） ， 根据题意得， （10﹣v）×40=200， 解得，v=5， 即：v 的值为 5 米/秒． 【点评】此题主要考查了一元一次方程的应用，利用路程、速度、时间之间的关系得出方程是 解题关键． 22． （9 分）已知数轴上两点 A、B 对应的数分别是 6，﹣8，M、N、P 为数轴上三个动点，点 M 从 A 点出发速度为每秒 2 个单位，点 N 从点 B 出发速度为 M 点的 3 倍，点 P 从原点出发速 度为每秒 1 个单位． （1）若点 M 向右运动，同时点 N 向左运动，求多长时间点 M 与点 N 相距 54 个单位？ （2）若点 M、N、P 同时都向右运动，求多长时间点 P 到点 M，N 的距离相等？【分析】 （1） 设经过 x 秒点 M 与点 N 相距 54 个单位， 由点 M 从 A 点出发速度为每秒 2 个单位， 点 N 从点 B 出发速度为 M 点的 3 倍，得出 2x+6x+14=54 求出即可； （2）首先设经过 t 秒点 P 到点 M，N 的距离相等，得出（2t+6）﹣t=（6t﹣8）﹣t 或（2t+6）﹣ t=t﹣（6t﹣8） ，进而求出即可． 【解答】解： （1）设经过 x 秒点 M 与点 N 相距 54 个单位． 依题意可列方程为：2x+6x+14=54， 解方程，得 x=5． 答：经过 5 秒点 M 与点 N 相距 54 个单位． （算术方法对应给分）（2）设经过 t 秒点 P 到点 M，N 的距离相等． （2t+6）﹣t=（6t﹣8）﹣t 或（2t+6）﹣t=t﹣（6t﹣8） ， t+6=5t﹣8 或 t+6=8﹣5tt= 或 t= ， 答：经过 或 秒点 P 到点 M，N 的距离相等． 【点评】此题主要考查了一元一次方程的应用，根据已知点运动速度得出以及距离之间的关系 得出等式是解题关键．六、解答题（本大题共 1 小题，共 12 分） 23． （12 分） 【问题提出】已知∠AOB=70°，∠AOD= ∠AOC，∠BOD=3∠BOC（∠BOC＜45°） ， 求∠BOC 的度数． 【问题思考】聪明的小明用分类讨论的方法解决． （1）当射线 OC 在∠AOB 的内部时，①若射线 OD 在∠AOC 内部，如图 1，可求∠BOC 的度数， 解答过程如下： 设∠BOC=α， ∴∠BOD=3∠BOC=3α， ∴∠COD=∠BOD﹣∠BOC=2α， ∴∠AOD= ∠ AOC， ∴∠AOD=∠COD=2α，∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°，∴α=14°，∴∠ BOC=14° 问：当射线 OC 在∠AOB 的内部时，②若射线 OD 在∠AOB 外部，如图 2，请你求出∠BOC 的度 数； 【问题延伸】 （2）当射线 OC 在∠AOB 的外部时，请你画出图形，并求∠BOC 的度数． 【问题解决】综上所述：∠BOC 的度数分别是 14°，30°，10°，42° ．【分析】 （1）②由已知条件得出∠COD、∠AOD、∠AOB 与∠BOC 的关系，求出∠BOC 的度数； （2）分类讨论，根据∠AOD、∠BOD．∠AOB 与∠BOC 的关系，得出∠BOC 的度数． 【解答】解： （1）②设∠BOC=α，则∠BOD=3α，②若射线 OD 在∠AOB 外部， 如图 2：∠COD=∠BOD﹣∠BOC=2α， ∵∠AOD= ∠AOC，∴∠AOD= ∠COD=， = =70°，∴∠AOB=∠BOD﹣∠AOD=3α﹣ ∴α=30°． ∴∠BOC=30°；（2）当射线 OC 在∠AOB 外部时，根据题意，此时射线 OC 靠近射线 OB， ∵∠BOC＜45°，∠AOD= ∠AOC， ∴射线 OD 的位置也只有两种可能； ①若射线 OD 在∠AOB 内部，如图 3 所示， 则∠COD=∠BOC+∠COD=4α， ∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°， ∴α=10°， ∴∠BOC=10°； ②若射线 OD 在∠AOB 外部，如图 4， 则∠COD=∠BOC+∠BOD=4α， ∵∠AOD= ∠AOC， ∴∠AOD= ∠COD= α， ∴∠AOB=∠BOD﹣∠AOD=3α﹣ ∴α=42°， ∴∠BOC=42°； 综上所述：∠BOC 的度数分别是 14°，30°，10°，42°． = =70°，【点评】根据 OC、OD 的不同位置分类讨论∠BOC 的计算方法；分类讨论是关键．。
2018-2019学年八年级上期末质量数学试卷含答案
2018-2019学年度第一学期期末教学质量检测八年级数学试卷一、选择题（共10个小题，每小题2分，共20分）下列各题均有四个选项，其中只有一个是符合题意的 .1有意义，则x 的取值范围是 A ．1x >-且1x ≠ B ．1x ≥-C ．1x ≠D ．x ≥-1且1x ≠2．下列各式从左到右的变形正确的是A ．yx y x -+-= －1B ．y x =11++y xC ．y x x +=y +11D ．2)3(y x -=223yx3．在实数722，3π23.14中，无理数有 A.2个 B.3个 C.4个 D.5个4．已知等腰三角形的两边长分别为4和9，则这个三角形的周长是 A ．22B ．19C ．17D ． 17或225.在下列四个图案中，是轴对称图形的是A. B. C. D.6. 在不透明口袋内有形状、大小、质地完全一样的5个小球，其中红球3个，白球2个，随机抽取一个小球是红球的可能性大小是 A ．25B ．35C ．13D ．127. 下列事件中，属于必然事件的是A. 2018年2月19日是我国二十四节气中的“雨水”节气，这一天会下雨B. 某班级11名学生中，至少有两名同学的生日在同一个月份C. 用长度分别为2cm ，3cm ，6cm 的细木条首尾相连能组成一个三角形D. 从分别写有π，2，0.1010010001⋅⋅⋅（两个1之间依次多一个0）三个数字的卡片中随机抽出一张，卡片上的数字是无理数 8．下列运算错误的是== = D.2(2=9. 如图，AD 是△ABC 的角平分线，DE ⊥AB 于点E ，S △ABC =10，DE =2，AB=4，则AC 长是 A.9B. 8C. 7D. 610. 我们根据指数运算，得出了一种新的运算，如表是两种运算对应关系的一组实例：根据上表规律，某同学写出了三个式子：①log216=4，②log525=5，③log212=﹣1．其中正确的是A．①②B．①③C．②③D．①②③二、填空题（共10个小题，每小题2分，共20分）11．25的平方根是.12．计算：2= .13．若实数x y，0y=，则代数式2xy的值是.14. 已知：ABC∆中，AB AC=，30B A∠-∠=︒，则A∠=.15．将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．16．边长为10cm的等边三角形的面积是.17.如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于12BC的同样长为半径画弧，两弧相交于两点M，N；②作直线MN交AB于点D，连结CD.请回答：若CD=AC，∠A=50°，则∠ACB的度数为.18．已知一个围棋盒子中装有7颗围棋子，其中3颗白棋子，4颗黑棋子，若往盒子中再放入x 颗白棋子和y颗黑棋子，从盒子中随机取出一颗白棋子的可能性大小是14，则y与x之间的关系式是．19．已知1132a b+=，则代数式254436a ab bab a b-+--的值为．（第17题图）20．已知: 如图，ABC △中，45ABC ∠=，H 是高AD 和BE的交点，12AD =,17BC =，则线段BH 的长为.三、解答题 （共12个小题，共60分）21．（4分）22.（5+23.（4分）1= ， 3(2)64x y += ，求代数式22x yx y ++的值.24. （5分）先化简，再求值：2532236x x x x x -⎛⎫+-÷ ⎪--⎝⎭，其中x 满足2310x x +-=.25.(5分).已知： 如图，点B 、A 、D 、E 在同一直线上，BD=AE ，BC ∥E F ，∠C ＝∠F ． 求证：AC ＝DF ．26.（5分） 解关于x 的方程：32211x x x +=-+ .27.（4分））在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个． (1)先从袋子中取出m (m >1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A ．请完成下列表格：(2)先从袋子中取出m 个红球，再放入m 个一样的黑球并摇匀，随机摸出1个球是黑球的可能性大小是，求m 的值．28.（5分） 某服装厂接到一份加工3000件服装的订单.应客户要求，需提前供货，该服装厂决定提高加工速度，实际每天加工的件数是原计划的1.5倍，结果提前10天完工.原计划每天加工多少件服装？29.(5分) 在ABC ∆中，AB ，BC ，AC 形的面积.小明同学在解答这道题时，先建立了一个正方形网格（每个小正方形的边长为1），再在网格中画出格点ABC ∆中，（即ABC ∆三个顶点都在小正方形的顶点处），如图1所示，这样不需要ABC ∆高，借用网格就能计算出它的面积.（1）△ABC 的面积为 ；（2）如果MNP ∆2的正方形网格（每个小正方形的边长为1）画出相应的格点MNP ∆，并直接写出MNP ∆的面积为 .30.（5分） 已知：如图，在ABC ∆中，90C ∠=︒．（1）求作：ABC ∆的角平分线AD （要求：尺规作图，不写作法，保留作图痕迹）; （2）在（1）的条件下，若6AC =，8BC =，求CD 的长．31.（5分）如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这 个分式为“和谐分式”.（1）下列分式: ①211x x -+；②222a b a b --；③22x y x y +-；④222()a b a b -+. 其中是“和谐分式”是(填写序号即可)； （2）若a 为正整数，且214x x ax -++为“和谐分式”，请写出a 的值; （3） 在化简22344a a bab b b -÷-时， 小东和小强分别进行了如下三步变形:小东：22344=a a ab b b b -⨯-原式223244a a ab b b =--()()222323244a b a ab b ab b b--=-小强：22344=a a ab b b b -⨯-原式()22244a a b a b b =--()()2244a a a b a b b--=- 显然，小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单，原因是： ，请你接着小强的方法完成化简. 32.（6分）已知：如图，D 是ABC ∆的边BA 延长线上一点，且AD AB =，E 是 边AC 上一点，且DE BC =. 求证：DEA C ∠=∠.顺义区2017---2018学年度第一学期期末八年级教学质量检测数学试题答案及评分参考二、填空题三、解答题21. 3分（各1分）＝4分22. 解：原式＝5(1512)--………………………………… 4分（前2分后2分）＝8-5分23 解：∵1= ， 3(2)64x y += ，∴ 124x y x y -=⎧⎨+=⎩………………………………………………2分（各1分）解得21x y =⎧⎨=⎩……………………………………………4分（各1分）∴2222213215x y x y ++==++………………………………………5分24 解：原式=(2)(2)5323(2)x x x x x x +---⎛⎫÷⎪--⎝⎭………………………1分 =293(2)23x x x x x --⨯--……………………………………………2分 =(3)(3)3(2)23x x x x x x +--⨯-- ……………………………3分=239x x +……………………………………………4分∵ 2310x x +-= ∴ 231x x +=∴ 原式=22393(3)313x x x x +=+=⨯=……………………5分25．证明：∵BD AE =，∴BD AD AE AD -=-．即AB DE =． ……………………………………………………………… 1分∵BC ∥EF ，∴B E ∠=∠． ……………………………………………………………… 2分又∵C F ∠=∠……………………………………………………………… 3分在ABC ∆和DEF ∆中，,,,B E C F AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ ABC ∆≌DEF ∆． ………………………………………………………4分 ∴ AC DF =． …………………………………………………………… 5分26. 解：方程两边同乘以(1)(1)x x +-，……………………………………………1分3(1)2(1)2(1)(1)x x x x x ++-=+-． ……………………………………………2分 223+32222x x x x +-=-． ……………………………………………3分解这个整式方程，得5x =-． …………………………………………… 4分 检验：当5x =-时，(1)(1)0x x +-≠．…………………………………………5分5x ∴=-是原方程的解．27.…………………………………………… 3分 (2)依题意，得64105m +=…………………………………………… 4分解得 2m =…………………………………………… 5分 所以m 的值为228. 解：设该服装厂原计划每天加工x 件服装，则实际每天加工1.5x 件服装.……………１分 根据题意，列方程得105.130003000=-xx …………………………………3分 解这个方程得100x = …………………………………………4分 经检验，100x =是所列方程的根. ………………………………5分 答：该服装厂原计划每天加工100件服装.29. 解： （1）ABC ∆的面积为 4.5 …………………………………………2分正确画图………………………………………4分 （2）MNP ∆的面积为 7 ………………………………………… 5分30. 解：（1）如图 ………………1分（2）过点D 作DE ⊥AB 于E . ………………2分∵DE ⊥AB ，∠C =90° ∴由题意可知DE =DC ， ∠DEB =90° 又∵DE =DC ，AD =AD ∴AD 2－ED 2=AD 2－DC 2 ∴AE =AC =6………………3分∵A B =10 ∴BE =AC －AE =4 ………………4分 设DE =DC =x ，则BD =8－x∴在Rt △BED 中 ()22168x x +=-∴x =3………………5分 ∴CD =3.31. （1）②………………1分 （2） 4，5………………3分（3）小强通分时，利用和谐分式找到了最简公分母. ………………4分解：原式()222444a a ab a b b-+=-()24ab a b b =-()4aa b b =-24a ab b =-………………5分32．证明：过点D 作BC 的平行线交CA 的延长线于点F ．……………… 1分∴C F ∠=∠．∵点A 是BD 的中点，∴AD=AB ． …………………………… 2分 在△ADF 和△ABC 中，,,,C F DAF BAC AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ADF ≌△ABC ．………………… 3分 ∴DF=BC ．…………………………… 4分 ∵DE=BC ， ∴DE=DF ．∴F DEA ∠=∠． ………………………………………………………… 5分 又∵C F ∠=∠，∴C DEA ∠=∠． …………………………………………………………… 6分其它证法相应给分。
(嘉兴)2018-2019学年第一学期七年级语文教学质量检测(二)参考答案及评分建议
2018-2019学年第一学期七年级语文教学质量检测（二）参考答案及评分建议一、积累（12分）1．（4分）绽；蕴；谐；淌2．（6分）（1）半江瑟瑟半江红（2）夜发清溪向三峡（3）乡书何处达？归雁洛阳边。
（4）非淡泊无以明志，非宁静无以致远（评分标准：每空1分，有错、漏、添字者，则该空不得分。
）3．（2分）C二、阅读（42分）4．（2分）他变成妖怪老母后，让妖怪割下八戒耳朵下酒。
5．（3分）八戒是巡山被银角及众小妖识破抓走。
沙僧则是银角大王使法压倒悟空后，将他和唐僧一并抓走的。
孙悟空开动脑筋，用计谋调换了紫金葫芦，战胜了金、银二怪。
6．（1）推介古典文学作品（2）搬出当代流行作品7．①他愤懑不平，不希望像他的父亲一样在工厂的流水生产线上作牛作马，累死累活地过一辈子。
或：他郁闷不平，不甘于受命运的安排。
②“我”屡次尝试后受挫的生气与不快，以及不信说服不了迪龙的心态。
8．他的作品真实地表现了自己的生活，充满生命力；字里行间又流露出迪龙的痛苦、挣扎、愤懑和暴戾，令人感到无比沉重。
9．同意。
迪龙在老师的理解与关爱下挣脱了命运的安排，并在其耐心地指导和激励下投身文学创作；老师从迪龙的身上获得了一个坚定的信念：年轻人的敢作敢为足以移山填海，改变命运，改变世界。
这就是“彼此唤醒心灵”。
10．【解析】本题考查考生筛选、提炼信息的能力。
首先审清题干，题干要求概括滥用抗生素的危害。
通读材料，明确四则材料都是围绕“抗生素”写的，材料一、二、三涉及了抗生素的危害。
【答案】①可能产生过敏反应，严重时会致聋；②使病菌产生耐药性；③使人体免疫力下降。
11．【解析】此题考查图文转换、材料探究能力。
首先，审清题干，题干要求从材料二中得出三条有意义的结论，就是要对“中外抗生素使用情况对比表”进行总结。
解答时要读懂材料二表格中的内容，注意表头文字、表格内每一列的名称及数据，然后对比分析，得出结论。
【答案】①与国外相比，我国滥用抗生素情况非常严重；②我国的抗生素不仅滥用于人体，还滥用于畜牧养殖业；③我国对药品销售的监管力度不够；④我国因滥用抗生素致聋的儿童比例非常大。
2018—2019学年度人教版八年级上学期期末教学质量监测语文试题及答案
2018—2019学年度上学期期末教学质量监测八年级语文试题请将所有答案填写在答题纸上一、积累运用（30分）1.下列词语中加点字每组读音都不相同的一项是（）（2分）A.狼藉．/慰藉．倦．怠/镌．刻遏．制／简明扼．要步履蹒跚．/春意阑珊．B.纤．维/拉纤．滞．留/窒．息记载．／千载．难逢鹤．立鸡群/以邻为壑．C.嶙．峋/遴．选倔．强/诀．别阻挡．／锐不可当．坦荡如砥．/同仇敌．忾D.濒．临/频．繁轩昂．/盎．然悄．然／春寒料峭．不屑．一顾/惟妙惟肖．2.下列各组词语中汉字书写完全正确的一项是( )(2分)A.仲裁娴熟不折不挠坦荡如砥B.浩翰踌躇巧妙绝伦为富不仁C.慰勉蒙寐连绵不断自出新裁D.雕镂推祟惮精竭虑诚惶成恐3.下列句子中加点词语使用有误的一项是( )(2分)A.燕子矶是一座山，山上丹崔翠壁，磴道盘曲，燕头跨江而出，宛然．．一只燕子，因而得名。
B.这部小说情节跌宕起伏，抑扬顿挫．．．．，具有很强的感染力。
C.今年“十·一”国庆节期间，前往苍马山观光的游客络绎不绝．．．．。
D.据调查：在各种不文明行为中，市民对不遵守交通法规乱闯红灯的行为深恶痛疾．．．．。
4.下列表述不正确的一项是（）（2分）A．新闻特写兼有新闻和文学的特点，要相对完整地记叙新闻事件，生动形象地展现新闻现场。
B．汪曾祺，江苏省高邮人，著有小说《受戒》《大淖记事》，被誉为“抒情的人道主义者，中国最后一个纯粹的文人，中国最后一个士大夫。
”C．《蝉》的作者法布尔，法国昆虫学家、作家，作品《昆虫故事》，又称《昆虫记》，世人称为“昆虫界的荷马”。
D.茅盾，现代作家，原名沈德鸿，字雁冰。
主要作品有长篇小说《蚀》《虹》《子夜》《腐蚀》；中篇小说《路》《三人行》；短篇小说《春蚕》《秋收》《残冬》《林家铺子》等。
5. 名著阅读（8分）【甲】几乎每次进餐后，它都要整理一下仪容。
譬如用前腿上的跗节把触须和上颚里里外外清扫干净。
【乙】嗉囊装满后，它用喙尖抓抓脚底，用沾着唾液的爪擦擦脸和眼睛，然后闭着双眼或者躺在沙上消化食物。
2018—2019学年度人教版八年级上学期期末教学质量监测语文试题(含参考答案)
2018—2019学年度上学期期末教学质量监测八年级语文试题请将所有答案填写在答题纸上一、积累运用（30分）1.下列词语中加点字每组读音都不相同的一项是（）（2分）A.狼藉．/慰藉．倦．怠/镌．刻遏．制／简明扼．要步履蹒跚．/春意阑珊．B.纤．维/拉纤．滞．留/窒．息记载．／千载．难逢鹤．立鸡群/以邻为壑．C.嶙．峋/遴．选倔．强/诀．别阻挡．／锐不可当．坦荡如砥．/同仇敌．忾D.濒．临/频．繁轩昂．/盎．然悄．然／春寒料峭．不屑．一顾/惟妙惟肖．2.下列各组词语中汉字书写完全正确的一项是( )(2分)A.仲裁娴熟不折不挠坦荡如砥B.浩翰踌躇巧妙绝伦为富不仁C.慰勉蒙寐连绵不断自出新裁D.雕镂推祟惮精竭虑诚惶成恐3.下列句子中加点词语使用有误的一项是( )(2分)A.燕子矶是一座山，山上丹崔翠壁，磴道盘曲，燕头跨江而出，宛然．．一只燕子，因而得名。
B.这部小说情节跌宕起伏，抑扬顿挫．．．．，具有很强的感染力。
C.今年“十·一”国庆节期间，前往苍马山观光的游客络绎不绝．．．．。
D.据调查：在各种不文明行为中，市民对不遵守交通法规乱闯红灯的行为深恶痛疾．．．．。
4.下列表述不正确的一项是（）（2分）A．新闻特写兼有新闻和文学的特点，要相对完整地记叙新闻事件，生动形象地展现新闻现场。
B．汪曾祺，江苏省高邮人，著有小说《受戒》《大淖记事》，被誉为“抒情的人道主义者，中国最后一个纯粹的文人，中国最后一个士大夫。
”C．《蝉》的作者法布尔，法国昆虫学家、作家，作品《昆虫故事》，又称《昆虫记》，世人称为“昆虫界的荷马”。
D.茅盾，现代作家，原名沈德鸿，字雁冰。
主要作品有长篇小说《蚀》《虹》《子夜》《腐蚀》；中篇小说《路》《三人行》；短篇小说《春蚕》《秋收》《残冬》《林家铺子》等。
5. 名著阅读（8分）【甲】几乎每次进餐后，它都要整理一下仪容。
譬如用前腿上的跗节把触须和上颚里里外外清扫干净。
【乙】嗉囊装满后，它用喙尖抓抓脚底，用沾着唾液的爪擦擦脸和眼睛，然后闭着双眼或者躺在沙上消化食物。
(嘉兴)2018-2019学年第一学期七年级科学教学质量检测(二)参考答案及评分建议
2018-2019学年第一学期七年级科学教学质量检测（二）参考答案及评分建议二、填空题（每空1分，共22分）21．(1)BC(2)A22．(1)E ；A(2)用铜丝线圈的总长度L2除以铜丝的圈数n，即得细铜丝的直径d(3)ABC23．(1)钢尺的胀、缩程度随温度的变化非常小(2)指针的偏转方向；放大24．菜粉蝶；蝗虫；棉铃虫；果蝇25．(1)内力；弯曲；断裂(2)地壳的升降运动26．(1)山地(2)山脊(3)自西向东(4)6(5)②三、实验探究题（每空1分，共18分）27．(1)海拔高度(2)b组；c组(3)平均值(4)D28．(2)对照组①同样的培养液；适宜的温度和光照②清水(3)实验组植株平均高度大于对照组29．(1)刻度尺、秒表(2)小球到固定点距离（或摆长）(3)摆动过程中受到空气阻碍作用(4)短30．(2)0.052 ①降低②小③13℃四、解答题（每题5分，共20分）31．解：(1)因为1标准大气压下沸水温度为100℃，冰水混合物温度为0℃所以该温度计的分度值为：1002 8030=-℃℃(2)100格代表的温度为(100－30)×2℃=140℃(3)q起点代表的温度最低为：(－30)×2℃=－60℃最上面的150处刻度对应的最高温度是：2℃×(150－30)=240℃所以该温度计的测量范围是：－60℃~240℃32．(1)刻度的画法；(2)小刚；由于小明分10次将水倒入到玻璃杯中，每一次都有少量的水没有倒到玻璃杯中，所以制成的量筒刻度误差较大33．(1)细胞分裂(2)细胞分化(3)染色体数量先加倍，然后平均分配到两个子细胞中这种变化保证了新细胞与亲代细胞具有相同的遗传物质(4)结缔组织结缔组织34．(1)牛、马、羊；(2)人类偷猎，栖息地丧失；栖息地丧失(3)食物链被破坏，生态平衡被破坏，如各种农林害虫失去天敌的控制，就大量繁殖起来，给农作物和树木造成严重的危害，导致生态系统被破坏。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018-2019 学年度第一学期期末教学质量检测七年级数学试卷一、选择题（本大题共10 小题，每小题 3 分，共 30 分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答题卡上将正确答案的代号涂黑．1．（3分）四个有理数﹣ 1，2，0，﹣ 3，其中最小的是（）A．﹣ 1B．2C．0D．﹣ 32．（3分）下列是﹣ 3 的相反数是（）A． 3B．﹣C．D．﹣ 33．（ 3 分）我国南海某海域探明可燃冰储量约为19 400 000 000 立方米， 19 400 000 000 用科学记数法表示为（）A． 19.4×109B．1.94×1010C．0.194×1010D．1.94× 1094．（3分）将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（）A．B．C．D．5．（3分）若代数式﹣ 5x6y3与 2x2n y3是同类项，则常数n 的值（）A． 2B．3C．4D．66．（3分）若 x=﹣1 是关于 x 的方程 2x+5a=3的解，则 a 的值为（）A．B．4C．1D．﹣ 17．（3分）下列运算中，正确的是（）A． 3a+2b=5ab B．3a2b﹣ 3ba2=0C． 2a3+3a2=5a5D．5b2﹣4b2=18．（3 分）程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100 个和尚分 100 个馒头，如果大和尚 1 人分 3 个，小和尚 3 人分 1 个，正好分完．大、小和尚各多少人？大和尚有x 人，依意列方程得（）A．+3（100 x）=100B．3（100 x）=100C． 3x+=100D．3x=1009．（3 分）在数上表示有理数a， a， b 1 的点如所示，（）A． b＜ aB．|b 1＜|a C．|a＞|b|D．b 1＜a+ |||10．（3 分）一列数，按一定律排列成1， 3， 9，27， 81，⋯，从中取出三个相的数，若三个数的和 a，三个数中最大的数与最小的数的差（）A． a B．|a C．|a|D．a |二、填空（本大共6 小，每小 3 分，共 18 分）下列各不需要写出解答程，将果直接填写在答卡指定位置．11．（3 分）某市 2018 年元旦的最低气温1℃，最高气温7℃，一天的最高气温比最低气温高℃．12．（3分） 30 ° 30 ′=度．13．（3分）式 2x2y 的次数是：．14．（3分）若一个角比它的角大36 °，个角°．15．（3分）已知点 A、B、C 在直 l 上，若 BC= AC，=．16．（3 分）如所示的运算程序中，若开始入的x100，我第 1 次出的果50，第 2 次出的果 25，⋯，第 2018 次出的果．三、解答（共8 小，共 72 分）17．（8 分）算：（1）（ 3）+7+8+（ 9）．（2）（﹣ 1）10×2+（﹣ 2）3÷4．18．（8 分）解方程：（1）3x+2=7﹣2x．（2）x﹣=3﹣．19．（8 分）先化简，再求值：x﹣2（x﹣y2）+（﹣x+y2），其中 x=﹣2，y=﹣1．20．（8 分）笔记本的单价是 x 元，圆珠笔的单价是y 元．小红买 3 本笔记本， 6 支圆珠笔；小明买 6 本笔记本， 3 支圆珠笔．（1）买这些笔记本和圆珠笔小红和小明一共花费多少元钱？（2）若每本笔记本比每支圆珠笔贵 2 元，求小明比小红多花费了多少元钱？21．（8 分）如图，∠ AOC与∠ BOC互余， OD 平分∠ BOC，∠ EOC=2∠AOE．（1）若∠ AOD=75°，求∠ AOE的度数．（2）若∠ DOE=54°，求∠ EOC的度数．22．（10 分）2018 年元旦，某商场将甲种商品降价40%，乙种商品降价 20%开展优惠促销活动．已知甲、乙两种商品的原销售单价之和为 1400 元，某顾客参加活动购买甲、乙各一件，共付1000 元．（1）甲、乙两种商品原销售单价各是多少元？（2）若商场在这次促销活动中甲种商品亏损25%，乙种商品盈利 25%，那么商场在这次促销活动中是盈利还是亏损了？如果是盈利，求商场销售甲、乙两种商品各一件盈利了多少元？如果是亏损，求销售甲、乙两种商品各一件亏损了多少元？23．（10 分）如图，点 B、C 在线段 AD 上， CD=2AB+3．（1）若点 C 是线段 AD 的中点，求 BC﹣AB 的值；（2）若 BC= AD，求 BC﹣AB 的值；（3）若线段 AC上有一点 P（不与点 B 重合）， AP+AC=DP，求 BP 的长．24．（ 12 分）如图 1，已知∠ AOB=120，°∠COD=60°，OM 在∠ AOC内，ON 在∠ BOD内，∠ AOM=∠AOC，∠ BON= ∠BOD．O 逆时针旋转到OC与 OB 重合时，如图 2，∠MON=°；（1）∠COD从图 1 中的位置绕点（2）∠ COD从图 2 中的位置绕点 O 逆时针旋转 n°（ 0＜ n＜ 120 且 n≠ 60），求∠ MON 的度数；O 顺时针旋转n°（0＜ n＜ 120），则 n=时，∠ MON=2（3）∠ COD从图 2 中的位置绕点∠BOC．参考答案与试题解析一、选择题（本大题共10 小题，每小题 3 分，共 30 分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答题卡上将正确答案的代号涂黑．1．（3 分）四个有理数﹣ 1，2，0，﹣ 3，其中最小的是（）A．﹣ 1B．2C．0D．﹣ 3【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．【解答】解：根据有理数比较大小的方法，可得﹣3＜﹣ 1＜0＜2，∴四个有理数﹣ 1，2，0，﹣ 3，其中最小的是﹣ 3．故选： D．【点评】此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于 0；②负数都小于 0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．2．（3 分）下列是﹣ 3 的相反数是（）A． 3B．﹣C．D．﹣ 3【分析】根据相反数的定义，即可解答．【解答】解：﹣ 3 的相反数是 3．故选： A．【点评】本题考查了相反数的定义，解决本题的关键是熟记相反数的定义．3．（ 3 分）我国南海某海域探明可燃冰储量约为19 400 000 000 立方米， 19 400 000 000 用科学记数法表示为（）A． 19.4×109B．1.94×1010C．0.194×1010D．1.94× 109【分析】科学记数法的表示形式为a× 10n的形式，其中 1≤|a| ＜ 10，n 为整数．确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞ 1 时， n 是正数；当原数的绝对值＜ 1 时， n 是负数．【解答】解： 19 400 000 000 用科学记数法表示为 1.94×1010，故选： B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a× 10n的形式，其中1≤| a| ＜ 10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值．4．（3 分）将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（）A．B．C．D．【分析】面动成体．由题目中的图示可知：此圆台是直角梯形转成圆台的条件是：绕垂直于底的腰旋转．【解答】解： A、是两个圆台，故A 错误；B、上面小下面大，侧面是曲面，故 B 正确；C、是一个圆台，故 C 错误；D、下面小上面大侧面是曲面，故 D 错误；故选： B．【点评】本题考查直角梯形转成圆台的条件：应绕垂直于底的腰旋转．5．（3 分）若代数式﹣ 5x6y3与 2x2n y3是同类项，则常数n 的值（）A． 2B．3C．4D．6【分析】根据同类项是字母相同且相同字母的指数也相同，可得答案．【解答】解：由﹣ 5x6y3与 2x2n y3是同类项，得2n=6，解得 n=3．故选： B．【点评】本题考查了同类项，同类项定义中的两个“相同”：相同字母的指数相同，是易混点，因此成了中考的常考点．6．（3 分）若x=﹣1 是关于x 的方程2x+5a=3的解，则 a 的值为（）A．B．4C．1D．﹣ 1【分析】把 x 的值代入方程计算即可求出 a 的值．【解答】解：把 x=1 代入方程得：﹣ 2+5a=3，解得： a=1，故选： C．【点评】此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．7．（3 分）下列运算中，正确的是（）A． 3a+2b=5ab B．3a2b﹣ 3ba2=0C． 2a3+3a2=5a5D．5b2﹣4b2=1【分析】直接利用合并同类项法则分别化简得出答案．【解答】解： A、 3a+2b 无法计算，故此选项错误；B、3a2b﹣ 3ba2=0，正确；C、2a3+3a2，无法计算，故此选项错；D、5b2﹣4b2=b2，故此选项错误；故选： B．【点评】此题主要考查了合并同类项，正确掌握运算法则是解题关键．8．（3 分）程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100 个和尚分100 个馒头，如果大和尚 1 人分3 个，小和尚 3 人分 1 个，正好分完．试问大、小和尚各多少人？设大和尚有x 人，依题意列方程得（）A．+3（100﹣x）=100B．﹣3（100﹣x）=100C． 3x+=100D．3x﹣=100【分析】根据100 个和尚分100 个馒头，正好分完．大和尚一人分 3 个，小和尚 3 人分一个得到等量关系为：大和尚的人数+小和尚的人数 =100，大和尚分得的馒头数 +小和尚分得的馒头数=100，依此列出方程即可．【解答】解：设大和尚有x 人，则小和尚有（ 100﹣x）人，根据题意得： 3x+=100；故选： C．【点评】本题考查了由实际问题抽象出一元一次方程，关键以和尚数和馒头数作为等量关系列出方程．9．（3 分）在数轴上表示有理数a，﹣ a，﹣ b﹣ 1 的点如图所示，则（）A．﹣ b＜﹣ aB．|b 1＜|a C．|a＞|b|D．b﹣1＜a+ |||【分析】因为 a 与﹣ a 互为相反数，所以根据图示知，a＜0＜﹣ a＜﹣ b﹣ 1，由此对选项进行一一分析．【解答】解：∵ a 与﹣ a 互为相反数，∴根据图示知， a＜0＜﹣ a＜﹣ b﹣1，∴|﹣ a| =| a| ＜| ﹣ b﹣1| =| b+1| ，则|b+1| ＞|a| ，故 B 选项错误；∴﹣ b＞﹣ a，故 A 选项错误；∴|a| ＞|b| ，故 C 选项错误；∴b﹣1＜a，故 D 选项正确．故选： D．【点】此合考了数、的有关内容，用几何方法借助数来求解，非常直，体了数形合的点．10．（3 分）一列数，按一定律排列成1， 3， 9，27， 81，⋯，从中取出三个相的数，若三个数的和 a，三个数中最大的数与最小的数的差（）A．a B．| a|C．| a|D．a【分析】三个数中第一个数x，另两个数分3x、9x，根据三个数的和a，即可得出关于 x 的一元一次方程，解之即可得出x 的，再根据 3x 与 9x 异号、x 与 9x 同号，即可求出三个数中最大的数与最小的数的差．【解答】解：三个数中第一个数 x，另两个数分 3x、 9x，根据意得： x3x+9x=a，解得： x= a．∵ 3x 与 9x 异号， x 与 9x 同号，∴ 三个数中最大的数与最小的数的差 |9x（ 3x）|=12| x| = | a| ．故： C．【点】本考了一元一次方程的用，找准等量关系，正确列出一元一次方程是解的关．二、填空（本大共 6 小，每小 3 分，共 18 分）下列各不需要写出解答程，将果直接填写在答卡指定位置．11．（3 分）某市 2018 年元旦的最低气温1℃，最高气温7℃，一天的最高气温比最低气温高8℃．【分析】直接利用有理数的加减运算法算得出答案．【解答】解：由意可得：一天的最高气温比最低气温高7（ 1） =8（℃）．故答案： 8．【点】此主要考了有理数的加减运算，正确掌握运算法是解关．12．（3 分） 30 ° 30 ′=30.5度．【分析】根据 1 度等于 60 分， 1 分等于 60 秒，由大位成小位乘以60，小位成大位除以 60，按此化即可．【解答】解：（1）∵ 30′= °=0.5，°∴30°30′=30°.5 °=30.．5°+故答案为30.5．【点评】本题主要考查的是度、分、秒的加法计算，相对比较简单，注意以60 为进制即可．13．（3 分）单项式 2x2y 的次数是： 3 ．【分析】根据单项式次数的定义来确定．单项式中所有字母的指数和叫做这个单项式的次数．【解答】解：根据单项式次数的定义，字母x、y 的次数分别是 2、1，和为 3，即单项式的次数为3．故答案为 3．【点评】本题考查单项式次数的定义，要记清，单项式中所有字母的指数和叫做这个单项式的次数．14．（3 分）若一个角比它的补角大36 °，则这个角为108°．【分析】设这个角为 x°，则这个角的补角为（ 180﹣x）°，根据题意可得方程x﹣（180﹣ x）=36，再解方程即可求解．【解答】解：设这个角为x°，则这个角的补角为（ 180﹣x）°，x﹣（ 180﹣x）=36，解得： x=108．故答案为： 108．【点评】此题主要考查了余角和补角，关键是掌握余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．15．（3 分）已知点 A、B、C 在直线 l 上，若 BC= AC，则=或．【分析】分类讨论： C 点在线段 AB 上，则 AB=AC+BC；当 C 点在线段 AB 的反向延长线上，则AB=BC﹣AC，然后把 BC= AC代入计算．【解答】解：当 C 点在线段 AB 上，如图 1，∵AB=AC+BC，BC= AC，∴==；当 C 点在线段 AB 的反向延长线上，如图2，∵AB=BC AC， BC= AC，∴==．故答案：或．【点】本考了两点的距离：两点之的段叫两点的距离．也考了分思想的运用．1 次出的果16．（3 分）如所示的运算程序中，若开始入的x100，我第50，第2 次出的果 25，⋯，第 2018 次出的果4．【分析】根据的程序行算，找到循的律，根据律推算．【解答】解：由的程序，知依次出的果是50，25，32， 16，8，4，2，1，8，4，2，1⋯，从 8 开始循．2018 4=2014， 2014÷ 4=503⋯2，故第 2018 次出的果是 4．故答案： 4．【点】此主要考了代数式求，正确循的律，根据循的律行推广．中除前 4 次不循外，后是 4 个一循．三、解答（共8 小，共 72 分）17．（8 分）算：（1）（ 3）+7+8+（ 9）．（2）（ 1）10×2+（ 2）3÷4．【分析】（ 1）原式合后，相加即可求出；（2）原式先算乘方运算，再算乘除运算，最后算加减运算即可求出．【解答】解：（1）原式 = 12+15=3；（2）原式 =2﹣2=0．【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．18．（8 分）解方程：（1）3x+2=7﹣2x．（2）x﹣=3﹣．【分析】（ 1）方程移项合并，把x 系数化为 1，即可求出解；（2）方程去分母，去括号，移项合并，把x 系数化为 1，即可求出解．【解答】解：（1）移项合并得： 5x=5，解得： x=1；（2）去分母得： 4x﹣2x﹣ 4=12﹣ x﹣ 1，移项合并得： 3x=15，解得： x=5．【点评】此题考查了解一元一次方程，解方程去分母时注意各项都乘以各分母的最小公倍数．19．（8 分）先化简，再求值：x﹣2（x﹣2x y2x= 2y= 1y ）+（﹣+），其中﹣，﹣．【分析】先去括号，然后合并同类项即可化简题目中的式子，然后将x、y 的值代入化简后的式子即可解答本题．【解答】解：x﹣2（x﹣y2）（﹣x+y2）+==﹣ 3x+y2，当x=﹣2，y=﹣1 时，原式 =﹣ 3×（﹣ 2）+（﹣ 1）2=6+1=7．【点评】本题考查整式的加减﹣化简求值，解答本题的关键是明确整式化简求值的方法．20．（8 分）笔记本的单价是 x 元，圆珠笔的单价是y 元．小红买 3 本笔记本， 6 支圆珠笔；小明买 6 本笔记本， 3 支圆珠笔．（1）买这些笔记本和圆珠笔小红和小明一共花费多少元钱？（2）若每本笔记本比每支圆珠笔贵 2 元，求小明比小红多花费了多少元钱？【分析】（ 1）分别用含 x、y 的代数式表示出小红、小明的花费，合并它们花费的代数式；（2）用含 x、y 的代数式表示出小明比小红多花费的钱数，把每本笔记本比每支圆珠笔贵 2 元代入化简后的代数式．【解答】（ 1）由题意，得3x+6y+6x+3y=9x+9y答：买这些笔记本和圆珠笔小红和小明一共花费了（9x+9y）元；（2）由题意，的（ 6x+3y）﹣（ 3x+6y）=3x﹣3y因为每本笔记本比每支圆珠笔贵 2 元，即 x﹣ y=2所以小明比小红多花费：3x﹣ 3y=3（x﹣y）=6（元）答：小明比小红多花费了 6 元钱．【点评】本题考查了列代数式及代数式的化简求值．理解题意是解决本题的关键21．（8 分）如图，∠AOC与∠BOC互余，OD 平分∠BOC，∠EOC=2∠AOE．（1）若∠ AOD=75°，求∠ AOE的度数．（2）若∠ DOE=54°，求∠ EOC的度数．【分析】设∠ AOE=x，表示出∠ EOC，从而得到∠ AOC和∠ BOC，再根据角平分线的定义表示出∠COD，（1）根据∠ AOD=∠AOC+∠ COD列方程求解即可；（2）根据∠ DOE=∠EOC+∠COD列方程求出 x 的值，再求解即可．【解答】解：设∠ AOE=x，∵∠ EOC=2∠AOE，∴∠ EOC=2x，∴∠ AOC=∠ AOE+∠ COE=3x，∵∠ AOC与∠ BOC互余，∴∠ BOC=90°﹣3x，∵OD 平分∠ BOC，∴∠ COD= ∠BOC=45°﹣x，（1）若∠ AOD=75°，则∠ AOD=∠AOC+∠ COD=75°，即3x+45°﹣ x=75°，解得 x=20°，即∠ AOE的度数为 20°；（2）若∠ DOE=54°，则∠ DOE=∠ EOC+∠ COD=54°，即2x+45°﹣ x=54°，解得 x=18°，2x=36 ，°即∠ EOC的度数是 36°．【点评】本题考查了余角和补角，角平分线的定义，准确识图是解题的关键，难点在于表示出∠COD．22．（10 分）2018 年元旦，某商场将甲种商品降价40%，乙种商品降价 20%开展优惠促销活动．已知甲、乙两种商品的原销售单价之和为1400 元，某顾客参加活动购买甲、乙各一件，共付1000 元．（1）甲、乙两种商品原销售单价各是多少元？（2）若商场在这次促销活动中甲种商品亏损25%，乙种商品盈利 25%，那么商场在这次促销活动中是盈利还是亏损了？如果是盈利，求商场销售甲、乙两种商品各一件盈利了多少元？如果是亏损，求销售甲、乙两种商品各一件亏损了多少元？【分析】（ 1）设甲商品原销售单价为x 元，则乙商品的原销售单价为（1400﹣x）元，根据优惠后购买甲、乙各一件共需1000 元，即可得出关于x 的一元一次方程，解之即可得出结论；（2）设甲商品的进价为 a 元/ 件，乙商品的进价为 b 元/ 件，根据甲、乙商品的盈亏情况，即可分别得出关于 a、b 的一元一次方程，解之即可求出a、b 的值，再代入 1000﹣a﹣b 中即可找出结论．【解答】解：（1）设甲商品原销售单价为x 元，则乙商品的原销售单价为（1400﹣x）元，根据题意得：（1﹣40%）x+（ 1﹣20%）（ 1400﹣ x）=1000，解得： x=600，∴1400﹣x=800．答：甲商品原销售单价为600 元，乙商品的原销售单价为800 元．（2）设甲商品的进价为 a 元/ 件，乙商品的进价为 b 元/ 件，根据题意得：（1﹣25%）a=（1﹣40%）× 600，（1+25%）b=（1﹣ 20%）× 800，解得： a=480，b=512，∴1000﹣a﹣b=1000﹣480﹣ 512=8．答：商场在这次促销活动中盈利，盈利了8 元．【点评】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．23．（10 分）如图，点 B、C 在线段 AD 上， CD=2AB+3．（1）若点 C 是线段 AD 的中点，求 BC﹣AB 的值；（2）若 BC= AD，求 BC﹣AB 的值；（3）若线段 AC上有一点 P（不与点 B 重合）， AP+AC=DP，求 BP 的长．【分析】设 AB=x， BC=y，则 CD=2x+3．（1）根据 AC=CD构建方程即可解决问题；（2）根据 AB+CD=3BC，构建方程即可解决问题；（3）设 BP=m，根据 AP+AC=DP，构建方程即可解决问题；【解答】解：设 AB=x，BC=y，则 CD=2x+3．（1）∵ C 是 AD 中点，∴AC=CD，∴x+y=2x+3∴y﹣x=3，即 BC﹣ AB=3．（2）∵ BC= AD，即 AB+CD=3BC，∴x+2x+3=3y，∴y﹣x=1，即 BC﹣ AB=1．（3）设 AP=m，∵ AP+AC=DP，∴m+x+y=2x+3+x+y﹣ m，∴m﹣x=，即BP=m﹣x=．【点评】本题考查两点间距离，线段的中点、线段的和差定义等知识，熟知各线段之间的和、差关系是解答此题的关键，学会利用参数构建方程解决问题．24．（ 12 分）如图 1，已知∠ AOB=120，°∠COD=60°，OM 在∠ AOC内，ON 在∠ BOD内，∠ AOM=∠AOC，∠ BON= ∠BOD．（1）∠COD从图 1 中的位置绕点 O 逆时针旋转到 OC与 OB 重合时，如图 2，∠MON= 100 °；（2）∠COD从图 2 中的位置绕点 O 逆时针旋转 n°（ 0＜ n＜ 120 且 n≠ 60），求∠ MON 的度数；（3）∠COD 从图 2 中的位置绕点 O 顺时针旋转 n（°0＜ n＜ 120），则 n= 50°或 70°时，∠MON=2∠BOC．【分析】（ 1）根据∠ MON=∠BOM+∠ BON 计算即可；（2）分两种情形分别计算即可；（3）分两种情形分别计算即可；【解答】解：（1）由题意；∠ MON= ∠AOB+∠COD=80°+20°=100，°故答案为 100；（2）①当 0＜n＜60°时，如图 1 中，∠AOC=120°﹣n°，∠ BOD=60°﹣ n°，∴∠ MON=∠MOC+∠ COB+∠ BON= （ 120°﹣n°）+n°+（60°﹣n°）=100°，②当 60°＜n＜120°时，如图 2 中，∠AOC=120°﹣n°，∠ COD=60°，∠ BOD=n°﹣60°M∴∠ MON∠ MOC+∠ COD+∠ DON= （120°﹣n°）+60°+（n°﹣60°）=100°．综上所述，∠ MON=100°（3）①0°＜n＜60°时，∠BOC=n°，∠MON=2n°，∠MON= （120°+n°）+60°﹣（60°+n°） =100°，∴n=50°．②当 60°＜n＜120°时，∠ AOC=360°﹣（ 120°+n°） =240°﹣n°，∠ BOD=60°+n°，∴∠ MON=360° ﹣∠ AOM﹣∠ AOB﹣∠ BON=360°﹣（ 240°﹣n°）﹣ 120°﹣（60°+n°）=140°∴n=70°．综上所述， n 的值为 50°或 70°．故答案为 50°或 70°．【点评】本题考查角的和差定义，解题的关键是学会用分类讨论的思想思考问题，学会利用参数解决问题．。