有限单元法3.4
有限单元法
F2
x
1
2
e T
EP 0 eT e EP B T EAl B l e eT (F q( x)N dx) 0 0
单元是平衡的
eT T eT l e 0
eT T
k B
其中
EAl B
1 / l EAl 1 / l 1 / l 1/ l EA 1 1 l 1 1 --局部坐标系下的单元刚度矩阵
有限单元法初步
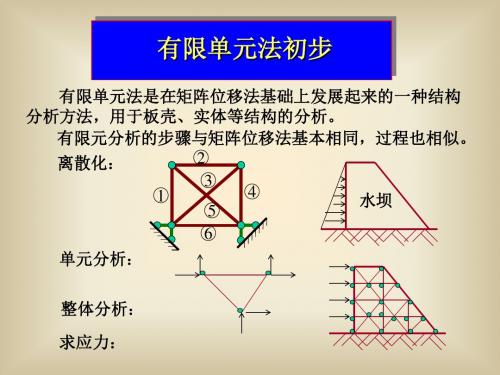
有限单元法是在矩阵位移法基础上发展起来的一种结构 分析方法,用于板壳、实体等结构的分析。 有限元分析的步骤与矩阵位移法基本相同,过程也相似。 2 离散化: 3 4 1 水坝 5 6
单元分析:
整体分析: 求应力:
§1 杆系结构的有限单元法
§1.1 泛函与变分
“最速落径问题”---质量为m的小环从A处自由滑下, 试选择一条曲线使所需时间最短。(不计摩擦)
§1.1 泛函与变分
y* ( x) y( x) y( x)
称 y ( x ) 为y(x)的变分,它是一个无穷小的任意函数。 变分运算在形式上与微分运算相同。
y 2 ( x) 2 y( x)y( x)
微分与变分运算次序可以交换。 d dy (y ) ( ) dx dx 积分与变分运算次序也可以交换。
杆中任一点应变
三、应力分析 ---用杆端位移表示杆中内力
杆中任一点应力
du dx d N e dx dN2 e dN 1 dx dx
E
EB
e
杆中任一截面的轴力
N A
B
B2
e
EAB
有限单元法课程设计

有限单元法课程设计一、引言有限单元法是结构力学和振动动力学中一个重要的数值分析方法,广泛应用于各种工程领域。
本文旨在介绍本人在有限单元法课程中完成的课程设计,包括设计目的、设计内容、设计方法和最终结果。
二、设计目的本课程设计旨在通过有限单元法对具有复杂边界条件的结构进行分析,掌握有限单元法的基本原理和方法,提高对有限单元法的理解和应用能力。
三、设计内容1. 课程背景本课程设计基于某高层建筑的振动分析,该建筑结构比较复杂,需要考虑建筑本身的振动和风荷载的影响。
2. 课程要求在完成本课程设计的过程中,学生需要掌握以下知识和技能:•掌握有限单元法和常见的单元类型;•掌握结构振动分析的基本原理;•能够编写MATLAB程序完成有限单元法分析,并绘制出振动模态图;•能够进行不同条件的分析和对比,并对结果进行分析和解释。
3. 设计流程3.1 建模首先,对建筑进行建模。
将建筑分为若干个部分,每个部分选择合适的单元类型和尺寸进行建模。
对于较为复杂的部分,可以采用多种单元类型进行分割。
3.2 材料参数和边界条件设定设定建筑结构的材料参数和边界条件。
根据建筑的实际情况进行选择,并进行数据输入。
3.3 有限元网格生成对建模后的结构进行有限元网格的生成。
根据建筑的精度要求和模型的复杂程度进行选择。
3.4 分析求解利用程序对有限元模型进行求解,得到结构的振动频率和模态。
3.5 结果分析对分析结果进行分析和解释。
分析建筑结构的振动模态和频率,分析不同条件下的差异和影响,制定相应的分析报告和结论。
4. 设计方法本课程设计采用MATLAB编程完成,具体包括以下步骤:•建模:采用MATLAB进行几何建模,根据建筑的实际情况进行部分分割和单元选择;•材料参数和边界条件设定:采用MATLAB进行数据输入;•有限元网格生成:采用MATLAB进行有限元网格的生成;•分析求解:编写MATLAB程序求解有限元模型;•结果分析:对结果进行分析并输出相应的报告和结论。
有限单元法ppt课件

06
有限单元法的发展趋势和展 望
发展趋势
工程应用领域拓展
随着科技的发展,有限单元法在解决 复杂工程问题上的应用越来越广泛, 不仅局限于结构分析,还涉及到流体 动力学、热传导等领域。
与其他方法的结合
有限单元法正与其他数值方法(如有 限差分法、边界元法等)进行交叉融 合,形成更为强大的数值分析工具。
05
有限单元法的优缺点
优点
灵活性
有限单元法允许对复杂的几何形状进 行离散化,适用于解决各种形状和大 小的问题。
高效性
有限单元法能够处理大规模问题,通 过使用计算机技术,可以快速求解。
广泛的应用领域
有限单元法被广泛应用于工程、物理 、生物等领域,是一种通用的数值分 析方法。
易于理解和实现
有限单元法的基本概念直观易懂,且 实现起来相对简单。
01
利用线性代数方法,将 各个单元的数学模型和 节点信息组合成整体方
程组。
03
将节点的未知量返回到 原问题中,得到问题的
解。
05
根据问题的物理性质和 边界条件,建立单元的 数学模型和节点信息。
02
解整体方程组,得到节 点的未知量。
04
有限单元法的特点
适用范围广
可以用于解决各种类型的问题,如弹性力学 、流体力学、传热学等。
高精度与高效率
研究者们致力于开发更高效、精确的 算法,以解决大规模、非线性、动态 等复杂问题。
并行化与云计算应用
随着计算资源的丰富,有限单元法的 计算过程正逐步实现并行化,利用云 计算平台进行大规模计算已成为趋势 。
展望
理论完善与创新
随着工程实践的深入,有限单元法的理论体系将进一步完善,同时会 有更多创新性的算法和模型出现。
有限单元法基础(1-3)

前言计算机仿真科学的发展,使我们能够在虚拟环境中瞬抚四海和纵览古今,而有限元方法(Finite Element Method) 及其计算机程序正是我们到达彼岸的桥梁,它是虚拟科学与工程研究的重要工具。
有限单元法的历史有限单元法的思想萌芽,可以追溯到十八世纪的欧拉(Euler)。
在十八世纪,欧位就曾经使用与现代有限单元法相同的方法计算过杆在轴力作用下的平衡问题; 现代可以追溯到Courant在1943年的工作,他第一次尝试应用定义在三角形区域上的分片连续函数和最小势能原理结合起来去求解圣维南(Saint-Venant) 扭转问题。
此后,基于工作需要,一些应用数学家、物理学家和工程师都涉足过有限单元概念的应用。
有限单元法第一个成功应用于弹性力学平面问题的是特纳(Turner)、克拉夫(Clough)、马丁(Martin)和托普(Top)等人于1956年在分析飞机结构时所获得的成果,他们把结构划分成一个个三角形和矩形的单元,把位移法应用到平面应力问题中去。
在他们的公式中,每一单元的特性是用一个单元结点上的力使之结点位移相联系的单元刚度矩阵来表示。
他们第一次给出了用三角形单元求得平面应力问题的正确解答。
他们的研究工作打开了利用电子计算机求解复杂平面弹性问题的新局面。
几乎与此同时,中国科学院的冯康教授也独立地提出了类似的方法。
于1960年,Clough进一步处理了弹性力学平面问题,并第一次提出了“有限单元法”的名称,从此,人们开始认识了有限单元法的功效。
在1999年慕尼黑的欧洲计算力学会议上,R.L. Taylor教授(“有限元方法:The Finite Element Method”第2作者)在主题报告中,形象生动地用三角形单元的3个顶点形容有限元方法的3位奠基人:R.W. Clough,J.H. Argyris,O.C. Zienkiewicz(“有限元方法”第1作者),足以证明“有限元方法”的两位作者对发展有限元方法的贡献。
有限单元法原理及应用简明教程

返 回 章 节 目 录
图2-31 铰接三角形
24
第二章 结构几何构造分析
结构的特征是:当它受载荷作用时会产生微小的 位移, 但位移一旦发生后, 即转变成一几何不变结 构,但结构的内力可能为无限大值或不定值,这样的 结构称为瞬变结构。显然,瞬变结构在工程结构设计 中应尽量避免。
(a) 瞬变结构
(b) 分离体分析 图2-32 瞬变结构
9
第一章 概述
图1-7 液压管路速度场分布云图
图1-8 磨片热应力云图
图1-9 支架自由振动云图
10
第二章 结构几何构造分析
2.1 结构几何构造的必要性 2.2 结构计算基本知识 2.3 结构几何构造分析的自由度与约束 2.4 自由度计算公式 2.5 结构几何不变结构组成规律
返 回 全 书 目 录
17
第二章 结构几何构造分析
对称结构在正对称载荷下,对称轴截面上只能产生 正对称的位移,反对称的位移为零;对称结构在反对称 载荷下,对称轴截面上只有反对称的位移,正对称的位 移为零。
(1) 具有奇数跨的刚架 ① 正对称载荷作用
2.2.3 结构对称性的利用
(a) 对称刚架
(b) 变形状态分析 图2-22对称性利用示意图
(c) 对称性利用
18
第二章 结构几何构造分析
② 对称刚架承受反对称载荷作用
(a) 对称刚架
(b) 变形状态分析 图2-23 反对称性利用示意图
(c) 反对称性利用
19
第二章 结构几何构造分析
(2) 具有偶数跨的刚架 ① 正对称载荷作用
(a) 变形状态分析
(b) 对称性利用
图2-24对称性利用示意图
规律3 一个几何不变结构( 或刚体 )与另一个几 何不变结构(或刚体)用六根即不平行也不相交于同一 条直线的链杆相联,所组成的结构是几何不变的结构, 且无多余约束。
《有限单元法》1-5章课后习题答案

δδ∏00且或∏,泛函极值性对于判断解的近似性质有意义,利用它可以对解的上下界做出估计。
思考题1.9什么是里兹法?通过它建立的求解方法有什么特点?里兹方法收敛性的定义是
什么?收敛条件是什么?
里兹法:在某一函数空间寻找试探函数,利用加权值的独立变分性将该函数的驻值问题转化
为该函数关于权值的极值问题。其特点是:试探函数是全域的,解的精度依赖于试探函数的
5qL L 5qL
wx L x当x , w
5 4
120EI + kl 2 480EI + 4kL
4
L 5qL
精确解w ???,应该是三角级数更接近精确解。因为是最小位能原理建立的
2 384EI
泛函,因此近似解比精确解要偏小。因此只要比较三角函数和幂函数的结果,就可以知道哪
个更精确了。另外,取不同的阶数,逼近速度不同,三角函数更快。
可得最终结果(略)。3 2 2 2 w ww ww
δδw n ds?+ n dsδ dxdy?
xx?∫∫3 2∫2 2
ΓΓ?x xx ?x ?x? 2 2 2 3? ww ?
+δ dxdy?+δδ n ds w n ds? y y
∫22∫2∫2ΓΓ
?y ?x ?y ?x y xD?
0
2 2 2 3 ww ?
12
23
L LL
3
x
上式中的最后一项前面没有待定系数,这是由于使用了在xL处φ1的强制边界条件。
3
L
从物理意义上说,相当于给定边界条件的解为齐次方程的通解加一个特解的缘故。将(1 )
式代入教材(1.2.26 )式,得到残量:
x 66 xx
R x a ?6 + a 2? + + Qx
第三章平面问题的有限单元法PPT课件
1
2A
ai aj am
bi bj bm
x ci c j cm
y
1
简记为
Ni N j Nm 1
这说明,三个形函数中只有二个是独立的。
(3-11)
2. 形函数在各单元结点上的值,具有“本点是1、它点
为零”的性质,即
在结点i上,
N i xi
,
yi
1 2A
ai
bi xi
ci yi
若令
Ni
1 2A
ai
bi x
ci y
(i , j , m轮换) (3-9)
这样,位移模式 就可以写为
u Niui Njuj Nkmukm Niui v Nivi Njvj Nkmvkm Nivi
[N] 形函数矩阵
u
u
v
Ni I
Nj I
NkmI e Ne
式中 I是二阶单位矩阵;Ni 、Nj 、Nm 是坐标的函数,它 们反映了单元的位移状态,所以一般称之为形状函数,简称形
y
Ym vm
m( xm
,
ym
)
X m um
Yi vi Xi
Fy Fx
Yj vj
i(xi , yi ) ui
j
(
x
j
,
X y
j j
u )
j
0
x
ai
xj xm
yj ym
x j ym xm y j
1
bi
1
yj ym
y j ym
(i , j , m轮换) (3-5)
1
ci 1
xj xm
x j xm
u N e
(3-1)
第三章 有限单元法
第3章有限单元法在工程技术领域内,工程师常常运用数学和力学的知识将实际问题抽象成它们应遵循的基本方程(常微分方程或偏微分方程)和相应的边界条件。
对于大多数的工程技术问题,由于物体的几何形状和载荷作用方式是很复杂的,除了方程性质比较简单且几何边界相当规则的少数问题之外,试图按经典的弹性力学和塑性力学方法获得解析解是十分困难的,甚至是不可能的。
为了克服这种困难,有两条解决途径:一是引入简化假设,将方程和边界条件简化为能够处理的问题,从而得到它在简化状态下的解答。
这种方法只在有限的情况下可行,因为过多的简化将可能导致不正确的甚至错误的答案。
另一条解决途径就是数值解法,如有限差分法、边界元法、有限单元法和离散元法等。
对于非线性问题,有限单元法更为有效,且已经出现了许多通用程序。
有限单元法的主要优点是:①建立于严格理论基础上的可靠性。
因为用于建立有限元方程的变分原理或加权余量法在数学上已被证明是微分方程和边界条件的等效积分形式。
只要原问题的数学模型是正确的,同时用来求解有限元方程的算法是稳定、可靠的,如果单元满足收敛准则,则近似解最后收敛于原数学模型的精确解;②适应性强,应用范围广,不仅能成功地分析具有复杂边界条件、非线性、非均质材料、动力学等难题,而且还可以推广到解答数学方程中的其它边值问题,如热传导、电磁场、流体力学等问题;③适合计算机实现的高效性。
由于有限元分析的各个步骤可以表达成规范化的矩阵形式,最后导致求解方程可以统一为标准的矩阵代数问题,特别适合计算机的编程和执行。
已经出现了许多大型结构分析通用程序,如:NASTRAN、ASKA、ADINA、ANSYS、ABAQUS等,可以直接应用。
这些优点使有限单元法得到了广泛的应用和发展。
3.1有限单元法分析的基本步骤在工程或物理问题的数学模型(基本变量、基本方程、求解域和边界条件等)确定以后,有限单元法作为对其进行分析的数值计算方法的基本步骤如下:(1) 离散化一个复杂的弹性体可以看成是由无限个质点组成的连续体,它具有无限个自由度。
有限单元法的基本概念和理论基础
可以证明,如果弹性体内任一点,已知这三个垂直方向的正应变及其相应的三个剪应变,则该点任意方向的正应变和任意二垂直线间的剪应变均可求出,当然也可求出它的最大和最小正应变。因此,这六个量可以完全确定该点的应变分量,它们就称为该点的应变分量。六个应变分量的总体,可以用一个列向量来表示:
1
2
应变分量向量
<<结构分析中的有限单元法>> By Xiaojun Wang
01
02
03
04
<<结构分析中的有限单元法>> By Xiaojun Wang
考察了体素在XOY一个平面内的变形情况,可得
考察体素在XOZ和YOZ平面内的变形情况,可得:
联立得到几何方程,表明应变分量与位移分量之间的关系。
应变分量与位移分量的关系来自<<结构分析中的有限单元法>> By Xiaojun Wang
简化得
剪应力互等
应力
<<结构分析中的有限单元法>> By Xiaojun Wang
考虑微元体各个面上的法向应力和剪应力与其体力平衡,注意应力从一个面到对面是变化的,即有增量,将作用于微元体各个方向的力求和,略去高阶项,可得平衡方程:
平衡微分方程
可以证明:如果 这六个量在P点是已知的,就可以求得经过该点的任何面上的正应力和剪应力,因此,这六个量可以完全确定该点的应力状态,它们就称为在该点的应力分量。
杆件系统有限单元法
(3)单元应力场的表达 由弹性力学中物理方程有:
σ e ( x ) = E eε e ( x ) = E e B e ( x ) ⋅ δ e = S e ( x ) ⋅ δ e
其中Se为单元的应力函数矩阵:
⎡ E S ( x) = E B ( x) = ⎢ − ⎣ l
e e e
e
E ⎤ ⎥ l ⎦
平面梁单元的节点位移δe和节点力Fe为:
δ =⎡ ⎣ui vi θi u j v j θ j ⎤ ⎦
e e
T
F =⎡ ⎣ FNi FQi M i FNj FQj M j ⎤ ⎦
相应的刚度方程为:
T
K e ⋅δ e = F e
将杆单元刚度矩阵与纯弯梁单元刚度矩阵进行组 合,可得到平面梁单元的刚度矩阵:
可以写出节点位移向量和节点力向量:
δ =⎡ ⎣ui u j ⎤ ⎦
e
e
T
T ⎡ ⎤ F = ⎣ FNi FNj ⎦
(1)单元位移模式的表达 由于每个节点只有一个轴向位移,即一个单元共有 两个自由度,因此可假设该单元的位移模式为具有 两个待定系数的函数模式:
u ( x ) = a 0 + a1 x
e
第三章
杆件结构的有限元分析 (FEA)
在杆件系统中根据单元受力的特点,我们可以 把它们分成两大类:杆和梁。为了以后描述的 方便,我们把两端铰接,只受轴向力的基本结 构称为杆单元,而受轴向力和弯矩、扭矩、剪 力共同作用的基本结构称为梁单元。
3.1 平面杆单元
局部坐标系中的杆单元描述
设有一任意的杆单元如图所示,i 和j 为单元的两 个结点,x 为该单元的局部坐标,其原点设在单 元的i 结点。设两个结点在x 方向的位移为 u i 和 u j ,它们的正方向如图3-1 所示,与它们相应的 结点力 FN δ e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5m
5kN
T
目录
上页 下页 退出
Ff
①
0 4 5 0 4 5
3.4 等效结点荷载和边界条件
单元②
Fxi Fxj 0 Fyi Fyj
② ②
② ②
Байду номын сангаас2.5m
12kN/m
O
B
y
① 8kN
M i ② M j ② 25kN
A 1(0 0 0)
5m
4(0 0 0) D
Ff ② 0 30 25 0 20 25
F = FE Fd
(3 81)
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
边界条件的处理
1.铰结点 ①铰结点上各杆具有相同的线位移,但 截面的转角位移不相同; ②结点上具有铰接杆端不承受弯矩作用
E H
6(9 10 11) E 9(15 16 17) H
目录
上页 下页 退出
D G B
ⓔ
a pa 1 2l
0 0
a2 p 2l
目录
上页 下页 退出
j x F fy ⓔ
0 0
y
M fⓔ
3.4 等效结点荷载和边界条件
m
i
a b l
F fx ⓔ
j x F fy
ⓔ
0
a2 a b m 2 3 l l l
0
a2 a b m 2 3 l l l
3.4 等效结点荷载和边界条件
引入弹性支承的具体做法:先解除弹 性支承点约束,在处给一个结点号,形 成总刚度矩阵,然后在总刚度矩阵中将 第i行的主元素Kii 加上弹性支承的刚度 系数k,此时第i行变为:
K i1 K i 2 K i 3 L K ii k L K in
目录
上页 下页 退出
同样也适应于角位移为弹性约束的情况.
F i
a b l
F fx ⓔ
j x F fy
ⓔ
0
b2 a F 2 1 2 l l
0
a2 b F 2 1 2 l l
a 2b F 2 l
目录
上页 下页 退出
y
Mf
ⓔ
ab2 F 2 l
3.4 等效结点荷载和边界条件
M
i
a b l
F fx ⓔ
j x F ⓔ fy
2(2 3 4) B 3(5 6 7)
D 4(5 6 8)
8(12 13 14) G
A
C
F
A
C
5(0 0 0)
F
7(0 0 0)
(a)
(b)
3.4 等效结点荷载和边界条件
2.弹性支承点
1 2 i-1
i
i i+1 n
k
FR k i
1 2 i-1 i i+1 n
FR
目录
上页 下页 退出
K i11 K i 2 2 L K ii i L K in n Fi FR K i11 K i 2 2 L ( K ii k ) i L K in n Fi
T
单元③
Fxi ③ Fxj ③ 0
Fyi ③ Fyj ③ 0kN
5m
30kN
x
2(1 2 3) ② 3(4 5 6) C ③
6kN 10kN· m 10kN
目录
上页
M i ③ M j ③ 25kN
Ff
③
0 0 0 0 0 0
T
下页 退出
3.4 等效结点荷载和边界条件
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
步骤: (1) 在局部坐标系下求单元的固端力F f ⓔ 假定单元的两端均固定,然后根据 静力平衡求得固定端的反力
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
常见载荷的单元固端力
F fx ⓔ
q
0
0
F fy
i
a b l
ⓔ
j x
y
M fⓔ
1 a 2 a3 1 qa 3 a qa 2 2 2 3 2 2 l l 2 l2 l qa 2 a a2 qa 3 a 68 3 2 43 12 l l 12l l
0
M 6ab l3 M
0
6ab l3
y
Mf
ⓔ
b b M 2 3 l l
M
a a 23 l l
F fx ⓔ
q i
a b l
0
0
目录
上页
j x
F fy Mf
ⓔ
qa a2 a 3 qa3 a 2 3 2 1.6 3 2 3 1.6 4 l l 4l l
y
Mf
ⓔ
ab2 m 2 l
a 2b m 2 l
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
(2) 由单元固端力求单元等效结点荷载 FE ⓔ
F f ⓔ T ⓔT F f ⓔ FE ⓔ F f ⓔ
(3 79) (3 80)
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
等效结点荷载
(2) 求整体坐标系下各单 元的等效结点载荷 单元①
Ff
①
2.5m
12kN/m
O
B
x y
8kN
2(1 2 3) ② 3(4 5 6) C ① ③
6kN 10kN· m 10kN
90o
①T
1
2 3
0
0 0
A 1(0 0 0)
5m
4(0 0 0) D
T
Ff
①
4 0 5 4 0 5 1 2 3 4 5
3.4 等效结点荷载和边界条件
例3-2 试求图示刚架的等效结点荷载。
2.5m
12kN/m 6kN 10kN· m 10kN
O
B
x y
8kN
2(1 2 3) ② 3(4 5 6) C ① ③
5m
A 1(0 0 0)
5m
4(0 0 0) D
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
解: 建立单元坐标系和结 构整体坐标系,结点 编码如图。 单元①
3.4 等效结点荷载和边界条件
整体平衡方程:基于结点。 载荷位置:结点载荷和非结点载 荷。
按静力等效的原 则等效到结点上, 形成等效结点载荷。
非结点 荷载?
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
非结点荷载的处理
按照虚功等效的原则等效到结点上,成为 等效结点荷载 FE 。 虚功等效:指原力系与等效结点荷载在任 何可能的微小位移(虚位移)上所做的虚功 相等。 前面已经介绍了求等效结点荷载的方法, (3-8)式、(3-17)式、(3-26)式分别可用来求不 同情况下的等效结点荷载。
y
ⓔ
qa 2 a a2 2 3 1.2 2 6 l l
qa 3 a 1 0.8 下页 4l l
退出
3.4 等效结点荷载和边界条件
F i
a b l
F fx ⓔ
j x
F
b l
F
a l
y
F fy ⓔ M fⓔ
0 0
0 0
F fx
p i
a b l
1 2 3 4 5 6
T
2.5m
12kN/m
O
B
x y
8kN
2(1 2 3) ② 3(4 5 6) C ① ③
6kN 10kN· m 10kN
A 1(0 0 0)
5m
4(0 0 0) D
F 4 30 20 14 36 10
5m
目录
上页 下页 退出
3.4 等效结点荷载和边界条件
目录
上页 下页 退出
2.5m
12kN/m
O
B
x y
8kN
2(1 2 3) ② 3(4 5 6) C ① ③
6kN 10kN· m 10kN
A 1(0 0 0)
5m
4(0 0 0) D
(1) 求各单元在局部坐标系下的固端力
Fxi ① Fxj ① 0 M i M j
① ①
Fyi ① Fyj ① 4kN
T
单元②
Ff
②
0o
②T
6
T
5m
T
Ff
②
0 30 25 0 30 25 4 5 6 0 0 0
③
目录
上页
单元③
Ff
③
90o
T
③T
Ff
0 0 0 0 0 0
T
下页 退出
3.4 等效结点荷载和边界条件
(3)由(3-80)式和(3-81)并利 用先处理法可得整体坐标 系下的总结点荷载矩阵。
