初一上学期角度计算典型题
新人教版七年级数学上册专题训练:角的计算(含答案)

专题训练角的计算类型1利用角度的和、差关系找出待求的角与已知角的和、差关系,根据角度和、差来计算.1.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD的度数.解:因为∠AOC=75°,∠BOC=30°,所以∠AO B=∠AOC-∠BOC=75°-30°=45°.又因为∠BOD=75°,所以∠AOD=∠AOB+∠BOD=45°+75°=120°.2.将一副三角板的两个顶点重叠放在一起.(两个三角板中的锐角分别为45°、45°和30°、60°)(1)如图1所示,在此种情形下,当∠DAC=4∠BAD时,求∠CAE的度数;(2)如图2所示,在此种情形下,当∠ACE=3∠BCD时,求∠ACD的度数.解:(1)因为∠BAD+∠DAC=90°,∠DAC=4∠B AD,所以5∠BAD=90°,即∠BAD=18°.所以∠DAC=4×18°=72°.因为∠DAE=90°,所以∠CAE=∠DAE-∠DAC=18°.(2)因为∠BCE=∠DCE-∠BCD=60°-∠BCD,∠ACE=3∠BCD,所以∠ACB=∠ACE+∠BCE=3∠BCD+60°-∠BCD=90°.解得∠BCD=15°.所以∠ACD=∠ACB+∠BCD=90°+15°=105°.类型2利用角平分线的性质角的平分线将角分成两个相等的角,利用角平分线的这个性质,再结合角的和、差关系进行计算.3.如图,点A,O,E在同一直线上,∠AOB=40°,∠EOD=28°46′,OD平分∠COE,求∠COB的度数.解:因为∠EOD=28°46′,OD 平分∠COE,所以∠COE=2∠EOD=2×28°46′=57°32′.又因为∠AOB=40°,所以∠COB=180°-∠AOB-∠COE=180°-40°-57°32′=82°28′.4.已知∠AOB=40°,OD 是∠BOC 的平分线.(1)如图1,当∠AOB 与∠BOC 互补时,求∠COD 的度数;(2)如图2,当∠AOB 与∠BOC 互余时,求∠COD 的度数.解:(1)因为∠AOB 与∠BOC 互补,所以∠AOB+∠BOC =180°.又因为∠AOB=40°,所以∠BOC=180°-40°=140°.因为OD 是∠BOC 的平分线,所以∠COD=12∠BOC=70°. (2)因为∠AOB 与∠BOC 互余,所以∠AOB+∠BOC=90°.又因为∠AOB=40°,所以∠BOC=90°-40°=50°.因为OD 是∠BOC 的平分线,所以∠COD=12∠BOC=25°.类型3 利用方程思想求解在解决有关余角、补角,角的比例关系或倍分关系问题时,常利用方程思想来求解,即通过设未知数,建立方程,通过解方程使问题得以解决.5.一个角的余角比它的补角的23还少40°,求这个角的度数. 解:设这个角的度数为x °,根据题意,得90-x =23(180-x)-40. 解得x =30.所以这个角的度数是30°.6.如图,已知∠AOE 是平角,∠DOE =20°,OB 平分∠AOC,且∠COD∶∠BOC=2∶3,求∠BOC 的度数.解:设∠COD=2x °,则∠BOC=3x °.因为OB 平分∠AOC,所以∠AOB=3x °.所以2x +3x +3x +20=180.解得x =20.所以∠BOC=3×20°=60°.7.如图,已知∠AOB=12∠BOC,∠COD =∠AOD=3∠AOB ,求∠AOB 和∠COD 的度数.解:设∠AOB=x °,则∠COD=∠AOD=3∠AOB=3x °.因为∠AOB=12∠BOC, 所以∠BOC=2x °.所以3x +3x +2x +x =360.解得x =40.所以∠AOB=40°,∠COD =120°.类型4 利用分类讨论思想求解在角度计算中,如果题目中无图,或补全图形时,常需分类讨论,确保答案的完整性.8.已知∠AOB=75°,∠AOC =23∠AOB,OD 平分∠AOC,求∠BOD 的大小. 解:因为∠AOB=75°,∠AOC =23∠AOB, 所以∠AOC=23×75°=50°.所以∠AOD=∠COD=25°.如图1,∠BOD =75°+25°=100°;如图2,∠BOD =75°-25°=50°.9.已知:如图,OC 是∠AOB 的平分线.(1)当∠AOB=60°时,求∠AOC 的度数;(2)在(1)的条件下,∠EOC =90°,请在图中补全图形,并求∠AOE 的度数;(3)当∠AOB=α时,∠EOC =90°,直接写出∠AO E 的度数.(用含α的代数式表示)解:(1)因为OC 是∠AOB 的平分线,所以∠AOC=12∠AOB. 因为∠AOB=60°,所以∠AOC=30°.(2)如图1,∠AOE =∠EOC+∠AOC=90°+30°=120°;如图2,∠AOE =∠EOC-∠AOC=90°-30°=60°.(3)90°+α2 或90°-α2.专题训练 整式的加减运算计算:(1)(钦南期末)a 2b +3ab 2-a 2b ;解:原式=3ab 2.(2)2(a -1)-(2a -3)+3;解:原式=4.(3)2(2a 2+9b)+3(-5a 2-4b);解:原式=-11a 2+6b.(4)3(x 3+2x 2-1)-(3x 3+4x 2-2);解:原式=2x 2-1.(5)(钦南期末)(2x 2-12+3x)-4(x -x 2+12); 解:原式=2x 2-12+3x -4x +4x 2-2 =6x 2-x -52.(6)3(x2-x2y-2x2y2)-2(-x2+2x2y-3);解:原式=3x2-3x2y-6x2y2+2x2-4x2y+6=5x2-7x2y-6x2y2+6.(7)-(2x2+3xy-1)+(3x2-3xy+x-3);解:原式=-2x2-3xy+1+3x2-3xy+x-3=x2-6xy+x-2.(8)(4ab-b2)-2(a2+2ab-b2);解:原式=4ab-b2-2a2-4ab+2b2=-2a2+b2.(9)-3(2x2-xy)+4(x2+xy-6);解:原式=-6x2+3xy+4x2+4xy-24=-2x2+7xy-24.(10)(钦州期中)2a2-[-5ab+(ab-a2)]-2ab. 解:原式=2a2+5ab-ab+a2-2ab=3a2+2ab.。
(完整)数学人教版七年级上册角的计算
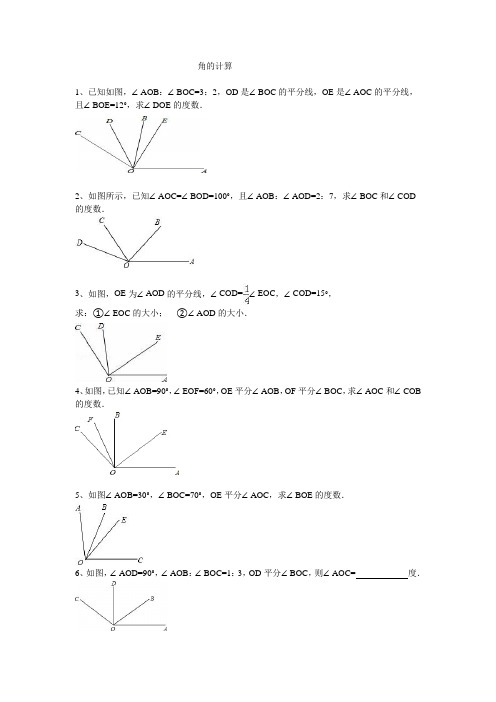
角的计算1、已知如图,∠AOB:∠BOC=3:2,OD是∠BOC的平分线,OE是∠AOC的平分线,且∠BOE=12°,求∠DOE的度数.2、如图所示,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,求∠BOC和∠COD 的度数.3、如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,求:①∠EOC的大小;②∠AOD的大小.4、如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB 的度数.5、如图∠AOB=30°,∠BOC=70°,OE平分∠AOC,求∠BOE的度数.6、如图,∠AOD=90°,∠AOB:∠BOC=1:3,OD平分∠BOC,则∠AOC=度.7、如图,已知OB 是∠AOC 的平分线,OD 是∠COE 的平分线,如果∠AOE=140°,∠BOC 比∠COD 的2倍还多10°,那么∠AOB 是多少度?8、如图,已知∠BOC=2∠AOC ,OD 平分∠AOB ,且∠COD=20°,求∠AOB 的度数.9、已知∠AOB=60°,从点O 引射线OC ,使∠AOC=40°,作∠AOC 的角平分线OD ,(1)依题意画出图形;(2)求∠BOD 的度数.10、(1)如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOC ,ON 平分∠BOC ,求∠MON 的度数;(2)如果(1)中的∠AOB=α,∠BOC=β,其它条件不变,请用求α或β来表示∠MON 的度数.11、 如图AOB α∠= ,OC 是一条射线,OM 平分AOC ∠ ,ON 平分BOC ∠ .(1)当15,45MOC NOC ∠=︒∠=︒时,求α的大小.(2)将射线OC 绕点O 按逆时针方向旋转一周.试用含 α的代数式表示MON ∠.12、已知∠AOD=α,射线OB、OC在∠AOD的内部,OM平分∠AOC,ON平分∠BOD.(1)如图1,当射线OB与OC重合时,求∠MON的大小;(2)在(1)的条件下,若射线OC绕点O逆时针旋转一定角度θ,如图2,求∠MON的大小;(3)在(2)的条件下,射线OC绕点O继续逆时针旋转,旋转到与射线OA的反向延长线重合为止,在这一旋转过程中,∠MON=.13、(1)如图1所示,已知∠AOB=120°,OC平分∠AOB,OD、OE分别平分∠AOC、∠COB,求∠DOE的度数;(2)如图2,在(1)中把“OC平分∠AOB”改为“OC是∠AOB内任意一条射线”,其他任何条件都不变,试求∠DOE的度数;(3)如图3,在(1)中把“OC平分∠AOB”改为“OC是∠AOB外的一条射线且点C与点B 在直线AO的同侧”,其他任何条件都不变,请你直接写出∠DOE的度数.余角与补角14、将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为.15、如图所示,点O为直线AB上一点∠AOC=∠DOE=90°,那么图中互余角的对数为( ) A.2对B.3对C.4对D.5对AB C D E FO 16、如图所示,将一副三角板叠放在一起,使直角顶点重合,且∠AOD=2∠BOC ,则∠AOC 的等于( )A .45°B .30°C .25°D .20°17、将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )18、如图,已知直线AB 和CD 相交于O 点,∠COE=90°,OF 平分∠AOE ,∠COF=28°,求∠BOD 的度数.19、(7分)如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,∠AOC =72°,OF ⊥CD .(1)写出图中互余的角;(3分)(2)求∠EOF 的度数.(4分)20、如图,点O 是直线AB 上一点,∠EOF=90°,OP 平分∠AOE ,OQ 平分∠BOF ,∠AOE=130°,求∠POQ 的度数.20、如图,∠AOB与∠BOC互补,OM平分∠BOC,且∠BOM=35°,则∠AOB=__________°.21、如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数;(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.22、如图,E、O、A三点共线,OB平分∠AOC,∠DOC=2∠EOD,已知∠AOB=30°.求∠EOD的度数.23、已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.(1)当点C、E、F在直线AB的同侧时(如图1所示)①若∠COF=28°,则∠BOE=°②若∠COF=α°,则∠BOE=°.(2)当点C与点E、F在直线AB的两旁(如图2所示)时,(1)中②是否仍然成立?请给出你的结论并说明理由.24、如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC (1)填空:与∠AOE互补的角是;(2)若∠AOD=36°,求∠DOE的度数;(3)当∠AOD=x°时,请直接写出∠DOE的度数.25、已知,如图,AO⊥BC,DO⊥OE.(1)在下面的横线上填上适当的角:∠DOE=∠__________+∠__________;∠BOE=∠__________﹣∠__________;(2)不添加其它条件情况下,请尽可能多地写出图中有关角的等量关系(至少4个).(3)如果∠COE=35°,求∠AOD的度数.26、如图,已知∠AOM与∠MOB互为余角,且∠BOC=30°,OM平分∠AOC,ON平分∠BOC.(1)求∠MON的度数;(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;(4)从(1)、(2)、(3)中你能看出有什么规律.27、如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)填空:与∠AOE互补的角是;(2)若∠AOD=36°,求∠DOE的度数;(3)当∠AOD=x°时,请直接写出∠DOE的度数.28、O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.(1)如图(1),若∠AOB=130°,求∠EOF的度数;(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.29、如图,OM是∠AOC的平分线,ON是∠BOC的平分线.(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.30、(1)如图1,将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=度;(2)如图2,将三个正方形的一个顶点重合放置,求∠1的度数;(3)如图3,将三个方形的一个顶点重合放置,若OF平分∠DOB,那么OE平分∠AOC 吗?为什么?31、已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).(1)如图1,当OB、OC重合时,求∠EOF的度数;(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.32、将矩形ABCD沿AE折叠,得到如图的图形.已知∠CEB′=50°,则∠AEB′=°.33、如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD(1)图中除直角外,还有相等的角吗?请写出三对:①②③(2)如果∠AOD=40°,求∠POF的度数.。
初中角度经典练习题(含详细答案)

初中角度经典练习题(含详细答案) ================================问题1:--------若一个角的度数是100°,则它是什么类型的角?答案1:--------这是一个锐角,因为它的角度小于90°。
问题2:--------已知角A的补角是120°,求角A的度数。
答案2:--------角A的度数为60°,因为补角的度数与原角的度数相加等于180°。
问题3:--------两个角互为余角,其中一个角的补角是30°,求这两个角的度数分别是多少?答案3:--------一个角的度数是60°,另一个角的度数是120°,因为余角的度数相加等于90°。
问题4:--------如果一根直线将一个角分成两个互补角,其中一个角度是40°,求另一个角的度数。
答案4:--------另一个角的度数是50°,因为两个互补角的度数相加等于90°。
问题5:--------如果两个角互为补角,其中一个角度是60°,求另一个角的度数。
答案5:--------另一个角的度数是30°,因为两个补角的度数相加等于90°。
问题6:--------如果两个角互为补角,其中一个角的度数是75°,求另一个角的度数。
答案6:--------另一个角的度数是15°,因为两个补角的度数相加等于90°。
初一上册数学角度题30道

初一上册数学角度题30道以下是30道初一上册数学角度题,涵盖了角度的基本概念、角度的计算、角度与直线的关系等内容。
请注意,这些题目可能需要根据具体的数学教材和教学大纲进行调整。
1. 一个角的补角比这个角的余角的3倍大10°,求这个角的度数。
2. 已知∠AOB = 70°,∠BOC = 30°,OM 平分∠AOC,求∠BOM 的度数。
3. 已知∠AOB = 90°,∠BOC = 30°,求∠AOC的度数。
4. 已知∠AOB = ∠COD = 90°,∠AOC = 30°,求∠BOD的度数。
5. 一个角的余角比这个角的补角的1/4还小10°,求这个角的度数。
6. 已知∠AOB = 120°,∠BOC = 30°,求∠AOC的度数。
7. 已知∠AOB = ∠COD,∠AOC = ∠BOD,求证:∠A = ∠D。
8. 一个角的补角是这个角的余角的4倍,求这个角的度数。
9. 已知∠AOB = 60°,∠BOC = ∠AOD,求∠COD的度数。
10. 已知∠AOB = ∠COD,∠AOC = ∠BOD,求证:∠A = ∠D。
11. 一个角的余角比这个角的补角的1/3大10°,求这个角的度数。
12. 已知∠AOB = 150°,∠BOC = 60°,求∠AOC的度数。
13. 已知∠AOB = ∠COD,∠AOC + ∠BOD = 90°,求证:∠AOC = ∠BOD。
14. 一个角的补角比这个角的余角的2倍小30°,求这个角的度数。
15. 已知∠AOB = 80°,∠BOC = ∠AOD,求∠COD的度数。
16. 已知∠AOB = ∠COD,且∠AOC = ∠BOD,求证:OC平分∠AOD。
17. 一个角的余角比这个角的补角的1/2大20°,求这个角的度数。
人教版七年级数学上册 角度的计算习题练习 (附答案)

七年级上册数学角度的计算习题一、选择题1.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于()A. 65°B. 50°C. 40°D. 25°2.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有()A. 1个B. 2个C. 3个D. 4个3.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A . 90°B . 120°C . 160°D . 180°4.一个钝角与一个锐角的差是( )A . 锐角B . 钝角C . 直角D . 不能确定 5.如图,∠AOB 是直角,∠COD 也是直角,若∠AOC =α,则∠BOD 等于 ( ).A .90°+αB .90°-αC .180°+αD .180°-α6.如图,射线OB 、OC 将∠AOD 分成三部分,下列判断错误的是( )DABC OA.如果∠AOB=∠COD,那么∠AOC=∠BODB.如果∠AOB>∠COD,那么∠AOC>∠BODC.如果∠AOB<∠COD,那么∠AOC<∠BODD.如果∠AOB=∠BOC,那么∠AOC=∠BOD二、填空题7.比较两角大小的方法有:(1)法;(2)法.三、解答题8.如图,将一副三角尺的两个直角顶点O重合在一起,在同一平面内旋转其中一个三角尺.(1)如图1,若∠BOC=70°,求∠AOD的度数.(2)如图2,若∠BOC=50°,求∠AOD的度数.(3)如图1,请猜想∠BOC与∠AOD的关系,并写出理由.9.下面是小马虎解的一道题题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.解:根据题意可画出图∵∠AOC=∠BOA-∠BOC=70°-15°=55°∴∠AOC=55°若你是老师,会判小马虎满分吗?若会,说明理由.若不会,给出你认为正确的解法.10.把一副三角尺如图所示拼在一起.(1)写出图中∠A、∠B、∠BCD、∠D、∠AED的度数;(2)用小于号“<”将上述各角连接起来.11.如图所示,点O在直线AB上,并且∠AOC=∠BOC=90°,∠EOF=90°,试判断∠AOE 和∠COF,∠COE和∠BOF的大小关系.12.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.答案解析1.【答案】A【解析】∵∠AOB是一直角,∠AOC=40°,∴∠COB=50°,∵OD平分∠BOC,∴∠COD=25°,∵∠AOD=∠AOC+∠COD,∴∠AOD=65°.故选A.2.【答案】C【解析】15°=45°-30°,65°不能画出,75°=30°+45°,135°=45°+90°,所以能用一副三角尺画出来的有15°、75°,135°共3个,故选C.3.【答案】D【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°-a,所以∠AOC+∠BOD=90°+a+90°-a=180°.故选D.4.【答案】D【解析】一个钝角与一个锐角的差可能是锐角、直角也可能是钝角.故选D.5.【答案】B6.【答案】D【解析】A、如果∠AOB=∠COD,那么∠AOC=∠BOD,本选项正确;B、如果∠AOB>∠COD,那么∠AOC>∠BOD,本选项正确;C、如果∠AOB<∠COD,那么∠AOC<∠BOC,本选项正确;D、如果∠AOB=∠BOC,那么∠AOC=∠BOD,本选项错误.故选D.7.【答案】(1)度量;(2)叠合【解析】角的大小比较的两种方法:(1)度量法,即用量角器量角的度数,角的度数越大,角越大.(2)叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,另一边都不落在重合边的同侧,观察另一边的位置,据此判断即可.8.【答案】解:(1)∵∠BOC+∠BOD=90,∠BOC=70°,∴∠BOD=20°,∴∠AOD=∠AOB+∠BOD=110°.(2)∵∠AOB=∠DOC=90°,又∵∠AOB+∠AOD+∠DOC+∠BOC=360°,∴∠BOC+∠AOD=180°∵∠BOC=50°,∴∠AOD=180-∠BOC=130°.(3)结论:∠BOC+∠AOD=180°.理由:∵∠AOB=90°,∠COD=90°,∴∠BOC+∠AOD=(90°-∠AOC)+(90°+∠AOC)=90°-∠AOC+90°+∠AOC=180°,∴∠BOC+∠AOD=180°.【解析】(1)∠BOC和∠BOD互余,故∠BOD=20°,故可知∠AOD的度数.(2)利用∠BOC与∠AOD互补求∠AOD度数.(3)根据角的互补,叠和部分恰好为∠AOD的补角,故∠BOC和∠AOD的和始终等于180度.9.【答案】解:不会,如图,当OC在∠AOB的内部时,∠AOC=∠BOA-∠BOC=55°,当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,故∠AOC的度数是55°或85°.【解析】在同一平面内,∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.10.【答案】解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;(2)∠A<∠D<∠B<∠AED<∠BCD.【解析】(1)一副三角尺一个是等腰直角三角形,另一个是一个角为30°的直角三角形,看图写出各个角的度数,(2)按角的大小顺序连接.11.【答案】解:因为∠EOF=∠COF+∠COE=90°,∠AOC=∠AOE+∠COE=90°,即∠AOE和∠COF都与∠COE互余,根据同角的余角相等得:∠AOE=∠COF,同理可得出:∠COE=∠BOF.【解析】根据已知得出∠AOE和∠COF都与∠COE互余,进而得出∠AOE=∠COF,即可得出:∠COE=∠BOF.12.【答案】解:∵∠AOC=75°,∠BOC=30°,∴∠AOB=∠AOC-∠BOC=75°-30°=45°,又∵∠BOD=75°,∴∠AOD=∠AOB+∠BOD=45°+75°=120°.故答案为120°.【解析】根据∠AOC=∠BOD=75°,∠BOC=30°,利用角的和差关系先求出∠AOB的度数,再求∠AOD.。
人教版七年级上册数学 角度的计算专题解析及训练(word版,有答案)

专题6 角一、单选题1.(新人教版数学七年级上册第四章几何图形初步4.3.2《角的比较与运算》课时练习)如图所示,从点O出发的5条射线,可以组成的角的个数是().A. 4B. 6C. 8D. 10【答案】D2.北京时间上午8:30时,时钟上时针和分针之间的夹角(小于平角)是()A. 85°B. 75°C. 70°D. 60°【答案】B【解析】在钟面上,被12小时划分为12大格,每1大格对应的度数是30度,上午8:30的时候,时针指向8时和9时的中间位置,分针指向6时,两针之间刚好间隔2.5格,∴8:30时,时针和分针之间的夹角为:30° 2.5=75°.3.如图,下列说法错误的是()A. OA的方向是北偏东40°B. OB的方向是北偏西75°C. OC的方向是西南方向D. OD的方向是南偏东40°【答案】A【解析】A选项中,由图可知“OA的方向是北偏东50°”,所以本选项说法错误;B选项中,由图可知:“OB的方向是北偏西75°”是正确的;C选项中,由图可知;“OC的方向是西南方向”是正确的;D选项中,由图可知:“OD的方向是南偏东40°”是正确的;故选A.4.下列说法正确的是()A. A在B的南偏东30°的方向上,则B也在A的南偏东30°的方向上;B. A在B的南偏东30°的方向上,则B在A的南偏东60°的方向上;C. A在B的南偏东30°的方向上,则B在A的北偏西30°的方向上;D. A在B的南偏东30°的方向上,则B在A的北偏西60°的方向上【答案】C5.(北师大版数学七年级上册第四章基本平面图形4.3角同步测试题)一个角是70°18′,则这个角等于()A. 70.18° B. 70.3° C. 70.018° D. 70.03°【答案】B【解析】70°18′=70°+18′ 60=70°+0.3°=70.3°.故选B.6.如图,射线OC,OD分别在∠AOB的内部、外部,下列结论错误的是()A. ∠AOB<∠AODB. ∠BOC<∠AOBC. ∠COD>∠AODD. ∠AOB>∠AOC【答案】C【解析】观察图形可知:A.∠AOB<∠AOD正确;B.∠BOC<∠AOB正确;C.∠COD>∠AOD错误;D.∠AOB>∠AOC正确.故选C.7.(新人教版数学七年级上册第四章几何图形初步4.3.2《角的比较与运算》课时练)下列语句中,正确的是().A. 比直角大的角钝角; B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角【答案】C8.(新人教版数学七年级上册第四章几何图形初步4.3.1《角》课时练习)已知α 、β都是钝角,甲、乙、丙、丁四个同学的计算16(α +β)的结果依次为28°、48°、60°、88°,其中只有一个同学计算结果是正确的,则得到正确结果的同学是()A. 甲B. 乙C. 丙D. 丁【答案】B【解析】甲、乙、丙、丁四个同学的计算16(α +β)的结果依次为28°、48°、60°、88°,那么这四个同学计算α+β的结果依次为168°、288°、360°、528°,又因为两个钝角的和应大于180°且小于360°,所以只有乙同学的计算正确,故选B.9.(山东省东昌府区梁水镇中心中学2016-2017学年七年级下学期期中考试数学试题)如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是()A. ∠AOB>∠DOCB. ∠AOB<∠DOCC. ∠AOB=∠DOCD. 无法比较【答案】C【解析】∵∠AOC=∠BOD,∴∠AOC-∠BOC=∠BOD-∠BOC,∴∠AOB=∠DOC.故选C.10.如图,OB、OC是∠AOD的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,则表示∠AOD的代数式为( )。
人教版七年级数学《角度换算》计算题专项练习(含答案)

人教版七年级数学《角度换算》计算题专项练习(含答案)人教版七年级数学《角度换算》计算题专项练1.计算:13°58′+28°37′×2.解答】13°58′+28°37′×2=13°58′+57°14′=71°12′.2.计算(结果用度、分、秒表示):22°18′20″×5﹣28°52′46″.解答】22°18'20''×5﹣28°52'46''=110°90'100''﹣28°52'46''=82°38'54''.3.计算:1)90°﹣36°12'15″2)32°17'53“+42°42'7″3)25°12'35“×5;4)53°÷6.解答】(1)90°﹣36°12'15″=53°′45″;2)32°17'53“+42°42'7″=74°59′60″=75°;3)25°12'35“×5=125°60′175″=126°2′55″;4)53°÷6=8°50′.5.计算:1)27°26′+53°48′2)90°﹣79°18′6″.解答】(1)27°26′+53°48′=81°14′;2)90°﹣79°18′6″=10°41′54″.6.计算1)25°34′48″﹣15°26′37″2)105°18′48″+35.285°.解答】(1)25°34′48″﹣15°26′37″=10°8′11″;2)105°18′48″+35.285°=140°28′48″.7.计算:1)40°26′+30°30′30″÷6;2)13°53′×3﹣32°5′31″.解答】(1)40°26′+30°30′30″÷6=45°31′;2)13°53′×3﹣32°5′31″=41°32′59″.8.计算:180°﹣48°39′40″.解答】180°﹣48°39′40″=131°20′20″.9.计算:26°21′30″+42°38′30″.解答】26°21′30″+42°38′30″=69°60′=70°.10.(1)180°﹣(34°55′+21°33′);2)(180°﹣91°31′24″)÷2.解答】(1)180°﹣(34°55′+21°33′)=123°12′;2)(180°﹣91°31′24″)÷2=44°14′18″.11.计算:72°35′÷2+18°33′×4.解答】72°35′÷2+18°33′×4=36°17′30″+74°12′=110°29′30″.12.计算:48°39′+67°41′.解答】48°39′+67°41′=116°20′.13.计算:18°20′32″+30°15′22″.解答】18°20′32″+30°15′22″=48°35′54″.14.计算:180°﹣22°18′×5.解答】180°﹣22°18′×5=67°30′.15.计算:56°31′+29°43′×6.解答】56°31′+29°43′×6=245°19′.16.计算:49°28′52″÷4.解答】49°28′52″÷4=12°22′13″.4.计算:(1) 27°26′+53°48′。
与角度有关的计算问题(35题提分练)(原卷版)—七年级数学上册(北师大版2024)

与角度有关的计算问题(解答题35题)(基础题&提升题&压轴题)题型一基础题1.(2023秋•同安区期末)如图,点O在直线AB上,∠BOC=20°,∠COD=90°,OE是∠BOD的角平分线,求∠COE的度数.2.(2023秋•吉安期末)如图,已知∠1:∠3:∠4=1:2:4,∠2=80°,求∠1、∠3、∠4的度数.3.(2023秋•西峡县期末)如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE 的度数.4.(2023秋•天心区期末)如图,O为直线AB上一点,OC平分∠AOD,∠AOC=60°,∠BOD=3∠DOE,求∠DOE的度数.5.(2023秋•泉港区期末)如图,∠COD=45°,∠BOD=13∠COD,OC是∠AOB的平分线,求∠AOD的度数.6.(2023秋•泸县校级期末)如图,OE是∠COA的平分线,∠AOB=∠COD.(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;(2)比较∠AOC和∠BOD7.(2023秋•南沙区期末)如图,将一副三角尺叠放在一起.三角尺ABC的三个角是45°,45°,90°,三角尺ADE的三个角是30°,60°,90°.(1)若∠CAE=58°,求∠BAE的度数;(2)若∠CAE=2∠BAD,求∠CAD的度数.8.(2023秋•大荔县期末)将一副直角三角板ABC和BDE的一个顶点B重合在一起,按如图所示方式摆放,其中∠ACB=∠DBE=90°,∠ABC=30°,三角板ABC在∠DBE内可任意转动.(1)以点B为顶点的所有锐角有 个.(2)求以点B9.(2023秋•九龙坡区校级期末)如图,∠AOB:∠BOC=1:4,OM平分∠AOB,∠BON:∠NOC=3:1,若∠MON=91°.(1)∠AOB ∠NOC(填“>”或“<”或“=”)(2)求∠AOC的度数.10.(2023秋•娄底期末)如图,点O在直线AB上,∠COD=60°,∠AOE=2∠DOE.(1)若∠BOD=60°,求∠COE的度数;(2)试猜想∠BOD和∠COE的数量关系,并说明理由.11.(2023秋•瑶海区校级期末)已知点O为直线AB上一点,∠MON=90°,在∠MON内部作射线OC,且OC恰好平分∠MOB.(1)若∠CON=20°,求∠AOM的度数;(2)若∠BON=2∠NOC,求∠AOM的度数.12.(2023秋•高安市期末)如图,已知∠AOB=80°,OC是∠AOB的平分线,OD是∠BOC的平分线.(1)求∠AOD的度数;(2)若∠COE=14∠COB,求∠的度数.题型二提升题13.(2023秋•福田区校级期末)如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.(1)求∠DOE的度数;(2)如果∠COD=65°,求∠AOE的度数;(3)如果∠COD:∠COE=3:2,求∠AOE的度数.14.(2023秋•慈溪市期末)如图,直角三角板DOE的直角顶点O在直线AB上,OD平分∠AOF.(1)比较∠EOF和∠EOB的大小,并说明理由;(2)若OF平分∠AOE,求∠的度数.15.(2023秋•武昌区期末)已知∠AOB=50°,∠COD=20°.(1)如图1,若∠AOD=80°,∠COD在OB的左侧,则∠BOC= ;(2)如图2,OP平分∠AOD,OQ平分∠BOC,求∠POQ.16.(2023秋•无为市期末)利用折纸可以作出角平分线,如图1折叠,则OC为∠AOB的平分线,如图2、图3,折叠长方形纸片,OC,OD均是折痕,折叠后,点A落在点A',点B落在点B',连接OA′.(1)如图2,若点B'恰好落在OA′上,且∠AOC=32°,则∠BOD= ;(2)如图3,当点B'在∠COA'的内部时,连接OB′,若∠AOC=44°,∠BOD=61°,求∠A'OB'的度数.17.(2023秋•彭水县期末)已知∠AOB内部有三条射线OD,OC,OE且在同一个平面内,∠AOC=2∠BOC,射线OD始终在射线OE的上方,∠AOB=108°,∠DOE=36°.(1)如图1,当OE平分∠BOC时,求∠AOD的度数;(2)如图2,若∠AOD=5∠COE时,求∠BOE的度数.18.(2023秋•沙坪坝区校级期末)如图1,已知∠AOC=160°,OB是∠AOC内的射线,且∠AOB=3 5∠BOC,射线OD、OE将∠AOC分割,使得∠AOD:∠BOD:∠COE=1:2:3.(1)求∠DOE.(2)如图2,作∠BOD,∠EOC的平分线OM,ON.求∠MON的值.19.(2023秋•渝北区期末)OC ,OD ,OE 在∠AOB 内,∠AOC =2∠BOC ,∠AOB =108°,∠DOE =66°.(1)如图1,当OE 为∠BOC 的角平分线时,求∠AOD 的度数;(2)如图2,当∠AOD =53∠COE ,求∠BOE 的度数.20.(2023秋•汉中期末)如图,已知∠AOB =120°,从∠AOB 的顶点O 引出一条射线OC ,射线OC 在∠AOB 的内部,将射线OC 绕点O 逆时针旋转到OD ,且∠COD =60°.(1)如图①,若∠AOD =90°,试判断∠AOC 与∠BOD 之间的大小关系并说明理由;(2)如图②,作射线OE ,射线OE 为∠AOD 的平分线,设∠AOC =α,当0°<α<60°时,若射线OC 恰好平分∠AOE ,求∠BOD 的度数.21.(2023秋•宿豫区期末)已知,将一副三角板的直角顶点O按如图所式叠放在一起.(1)若∠BOD=55°,则∠BOC= ,∠BOC ∠AOD(填>、<、=);(2)①若∠BOD=50°,则∠AOC= ;若∠AOC=120°,则∠BOD= ;②猜想∠BOD与∠AOC之间的数量关系,并说明理由.22.(2023秋•庄河市期末)如图,点O为直线上AB一点,∠COD=90°,∠BOD=18°,若OE是∠BOC 的平分线,(1)求∠BOE的度数;(2)若点F是平面内一点,连接射线OF,且∠AOF=13∠AOC,求∠COF的度数.23.(2023秋•黄陂区校级期末)将三角板COD的直角顶点O放置在直线AB上.(1)如图,且∠AOC=40°射线OE平分∠BOC,则∠BOE的大小为 ;(2)在(1)的条件下,射线OE平分∠BOC,射线OF平分∠BOD,求∠EOF的度数;(3)若将三角板COD绕点O旋转,射线OE平分∠BOC,射线OF平分∠BOD.请写出∠COD与∠EOF 度数的等量关系: .题型二压轴题24.(2023秋•斗门区期末)如图①,OC是∠AOE内部的一条射线,OB、OD分别平分∠AOC,∠EOC.(1)若∠AOE=140°,∠COD=30°,求∠BOC= ;(2)∠AOE与∠BOD的大小有什么关系,写出你的结论并说明理由.(3)如图②,如果OC是∠AOE外部的一条射线,OB、OD分别平分∠AOC,∠EOC.那么(2)中∠AOE与∠BOD的大小关系还成立吗?请说明理由.25.(2023秋•海陵区校级期末)已知∠AOB=2∠COD=140°,OE平分∠AOD.(1)如图①,若∠COE=10°,求∠AOC的度数;(2)将∠COD绕顶点O按逆时针方向旋转至如图②的位置,∠BOD和∠COE有怎样的数量关系?请说明理由;(3)将∠COD绕顶点O按逆时针方向旋转至如图③的位置,(2)中的关系是否成立?请说明理由.26.(2023秋•思明区校级期末)如图,点M,O,N在同一条直线上,将一直角三角板的60°锐角顶点放在点O处,一边OA在射线OM上,另一边OB在直线MN的上方.OC平分∠BON,OD平分∠CON.(1)求∠BOD的度数;(2)把三角板绕点O沿逆时针方向旋转,当OB转到射线OM上时停止,若在旋转过程中,∠AOM=(x﹣120)°,同时在∠BOC内部有一条射线OE,使得∠BOE=(34x―90)°,试探究在旋转过程中,射线OE始终是哪个角的平分线?27.(2023秋•宝安区期末)将一副三角板如图1放置(∠AOB=90°,∠A=45°,∠OCD=90°,∠COD =30°),在∠BOD、∠AOC(∠BOD≤180°、∠AOC≤180°)内作射线OM、ON,且∠MOB=2∠DOM,∠NOA=2∠NOC,将三角板OCD绕着点O顺时针旋转.(1)如图1,当点O、A、C在一条直线上时,∠MON= ;(2)如图2,若旋转角为α(0°<α<90°),∠MON的度数是否会发生改变?若不变,求其值;若变化,说明理由.(3)如图3,当三角板OCD旋转到∠AOB内部时,求∠MON的值.28.(2024•两江新区校级开学)将一副三角板的两个锐角顶点重合,∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD(1)如图①所示,当OB与OC重合时,则∠MON的大小为 ;(2)当∠COD绕着点O旋转至如图②所示,当∠BOC=14°,则∠MON的大小为多少?(3)当∠COD绕着点O旋转至如图③所示,当∠BOC=α时,求∠MON的大小.29.(2023秋•于洪区期末)【提出问题】已知点O是直线AB上一点,∠COD=90°,射线OE是∠AOD的平分线.(1)如图1,若∠BOD=110°,求∠COE的度数.请补充完成下列解答过程:解:∵∠AOB=180°,∠BOD=110°,∴∠AOD= °.∵∠COD=90°,∴∠AOC=∠COD﹣∠AOD= °.∵OE是∠AOD的平分线,∴∠AOE= ∠AOD= °.∴∠COE=∠AOC+ = °.【类比分析】(2)如图2,设∠COE=α,求∠BOD的度数(用含α的代数式表示).【变式探索】(3)如图3,若3∠COE﹣2∠BOD=78°,求∠COE的度数.30.(2023秋•渑池县期末)如图.已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB.(1)在图①中.若∠AOC=40°,则∠BOC= °.∠NOB= °;(2)在图①中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);(3)在图①中,当∠AOB绕着点O顺时针转动到如图②的位置时,(2)中α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.31.(2023秋•青岛期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.(1)如图1,当∠AOB是直角,∠BOC=60°时,求∠MON的度数是多少?(2)如图2,当∠AOB=α,∠BOC=60°时,尝试发现∠MON与α的数量关系.(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON与α、β有数量关系吗?直接写出结论即可.32.(2024春•高青县期末)【实践活动】如图1,将一副三角板的直角顶点重合摆放.(1)∠ACE与∠BCD的大小关系是∠ACE ∠BCD.(填“>”“=”或“<”)(2)∠ACB与∠DCE之间的数量关系是 .【拓展探究】(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.33.(2023秋•和平区校级期末)已知∠AOB=120°,从∠AOB的顶点O引出一条射线OC,射线OC在∠AOB的内部,将射线OC绕点O逆时针旋转60°形成∠COD.(1)如图1,若∠AOD=90°,比较∠AOC和∠BOD的大小,并说明理由;(2)作射线OE,射线OE为∠AOD的平分线,设∠AOC=α.①如图2,当0°<α<60°,若射线OC恰好平分∠AOE,求∠BOD的度数;②当α≠60°时,请探究∠EOC与∠BOD之间的数量关系.34.(2023秋•山西期末)综合与探究特例感知:(1)如图1.线段AB=16cm,C为线段AB上的一个动点,点D,E分别是AC,BC的中点.①若AC=4cm,则线段DE的长为 cm.②设AC=a cm,则线段DE的长为 cm.知识迁移:(2)我们发现角的很多规律和线段一样,如图2,若∠AOB=120°,OC是∠AOB内部的一条射线,射线OM平分∠AOC,射线ON平分∠BOC,求∠MON的度数.拓展探究:(3)已知∠COD在∠AOB内的位置如图3所示,∠AOB=α,∠COD=30°,且∠DOM=2∠AOM,∠CON=2∠BON,求∠MON的度数.(用含α的代数式表示)35.(2023秋•青羊区校级期末)如图所示,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=30°,求∠DOE的度数.(2)在图1中,若∠AOC=α,直接写出∠DOE的度数: (用含α的代数式表示).(3)将图1中的∠COD绕顶点O顺时针开始旋转.①当∠COD旋转至如图2的位置时,请探究∠AOD与∠BOE的度数之间的关系,写出你的结论,并说明理由;②过点O的一条射线OF,使得OC恰好平分∠BOF,在图1和图2中分别探究∠AOF与∠DOE的度数之间的关系,请直接写出结论.。
