2017年江苏省中考数学真题《圆》专题汇编(解)
2017江苏中考数学试题及答案

2017江苏中考数学试题及答案一、选择题1. (2017江苏中考数学试题) 在(a+2b)(3a-b)的展开式中,a与b的系数之和为________。
A. 2B. 4C. 6D. 8解析:展开后的表达式为3a^2 - 5ab + 2b^2,a与b的系数之和为3 - 5 = -2。
答案:选项A. 22. (2017江苏中考数学试题) 设a:b=2:3,且a:b=3:4,则a:b=:________。
A. 6:7B. 2:3C. 1:1D. 4:9解析:由已知条件得到a:b=6:9,a:b: = 6:9:4。
答案:选项D. 4:9二、填空题3. (2017江苏中考数学试题) 扇形的周长为20π cm,半径为________cm。
解析:周长等于半径乘以圆周率的两倍,所以半径=10cm。
答案:104. (2017江苏中考数学试题) 在△ABC中,已知∠A=40°,AB=6 cm,BC=8 cm,CD是BC的平分线,求BD的长度。
解析:由平分线定理可知BD:DC=AB:AC,代入已知条件求解得BD=4 cm。
答案:4三、解答题5. (2017江苏中考数学试题) 已知点A(1, -2)、B(-3, 4),求线段AB的中点坐标。
解析:线段的中点坐标等于两个端点坐标的x坐标和y坐标分别取平均值,所以中点坐标为((-3+1)/2, (4-2)/2) = (-1, 1)。
答案:(-1, 1)6. (2017江苏中考数学试题) 某公司以一件货物的进价520元售出,若利润率为25%,则售价是多少?解析:利润率等于利润除以进价的百分数,利润率为25%,则利润为520元乘以25% = 130元。
售价等于进价加上利润,所以售价为520元 + 130元 = 650元。
答案:650综上所述,2017江苏中考数学试题的部分题目及答案如上所示。
这些题目涵盖了选择题、填空题和解答题,通过解析和计算可以得出正确的答案。
在中考数学考试中,熟练掌握各类题型的解题技巧是提高得分的关键。
2017江苏中考数学试题及答案

2017江苏中考数学试题及答案一、选择题(每题3分,共30分)1. 下列各数中,最小的数是()A. -3B. 0C. 1D. 2答案:A2. 一个数的平方根是2,那么这个数是()A. 4B. -4C. 2D. -2答案:A3. 一个等腰三角形的两边长分别为3和5,那么这个三角形的周长是()A. 11B. 13C. 14D. 16答案:C4. 下列各数中,是无理数的是()A. 0.5B. πC. √2D. 0.33333答案:C5. 已知一个数列的前三项为1,2,3,那么这个数列的通项公式是()A. nB. n+1C. n^2D. n(n+1)/2答案:D6. 一个圆的半径为3,那么它的面积是()A. 9πB. 18πC. 27πD. 36π答案:C7. 函数y=2x+3的图象与x轴的交点坐标是()A. (-3/2, 0)B. (3/2, 0)C. (-1.5, 0)D. (1.5, 0)答案:B8. 已知一个二次函数的顶点坐标为(1, -2),且开口向上,那么它的解析式是()A. y=(x-1)^2-2B. y=(x+1)^2-2C. y=-(x-1)^2-2D. y=-(x+1)^2-2答案:A9. 一个正方体的体积为8cm³,那么它的表面积是()A. 16cm²B. 24cm²C. 32cm²D. 64cm²答案:B10. 已知一个等差数列的前四项为2,5,8,11,那么它的公差是()A. 3B. 4C. 5D. 6答案:A二、填空题(每题3分,共15分)1. 一个数的立方根是3,那么这个数是______。
答案:272. 一个直角三角形的两条直角边长分别为3和4,那么它的斜边长是______。
答案:53. 一个数的绝对值是5,那么这个数可以是______或______。
答案:5 或 -54. 一个函数的图象经过点(2, 3),那么这个函数的解析式可以是y=kx+b,其中k=______,b=______。
江苏省苏州市2017年中考数学试题(解析版)

第Ⅰ卷(共30分)一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.()217-÷的结果是 A .3B .3-C .13D .13- 【答案】B. 【解析】试题分析:()217-÷2137=-=-故答案选B. 考点:有理数的除法.2.有一组数据:2,5,5,6,7,这组数据的平均数为 A .3B .4C .5D .6 【答案】C.考点:平均数的求法3.小亮用天平称得一个罐头的质量为2.026kg ,用四舍五入法将2.026精确到0.01的近似值为 A .2B .2.0C .2.02D .2.03 【答案】D. 【解析】试题分析:2.026 2.03≈故答案选D. 考点:近似数4.关于x 的一元二次方程220x x k -+=有两个相等的实数根,则k 的值为 A .1B .1- C.2D .2- 【答案】A.【解析】试题分析:=4401k k ∆-=⇒=故答案选A. 考点:根的判别式的性质.5.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有2400名学生中随机征求了100名学生的意见,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为 A .70B .720C.1680D .2370 【答案】C. 【解析】 试题分析:702400=1680100⨯故答案选C. 考点:用样本估计总体的统计思想.6.若点(),m n A 在一次函数3y x b =+的图像上,且32m n ->,则b 的取值范围为 A .2b >B .2b >- C.2b <D .2b <- 【答案】D.考点:一次函数上的点的特征.7.如图,在正五边形CD AB E 中,连接BE ,则∠ABE 的度数为 A .30B .36C.54D .72【答案】B. 【解析】试题分析:∠ABE =3601=3652︒⨯︒故答案选B. 考点:多边形的外角,等腰三角形的两底角相等8.若二次函数21y ax =+的图像经过点()2,0-,则关于x 的方程()2210a x -+=的实数根为 A .10x =,24x =B .12x =-,26x = C.132x =,252x =D .14x =-,20x = 【答案】A.考点:一元二次方程的解法9.如图,在Rt C ∆AB 中,C 90∠A B =,56∠A =.以C B 为直径的O 交AB 于点D ,E 是O 上一点,且C CD E =,连接OE ,过点E 作F E ⊥OE ,交C A 的延长线于点F ,则F ∠的度数为 A .92B .108C.112D .124【答案】C. 【解析】 试题分析:C 90∠A B =,56∠A =,34B ∴∠=︒1C CD 682B CBD COE E =∴∠=∠=∠=︒,112F ∴∠=︒故答案选C.考点:圆心角与圆周角的关系.10.如图,在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点.过点F 作F D E ⊥A ,垂足为E .将F ∆AE 沿点A 到点B 的方向平移,得到F '''∆A E .设P 、'P 分别是F E 、F ''E 的中点,当点'A 与点B 重合时,四边形CD 'PP 的面积为A .283B .243C.323D .3238-【答案】A.7382832S ∴=⨯= L K H故答案选A.考点:平行四边形的面积,三角函数.第Ⅱ卷(共100分)二、填空题(每题3分,满分24分,将答案填在答题纸上)11.计算:()22a= .【答案】4a . 【解析】 试题分析:()()()22224=aa a a=⋅.考点:幂的乘方的运算.12.如图,点D 在∠AOB 的平分线C O 上,点E 在OA 上,D//E OB ,125∠=,则D ∠AE 的度数为 .【答案】50.考点:平行线的性质,外角的性质.13.某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知,11名成员射击成绩的中位数是 环.【答案】8. 【解析】试题分析:先按照从小到大的顺序排列,11个数据的中位数由第6个数据决定,故中位数是8. 考点:中位数的求法.14.因式分解:2441a a -+= . 【答案】2(21)a -.考点:公式法因式分解.15.如图,在“33⨯”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是 .【答案】13. 【解析】试题分析:有6种等可能的结果,符合条件的只有2种,则完成的图案为轴对称图案的概率是13. 21.考点:轴对称图形的定义,求某个事件的概率. 16.如图,AB 是O 的直径,C A 是弦,C 3A =,C 2C ∠BO =∠AO .若用扇形C OA (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .【答案】12考点:圆锥的侧面展开图的弧长等于地面圆的周长.17.如图,在一笔直的沿湖道路l 上有A 、B 两个游船码头,观光岛屿C 在码头A 北偏东60的方向,在码头B 北偏西45的方向,C 4A =km .游客小张准备从观光岛屿C 乘船沿C A 回到码头A 或沿C B 回到码头B ,设开往码头A 、B 的游船速度分别为1v 、2v ,若回到A 、B 所用时间相等,则12v v = (结果保留根号).【答案】2.D.考点:特殊角三角函数的应用.18.如图,在矩形CD AB 中,将C ∠AB 绕点A 按逆时针方向旋转一定角度后,C B 的对应边C ''B 交CD 边于点G .连接'BB 、CC ',若D 7A =,CG 4=,G ''AB =B ,则CC '='BB (结果保留根号).【答案】745.考点:旋转的性质,勾股定理.三、解答题(本大题共10小题,共76分.解答应写出文字说明、证明过程或演算步骤.)19.(本题满分5分) 计算:()0143π-+--. 【答案】2 【解析】试题分析:先算绝对值、算术平方根、0次幂. 试题解析:原式1212=+-=. 考点:实数的运算. 20.(本题满分5分)解不等式组:()142136x x x +≥⎧⎪⎨->-⎪⎩.【答案】34x ≤<考点:一元一次不等式组的解法 21.(本题满分6分)先化简,再求值:259123x x x -⎛⎫-÷⎪++⎝⎭,其中32x =-. 【答案】12x +,33【解析】试题分析:先将括号里面进行通分,各分子、分母因式分解,再约分.试题解析:原式()()()()333331232332x x x x x x x x x x x -+--+=÷=⋅=++++-+.当32x =-时, 原式11333223===-+. 考点:分式的化简求值.22.(本题满分6分)某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y (元)是行李质量x (kg )的一次函数.已知行李质量为20kg 时需付行李费2元,行李质量为50kg 时需付行李费8元.(1)当行李的质量x 超过规定时,求y 与x 之间的函数表达式; (2)求旅客最多可免费携带行李的质量. 【答案】(1)求y 与x 之间的函数表达式为125y x =-;(2)10 【解析】试题分析:(1)用待定系数法求一次函数的表达式;(2)旅客最多可免费携带行李的质量就是0y =时x 的值.(2)当0y =时,1205x -=,得10x =. 答:旅客最多可免费携带行李10kg .考点:一次函数的实际应用23.(本题满分8分)初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.根据以上信息解决下列问题:(1)m = ,n = ;(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ;(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率. 【答案】(1)8,3m n ==;(2)144;(3)23【解析】试题分析:(1)利用航模小组先求出数据总数,再求出n.(2)小组所占圆心角=该组频数数据总数360⨯︒;(3)列表格求概率.试题解析:(1)8,3m n ==; (2)144;(3)将选航模项目的2名男生编上号码1,2,将2名女生编上号码3,4.用表格列出所有可能出现的结果:由表格可知,共有12种可能出现的结果,并且它们都是第可能的,其中“1名男生、1名女生”有8种可能.P ∴(1名男生、1名女生)82123==.(如用树状图,酌情相应给分) 考点:统计与概率的综合运用.24.(本题满分8分)如图,∠A =∠B ,AE =BE ,点D 在C A 边上,12∠=∠,AE 和D B 相交于点O . (1)求证:C ∆AE ≌D ∆BE ; (2)若142∠=,求D ∠B E 的度数.【答案】(1)详见解析;(2)69BDE ∠=考点:全等三角形的判定与性质25.(本题满分8分)如图,在C ∆AB 中,C C A =B ,x AB ⊥轴,垂足为A .反比例函数ky x=(0x >)的图像经过点C ,交AB 于点D .已知4AB =,5C 2B =. (1)若4OA =,求k 的值;(2)连接C O ,若D C B =B ,求C O 的长.【答案】(1)5k =(2)972OC = 【解析】试题分析:(1)利用勾股定理,先求出C 的坐标,再代入反比例函数即可.(2)利用勾股定理,求OC 的长度.试题解析:(1)作CE AB ⊥,垂足为,,4E AC BC AB ==,2AE BE ∴==.在Rt ∆BCE 中,53,2,22BC BE CE ==∴=,4,OA C =∴点的坐标为5,22⎛⎫⎪⎝⎭,点C 在k y x =的图象上,5k ∴=.考点:反比例函数与三角形的综合运用.26.(本题满分10分)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A 出发,在矩形CD AB 边上沿着C D A →B →→的方向匀速移动,到达点D 时停止移动.已知机器人的速度为1个单位长度/s ,移动至拐角处调整方向需要1s (即在B 、C 处拐弯时分别用时1s ).设机器人所用时间为()s t 时,其所在位置用点P 表示,P 到对角线D B 的距离(即垂线段Q P 的长)为d 个单位长度,其中d 与t 的函数图像如图②所示. (1)求AB 、C B 的长;(2)如图②,点M 、N 分别在线段F E 、G H 上,线段MN 平行于横轴,M 、N 的横坐标分别为1t 、2t .设机器人用了()1s t 到达点1P 处,用了()2s t 到达点2P 处(见图①).若12C C 7P +P =,求1t 、2t 的值.【答案】(1)AB=8,BC=6;(2)1212,20.t t == 【解析】试题分析:(1)利用勾股定理求出BT,再利用正切值求出BC ;(2)平行线分线段成比例定理列出方程,求解.(2)在图①中,连接12.PP 过12,P P 分别作BD 的垂线,垂足为12,.Q Q 则1122PQ PQ . 在图②中,线段MN 平行于横轴,12,d d ∴=即1122PQ PQ =.1212..CP CP PP BD CB CD∴∴= 即12.68CP CP =又12127,3, 4.CP CP CP CP +=∴==设,M N 的横坐标分别为12,t t ,由题意得, 11221215,16,12,20.CP t CP t t t =-=-∴==考点:三角函数的应用,平行线分线段成比例定理. 27.(本题满分10分)如图,已知C ∆AB 内接于O ,AB 是直径,点D 在O 上,D//C O B ,过点D 作D E ⊥AB ,垂足为E ,连接CD 交OE 边于点F .(1)求证:D ∆OE ∽C ∆AB ; (2)求证:DF D ∠O =∠B E ;(3)连接C O ,设D ∆OE 的面积为1S ,四边形C D B O 的面积为2S ,若1227S S =,求sin A 的值.【答案】(1)详见解析;(2)详见解析;(3)2sin 3A = 【解析】试题分析:(1)利用两角对应相等,两三角形相似证明;(2)相似三角形对应角相等,同弧所对的圆周角相等;(3)转化角度,放在直角三角形求正弦值.(3)21,4DOE ABC S OD DOEABC S AB ∆∆⎛⎫∆∆∴== ⎪⎝⎭,即144ABC DOE S S S ∆∆==,OA OB =,12BOC ABC S S ∆∆∴=,即12B O CS S ∆=.121122,27BOC DOE DBE DBE S S S S S S S S S ∆∆∆∆==++=++,112DBE S S ∆∴=,12BE OE ∴=,即222,sin sin 333OE OE OB OD A ODE OD ==∴=∠== 考点:圆、三角函数、相似三角形的综合运用.28.(本题满分10分)如图,二次函数2y x bx c =++的图像与x 轴交于A 、B 两点,与y 轴交于点C ,C OB =O .点D 在函数图像上,CD//x 轴,且CD 2=,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求b 、c 的值;(2)如图①,连接BE ,线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上,求点F 的坐标; (3)如图②,动点P 在线段OB 上,过点P 作x 轴的垂线分别与C B 交于点M ,与抛物线交于点N .试问:抛物线上是否存在点Q ,使得Q ∆P N 与∆APM 的面积相等,且线段Q N 的长度最小?如果存在,求出点Q 的坐标;如果不存在,说明理由.【答案】(1)2b =-, 3.c =-;(2)点F 的坐标为()0,2-;(3)点Q 的坐标为115,24⎛⎫- ⎪⎝⎭和315,.24⎛⎫- ⎪⎝⎭【解析】试题分析:(1)根据二次函数的对称轴公式,抛物线上的点代入,即可;(2)先求F 的对称点,代入直线BE ,即可;(3)构造新的二次函数,利用其性质求极值.21世纪教育网(2)设点F 的坐标为()0,.m 对称轴为直线1,l x =∴:点F 关于直线l 的对称点F 的坐标为()2,m .直线BE 经过点()()3,0,1,4,B E -∴利用待定系数法可得直线BE 的表达式为26y x =-. 因为点F 在BE 上,∴2262,m =⨯-=-即点F 的坐标为()0,2.-(3)存在点Q 满足题意.设点P 坐标为(),0n ,则21,3,2 3.PA n PB PM n PN n n =+==-=-++作,QR PN ⊥垂足为,R ()()()211,1323,22PQN APM S S n n n n QR ∆∆=∴+-=-++ 1.QR ∴= ①点Q 在直线PN 的左侧时,Q 点的坐标为()21,4,n n n R --点的坐标为()2,4,n n n N -点的坐标为()2,23.n nn --∴在Rt QRN ∆中,()223123,2NQ n n =+-∴=时,NQ 取最小值1.此时Q 点的坐标为115,.24⎛⎫- ⎪⎝⎭考点:二次函数的综合运用.。
2017年中考数学试卷汇编——圆(带答案)

2017年中考数学试卷汇编——圆(带答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学试卷汇编——圆(带答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学试卷汇编——圆(带答案)(word版可编辑修改)的全部内容。
圆的有关性质一、选择题1.(2016·山东省滨州市·3分)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD 分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤【考点】圆的综合题.【分析】①由直径所对圆周角是直角,②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,③由平行线得到∠OCB=∠DBC,再由圆的性质得到结论判断出∠OBC=∠DBC;④用半径垂直于不是直径的弦,必平分弦;⑤用三角形的中位线得到结论;⑥得不到△CEF和△BED中对应相等的边,所以不一定全等.【解答】解:①、∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,∴∠AOC≠∠AEC,③、∵OC∥BD,∴∠OCB=∠DBC,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠DBC,∴CB平分∠ABD,④、∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,∵OC∥BD,∴∠AFO=90°,∵点O为圆心,∴AF=DF,⑤、由④有,AF=DF,∵点O为AB中点,∴OF是△ABD的中位线,∴BD=2OF,⑥∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,故选D【点评】此题是圆综合题,主要考查了圆的性质,平行线的性质,角平分线的性质,解本题的关键是熟练掌握圆的性质.2.(2016·山东省德州市·3分)《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?"( )A.3步B.5步C.6步D.8步【考点】三角形的内切圆与内心.【专题】圆的有关概念及性质.【分析】根据勾股定理求出直角三角形的斜边,即可确定出内切圆半径.【解答】解:根据勾股定理得:斜边为=17,则该直角三角形能容纳的圆形(内切圆)半径r==3(步),即直径为6步,故选C【点评】此题考查了三角形的内切圆与内心,Rt△ABC,三边长为a,b,c(斜边),其内切圆半径r=.(2016·山东省济宁市·3分)如图,在⊙O中, =,∠AOB=40°,则∠ADC的度数是( )3.A.40°B.30°C.20°D.15°【考点】圆心角、弧、弦的关系.【分析】先由圆心角、弧、弦的关系求出∠AOC=∠AOB=50°,再由圆周角定理即可得出结论.【解答】解:∵在⊙O中, =,∴∠AOC=∠AOB,∵∠AOB=40°,∴∠AOC=40°,∴∠ADC=∠AOC=20°,故选C.4. (2016·云南省昆明市·4分)如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O 于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )A.EF∥CD B.△COB是等边三角形C.CG=DG D.的长为π【考点】弧长的计算;切线的性质.【分析】根据切线的性质定理和垂径定理判断A;根据等边三角形的判定定理判断B;根据垂径定理判断C;利用弧长公式计算出的长判断D.【解答】解:∵AB为⊙O的直径,EF切⊙O于点B,∴AB⊥EF,又AB⊥CD,∴EF∥CD,A正确;∵AB⊥弦CD,∴=,∴∠COB=2∠A=60°,又OC=OD,∴△COB是等边三角形,B正确;∵AB⊥弦CD,∴CG=DG,C正确;的长为: =π,D错误,故选:D.5。
2017江苏中考数学试题及答案

2017江苏中考数学试题及答案2017年江苏中考数学试题及答案一、选择题(本题共10小题,每小题3分,共30分)1. 以下哪个数是无理数?A. 2B. √2C. 0.33333…D. π答案:B2. 已知函数y=x^2+2x+1,该函数的顶点坐标为:A. (-1, 0)B. (1, 0)C. (-1, 2)D. (1, 2)答案:C3. 若一个三角形的三边长分别为3、4、5,则该三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形答案:B4. 已知一个圆的半径为5,那么它的面积是:A. 25πB. 50πC. 75πD. 100π答案:C5. 以下哪个选项不是单项式?A. 3x^2B. 5xC. -2D. x/y答案:D6. 计算(3x^2-2x+1)-(2x^2-x+3)的结果是:A. x^2+x-2B. x^2-3x-2C. x^2-x-2D. x^2+x+2答案:C7. 若方程2x+3=7的解是x=2,则方程4x+6=14的解是:A. x=1B. x=2C. x=3D. x=4答案:C8. 已知一个扇形的圆心角为60°,半径为4,则该扇形的面积是:A. 4πB. 8πC. 12πD. 16π答案:A9. 以下哪个选项是二次函数?A. y=3x+2B. y=x^2+2x+1C. y=x^3-2x+3D. y=1/x答案:B10. 一个数的相反数是-5,那么这个数是:A. 5B. -5C. 0D. 1答案:A二、填空题(本题共5小题,每小题4分,共20分)11. 计算√16的结果是______。
答案:412. 已知一个正比例函数y=kx,当x=2时,y=4,则k的值是______。
答案:213. 一个等腰三角形的底角为45°,那么顶角的度数是______。
答案:90°14. 计算(2x+3)(x-1)的结果是______。
答案:2x^2+x-315. 一个数的绝对值是5,那么这个数可以是______。
2017江苏中考数学试题及答案

2017江苏中考数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正整数?A. -2B. 0C. 1.5D. 2答案:D2. 已知一个圆的半径为5cm,那么它的面积是多少平方厘米?A. 25πB. 50πC. 75πD. 100π答案:B3. 以下哪个函数是一次函数?A. y = x^2B. y = 2x + 3C. y = 1/xD. y = x^3答案:B4. 一个等腰三角形的底边长为6cm,腰长为8cm,那么它的周长是多少?A. 22cmB. 26cmC. 30cmD. 34cm答案:B5. 下列哪个数是无理数?A. 0.5B. √2C. 0.33333...D. 3答案:B6. 一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 10答案:A7. 以下哪个选项是不等式?A. 3x + 2 = 7B. 2x - 5 > 3C. 4y - 6 = 0D. 5z + 3 ≤ 8答案:B8. 一个长方体的长、宽、高分别为3cm、4cm、5cm,那么它的体积是多少立方厘米?A. 60B. 120C. 180D. 240答案:A9. 以下哪个选项是二次函数?A. y = x^2 + 2x + 1B. y = 3x + 2C. y = 1/x^2D. y = x^3 - 2x^2 + 3答案:A10. 一个数的绝对值是5,那么这个数可能是?A. 5B. -5C. 5或-5D. 0答案:C二、填空题(每题4分,共20分)11. 一个数的平方等于25,那么这个数是________。
答案:±512. 一个等差数列的首项是2,公差是3,那么它的第5项是________。
答案:1713. 一个直角三角形的两直角边长分别为3cm和4cm,那么它的斜边长是________。
答案:5cm14. 一个数的立方根是2,那么这个数是________。
答案:815. 一个扇形的圆心角是60°,半径是4cm,那么它的面积是________。
2017中考数学全国试题汇编------圆(含详细解析)

FhseFhee2017中考数学全国试题汇编-■■■■■圆24 (2017.北京)如图,AB是LI O的一条弦,LI O的切线交CE的延长线于点D .(1)求证:DB 二DE ;(2)若AB =12, BD =5,求LI O 的半径.【解析】E是AB的中点,过点E作EC_OA于点C ,过点B作试题分析:(1)由切线性质及等量代换推出/ 4=7 5,再利用等角对等边可得出结论;(2)由已知条件得出sin7 DEF和sin7 AOE的值,禾用对应角的三角函数值相等推出结论.试题解析:(1)证明:T DC 丄OA, A / 1 + 7 3=90°, v BD 为切线,二OB 丄BD, /-Z 2+7 5=90°, v OA=OB, •••7 1=7 2,v/ 3=7 4,A/ 4=7 5,在厶DEB中, 7 4=7 5,A DE=DB.⑵作DF丄AB 于F,连接OE, ・,.EF^-EE=3/在RTADEF中,EA3, DE=BD=5J EQ3 , J.f~nj jQ-F* 4Y彗一3 =斗——=-3「.在irrAAOE 中rDE5TAEh,二曲二二■ ■考点:圆的性质,切线定理,三角形相似,三角函数27 (2017甘肃白银)•如图,AN是L M的直径,NB//X轴, ~A OAB交L M于点C .(1)若点A 0,6 , N 0,2厂ABN =30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是L M的切线.解:(1)v A 的坐标为(0, 6), N (0, 2)••• AN=4, .............................................................................................................. 1 分vZ ABN=30°, / ANB=90°,••• AB=2AN=8, ...................................................................................................... 2分•••由勾股定理可知:NB=4..3 ,••• B ( 4 3 , 2) ....................................................... 3 分(2)连接MC , NC ........................................................................................... 4 分v AN是O M的直径,•••Z ACN=90°°•••Z NCB=90° ° ................................................................................................... 5 分在Rt A NCB中,D为NB的中点,1•CD= = N B=ND ,2•Z CND=Z NCD, .............................. 6 分v MC=MN ,•Z MCN=Z MNC.vZ MNC+Z CND=90°°• Z MCN+Z NCD=90° ° ...................... 7 分即MC I CD.•直线CD是。
江苏省中考数学真题《圆》专题汇编(解答题)
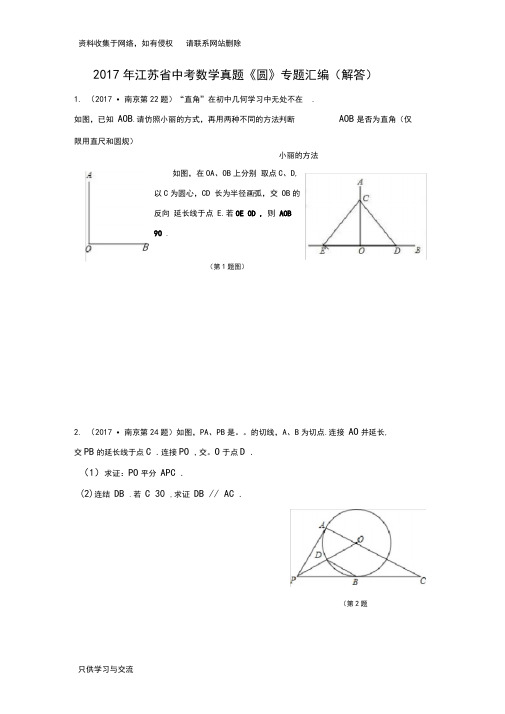
2017年江苏省中考数学真题《圆》专题汇编(解答)1.(2017 •南京第22题)“直角”在初中几何学习中无处不在.如图,已知AOB.请仿照小丽的方式,再用两种不同的方法判断AOB是否为直角(仅限用直尺和圆规)小丽的方法如图,在OA、OB上分别取点C、D,以C为圆心,CD 长为半径画弧,交OB的反向延长线于点E.若OE OD , 则AOB90 .B(第1题图)2.(2017 •南京第24题)如图,PA、PB是。
的切线,A、B为切点.连接AO并延长,交PB的延长线于点C .连接PO ,交。
O于点D .(1)求证:PO平分APC .(2)连结DB .若C 30 ,求证DB // AC .(第2题图)4. (2017 ・无锡第27题)如图,以原点 。
为圆心,3为半径的圆与 x 轴分别交于 A, B 两 点(点B 在点A 的右边),P 是半径OB 上一点,过 P 且垂直于AB 的直线与。
分别交于 C, D 两点(点 C 在点D 的上方),直线 AC, DB 交于点E.若AC: CE=1 : 2,求点P 的 坐标.3. (2017 ・无锡第24题)如图,已知等边△ ABC,要求作图(不要求写作法,但要保留作图痕迹):(1)作4ABC 的外心O;(2)设D 是AB 边上一点,在图中作出一个正六边形和AC 上.请用直尺(不带刻度)和圆规,按下列DEFGHI ,使点F,点H 分别在边 BC(第4题图)5. (2017 •常州第28题)如图,已知一次函数 y与y 轴、x 轴交于点A B.(1)求线段AB 的长度;(2)设点M 在射线AB 上,将点M 绕点A 按逆时针方向旋转 90°到点N ,以点N 为圆心, NA 的长为半径作e N .①当e N 与x 轴相切时,求点 M 的坐标;②在①的条件下,设直线 AN 与x 轴交于点C ,与e N 的另一个交点为 D ,连接MD 交x 轴于点E ,直线m 过点N 分别与y 轴、直线l 交于点P 、Q ,当 APQ 与 CDE 相似时, 求点P 的坐标.4-x 4的图像是直线l ,设直线l 分别 36. (2017 •苏州第27题)如图,已知△ ABC 内接于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年江苏省中考数学真题《圆》专题汇编(解答)
1.(2017·南京第22题)“直角”在初中几何学习中无处不在.如图,已知
AOB .请仿照小丽的方式,再用两种不同的方法判断AOB 是否为直角(仅
限用直尺和圆规).
2.(2017·南京第24题)如图,PA 、PB 是⊙O 的切线,A 、B 为切点.连接AO 并延长,
交PB 的延长线于点C .连接PO ,交⊙O 于点D .(1)求证:PO 平分APC .(2)连结DB .若
30C
,求证DB ∥AC .
小丽的方法
如图,在OA 、OB 上分别取点C 、D ,以C 为圆心,CD 长为半径画弧,交
OB 的反向
延长线于点 E.若OD OE ,
则
90AOB
.
(第1题图)
(第2题图)
3.(2017·无锡第24题)如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列
要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC 和AC上.
(第3题图)
4.(2017·无锡第27题)如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2,求点P的坐标.
(第4题图)
5.(2017·常州第28题)如图,已知一次函数
4
4
3
y x的图像是直线l,设直线l分别
与y轴、x轴交于点A B
、.
(1)求线段AB的长度;
(2)设点M在射线AB上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作N.
①当N与x轴相切时,求点M的坐标;
②在①的条件下,设直线AN与x轴交于点C,与N的另一个交点为D,连接MD交x 轴于点E,直线m过点N分别与y轴、直线l交于点P Q
、,当APQ与CDE相似时,求点P的坐标.
(第5题图)
6.(2017·苏州第27题)如图,已知△ABC 内接于⊙O ,AB 是直径,点D 在⊙O 上,OD ∥BC ,过点D 作DE ⊥AB ,垂足为E ,连接CD 交OE 边于点F .(1)求证:△DOE ∽△ABC ;(2)求证:∠ODF=∠BDE ;
(3)连接OC ,设△DOE 的面积为S 1,四边形BCOD 的面积为S 2,若7
22
1S S ,求sinA
的值.
7.(2017·南通第24题)如图,Rt △ABC 中,∠C=90°,BC=3,点O 在AB 上,OB=2,以OB 为半径的⊙O 与AC 相切于点D ,交BC 于点E ,求弦BE 的长.
(第6题图)
(第7题图)
8.(2017·淮安第25题)如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
(第8题图)
9.(2017·盐城第24题)如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
(第9题图)
10.(2017·盐城第25题)如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F 恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
(第10题图)
11.(2017·扬州第25题)如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.
(第11题图)
12.(2017·扬州第28题)如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O.
(1)若AP=1,则AE=;
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;
(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心
到AB边的距离的最大值.
(第12题图)。
