正态分布图作图指导-Normal distribution curve
正态分布

2、医学参考值范围的用途:
①作为诊断标准,划分正常与异常的界限; ②根据传染病传染期的长短确定该病患者的隔离期限,或根据潜伏期 长短确定接触者的留验期限。 ③制订卫生标准及有害物质的容许浓度,作为保护健康的安全界限。 ④制订不同性别、年龄儿童某项生长发育指标的等级标准。 ⑤在质量控制中制订各种控制限。
不变, 发生变化
不变, 发生变化
正态分布的特征
(4)正态分布在 处各有一个拐点。
凸
凹
凹
+
(5)正态曲线下的面积分布有一定规律。(见下文)
三、标准正态分布 (standard normal distribution)
1. 概念:均数为 0,方差为1的正态分布称为标准正态分布, 记为 N ( 0, 1 )。 2. 概率密度函数:
提 纲
• • • • • 正态分布的概念 正态分布的特征 标准正态分布 正态曲线下的面积分布规律 正态分布的应用
1.制定医学参考值范围 2.正态分布是许多统计方法的理论基础
一、正态分布的概念
1、定义:
若随机变量 x 的概率密度函数可以表示为:
f (x)
1
2
。
e
1 x 2 _ ( ) 2
则称x服从正态分布,记为 x ~N(,2),其中 x Biblioteka , 2、正态分布的图形
f(x)
x
二、正态分布的特征
(1)正态曲线(normal curve)在横轴上方均数处最高。 (2)正态分布以均数为中心,左右对称。 (3)正态分布有2个参数,即均数 和标准差。 是位置 参数,当 固定不变时, 越大,曲线沿横轴越向右移动; 反之, 越小,则曲线沿横轴越向左移动。 是形状参数 (亦称变异度参数),当 固定不变时, 越大,曲线越 平阔; 越小,曲线越尖峭。通常用N( , 2)表示均数为 ,方差为 的正态分布。 (4)正态分布在 处各有一个拐点。 (5)正态曲线下面积的分布有一定规律。
C++normal_distribution高斯正态分布函数的用法示例

C++normal_distribution⾼斯正态分布函数的⽤法⽰例图 1 显⽰的是正态(或⾼斯)分布。
它是⼀条连续的贝尔曲线,期望两边的值是相等的,可以理解为期望就是平均值。
它是⼀个概率分布,因此曲线下⽅的⾯积是1。
正态分布是由两个参数完全定义的:期望和标准差,它们是衡量期望两边的值如何分布的⼀种⽅式。
图 1 正态分布期望和标准差分别是⽤希腊字母 µ 和σ来表⽰的,变量 x 有 n 个样本,这些是由下⾯的公式定义的:因此,期望就是值的和除以值的个数⼀换句话说,也就是平均值。
可以通过值和期望的差值的平⽅⼦和除以 n-1,然后对结果开⽅来得到标准差。
对于不同的期望和标准差的值,正态分布的相对宽度和⾼度分布曲线的变化是相当⼤的。
但是,分布值总是如图 1 所⽰。
这意味着,如果知道⼀个符合正态分布的变量的期望和标准差,例如在⼤量⼈⼝中个体的⾝⾼,就可以知道95% 的⼈⾝⾼不超过期望的 2σ。
标准正态分布的期望为 0,标准差为 1。
uniform_distribution 模板定义了可以产⽣随机浮点值的分布对象类型,默认是 double 类型。
默认构造函数创建的是标准正态分布,因此期望是 0,⽅差是 1.0:std::normal_distribution<> dist; // mu: 0 sigma: 1下⾯展⽰了如何创建⼀个有特定值和标准差的正态分布:double mu {50.0}, sigma {10.0};std::normal_distribution<> norm {mu, sigma};这⾥定义了⼀个⽣成 double 值的分布对象,期望为 50.0,标准差是 10.0。
为了⽣成值,可以将⼀个随机数⽣成器传给 norm 函数对象。
例如:std::random_device rd;std::default_random_engine rng {rd()};std::cout << "Normally distributed values: "<< norm (rng) << " " << norm (rng) << std::endl; // 39.6153 45.5608可以通过调⽤对象的成员函数 mean() 和 stddev() 来获取它的期望值和标准差:std::cout<<"mu: "<< norm.mean () << " sigma: " << norm.stddev ()<< std::endl; // mu: 50 sigma: 10通过调⽤⽆参数的成员函数 param(),可以得到⼀个封装了这两个值的 param_type 对象。
定性数据的统计描述、正态分布以及应用(normaldistribution)

-2.58 -1.96 -1
0
1 1.96 2.58
标准正态分布
-1~1 -1.96~1.96 -2.58~2.58
面积或概率 68.27% 95.00% 99.00%
曲线下面积分布规律
68.27%
68.27%
95.00%
95.00%
-2.58 -1.96 -1
99.00%
0
1 1.96 2.58μ-2.58σ μ-1.96σ μ-σ
标准正态分布
标准正态分布 (standard normal distribution) 的两个参数为:μ=0,σ=1 记为 N(0,1)
一般正态分布为一个分布族:N(m,2) ;标准
正态分布只有一个 N(0,1) ;这样简化了应 用
u曲线下面积
0.5
f(X)
1 u X2
0.4
-∞
u0.3
(u)
五. 正态分布的应用
1.许多医学指标服从正态分布或近似 正态分布,如同性别、同年龄儿童的身 高,同性别健康成人的红细胞数、血红 蛋白量等,及实验中的误差。
2. 估计医学参考值范围 医学正常值范围
定义:又称参考值范围,是指特定健康人群的 解剖、生理、生化等各种数据的波动范围。习 惯上是确定包括95%的人的界值。
e 2dX
2
0.2
附表(标准正态分布
0.1
左侧曲线下面积)就
0.0
是根据此公式和图形
-4 -3 -2 -1 0 1 X
2
3
4
制定的
曲线下面积分布规律
查附表
68.27%
( 1 .9 6 ) P (u 1 .9 6 ) ?
95.00%
正态分布图作图指导-Normaldistributioncurve

1. 双击Origin Pro的图标,
2. 将数据从text 文件里复制粘贴到数据区域
3. 按照如下路径,选择频率分
析.Frequency Count
4. 设置起点终点和步进,一般
步进50,单击ok
5. 选择生成的 X,Y列数据,点
击plot,按如下路径画图,
--------------------
6. 对得到的柱形图进行颜色调整,默认是红色。
7. 单击菜单栏的Analysis选项,按照图中路径,选择高级拟合(Advanced Fitting Tool)
8. 在Advanced Fitting Tool 菜单界面选择Action-Fit
9. 弹出的对话框,选择
Active Dateset。
10. 选择100Iter,单击Done。
11. 对模型的解释框内容进行删除,只保留Model,Equation,and R2的信息。
12. 右击边框,在属性Properties窗口中去掉边框。
13. 对坐标轴进行命名
14. 右击空白区域,弹出菜单中单击添加Text选项,添加本图表的制作日期。
15. 右击图标空白区域,探出菜单中选择Export Page 导出图片,图片DPI选择200,格式选择png or jpg
16. 最后,保存数据
继续阅读。
医学统计学课件之正态分布(Normal Distribution)
Ⅱ类错误 本质为不拒绝实际上不成立的H0 犯该类错误的最大概率为 “存伪”、“假阴性”、“漏诊”
两类错误此消彼长,欲同时减少他们的唯 一手段——增大样本含量
返回
严密的科研设计是保证假设检验结论正确性 的前提
选用合适的检验方法,必须以符合其适用条 件为前提
正确理解假设检验的统计意义
假设检验与可信区间的联系与区别
返回
计量资料的t检验 计量资料的ANOVA 计数资料的卡方检验 非参数的秩和检验
Example
从
总体中重复随机抽样10000次,
每次抽取n为9的样本
其中,2个样本的观测值及其均数和标准差:
身高观测值
均数 标准差
1 125 124 117 116 125 132 122 118 115 121.56 5.55
准差进行反映的,也叫标准误。
结论
只要抽样,则必定存在抽样误差
标准误越小,意味着抽样误差越小;反之,则大
抽样误差的大小反映的就是样本统计量对总体参 数的偏离程度
尽量减少抽样误差的最佳方法——增大样本含量 均为反映离散程度的统计指标
不同
定义 单个原始观测值对均数 样本均数对总体均数
正态分布(Normal Distribution)
u变换
标准正态变换
目的
标准正态分布曲线下面积规律
双侧95%或99%面积(1.96与2.58)
单侧95%或99%面积(1.645与2.32)
正态性检验(Normality test)
符合正态概率密度函数 矩法 偏度系数与峰度系数 W检验或D检验 原始目测法 P-P plot Q-Q plot
返回
可信区间
正态分布(Normal distribution).

系 X 1.96S 35.92-37.22
X 2.58S 35.71-37.43
137 94.48 95.00 144 99.31 99.00
医学参考值范围的制定
公 (一)、概念: 共 医学参考值是指包括绝大多数“正常人”
卫 的各种生理及生化指标常数,也称正
生
常值。 由于存在个体差异,正常值并非为常数,
共 (二)、区间面积: 区间表示方法:μ±uσ
x us
卫
u=1时,区间面积为68.25%
u=1.96时,区间面积为95%
生
u=2.58时,区间面积为99%
系
区间面积含义:
表示此区间的变量值个数占全部变量值
个数的百分比或表示变量值在此区间出 现的概率(P)
四、正态分布的应用
公 1.根据样本分布判断总体分布情 共况
系 而是在一定范围内波动,医学上常用
95% 或 99% 的 分 布 范 围 作 为 判 定 正 常
和异常的参考标准。
(二)、参考值范围的制定方法 公 1、百分位数法:偏态分布,样本含量足够大
共 ⑴求正常成年人尿铅的95%的参考值范围
卫 ⑵求正常成年男子肺活量的95%的参考值范围 生 单侧参考值范围
0 12.0 14.5 17.0 19.5 22.0 24.5 27.0 29.5 32.0
(3)
(4)
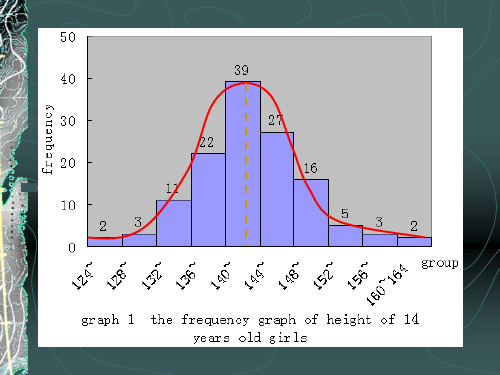
图2-4 频数分布与正态分布示意图
二、正态分布曲线的特征
公 (1)以X= μ为中心,μ左右X值对称性减少。 (2)在X= μ处曲线最高,f(X=μ)为最大值。
共 (3)μ 、σ决定 正态分布曲线位置和形状:
系 ⑶求正常成年男子白细胞的95%的参考值范围
双侧参考值范围
excel画正态分布曲线图

excel画正态分布曲线图正态分布是一种被广泛应用的概率分布,它的概率密度函数是一个标准的钟形曲线,它的简称为NDF(Normal Distribution Function),或者叫作正态分布曲线。
正态分布在做实验中经常使用,但人们不得不用许多繁琐的统计学公式来绘制出正态分布曲线。
为了使用更简便的方法来绘制正态分布曲线,本文将介绍如何使用微软的Excel构建正态分布曲线图。
首先,需要准备一份Excel表格,将某一维度的分布曲线数据记录在一列中。
这里以“height”(身高)为例,在第一列的表格中,列出人的身高(以厘米为单位),在第二列的表格中,记录身高的频数(以人数为单位)。
接下来,在Excel中选择插入“图表”,选择“线形图”,把第一列的数据作为图表的X轴,第二列的数据作为图表的Y轴。
然后,在图表右上角的菜单中,点击“选项”,勾选“折线”并且把它改为“曲线”,当把曲线拖动到正常位置时,图表就出来了。
最后,可以给正态分布曲线图添加标题和比例尺,使其更加易于理解。
正态分布曲线图主要用于表示一组数据的分布特征。
例如,可以用正态分布曲线图来表示全国人口的年龄分布情况,或是某类测试成绩的分布特征,或是市场消费行为的变化情况。
另外,正态分布曲线图也可以用于比较两个不同维度的数据分布特征,从而更好地表现出这些数据之间的相关性。
正态分布曲线图被广泛应用于商业决策分析、统计学、有限元素分析等领域中,可以帮助人们对数据的变化趋势进行更加客观的分析,从而准确地了解现象背后的规律性。
使用Excel绘制正态分布曲线图不但简单易操作,而且能够获得较为准确的曲线图,因此得到了广泛的应用。
以上就是本文关于如何使用Excel画正态分布曲线图的介绍,希望读者通过本文的介绍,能够对Excel构建正态分布曲线图有一个较为完整的了解,可以灵活运用Excel技术来解决一些数据处理问题。
标准正态分布示意图

lgG = lg(12571032040)=lg(571032040)1/12=1/1 2(7lg5+3lg10+lg20+lg40)=0.89966
为简化计算, 可两边取对数
G = lg-1(lgG)= lg-10.89966 = 7.94
加权法: G=lg-1( lgx/ ), 当变量值个数 较多或变量值为频数表资料时
(3) (4)=(2)(3) (5)=(2)(4)
1 127
16129
• 129 131
4 524
68644
• 133 135
9 1215
164025
• 137 139
28 3829
540988
• 141 143
35 5005
715715
• 145 147
27 3969
583443
• 149 151
11 1661
250811
• 153 155
4 620
96100
• 157161 159 • 合计 •
1 159
120 17172
(ƒ)( ƒx)
25181
2461136
( ƒx2)
•
2461136 - (17172)2/120
• s=
•
120 - 1
•
• 三、变异系数: 又称离散系数。代号为CV。
甲的变异程度>乙组
一、极差和四分位间距
• (一)全距: R(range), 亦称极差。即一组变量 值中最大值与最小值之差。
• R甲=4.0 - 2.8 = 1.2 • R乙=3.8 - 3.0 = 0.8 • 优点: 简单明了 • 缺点: 仅考虑了资料的最大值与最小值, 不能反
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.双击Origin
Pro的图标,
2.将数据从text
文件里复制
粘贴到数据
区域
3.按照如下路
径,选择频率
分
析.Frequency
Count
4.设置起点终
点和步进,一
般步进50,单
击ok
5.选择生成的
X,Y列数据,点
击plot,按如
下路径画图,
--------------------
6.对得到的柱
形图进行颜
色调整,默认
是红色。
7.单击菜单栏
的Analysis选
项,按照图中
路径,选择高
级拟合
(Advanced
Fitting Tool)
8.在Advanced
Fitting Tool
菜单界面选
择Action-Fit
9.弹出的对话
框,选择
Active
Dateset。
10.选择100Iter,
单击Done。
11.对模型的解
释框内容进
行删除,只保
留Model,
Equation,and
R2的信息。
12.右击边框,在
属性
Properties窗
口中去掉边
框。
13.对坐标轴进
行命名
14.右击空白区
域,弹出菜单
中单击添加
Text选项,添
加本图表的
制作日期。
15.右击图标空
白区域,探出
菜单中选择
Export Page
导出图片,图
片DPI选择
200,格式选
择png or jpg
16.最后,保存数
据。
