钢结构第四章答案
钢结构—第四章课后答案

P1084.1解: 示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270⨯300=81kN.mI x =[0.8⨯(38-2⨯0.8)3]/12+[(15-2)⨯1⨯19.52]⨯2=13102cm 4=腹板A e =0.8⨯(38-2⨯0.8)=29.12 cm 2截面最大正应力σmax =M/W= 81⨯106⨯200/13102⨯104=123.65 N/mm 2≤f t w =185N/mm 2剪力全部由腹板承担τ=V/A w =270⨯103/2912≤=92.72 N/mm 2 =f v w =125N/mm 2腹板边缘处”1”的应力σ1=(M/W)(190/200)=123.65(190/200)=210.19=117.47腹板边缘处的折算应力应满足1.1w zs t f σ=≤=2≤1.1f t w =203.5N/mm 2焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN连接为不等边角钢长肢相连 题意是两侧焊肢背分配的力N 1=0.65 ⨯420=273 kN肢背分配的力N 2=0.35 ⨯420=147 kNh fmin =1.5(t max )1/2=1.5(10)1/2=4.74mmh fmax =1.2(t min )=1.2(6)=7.2mm取h f =6mm肢背需要的焊缝长度l w1=273⨯103/(2⨯0.7⨯6⨯160)+2⨯6=203.12+12=215.13mm肢尖需要的焊缝长度l w2=147⨯103/(2⨯0.7⨯6⨯160)+2⨯6=109.38+12=121.38mm端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
l wmax =60h f =360mm ;l wmin =8h f =48mm ;焊缝“A ”满足要求4.3解:节点板与端板间的连接焊缝“B ”承受拉力N 对焊缝“B ”有偏心,焊缝“B ”承受拉力N=(1.5/1.8) ⨯420=350kN ;剪力V=(1/1.8) ⨯420=233.33 kN ;弯矩M=350⨯50=17.5 kN.mh fmin =1.5(t max )1/2=1.5(20)1/2=6.71mmh fmax =1.2(t min )=1.2(10)=12mm焊缝“B ”h f =7mm焊缝“B ”A 点的力最大焊缝“B ”承受的剪应力τ=233.33⨯103/(2⨯0.7⨯7⨯386)=61.68 N/mm 2焊缝“B ”承受的最大正应力σ=N/Ae+M/W=350⨯103/(2⨯0.7⨯7⨯386)+17.5⨯106⨯200/(2⨯0.7⨯7⨯3863/12)=92.52+71.91 =164.43 N/mm 2验算焊缝“B ”的强度=148.19 N/mm 2<f f w 焊缝“B ”满足要求。
陈绍蕃 钢结构第四章答案

第四章4. 1有哪些因素影响轴心受压杆件的稳定系数? 答:①残余应力对稳定系数的影响;②构件的除弯曲对轴心受压构件稳定性的影响; ③构件初偏心对轴心轴心受压构件稳定性的影响; ④杆端约束对轴心受压构件稳定性的影响;4.3影响梁整体稳定性的因素有哪些?提高梁稳定性的措施有哪些? 答:主要影响因素:①梁的侧向抗弯刚度y EI 、抗扭刚度t GI 和抗翘曲刚度w EI 愈大,梁越稳定; ②梁的跨度l 愈小,梁的整体稳定越好;③对工字形截面,当荷载作用在上翼缘是易失稳,作用在下翼缘是不易失稳; ④梁支撑对位移约束程度越大,越不易失稳; 采取措施:①增大梁的侧向抗弯刚度,抗扭刚度和抗翘曲刚度; ②增加梁的侧向支撑点,以减小跨度;③放宽梁的受压上翼缘,或者使上翼缘与其他构件相互连接。
4.6简述压弯构件中等效弯矩系数mx β的意义。
答:在平面内稳定的计算中,等效弯矩系数mx β可以把各种荷载作用的弯矩分布形式转换为均匀守弯来看待。
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N =1500kN 。
解:由支承条件可知0x 12m l =,0y 4m l =23364x 1150012850025012225012476.610mm 12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012500810000mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cm i ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa 0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
钢结构基础第四章课后习题答案
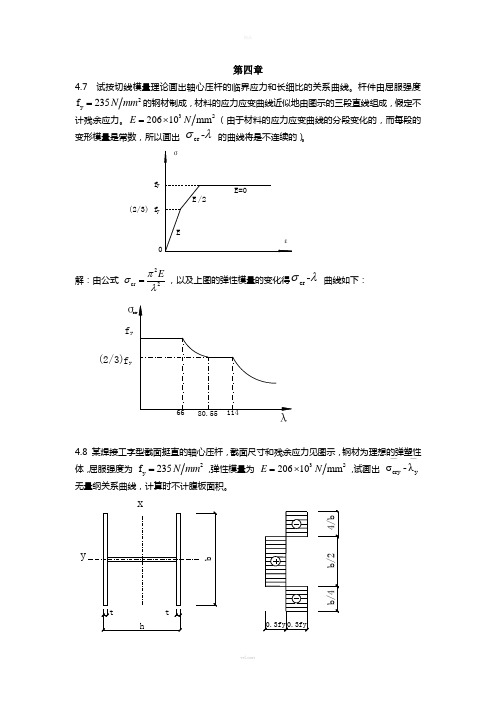
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构基础(第二版)课后习题第四章答案
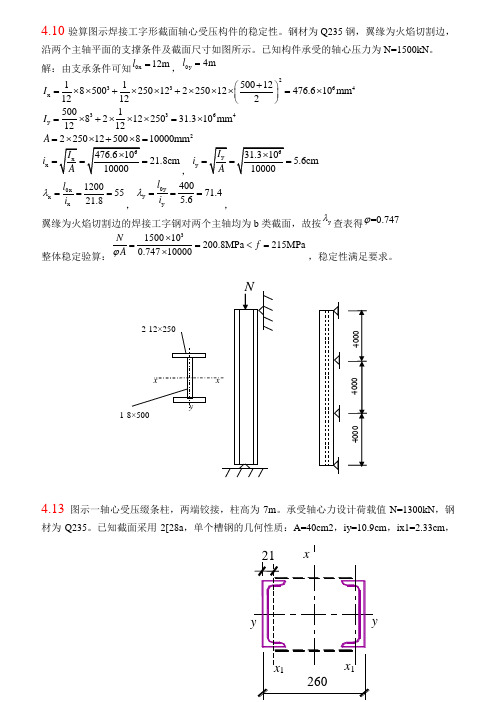
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN 。
解:由支承条件可知0x 12m l =,0y 4ml =23364x 1150012850025012225012476.610mm12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭ 3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012*********mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cmi ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值N=1300kN ,钢材为Q235。
已知截面采用2[28a ,单个槽钢的几何性质:A=40cm2,iy=10.9cm ,ix1=2.33cm ,Ix1=218cm4,y0=2.1cm ,缀条采用∟45×5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7ml l ==224x x10262221840 2.19940.8cm 22b I I A y ⎡⎤⎡⎤⎛⎫⎛⎫=+-=+-=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦x 11.1cm i === 0x xx 70063.111.1l i λ=== 0y y y 70064.210.9l i λ===0x 65.1λ===格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
钢结构第四章答案【范本模板】

第四章4。
10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N =1500kN 。
解:由支承条件可知0x 12m l =,0y 4m l =23364x 1150012850025012225012476.610mm 12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012500810000mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cm i ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa 0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
4。
13图示一轴心受压缀条柱,两端铰接,柱高为7m 。
承受轴心力设计荷载值N =1300kN ,钢材为Q235。
已知截面采用2[28a ,单个槽钢的几何性质:A =40cm 2,i y =10。
9cm ,i x1=2.33cm ,I x1=218cm 4,y 0=2。
1cm ,缀条采用∟45×5,每个角钢的截面积:A 1=4。
29cm 2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7m l l ==224x x10262221840 2.19940.8cm 22b I I A y ⎡⎤⎡⎤⎛⎫⎛⎫=+-=+-=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦x 11.1cm i === 0x x x 70063.111.1l i λ=== 0y y y 70064.210.9l i λ===0x 65.1λ=== 格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
钢结构第四章习题答案

截面轮廓尺寸 h =
两个槽钢翼缘间净距为 300 − 2 × 84 = 132mm > 100mm ,满足构造要求。 分肢形心轴之间的间距 a = 300 − 2 × 20.2 = 259.6mm (3)绕 y 轴整体稳定检算 分肢形心轴与 y 轴的间距 x1 = a / 2 = 259.6 / 2 = 129.8mm 绕 y 轴名义惯性距: I y = 2( I1 + x1 A1 ) =2(241.5+12.98 ×45.6) =15849cm
58.8
= 122.4mm
2 iy − 2i12 = 122.42 − 2 × 20.22 = 119mm
分肢形心至 y 轴: x1 =
分肢间距: b = 2( x1 + z0 ) = 2(119 + 20.2) = 278.4mm , 取 b = 300mm ,则实际分肢间距为 300-20.2×2=259.6mm 也可根据截面与回转半径的近似关系确定。 b=122.4/0.44=278mm,取 b=300mm (3)绕 y 轴整体稳定检算 分肢形心至 y 轴: x1 =300/2-20.2=129.8mm 绕 y 轴名义惯性距: I y = 2( I1 + x1 A1 ) =2(241.5+12.98 ×45.6) =15849cm
解:lox=9m,loy=3m,可选择窄翼缘热轧 H 型钢。 截面类型:绕 X 轴截面为 a 类截面, 绕 Y 轴截面为 b 类截面 假定长细比 λ = 100 ,查表 4.5(a)和 4.5(b),得 ϕ x = 0.638, ϕ y = 0.555 所需截面 A =
N 400 × 103 = = 33.52cm 2 ϕ f 0.555 × 215
钢结构计算题答案

第四章 轴心受力构件4。
1 验算由2∟635⨯组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼(图4。
37),钢材为Q235钢。
如截面尺寸不够,应改用什么角钢? 注:计算时忽略连接偏心和杆件自重的影响。
解:(1)强度 查表得 ∟635⨯的面积A=6。
14cm 2,min 1.94x i i cm ==,22()2(614205)1028n A A d t mm =⨯-⋅=⨯-⨯=, N=270KN 327010262.62151028n N Mpa f Mpa A σ⨯===≥=,强度不满足,所需净截面面积为32270101256215n N A mm f ⨯≥==,所需截面积为212562057282n A A d t mm =+⋅=+⨯=, 选636⨯,面积A=7。
29cm 22729mm =2728mm ≥ (2)长细比[]min3000154.635019.4o l i λλ===≤= 4。
2 一块—40020⨯的钢板用两块拼接板-40012⨯进行拼接。
螺栓孔径为22mm ,排列如图4。
38所示。
钢板轴心受拉,N=1350KN (设计值).钢材为Q235钢,解答下列问题; (1)钢板1—1截面的强度够否? (2)是否需要验算2-2截面的强度?假定N 力在13个螺栓中平均分配,2-2截面应如何验算? (3)拼接板的强度够否?解:(1)钢板1—1截面强度验算:210min (3)(400322)206680n A b d t mm =-⋅⋅=-⨯⨯=∑, N=1350KN 31135010202.12056680n N Mpa f Mpa A σ⨯===≤=,强度满足.(2)钢板2—2截面强度验算:(a),种情况,(a)是最危险的。
222 2()0(5)(400808080522)206463n aA l d t mm=-⋅⋅=-++-⨯⨯=, N=1350KN32135010208.92056463nNMpa f MpaAσ⨯===≥=,但不超过5%,强度满足。
陈绍蕃钢结构第四章答案

第四章4. 1有哪些因素影响轴心受压杆件的稳定系数?答:①残余应力对稳定系数的影响;② 构件的除弯曲对轴心受压构件稳定性的影响; ③ 构件初偏心对轴心轴心受压构件稳定性的影响; ④ 杆端约束对轴心受压构件稳定性的影响;4.3影响梁整体稳定性的因素有哪些?提高梁稳定性的措施有哪些? 答:主要影响因素:① 梁的侧向抗弯刚度 El y 、抗扭刚度Gi t 和抗翘曲刚度EI w 愈大,梁越稳定; ② 梁的跨度丨愈小,梁的整体稳定越好;③ 对工字形截面,当荷载作用在上翼缘是易失稳,作用在下翼缘是不易失稳; ④ 梁支撑对位移约束程度越大,越不易失稳; 采取措施:① 增大梁的侧向抗弯刚度,抗扭刚度和抗翘曲刚度; ② 增加梁的侧向支撑点,以减小跨度;③ 放宽梁的受压上翼缘,或者使上翼缘与其他构件相互连接。
4.6简述压弯构件中等效弯矩系数P mx 的意义。
答:在平面内稳定的计算中,等效弯矩系数P mx 可以把各种荷载作用的弯矩分布形式转换为均匀守弯来看待。
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为 解:由支承条件可知l 0x =12m , l 0y =4m11 f 500+12 I x =—x8x5003 +—x250>d23+2咒250"2咒 I --------12 12 12/I500X 83+2」X 12X 2503=31.3x106mm 412 122A =2X250X12 +500x8 = 10000mm/476.6咒106 … . P7 /31.3X 106匕厂lx = ---------- = J ------------------------- = 21.8cm , i y =J — =J ----------- = 5.6cmV 10000 yV A V 10000,一直=僭=55」上=型=71.4,i x 21.8yi y 5.6翼缘为火焰切割边的焊接工字钢对两个主轴均为 整体稳定验算: 器 =—= 200.8MPac f =215MPa ,稳定性满足要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章4. 1有哪些因素影响轴心受压杆件的稳定系数?答:①残余应力对稳定系数的影响;② 构件的除弯曲对轴心受压构件稳定性的影响; ③ 构件初偏心对轴心轴心受压构件稳定性的影响; ④ 杆端约束对轴心受压构件稳定性的影响;4.3影响梁整体稳定性的因素有哪些?提高梁稳定性的措施有哪些? 答:主要影响因素:① 梁的侧向抗弯刚度 El y 、抗扭刚度Gi t 和抗翘曲刚度EI w 愈大,梁越稳定; ② 梁的跨度I 愈小,梁的整体稳定越好;③ 对工字形截面,当荷载作用在上翼缘是易失稳,作用在下翼缘是不易失稳; ④ 梁支撑对位移约束程度越大,越不易失稳; 采取措施:① 增大梁的侧向抗弯刚度,抗扭刚度和抗翘曲刚度; ② 增加梁的侧向支撑点,以减小跨度;③ 放宽梁的受压上翼缘,或者使上翼缘与其他构件相互连接。
4.6简述压弯构件中等效弯矩系数mx 的意义。
答:在平面内稳定的计算中,等效弯矩系数 mx可以把各种荷载作用的弯矩分布形式转换为均匀守弯来看待。
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN 。
解: 由支承条件可知l 0x12m , l 0y 4mI x18 5003 1212250 1232 250 122500 12476.6 106mm 4I y型83122 250 1212 12500 2503 31.3 106mm 8 476.6 106 210000mm1000021.8cm , i y 31.3 106 100005.6cm1200 55,21.8l °y 400 i y5.6翼缘为火焰切割边的焊接工字钢对两个主轴均为 71.4,b 类截面,故按y 查表得=0.747整体稳定验算:1500 103 A 0.747 10000200.8MPa 215MPa ,稳定性满足要求。
AI xl 0xI x I y因此板件局部稳定满足要求。
4.11解:先计算杆件截面特性l 0x 1200cm,l 0y 900cm A 2 1 25 0.6 50 62cm 2l x 0.6 203 12 1 25 10.52 2 5912.5cm 4 I y 2 1 253 12 2604.2cm 4 i x ... I x A 5912.5 62 9.77cm i y . I y —A , 2604.2 62 6.48cmx l 0x . i x1200 9.77 122.8y l oy i y900 6.48138.9对强轴x 和弱轴y 均为b 类截面,查表得minN y A 0.349450 103. 0.349 6200208 N mm 2215 N mm 2满足整体稳定要求! 验算板件稳定性 翼缘的宽厚比为:94.45腹板的高厚比为:33.3 (25 0.54.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值N=1300kN ,钢材为Q235。
已知截面采用2[28a,单个槽钢的几何性质:A=40cm2,i y=10.9cm , i xi=2.33cm , l xi=218cm4, y o=2.1cm,缀条采用L 45 >5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?214.15某压弯格构式缀条柱如图所示,两端铰接,柱高为8m。
承受压力设计荷载值N=600kN , 弯矩M 100kN m,缀条采用L 45X5,倾角为45°,钢材为Q235,试验算该柱的整体稳定性是否满足?已知:I22a A=42cm2, l x=3400cm4, I y1=225cm4;[22a A=31.8cm2, l x=2394cm4, I y2=158cm4;L 45 X5 A1 =4.29cm 2。
解: 柱为两端铰接,因此柱绕x、y轴的计算长度为:X i26010x by 7mX1A £ y。
22 218 40 262 2.149940.8cm0x9940.82 4011.1cmx 7~l x70011.1 册l0yiy200 64.210.9x2 27 A x 63・12 2722蟲边格构柱截面对两轴均为b类截面,按长细比较大者验算整体稳定既可。
由0x 65.1, b类截面,查附表得0.779 ,1300 103整体稳定验算:—2208.6MPaA 0.779 2 40 10所以该轴心受压的格构柱整体稳定性满足要求。
215MPa解:①求截面特征参数 截面形心位置: 31.8 26 X 1112mm ,x 2 A I x42 31.82 42 31.8 73.8cm 2 43400 2394 5794cm 260 112 148mm 225 42 11.22 158 31.8 14.82 12616.952cm 4 Iy该压弯柱两端铰接因此柱绕 x 、y 轴的计算长度为:l 0xl0y8m0x 0yAi x i x l0xI x 5794 73.88.86cm , i y800J^^213.08cm;73.8 观90.3, 8.86Lyy I y 13.08 61.2:27 A,.'61.22 27 73.8y A 1y ,2 4.29 ②弯矩作用平面内稳定验算(弯矩绕虚轴作用) 由 0y63.1N 10y 63.1,b 类截面,查附表得 匹陛竺空38 726kN 0.791 N 2 说明分肢 I y a 260 260 N 1 600 726 126kN 1受压,分肢2受拉, 12616.952 31126.5cm 3 N Ey 2EA11.22 206 103 73803425.9kN1.1 63.12由图知,M 2=0,M 1 100kN m ,等效弯矩系数 my0.65 0.35M 2 M 1 0.654.17焊接简支工字形梁如图所示,跨度为 12m ,跨中6m 处梁上翼缘有简支侧向支撑,材料为Q345钢。
集中荷载设计值为 P=330kN ,间接动力荷载,验算该梁的整体稳定是否满足要 求。
如果跨中不设侧向支撑,所能承受的集中荷载下降到多少?_-280 X 14l 1 6000-21.4 13,需验算整体稳定t 1 280y A W 1y 1my Myy N N Ey 600 1030.65 100 10630.791 7380 1126.5 10 1 0.791 600 3425.9 152.5MPa 因此柱在弯矩作用平面内的稳定性满足要求。
③弯矩作用平面外的稳定性验算 弯矩绕虚轴作用外平面的稳定性验算通过单肢稳定来保证, 只需对分肢 215MPa 因此对单肢稳定性进行验算: 8m ,1进行稳定验算。
“ 260mm 单肢对 l 0x1 34008.9cm , 42 2.31cm I y 1 N i 800 89.9,8.9 I x1 x 轴和y 轴分别为 726 1030.715 4200yi a 、l 0y1 I y1 b 类截面,241.8MPa 竺11.3 2.31查附表得:f 215MPax1 A因此柱在弯矩作用平面外的整体稳定性不满足要求。
x10.715, y1 0.99跨中弯矩M xPL 4330 12 4990kN mPhx”rr -- ---- ■ ■、-1000 X 8I ~I -280 X 14解:①梁跨中有一个侧向支承点I x 18 10003 2 280 14 50722682 106mm4121000 3 1 3 4I y 8 2 14 280 51264000mm12 12A 2 280 14 1000 8 215840mmIy51264000 56.89cm15840l0yI y 6000 105.47 12056.8923599,所以不能用近似公式计算345l x 2682 1063Wx -5218015.6mmy i 514查附表15,跨度中点有一个侧向支承点、集中荷载作用在截面高度高度上任意位置,1.754.18题:如图所示两焊接工字型简支梁截面,其截面积大小相同,跨度均为12m ,跨间无侧向支承点,均布荷载大小相同,均作用于梁的上翼缘,钢材为 Q235,试比较说明何者稳定性更好。
解:均布荷载作用,受弯构件的弯扭失稳,计算其整体稳定性。
1 2Mmax — ql(1 )、梁的跨中最大弯矩:8;梁的几何特征参数如下:需对M x 4320 Ah 1 b : W q 4.4h235b可4320 15840 1028 105.47 14 2351.752 1105.4725218015.6 \b 进行修正,b1.07 0.282, b990 1064.4 1028345 1.52 0.61.07 0.282 1.520.884214.6MPa W 0.884 5218015.6该梁的整体稳定性满足要求。
②梁跨中没有侧向支承点l °y y — i yb]h輕 210.9456.89竺也上0.586 2.0280 1024 f 310MPa梁跨中无侧向支承点,集中荷载作用在上翼缘, 0.586 0.73 0.180.73 0.18则有:0.8354320 Ah r 证\14.4h235b ~~0.8354320 210.942 1028 :121°94 14 2 2350.205 5218015.6「4.4 1028 34515840 M bW x4M x 4 331.6P x110.5kNL12所以,如果跨中不设侧向支撑,所能承受的集中荷载下降到 M 0.205 5218015.6310MPa M x 331.6kN m110.5kN 。
I x1 3 3(300 12323290 12003)124.989 109mm4W x I x 4.989 109 212328.099 106mm3l x4.989 10921600480.6mmI y 丄(16123300 2 1200 103) 7.21 10 4mmW yI y 7.21 107 2h y 2 3004.807 105mm3i y;7.21 1072160057.8mm12000l y 57.8207.6112000 16梁的整体稳定系数b|h 300 12320.520.69 0.13 0.7584320 Ah [ y2W x L- 1心2]235b]下0.7584320 21600 1232207.6128.099 1061 (207.61 16)2(4.41232)0]空0.2928235M max b W x f 0.2928 8.099 106215 509.85kNq max 8M max 8 509.8512228.33kN /m 28.33N/mmM max(2 )、梁的跨中最大弯矩: 梁的几何特征参数如下:l 0x l0y l012000 mm A 240 20 22 1200 10 21600mm -I x —(240 124032301231200 )9 45.013 10 mmI x 5.013 109 21240 8.086 6 310 mmI y 1 3 3(20 2403 2 1200 103) 12 4.618 107mm4.20图中所示为Q235钢焰切边工字形截面柱,两端铰接,截面无削弱,承受轴心压力的设 计值N=900kN ,跨中集中力设计值为F=100kN 。
