2020年高中物理竞赛辅导课件★★磁场的能量(PPT)
合集下载
高中物理竞赛课件：磁场(共80张PPT)
I
6 10
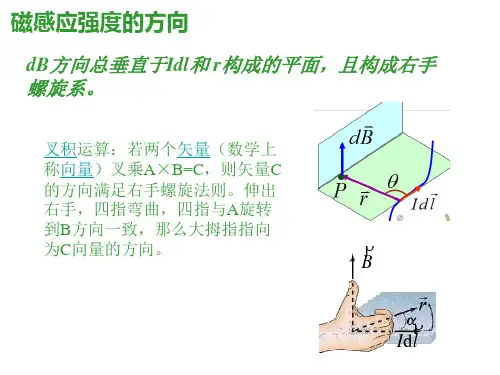
专题21-例4 一N匝密绕的螺线管长L，半径r，且L >> r．当通有
恒定电流I时，试求作用在长螺线管侧面上的压强p ．
解:解题方向: 求出电流元所处磁场磁感 应强度,即可求安培力及其对螺线管
Fi
侧面压强
电流元所在处磁场设为B其它;
B其余 Bi
Bi
电流元内侧有
B B其余 Bi B I
dB 只有x，y方向上的分量
B dB
dx I
2b
o
r
d
r
dB
P
dB
y
x
iˆ
dB x
ˆj
dB y
dx
由于铜片对y 轴对称，所有长条电流的
dB
dBy
dB
x
dB 分量的代数和等于零 y
dB y
B
iˆ
dB x
dI I dx dB 0dI
x
2b
2r
I
n 1
2
a
P
变式训练
电流为I的一无限长直导线在C点被折成60°角，若用同样导 线将A,B两点连接，且AB=BC=L，求三角形中心点O的磁感 应强度。
变式训练
从无限远来的直电流从A点流入正方形导体框，又从B点沿 直线流向无限远。若正方形边长为l，且导体粗细均匀，流 入的总电流强度为I。求正方形中心O处的磁感应强度。
电流元外侧有
0 B其余 Bi
B其余
B 2 Fi Fi
0BrIN2lI 2
2nL
P Fi 0 N 2 I 2
6 10
专题21-例4 一N匝密绕的螺线管长L，半径r，且L >> r．当通有
恒定电流I时，试求作用在长螺线管侧面上的压强p ．
解:解题方向: 求出电流元所处磁场磁感 应强度,即可求安培力及其对螺线管
Fi
侧面压强
电流元所在处磁场设为B其它;
B其余 Bi
Bi
电流元内侧有
B B其余 Bi B I
dB 只有x，y方向上的分量
B dB
dx I
2b
o
r
d
r
dB
P
dB
y
x
iˆ
dB x
ˆj
dB y
dx
由于铜片对y 轴对称，所有长条电流的
dB
dBy
dB
x
dB 分量的代数和等于零 y
dB y
B
iˆ
dB x
dI I dx dB 0dI
x
2b
2r
I
n 1
2
a
P
变式训练
电流为I的一无限长直导线在C点被折成60°角，若用同样导 线将A,B两点连接，且AB=BC=L，求三角形中心点O的磁感 应强度。
变式训练
从无限远来的直电流从A点流入正方形导体框，又从B点沿 直线流向无限远。若正方形边长为l，且导体粗细均匀，流 入的总电流强度为I。求正方形中心O处的磁感应强度。
电流元外侧有
0 B其余 Bi
B其余
B 2 Fi Fi
0BrIN2lI 2
2nL
P Fi 0 N 2 I 2
高二物理竞赛磁场的能量课件
单位长度传输线上
I
wm
0I 2 8 2r 2
Wm ' Wm1'Wm2 '
0I 2 16
0I 2 4
ln
R2 R1
引言
(1)中断的传导电流 I 由位移电流ID接替，使电路中的电流保持连续 (2)传导电流和位移电流之和：全电流 (1)中断的传导电流 I 由位移电流ID接替，使电路中的电流保持连续 自感为L的线圈通有电流 I 时 [例]一长直圆柱导体，有电流 I 均匀地流过。 [例]半径R1的圆柱导体和半径R2的圆柱壳同轴组成传输线，电流I由内管流入，外管流出，求单位长度上储存的磁能。 A’是由储存在磁场中的能量提供的 问题：能量从哪里来的呢？ 由安培环路定律，导体内 设极板面积为S，某时刻极板上的自由电荷面密度为 ，则 取环绕导线的环路L，以L为边界作S1、S2 两曲面 长直螺线管内的磁场均匀分布 长直螺线管内的磁场均匀分布 ——稳恒磁场安培环路定律不再适用 [例]半径R1的圆柱导体和半径R2的圆柱壳同轴组成传输线，电流I由内管流入，外管流出，求单位长度上储存的磁能。 ——回路中传导电流不连续
1 2
ED
两极板间：无传导电流存在 ——等于电流增大时 反抗 L所作的功 自感为L的线圈通有电流 I 时
——该结果适用于一切磁场
[例]一长直圆柱导体，有电流 I 均匀地流过。
对不均匀磁场 自感为L的线圈通有电流 I 时
设极板面积为S，某时刻极板上的自由电荷面密度为 ，则 (1)中断的传导电流 I 由位移电流ID接替，使电路中的电流保持连续
A’是由储存在磁场中的能量提供的
自感为L的线圈通有电流 I 时
磁场能量
Wm
1 2
LI
2
对长直螺线管有
2020-2021学年高二物理竞赛课件：第9章磁场的能量
K
1
L
L
di dt
dA Lidt Lidi
3
§9.6 磁场的能量
AL
0
dAL I Lidi
1 LI 2 2
自感为 的L自感线圈，当通电流 时所I 储存的 能量为:
WL
1 2
LI 2
4
§9.6 磁场的能量
二、磁场的能量
1.磁场强度:
H
B
B
0真空磁导率. r相对磁导率
0r 0r介质磁导率
② I传只存在于导体中，而 I位 ，哪里有变化的 电场，哪里有 I位 ，导体、介质、真空都可以存 在位移电流；
③ I传 通过导体时放出焦耳热，I位 通过导体、 介质、真空时不放出焦耳热。
15
二、麦克斯韦方程组
1、静电场与稳恒电流磁场规 律
静电场的高斯定理 D dS dV q
静电场的环流定理
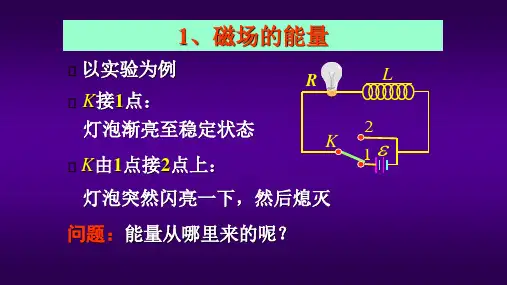
为 r 的绝缘材料.求该同轴电缆中长为 l 的一段
的磁场能量及其自感。
[解]： 当R1 r R2时，
H
I
2r
;B
r0H
r0I 2r
.
磁能密度：wm
1 BH 2
r0I 2 8 2r 2
总磁能：Wm
R2 R1
wm
2rldr
0
R1 r R2
8
§9.6 磁场的能量
r 0 I 2l R2 dr r 0 I 2l ln R2
第九章 变化的电磁场
§9.1电源 电动势 §9.2 电磁感应的基本规律
§9.3 动生电动势 §9.4 感生电动势 感生电场 §9.5 自感和互感 §9.6 磁场的能量 §9.7 位移电流 麦克斯韦电磁场方程组
1
高二物理竞赛磁场的能量课件
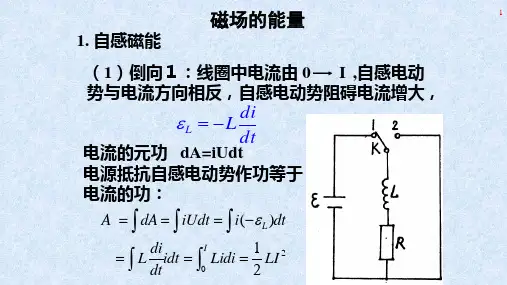
求磁场0 ,能量。
R1
R2
o
b
r
解 设长直导线为回路1， 电流 I1；螺线环为回路2，
6
b
(1) 互感
R1
M 21 N221
I1
I1
R2
o
r
N
R2 0 I1bdr
I1 R1 2r
0 Nb ln R2
2
R1
（2） 长直导线的互感电动势
7
12 M
di2 , dt
i2 I0 cos(2ft)
I02I02Irln
1
2
dr
b 2r
2
（3）求磁能变化（I不变）
W 1 LI 2 1 LI 2
2
2
1 I 2 ( 0 ln 2b a ) 0I 2 ln b a
2
a
2
a
0I 2 ln 2b a 0I 2 ln 2 2 b a 2
一、RL电路的态过程
11
暂态过程、过电压、过电流
0 N 2 I02b ln 4
R2 R1
例 两根长直导线平行放置（ a 、b）, (b>>a)，通
8
有大小相等方向相反的电流I. (1) 求这两导线单位
长度的自感系数(忽略导线内磁通); (2) 若将导线间
距由b增到2b（I不变）,求磁场对单位长度导线做
的功; (3) 导线间距由b增到2b，导线方向上单位长
WM
1 BHV 2
2
磁能密度
wM
WM V
1
B
H
2
B2
2
非均匀磁场总磁能 :WM
v
wdv
1 2
v
B Hdv
2020年高中物理竞赛-电磁感应：磁场的能量 磁场能量密度(含习题一)(共10张PPT)
Ei (vB sin90)o)dldlco csos180o a
I
vBB
v
dl
Blv sin
o
m
x
n x
若棒右移 ，则 Ei 指向：a
b；
a
b
若棒左移，则 Ei 指向： b a。
13 – 5 磁场的能量 磁场能量密度 第十三章电磁感应 电磁场
例 如图，∞载流 I 直导线与导体棒相互垂直，棒以 v 沿
idt
1
LI2
t Ri 2dt
0
2
0
电
电源反 回路电
源
抗自感 阻所放
作 功
电动势 出的焦 作的功 耳热
13 – 5 磁场的能量 磁场能量密度 第十三章电磁感应 电磁场
自感线圈磁能
Wm
1 LI 2 2
IL
L n2V , B nI
Wm
1 2
LI 2
1 2
n
2V
(
B
n
)
2
1 2
B2 V
wmV
磁场能量密度
平面内以 v 运动，已知 θ 。求导体棒的电动势。
提示
dl : a b
(b)
Ei (vB sin )dl cos (a) l
vB
b
v
(vB sin90o ) dl cos(90o )
0
dl
a B
13 – 5 磁场的能量 磁场能量密度 第十三章电磁感应 电磁场
13 – 5 磁场的能量 磁场能量密度 第十三章电磁感应 电磁场
谢谢观看！
wm
B2
2
1 2
H 2
1 2
BH
磁场能量
2020年高中物理竞赛—普通物理学A版-电磁学(第二课时)(共35张PPT) 课件
2020高中物理竞赛
普通物理学A版
2-3.磁聚焦
带电粒子的速度v0与B之间有任意夹角时,它作螺旋运动
把初速v0分解为v//和
v⊥ v⊥
v0
v⊥ v0
B
v//
R z
v//
v// = v0cos v⊥ = v0sin
d
d
螺旋线半径 R mv mv0 sin 由以上结果可实现磁聚焦
qB
qB
回旋周期为 T 2 R 2 m
t
0
RI
2dt
为导体消耗的能量(释放的焦耳热)
1 LI 2 则为电源反抗自感电动势而做的功
2
它作为磁能被储存, 或说转化为磁场的能量.
磁能的建立过程满足能量守恒. 结论: 对自感为L的线圈,储能为:
Wm
1 2
LI 2
二. 磁场能量密度 自感储能为:
Wm
1 2
LI 2
如对体积为V的长直螺线管: L n2V B nI
(电动势的定义:ℰi= ∮Ek·dl , —Ek为非静电场)
感生电场比感生电动势更本质. 即无论是否有导线回路,
只要存在变化的磁场,就一定有感生电场存在.
感生电场Ek与静电场E 的比较: 相同点: 两者都对电荷有力的作用; 不同点: (1)静电场是由电荷激发的,感生电场是变化的磁场激发的; (2)静电场线始于正电荷、止于负电荷,是不闭合的.感生
例题1.
如图所示,半径为0.20m,电流为20A, 可绕Oy 轴旋转的圆形载流线圈 放在均匀磁场中, 磁感强度为B 的大小为0.08T,方向沿x 轴正向.问线 圈受力情况如何? 线圈受的磁力矩又为多少?
解：把圆满线圈分为两个半圆考虑
由上节例题，对半圆JKP
普通物理学A版
2-3.磁聚焦
带电粒子的速度v0与B之间有任意夹角时,它作螺旋运动
把初速v0分解为v//和
v⊥ v⊥
v0
v⊥ v0
B
v//
R z
v//
v// = v0cos v⊥ = v0sin
d
d
螺旋线半径 R mv mv0 sin 由以上结果可实现磁聚焦
qB
qB
回旋周期为 T 2 R 2 m
t
0
RI
2dt
为导体消耗的能量(释放的焦耳热)
1 LI 2 则为电源反抗自感电动势而做的功
2
它作为磁能被储存, 或说转化为磁场的能量.
磁能的建立过程满足能量守恒. 结论: 对自感为L的线圈,储能为:
Wm
1 2
LI 2
二. 磁场能量密度 自感储能为:
Wm
1 2
LI 2
如对体积为V的长直螺线管: L n2V B nI
(电动势的定义:ℰi= ∮Ek·dl , —Ek为非静电场)
感生电场比感生电动势更本质. 即无论是否有导线回路,
只要存在变化的磁场,就一定有感生电场存在.
感生电场Ek与静电场E 的比较: 相同点: 两者都对电荷有力的作用; 不同点: (1)静电场是由电荷激发的,感生电场是变化的磁场激发的; (2)静电场线始于正电荷、止于负电荷,是不闭合的.感生
例题1.
如图所示,半径为0.20m,电流为20A, 可绕Oy 轴旋转的圆形载流线圈 放在均匀磁场中, 磁感强度为B 的大小为0.08T,方向沿x 轴正向.问线 圈受力情况如何? 线圈受的磁力矩又为多少?
解：把圆满线圈分为两个半圆考虑
由上节例题，对半圆JKP
高二物理竞赛课件：磁场的能量(共15张PPT)
磁场的能量
磁场的能量
一、磁能的来源
LR
电流建立过程 磁场储存能量 稳态时：电源作功 = 焦耳热
当K1 电路接通
1K 2
I 增加：电源作功=反抗L作功+焦耳热
电源作功＞焦耳热 有能量储存 K由12 电路断开
结论：电源 提供的能量 的一部分储 存在线圈的 磁场内。
I 减小：L作功=焦耳热
有能量放出
LI L
自感线圈也是一个储 能元件，自感系数反 映线圈储能的本领
磁场能量密度与电场能量密度公式的比较
dV
w
V 在有限区域内
磁场能量公式与电场能量公式具有完全对称的形式!
自感系数只与 装置的几何因 素和介质有关
例题2 有一同轴电缆，由半径为a和b的同轴长圆筒组 成，电流I 由内筒一端流入，经外筒的另一端流出，两
筒间充满磁导率为μ的均匀介质，求单位长度同轴电缆
的自感系数。
解：由安培环路定律可以证明
磁场只存在于两筒之间，距轴为r (a<r<b)处的磁感应强度为
ba
B I
1 2
LI 2
W 1 L I 2 1 n2V I 2 1 ( nI )2V B2 V
m2
2
2
2
磁场能量密度为： w Wm B2
m V 2
wm
B2
2
wm
1 2
BH
1 2
H2
HB
电场能量密度
磁场的能量为： Wm V wmdV
we
1 2
E2
V 是磁场分布的整个空间。
自感储能与电容储能比较
例题3 一长直螺线管,单位长度上的匝数为n，有一 半径为r的圆环放在螺线管内，环平面与管轴垂直，求 螺线管与圆环的互感系数。
磁场的能量
一、磁能的来源
LR
电流建立过程 磁场储存能量 稳态时：电源作功 = 焦耳热
当K1 电路接通
1K 2
I 增加：电源作功=反抗L作功+焦耳热
电源作功＞焦耳热 有能量储存 K由12 电路断开
结论：电源 提供的能量 的一部分储 存在线圈的 磁场内。
I 减小：L作功=焦耳热
有能量放出
LI L
自感线圈也是一个储 能元件，自感系数反 映线圈储能的本领
磁场能量密度与电场能量密度公式的比较
dV
w
V 在有限区域内
磁场能量公式与电场能量公式具有完全对称的形式!
自感系数只与 装置的几何因 素和介质有关
例题2 有一同轴电缆，由半径为a和b的同轴长圆筒组 成，电流I 由内筒一端流入，经外筒的另一端流出，两
筒间充满磁导率为μ的均匀介质，求单位长度同轴电缆
的自感系数。
解：由安培环路定律可以证明
磁场只存在于两筒之间，距轴为r (a<r<b)处的磁感应强度为
ba
B I
1 2
LI 2
W 1 L I 2 1 n2V I 2 1 ( nI )2V B2 V
m2
2
2
2
磁场能量密度为： w Wm B2
m V 2
wm
B2
2
wm
1 2
BH
1 2
H2
HB
电场能量密度
磁场的能量为： Wm V wmdV
we
1 2
E2
V 是磁场分布的整个空间。
自感储能与电容储能比较
例题3 一长直螺线管,单位长度上的匝数为n，有一 半径为r的圆环放在螺线管内，环平面与管轴垂直，求 螺线管与圆环的互感系数。
2020年高中物理竞赛辅导课件(电磁学基础篇)01磁感应强度(共28张PPT)
明代航海用水罗盘
南宋咸淳年间(1265～ 1274)吴自牧在 《梦梁录》里记道：“风雨冥晦时，惟凭 针盘而行，乃火长掌之，毫厘不取差误， 盖一舟人命所系也。”这是中国航海中使 用罗盘的最早记载。
航 海 木
帆 船 用
的 “ 旱
罗 盘 ”
磁感应强度 磁场的高斯定理 一、基本磁现象 磁铁间的相互作用
木龟 磁石 黄蜡 针
点的装钉子上， 可以自由旋转，旋
竹钉 木板
定以后也会指南。
元指代南指南龟龟
自南宋至明中叶，中国航海中所用的罗盘， 都是“水罗盘”。所谓水罗盘，是指磁针浮于水面 没有固定支点的水,浮针盘。明初随郑,和下西洋的 巩珍，在他的《西洋番国志》自序中曾对这种水 罗盘作了记述： “皆□木为盘，书刻干支之字， 浮针于水,指向行舟。”(1522～1566)
1.磁力大小和电荷运动方向有关； 2.当电荷沿某一特定方向运动时磁力为零， 定义磁力为零的方向为磁场的方向（磁场指 向另行规定）。
3.当电荷运动方向和磁场方向垂直时，所
受磁力最大。并且：Fm ∝ q v
而比值 Fm 和 q v 无关,它反映了该点磁场 qv
的强弱,为此定义:
磁感应强度B 的大小:
B=
Fm qv
磁感应强度B 的方向:
Fm × v
（式中 v 为正电荷运动方向）
Bv q
Fm
Bv Fm
磁感应强度B 的单位：特斯拉(Tesla) T
[B] =
[Fm ] [q ] [v ]
=
N C . m/s
= T（特斯拉）
(注：[q ] 表示q 的单位)
1T = 104 Gs（高斯）
三、磁感应线： 直线电流的磁感应线 I
司南
南宋咸淳年间(1265～ 1274)吴自牧在 《梦梁录》里记道：“风雨冥晦时，惟凭 针盘而行，乃火长掌之，毫厘不取差误， 盖一舟人命所系也。”这是中国航海中使 用罗盘的最早记载。
航 海 木
帆 船 用
的 “ 旱
罗 盘 ”
磁感应强度 磁场的高斯定理 一、基本磁现象 磁铁间的相互作用
木龟 磁石 黄蜡 针
点的装钉子上， 可以自由旋转，旋
竹钉 木板
定以后也会指南。
元指代南指南龟龟
自南宋至明中叶，中国航海中所用的罗盘， 都是“水罗盘”。所谓水罗盘，是指磁针浮于水面 没有固定支点的水,浮针盘。明初随郑,和下西洋的 巩珍，在他的《西洋番国志》自序中曾对这种水 罗盘作了记述： “皆□木为盘，书刻干支之字， 浮针于水,指向行舟。”(1522～1566)
1.磁力大小和电荷运动方向有关； 2.当电荷沿某一特定方向运动时磁力为零， 定义磁力为零的方向为磁场的方向（磁场指 向另行规定）。
3.当电荷运动方向和磁场方向垂直时，所
受磁力最大。并且：Fm ∝ q v
而比值 Fm 和 q v 无关,它反映了该点磁场 qv
的强弱,为此定义:
磁感应强度B 的大小:
B=
Fm qv
磁感应强度B 的方向:
Fm × v
（式中 v 为正电荷运动方向）
Bv q
Fm
Bv Fm
磁感应强度B 的单位：特斯拉(Tesla) T
[B] =
[Fm ] [q ] [v ]
=
N C . m/s
= T（特斯拉）
(注：[q ] 表示q 的单位)
1T = 104 Gs（高斯）
三、磁感应线： 直线电流的磁感应线 I
司南
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I
不变。（单位长度上的自感
L
0
ln
d a
）
求：（1）当d→d’时，磁力做的功。 I
（2）磁能改变多少？增加？ 减少？说明能量来源？
I I
解：（1）根据
F
L
0
Idl
B
单位长度受力
F
IlB
I
0 I 2 r
A
d
d
F
dr
d
d
0I 2 2 r
dr
0I 2 2
ln
d d
>
0
r F
d d'
48
（2）磁能改变多少？
以热能形式散发：
Q
Ri 2dt
R( I
2e
2
R L
t
)dt
RI 2
e
2
R L
t
dt
0
1 LI 2 2
L R
i
i
R
e
Rt
L
42
二、磁能与磁能密度
由上可知，通有电流 I 的自感线圈中储能： W 1 LI 2 2
那么,Wm→磁场（ B、 H）,如何联系？
以长直螺线管为例
我们已知长直螺线管的自感为
在回路2的磁场储存的能量为
21
M21
di2 dt
W2
1 2
L2 I22
但此过程在回路1中产生了互感电动势
46
W1
1 2
L1I12
W2
1 2
L2 I22
21
M21
di2 dt
为保持I1不变,回路1的电源 要克服这个电动势作功:
12
A
21dq
I2
M21 0
di2 dt
I1dt
I1
I2
M21I1I2
第4节 磁场的能量
Energy of Magnetic fields
一、自感储存磁能 当线圈通有电流时，
电容器充电后就
储存了电场能量：We
1 2
CU
2
在其周围建立了磁场，所储存的
磁能等于建立磁场过程中，电源
反抗自感电动势所做的功。
若回路电流以di/dt >0变化时，
电流增加di，电源克服L作功为dA
ln d d
A磁力 W 能量守恒
49
本章小结：
1.
法拉第电磁感应定律： i
d
dt
2. 动生电动势 i L Ek dl L(v B) dl
3. 感生电动势
i
Ei
dl
对闭合回路：i
L
Ei
dl
B t
dS
4. 自感、互感的意义， 自感系数L、互感系数M的计算。
5. 磁场能量和磁场能量密度的概念及计算
以上结论对任意形式的磁场都成立！
一般地，对非均匀磁场：
Wm
wmdV
V
1 2
B
HdV
44
三、磁能的计算
例11.一圆柱形同轴电缆,由半径为a、b的薄圆筒构
成, 其间充满磁导率为µ介质,并通有电流 I。
求：长度为h 的电缆内磁场的能量Wm和L？
解：两圆柱面间的磁场为
B
I 2 r
b ra
Wm
1
2
B2dV
II
h
b
a
1 2
I2 (2 r)2
h2 rdr
I 2h 4
ln
b a
由Wm → L
2Wm I2
h 2
ln
b a
45
例12. 证明两个导体回路的互感系数相等。 解: 设两个回路开始处在开路状态 1 2
先接通回路1的电源,
其电流从0I1,
I1
I2
电源W力1 12作L1I12功,储存在磁场的能量为
再接通回路2的电源, 其电流从0I2,
两回路电流分别达到I1, I2时,整个系统的磁能为
Wm
1 2
L1I12
1 2
L2 I22
M21I1I2
若先接通回路2的电源, 则有
Wm
1 2
L1I12
1 2
L2 I 22
M12 I1 I 2
而系统的总能量与建立电流的过程无关:
M21 M12 M 命题得证
47
例13. 两根平行输电线相距为d, 半径为a, 若维持
解：
W
Wd
Wd
1 2
LI 2
1 2
LI 2
0 I 2
2
ln
d d
>0
L
0
ln
d a
I
I
I
能量从何而来?
Li
导线移动时自感电动势
r F
L
d
dt
L
di dt
0I
dL dt
维持I 不变,电源力克服L做功:
A外
Ldq
L
L
I
2dL
I 2 ( L
L)
d d'
I
2
(
0
ln
d a
0
ln
d a
)
0I 2
L 0n2V体
设螺线管通有电流I，则其存储的磁能为：
Wm
1 2LI 2源自1 20n2V体I2
而 B 0nI
即
Wm
B2
20
V体
43
通有电流 I 的长直螺线管储存的磁能为
Wm
B2
20
V体
又长直螺线管管内为均匀磁场!
单位体积储存的磁场能量为
wm
Wm V
B2
20
1 2
B
H
——磁能密度
其中
H
B
0
——磁场强度
50
L R
i
dA= –Ldq = –Lidt
L
L
di dt
dA Lidi
A
dA
I
0Lidi
1 2
LI 2
储存
Wm
1 2
LI 2
41
A
Wm
1 2
LI 2
自感为L的线圈通有电流I 时所储存的磁能， 就等于这电流消失时自感电动势所做的功:
AL
L i dt
0
I
Li
di
1 2
LI 2
Wm
自感电动势所做的功，电阻R