八年级不等式培优提高练习.doc
不等式复习专题培优训练【含答案】
三、不等式（组）一、学习目标1、一元一次不等式（组）的解法.2、一元一次不等式（组）的整数解.3、一元一次不等式（组）的实际应用题二、知识要点1、不等式的概念；2、不等式的解集3、用数轴表示不等式的方法4、不等式的基本性质5、一元一次不等式的概念及解法6、一元一次不等式组的概念及解法7、一元一次不等式（组）的实际应用题三、考点再现1、不等式x 8x 25-≤-的负整数解是_________________.2、（2009泸州）关于x 的方程的解为正实数，则k 的取值范围是x kx 21=-3、（08山东日照）在平面直角坐标系中，若点P(m －3，m ＋1)在第二象限，则m 的取值范围为 （ ）A 、 －1＜m ＜3B 、 m ＞3C 、 m ＜－１D 、 m ＞－１ 4、（2009恩施市）如果一元一次不等式组的解集为．则的取值范围是（ ）3x x a>⎧⎨>⎩3x >a A ． B ． C ． D ．3a>a ≥3a ≤33a <5、（08永州） 如图，a 、b 、c 分别表示苹果、梨、桃子的质量，同类水果质量相等，则下列关系正确的是（ ）A a ＞c ＞bB b ＞a ＞cC a ＞b ＞cD c ＞a ＞b6、（08湖北咸宁）直线与直线在同一平面直角坐标系中的图象如:1l b x k y +=11:2l x k y 22=图所示，则关于的不等式的解集为 ；x b x k x k +>12四、典例剖析考查目标一：一元一次不等式（组）的解法.例1.（2009年内蒙古包头）解不等式：x 121x ≥+-，并把解集表示在数轴上.解：去分母得：x221x ≥+-移项，合并同类项得：1x -≥-系数化为1，得：1x ≤解集在数轴上表示为：评注：熟练掌握不等式的基本性质是正确的解一元一次不等式的基础.解不等式的一般步骤与解方程的步骤相同.但要特别注意“不等式两边同乘以（或除以）一个负数时，必须改变不等号的方向”，这是一个难点和易错点.例2.（2009恩施市）若不等式组⎩⎨⎧>->-0x 2b 2a x 的解集是1x 1<<-，则=_______.2009()a b +解：解原不等式组得 ⎪⎩⎪⎨⎧<+>2bx a 2x 因为不等式组的解集为：1x 1<<-⎩⎨⎧=-=∴⎪⎩⎪⎨⎧=-=+∴2b 3a ，12b 12a 200920091()(32)a b ==-+-+评注：一元一次不等式组的解集的求法是：（1）先分别求出各不等式的解集；（2）再利用数轴求出多个解集的公共部分就是这个不等式组的解集，若各不等式的解集没有公共部分，则这个不等式组无解.考查目标二：一元一次不等式（组）的整数解.例3. （2009年崇左）解不等式组⎪⎩⎪⎨⎧+<-≤-②①)1x (42x 121x ，并写出不等式组的正整数解.解：解不等式①得：3x ≤ 解不等式②得：2x->3,2,13x 2不等式组的正整数解是不等式组的解集是∴≤<-∴评注：求一元一次不等式（组）的整数解的一般步骤是：先求出一元一次不等式（组）的解集，再确定适合解集范围的整数解、正整数解、非负整数解（自然数解）等特殊解，有时借助于数轴会更直观.考查目标三：一元一次不等式（组）的实际应用题例4（2009年湖北十堰）为执行中央“节能减排，美化环境，建设美丽新农村”的国策，我市某村计划建造A 、B 两种型号的沼气池共20个，以解决该村所有农户的燃料问题．两种型号沼气池的占地面积、使用农户数及造价见下表：型号占地面积(单位:m 2/个 )使用农户数(单位:户/个)造价(单位: 万元/个)A 15182B20303已知可供建造沼气池的占地面积不超过365m 2，该村农户共有492户．(1)满足条件的方案共有几种?写出解答过程．(2)通过计算判断，哪种建造方案最省钱．解: (1) 设建造A 型沼气池 x 个，则建造B 型沼气池(20－x )个依题意得: ()()⎩⎨⎧≥-+≤-+492203018365202015x x x x解得：7≤ x ≤ 9∵ x 为整数 ∴ x = 7，8 ，9 ，∴满足条件的方案有三种．(2)设建造A 型沼气池 x 个时，总费用为y 万元，则： y = 2x + 3( 20－x) = －x+ 60∵－1< 0，∴y 随x 增大而减小，当x=9 时，y 的值最小，此时y= 51( 万元 )∴此时方案为：建造A 型沼气池9个，建造B 型沼气池11个． ∴方案三最省钱.评注：一元一次不等式（组）在实际生活中有着广泛的应用，解此类实际问题时，需从题目中捕捉不等关系，用不等式（组）将它们表示出来，通过解不等式（组）找出符合题意的解.五、达标训练(一)选择题1．(2009临沂中考) 若，则下列式子错误的是（ ）x y >A ． B ． C ．D ．33x y ->-33xy ->-32x y +>+33x y >2．（2009年四川泸州）不等式组 的解集是 （ ）2131x x -<⎧⎨≥-⎩A. B. C. D ．无解2x<1-≥x 12x -≤<3. （2010南宁）不等式组的正整数解有：24,241x x x x +⎧⎨+<-⎩≤（Ａ）1个 （Ｂ）2个 （Ｃ）3个 （Ｄ）4个4.（2010年福建模拟）关于x 的不等式22≤+-a x 的解集如图所示，那么a 的值是…（ ）Ａ．－4 Ｂ．－2Ｃ．0 Ｄ．２5、（2009湖北省荆门市）若不等式组0,122x a x x +⎧⎨->-⎩≥有解，则a 的取值范围是（ ）A ．B ．C ．D ．1a>-1a -≥1a ≤1a <6．（2009年山东日照）不等式组 的解集在数轴上表示正确的是（ ）⎪⎩⎪⎨⎧≥--+2321123x ,x x ＞ABC-310D7．已知(x+3)2+＝0中，y 为负数，则m 的取值范围是m y x ++3A.mB.mB.m B.m ＜9 CD.mD.m D.m ＜－98．观察图像，可以得出不等式组 的解集是⎩⎨⎧>+->+015.0013x x A.x ＜B.－＜x ＜0C.0＜x ＜2D.－＜x ＜2313131（二）填空题1（2010潍坊）已知不等式，则的最小)2(2643-+≤+x x 1+x 值等于——2．（2009年杭州）已知关于的方程的解是正数，则m 的取值范围为________x 322=-+x mx 3．已知二次函数和直线)0(21≠++=a c bx ax y )0(2≠+=k b kx y 如图，则当时，；______x 21y y >4．(2009武汉)．如图，直线y kx b =+经过(21)A ，，(12)B --，两点，则不等式122x kx b >+>-的解集为 ． 5、（2009长沙）已知关于的不等式组只有四个整数解，则的取值范围是x 0521x a x -⎧⎨->⎩≥，．6．（2009年烟台市）如果不等式组的解集是，那么的值为 ．2223xa xb ⎧+⎪⎨⎪-<⎩≥01x <≤a b +（三）解答题1、（2009年天津市）解不等式组，并在数轴上把解集表示出来.⎪⎩⎪⎨⎧-<--≥+-)2(x8)1x (31)1(x 323x 2、当关于、的二元一次方程组的解为正数，为负数，则求此时的取x y ⎩⎨⎧-=--=+my x m y x 432522x y m 值范围？3、（2009年青岛市）北京奥运会开幕前，某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．（1）该商场两次共购进这种运动服多少套？（2）如果这两批运动服每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？（利润率）100%=⨯利润成本4、( 2009年威海)响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超过元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200元/台、1 600元/台、2 000元/台．(1)至少购进乙种电冰箱多少台？(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？六、学习感悟三、不等式答案考点再现：1、-3，-2，-1；2、K ＞2；3、A; 4、C; 5、C; 6、x ＜-1. 达标训练：（一）选择题1、B;2、C;3、C;4、c;5、A;6、A;7、B;8、D.(二)填空题1、=1；2、m ＞-6;3、-5＜x ＜1;4、-1＜x ＜2;5、-3＜a≤-2;6、1;7、a ＞4.(三)解答题1、-2＜x≤3; 2、m ＜-1.3、解：（1）设A 、B 两种纪念品的进价分别为x 元、y 元。
初二数学《不等式分式》提高练习题
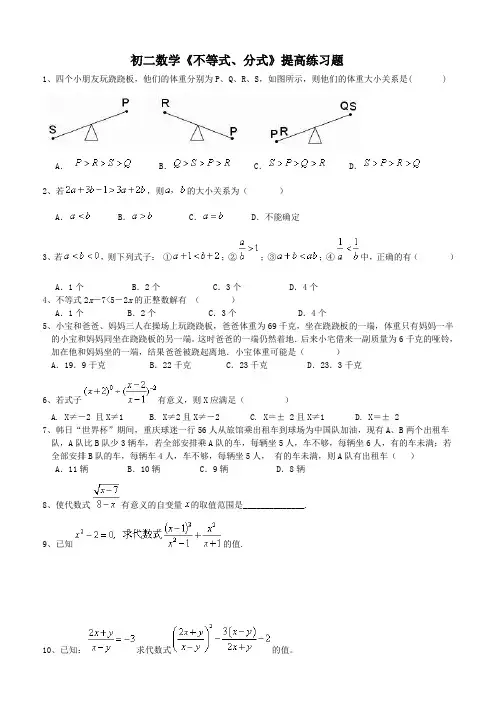
初二数学《不等式、分式》提高练习题1、四个小朋友玩跷跷板，他们的体重分别为P、Q、R、S，如图所示，则他们的体重大小关系是( )A．B． C． D．2、若，则的大小关系为（）A． B．C． D．不能确定3、若，则下列式子：①；②；③；④中，正确的有（）A．1个 B．2个 C．3个 D．4个4、不等式2x－7<5－2x的正整数解有（）A．1个B．2个 C．3个 D．4个5、小宝和爸爸、妈妈三人在操场上玩跷跷板，爸爸体重为69千克，坐在跷跷板的一端，体重只有妈妈一半的小宝和妈妈同坐在跷跷板的另一端。
这时爸爸的一端仍然着地．后来小宅借来一副质量为6千克的哑铃，加在他和妈妈坐的一端，结果爸爸被跷起离地．小宝体重可能是（）A．19．9于克 B．22千克 C．23千克 D．23．3千克6、若式子有意义，则X应满足（）A. X≠－2 且X≠1B. X≠2且X≠－2C. X＝± 2且X≠1D. X＝± 27、韩日“世界杯”期间，重庆球迷一行56人从旅馆乘出租车到球场为中国队加油，现有A、B两个出租车队，A队比B队少3辆车，若全部安排乘A队的车，每辆坐5人，车不够，每辆坐6人，有的车未满；若全部安排B队的车，每辆车4人，车不够，每辆坐5人，•有的车未满，则A队有出租车（）A．11辆 B．10辆 C．9辆 D．8辆8、使代数式有意义的自变量的取值范围是______________.9、已知的值.10、已知：求代数式的值。
11每户每月用水量不超过10吨（含10吨）超过10吨的部分水费单价 1.30元/吨 2.00元/吨（1（2）若小华家四月份付水费17元，问他家四月份用水多少吨？（3）已知某住宅小区100户居民五月份交水费共1682元，且该月每户用水量均不超过15吨（含15吨），求该月用水量不超过10吨的居民最多可能有多少户？12、县公路局为了对某段公路进行绿化，计划购买A、B两种树共900棵，A、B两种树的相关信息如下表：项目单价(元／棵) 成活率品种A 80 92％B 100 98%设购买A种树x棵，购树所需的总费用为y元．(1)求y与x之间的函数关系式；(2)若购树的总费用不超过82000元，则购A种树不少于多少棵?(3)若希望这批树的成活率不低于94％，且使购树的总费用最低，应选购A、B两种树各多少棵?此时最低费用为多少?13、某公司有型产品40件，型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：型利润型利润甲店200 170乙店160 150（1）设分配给甲店型产品件，这家公司卖出这100件产品的总利润为（元），求关于的函数关系式，并求出的取值范围；（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；（3）为了促销，公司决定仅对甲店型产品让利销售，每件让利元，但让利后型产品的每件利润仍高于甲店型产品的每件利润．甲店的型产品以及乙店的型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？14、求不等式的整数解。
八年级不等式培优题
不等式提高练习一、选择题(每小题3分，共30分)1..下列不等式一定成立的是( )A.5a ＞4aB.x +2＜x +3C.－a ＞－2aD.aa 24> 2.不等式－3x +6＞0的正整数有( )A.1个B.2个C.3个D.无数多个3. .在数轴上与原点的距离小于8的点对应的x 满足( )A.－8＜x ＜8B.x ＜－8或x ＞8C.x ＜8D.x ＞84.若不等式组⎩⎨⎧>≤11x m x 无解，则m 的取值范围是( )A.m ＜11B.m ＞11C.m ≤11D.m ≥115.要使函数y =(2m －3)x +(3n +1)的图象经过x 、y 轴的正半轴，则m 与n 的取值应为( )A.m ＞23，n ＞－31B.m ＞3，n ＞－3C.m ＜23，n ＜－31D.m ＜23，n ＞－31 6. 如右图，当0<y 时，自变量 x 的范围是（ ）A 、2-<xB 、2->xC 、2<xD 、2>x7. 如果10<<x ，则下列不等式成立的（ ）A 、x x x 12<<B 、x x x 12<<C 、21x x x <<D 、x x x<<21 8. 若a>b>0, 则下列结论正确的是 （ ）(A) -a>-b (B)ba 11> (C)a 3<0 (D)a 2>b 29.某射击运动员在一次比赛中前6次射击共中52环,如果他要打破89环(10次射击)的记录，第七次射击不能少于（ ）环（每次射击最多是10环）A 、5B 、6C 、7D 、810.初三的几位同学拍了一张合影作留念，已知冲一张底片需要0.80元，洗一张相片需要0.35元．在每位同学得到一张相片、共用一张底片的前提下，平均每人分摊的钱不足0.5元，那么参加合影的同学人数 .Ａ．至多6人 Ｂ．至少6人 Ｃ．至多5人 Ｄ．至少5人11.不等式组⎪⎩⎪⎨⎧≤-->84332x x 的最小整数解为 ( ) (A)–1 (B) 0 (C)1 (D) 412、如果10<<x ，则下列不等式成立的（ ）A 、x x x 12<<B 、x x x 12<<C 、21x x x <<D 、x x x<<21 13、在平面直角坐标系内，点P （3-m ，5-m ）在第四象限，则m 的取值范围是（ ）A 、35<<-mB 、53<<-mC 、53<<mD 、35-<<-m二、填空题：（每题3分，共15分）1、若11|1|-=--x x ，则x 的取值范围是_______ 2、 如果关于x 的不等式5)1(+<-a x a 和42<x 的解集相同，则a 的值为________．3、若b a <，用“＜”或“＞”号填空：2a______b a +，33a b -_____． 4、 点A （－5，1y ）、B （－2，2y ）都在直线x y 2-=上，则1y 与2y 的关系是 。
第3章 一元一次不等式 浙教版数学八年级上册培优试卷(含答案)
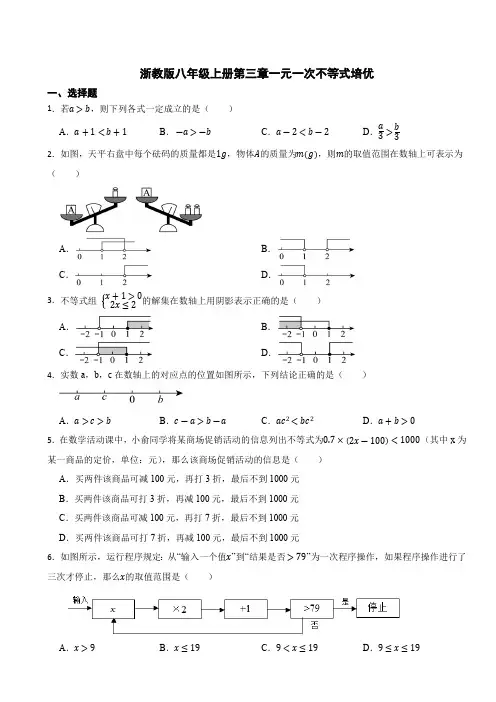
浙教版八年级上册第三章一元一次不等式培优一、选择题1．若a>b，则下列各式一定成立的是（ ）A．a+1<b+1B．―a>―b C．a―2<b―2D．a3>b32．如图，天平右盘中每个砝码的质量都是1g，物体A的质量为m(g)，则m的取值范围在数轴上可表示为（ ）A．B．C．D．3．不等式组x+1>02x≤2的解集在数轴上用阴影表示正确的是（ ）A．B．C．D．4．实数a，b，c在数轴上的对应点的位置如图所示，下列结论正确的是（ ）A．a>c>b B．c―a>b―a C．a c2<b c2D．a+b>05．在数学活动课中，小俞同学将某商场促销活动的信息列出不等式为0.7×(2x―100)<1000（其中x为某一商品的定价，单位：元），那么该商场促销活动的信息是（ ）A．买两件该商品可减100元，再打3折，最后不到1000元B．买两件该商品可打3折，再减100元，最后不到1000元C．买两件该商品可减100元，再打7折，最后不到1000元D．买两件该商品可打7折，再减100元，最后不到1000元6．如图所示，运行程序规定：从“输入一个值x”到“结果是否>79”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（ ）A．x>9B．x≤19C．9<x≤19D．9≤x≤197．若关于x 的不等式组4―(x ―2)≥33x ―a >2x有且只有4个整数解，则a 的取值范围是（ ）A ．―1≤a <0B ．―1<a ≤0C ．0<a ≤1D ．0≤a <18．若x 为实数，则[x ]表示不大于x 的最大整数，例如[1,6]=1,[π]=3,[―2,82]=―3等．[x ]+1是大于x 的最小整数，则方程6x ―3[x ]+9=0的解是（ ）A ．x =―83B ．x =―196C ．x =―72或x =―3D ．x =―83或x =―1969．已知三个实数a ，b ，c 满足a ―2b ―c =0，a +2b ―c <0，则（ ）A ．b <0，b 2+ac ≤0B ．b <0，b 2+ac ≥0C ．b >0，b 2+ac ≤0D ．b >0，b 2+ac ≥010． 已知关于x 的分式方程mx(x ―2)(x ―6)+2x ―2=3x ―6无解，且关于y 的不等式组m ―y >4y ―4≤3(y +4)有且只有三个偶数解，则所有符合条件的整数m 的乘积为（ ）A ．1B ．2C ．4D ．8二、填空题11．若(m ―1)x >(m ―1)的解集是x <1，则m 的取值范围是 ；12．一罐饮料净重300g ，罐上标注有“蛋白质含量≥0.5%”，其中蛋白质的含量至少为 g ．13．若关于x 的不等式组x <1x ≤a 的解集是x <1，则a 的值可以是 （写出一个即可）．14．关于x 的方程k ―2x =3(k ―2)的解为非负数，且关于x 的不等式x ―2(x ―1)≤32k +x 3≥x 有解，求符合条件的所有整数k 的值的积为 ．15．若关于x 的不等式组―6<x <2x ―m <m无解，那么m 的取值范围是 16．对非负实数x“四舍五入”到个位的值记为＜x ＞，即：当n 为非负整数时，如n ﹣12≤x ＜n+12，则＜x ＞＝n ．如：＜0.48＞＝0，＜3.5＞＝4．如果＜x ＞＝97x ，则x ＝ ．三、解答题17．课堂上，老师设计了“接力游戏”，规则：一列同学每人只完成解不等式的一步变形，即前一个同学完成一步，后一个同学接着前一个同学的步骤进行下一步变形，直至解出不等式的解集．请根据下面的“接力游戏”回答问题．接力游戏老师：3x +12―1>5x ―43甲同学：3(3x +1)―6>2(5x ―4)乙同学：9x+3―6>10x―8丙同学：9x―10x>―8―3+6丁同学：―x>―5戊同学：x>5任务一：①在“接力游戏”中，乙同学是根据______进行变形的．A．等式的基本性质B．不等式的基本性质C．乘法对加法的分配律②在“接力游戏”中，出现错误的是______同学，这一步错误的原因是______．任务二：在“接力游戏”中该不等式的正确解集是______．任务三：除纠正上述错误外，请你根据平时的学习经验，针对解不等式时还需要注意的事项给同学们提一条建议．18．解不等式1―x3―x<3―x+24．并把解集表示在数轴上．19．解不等式组：5x―6≤2(x+2) x4―1<x―3320．如图，点A，B均在数轴上，点B在点A的右侧，点A对应的数字是―4，点B对应的数字是m．（1）若AB=2，求m的值；（2）将AB线段三等分，这两个等分点所对应数字从左到右依次是a1，a2，若a2>0，求m的取值范围．21．如图所示的是某大院窗格的一部分，其中“O”代表窗格上所贴的剪纸，设第x个窗格上所贴“O”的个数为y．（1）填写下表．x12345xy581117（用含x的式子表示）（2）若第x个窗格上所贴的“O”的个数大于50，求x的取值范围．22．如图，在平面直角坐标系xOy中，已知A(1,a)，B(b,3)，E(3―a,0)，其中a，b满足|a―5|+b―4=0．平移线AB段得到线段CD，使得C，D两点分别落在y轴和x轴上．（1）①点A的坐标是____________；点B的坐标是____________；②求三角形OCD的面积．（2）将点E向下移动1个单位长度得到点F，连接FC，FD，Q(m,0)是x轴负半轴上一点．若三角形QCD 的面积不小于三角形FCD的面积，求m的取值范围．23．如图，在平面直角坐标系中，三角形ABC的三个顶点的坐标分别为A(a,0)，B(0,b)，C(2,4)，且2a+b+10+|3a―2b+8|=0．（1）求a，b的值；，求t的取值范围；（2）点D(t,0)为x轴上一点，且S三角形ABD≤13S三角形ABC（3）平移三角形ABC到三角形EFG（其中点A，B，C的对应点分别为点E，F，G），设E(m,n)，F (p,q)，且满足5m―n=43p―q=4，请直接写出点G的坐标．答案解析部分1．【答案】D 2．【答案】A 3．【答案】C 4．【答案】C 5．【答案】C 6．【答案】C 7．【答案】A 8．【答案】C 9．【答案】B 10．【答案】B 11．【答案】m <112．【答案】1.513．【答案】2（答案不唯一）14．【答案】015．【答案】m ≤―316．【答案】0或79或149．17．【答案】任务一：①C ；②戊；不等式的两边同时乘以―1，不等号的方向没有改变任务二：x <5任务三：去括号时，括号前面是“―”，去括号后，括号的每一项都要变号，或移项要变号18．【答案】x >―219．【答案】0<x ≤10320．【答案】（1）―2（2）m >221．【答案】（1）14，3x +2（2）x >16．22．【答案】（1）①A (1,5)，B (4,3)，②3（2）m ≤―7223．【答案】（1）a 的值为―4，b 的值为―2（2）―10≤t ≤2（3）G(8，10)。
初中不等式提高试题(初二)(整理)
初中不等式提高试题1.不等式2(x + 1) - 12732x x 的解集为_____________。
2．同时满足不等式7x + 4≥5x – 8和523x x的整解为______________。
3．如果不等式33131x mx 的解集为x >5，则m 值为___________。
4．不等式7 x – 2kx <2k +6的解集为_____________。
5．关于x 的不等式(5 – 2m)x > -3的解是正数，那么m 所能取的最小整数是__________。
1、解不等式252133x 2、求下列不等式组的整数解2(2)83373(2)82xx x x x x3、解不等式：（1）0)2)(1(x x （2）0121x x4、对于1x 的一切有理数，不等式12x a a 都成立，求a 的取值范围。
5、已知1x 是不等式组352,23425x x a x a x 的解，求a 的取值范围.6、如果35x a 是不等式11233x x 的解，求a 的取值范围。
7、若不等式组841,x x x m 的解集为3x ，求m 的取值范围。
8、如果不等式组237,635x a b b x a 的解集为522x ，求a 和b 的值。
9、不等式组622131m x m x 的解集是36m x ，求m 的取值范围。
10、已知关于x 的不等式12a x 的解在2x 的范围内，求a 的取值范围。
11、已知关于x 的不等式组010x a x ，的整数解共有3个，求a 的取值范围。
12、已知关于x 的不等式组0321x ax 的整数解共有5个，求a 的取值范围。
13、若关于x 的不等式组2145,x x x a 无解，求a 的取值范围。
14、设关于x 的不等式组22321x mx m 无解，求m 的取值范围15、若不等式组a x a x 无解，那么不等式11a x a x 有没有解？若有解，请求出不等式组的解集；若没有请说明理由？16、若不等式组372,x x a a有解，求a 的取值范围。
初中数学不等式与不等式组提高题与常考题和培优题(含解析)
初中数学不等式与不等式组提高题与常考题和培优题(含解析)一．选择题（共13小题）1．已知a＞b，下列关系式中一定正确的是（）A．a2＜b2B．2a＜2b C．a+2＜b+2 D．﹣a＜﹣b2．不等式2x+3＞3x+2的解集在数轴上表示正确的是（）A．B．C．D．3．若关于x的不等式3﹣x＞a的解集为x＜4，则关于m的不等式2m+3a＜1的解为（）A．m＜2 B．m＞1 C．m＞﹣2 D．m＜﹣14．关于x的不等式x﹣b≥0恰有两个负整数解，则b的取值范围是（）A．﹣3＜b＜﹣2 B．﹣3＜b≤﹣2 C．﹣3≤b≤﹣2 D．﹣3≤b＜﹣2 5．不等式组的最小整数解是（）A．0 B．﹣1 C．﹣2 D．36．已知点P（1﹣2a，a+3）在第二象限，则a的取值范围是（）A．a＜﹣3 B．a＞C．﹣＜a＜3 D．﹣3＜a＜7．不等式组的整数解的个数是（）A．4 B．5 C．6 D．无数个8．已知且﹣1＜x﹣y＜0，则k的取值范围为（）A．﹣1＜k＜﹣B．＜k＜1 C．0＜k＜1 D．0＜k＜9．不等式组的解集，在数轴上表示正确的是（）A．B．C．D．10．当0＜x＜1时，x2、x、的大小顺序是（）A．x2B．＜x＜x2C．＜x D．x＜x2＜11．三个连续正整数的和小于39，这样的正整数中，最大一组的和是（）A．39 B．36 C．35 D．3412．“一方有难，八方支援”，雅安芦山4•20地震后，某单位为一中学捐赠了一批新桌椅，学校组织初一年级200名学生搬桌椅．规定一人一次搬两把椅子，两人一次搬一张桌子，每人限搬一次，最多可搬桌椅（一桌一椅为一套）的套数为（）A．60 B．70 C．80 D．9013．运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（）A．x≥11 B．11≤x＜23 C．11＜x≤23 D．x≤23二．填空题（共12小题）14．不等式组的解集是．15．不等式5x﹣3＜3x+5的所有正整数解的和是．16．若关于x的不等式3m﹣2x＜5的解集是x＞3，则实数m的值为．17．若不等式x＜2的解集都能使关于x的一次不等式（a﹣3）x＜a+5成立，则a的取值范围是．18．若关于x的一元一次不等式组有解，则a的取值范围是．19．在实数范围内规定新运算“△”，其规则是：a△b=2a﹣b．已知不等式x△k ≥1的解集在数轴上如图表示，则k的取值范围是．20．已知满足不等式3（x﹣2）+5＜4（x﹣1）+6的最小整数解是方程：2x﹣ax=3的解，则a的值为．21．关于x的不等式组的解集为x＜3，那么m的取值范围是．22．已知x=2是不等式ax﹣3a+2≥0的解，且x=1不是这个不等式的解，则实数a的取值范围是．23．四个小朋友玩跷跷板，他们的体重分别为P，Q，R，S，如下图所示，则他们的体重从小到大是（用“＜”号连接）．24．下列判断中，正确的序号为．①若﹣a＞b＞0，则ab＜0；②若ab＞0，则a＞0，b＞0；③若a＞b，c≠0，则ac＞bc；④若a＞b，c≠0，则ac2＞bc2；⑤若a＞b，c≠0，则﹣a﹣c＜﹣b﹣c．25．小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入小球时有水溢出．三．解答题（共15小题）26．解不等式﹣1≤，并把解集在数轴上表示出来．27．解不等式组：．28．x取哪些整数值时，不等式5x+2＞3（x﹣1）与x≤2﹣都成立？29．已知关于x的不等式组有四个整数解，求实数a的取值范围．30．已知关于x，y的方程组的解满足不等式组，求满足条件的m的整数值．31．已知x=3是关于x的不等式的解，求a的取值范围．32．已知关于x、y的方程组的解满足不等式x+y＜3，求实数a的取值范围．33．关于x的两个不等式①＜1与②1﹣3x＞0（1）若两个不等式的解集相同，求a的值；（2）若不等式①的解都是②的解，求a的取值范围．34．解不等式组．把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解．35．某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：A B进价（元/件）12001000售价（元/件）13801200（1）该商场购进A、B两种商品各多少件；（2）商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？36．某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．（1）请问榕树和香樟树的单价各多少？（2）根据学校实际情况，需购买两种树苗共150棵，总费用不超过10840元，且购买香樟树的棵树不少于榕树的1.5倍，请你算算，该校本次购买榕树和香樟树共有哪几种方案．37．某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元，40元，商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．（1）求商场销售A、B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）（2）商场准备用不多于2500元的资金购进A、B两种型号计算器共70台，问最少需要购进A型号的计算器多少台？38．某工程机械厂根据市场需求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22400万元，但不超过22500万元，且所筹资金全部用于生产此两种型号挖掘机，所生产的此两种型号挖掘机可全部售出，此两型挖掘机的生产成本和售价如下表：型号A B成本（万元/台）200240售价（万元/台）250300（1）该厂对这两型挖掘机有哪几种生产方案？（2）该厂如何生产能获得最大利润？（3）根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高m万元（m＞0），该厂应该如何生产获得最大利润？（注：利润=售价﹣成本）39．暑期中，哥哥和弟弟二人分别编织28个中国结，已知弟弟单独编织一周（7天）不能完成，而哥哥单独编织不到一周就已完成．哥哥平均每天比弟弟多编2个．求：（1）哥哥和弟弟平均每天各编多少个中国结？（答案取整数）（2）若弟弟先工作2天，哥哥才开始工作，那么哥哥工作几天，两人所编中国结数量相同？40．冷饮店每天需配制甲、乙两种饮料共50瓶，已知甲饮料每瓶需糖14克，柠檬酸5克，乙饮料每瓶需糖6克，柠檬酸10克，现有糖500克，柠檬酸400克．（1）请计算有几种配制方案能满足冷饮店的要求；（2）冷饮店对两种饮料上月的销售情况作了统计，结果如下表，请你根据这些统计数据确定一种比较合理的配制方案，并说明理由．两种饮料的日销量甲101214 16 21 253038 4050乙4038363429252012100天数3444811122初中数学一元一次不等式提高题与常考题和培优题(含解析)参考答案与试题解析一．选择题（共13小题）1．（2017•青浦区一模）已知a＞b，下列关系式中一定正确的是（）A．a2＜b2B．2a＜2b C．a+2＜b+2 D．﹣a＜﹣b【分析】根据不等式的性质分别进行判断，即可求出答案．【解答】解：A，a2＜b2，错误，例如：2＞﹣1，则22＞（﹣1）2；B、若a＞b，则2a＞2b，故本选项错误；C、若a＞b，则a+2＞b+2，故本选项错误；D、若a＞b，则﹣a＜﹣b，故本选项正确；故选：D．【点评】此题考查了不等式的性质，掌握不等式的性质是解题的关键，不等式的基本性质：（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变．（2）不等式两边乘（或除以）同一个正数，不等号的方向不变．（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．2．（2017•朝阳区校级一模）不等式2x+3＞3x+2的解集在数轴上表示正确的是（）A．B．C．D．【分析】先根据不等式的性质求出此不等式的解集，再根据不等式的解集在数轴上的表示方法即可求解．【解答】解：2x+3＞3x+2，解得x＜1，故选D．【点评】本题考查了在数轴上表示不等式的解集，用数轴表示不等式的解集时，要注意“两定”：一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点；二是定方向，定方向的原则是：“小于向左，大于向右”．也考查了解不等式．3．（2017•邢台县一模）若关于x的不等式3﹣x＞a的解集为x＜4，则关于m的不等式2m+3a＜1的解为（）A．m＜2 B．m＞1 C．m＞﹣2 D．m＜﹣1【分析】首先求出不等式的解集，与x＜4比较，就可以得出a的值，然后解不等式即可．【解答】解：解不等式3﹣x＞a，得x＜3﹣a，又∵此不等式的解集是x＜4，∴3﹣a=4，∴a=﹣1，∴关于m的不等式为2m﹣3＜1，解得m＜2．故选A．【点评】此题主要考查了一元一次不等式的解法．解一元一次不等式的一般步骤是：去分母，去括号，移项，合并同类项，系数化为1．4．（2017•兴化市校级一模）关于x的不等式x﹣b≥0恰有两个负整数解，则b 的取值范围是（）A．﹣3＜b＜﹣2 B．﹣3＜b≤﹣2 C．﹣3≤b≤﹣2 D．﹣3≤b＜﹣2【分析】解不等式可得x≥b，根据不等式的两个负整数解为﹣1、﹣2即可得b 的范围．【解答】解：解不等式x﹣b≥0得x≥b，∵不等式x﹣b≥0恰有两个负整数解，∴不等式的两个负整数解为﹣1、﹣2，∴﹣3＜b≤﹣2，故选：B．【点评】本题考查了不等式的正整数解，解题的关键是注意能根据整数解的具体数值，找出不等式解集的具体取值范围．5．（2017•茂县一模）不等式组的最小整数解是（）A．0 B．﹣1 C．﹣2 D．3【分析】首先解不等式组确定不等式组的解集，即可确定不等式组的最小整数解．【解答】解：解不等式（1）得：x＞﹣，则不等式组的解集是：﹣＜x≤3，故最小的整数解是：﹣1．故选B．【点评】本题主要考查了不等式组的整数解的确定，关键是正确解得不等式组的解集．6．（2017•南雄市校级模拟）已知点P（1﹣2a，a+3）在第二象限，则a的取值范围是（）A．a＜﹣3 B．a＞C．﹣＜a＜3 D．﹣3＜a＜【分析】根据第二象限内点的横坐标小于零，纵坐标大于零，可得不等式组，根据解不等式组，可得答案．【解答】解：由点P（1﹣2a，a+3）在第二象限，得．解得a＞，故选B．【点评】本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．7．（2017•邢台县一模）不等式组的整数解的个数是（）A．4 B．5 C．6 D．无数个【分析】先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求其整数解即可．【解答】解：，由①得：x＞﹣2，由②得：x≤4．则不等式组的解集是：﹣2＜x≤4．则整数解是：﹣1，0，1，2，3，4共6个．故选C．【点评】本题考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．8．（2017春•萧山区校级月考）已知且﹣1＜x﹣y＜0，则k的取值范围为（）A．﹣1＜k＜﹣B．＜k＜1 C．0＜k＜1 D．0＜k＜【分析】先根据方程组将两式相减，得到x﹣y=1﹣2k，再代入﹣1＜x﹣y＜0，得到关于k的不等式组，进而得出k的取值范围．【解答】解：∵∴（2x+y）﹣（x+2y）=（2k+1）﹣4k，∴x﹣y=1﹣2k，又∵﹣1＜x﹣y＜0，∴﹣1＜1﹣2k＜0，解得＜k＜1．故选：B．【点评】本题主要考查了解一元一次不等式组以及解二元一次方程组，解决问题的关键是根据方程组求得x﹣y=1﹣2k，运用整体思想进行代入计算．9．（2016•）不等式组的解集，在数轴上表示正确的是（）A．B．C．D．【分析】解出不等式组的解集，即可得到哪个选项是正确的，本题得以解决．【解答】解：由①，得x＜4，由②，得x≤﹣3，由①②得，原不等式组的解集是x≤﹣3；故选A．【点评】本题考查解一元一次不等式组、在数轴上表示不等式的解集，解题的关键是明确解一元一次不等式组的方法．10．（2016•）当0＜x＜1时，x2、x、的大小顺序是（）A．x2B．＜x＜x2C．＜x D．x＜x2＜【分析】先在不等式0＜x＜1的两边都乘上x，再在不等式0＜x＜1的两边都除以x，根据所得结果进行判断即可．【解答】解：当0＜x＜1时，在不等式0＜x＜1的两边都乘上x，可得0＜x2＜x，在不等式0＜x＜1的两边都除以x，可得0＜1＜，又∵x＜1，∴x2、x、的大小顺序是：x2＜x＜．故选A【点评】本题主要考查了不等式，解决问题的关键是掌握不等式的基本性质．不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变，即：若a＞b，且m＞0，那么am＞bm或＞．11．（2016•）三个连续正整数的和小于39，这样的正整数中，最大一组的和是（）A．39 B．36 C．35 D．34【分析】设三个连续正整数分别为x﹣1，x，x+1，列出不等式即可解决问题．【解答】解：设三个连续正整数分别为x﹣1，x，x+1．由题意（x﹣1）+x+（x+1）＜39，∴x＜13，∵x为整数，∴x=12时，三个连续整数的和最大，三个连续整数的和为：11+12+13=36．故选B．【点评】本题考查一元一次不等式的应用，解题的关键是构建不等式解决问题，属于中考常考题型．12．（2016•）“一方有难，八方支援”，雅安芦山4•20地震后，某单位为一中学捐赠了一批新桌椅，学校组织初一年级200名学生搬桌椅．规定一人一次搬两把椅子，两人一次搬一张桌子，每人限搬一次，最多可搬桌椅（一桌一椅为一套）的套数为（）A．60 B．70 C．80 D．90【分析】设可搬桌椅x套，即桌子x张、椅子x把，则搬桌子需2x人，搬椅子需人，根据总人数列不等式求解可得．【解答】解：设可搬桌椅x套，即桌子x张、椅子x把，则搬桌子需2x人，搬椅子需人，根据题意，得：2x+≤200，解得：x≤80，∴最多可搬桌椅80套，故选：C．【点评】本题主要考查一元一次不等式的应用能力，设出桌椅的套数，表示出搬桌子、椅子的人数是解题的关键．13．（2016•潍坊）运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（）A．x≥11 B．11≤x＜23 C．11＜x≤23 D．x≤23【分析】根据运算程序，前两次运算结果小于等于95，第三次运算结果大于95列出不等式组，然后求解即可．【解答】解：由题意得，，解不等式①得，x≤47，解不等式②得，x≤23，解不等式③得，x＞11，所以，x的取值范围是11＜x≤23．故选C．【点评】本题考查了一元一次不等式组的应用，读懂题目信息，理解运输程序并列出不等式组是解题的关键．二．填空题（共12小题）14．（2016•）不等式组的解集是﹣3＜x≤1．【分析】分别解两个不等式得到x≤1和x＞﹣3，然后利用大小小大中间找确定不等式组的解集．【解答】解：，解①得x≤1，解②得x＞﹣3，所以不等式组的解集为﹣3＜x≤1．故答案为﹣3＜x≤1．【点评】本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．15．（2016•新县校级模拟）不等式5x﹣3＜3x+5的所有正整数解的和是6．【分析】先根据不等式的性质求出不等式的解集，再根据不等式的解集找出所有正整数解即可．【解答】解：移项，得：5x﹣3x＜5+3，合并同类项，得：2x＜8，系数化为1，得：x＜4，∴不等式所有正整数解得和为：1+2+3=6，故答案为：6．【点评】本题考查了不等式的性质，解一元一次不等式，一元一次不等式的整数解的应用，解此题的关键是求出不等式的解集．16．（2017春•萧山区月考）若关于x的不等式3m﹣2x＜5的解集是x＞3，则实数m的值为．【分析】根据解不等式，可得不等式的解集，根据不等式的解集，可得关于m 的方程，根据解方程，可得答案．【解答】解：解3m﹣2x＜5，得x＞．由不等式的解集，得=3．解得m=．故答案为：．【点评】本题考查了不等式的解集，利用不等式的解集得出关于m的方程是解题关键．17．（2016•郑州校级模拟）若不等式x＜2的解集都能使关于x的一次不等式（a ﹣3）x＜a+5成立，则a的取值范围是3＜a≤．【分析】先求出x的取值范围，再由不等式的基本性质即可得出a的取值范围．【解答】解：解不等式x＜2得，x＜4．∵不等式x＜2的解集都能使关于x的一次不等式（a﹣3）x＜a+5成立，∴，解得3＜a≤．故答案为：3＜a≤．【点评】本题考查的是不等式的解集，根据题意得出关于a的不等式组是解答此题的关键．18．（2016•如皋市校级二模）若关于x的一元一次不等式组有解，则a的取值范围是a＜1．【分析】不等式组中两不等式分别求出解集，由不等式组有解确定出a的范围即可．【解答】解：不等式整理得：，由不等式有解，得到a＜1，则a的范围是a＜1，故答案为：a＜1【点评】此题考查了不等式的解集，熟练掌握不等式组取解集的方法是解本题的关键．19．（2016•杭州模拟）在实数范围内规定新运算“△”，其规则是：a△b=2a﹣b．已知不等式x△k≥1的解集在数轴上如图表示，则k的取值范围是k=﹣3．【分析】根据新运算法则得到不等式2x﹣k≥1，通过解不等式即可求k的取值范围，结合图象可以求得k的值．【解答】解：根据图示知，已知不等式的解集是x≥﹣1．则2x﹣1≥﹣3∵x△k=2x﹣k≥1，∴2x﹣1≥k且2x﹣1≥﹣3，∴k=﹣3．故答案是：k=﹣3．【点评】本题考查了在数轴上表示不等式的解集、解一元一次不等式．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．20．（2016•乌审旗模拟）已知满足不等式3（x﹣2）+5＜4（x﹣1）+6的最小整数解是方程：2x﹣ax=3的解，则a的值为．【分析】首先解不等式求得不等式的解集，然后确定解集中的最小整数值，代入方程求得a的值即可．【解答】解：解不等式3（x﹣2）+5＜4（x﹣1）+6，去括号，得：3x﹣6+5＜4x﹣4+6，移项，得3x﹣4x＜﹣4+6+6﹣5，合并同类项，得﹣x＜3，系数化成1得：x＞﹣3．则最小的整数解是﹣2．把x=﹣2代入2x﹣ax=3得：﹣4+2a=3，解得：a=．故答案是：．【点评】本题考查了一元一次不等式的解法以及方程的解的定义，正确解不等式求得x的值是关键．21．（2016•包头二模）关于x的不等式组的解集为x＜3，那么m的取值范围是m≥3．【分析】首先解第一个不等式，然后根据不等式组的解集即可确定m的范围．【解答】解：，解①得x＜3，∵不等式组的解集是x＜3，∴m≥3．故答案是：m≥3．【点评】本题考查了一元一次不等式组的解法，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．22．（2016春•扬州校级期末）已知x=2是不等式ax﹣3a+2≥0的解，且x=1不是这个不等式的解，则实数a的取值范围是1＜a≤2．【分析】根据x=2是不等式ax﹣3a+2≥0的解，且x=1不是这个不等式的解，列出不等式，求出解集，即可解答．【解答】解：∵x=2是不等式ax﹣3a+2≥0的解，∴2a﹣3a+2≥0，解得：a≤2，∵x=1不是这个不等式的解，∴a﹣3a+2＜0，解得：a＞1，∴1＜a≤2，故答案为：1＜a≤2．【点评】本题考查了不等式的解集，解决本题的关键是求不等式的解集．23．（2016春•召陵区期末）四个小朋友玩跷跷板，他们的体重分别为P，Q，R，S，如下图所示，则他们的体重从小到大是（用“＜”号连接）S＞P＞R＞Q．【分析】由图一、二得，S＞P＞R，则S﹣P＞0，由图三得，P+R＞Q+S，则S﹣P ＜R﹣Q，所以，R﹣Q＞0，即R＞Q；即可解答．【解答】解：由图一、二得，S＞P＞R，∴S﹣P＞0，由图三得，P+R＞Q+S，∴S﹣P＜R﹣Q，∴R﹣Q＞0，∴R＞Q；综上，S＞P＞R＞Q．故答案为：S＞P＞R＞Q．【点评】本题主要考查了不等式的性质，①不等式两边加（或减）同一个数（或式子），不等号的方向不变；②不等式两边乘（或除以）同一个正数，不等号的方向不变；③不等式两边乘（或除以）同一个负数，不等号的方向改变．24．（2016春•济南校级期末）下列判断中，正确的序号为①④⑤．①若﹣a＞b＞0，则ab＜0；②若ab＞0，则a＞0，b＞0；③若a＞b，c≠0，则ac＞bc；④若a＞b，c≠0，则ac2＞bc2；⑤若a＞b，c≠0，则﹣a﹣c＜﹣b﹣c．【分析】①若﹣a＞b＞0，则a＜0，b＞0，所以ab＜0，据此判断即可．②若ab＞0，则a＞0，b＞0或a＜0，b＜0，据此判断即可．③若a＞b，c≠0，则c＞0时，ac＞bc；c＜0时，ac＜bc；据此判断即可．④若a＞b，c≠0，则c2＞0，所以ac2＞bc2，据此判断即可．⑤若a＞b，c≠0，则﹣a＜﹣b，所以﹣a﹣c＜﹣b﹣c，据此解答即可．【解答】解：∵﹣a＞b＞0，∴a＜0，b＞0，∴ab＜0，①正确；∵ab＞0，∴a＞0，b＞0或a＜0，b＜0，②错误；∵a＞b，c≠0，∴c＞0时，ac＞bc；c＜0时，ac＜bc；③错误；∵a＞b，c≠0，∴c2＞0，∴ac2＞bc2，④正确；∵a＞b，c≠0，∴﹣a＜﹣b，∴﹣a﹣c＜﹣b﹣c，⑤正确．综上，可得判断中，正确的序号为：①④⑤．故答案为：①④⑤．【点评】此题主要考查了不等式的基本性质：（1）不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变；（2）不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变；（3）不等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变．25．（2016春•扶沟县期末）小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入10小球时有水溢出．【分析】设放入球后量桶中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式为y=kx+b，由待定系数法就可求出结论；当y＞49时，建立不等式求出其解即可．【解答】解：设放入球后量桶中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式为y=kx+b，由题意，得：，解得：，即y=2x+30；由2x+30＞49，得x＞9.5，即至少放入10个小球时有水溢出．故答案为：10．【点评】本题考查了列一元一次方程解实际问题的运用，待定系数法求函数的解析式的运用，列不等式解实际问题的运用，解答时求出函数的解析式是关键．三．解答题（共15小题）26．（2016•）解不等式﹣1≤，并把解集在数轴上表示出来．【分析】利用解一元一次不等式的方法解出不等式的解集，再将其表示在数轴上即可得出结论．【解答】解：不等式两边同时×6得：3x﹣6≤14﹣2x，移项得：5x≤20，解得：x≤4．将其在数轴上表示出来如图所示．【点评】本题考查了解一元一次不等式以及在数轴上表示不等式的解集，熟练掌握解一元一次不等式的方法是解题的关键．27．（2016•）解不等式组：．【分析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．【解答】解：，解①得x＜2，解②得x≥﹣1，则不等式组的解集是﹣1≤x＜2．【点评】本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．28．（2016•）x取哪些整数值时，不等式5x+2＞3（x﹣1）与x≤2﹣都成立？【分析】根据题意分别求出每个不等式解集，根据口诀：大小小大中间找，确定两不等式解集的公共部分，即可得整数值．【解答】解：根据题意解不等式组，解不等式①，得：x＞﹣，解不等式②，得：x≤1，∴﹣＜x≤1，故满足条件的整数有﹣2、﹣1、0、1．【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．29．（2016•呼和浩特）已知关于x的不等式组有四个整数解，求实数a的取值范围．【分析】分别求出不等式组中两不等式的解集，根据不等式组有四个整数解，即可确定出a的范围．【解答】解：解不等式组，解不等式①得：x＞﹣，解不等式②得：x≤a+4，∵不等式组有四个整数解，∴不等式组的解集再数轴上表示为：∴1≤a+4＜2，解得：﹣3≤a＜﹣2．【点评】此题考查了一元一次不等式组的整数解，熟练掌握运算法则是解本题的关键．30．（2013•）已知关于x，y的方程组的解满足不等式组，求满足条件的m的整数值．【分析】首先根据方程组可得y=，把y=代入①得：x=m+，然后再把x=m+，y=代入不等式组中得，再解不等式组，确定出整数解即可．【解答】解：①×2得：2x﹣4y=2m③，②﹣③得：y=，把y=代入①得：x=m+，把x=m+，y=代入不等式组中得：，解不等式组得：﹣4＜m≤﹣，则m=﹣3，﹣2．【点评】此题主要考查了一元一次不等式组的整数解，以及二元一次方程的解，关键是掌握消元的方法，用含m的式子表示x、y．31．（2013•凉山州）已知x=3是关于x的不等式的解，求a的取值范围．【分析】先根据不等式，解此不等式，再对a分类讨论，即可求出a的取值范围．【解答】解：解得（14﹣3a）x＞6当a＜，x＞，又x=3是关于x的不等式的解，则＜3，解得a＞4；当a＞，x＜，又x=3是关于x的不等式的解，则＞3，解得a＜4（与所设条件不符，舍去）；综上得4＜a＜．故a的取值范围是4＜a＜．【点评】本题考查了不等式的解的定义及一元一次不等式的解法，比较简单，注意分类讨论是解题的关键．32．（2011•）已知关于x、y的方程组的解满足不等式x+y＜3，求实数a的取值范围．【分析】先解方程组，求得x、y的值，再根据x+y＜3，解不等式即可．【解答】解：，①+②得，3x=6a+3，解得x=2a+1，将x=2a+1代入①得，y=2a﹣2，∵x+y＜3，∴2a+1+2a﹣2＜3，即4a＜4，a＜1．【点评】本题是一元一次不等式和二元一次方程组的综合题，是中档题，难度适中．33．（2016•）关于x的两个不等式①＜1与②1﹣3x＞0（1）若两个不等式的解集相同，求a的值；（2）若不等式①的解都是②的解，求a的取值范围．【分析】（1）求出第二个不等式的解集，表示出第一个不等式的解集，由解集相同求出a的值即可；（2）根据不等式①的解都是②的解，求出a的范围即可．【解答】解：（1）由①得：x＜，由②得：x＜，由两个不等式的解集相同，得到=，解得：a=1；（2）由不等式①的解都是②的解，得到≤，解得：a≥1．【点评】此题考查了不等式的解集，根据题意分别求出对应的值利用不等关系求解．34．（2013•毕节地区）解不等式组．把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解．【分析】分别计算出两个不等式的解集，再根据大小小大中间找确定不等式组的解集即可，再找出解集范围内的非负整数即可．【解答】解：，由①得：x≥﹣1，由②得：x＜3，不等式组的解集为：﹣1≤x＜3．在数轴上表示为：．不等式组的非负整数解为2，1，0．【点评】此题主要考查了解一元一次不等式组，解决此类问题的关键在于正确解得不等式组或不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件进而求得不等式组的整数解．35．（2014•）某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：A B进价（元/件）12001000售价（元/件）13801200（1）该商场购进A、B两种商品各多少件；（2）商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？【分析】（1）设购进A种商品x件，B种商品y件，列出不等式方程组可求解．（2）由（1）得A商品购进数量，再求出B商品的售价．【解答】解：（1）设购进A种商品x件，B种商品y件，根据题意得化简得，解之得．答：该商场购进A、B两种商品分别为200件和120件．。
完整版八年级不等式培优提高练习
是（ ）v 0的解集是（ ）A . x >--B . x v-丄C . x >-丄D . x v 丄5 5553.若不等式（ax - 1） （x+2）> 0的解集是-3v x v- 2,那么a 等于（）A . 4B . 2C . 3D .丄2 25.若关于x 的不等式组｛;浆畀整数解共有3个，则m的取值范围是（）A . 5v m < 6B . 5< m v 6C . 5< m < 6D . 5v m v 66.已知a >b , CM 0,则下列关系一定成立的是()A . ac >beB .丄•一C . C - a >C - bD . c+a >c+bc c7. 下列命题中:① 如果a v b ,那么ae 2v be 2；② 关于x 的不等式（a- 1） x > 1 - a 的解集是x v- 1,贝U a v 1； ③ 若一^是自然数，则满足条件的正整数 x 有4个.6-x 正确的命题个数是（） A . 0B . 1C . 2D . 38.若x 是方程2x+m - 3 （m - 1） =1+x 的解为负数，贝U m 的取值范围是（ ）A . m >-1B . m v-1C . m > 1D . m v 11 •若关于x 的不等式组 2恰好只有四个整数解，则 a 的取值范围2x+2<3(x+a)A- a" '2 .设a , b 是常数,D. - 2 1-—,则关于x 的不等式 bx - aB . 不等式43C .- 2 1 ：-— 3>0的解集为x v£54.不等式二了-厂」—：-厂的解集为x >2,则m 的值为（9.按下面的程序计算:若输入x=100,输出结果是501，若输入x=25，输出结果是631，若开始输入的 x 值为正整数，最后输出的结果为 556,则开始输入的x 值可能有（ ）A . 1种B . 2种C . 3种D . 4种10. 若x 为任意实数时，二次三项式x 2-6x+c 的值都不小于0,则常数c 满足的 条件是（ ）A . c >0B . c >9C . c >0D . c >911. 关于x 的方程mx -仁2x 的解为正实数，则 m 的取值范围是（ ）A . m > 2B . m < 2C . m > 2D . m v 2C-1 d （ y —1 }12 .关于x 的不等式组的解集为x v 3,那么m 的取值范围为（ ） A . m=3B . m > 3C . m v 3D . m > 313 .已知△ ABC 的边长分别为2x+1，3x ，5,则厶ABC 的周长L 的取值范围是（ ） A . 6v L v 36B . 10v L < 11C . 11< L v 36D . 10v L v 3614 .已知实数x 、y 同时满足三个条件：①3x - 2y=4 - p ,②4x - 3y=2+p ，③x > y ，那么实数p 的取值范围是（ ）A . p >- 1B . p v 1C . p v- 1D . p > 115 .关于x 的不等式组 、 的解集是x >- 1,则m= _________ .x>ir+216 .若不等式组 <2x _a <^ jJ 二 的解集为-1 v x v 1，那么(a+1) (b - 1)的值等 于范围是17 .已知关于x 、y 的二元一次方程组xf2y--2的解满足x+y >2,则k 的取值18 .若不等式组 有解，那么a 必须满足19 .已知a 、b 都是实数，且a=y-，b=—,b v*v 2a ,那么实数x 的取值范围是________20. 若关于x 、y 的二元一次方程组* *于加'1的解满足x+y >0,则m 的取值范x+3y=3 围是 _______ .21.关于x的不等式x - 3>丄一的解集在数轴上表示如图所示，则 a 的值是 _______ ._1~ 1 2 3 4 5 7^22.已知关于x 的分式方程 的解为负数，那么字母 a 的取值范围 R +2 JJ +2是 _______ .23. 求不等式(2x - 1) (x+3)> 0的解集.请你仿照上述方法解决下列问题: (1) 求不等式(2x - 3) (x+1)v 0的解集.解：根据 同号两数相乘，积为正”可得：① r2x-l>0K +3>0r2x-l<0解①得x；解②得x V- 3.•••不等式的解集为x或 x v- 3.(2)求不等式> 0的解集.24. x取哪些整数值时，不等式5x+2>3 (x- 1)与丄x- K 7-一二都成立?25.已知关于x的不等式组恰好有两个整数解, 求实数a的取值范围.26. 已知一元一次不等式mx - 3> 2x+m.(1)若它的解集是XV-—，求m的取值范围；rn-2(2)若它的解集是x>-，试问：这样的m是否存在？如果存在，求出它的值;4如果不存在，请说明理由.27. 用等号或不等号填空：(1)比较4m与m2+4的大小当m=3 时，4m ______ m2+4当m=2 时，4m ______ m2+4当m= - 3 时，4m ____ m2+4(2)无论取什么值，4m与m2+4总有这样的大小关系吗？试说明理由.(3)比较x2+2与2x2+4x+6的大小关系，并说明理由.(4)比较2x+3与-3x- 7的大小关系.28.是否存在整数m ,使关于x 的不等式1七厶—与关于x 的不等式x+1> m m m的解集相同？若存在，求出整数 m 和不等式的解集；若不存在，请说 明理由.29. 已知关于x 的不等式(2a- b ) x+a- 5b >0的解集为x<—, (1) 求丄的值.(2) 求关于x 的不等式ax > b 的解集.值.31. 小明把三个数-1, 2 -a, 丄在数轴上从左到右依次排列在三个对应点上, 你能确定a 的取值范围吗？请写出你的解答过程.32. 阅读下面的例题，并回答问题.30. 若不等式组的偶数解a 满足方程组I" ax-y--7 |2x4-3y=7.求x 2+y 2的【例题】解一元二次不等式：x2- 2x- 8>0.解：对x2- 2x- 8分解因式，得x2- 2x- 8= (x - 1) 2- 9= (x - 1) 2-32= (x+2) (x - 4), •'•(x+2) (x - 4)> 0.由两实数相乘，同号得正，异号得负”，可得解①得x>4;解②得X V- 2.故x2- 2x - 8>0的解集是x>4或x V- 2.(1)_____________________________ 直接写出x2- 9>0的解是;(2)仿照例题的解法解不等式：x2+4x- 21V0；(3)求分式不等式：二一w 0的解集.x-2。
【湘教版】八年级数学上4.1不等式能力培优训练(含答案)
专题列不等式 1.四个小朋友玩跷跷板，他们的体重分别为 P , Q , R , S ,如图所示，则他们的体重大小关P > R >S > Q B . Q >S > P >R C . S >P > Q > R 2. 下列关于 a a 用不等式表示正确的是A. a a 0B. a a 0C. |a a 0D. a a 03. 某工地实施爆破，操作人员点燃导火线后，必须在炸药爆炸前跑到400m 外安全区域， 若导火线燃烧的速度为 1.1cm/秒，人跑步的速度为5m/秒，则导火线的长xcm 应满足的不 等式是： ____________________ .4.辽宁崗部忒冇“半駅之乡 F 勺关称―臬字细织 衲汽乍装运A Ji 阴种苹果到外地硝宙”按规足冊辆乍H 装冋一种 申杲-冃.必须较满”已血每辆仆的运鞍葷型毎吨苹果的获利情况如下表所示1A毎轴1 A 车运4* W （ im ? :<2 审汆抿利E n 儿>5 . y J（1）変求」戏运小苹生节加裝运种 苹 跟的汽乍散M <辆了 z 满足的不等式5 < 3芒荻刑」彳“少 F 12 600丿C ・试"J f I ］隨迖A 种苹果的汽车数 d: J （辆》炖满足的知一伞 不警式.状元笔记【知识要点】不等式：用不等号 >”.N”. “N”“W”“壬连接而成的式子叫作不等式.【温馨提示】注意 不大于“.不小于“.不超过”等字表示不等时要带上 “=号.4. 1 不等式玄阜系疋D . S > P > R >Q【方法技巧】1仔细审题，抓住题中的关键字小于”.大于”.不大于”.不小于”.不超过”列不等式. 2•列不等式时还应掌握常见的数量关系式，如：速度刘寸间=路程，单价W数量=总价，工作效率 >工作时间=工作总量等.参考答案：1. D 解析：观察前两幅图易发现S> P > R,再观察第一幅和第三幅图可以发现R> Q.2. D 解析：分两类讨论：a 0时，|a| a 2a ,显然|a| a 0 ；当a 0时，a a a a 0，故同a 0.x3. 5 4001.14.解：(1) 3x 2(10 x) 26 ;(2) 5x 9(10 x) 126 .。
八年级三角形和不等式培优提高题
1、等腰三角形的两边长分别为4厘米和9厘米，则这个三角形的周长为（）A、22厘米B、17厘米C、13厘米D、17厘米或22厘米2、下列关于等腰三角形的性质叙述错误的是（）A、等腰三角形的两底角相等B、等腰三角形是轴对称图形C、等腰三角形是轴对称图形D、等腰三角形底边上的高、底边上的中线、顶角的平ABC D分线互相重合3．已知△ABC 的三边长分别是6cm 、8cm 、10cm ，则△ABC 的面积 是（ ）A.24cm 2B.30cm 2C.40cm 2D.48cm 24. 如图，在△ABC 和△DEF 中，已知AC=DF ，BC=EF ，要使△ABC ≌△DEF ，还需要的条件是（ ）A.∠A=∠DB.∠ACB=∠FC.∠B=∠DEFD.∠ACB=∠D 5．如图，△ABC 中，AB=AC ，点D 在AC 边上，且BD=BC=AD ， 则∠A 的度数为（ ）A.30°B.36°C.45°D.70° 6．如图，△ABC ≌△AEF ，AB ＝AE ，∠B ＝∠E ，则对于结论①AC ＝AF ；②∠FAB ＝∠EAB ；③EF ＝BC ；④∠EAB ＝∠FAC ，其中正确结论的个数是（ ）A.1个B.2个C.3个D.4个（4题图） （5题图） （6题图） （第10题图）7. 到三角形三个顶点的距离相等的点是三角形（ ）的交点.A. 三个内角平分线B. 三边垂直平分线C. 三条中线D. 三条高 8. 面积相等的两个三角形（ ）A.必定全等B.必定不全等C.不一定全等D.以上答案都不对 二、填空题09.如果等腰三角形的有一个角是80°，那么顶角是 度.10.如图，△ABC 中，∠C=90°，∠A ＝30° ，BD 平分∠ABC 交AC 于D ，若CD ＝2cm ，则AC= .11.“等边对等角”的逆命题是______________________________．12．在△ABC 中，边AB 、BC 、AC 的垂直平分线相交于P ，则PA 、PB 、PC 的大小关系是 . 13．已知⊿ABC 中，∠A = 090，角平分线BE 、CF 交于点O ，则∠BOC = . 14．在△ABC 中，∠A=40°，AB=AC ，AB 的垂直平分线交AC 与D ，则∠DBC 的度数为 ． 15．Rt ⊿ABC 中，∠C=90º，∠B=30º，则AC 与AB 两边的关系是 ， 16.等腰三角形一腰上的高与另一腰的夹角为300，腰长为6，则其底边上的高是 。
初二数学不等式专项经典培优练习
初二数学 不等式专项训练一、选择题1．（2010江苏南通） 关于x 的方程12mx x -=的解为正实数，则m 的取值范围是（ ）A ．m ≥2B ．m ≤2C ．m ＞2D ．m ＜22．（2010台湾）有数颗等重的糖果和数个大、小砝 码，其中大砝码皆为5克、大砝码 皆为1克，且图(三)是将糖果与砝码放在等臂天平上的两种情形。
判断下列哪一种情形是正确的？（ ）3．（2010浙江杭州） 已知a ，b 为实数，则解可以为 – 2 < x < 2的不等式组是A.⎩⎨⎧>>11bx axB. ⎩⎨⎧<>11bx axC. ⎩⎨⎧><11bx axD. ⎩⎨⎧<<11bx ax4．（2010山东泰安）若关于x 的不等式0721x m x -<⎧⎨-≤⎩的整数解共有4个,则m 的取值范围是( ) A.6<m<7 B.6≤m<7 C.6≤m≤7 D.6<m≤75．（2010 甘肃）若不等式组,420x a x >⎧⎨->⎩的解集是12x -<<，则a = ． 6．（2010 山东荷泽）若关于x 的不等式3m －2＜5的解集是x ＞2，则实数m 的值为 ．（A ） （B ）（C ） （D ） 5 5 5 5 1 1 5 5 5 5 1(A)5 1 5 1 1(B) (C) 5 5 5 5 1圖(三)7．（2010宁夏回族自治区）若关于x 的不等式组⎩⎨⎧>>m x x 2的解集是2>x ，则m 的取值范围是 ． 8．（2010山东威海）解不等式组：9．（2010湖北荆门）试确定实数a 的取值范围，使不等式组)(⎪⎪⎩⎪⎪⎨⎧++++++a x ＞a x ＞x x 1343450312恰有两个整数解。
【答案】解：由不等式0312＞x x ++两边同乘以6得到3x+2（x+1）＞0，可以求出x ＞－52，由不等式)(a x ＞a x ++++134345两边都乘以3得到3x+5a+4＞4x+4+3a 可以解出x ＜2a ，所以不等式组的解集为a ＜x＜252-，因为该不等式组恰有有两个整数解，所以1＜2a ≤2，所以21＜a ≤1。
八年级不等式提高练习题
八年级数学（下）《不等式》测试题一、填空题（每题2分，共计20分）1.用恰当的不等号表示下列关系：①x 的3倍与8的和比y 的2倍小： ； ②老师的年龄a 不小于你的年龄b ： . 2.不等式3(x+1)≥5x —3的正整数解是 3.当a 时，不等式(a —1)x ＞1的解集是x ＜11-a .4.已知x ＝3是方程2a x -—2＝x —1的解，那么不等式(2—5a )x ＜31的解集是5.已知函数y=2x —3，当x 时，y ≥0；当x 时，y ＜5.6.若不等式组 的解集是x ＞3，则m 的取值范围是7.已知关于x 的不等式组 的整数解共有5个，则a 的取值范围是8.若不等式组 的解集为-1＜x ＜1，那么(a-1)(b-1)的值等于9.小明用100元钱购得笔记本和钢笔共30件，已知每本笔记本2元，每只钢笔5元.那么小明最多能买 只钢笔.10.2012年某省体育事业成绩显著，据统计，在有关大赛中获得奖牌数如右表所示(单位：枚)如果只获得1枚奖牌的选手有57人，那么荣获3枚奖牌的选手最多有 人. 二、选择题（每题4分，共计40分）11.已知“①x+y=1；②x ＞y ；③x+2y ；④x 2—y ≥1；⑤x ＜0”属于不等式的有 个.A.2；B. 3；C.4；D. 5. 12.如果m<n<0，那么下列结论错误的是A.m －9<n －9；B.—m>—n ；C.n1>m1； D.nm >1.13.设“●”、“▲”、“■”表示三种不同的物体，现用天平称了两次，情况如图所示，那么●、▲、■这三种物体按质量从大到小的顺序排列为 A.■、●、▲。
B.■、▲、●。
C .▲、●、■。
D.▲、■、●。
mx x x >-<+1481230->-≥-x a x 3212>-<-b x a x14.已知a ，b 两数在数轴上的位置如图所示，设M=a+b,N=—a+b,H=a —b ，则下列各式正确的是A.M>N>H ；B.H>M>N ；C.H>M>N ；D.M>H>N. 15.不等式组⎩⎨⎧>≤35x x 的解集在数轴上表示，正确的是A. B. C. D16.已知(x+3)2+m y x ++3＝0中，y 为负数，则m 的取值范围是A.m>9B.m<9C.m>－9D.m<－917.观察下列图像，可以得出不等式组的解集是A. x 〈31 B. －31〈x 〈0C. 0〈x 〈2D. －31〈x 〈218.某种出租车的收费标准是：起步价7元（即行驶的距离不超过3千米都需付7元车费）,超过3千米，每增加1千米，加收2.4元（不足1千米按1千米计算）某人乘这种出租车从甲地到乙地共付车费19元，那么此人从甲地到乙地经过的路程的最大值是 千米.A.11B.8C.7D.519.某种肥皂原零售价每块2元，凡购买2块以上（包括2块）,商场推出两种优惠销售办法.第一种：一块肥皂按原价，其余按原价的七折销售；第二种：全部按原价的八折销售.你在购买相同数量肥皂的情况下，要使第一种方法比第二种方法得到的优惠多，最少需要买 块肥皂.A.5B.4C.3D.220.韩日“世界杯” 期间，重庆球迷一行若干人从旅馆乘车到球场为中国队加油，现有某个车队，若全部安排乘该车队的车，每辆坐4人则多16人无车坐，若每辆坐6人，则坐最后一辆车的人数不足一半.这个车队有 辆车A.11B.10C.9D.12 三、解答题21.解下列不等式（组）：（每题8分，共计24分）（1） 5（x+2）≥1―2(x ―1) （2）()1273212-≤-++x x x 015.0013>+->+x x（3）解不等式组：⎪⎩⎪⎨⎧>-+<+02)8(21042x x22.若方程组 的解x 、y 都是正数，求a 的取值范围. （6分）23.如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像．根据图像解答下列问题：（6分）（1）在轮船快艇中，哪一个的速度较大？（2）当时间x 在什么范围内时，快艇在轮船的后面？当时间x 在什么范围内时，快艇在轮船的前面？（3）问快艇出发多长时间赶上轮船？四、实际应用题（每题8分，共计24分）24.某校长暑假将带领该校市级“三好学生”去北京旅游，甲旅行社说：“如果校长买全票一张，则其余的学生可享受半价优惠.”乙旅行社说：“包括校长在内全部按票价的六折优惠.”若全票价为240元，两家旅行社的服务质量相同，根据“三好学生”的人数你认为选择哪一家旅行社才比较合算？⎩⎨⎧-=-=+323a y x y x25.某工厂现有甲、乙原料分别360千克、290千克，计划利用两种原料生产A、B两种产品共50件，已知生产一件A种产品需要甲种原料9千克，乙种原料3千克；生产一件B种，需要甲种原料4千克，乙种原料10千克，按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来。
八年级数学不等式能力提高题
不等式能力提高题一、选择题：1、若不等式(a+1)x ＞a+1的解集为x ＜1,则a 必须满足（ ） A 、a ＜0 B 、a ＜1 C 、a ＜-1 D 、a ＞-12、如果不等式3x-m ≤0的正整数解是1、2、3，那么m 的取值范围是（ ） A 、9≤m ＜12 B 、9＜m ＜12 C 、m ＜12 D 、m ≥93、已知a 、b 为常数，若ax+b ＞0的解集是x ＜31,则bx-a ＜0的解集是（ ）A 、x ＞-3B 、x ＜-3C 、x ＞3D 、x ＜3 4、设m=32++a a n=21++a a p= 1+a a若a ＜-3则（ ） A 、 m ＜n ＜p B 、n ＜p ＜m C 、p ＜n ＜m D 、p ＜m ＜n 5、要使a 5＜a 3＜a ＜a 2＜a 4＜成立，则a 的取值范围是（ ） A 、0＜a ＜1 B 、a ＞1 C 、-1＜a ＜0 D 、a ＜-1 6、有四个叙述：其中正确的叙述是（ ）（1）、当0＜x ＜1 时,x +11＜1-x-x 2 （2）、当0＜x ＜1 时, x +11＞1-x-x 2 （3）、当-1＜x ＜0 时, x +11＜1-x-x 2 （4）、当-1＜x ＜0 时, x+11＞1-x-x 2A 、 （1）、（3）B 、（2）、（4）C 、（1）、（4）D 、（2）、（3） 7、若a ＜b ＜0＜c ＜d 则以下四个结论中正确的是（ ） A 、 a+b+c+d 一定是正数 B 、d+c-a-b 可能是负数 C 、 d-c-b-a 一定是正数 D 、c-d-a-b 一定是正数8、若关于x 不等式组⎩⎨⎧-≥-0809 b x a x 的整数解仅为1、2、3；则适合不等式组的整数a 、b 的有序数对是（ ）A 、17B 、64C 、72D 、81二、填空题：9、已知不等式3x-a ≤0只有三个正整数解，则正数a 的取值范围是10、已知58≤x ＜2 化简2-x +6480252+-x x 的结果是11、化简a .8a - 的结果是12、设m ＞0 3+x -1-x = m 则代数式3+x +1-x 的值是 13、设0＜a ＜1 -2＜b ＜-1 则a 1、b a -1 、b a +1 和221ba - 四个式子中，值最大的是 最小的是14、设a 、b 、c 是△ABC 三条，满足c b a c -+＜a c b a -+＜ba c b-+ 则三边中最长的是15、关于x 不等式3-x +5-x ≤3的所有整数解的和是16、已知M=121220012000++ N=121220022001++ 那么M 、N 大小关系是17、不等式a(x-a)＞x-1的解集为 18、不等式21-x ≤31+x 的所有整数解之和为19、不等式(x +x)(2-x)＜0 的解集是 20、已知6＜a ＜102a＜b ＜2a c=a+b 则c 取值范围是 21、关于x 不等式组⎪⎩⎪⎨⎧+++01456 m x xx 的解集为x ＜4 则m 的取值范围是 22、(2a-b)x+3a-4b ＜0的解集是x ＞49, 则不等式(a-4b)x+2a-3b ＞0的解集是 23、满足x+2y ≤3 x ≥0 y ≥0 条件下，2x+y 能达到的最大值是 24、(x+1)(x-1)＜0 的解集 (x+3)(x-2)＞0的解集 25、比较大小3a 2-3b 2+6 2a 2-4b 2+126、 已知-4是不等式ax ＞-5的解集中的一个，则a 的取值范围是 27、已知a=x+2 b=x-1 且a ＞3＞b 则x 的取值范围是28、已知-1＜x ＜0则x 、 x 2 、x1三者的大小关系是 29、关于x 的不等式组⎩⎨⎧+-011x a x 只有4个整数解，则a 的取值范围是30、已知x ＜a 的解集中的最大整数为3，则a 的取值范围是 已知x ＞a 的解集中的最小整数为－2，则a 的取值范围是 三、计算题： 31、解关于x 的不等式2[])2(3--x x ≥6(x 332-) ⎥⎦⎤⎢⎣⎡--2)14(3223x -x ＜232、解关于X 的不等式组：⎪⎩⎪⎨⎧+--+-1413158.55.0)3.0(4x x x x 整数a 、b 、c 满足 ⎪⎪⎪⎩⎪⎪⎪⎨⎧+++b c a b a c b a c b a c 4112535232611试确定abc 的大小关系33、解关于x 的不等式mx-2＞3m+5x (m ≠5)34、关于x 的不等式2a1+x －1＞a x31-的解35、若m(x-2)＞x+1 和3x-5＜0是同解不等式，求m 的值36、关于X 的不等式组⎪⎩⎪⎨⎧+++-a x x x x 4231)3(32 有四个整数解，则a 的取值范围是37、m 为何值时，关于x 的方程2153166--=--m x m x 的解大于1.38、关于x 、y 的方程组⎩⎨⎧-=++=+134123p y x p y x 的解满足x ＞y ，求p 的取值范围39、关于x 的不等式mx ＞n 解集为x ＜53则关于x 的不等式(2m-n)x+m-5n ＞0 的解集40、八年级某班部分同学去植树，若每人平均植树7棵，还剩9棵；若每人平均植树9棵，则有1名同学植树的棵数不到8棵，则一共去了 学生，共植树 棵。
北师大八年级不等式培优0001
第一章一兀一次不等式和一兀一次不等式组【知识总结】一. 不等关系探1.一般地,用符号“ V” (或“W” ), “>” (或“》”)连接的式子叫做不等式...•O2.要区别方程与不等式：方程表示的是相等的关系；不等式表示的是不相等的关系• 探3.准确“翻译”不等式，正确理解“非负数”、“不小于”等数学术语.非负数<===> 大于等于0( > 0) <===> 0和正数<===> 不小于0非正数<===> 小于等于0( < 0) <===> 0和负数<===> 不大于0二. 不等式的基本性质探1.掌握不等式的基本性质，并会灵活运用：(1) 不等式的两边加上(或减去)同一个整式，不等号的方向不变，即：如果a>b,那么a+c>b+c, a-c>b-c.(2) 不等式的两边都乘以(或除以)同一个正数，不等号的方向不变，即如果a>b,并且c>0,那么ac>bc, a b .c c(3) 不等式的两边都乘以(或除以)同一个负数，不等号的方向改变，即：如果a>b,并且c<0,那么ac<bc,—:::-c c三•不等式的解集：探1.能使不等式成立的未知数的值，叫做不等式的解一个不等式的所有解，组成这个不等式的解集；求不等式的解集的过程,叫做解不等式.•探2.不等式的解可以有无数多个，一般是在某个范围内的所有数，与方程的解不同•O3.不等式的解集在数轴上的表示：用数轴表示不等式的解集时，要确定边界和方向：①边界:有等号的是实心圆圈，无等号的是空心圆圈；②方向：大向右，小向左四.一元一次不等式：探1.只含有一个未知数，且含未知数的式子是整式，未知数的次数是1•像这样的不等式叫做一元一次不等式...探2.解一元一次不等式的过程与解一元一次方程类似，特别要注意，当不等式两边都乘以一个负数时，不等号要改变方向.探3.解一元一次不等式的步骤：①去分母；②去括号；③移项；④合并同类项；⑤系数化为1（不等号的改变问题）探4. 一元一次不等式基本情形为ax>b（或axvb）①当a>0时,解为x b;a②当a=0时,且b<0,则x取一切实数；当a=0时，且b>0,则无解;③当a<0时，解为x：：：b;a五.一元一次不等式组探1.定义：由含有一个相同未知数的几个一元一次不等式组成的不等式组，叫做一元一次不等式组..探2. 一元一次不等式组中各个不等式解集的公共部分叫做不等式组的解集.如果这些不等式的解集无公共部分，就说这个不等式组无解.几个不等式解集的公共部分，通常是利用数轴来确定.探3.解一元一次不等式组的步骤：（1）分别求出不等式组中各个不等式的解集；（2）利用数轴求出这些解集的公共部分，即这个不等式组的解集.两个一元一次不等式组的解集的四种情况（a、b为实数,且a<b）【培优训练】一、选择题（每小题3分，共30分）1.. 下列不等式一定成立的是（）4 2A.5a> 4aB.x+2v x+3C. —a>—2aD.-a a2•不等式—3x+6> 0的正整数有（）A.1个B.2个C.3个D.无数多个 3..在数轴上与原点的距离小于 8的点对应的x 满足（）A. — 8v x v 8B.x v — 8 或 x > 8C.x v 8D.x > 84•若不等式组/"m 无解，则m 的取值范围是（）x>11A. m v 11B.m > 11C.m < 11D.m > 115. 要使函数y=（2m — 3）x+（3n+1）的图象经过x 、y 轴的正半轴，则片需要0.35元.在每位同学得到一张相片、共用一张底片的前提下，平均每人分摊的钱不足 0.5元，那么参加合影的同学人数m 与n 的取值应为()3 A. m > n >— 1B.m >3， n >— 32 3> _ 136. 如右图，当 y 0时, 自变量x 的范围是（A 、 x ：： -2B 、 x -2C 、 x 27.如果0 x 1，则下列不等式成立的（xx8.若 a>b>0, 则下列结论正确的是 (A) -a>-b(B)i1 (C)a- 3 1_ 3C.m v -，nv —D.m v 一 ，n2 32I,)丄LD、x 21i)1、x x 2D1、—X 2Xxx( )3<0 (D)a2 2>b6次射击共中52环,如果他要打破89环（10次射击）的记录，第七次射击不能少于（ ）环（每次射击最多是 10环）10.初三的几位同学拍了一张合影作留念, 已知冲一张底片需要 0.80元，洗一张相A x x 2- B 、 x 2：： x ：丄 C 9.某射击运动员在一次比赛中前A.至多6人 E.至少6人 C.至多5人 D.至少5人[ 211.不等式组v vi vii viii ix x• -3的「最小整数解为()3x -4 乞8(A) - 1 (B)0 (C)1(D) 412、如果0 ：：: x :: 1，则卜夕U不等式成立的（)1A、x < x2£—B 、21Cx : x C 、1 2X x D 、1 2x ::: x x x x x13、在平面直角坐标系内，点P ( m - 3，m - 5 ）在第四象限，则m的取值范围是( )A、一B> -3 m 5 C、3 m 5D> -5 m ： -3二、填空题：（每题3分，共15分）1、若区也=—1,则x的取值范围是x _12、如果关于x的不等式（a -1）x ：：：a 5和2x ：：： 4的解集相同，则a的值为__3、若a ：：： b，用“v” 或“〉”号填空：2a a b , - - a .3 34、点A （—5 , y i ） > B （—2 , y?）都在直线y = -2x上，贝U y i与y的关系5、若不等式组匸》3的解集为"2，那么A3"*）的值等于——6、不等式ax b的解集是x -，则a的取值范围是_______________________a三、解不等式（组）（每题5分）5x -6 乞2(x 3)x .4_1 ：:2x-1 5x + 1 (4)」3 一 2'5x -1 c 3(x + 1)四、解答题(1) 不等式组 a —「x ：：a2的解集是3< x v a+2，则a 的取值范围3 <x <5.：2x-1.(2) 若关于x 的不等式组 ^1,的解集为x<2，求k 的取值范围x - k :: 0(3) 若不等式组 X m 1,无解，求m 的取值范围x 》2m -1(4) 已知关于x ，y 的方程组』x +y =m的解为非负数，求整数 m 的值Qx+3y =31(5) 画出函数y=3x+12的图象，并回答下列问题：(6分)(1) 当x 为什么值时，y >0?⑵如果这个函数y 的值满足一6<y <6,求相应的x 的取值范围. (6)已知方程组丿2x + y-— m的解％、y 满足x +y > 0，求m 的取值范围.(6 分) £ +2y =2四.应用题某汽车租赁公司要购买轿车和面包车共10辆•其中轿车至少要购买 3辆，轿车每辆7万元，面包车每辆 4万元，公司可投入的购车款不超过 55万元.(10分)(1) 符合公司要求的购买方案有哪几种？请说明理由.(2) 如果每辆轿车的日租金为 200元，每辆面包车的日租金为 110元.假设新购 买的这10辆车每日都可租出，要使这 10辆车的日租金收入不低于 1500元，那么 应选择以上哪种购买方案？ 考点1不等式(3)"x - 5 £ -3 2x 龙—2(1)不等式的概念：用不等号表示不等关系的式子叫做不等式（2）不等式的解、解集能使不等式成立的未知数的值叫做不等式的解；一个含有未知数的不等式的解的全体叫做这个不等式的解集。
八年级不等式培优练习题
八年级不等式培优练习题一、选择题1. 若 a > b，则下列哪个选项一定成立？A. a b > 0B. a + b > 0C. a < bD. a² > b²2. 已知不等式 2x 3 > 5，解集是（）。
A. x > 4B. x > 2C. x < 4D. x < 23. 下列哪个不等式的解集是全体实数？A. x² > 0B. x² = 0C. x² < 0D. x² ≠ 0二、填空题1. 若 a > b，则 a 2 > b _______。
2. 不等式 3(x 1) < 2x + 3 的解集是 _______。
3. 若 |x 2| < 3，则 x 的取值范围是 _______。
三、解答题1. 解不等式组：$\begin{cases} 2x 3 > x + 1 \\ x 4 < 2x2 \end{cases}$。
2. 已知不等式 |2x 5| > 3，求 x 的取值范围。
3. 设 a、b 为实数，且 a > b，证明：a² > b²。
4. 在直角坐标系中，点 A(a, b) 满足 a > 0，b > 0，求点 A 到原点 O 的距离范围。
5. 已知不等式 3(x 1) < 2x + 3，求 x 的取值范围。
6. 若 a、b 为实数，且 a > b，证明：a + 2 > b + 2。
7. 解不等式：$\frac{2x 3}{5} > \frac{x + 1}{2}$。
8. 已知不等式 |x 4| + |x + 2| > 6，求 x 的取值范围。
9. 设 a、b、c 为实数，且 a > b，b > c，证明：a > c。
10. 在直角坐标系中，点 A(a, b) 满足 a < 0，b > 0，求点 A 到 y 轴的距离范围。
初二数学解含字母的不等式组培优详细解析
解含字母不等式（组）培优训练一.选择题1.已知关于x的不等式组恰有3个整数解，则a的取值范围是（）3a-2x>0LA.二-一B・「二C D2.不等式0&ax+5&4的整数解是1, 2, 3, 4,则a的取值范围是（）A. —aV -1B. a 0 -C. & a< - 1D. a》—3,若实数abc 满足a2+b2+c2=9,代数式（a- b）2+ （b-c）2+ （c-a）2的最大值是（）A. 27B. 18C. 15D. 124.已知非负数a, b, c满足条件a+b=7, c- a=5,设S=#b+c的最大值为m,最小值为n,则m - n的值（）A. 5B. 6C. 7D. 85.某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分，小明得分要超过120分，他至少要答对多少道题？如果设小明答对x道题，则他答错或不答的题数为20-x.根据题意得（A. 10x- 5 (20-x) >120B. 10x- 5 (20-x) < 120C. 10x-5 (20-x) >120D. 10x- 5 (20-x) <120r 2 宜一］>3 (上=2)6.若关于x的一元一次不等式组•/ 的解集是x<5,则m的取值范围是( )A. m>5 B, m>5 C. m<5 D, m<57.若x>0, y>0,且x+y=12.则寸7•^+^^二的最小值是8.已知实数a, b, c满足不等式| a|引b+c| , | b|引c+a| , | c|引a+b| ,求证: a+b+c=0..选择题（共9小题）2.已知关于x 的不等式组一 ：恰有3个整数解，则a 的取值范围是（）l3a-2x>0A 二3二 BC 二―三D q 一二3 2 3 2 3 2 3 2【考点】CC 一元一次不等式组的整数解.【分析】先求出不等式组的解集（含字母 a ）,因为不等式组有3个整数解，可 逆推出a 的值.（试题来源：阉蔡小丽丽）保》1专I ，，三个整数解不可能是-2, -1, 0. 若三个整数解为-1, 0, 1,则不等式组无解;2<ya<3一14~^a<01,:l解得a<3<率 故选：B.【点评】解答此题要先求出不等式组的解集，求不等式组的解集要遵循以下原则:同大取较大，同小取较小，小大大小中间找，大大小小解不了.3.不等式0&ax+5&4的整数解是1, 2, 3, 4,则a 的取值范围是（ ）A.-1 B. a0C. ^^W a < - 1D. a>【考点】CC 一元一次不等式组的整数解.【分析】先求出不等式组的解集，然后根据整数解是 1, 2, 3, 4得到关于a 的参考答案与试题解析【解答】解：由于不等式组有解，则 2a <其（四，必定有整数解0, £若三个整数解为0, 1, 2,则〕不等式组，解不等式组即可求解.注意要根据a的正负分情况讨论.【解答】解：不等式0&ax+5&4可化为ax+544। ax+5>0解得卜(1)当a=0时，得00 - 1,不成立；(2)当a>0时，得-$0x&-1，因为不等式0&ax+5&4的整数解是1, 2, a a3, 4,所以-301, -1>4,解得-5<a< -1,与a>0不符；a a 4(3)当a<0时，得-J_&x&-M；因为不等式0&ax+5&4的整数解是1, 2, a a3, 4,所以—<a< - 1.4故选：C.【点评】本题旨在考查不等式组的解法及整数解的确定. 求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了. 4,若实数abc 满足a2+b2+c2=9,代数式(a- b) 2+ (b-c) 2+ (c-a) 2的最大值是( )A. 27B. 18C. 15D. 12【考点】C2:不等式的性质.【分析】根据不等式的基本性质判断.【解答】解：: a2+b2+c2= (a+b+c) 2- 2ab - 2ac- 2bc,•• - 2ab- 2ac- 2bc=a2+b2+c2 - (a+b+c) 2①(a-b) 2+ (b-c) 2+ (c- a) 2=2a2+2b2+2c2-2ab-2ac- 2bc；又(a-b) 2+ (b-c) 2+ (c- a) 2=3a2+3b2+3c2- (a+b+c) 2=3 (a2+b2+c2) - ( a+b+c) 2②①代入②，得3 (a2+b2+c2) - (a+b+c) 2=3X9- (a+b+c) 2=27- (a+b+c) 2,=(a+b+c) 2>0,其值最小为0,故原式最大值为27.故选：A.【点评】本题主要考查了不等式a2+b2 >2ab.5.已知非负数a, b, c满足条件a+b=7, c- a=5,设S=#b+c的最大值为m,最小值为n,则m - n的值（）A. 5B. 6C. 7D. 8【考点】CE 一元一次不等式组的应用.【分析】由于已知a, b, c为非负数，所以m、n一定>0；根据a+b=7和c- a=5 推出c的最小值与a的最大值；然后再根据a+b=7和c- a=5把S=aHb+c转化为只含a或c的代数式，从而确定其最大值与最小值.【解答】解：: a, b, c为非负数；S=ahb+c>0；又 = c- a=5;c=a+5;.二c>5;a+b=7；S=ahb+c=7+c；又c> 5;；c=5时S最小，即S最小=12,即n=12;a+b=7；a0 7；.二S=ahb+c=7+c=7+a+5=12+a；；a=7时S最大，即S最大=19,即m=19;m - n=19 - 12=7.故选：C.【点评】本题考查了一元一次不等式组的应用，解答本题的关键是熟练掌握不等式的性质，求出S的最大值及最小值，难度较大.6.某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分，小明得分要超过120分，他至少要答对多少道题？如果设小明答对x道题，则他答错或不答的题数为20-x.根据题意得( )A. 10x- 5 (20-x) >120B. 10x- 5 (20-x) < 120C. 10x-5 (20-x) >120D. 10x- 5 (20-x) <120【考点】C8:由实际问题抽象出一元一次不等式.【分析】小明答对题的得分：10x;小明答错题的得分：-5 (20-x).不等关系：小明得分要超过120分.【解答】解：根据题意，得10x- 5 (20-x) >120.故选：C.【点评】此题要特别注意：答错或不答都扣5分.至少即大于或等于.7.若关于x的一元一次不等式组,二的解集是x<5,则m的取值范围是( )A. m>5 B, m>5 C. m<5 D, m<5【考点】CB:解一元一次不等式组.【分析】求出第一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了即可确定m的范围.【解答】解：解不等式2x-1>3 (x-2),得：x<5,•••不等式组的解集为x<5,m>5,故选：A.【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键.11.某射击运动爱好者在一次比赛中共射击10次，前6次射击共中53环(环数均是整数)，如果他想取得不低于89环的成绩，第7次射击不能少于6环.【考点】C9 一元一次不等式的应用.【分析】他想取得不低于89环的成绩，就是成绩要大于或等于89环，根据这个不等关系就可以列出不等式.【解答】解：已知前6次射击共中53环，不低于89环，故89-53=36环假设让最后3枪打最大值，则第7枪不得低于36- 10X 3=6环，如果少于6环, 即使后面3枪都是10环，也不能打到89环.【点评】本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解.【点评】本题考查了等腰三角形的性质；题目充分运用三个相似的等腰三角形的对应边成比例的性质解题，体现了形数结合的思想.17.若x>0, y>0,且x+y=12.贝U 后工+阴己的最小值是」3_.【考点】PA轴对称-最短路线问题.［分析］将代数式"工芯石转化为。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学习必备欢迎下载
1．若关于 x 的不等式组恰好只有四个整数解，则 a 的取值范围是（）
A ．a B．C．﹣ 2 D．﹣ 2
2．设 a，b 是常数，不等式 + ＞0 的解集为 x＜，则关于 x 的不等式 bx﹣a ＜0 的解集是（）
A ．x＞B．x＜﹣C． x＞﹣D． x＜
3．若不等式（ ax﹣1）（x+2）＞ 0 的解集是﹣ 3＜x＜﹣ 2，那么 a 等于（）
A ．B．C． 3 D．一 3
4．不等式的解集为 x＞ 2，则 m 的值为（）
A ．4 B．2 C．D．
5．若关于 x 的不等式组的整数解共有 3 个，则 m 的取值范围是（）
A ．5＜m≤ 6 B．5≤m＜6 C． 5≤ m≤6 D． 5＜m＜6 6．已知 a＞b，c≠0，则下列关系一定成立的是（）
A ．ac＞ bc B．C． c﹣a＞c﹣b D． c+a＞ c+b 7．下列命题中：
①如果 a＜b，那么 ac2＜bc2；
②关于 x 的不等式（ a﹣1）x ＞1﹣a 的解集是 x ＜﹣ 1，则 a＜1；
③若是自然数，则满足条件的正整数x 有 4 个．
正确的命题个数是（）
A ．0 B．1 C． 2 D． 3
8．若 x 是方程 2x+m﹣3（m﹣ 1）=1+x 的解为负数，则 m 的取值范围是（）
A ．m＞﹣ 1 B．m＜﹣ 1 C． m＞1 D． m＜1
9．按下面的程序计算：
若输入 x=100，输出结果是 501，若输入 x=25，输出结果是631，若开始输入的x 值为正整数，最后输出的结果为556，则开始输入的x 值可能有（）A．1 种B．2 种C．3 种D．4 种
10．若 x 为任意实数时，二次三项式 x2﹣ 6x+c 的值都不小于 0，则常数 c 满足的条件是（）
A ．c≥0 B．c≥9 C． c＞0 D． c＞9
11．关于x 的方程mx﹣1=2x 的解为正实数，则m 的取值范围是（）
A ．m≥ 2 B．m≤2 C． m＞2 D． m＜2
12．关于x 的不等式组的解集为x＜3，那么m 的取值范围为
（）
A ．m=3 B．m＞3 C． m＜3 D． m≥3
13．已知△ ABC 的边长分别为 2x+1，3x， 5，则△ ABC 的周长 L 的取值范围是（）
A．6＜L＜36B．10＜L≤11C．11≤L＜36D．10＜L＜36 14．已知实数 x、y 同时满足三个条件：① 3x﹣2y=4﹣p，② 4x ﹣3y=2+p，③ x＞y，那么实数 p 的取值范围是（）
A ．p＞﹣ 1 B．p＜1 C． p＜﹣ 1 D． p＞1
15．关于 x 的不等式组的解集是x＞﹣1，则m=．
16．若不等式组的解集为﹣1＜x＜1，那么（a+1）（b﹣1）的值等于．
17．已知关于x、y 的二元一次方程组的解满足x+y＞2，则k 的取值范围是．
18．若不等式组有解，那么 a 必须满足．
19．已知a、b 都是实数，且a= ，b= ，b＜＜2a，那么实数x 的取值
范围是．
20．若关于
围是
21．关于 x
是
x 、y 的二元一次方程组
．
的不等式 x ﹣ 3＞
．
的解满足 x+y ＞ 0，则 m 的取值范
的解集在数轴上表示如图所示，则 a 的值
22．已知关于 x 的分式方程
的解为负数，那么字母
是
．
23．求不等式（ 2x ﹣1）（ x+3）＞ 0 的解集． 解：根据 “同号两数相乘，积为正 ”可得：① 或 ②
解①得 x ＞
；解②得 x ＜﹣ 3．
a 的取值范围
．
∴不等式的解集为 x ＞ 或 x ＜﹣ 3．
请你仿照上述方法解决下列问题：
（ 1）求不等式（ 2x ﹣ 3）（x+1）＜ 0 的解集．
（ 2）求不等式≥ 0 的解集．
24．x 取哪些整数值时，不等式 5x+2＞ 3（ x ﹣ 1）与 x ﹣ 1≤ 7﹣ 都成立？
25．已知关于 x 的不等式组恰好有两个整数解，求实数a的取值范围．
26．已知一元一次不等式（ 1）若它的解集是 x＜mx﹣3＞2x+m．
，求 m 的取值范围；
（2）若它的解集是 x＞，试问：这样的 m 是否存在？如果存在，求出它的值；如果不存在，请说明理由．
27．用等号或不等号填空：
（ 1）比较 4m 与 m2+4 的大小
当 m=3 时， 4m m2+4
当 m=2 时， 4m m2+4
当 m=﹣3 时， 4m m2+4
（2）无论取什么值， 4m 与 m2+4 总有这样的大小关系吗？试说明理由．
（3）比较 x2+2 与 2x2+4x+6 的大小关系，并说明理由．
（4）比较 2x+3 与﹣ 3x﹣ 7 的大小关系．
28．是否存在整数 m，使关于 x 的不等式 1+＞+ 与关于 x 的不等式 x+1＞
的解集相同？若存在，求出整数 m 和不等式的解集；若不存在，请说明理由．
29．已知关于 x 的不等式（ 2a﹣ b）x+a﹣ 5b＞0 的解集为 x＜，
（1）求的值．
（2）求关于 x 的不等式 ax＞b 的解集．
．若不等式组
的偶数解 a 满足方程组
，求 x
2+y2 的
30
值．
31．小明把三个数﹣ 1，2﹣a，在数轴上从左到右依次排列在三个对应点上，你能确定 a 的取值范围吗？请写出你的解答过程．
32．阅读下面的例题，并回答问题．
【例题】解一元二次不等式：x2﹣ 2x﹣8＞0．
解：对 x2﹣2x﹣ 8 分解因式，得 x2﹣2x﹣ 8=（x ﹣1）2﹣ 9=（x﹣1）2﹣32=（x+2）（x﹣4），
∴（x+2）（ x﹣ 4）＞ 0．由“两实数相乘，同号得正，异号得负”，可得
①
或②
解①得 x＞ 4；解②得 x＜﹣ 2．
故 x2﹣2x﹣8＞0 的解集是 x＞4 或 x＜﹣ 2．
（ 1）直接写出 x2﹣ 9＞ 0 的解是；
（2）仿照例题的解法解不等式： x2+4x﹣ 21＜0；
（3）求分式不等式：≤0的解集．。