流体力学课后习题答案第六章
流体力学课后习题答案第六章

6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l /s ,水温为10oC ,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-= 由214Q nd v π= ①及临界雷诺数R e 2300vdν== ② 联立有 14d m m = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510ggJ 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510ggJ 1.0109.80.20147Pa 2l22τρρ-⨯===⨯⨯⨯⨯=2'3r1010gJ 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯=6.9为了确定圆管内径,在管内通过ν为0.013 cm 2/s 的水,实测流量为35cm 3/s ,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gdlQgdl gd l d h f πνυνυυν===11441281280.013150035 1.949802f lQ d cm ghνππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Qd 层流6-18 利用圆管层流Re64=λ,紊流光滑区25.0Re3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v∝f h ,光滑区75.1v∝f h ,粗糙区0.2v∝f h ;(2) 在不计局部损失h m 的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失h f 不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失h m 的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失h f 减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几? 解:(1)由R e vdν=,22f l vh d gλ=有1232f l h v gdν=即在层流 1.0f h v∝由0.250.3164R eλ=得0.251.752 1.250.1582f lvh dgν=光滑区 1.752f h v∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505sf k lh v dg=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为14128f lQh d gνπ=Q 变为16倍0.251.752 4.751.750.7898f lQh dg νπ=Q 变为6.56倍0.2523 5.2520.808sf k lQh dg π=Q 变为6.17倍(3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比h f 圆/h f 方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少? 解:(1)2214d a π=224a dπ=当量直径de a = 层流时 226464R e 22f l vlv h d gd gν==22220.7854f h de a h ddπ====圆方紊流粗糙区22f l vh d gλ=,λ相等0.886f h de a h dd====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 l/s ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
流体力学6,7,8章课后题答案

第六章 6-1解:层流状态下雷诺数Re 2000< 60.1Re 6.710vdv υ-⨯==⨯ ⇒60.120006.710v -⨯<⨯⇒62000 6.710/0.10.134(/)v m s -<⨯⨯= 即max 0.134/v m s =223max max max 0.13.140.1340.00105/ 1.05/44d Q Av v ms L sπ===⨯⨯≈=6-2解:层流状态下雷诺数Re 2000<3Re 20000.910120000.0450.1()vd d m d ρυ-=<⨯⨯⨯⇒<⇒<6-3解:3221.66100.21(/)0.13.1444Q v m s d π-⨯==≈⨯临界状态时Re 2000=52533Re Re0.210.1 1.0510(/)20001.05100.88109.2410()vd vd m s Pa s υυυμυρ---=⇒=⨯⇒==⨯⇒==⨯⨯⨯=⨯⋅ 6-4解:当输送的介质为水时:32210101270131444.(/)..Q v m s d π-⨯===⨯ 612701838632000151910..Re .vd υ-⨯===>⨯水 3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力粗糙。
当输送的介质为石油时:质量流量与水相等3310101010(/)Q kg s -=⨯⨯=31000118850.(/)Q m s == 2200118150********..(/)..Q v m s d π===⨯ 415030113184200011410..Re .vd υ-⨯===>⨯水3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力光滑。
6-5解:判断流态需先求出雷诺数()2900036009000088023144./..Re Q v m s Avd υ÷===⨯=冬季:421101./m s υ-⨯=40088021608820001110..Re ..vd υ-⨯===<⨯ ⇒ 流态为层流。
流体力学课后习题及答案-第6章
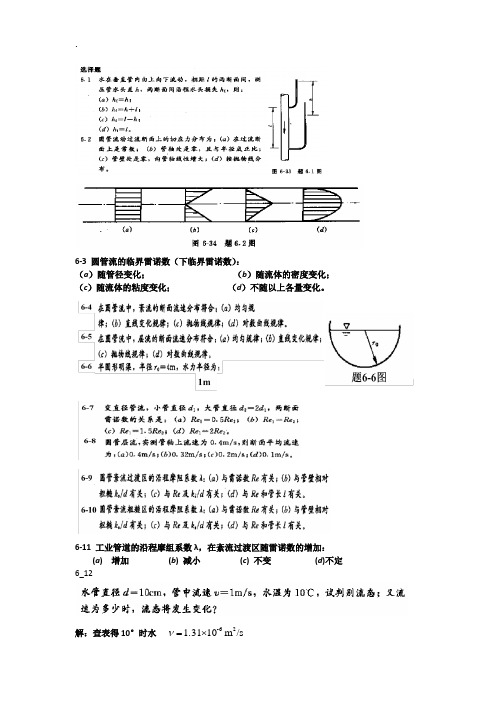
6-3 圆管流的临界雷诺数(下临界雷诺数):(a )随管径变化; (b )随流体的密度变化; (c )随流体的粘度变化; (d )不随以上各量变化。
6-11 工业管道的沿程摩组系数λ,在紊流过渡区随雷诺数的增加: (a ) 增加 (b ) 减小 (c ) 不变 (d )不定 6_12解:查表得10°时水 /s m 101.312-6⨯=ν230076341031.11.01Re 6>=⨯⨯==-νvd紊流m /s 30.01.023001031.1Re 6=⨯⨯==-d v cc ν 流速为0.30m/s 时流态将发生变化6-13解:查表得20°时空气 /s m 101.57 ,kg/m 20.12-53⨯==νρm /s 144.025.023001057.1Re 5=⨯⨯==d v cc νL/s 07.7/s m 00707.0425.014.3144.04322==⨯⨯==d v Q cc π c mQ Q Q >=⨯==/s m 0462.020.136002003v ρ紊流6-14解:查表得10°时水 /s m 101.312-6⨯=ν cm 61522015202=⨯+⨯=+=h b bh R 57568701031.106.015.0Re 6>=⨯⨯==-νvR 紊流6-15解:m/s 2563.0360015.014.33.164422=⨯⨯⨯==d Q v π 1922102.015.02563.0Re 4=⨯⨯==-νvd0333.0192264Re 64===λ m 744.06.192563.015.010000333.0222=⨯⨯==g v d l h f λ6-16见教材 P 137例6-36-17解:先按层流计算,由泊肃叶公式 408πr μρgJ Q =得 cm 97.0298014.3150035013.08884440=⨯⨯⨯⨯⨯===f gh Ql gJ Q r πνπρμ cm 94.120==r d 检验是不是层流 2300176994.114.3013.03544Re <=⨯⨯⨯===d Q vdνπν是层流,说明计算正确6-18解:皮托管测定的是管轴处的速度m/s 35.202.0)190113600(6.19)1(2=⨯-⨯=-=p p h g u ρρ以管轴处速度为特征流速计算雷诺数 23001958109075.035.2Re 5<=⨯⨯==-νud流动是层流 m/s 175.12==uv L/s 19.5/s m 00519.04075.014.3175.14322==⨯⨯==d v Q π6-19解:铸铁管道,取k s =1.25mm (平均值)3101.430025.1-⨯==d k s m/s 236.03.014.33600/604422=⨯⨯==d Q v π 46104.51031.13.0236.0Re ⨯=⨯⨯==-νvd 查穆迪图得 031.0=λ m 176.06.19236.03.0600031.0222=⨯⨯==g v d l h f λ6-20解:查表,取n =0.135m 075.04==d R 002.05001===l h J f 10.4816/1==R nC 管中流速 m /s 59.0==RJ C v6-21解:m/s 2.166.02.13600/42000=⨯==A Q v m 8.0)6.02.1(26.02.144=+⨯⨯==R d e 得由221v d l p e ρλ=∆ 0145.02.1611.15.06.31128.02122=⨯⨯⨯=∆=v p l d e ρλ 6-22解: πAd A AA d e 2 , 44===圆方 (1)层流 v gd lh f 232ρμ= 785.0422===π圆方方圆e e f f d d h h (2)紊流 g v d l h f 22λ= 886.04===π圆方方圆e e f f d d h h6-23解; m/s 702.105.014.300334.04422=⨯⨯==d Q v π 79.126.1215.0702.16.19222=⨯⨯==j h v g ζ 6-24解:由伯努利方程得 gv g v d l g v l H 222222ζλ++=+d l l H g v λζ+++=1)(2222)1()1(2d )(d dl d Hg l v λζλζ++-+=⇒ 当0d )(d 2<lv 时,管中流速随管长增加而减小,因管直径不变,流量也随管长增加而减小,即 01<-+dHλζ小时流量随管长增加而减λζdH )1(+>⇒6-25解:由伯努利方程得 gv v g v h g v 2)(222212221-++= 由连续性方程得 122212v d d v =)1(])1(1[2222122212122221424121d d d d g v d d d d g v h -=---=⇒ ⇒=0)(d )(d 2d h 由0122221=-d d 122d d = g v h 421m ax =6-26解:由伯努利方程得gv d l g v g v H 222222λζ++=进 m/s 36.6025.0602.05.01136.1912=⨯++⨯=++=dlgH v λζ进流量: L/s 12.3/s m 00312.04025.014.336.64322==⨯⨯==d v Q π 65.16.1936.6025.0102.02122=⨯⨯===g v d l h J fλ 切应力: Pa 1.10165.14025.08.910000=⨯⨯⨯==gRJ ρτ6-27解:m/s 06.305.014.3006.04422=⨯⨯==d Q v π m 15.325.06.12)1(=⨯=-=p f h h 水汞ρρ 022.006.3156.1905.015.3222=⨯⨯⨯==gv d l h f λ 6-28解; m/s 28.81.014.3065.04422=⨯⨯==d Q v π 由伯努利方程得gv d l H 2)3(2λζζζζ++++=出阀弯进6.1928.8)1.020042.0126.08.035.0(2⨯⨯+++⨯+=m 9.43=6-29 如图所示,水池中的水经弯管流入大气中。
(完整word版)流体力学习题及答案-第六章

第六章 水波理论6-1 求波长为145m 的海洋波传播速度和波动周期,假定海洋是无限深的。
答:052.1514525.125.1=⨯==λc (m/s ),633.91458.08.0=⨯==λτ(s );即传播速度为15.052(m/s ),波动周期为9.633(s )。
6-2 海洋波以10m/s 移动,试求这些波的波长和周期。
答:6425.1/1025.1/2222===c λ(m ), 4.6648.08.0=⨯==λτ(s );即波长为64(m ),波浪周期为6.4(s )。
6-3 证明()t iH A z W Ω-+=ςλπ2cos )(为水深为H 的进行波的复势,其中iy x +=ς为复变数,y 轴垂直向上,原点在静水面上。
并证明λπλπHth 222=Ω(提示:()xshy i xchy iy x sin cos cos -=+)。
答:在图示坐标系中,平面进行波的速度势为:()()t kx chkHH y chk ag ωωϕ-+=sin 在x 、y 方向的速度分别为: ()()t kx shkHH y chk a x u ωωϕ-+=∂∂=cos , ()()t kx shkH H y shk a y v ωωϕ-+=∂∂=sin ; 由上述速度分布得到二维波浪运动的流函数为:()()()()()()()()t kx chkHH y shk ag t kx shkHH y shk k a dy t kx shkHH y chk a dx t kx shkH H y shk a udy vdx ωωωωωωωωψ-⋅+⋅=-⋅+⋅=-++-+-=+-=⎰⎰cos cos cos sin 因此,二维波浪运动的复势为:()()()()()()()()()()()[]t kx H y ishk t kx H y chk chkHag t kx chkHH y shk ag i t kx chkH H y chk ag t y x i t y x z W ωωωωωωωψϕ-++-+⋅=-+⋅+-+⋅=+=cos sin 1 cos sin ,,,, 在上式中,令:chkH ag A 1⋅=ω,t kx X ω-=,()H y k Y +=; 则可得到:()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅-⎪⎭⎫ ⎝⎛-⋅=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅+⎪⎭⎫ ⎝⎛-⋅=⋅+⋅=2sin 2cos 2sin 2cos cos sin ππππX ishY X chY A X ishY X chY A X ishY X chY A z W 由提示()xshy i xchy iy x sin cos cos -=+,可以得到:()()()⎥⎦⎤⎢⎣⎡--++=⎪⎭⎫ ⎝⎛++--=⎪⎭⎫ ⎝⎛+-=2cos 2cos 2cos πωπωπt ikH iy x k A H y ik t kx A iY X A z W6-4 在水深为d 的水平底部(即d z -=处),用压力传感器记录到沿x 方向传播的进行波的波压力为()t p 。
流体力学龙天渝课后答案第六章

流体力学龙天渝课后答案第六章1、重100N的物体放在地面上,物体对地面的压力一定为100N [判断题] *对错(正确答案)答案解析:水平地面上2、与头发摩擦过的气球能吸引细小水流,是因为气球和水流带上了同种电荷[判断题]对错(正确答案)答案解析:气球经过摩擦后带电,可以吸引轻小的水流3、56.在没有任何其他光照的情况下,舞台追光灯发出的紫光照在穿白上衣、红裙子的演员身上,观众看到她()[单选题] *A.全身呈紫色B.上衣呈紫色,裙子不变色C.上衣呈黑色,裙子呈紫色D.上衣呈紫色,裙子呈黑色(正确答案)4、若以M表示水的摩尔质量,v表示水的摩尔体积,ρ表示水的密度。
Na为阿伏加德罗常数,m表示水的分子质量,V’表示水分子体积。
则下列关系中正确的是()*A.Na=V/V’(正确答案)B.V=M/ρ(正确答案)C.m=M/NA(正确答案)D.v=ρM5、41.下列物态变化现象中,说法正确的是()[单选题] *A.夏天从冰箱取出的冰棍周围冒“白气”,这是空气中水蒸气的凝华现象B.市场上售卖“冒烟”的冰激凌,是由于其中的液氮汽化吸热致使水蒸气液化形成(正确答案)C.在饮料中加冰块比加冰水的冰镇效果更好,是因为冰块液化成水的过程中吸热D.手部消毒可以用酒精喷在手上,感到凉爽是因为酒精升华吸热6、15.下列有关托盘天平的使用说法正确的是()[单选题] *A.称量前,应估计被测物体的质量,以免超过量程(正确答案)B.称量前,应调节平衡螺母或移动游码使天平平衡C.称量时,左盘放砝码,右盘放物体D.称量时,向右移动游码,相当于向左盘加砝码7、3.对匀减速直线运动,公式v2-v02=2ax中的a必须取负值.[判断题] *对错(正确答案)8、35.已知甲液体的密度ρ甲=5g/cm3,乙液体的密度ρ乙=2g/cm3,现在取一定量的甲乙液体混合,混合液体的密度为3g/cm3,液体混合前后总体积保持不变,则所取甲乙体积比V甲:V乙=()[单选题] *A.5:2B.2:5C.1:2(正确答案)D.2:19、若跳高运动员竖直向下蹬地的力大于他的重力,运动员就能从地上跳起来[判断题]*对(正确答案)错答案解析:运动员竖直向下蹬地的力与地面给他的支持力是一对相互作用力,大小相等。
工程流体水力学第六章习题答案

第六章 量纲分析和相似原理答案6-1由实验观测得知,如图6-1所示的三角形薄壁堰的流量Q 与堰上水头H 、重力加速度g 、堰口角度θ以及反映水舌收缩和堰口阻力情况等的流量系数m 0(量纲一的量)有关。
试用π定理导出三角形堰的流量公式。
解:()00θ=,,,,f Q H g m 选几何学的量H ,运动学的量g 作为相互独立的物理量,有3个π项。
111πa H g Q β=,222a H g,3330πa H g m对1π,其量纲公式为11000-23-1L T M =L (LT )L T11L :03αβ=++,1T :021β=--解出152α=-,112β=-,则可得 152πQg H对2π,其量纲公式为220002L T M L (LT )22L :0αβ=+,2T :02β=-联立解上述方程组,可得02=α,02=β,02=γ,则可得2π对3π,其量纲公式为33000-2L T M L (LT )33L :0αβ=+,3T :02β=-联立解上述方程组,可得03=α,03=β,03=γ,则可得30πm123πππ0F ,,即052()0Q F m g H,,或1052()Q F m g H,2501),(H g m F Q θ=式中,θ要视堰口的实际角度而定,量纲一的量0m 要由实验来确定。
第十章三角形薄壁堰的理论分析解5204tan 252Qm gh 与上式形状相同。
6-2 根据观察、实验与理论分析,认为总流边界单位面积上的切应力τ0,与流体的密度ρ、动力粘度μ、断面平均流速v ,断面特性几何尺寸(例如管径d 、水力半径R )及壁面粗糙凸出高度Δ有关。
试用瑞利法求τ0的表示式; 若令沿程阻力系数8(,)λ∆=f Re d,可得208λτρ=v 。
解:351240τkv d将上式写成量纲方程形式后得35124-1-23-1-110dim ML T =(ML )(ML T )(LT )(L)(L)ααααατ--=根据量纲和谐原理可得:12M :1αα=+12345L :13ααααα-=--+++ 23T :2αα-=--选53αα、为参变量,联立解上述方程组可得:131αα=-,232αα=-,4352ααα=-+-。
工程流体力学禹华谦习题答案第6章

工程流体力学禹华谦习题答案第6章本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March第六章 理想流体动力学6-1平面不可压缩流体速度分布为Vx=4x+1;Vy=-4y.(1) 该流动满足连续性方程否 (2) 势函数φ、流函数ψ存在否(3)求φ、ψ 解:(1)由于044=-=∂∂+∂∂y Vy x Vx ,故该流动满足连续性方程 (2)由ωz =21(y Vx xVy ∂∂-∂∂)=)44(21+-=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程, 流函数ψ存在,.(3)因 Vx yx ∂∂=∂∂=ψϕ=4x+1 Vy=y ∂∂φ=-x∂∂ψ=-4y d φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(4x+1)dx+(-4y)dy φ= ⎰d φ=⎰x ∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy=⎰ (4x+1)dx+(-4y)dy =2x 2-2y 2+xd ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdy=4ydx+(4x+1)dy ψ= ⎰d ψ=⎰x ∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰ 4ydx+(4x+1)dy =4xy+y6-2 平面不可压缩流体速度分布:Vx=x 2-y 2+x; Vy=-(2xy+y).(1) 流动满足连续性方程否 (2) 势函数φ、流函数ψ存在否 (3)求φ、ψ .解:(1)由于x Vx ∂∂+xVy ∂∂=2x +1-(2x +1)=0,故该流动满足连续性方程,流动存在.(2)由ωz =21(y Vx xVy ∂∂-∂∂)=))2(2(21y y ---=0, 故流动有势,势函数φ存在,由于该流动满足连续性方程,流函数ψ也存在.(3)因 Vx=x∂∂φ =y ∂∂ψ= x 2-y 2+x, Vy=y ∂∂φ=-x ∂∂ψ=-(2xy+y). d φ=x∂∂φdx+y ∂∂φdy=Vxdx+Vydy=(x 2-y 2+x )dx+(-(2xy+y).)dy φ= ⎰d φ=⎰x ∂∂φdx+y ∂∂φdy=⎰Vxdx+Vydy =⎰ (x 2-y 2+x )dx+(- (2xy+y))dy =33x -xy 2+(x 2-y 2)/2 d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdy ψ= ⎰d ψ=⎰x ∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy =⎰(2xy+y)dx+ (x 2-y 2+x)dy =x 2y+xy-y 3/36-3平面不可压缩流体速度势函数 φ=x 2-y 2-x,求流场上A(-1,-1),及B(2,2)点处的速度值及流函数值解: 因 Vx=x ∂∂φ =y ∂∂ψ=2x-1,V y =y x y 2-=∂∂-=∂∂ψφ,由于x Vx ∂∂+xVy ∂∂=0,该流动满足连续性方程,流函数ψ存在d ψ=x∂∂ψdx+y ∂∂ψdy=-Vydx+Vxdy ψ= ⎰d ψ=⎰x ∂∂ψdx+y ∂∂ψdy=⎰-Vydx+Vxdy=⎰2ydx+(2x-1)dy=2xy-y 在点(-1,-1)处 Vx=-3; Vy=2; ψ=3在点(2,2)处 Vx=3; Vy=-4; ψ=66-4已知平面流动速度势函数 φ=-π2q lnr,写出速度分量Vr,V θ,q 为常数。
流体力学吴望一教材第六章作业参考答案

第六章作业参考答案18.求理想不可压重力作用下的流体,在开口曲管中的振动规律.假定管为等截面的,管中流柱长为,,l αβ围曲管于水平线间的夹角,运动的初始条件是由平衡位置开始振动.解:设流体离开平衡位置的位移为x ,则由lagrange 积分得:()222212121102P P v v xds g z z t ρ--∂+++-=∂⎰ ()212121,,sin sin a P P P v v z z x αβ===-=+()sin sin 0xlg x αβ∴++=∴振动周期为2T π=ω=20.从充满空间的理想不可压缩流体中突然取出半径为c 的球状体积,设在无穷远处各点作用着压力()p 常数.无外力作用,求流体的运动规律.习题册25.宽为b 的二维理想不可压缩流体喷柱,正击于一静止的平板后,向两边分流.设来流速度为v ,密度为ρ.如果不考虑重力影响,试求平板所受的冲击力.解:取一正方形计算动量通量,x 方向动量通量为0,合面力为0。
y 方向动量通量为: v vb y ρ-= 方向面力()ap p nds P =-=-⎰⎰ 2aP V b bp ρ=+板 28.设流体是理想不可压缩的,流动是定常的.流体高度为h ,流速为V ,在重力作用下流过闸门(如图).闸门下游流体深为l .要固定闸门,求闸门单位宽度上所需的力R ,用,,g h l ρ和表示.解:我们取沿表面一圈为控制体CS ,通过CS 的动量通量=合面力+合体力我们只考虑水平方向的动量通量:设来流速度为1v ,出口速度为2v 则12v h v l =又()11221200hla v v h v v l p dy p dy p D l R ρρ-+=+---⎰⎰ 其中()1a p p g h y ρ=+-()2a p p gl y ρ=+-闸门的合力为()a R P h D --2. 证明在不可压缩的平面运动中,速度分布()()11,k n k n n n v akr e v ar e r θθθ-+-+== 是一种可能的速度分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6-5 某蒸汽冷凝器内有250根平行的黄铜管,通过的冷却水流量Q =8 l ,水温为10,为了使黄铜管内冷却水保持为紊流(此时黄铜管的热交换性能比层流时好),问黄铜管的直径不得超过多少?解:查表1.3有10℃的水621.310*10/m s ν-= 由214Q n d v π= ① 与临界雷诺数Re 2300vdν== ②联立有 14d mm = 即为直径最大值6.7 某管道的半径0r 15cm =,层流时的水力坡度J 0.15=,紊流时的水力坡度J 0.20=,试求管壁处的切应力0τ和离管轴r 10cm =轴处的切应力。
解:层流时:2f 3000h r r 1510g g J 1.0109.80.15110.25Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=23r 1010g J 1.0109.80.1573.5Pa 22τρ-⨯==⨯⨯⨯⨯=紊流时:2f 3000h r r 1510g g J 1.0109.80.20147Pa 2l 22τρρ-⨯===⨯⨯⨯⨯=2'3r 1010g J 1.0109.80.2098Pa 22τρ-⨯==⨯⨯⨯⨯= 6.9为了确定圆管内径,在管内通过ν为0.013 2的水,实测流量为353,长15m ,管段上的水头损失为2㎝水柱,试求此圆管的内径。
解: 设管内为层流42212832264gdlQ gd l g d l d h f πνυνυυν=== 11441281280.013150035 1.949802f lQ d cm gh νππ⎛⎫⨯⨯⨯⎛⎫===⎪ ⎪⎪⨯⨯⎝⎭⎝⎭校核 1768013.094.13544Re =⨯⨯⨯===πνπνυd Q d 层流 6-18 利用圆管层流Re64=λ,紊流光滑区25.0Re3164.0=λ和紊流粗糙区25.011.0⎪⎭⎫⎝⎛=d k s λ这三个公式,(1)论证在层流中0.1v ∝f h ,光滑区75.1v ∝f h ,粗糙区0.2v ∝f h ;(2) 在不计局部损失的情况下,如管道长度l 不变,若使管径d 增大一倍,而沿程水头损失不变,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,流量各为原来的多少倍?(3) 在不计局部损失的情况下, 如管道长度l 不变,通过流量不变,欲使沿程水头损失减少一半,试讨论在圆管层流、紊流光滑区和紊流粗糙区三种情况下,管径d 各需增大百分之几?解:(1)由Re vdν=,22f l v h d g λ=有1232f l h v gd ν=即在层流 1.0f h v ∝由0.250.3164Reλ= 得0.25 1.752 1.250.1582f lv h d g ν=光滑区 1.752f h v ∝由0.250.11s k d λ⎛⎫= ⎪⎝⎭得0.2523 1.250.0505s f k l h v d g=粗糙区 2.03f h v ∝(2)由214Q d v π=,以上公式变为14128f lQh d gνπ=Q 变为16倍0.25 1.7524.75 1.750.7898f lQ h d g νπ=Q 变为6.56倍0.25235.2520.808s f k lQ h d g π=Q 变为6.17倍(3)由以上公式计算可知分别19%,16%,14%6-19 两条断面面积、长度、相对粗糙高度都相等的风管,断面形状分别为圆形和正方形,试求(1)若两者通过的流量相等,当其管内流动分别处在层流和紊流粗糙区两种情况下时,两种管道的沿程水头损失之比圆方分别为多少?(2)若两者的沿程水头损失相等,且流动都处在紊流粗糙区,哪条管道的过流能力大?大多少? 解:(1)2214d a π= 224a d π=当量直径de a = 层流时226464Re 22f l v lvh d g d gν==22220.7854f h de a h d d π====圆方紊流粗糙区22f l v h d gλ=,λ相等0.886f h de a h d d ====圆方(2)Q Q =圆方此时圆管流通能力大,大6%6.20 水管直径为50㎜,1、2两断面相距15 m ,高差3 m ,通过流量Q =6 ,水银压差计读值为250㎜,试求管道的沿程阻力系数。
解:()s m d Q /06.305.0006.04422=⨯==ππυ2211221222fp p Z Z h g g g g υυρρ++=+++121212.612.60.25 3.15fp p p Z Z h g g h mρρ⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭==⨯=mg d l h f 15.322==υλ23.1515 3.060.0519.60.022λ==⨯6-23测定某阀门的局部阻力系数ζ,在阀门的上下游共设三个测压管某间距L 1=12=2m.若直径50,实测H 1=1502=1253=40,流速3,求阀门的ζ值。
解:2112h H H (150125)100.25m -∆=-=-⨯=1111L h dh d 0.250.050.0125L 1λλ∆=∆⨯⨯=== 2223h H H (12540)100.85m -∆=-=-⨯=2222222L v h d 2gL 2(h )2g (0.850.0125)29.8d 0.050.762v 3λζλζ∆=+∆-⨯-⨯⨯⨯=== 6-24 用突然扩大使管道的平均流速由v1减到v2,若直径d1与流速v1一定,试求使测压管液面差h 成为最大的v2与d2是多少?并求最大h 值。
解: ()22212112212222p p Z Z g g g g gυυυυρρ-++=+++()22212211221221222 p p h Z Z g g g g g gυυυυρρυυυ-⎛⎫⎛⎫-=+-+=- ⎪ ⎪⎝⎭⎝⎭=-+02122=+-=gg d dhυυυ211221max 24d h g υυυ===6-25 速由变到的突然扩大管,如分两次扩大,中间流速取何值时局部水头损失最小?此时的局部水头损失为多少?并与一次扩大时比较。
解:222211m 2A v A v h 11A 2g A 2g ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭其中11Q A v =,QA v=,12Q A v =()2221212m 2v 2v v v v v h 2g-+++=要使m h 最小,则mdh 0dv= 即 ()124v 2v v =+所以 12v v v 2+=时局部水头损失最小()212m v v h 4g-=一次扩大时:()2221211m 2v v A v h 1A 2g 2g -⎛⎫=-= ⎪⎝⎭是两次扩大时的两倍6-26 水箱中的水通过等直径的垂直管道向大气流出。
已知水箱的水深H ,管道直径d ,管道长l ,沿程阻力系数λ,局部阻力系数之和为∑ζ,试问在什么条件下:(1)流量Q 不随管长l 而变化?(2)Q 随l 的增加而减小?(3)Q 随管l 的增加而增加? 解(1)水箱水面进出口断面能量方程由212l vH L d g λξ⎛⎫+=++ ⎪⎝⎭∑得,v =21144Q d d v ππ==因为0dQ dL =,解得()1dH ξλ=+∑ (2)0dQ dL ,即()1dH ξλ+∑(3)0dQ dL ,即()1dH ξλ+∑6-28 水池中的水经弯管流入大气中(题6-26图),已知管道的直径100,水平段和倾斜段的长度均为50m ,高差h 1=22=25m ,段设有阀门,沿程阻力系数λ=0.035,管道入口与转弯的局部水头损失不计。
试求:为使段末段B 处的真空高度不超过7m,阀门的局部阻力系数ζ最小应是多少?此时的流量是多少?解:取水池自由液面和 B 处断面列伯努利方程:2211221222p p Z Z h g g g gυυρρ++=+++因为:121Z Z h -=1p =0 1p 7g ρ 1v =0所以:2v =3.088取B 处断面和C 处断面列伯努利方程:2233222322p p Z Z h g g g gυυρρ++=+++因为:232Z Z h -= 2v =3v 3p =0所以:h 18m =()222l v h ()d 2gh 2g l 1829.8500.03519.498v d 0.13.088ζλζλ=+⨯⨯⨯=-=-⨯=此时22d 3.088(0.1)Q v 24.25l /s 44ππ⨯⨯=== 6.29略6-31自水池中引出一根具有三段不同直径的水管,已知直径d =50㎜,D =200㎜,长度l =100 m ,水位H =12 m ,沿程阻力系数λ=0.03,局部阻力系数ζ阀=5.0,试求通过水管的流量并绘总水头线与测压管水头线。
解:由连续性方程116D υυ=列1、2断面伯努利方程200002fm H h h gυ++=++++22222.512.5150.05822225642D f l l l h d g D g d g gυυυυλλλ⎛⎫=+=+= ⎪⨯⎝⎭(ζ入口+ζ突扩+ζ突缩+ζ阀)22gυ879.01615411122222=⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=D d 扩ζ 469.016155.015.02=⨯=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=D d 缩ζ()220.50.8790.469 5.0 6.84822m h gg υυ=+++=()221150.058 6.848157.922H gg υυ=++=s m /22.19.157126.19=⨯=υ()220.05 1.22 2.39 /44dQ l s ππυ==⨯=6-32某闸板阀的直径d =100,该阀门在开度0.125时局部阻力系数ζ1=97.3,开度0.5时的ζ2=2.06,该管道的沿程阻力系数为0.03。
试求两不同开度情况下的折算长度。
解:221 2,22324.36.87v l vl d g d gl m l m ζζλλ== ==。
