2021年正态概率图(normal probability plot)
如何检验数据是否服从正态分布

如何检验数据是否服从正态分布正态分布是概率论和统计学中的一个重要分布,也称为高斯分布。
在很多实际问题中,需要确定一个数据集是否服从正态分布。
本文将介绍几种常用的方法来检验数据是否服从正态分布。
1.直方图检验法:直方图是用来表示数据频数分布的常用图形方法。
通过绘制数据集的直方图,我们可以观察数据的分布情况。
对于服从正态分布的数据,其直方图应该是呈现出一座钟形曲线的形状。
如果数据集的直方图呈现出钟形曲线的形状,那么可以初步判断数据服从正态分布。
但这种方法仅适用于大样本量和精确的直方图。
2.正态概率图法:正态概率图(Probability Plot)是另一种判断数据是否服从正态分布的方法。
正态概率图是将数据按照大小排序后,将每个数据点的累积分布函数的值(即标准正态分布分位数)在纵坐标上绘制,而横坐标则表示数据点的实际值。
如果数据集的正态概率图上的点大致沿着一条直线排列,则可以认为数据服从正态分布。
4.统计检验法:统计检验是通过计算统计量来得出结论的方法。
常用的统计检验方法有Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Anderson-Darling检验。
- Kolmogorov-Smirnov检验:该检验利用累积分布函数(CDF)来判断观测样本与理论分布之间的差异,若与理论分布没有显著差异,则可认为服从正态分布。
- Shapiro-Wilk检验:该检验是一种适用于小样本量的检验方法,利用观察数据与正态分布之间的相关系数来判断数据是否服从正态分布。
- Anderson-Darling检验:该检验适用于中等样本量,通过计算观察数据与理论分布之间的差异来判断数据服从的分布类型。
总结:。
SIMCA-P_11.5_指南(中文)要点

SIMCA-P,SIMCA-P+指南11.0版本Umetrics AB1992-2005 Umetrics AB本篇文章诣在告诉本软件使用者一些该软件的注意事项,并且该文件并不能作为Umetrics AB 公司承担义务的一部分。
该软件中的信息(包括所包含的所有数据库)均需要得到已公布或未公布的许可协议方可使用,并且必须在获得许可协议的前提下方可以使用或拷贝,在未得到已公布或未公布的许可协议下擅自的进行软件的拷贝是一种违法行为,在未得到Umetrics AB公司书面许可的前提下,该产品的任何部分不可以再次安装或以任何形式、任何传播方式(包括电子传播方式、机械传播方式)进行软件的传播。
SIMCA是Umetrics 公司的注册商标,Windows是Microsoft 公司的注册商标。
包括以下商品:SIMCA-P,SIMCA-P+编辑日期:2005年5月16日目录SIMCA软件的启动基本操作规程基础信息SIMCA-P软件是以工程(projects)的形式来进行数据的建模处理。
一个工程就是一个包含着主要的数据集(dataset)分析结果(没有模型数量的限制)的集合。
你可以通过输入数据(主要是数据集)来进行一个新的工程的建立。
当你选择活动模型类型(Active Model Type)并列举一个新的工作集或一个已经存在的工作集时,SIMCA-P软件将自主建立不合适的模型。
在一个工程建立的最初,系统默认的工作集包含所有的数据,包含所有的居中变量及方差的变化范围,并将其视作变量X,并且模型是变量X的重要组成部分。
一个工程窗口可以显示每一个模型的分析结果,每一行数据及时对一个模型的分析结果进行总结。
活动模型(即所需要进行建模处理的模型),也可以在灰色区域(status bar)左边的显示框中显示,即在命令菜单的下方。
如果你想打开一个模型,在工程窗口中双击该模型,将打开一个包含模型结果所有信息(一行一个分类)的模型窗口。
分式析因设计资料
1
1
1 P -1 1
11
T
1
-1 -1 S
2
1
1
P -1
1
-1
M
1
9
符号
分式析因设计的符号表示如下:
2
k R
p
• 2 --每个因素的水平数
• k --因素个数
• 2-p --分式大小 (p=1 1/2 分式,
分式, etc.)
p=2 1/4
• 2k-p --试验次数
• R -24-IV分1 辨度(resolution)
并估计这一变量关系. 注意:这一未知的真实方程式中, ST和PM 都很重要. ST和PM 呈别名关系. 该别名关系影响对过程模型的推导和解释?
15
线性组合
如用Minitab运行1/2方式析因设计, 将显示如下结 果(不包括误差)
Y 505 S 2.5T 1.9 S T 2.1 P M 真实模型
Term Constant S T P M S*T S*P S*M
Effect
10.000 5.000
-0.000 0.000
-8.000 -0.000
0.000
Coef 50.000
5.000 2.500 -0.000 0.000 -4.000 -0.000 0.000
Alias Structure
分式析因设计主要用于因素筛选:实验包含的因素相 对较多而试验次数相对较少
因素筛选实验通常在过程改进项目的初期实施
3
如何分配实验资源$$?
k=#
# main # 2 # 3 # 4 # 5 #6 #7
factors # runs effects ways ways ways ways ways ways
SPSS-5-假设检验与推断统计

二、SPSS的实现
3、正态性检验
许多统计过程,如方差分析,要求各组样本数据来自是有相同方差 的正态总体。因此,在选定统计假设之前,我们需要检验假设:各组数 据有相同方差,或者,所有样本来自正态总体。 由于正态分布对于统计推断非常重要,因此,我们经常想考察“我 们的数据来自一个正态分布”这样一个假设。
原假设 H0:各分组数据的方差是相等的(或齐性的); 研究假设 H1:各分组数据的方差是不等的(或非齐性的) 。 SPSS实现:
Analyze → Descriptive Statistics → Explore →Plots… → Untransformed
4、方差齐性检验(Levene检验)
案例分析:检验2000级学生课堂调查数据.sav中男女生“身高”数据的离散程度
一、相关的概念
3、假设检验(Hypothesis Test)
(1)根据实际问题的需要提出假设,包括: 原假设: H0 研究假设:H1 原假设被否定时,即接受研究假设。
例:某高校的英语四级平均成绩是67.5分,改进教学 方法后,学生的英语四级成绩是否有显著变化?是 否有显著提高?是否有显著下降? 是否有显著变化? H : 1000
0
H1 :
1000
是否有显著提高? 是否有显著下降?
H0 : H1 : H0 : H1 :
1000 1000 1000 1000
一、相关的概念
3、假设检验(Hypothesis Test)
(2)选择适当统计量及其分布
假设检验,基本上是根据抽样分布的原理。根 据H0假设来确定一个抽样分布,由此抽样分布来计 算各种情况出现的概率,如果实际样本出现的事件 属于小概率事件,然而小概率事件在一次抽样中就 出现了,这时我们就要怀疑所作的H0假设了,即: 否定H0,接受H1。
解读正态概率图正态概率图纸的秘密.doc

解读正态概率图-正态概率图纸的秘密本文是对解读Minitab的正态概率图一文中注解3-正态概率图图纸的说明1上图的H0假设1)上图单组数据为34,35,36,37,38,39,40,40,41,42,43,44,45,46共N=14个2)计算得平均值为Xbar=40,标准差为s=3.741657 (图示为3.742)3)上图的H0假设数据源自正态分布,相对H1就是非正态分布4)基于正态分布的假设,所以根据样本数可以估计此正态分布的2个参数,平均值μ为40,标准差σ为3.7416572正态分布的特性x、z与累积分配函数1)正态分布z值有人称z score,是正态分布的变量x,转换为标准正态分布时对应值为z,关系是为z=(x-μ)/σ2)正态分布下变量x,经转换为标准正态分布对应值z,就可经由正态分布数值表或软件等求得x的累积分配函数(cdf),cdf一般统计符号写成F(x)= P(X≦x),P就是X≦x累积机率,正态概率图的纵坐标Percent就是F(x)3)鼠标移到Minitab蓝色直线上,就会出现如下图中的黄底的Percent与x数值表4)Percent与x数值表说明黄底的Percent与x数值表,Percent就是F(x),F(x)是指定的解于0与1之间,表上所示数值系为%,透过标准正态分布,就可求F(x)的反函数z,然后以公式x=zσ+μ得到x值3正态性检定使用的正态概率图图纸1)下表为手工计算,结果与minitab的Percent与x数值表相符的作成蓝色参考值线的数据x、z、F(x)关系表如下表,表中系先指定F(x),就是表中Percent栏,然后基于正态分布求x=F-1(x),再使用正态分布标准化公式计算z=(x-Xbar)/s2)若以Percent vs x畫散佈圖是S型曲線並非直線,如下圖,所以常態機率圖的繪製有點竅門3)理解正态概率图图纸解读正态概率图的第一要务是理解所谓机率图图纸,常用有常态与Weibull二种机率图图纸,下图是正态概率图图纸的示意图,图中蓝色直线是基于H0的正态分布假设下,自样本数据去估计平均Xbar=40与标准差s=3.741657,并制作x、z、F(x)关系表(如上表)所作成4正确制作正态概率图图纸步骤1)作z vs x作散布图为了能够显示一直线,于是以z vs x作散布图,并于每个点上,标出该数据x对应的F(x)值,每一个点上也画出网格线如下图,观看网格线,似乎类似对数坐标(实际上并不是)2)將各點百分比值F(x)作為新座標Y軸3) 若将纵坐标Y轴隐藏或者是移到次坐标轴,而将数据卷标F(x)值作为纵坐标Y轴的坐标刻度,此时就是正态概率图纸5正态概率图的应有认识一张正态概率图表面上为F(x) vs x,实质上还是存在z vs x关系,构成正态概率图的二个轴分别为1)排序数据x2) 数据x对应累积比例(标准正态分布的百分位数值)至于数据x置于横轴或纵轴,不同软件表现不同,Minitab放在横轴,JMP放在纵、横轴均可指定,而Excel是放在在纵轴。
正态概率图(normal probability plot)精编版
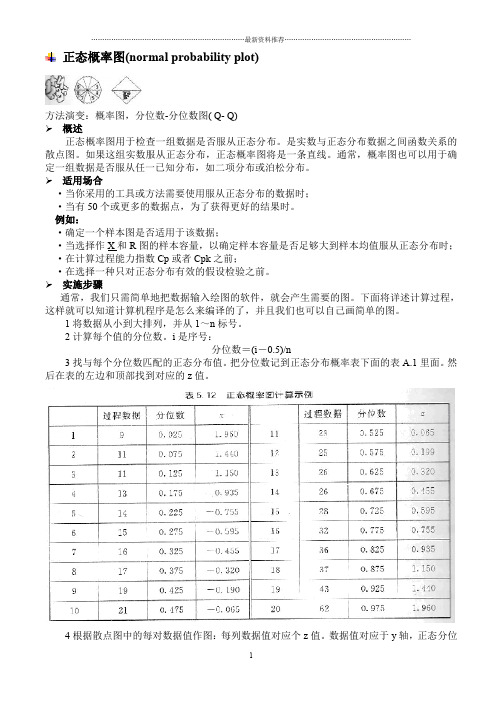
正态概率图(normal probability plot)方法演变:概率图,分位数-分位数图( Q- Q)概述正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
适用场合·当你采用的工具或方法需要使用服从正态分布的数据时;·当有50个或更多的数据点,为了获得更好的结果时。
例如:·确定一个样本图是否适用于该数据;·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;·在选择一种只对正态分布有效的假设检验之前。
实施步骤通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
示例为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20以此类推直到最后1个分位数=19. 5÷20。
spc专业词汇

quality improvement 质量改进quality control and improvement 质量控制及改进statistical 统计学reliability 可靠性conformance to Standards 符合标准characteristic 特性,性能regression analysis 回归分析random 随机的rectifying inspection 挑选型检验systematic reduction of variability 减少系统性波动acceptance sampling 验收抽样total quality management 全面质量管理company-wide quality control 全公司质量控制total quality assurance 全面质量保证quality standards and registration 质量标准和注册process control 过程控制quality system 质量体系internal audits 内部审核第二章专业词汇binomial distribution 二项分布mean 平均值variance 方差sample fraction defective 样本不合格品率sample fraction nonconforming 样本不合格品率Poisson distribution 泊松分布stem-and-leaf plot 茎叶图frequency distribution and histogram 频率分布和直方图box plot 箱线图probability distributions 概率分布hypergeometric distribution 超几何分布Pascal and related distributions 帕斯卡及其相关分布normal distribution 正态分布exponential distribution 指数分布the first quartile 第一四分位数the third quartile 第三四分位数Inter quartile range 四分位距sample mean 样本均值sample variance 样本方差sample standard deviation 样本标准差sample median 样本中位值mode 众数continuous distributions 连续分布discrete distributions 离散分布Bernoulli trials 伯努利试验(或贝努利试验)第三章专业词汇statistical process control (SPC) 统计过程控制check sheet 检查表Pareto chart 排列图cause-and-effect diagram 因果图defect concentration diagram 缺陷位置图scatter diagram 散布图control chart 控制图in statistical control 处于统计控制状态assignable causes 非随机原因,可查明的原因standard deviation 标准差average to signal(ATS) 平均报警时间(指:过程发生变化后平均发信号时间)average run length(ARL) 平均链长ATS=ARL×h(h 为时间)false alarms 误发警报missing alarms 漏发警报positive correlation 正相关causality 因果关系capability 能力(第四章出现该词通常指过程能力的意思)trial control limits 试验用控制限(指试验用控制图的控制限)specification limits 规范限,规格限current control 当前(生产)控制X bar and R chart 均值-极差控制图in control 受控(状态)out of control 失控(状态)process variability 过程波动unbiased estimator 无偏估计量departures 偏离variable sample size 可变样本容量exhibited 呈现recompute 重新计算parameter 参数equation 等式,公式standard values 标准值(指过程参数)the process mean 过程均值make process modifications 过程改进Cyclic patterns 周期性(变化)模式A shift in process level 过程水平发生偏移standard normal cumulative distribution function 标准正态累积分布函数quality characteristic 质量特性range 极差nonconforming 不符合,不合格nominal value 标称值subgroup 子组rational subgroup 合理子组range method 极差法weighted average approach 加权平均法the moving range 移动极差control chart for individual measurement 单值控制图operating-characteristic curves 操作特性曲线Over control 过度控制a shift in process level 过程水平偏移第五章专业词汇fraction nonconforming 不合格品率target value 目标值variable-width control limit 可变宽度控制界限individual sample 每个样品specific sample size 特定样本大小the upper control limit 控制上限the lower control limit 控制下限square root 平方根estimate of the standard deviation 标准偏差估计average sample size 平均样本容量approximate set of control limits 近似的一组控制限the standardized control chart 将控制图标准化(指通用控制图)nonrandom 非随机的nonconformities per unit 单位不合格数the preliminary data 原始数据the average number of nonconformities per unit 平均单位不合格数the number of inspection units 检验单位个数variable control limits 可变控制限center line 中心线process fraction nonconforming 过程不合格品率不合格品率控制计算公式:nonconformity 不符合、不合格第六章专业词汇process capability analysis 过程能力分析probability plot 概率图process capability ratio (PCR)过程能力指数off-center process (分布中心)偏离公差中心的过程confidence interval 置信区间uniformity 一致性quality characteristic 质量特性product characteristic 产品特性tolerance 公差vendor 供方designed experiments 实验设计chi-square distribution 卡方分布process performance indices 过程性能指数normal probability plot 正态概率图variables 计量,计量值(注意:variable 意思是“可变的,变量”)第七章专业词汇sampling plan 抽样方案sampling scheme 抽样计划acceptance sampling 验收抽样items 项目,产品liability risk 可靠性风险、责任风险Lots 批lot-by-lot 逐批attributes 计数,计数值single-sampling plan 一次抽样方案acceptance number 接收数inspection 检验OC curve(the operating characteristic curve)操作特性曲线probability of acceptance 接收概率discriminatory power 判别力、鉴别力(指判别批质量好坏的能力)acceptable quality limit(AQL)接收质量限lot tolerance percent defective(LTPD) 批允许不合格品率rejectable quality level(RQL) 拒收质量水平limiting quality level(LQL) 极限质量水平probability distribution 概率分布finite size 有限(样本)容量lot fraction defective 批不合格品率fixed percentage 固定百分比double sampling 二次抽样a final lot dispositioning decision 批的最终处置决定the fraction defective 不合格品率sample size code letter 样本大小字母tightened inspection 加严检验nonconformities per 100 items 每百单位产品不合格数lot size 批量100% inspection 全数检验,100% 检验rejection number 拒绝数reduced inspection 放宽检验skip-lot sampling 跳批抽样sampling procedures 抽样程序defective 不合格品average sample number curve 平均样本量曲线double-sampling plan 二次抽样方案curtailed inspection 截尾检验multiple-sampling plan 多次抽样方案disposition decision (批)处置决定subsequent sample 后续样本specified values 规定值sequential-sampling plan 序贯抽样方案sampling procedures for inspection by attributes 计数抽样检验程序continuing series of lot 连续多批LQ 极限质量poor lot 劣质批lots in isolation 孤立批percent nonconforming(in a sample) (样本)不合格品百分数responsible authority 负责部门limiting quality 极限质量isolated lot inspection 孤立批检验skip-lot sampling procedures 跳批抽样程序sentence 判别audit tool 审核工具accept with no inspection 免检average outgoing quality 平均检出质量AOQ rectifying inspection 挑选型抽样方案lot sentencing 批的判断random sampling 随机抽样ideal OC curve 理想 OC 曲线the producer's risk point 生产方风险点the consumer's risk point 使用方风险点P96--P98 Trial control limits 试验用控制限Current control 实时控制X bar and R chart 均值-极差控制图Statistical background 统计背景In control 受控Out of control 不受控Process variability 过程变量。
数据的正态分布

数据的正态性检验汇总2012-11-21 00:01:04| 分类:统计学习|字号订阅如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的"偏度和峰度都接近0……可以认为……近似服从正态分布"并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。
由此可见,部分SPSS教材里面关于"Shapiro – Wilk 适用于样本量3-50之间的数据"的说法实在是理解片面,误人子弟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态概率图(normal probability plot)
欧阳光明(2021.03.07)
方法演变:概率图,分位数-分位数图( Q- Q)
➢概述
正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
➢适用场合
·当你采用的工具或方法需要使用服从正态分布的数据时;
·当有50个或更多的数据点,为了获得更好的结果时。
例如:
·确定一个样本图是否适用于该数据;
·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;
·在计算过程能力指数Cp或者Cpk之前;
·在选择一种只对正态分布有效的假设检验之前。
➢实施步骤
通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:
分位数=(i-0.5)/n
3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表 A.1里面。
然后在表的左边和顶部找到对应的z 值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n 个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
➢示例
为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个
值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:
分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:
分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075
可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20
以此类推直到最后1个分位数=19. 5÷20。
现在可以在正态分布概率表中查找z值。
z的前两个阿拉伯数字在表的最左边一列,
最后1个阿拉伯数字在表的最顶端一行。
如
第1个分位数=0. 025,它位于-1.9在行与
0.06所在列的交叉处,故z=-1.96。
用相
同的方式找到每个分位数。
如果分位数在表的两个值之间,将需要用插值法进行求解。
例如:第4个分位数为0. 175,它位于0.1736与0.1762之间。
0.1736对应的z值为-0.94,0.1762对应的z值为-0.93,故
这两数的中间值为z=-0.935。
现在,可以用过程数据和相应的z值作图。
图表5. 127显示了结果和穿过这些点的直线。
注意:在图形的两端,点位于直线的上侧。
这属于典型的右偏态数据。
图表 5.128显示了数据的直方图,可进行比较。
➢概率图( probability plot)
该方法可以用于检验任何数据的已知分布。
这时我们不是在正态分布概率表中查找分位数,而是在感兴趣的已知分布表中查找它们。
➢分位数-分位数图(quantile-quantile plot)
同理,任意两个数据集都可以通过比较来判断是否服从同一分布。
计算每个分布的分位数。
一个数据集对应于x轴,另一个对应于y轴。
作一条45°的参照线。
如果这两个数据集来自同一分布,
那么这些点就会靠近这条参照线。
➢注意事项
·绘制正态概率图有很多方法。
除了这里给定的程序以外,正态分布还可以用概率和百分数来表示。
实际的数据可以先进行标准化或者直接标在x轴上。
·如果此时这些数据形成一条直线,那么该正态分布的均值就是直线在y轴截距,标准差就是直线斜率。
·对于正态概率图,图表5.129显示了一些常见的变形图形。
短尾分布:如果尾部比正常的短,则点所形成的图形左边朝直线上方弯曲,右边朝直线下方弯曲——如果倾斜向右看,图形呈S 型。
表明数据比标准正态分布时候更加集中靠近均值。
长尾分布:如果尾部比正常的长,则点所形成的图形左边朝直线下方弯曲,右边朝直线上方弯曲——如果倾斜向右看,图形呈倒S 型。
表明数据比标准正态分布时候有更多偏离的数据。
一个双峰分布也可能是这个形状。
右偏态分布:右偏态分布左边尾部短,右边尾部长。
因此,点所形成的图形与直线相比向上弯曲,或者说呈U型。
把正态分布左边截去,也会是这种形状。
左偏态分布:左偏态分布左边尾部长,右边尾部短。
因此,点所形成的图形与直线相比向下弯曲。
把正态分布右边截去,也会是这种形状。
·如果翻转正态概率图的数轴,那么弯曲的形状也跟着翻转。
比如,左偏态分布将是一个U型的曲线。
·记住过程应该在受控状态下对图形作出有效判断。
·尽管作直方图能马上知道数据的分布,但它却不是判断这些数据是否来自同一特定分布的好办法。
人眼不能很好地判别曲线,其他的分布也可能形成相似的形状。
并且,用服从正态分布的少量数据集作成的直方图可能看起来不是正态的。
因此,正态概率图是判断数据分布的较好方法。
·判断数据分布的另一种方法是使用拟合良好性检定,比如Shapiro-Wilk检验,Kolmogorov-Smirnov检验,或者Lilliefors检验。
关于这些检验的具体描述,不在本书的讨论范围,这些检验在大多数的统计软件上都能实现。
向统计学家咨询如何选择正确的检验并解释其结果。
请参阅“假设检验”以理解这些检验和所得到的结论的一般原则。
·最好的方法是使用统计软件得到正态概率图并作拟合性检验。
结合使用可以对数据和统计标准有直观的理解,以此判定是否为正态。
END。
