广义表
第5章 广义表
12
例:求下列广义表操作的结果(严题集5.10②) (k, p, h) ; 1. GetTail【(b, k, p, h)】=
2. GetHead【( (a,b), (c,d) )】= 3. GetTail【( (a,b), (c,d) )】=
(c,d)
((c,d)) ;
;
4. GetTail【 GetHead【((a,b),(c,d))】】=(b) ; 5. GetTail【(e)】= 6. GetHead 【 ( ( ) )】= 7. GetTail【 ( ( ) ) 】= () ; . .
讨论:广义表与线性表的区别和联系? 广义表中元素既可以是原子类型,也可以是列表; 当每个元素都为原子且类型相同时,就是线性表。
3
广义表是递归定义的线性结构,
LS = ( 1, 2, , n ) 其中:i 或为原子 或为广义表
例如: A = ( ) F = (d, (e)) D = ((a,(b,c)), F) C = (A, D, F) B = (a, B) = (a, (a, (a, , ) ) )
13
(a,b)
()
()
5.5 广义表的存储结构
由于广义表的元素可以是不同结构(原子或列表),难以用 顺序存储结构表示 ,通常用链式结构,每个元素用一个结 点表示。 注意:列表的“元素”还可以是列表,所以结点可能有两种形 式 1.原子结点:表示原子,可设2个域或3个域,依习惯而选。 法1:标志域,数值域 tag=0 标志域 value 数值域 法2:标志域、值域、表尾指针 tag=0 atom
} ADT Glist
10
基 结构的创建和销毁 InitGList(&L); DestroyGList(&L); 本 CreateGList(&L, S); CopyGList(&T, L); 操 作 状态函数
广义表的定义(精)

f(g)=
1 MAX{f(subg)}+1
int GLDepth(GLNode *g) /*求带头结点的广义表g的深度*/ { int max=0,dep; if (g->tag==0) return 0; /*为原子时返回0*/ g=g->val.sublist; /*g指向第一个元素*/ if (g==NULL) return 1; /*为空表时返回1*/ while (g!=NULL) /*遍历表中的每一个元素*/ { if (g->tag==1) /*元素为子表的情况*/ { dep=GLDepth(g); /*递归调用求出子表的深度 */ /*max为同一层所求过的子表中深度的最大值*/ if (dep>max) max=dep; } g=g->link; /*使g指向下一个元素*/ } return(max+1); /*返回表的深度*/ }
C a b c d
C a b c d
广义表的存储结构
广义表的情况 :
g2 1
∧
g1
1
∧
∧
*
*
*
*
…
*
*
∧
第 1 个元素 (a)空表
第 2 个元素 (b)非空表
第 n 个元素
为原子的情况 :
g3 0 a
∧
typedef struct lnode { int tag; union { ElemType data; /*结点类型标识*/
A()
A B e a b c d C A e
B(e)
D B a b c d C
C(a,(b,c,d))
数据结构广义表

结点结构是无论什么结点都有三个域:
第一个域是结点类型标志tag; 第二个域是指向一个列表的指针(当tag=1时) 或一个原子(当tag=0时); 第三个域是指向下一个结点的指针tp。
3 广义表的存储结构
形式描述为:
typedef enum{ ATOM, LIST }ElemTag typedef struct GLNode { //定义广义表结点 ElemTage tag; //公共部分,用以区分 原子结点和表结点 Unin{ //原子结点和表结点的联合部分 AtomType atom;//原子类型结点域, // AtomType由用户定义 struct GLNode *hp,; //表结点的表头指针域 }; struct GLNode *tp; //指向下一个结点的指针 }*Glist; //广义表类型
5. E=(a,E)
这是一个递归列表,其元素中有自己。
广义表也可以用图形表示,例如前述的广义表D和E可表示为:
广义表D
D
广义表E
E
C
A
B
a
e
a b c d
2 广义表的基本运算
广义表的基本运算 ⑴ 取表头 HEAD(LS); ⑵ 取表尾 TAIL(LS)。
3 广义表的存储结构
广义表中的数据元素可以是单元素,或是广义表, •很难用顺序存储结构表示,常采用链式存储结构。 1.表头表尾链存储结构 有两类结点:表结点和单元素结点。
P 1 3 1 1
A=y((c,3),(D,2)) C=x((1,10),(2,6))
^
1 2
A
z y 1 1 1 3
C
x 0 0 15 ^
B
1 2
1 2
^
广义表名词解释

广义表名词解释
广义表(英语:Generalized List)是一种非线性的数据结构。
但如果广义表的每个元素都是原子,它就变成了线性表。
广义表广泛地用于人工智能等领域的LISP语言。
广义表一般记作LS = (a1, a2, ···, an), n是它的长度,ai可以是单个元素(原子),也可以是广义表(子表),当广义表非空时,称第一个元素a1为LS的表头,称其余元素组成的表为LS 的表尾。
注意:表头是元素(可以是原子,也可以是广表),表尾一定是广义表。
E=(a, E)是一个递归的表。
D=(( ),(e),(a,(b,c,d)))是多层次的广义表,长度为3,深度为3。
例:((a),a)的表头是(a),表尾是(a),((a))的表头是(a),表尾是( )。
广义表

5.4 广义表的类型定义ADT Glist {数据对象:D={e i | i=1,2,..,n; n≥0;e i∈AtomSet 或e i∈GList,AtomSet为某个数据对象} 数据关系:LR={<e i-1, e i >| e i-1 ,e i∈D, 2≤i≤n }广义表是递归定义的线性结构,LS = ( α1, α2, ⋅⋅⋅, αn )其中:αi 或为原子或为广义表换句话说,广义表是一个多层次的线性结构。
例如:D = (E, F)E = (a, (b, c))F = (d, (e))A = ( )B = (a, B) = (a, (a, (a, ⋅⋅⋅ , ) ) )C = (A, D, F)广义表的结构特点:1) 广义表中的数据元素有相对次序;2) 广义表的长度定义为最外层包含的元素个数;3) 广义表的深度定义为所含括弧的重数;注意: “原子”的深度为“0”;“空表”的深度为14) 广义表可以共享;5) 广义表可以是一个递归的表;递归表的深度是无穷值,长度是有限值。
6) 任何一个非空广义表LS = ( α1, α2, …, αn)均可分解为表头Head(LS) = α1 和表尾Tail(LS) = ( α2, …, αn)两部分例如:LS = ( A, D )Head(LS) = A Tail(LS) = ( D )Head( D ) = E Tail( D ) = ( F )Head( E ) = a Tail( E ) = ( ( b, c) )Head( (( b, c)) ) = ( b, c) Tail( (( b, c)) ) = ( ) Head( ( b, c) ) = b Tail( ( b, c) ) = ( c )Head( ( c ) ) = c Tail( ( c ) ) = ( )基本操作:∙结构的创建和销毁InitGList(&L); DestroyGList(&L);CreateGList(&L, S); CopyGList(&T, L);∙状态函数GListLength(L); GListDepth(L);GListEmpty(L); GetHead(L); GetTail(L); ∙插入和删除操作InsertFirst_GL(&L, e);DeleteFirst_GL(&L, &e);∙遍历Traverse_GL(L, Visit());} ADT GList5.5 广义表的表示方法头、尾指针的链表结构表结点: tag=1 hp tp原子结点:tag=0 data构造存储结构的分析方法:1)空表ls= NIL2)空表ls = NIL•••α1α2αn 若子表为原子5.6 递归函数的设计方法递归函数一个含直接或间接调用本函数语句的函数被称之为递归函数,它必须满足以下两个条件:1) 在每一次调用自己时,必须是(在某种意义上)更接近于解;2) 必须有一个终止处理或计算的准则。
广义表中原子的深度

广义表中原子的深度什么是广义表广义表(Generalized List),简称GList,是一种拓展了线性表的数据结构。
与线性表只能存储单一类型元素不同,广义表可以存储原子和子表两种类型的元素。
在广义表中,原子是不可再分的最小单位,可以是数字、字符、布尔值等。
而子表则是由多个元素组成的序列,可以是空表或者由原子和/或其他子表组成。
举个例子,下面是一个简单的广义表示例:L = [1, 2, [3, 4], [5, [6, 7]]]在这个示例中,数字1和2是广义表L的原子;[3, 4]和[5, [6, 7]]则是L的两个子表。
广义表中原子的深度在广义表中,一个原子所处的层次称为它的深度。
深度为0表示该原子直接位于广义表最外层;深度为1表示该原子位于第一层子表内;以此类推。
对于上述示例L来说: - 数字1和2的深度为0; - 子列表[3, 4]的深度为1;- 子列表[5, [6, 7]]中数字5的深度为1,子列表[6, 7]的深度为2。
计算广义表中原子的深度计算广义表中原子的深度可以使用递归的方法。
首先,我们需要定义一个函数来计算广义表中原子的深度。
假设我们将这个函数命名为calculate_depth,它接受一个广义表作为参数,并返回该广义表中所有原子的深度。
def calculate_depth(glist):depth = 0if isinstance(glist, list):for item in glist:if isinstance(item, list):depth = max(depth, calculate_depth(item) + 1)else:depth = max(depth, 0)return depth在上述代码中,我们首先初始化深度为0。
然后,判断传入的参数是否是列表类型。
如果是列表类型,则遍历列表中的每个元素。
对于每个元素,如果它仍然是一个列表,则递归调用calculate_depth函数来计算该元素内部原子的深度,并将结果加1。
数据结构广义表

{ printf("("); /*输出'('*/
if (g->val.sublist==NULL) printf(""); /*输出空子表*/
else DispGL(g->val.sublist); /*递归输出子表*/
}
else printf("%c", g->val.data); /*为原子时输出元素值*/
假如把每个表旳名字(若有旳话)写在其表旳前面,则 上面旳5个广义表可相应地体现如下:
A()
B(e)
C(a,(b,c,d))
D(A(),B(e),C(a,(b,c,d)))
E((a,(a,b),((a,b),c)))
若用圆圈和方框分别体现表和单元素,并用线段把表 和它旳元素(元素结点应在其表结点旳下方)连接起来,则 可得到一种广义表旳图形体现。例如,上面五个广义表 旳图形体现如下图所示。
A() B(e) C(a,(b,c,d)) D(A(),B(e),C(a,(b,c,d))) E((a,(a,b),((a,b),c)))
AB e
C A
a b cd
D BC
ea b cd
E
a
ab
c
ab
8.2 广义表旳存储构造
广义表是一种递归旳数据构造,所以极 难为每个广义表分配固定大小旳存储空间,所
GLNode *CreatGL(char *&s)
{ GLNode *h;char ch=*s++; /*取一种扫描字符*/
if (ch!='\0')
/*串未结束判断*/
{ h=(GLNode *)malloc(sizeof(GLNode));/*创建新结点*/
数据结构第06章广义表

第6章广义表z6.1 广义表的基本概念z6.2 广义表的存储结构z6.3 广义表的操作算法16.1 广义表的基本概念广义表(列表)的概念-n( ≥0 )个表元素组成的有限序列,记作LS= ( a1, a1, a2, …, a n)LS是表名,a i是表元素,它可以是单个元素(称为原子) ,可以是表(称为子表) 。
n为表的长度。
n= 0 的广义表为空表。
n> 0时,表的第一个表元素称为广义表的表头(head),除此之外,其它表元素组成的表称为广义表的表尾(tail)。
2广义表举例:(1)A=()(2)B=(e)(3)C=(a, (b, c, d) )(4)D=(A,B,C)(5)E= (a , E)9任意一个非空广义表,均可分解为表头和表尾。
9对于一个非空广义表,其表头可能是原子,也可能是子表;而表尾一定是子表。
3广义表的基本操作:•结构的创建和销毁InitGList(&L); DestroyGList(&L); CreateGList(&L, S); CopyGList(&T, L);•状态函数GListLength(L); GListDepth(L);GListEmpty(L); GetHead(L); GetTail(L);•插入和删除操作InsertFirst_GL(&L, e);DeleteFirst_GL(&L, &e);•遍历Traverse_GL(L, Visit());66. 2 广义表的存储结构z由于广义表中的元素不是同一类型,因此难以用顺序结构表示,通常采用链接存储方法存储广义表,并称之为广义链表。
z由于广义表中有两种数据元素,原子或子表,因此,需要两种结构的结点:一种是表结点,一种是原子结点。
z下面介绍一种广义表的链式存储结构。
78扩展的线性链表表示法:-子表结点由三个域组成:标志域、表头指针域和指向下一个元素的指针域;-原子结点的三个域为:标志域、值域和指向下一个元素的指针域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的结构特点: 广义表 LS = ( α1, α2, …, αn )的结构特点
1) 广义表中的数据元素有相对次序 次序; 次序 2) 广义表的长度 长度定义为最外层包含元素个数; 长度 3) 广义表的深度 深度定义为所含括弧的重数; 深度 注意:“原子”的深度为 0 ; “空表”的深度为 1 。 4) 广义表可以共享 共享; 共享 5) 广义表可以是一个递归 递归的表; 递归 递归表的深度是无穷值,长度是有限值。
4. GetTail【 GetHead【((a,b),(c,d))】】=(b) ; 】】= ) 【 【 】】 5. GetTail【(e)】= 【 ) 6. GetHead 【 ( ( ) )】= 】 7. GetTail【 ( ( ) ) 】= 【 () () () . .
13
;
(a,b)
5.5 广义表的存储结构
0 d
0
b
0
c
⑤ E=(a, E)
1 1
(参见教材P109图) 参见教材P109图 ^
0
a
16
构造存储结构的两种分析方法: 构造存储结构的两种分析方法:
1) 表头、表尾分析法 表头、表尾分析法: 空表 ls = NIL tag=1 指向表尾的指针
非空表 ls
指向表头的指针 若表头为原子, 若表头为原子,则为 tag=0 data 否则,依次类推。 否则,依次类推。
24
5.6 m元多项式的广义表表示 m元多项式的广义表表示
P(x P(x,y,z) = x10y3z2+2x8y3z2+3x8y2z2+x4y4z+6x2y4z+2yz = ((x10+2x8)y3+3x8y2)z2+((x4+6x2)y4+2y)z ((x +((x +2y P(z Az +Bz P(z) = Az2+Bz A(x A(x,y) = (x10+2x8)y3+3x8y2 B(x,y) = (x4+6x2)y4+2y (x +2x +3x B(x (x +2y B(y Ey +Fy B(y) = Ey4+Fy A(y Cy +Dy A(y) = Cy3+Dy2 C(x C(x) = x10+2x8 +2x D(x 3x D(x) = 3x8 E(x E(x) = x4+6x2 +6x F(x 2x F(x) = 2x0
3
广义表是递归 递归定义的线性结构 线性结构, 递归 线性结构
LS = ( α1, α2, ⋅⋅⋅, αn ) 其中:αi 或为原子 或为广义表
例如: 例如 A = ( ) F = (d, (e)) D = ((a,(b,c)), F) C = (A, D, F) B = (a, B) = (a, (a, (a, ⋅⋅⋅ , ) ) )
指向下一结点
1
指向子表
例: ① A =( )
② B=( e )
1
A=NULL
^
^
③ C =( a ,( b , c , d ) ) ^
1 1
^
1 1
0
e
0
a
1
^
0 d
0
b
0
c
15
④ D=( A , B ,C )=(( ),(e),(a,(b,c,d))) =
1
^
1
1
1
^
1
^
0 e
1
^
1 1
0
a
1
^
ADT Glist { 数据对象:D={ei | i=1,2,..,n; n≥0; 数据对象 ei∈AtomSet 或 ei∈GList, AtomSet为某个数据对象 } 数据关系: 数据关系: LR={<ei-1, ei >| ei-1 ,ei∈D, 2≤i≤n} 基本操作: 基本操作
} ADT Glist
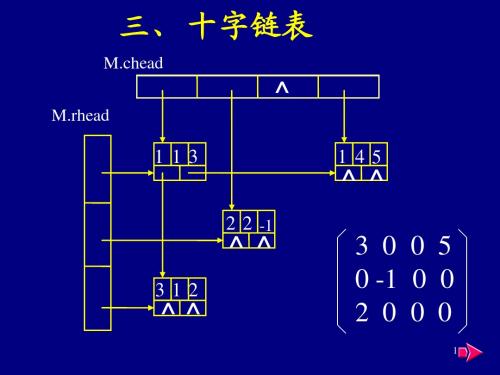
三、 十字链表
M.chead M.rhead
^
1 13 1 45
^^
2 2 -1
^^
312
^^
3 0 0 5 0 -1 0 0 2 0 0 0
1
广义表(LisΒιβλιοθήκη s) 广义表(Lists)广义表的特点:一种特殊的线性表 广义表的特点:
① 元素的值并非原子类型,可以再分解,表中元素也是一 元素的值并非原子类型,可以再分解, 个线性表(即广义的线性表)。 个线性表(即广义的线性表)。 所有数据元素仍属同一数据类型 同一数据类型。 ② 所有数据元素仍属同一数据类型。
D=(A,B,C)=(( ),(e),(a,(b,c,d))),共享表 , E=(a,E)=(a,(a,E))= (a,(a,(a,…….))),E为递归表 , 为递归表
7
例2:试用图形表示下列广义表. 试用图形表示下列广义表.
代表原子, (设 e 代表原子, 代表子表) 代表子表) ② A=( a , (b, A) ) A A B a e b c d ②的长度为2,深度为∞ 的长度为 ,深度为∞ b C a ① D=(A,B,C)=( ( ),(e),( a, (b,c,d) ) ) D
• •
和
InsertFirst_GL(&L, e); DeleteFirst_GL(&L, &e); Traverse_GL(L, Visit());
11
教材P107 广义表的抽象数据类型定义见教材P107广义表的抽象数据类型定义见教材P107-108
介绍两种特殊的基本操作: 介绍两种特殊的基本操作: GetHead( L) ——取表头 可能是原子或列表 取表头(可能是原子或列表 取表头 可能是原子或列表); GetTail(L ) ——取表尾 一定是列表 。 取表尾(一定是列表 取表尾 一定是列表)
19
( ) (x) ( )
L = ( a ( x, y ), ( ( x ) ) ) L = ( a, ) ) L
1 0 a 1 1 1 1 1 0 x
20
∧ ∧ ∧
2) 子表分析法 子表分析法: 空表 非空表 ls 1 1 ls=NIL
…
1
∧
指向子表1 指向子表2 的指针 的指针
指向子表n 的指针
6
例1:求下列广义表的长度。 :求下列广义表的长度。 1)A =( ) ) 2)B = ( e ) ) n=0,因为A是空表 ,因为 是空表 n=1,表中元素 是原子 ,表中元素e是原子
3)C =( a ,( b , c , d ) ) n=2,a 为原子,(b,c,d)为子表 ) , 为原子, 为子表 4)D=( A , B ,C ) ) 5)E=(a, E) ) n=3,3个元素都是子表 , 个元素都是子表 n=2,a 为原子,E为子表 , 为原子, 为子表
12
例:求下列广义表操作的结果(严题集 求下列广义表操作的结果(严题集5.10②) ② (k, p, h) ; 1. GetTail【(b, k, p, h)】= 【 】 2. GetHead【( (a,b), (c,d) )】= 【 】 3. GetTail【( (a,b), (c,d) )】= 【 】 (c,d) ((c,d)) ; ;
23
广义表的头尾链表存储表示: 广义表的头尾链表存储表示:
typedef enum {ATOM, LIST} ElemTag;
//ATOM==0:原子, LIST==1:子表
typedef struct GLNode { ElemTag tag; //标志域 union{ AtomType atom; //原子结点的数据域 struct {struct GLNode *hp, *tp;} ptr; }; 表结点 tag=1 hp tp } *GList ptr
17
广义表的表示方法
通常采用头、尾指针的链表结构 表结点: 表结点 tag=1 hp tp
原子结点: 原子结点: tag=0 data
18
例如: 例如
L=(a, (x, y), ((x)) ) a x y ((x, y), ((x)) ) (x, y) (y) x ( ((x)) ) ((x)) ( ) ( )
Tail( D ) = ( F ) Tail( E ) = ( ( b, c) )
Head( (( b, c)) ) = ( b, c) Tail( (( b, c)) ) = ( ) Head( ( b, c) ) = b Tail( ( b, c) ) = ( c ) Head( ( c ) ) = c Tail( ( c ) ) = ( )
由于广义表的元素可以是不同结构(原子或列表),难以用 由于广义表的元素可以是不同结构(原子或列表),难以用 ), 通常用链式结构,每个元素 元素用一个结 顺序存储结构表示 ,通常用链式结构,每个元素用一个结 点表示。 点表示。 注意:列表的“元素”还可以是列表,所以结点可能有两种形 注意:列表的“元素”还可以是列表, 式 1.原子结点 表示原子,可设2个域或3个域,依习惯而选。 1.原子结点:表示原子,可设2个域或3个域,依习惯而选。 原子结点: 法1:标志域,数值域 标志域, tag=0 标志域 value 数值域
25
若链结点的构造设计为
相当于data域 相当于data域
coef exp link 其中, 其中,coef 表示多项式的某一项的系数, 表示多项式的某一项的系数, exp 表示多项式的某一项的指数, 表示多项式的某一项的指数, link 为链接多项式中同一层各链结点的指针. 为链接多项式中同一层各链结点的指针.
广义表的定义 广义表的存储结构 广义表的应用 广义表的递归算法
2
