假设检验临界值
假设检验的公式运用总结
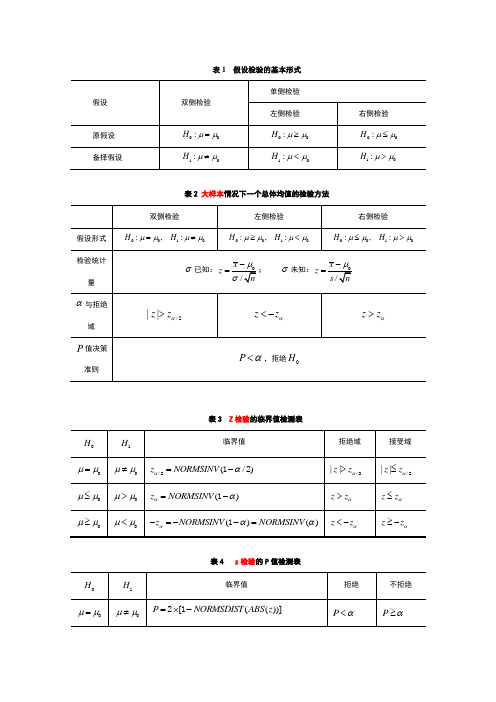
表1 假设检验的基本形式
表2 大样本情况下一个总体均值的检验方法
表3 Z检验的临界值检测表
表4 z检验的P值检测表
表5 小样本情况下一个总体均值的检验方法
表6 t检验的临界值检测表
表7 t检验的P值检测表
总体比率的检验与总体均值的检验基本上是相同的,区别只在于参数和检验统计量的形式不同。
所以总体均值检验的整个程序可以作为总体比率检验的参考,甚至有很多内容可以完全“照搬”。
表8 大样本情况下一个总体比率的检验方法
与总体均值和总体比率检验所通常使用的抽样分布(正态分布或t 分布)不同,一个总体方差的检验用的是卡方2()χ分布。
此外,总体方差的检验,不论样本容量n 的大小,都要求总体服从正态分布,这是由检验统计量的抽样分布决定的。
表9 一个总体方差检验的方法。
假设检验的基本概念2

二、假设检验旳基本原理
在大量观察中频频出现旳事件具有较大旳概率, 出现次数较小旳事件,具有小旳概率。
在日常生活中,人们习惯于把概率很小旳事件, 看成在一次观察中是不可能出现旳事件,这个原理 称作小概率原理。
举例说,我们几乎每天从电视、报纸、甚至街头 广告牌上都能看到交通事故旳统计,但人们绝不所 以而放弃交通工具旳使用 ,可见,在日常生活中, 人们是在不自觉利用小概率原理。
统计假设检验旳基本原理是小概率原理。
小概率原理能够归纳为两个方面:
能够以为小概率事件在一次观察中是不 可能出现旳。
假如在一次观察中出现了小概率事件, 那么,合理旳想法是否定原有事件具有小 概率旳说法(或称假设)。
即直接检验H0,间接检验H1。
•小概率 原理:
假如对总体旳某种假设是真实旳,那么不利于 或不能支持这一假设旳事件A(小概率事件)在 一次试验中几乎不可能发生旳;要是在一次试 验中A居然发生了,就有理由怀疑该假设旳真实 性,拒绝这一假设。
总体
抽样
(某种假设)
检验
(接受)
小概率事件 未发生
样本 (观察成果)
(拒绝) 小概率事件 发生
三、假设检验旳基本形式
虚无假设HO如前面所举女青年初婚年龄=20。原假设
在不会研被究假否中设定是,稳一不定般然、涉也受就到及失保两去护其旳部研,分究但意另:义一虚。方当面无经也假过并抽不设样表H调达O查永和,远研 究当假实际设数H据1。否定了原有假设H0时,就产生了需要接受其逻辑
拟定α,就拟定了 临界点c。拟定了 临界点c,就拟定 了否定域旳大小。
minitab教程-假设检验

案例分析
• 案例背景:研究某药物对血压的影响,选取了10名患者, 分别在服药前和服药后测量其血压。
案例分析
服药前血压
120/80, 115/75, 118/82, ..., 125/85
服药后血压
110/70, 112/72, 116/76, ..., 120/80
案例分析
案例1
比较两个不同品牌手机的待机时间均值。
案例2
比较两种不同类型轮胎的抗滑性能均值。
05
配对样本t检验
适用场景与条件
适用场景
当需要对两组配对观测值进行比较时,例如同一组实验者在两种不同情境下的表现。
条件要求
数据应满足独立、正态分布、方差齐性等假设。
检验步骤与解读
1. 计算差值
计算每对观测值的差值。
当需要检验一个总体均数与已知值或 理论值之间的差异是否显著时,可以 使用单样本Z检验。
条件
数据需要来自正态分布的总体,且总 体方差已知。
检验步骤与解读
01
2. 计算Z统计量
Z = (样本均数 - 已知值或理论值) / 样本标准差。
02
3. 根据Z值查找对应的P值
P值表示拒绝原假设的概率,通常选择显著性水平(如0.05或0.01)作
03
单样本t检验
适用场景与条件
适用场景
当需要检验一个样本均值与已知的某 个值是否显著不同时,可以使用单样 本t检验。
条件要求
样本数据需要符合正态分布,且总体 方差未知但具有同质性。
检验步骤与解读
01
02
03
04
步骤1
提出原假设和备择假设。原假 设通常是样本均值与已知值相 等,备择假设则是样本均值与 已知值不等。
假设检验完整版

几个重要的分布介绍 标准正态分布 定义: 设 X1,X2,......Xn相互独立, 都服从标准正态分布N(0,1), 则称 随机变量χ2=X12+X22+......+Xn2所服从的分布为自由度为 n 的χ2 分布.
几个重要的分布介绍
几个重要的分布介绍
双侧检验与单侧检验的假设形式
假设 原假设
计算检验统计量值:
t 986 1000 1.75 24 9
∵t值落入接受域,∴在 a =0.05的显著性水平上 接受H0
例四(和spss结合)
正常人的脉搏平均 数为72次/分。现测得15名患者的脉搏:71,55,76,68,
72,69,56,70,79,67,58,77,63,66,78 试问这15名患者的脉搏与正
描述统计
推断统计
参数估计 假设检验
假设检验一般问题
1、假设问题的提出和基本思想 2、几个重要的分布介绍 3、双侧检验和单侧检验 4、假设检验的步骤 5,总体均值的检验 6,举例
假设问题的提出
根据1989年的统计资料,某地女性新生儿的平均体重为 3190克,现从1990年的女性新生儿中随机抽取30人,测得 其平均体重为3210克,问1990年的女性新生儿和1989年的 新生儿相比,体重有无显著性差异?
显著性为0.088>0.05,接受原假设,无明显差异。
态分布,其总体均值为X0=0.081mm,总体标准差为 =0.025 。今换一 种新机床进行加工,抽取n=200个零件进行检验,得到的椭圆度均值为
0.076mm。试问新机床加工零件的椭圆度均值与以前有无显著差异?(a=
0.05)
解:已知:X0=0.081mm, =0.025,n=200,
常见的统计学中的假设检验方法

常见的统计学中的假设检验方法介绍假设检验是统计学中常用的一种方法,用于对给定的样本数据进行推断和决策。
它通过对样本数据与之前建立的假设进行比较,来确定是否拒绝或接受假设。
以下是一些常见的统计学中的假设检验方法的简要介绍。
单样本t检验单样本t检验适用于对一个样本的均值是否与已知的总体均值有显著差异进行检验。
假设检验的步骤包括设置原假设和备择假设、计算样本均值和标准差、计算t值并与临界值进行比较以得出结论。
独立样本t检验独立样本t检验用于比较两个独立样本的均值是否有差异。
这个方法适用于当我们有两个独立的样本,想要确定它们的均值是否来自于同一个总体。
假设检验的步骤与单样本t检验类似。
配对样本t检验配对样本t检验适用于比较同一组被试在两个不同条件下的均值是否有差异。
这个方法适用于当我们有同一组被试在两个不同条件下的成对观测数据时,想要确定这两个条件是否对其均值产生了显著影响。
假设检验的步骤与单样本t检验类似。
卡方检验卡方检验用于比较观察到的频数与期望频数之间的差异是否显著。
这个方法适用于分类数据的分析,可以确定观察到的频数是否符合预期的分布。
假设检验的步骤包括计算卡方统计量、确定自由度,并与临界值进行比较以得出结论。
方差分析方差分析用于比较两个或更多个样本均值之间的差异是否显著。
这个方法适用于当我们有多个样本需要进行比较时,可以确定它们的均值是否存在显著差异。
假设检验的步骤包括设置原假设和备择假设、计算组内和组间均方、计算F统计量并与临界值进行比较以得出结论。
总结以上是常见的统计学中的几种假设检验方法。
每种方法都有其适用的场景和步骤,正确理解和运用这些方法可以帮助我们进行数据分析和推断。
在实际应用中,我们应根据具体问题和数据的特点选择合适的假设检验方法,并进行可靠的统计推断。
假设检验的五个具体步骤

假设检验的五个具体步骤
1. 提出假设,假设检验的第一步是明确研究者要检验的假设。
通常有两种假设,即零假设(H0)和备择假设(H1)。
零假设通常
是研究者想要进行推翻的假设,而备择假设则是对零假设的补充或
对立假设。
2. 确定显著性水平,显著性水平(α)是在假设检验中用来判
断是否拒绝零假设的临界值。
通常取0.05或0.01。
选择显著性水
平时需要考虑研究的具体情况以及对错误类型的容忍程度。
3. 计算统计量,根据样本数据计算出一个统计量,该统计量用
于衡量样本数据与零假设的一致性。
常见的统计量包括t值、z值、F值等,具体的选择取决于研究问题和数据类型。
4. 做出决策,根据计算得到的统计量和显著性水平,判断是否
拒绝零假设。
如果计算得到的统计量落在拒绝域(即落在显著性水
平内),则拒绝零假设;否则接受零假设。
5. 得出结论,最后一步是根据对零假设的拒绝或接受做出结论,并对研究结果进行解释。
如果拒绝了零假设,则可以根据备择假设
对研究问题进行解释;如果接受了零假设,则需要说明样本数据不足以支持对总体参数的改变。
这五个步骤构成了假设检验的基本流程,通过严格按照这些步骤进行推断,可以确保统计推断的准确性和科学性。
假设检验基本方法

假设检验基本方法假设检验就像是数据世界里的超级侦探,总是对那些看似平常的数据提出各种怀疑。
你看,数据就像是一群性格各异的小怪物,在一个巨大的数字王国里生活着。
假设检验这个侦探呢,他可不是随便怀疑的,就像一个经验老到的侦探不会随便指认嫌疑人一样。
他会先提出一个假设,这个假设就像是一个“嫌疑犯画像”,比如说这个小怪物群落里的某个数据可能存在某种特殊的情况。
有时候,这个假设是很离谱的,就像说所有的兔子都能像鸟一样飞一样。
但是呢,我们的侦探可不会放过任何一种可能性。
他开始收集证据,这些证据就是我们的样本数据。
样本数据就像是小侦探的小跟班,带着各种关于数字王国的信息。
然后呢,这个侦探就开始施展他的魔法啦。
他会计算各种神奇的数值,这些数值就像是魔法咒语一样。
他把样本数据这个小跟班提供的信息按照特殊的规则进行组合,就好像是把一堆乱七八糟的拼图碎片按照特定的图案拼凑起来。
要是这个计算出来的结果看起来特别奇怪,就像是你在正常的水果篮子里发现了一块石头一样,那这个假设可能就有问题啦。
但如果结果看起来还比较合理,就像在一群白鹅里发现一只稍微白一点的鹅,也许这个假设还能勉强站得住脚。
假设检验还特别讲究一个“临界值”,这临界值就像是一道神秘的大门。
如果计算出来的结果轻易地就越过了这道大门,那就像是一个小偷大摇大摆地闯进了禁地,我们就有足够的理由拒绝原来的假设。
但如果结果在大门这边晃悠,就像一个胆小的孩子在门口徘徊,那我们可能就得暂时接受这个假设。
这个过程中还会有各种类型的错误,就像侦探有时候也会抓错人或者放走坏人一样。
第一类错误就像是把一个无辜的路人当成了罪犯,而第二类错误则是放走了真正的坏蛋。
不过呢,假设检验这个侦探可不会因为这些困难就放弃。
他总是在数字王国里反复穿梭,不断地提出假设,验证假设,就像一个不知疲倦的小蚂蚁在寻找食物一样。
在这个数据的世界里,假设检验就是这样一个有趣又充满挑战的过程,就像一场刺激的冒险,每一次的假设和验证都是在探索数字背后的秘密。
假设检验完整版PPT课件

消费者协会接到消费者投诉,指控品牌纸包装 饮料存在容量不足,有欺骗消费者之嫌。包装 上标明的容量为250毫升。消费者协会从市场上 随机抽取50盒该品牌纸包装饮品进行假设检验。 试陈述此假设检验中的原假设和备择假设。
解:消费者协会的意图是倾向于证实饮料厂包装 饮料小于250ml 。建立的原假设和备择假设为
显著性水平和拒绝域
(右侧检验 )
抽样分布
置信水平
1-
拒绝H0
0 观察到的样本统计量
样本统计量 临界值
显著性水平和拒绝域
(右侧检验 )
抽样分布
置信水平
1-
拒绝H0
0
样本统计量
临界值
第一节 假设检验概述
1、假设检验的基本思想 2、假设检验的步骤 3、两类错误和假设检验的规则
三、两类错误和假设检验的规则
(单侧检验 )
抽样分布
置信水平
拒绝H0
1-
拒绝域 临界值
0 接受域
样本统计量
显著性水平和拒绝域
(左侧检验 )
抽样分布
置信水平
拒绝H0
1-
临界值
0
样本统计量
观察到的样本统计量
显著性水平和拒绝域
(左侧检验 )
抽样分布
置信水平
拒绝H0
1-
临界值
0
观察到的样本统计量
样本统计量
•【例2】一种罐装饮料采用自动生产线生产,每罐的容量 是255ml,标准差为5ml,服从正态分布。换了一批工人后, 质检人员在某天生产的饮料中随机抽取了16罐进行检验,
一个总体的检验
一个总体
