二向应力状态分析
合集下载
应力状态概述二向和三向应力状态的实例二向
2．作应力圆 主应力为 1 , 3 ，并可 确定主平面的法线。
材料力学
第七章
应力和应变分析
3．分析 纯剪切应力状态的两个主应力绝对值相等， 但一为拉应力，另一为压应力。由于铸铁抗拉强度较 低，圆截面铸铁构件扭转时构件将沿倾角为 45º 的螺旋面因拉伸而发生断裂破坏。
材料力学
第七章
2 2
x y
xy
n
材料力学
y a xy
y On D( x , ) a a
a
第七章
n
应力和应变分析
二、应力圆的画法
建立应力坐标系，如下图所 示，（注意选好比例尺） 在坐标系内画出点A( x， xy)和B(y，yx)
x
C O
2a
AB与a 轴的交点C便是圆 A( x , xy) 心。
150°
第七章
应力和应变分析
x y 2 2 1 x y （ ） xy 2 2 2
解法2—解析法：分析——建立坐标系如图
95
60°
y 45MP a yx 25 3MP a xy
25 3
x ?
y O x
60 95MPa 60 25 3MPa
材料力学
第七章
应力和应变分析
应力表示——单元体：
①dx、dy、dz（微小的正六面体） ②单元体某斜截面上的应力就代表了构件内 对应点同方位截面上的应力。
B P
dz
dx
dy
A
C
பைடு நூலகம்
B
D
C
B、C——单向受力，τ ＝0 A——纯剪切， σ ＝0
D
D——既有 σ ，又有τ
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(应力和应变分析强度理论)【圣才出品】
平面的外法线方向。
7 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、三向应力状态分析 1．三向应力圆 如图 7-1-4 所示，以三个主应力表示的单元体，由三个相互垂直的平面分别作应力圆， 将三个平面的应力圆绘在同一平面上得到三向应力状态下的应力圆，如图 7-1-5 所示。与 每一主应力所对应的应力圆可由与该主平面相正交的其余面上的应力作出。 注意：作三向应力圆应至少知道一个主应力的大小和方向。
1 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
实例：在滚珠轴承中，滚珠与外圈接触点处的应力状态，可以作为三向应力状态的实例。 二、二向应力状态分析 1．解析法 如图 7-1-1（a）所示，一单元体 abcd 处于平面应力状态，采用截面法取左边部分单 元体 eaf 为研究对象，如图 7-1-1（b）所示。
5 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-1-3（a）
图 7-1-3（b） ③求主应力数值和主平面位置 a．求主应力数值的方法 如图 7-1-3（b）所示，点 A1 和点 B1 分别为代表最大主应力和最小主应力，其大小为
6 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 7 章 应力和应变分析强度理论
7.1 复习笔记
一、应力状态 一点的应力状态：过一点不同方向面上应力的集合。 应力状态的研究对象是单元体，其特征为：①单元体的尺寸无限小，每个面上应力均匀 分布；②任意一对平行平面上的应力相等。 主单元体是指各侧面上切应力均为零的单元体。其中，单元体上切应力为零的面称为主 平面，主平面上的正应力称为主应力。 说明：一点处必定存在一个单元体，使得三个相互垂直的面均为主平面，三个互相垂直 的主应力分别记为 σ1、σ2、σ3，且规定按代数值大小的顺序来排列，即 σ1≥σ2≥σ3。 应力状态分类及实例 （1）单向应力状态：也称为简单应力状态，三个主应力 σ1、σ2、σ3 中只有一个不等 于零。 实例：简单的拉伸或压缩。 （2）平面（二向）应力状态：三个主应力 σ1、σ2、σ3 中有两个不等于零。 实例：薄壁圆筒横截面上的点和圆形容器包含直径的任意横截面上的点。 （3）空间（三向）应力状态：和平面应力状态统称为复杂应力状态，三个主应力 σ1、 σ2、σ3，均不等于零。
材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)
x
y
2
R cos[180o
(2
20 )]
xy
x
2
y
R cos(2
20 )
O
xy
x
y
2
R(cos 2
cos 20
sin 2
sin 20 )
x
y
2
x
2
y
cos 2
xy
sin
2
D
A ( x , xy )
y R 2 20
E
C
x
B ( y , xy )
13
单元体与应力圆的对应关系
y y
y
10
a
64103 110103 3.206107 1012
219.6MPa
200
b
64103 100103 3.206107 1012
199.6MPa
10
c
64103 0 3.206107 1012
0.0MPa
120
10
c z
b a y
30
(Fs 160kN; M 64kN m)
xy
（3）以C 为圆心，AC为半径画圆
—应力圆或莫尔圆
O
xy
y
y
xy x
Ox
A ( x , xy )
y C
B ( y , xy )
x
10
3、单元体公式与应力圆的关系
以上由单元体公式
应力圆（原变换）
下面寻求由应力圆
单元体公式（逆变换）
只有这样，应力圆才能与公式等价 换句话，单元体与应力圆是否有一一对应关系？
x
x
x
0
y 1
材料力学第9章 应力状态分析
B
方位角α, 对应于应力圆上为2 α
a τy σy τx e σα σx a ταf
n
c
τ
a
B 2a
τσx x x o C
角, 自起始半径旋转, 且与α转向 一致；
A 单元体上A、B面夹角α, σ 应力圆上弧长AB的圆心角
b
σyτy d
为2 α角, 且转向一致。
3、主应力、主平面与主单元体
t
图解法
tadA (t xdAcosa ) cosa (s xdAcosa )sina (t ydAsina )sina (s ydAsina) cosa 0
关系式
t x =t
(负号已包含在指向中）；
y
sin
2a
2 sin a
cosa；
cos2 a 1 cos 2a ； sin2 a 1 cos 2a
t
图解法
注意A1、A2点
σx
σ( 2,0)
A2 B2
σ τ E(
2a
Dα1，σ( xα,)τ x )
2a
数值 方位
τy τx
o
σ a C B1 A1 σ
( 1,0) 主点法
s1 = sx s y
s2
2
s
(
x
s
2
y
)2
t
2 x
tan
2a0
2t x sx s
y
(σy ,Dτ2y) σy
K
s1的方位
作D1K⊥σ轴, 交圆与K点, 则A2K方向
2
2
sa、ta
计算公式
sa
ta
sx sx
sy
2
s y
二向应力状态分析—图解法
§7–4 二向应力状态分析—图解法
x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
1、 莫尔圆的概念
(
x
y 2
)2
2
(x
y )2 2
2 x
(
x
y 2
)2
2
(x
y 2
)2
2x
当斜截面随方位角 变化时, 其上的应力 ， 在 - 直角坐标系内的轨迹是一个圆 。
圆心的坐标为(the coordinates of MOHR circle’s center)
y
xm
900
t
450
k
D
y
xm
900
t
450
k
D
y
3
τ max
x
τ max
k
450
1
解: 从圆筒表面 k 点处取出单元体, 其各面上的应力分量如图 所示
可求得
y 1 max 80MPa
x 3 max 80MPa
z 0
k点处的线应变 x , y 为
y
x
1 E
(x
y )
1 E
(max
z
x
二、纯剪的本构关系
xy
xy
G
i 0 ( i x,y,z ) yz zx 0
y
xy
z
x
三、复杂状态下的本构关系
y
依叠加原理,得
y
z
z
x
xy
x
x
x
E
y
E
x
2
y
x
2
y
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2
1、 莫尔圆的概念
(
x
y 2
)2
2
(x
y )2 2
2 x
(
x
y 2
)2
2
(x
y 2
)2
2x
当斜截面随方位角 变化时, 其上的应力 ， 在 - 直角坐标系内的轨迹是一个圆 。
圆心的坐标为(the coordinates of MOHR circle’s center)
y
xm
900
t
450
k
D
y
xm
900
t
450
k
D
y
3
τ max
x
τ max
k
450
1
解: 从圆筒表面 k 点处取出单元体, 其各面上的应力分量如图 所示
可求得
y 1 max 80MPa
x 3 max 80MPa
z 0
k点处的线应变 x , y 为
y
x
1 E
(x
y )
1 E
(max
z
x
二、纯剪的本构关系
xy
xy
G
i 0 ( i x,y,z ) yz zx 0
y
xy
z
x
三、复杂状态下的本构关系
y
依叠加原理,得
y
z
z
x
xy
x
x
x
E
y
E
理论力学14应力状态分析
T
Wt
16M e πd3
联立解得扭转外力偶矩
Me
πd 3E45o
161
π
50103 3 210109
161 0.28
300 106
试求该扭转外力偶矩。
解： 在测点截取单元体
该点为纯剪切应力状态，与母线成45° 方向即为主方向，其主应力
1 2 0
根据广义胡克定律
3
45oBiblioteka 11 E
1
2
3
1
E
1
E
45o
1
E
圆轴表面的最大扭转切应力
2
MPa
80 MPa
第六节 广义胡克定律
一、二向应力状态下的胡克定律
x
1 E
x
y
y
1 E
y
x
二、三向应力状态下的胡克定律
x
1 E
x
y z
y
1 E
y
z
x
x
2
y
2
2 xy
切应力最大值
max
1
3
2
注意：切应力极大值不一定就是切应力最大值
四、纯剪切应力状态
1. 斜截面上的应力
sin 2
cos 2
2. 主平面和主应力
主平面： 45°斜截面
主应力： 1
《材料力学 第2版》_顾晓勤第09章第2节 二向应力状态分析
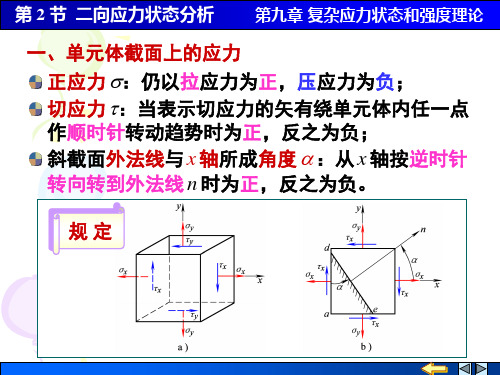
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
最大主应力和最小主应力的计算式
max m in
x
y
2
x
2
y
2
2 x
确定 max 和 min 所在平面的方法
1）若x>y，则所求的两个角度0 和 90º+0 中， 绝对值较小的一个确定max 所在的平面；
2）若x <y，则所求的两个角度0 和 90º+0 中， 绝对值较小的一个确定min 所在的平面；
2
及
2sin cos sin 2 对以上二式进行整理得到：
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
利用上述两式可以求得 de 斜截面上的正应力和切
设 de 斜截面面积为 dA，则 ae 面的面积为 dAsin ， ad面的面积为 dAcos 。取 t 和 n 为参考轴，建立棱
柱体 ade 的受力平衡方程如下：
dA ( xdAcos ) sin ( xdAcos ) cos ( ydAsin ) cos ( ydAsin ) sin 0
y
2
2 x
105 MPa
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
0
1 2
arctan(
2 x x
一般二向应力状态下求解主应力方法
一般二向应力状态下求解主应力方法1.引言二向应力状态是指材料在受力情况下同时受到两个不同方向的应力作用。
在工程实践中，很多材料都会出现二向应力状态，因此如何准确求解在这种情况下的主应力是非常重要的。
本文将介绍一般二向应力状态下求解主应力的方法。
2.二向应力状态的概念在材料受力的情况下，如果同时存在两个不同方向的应力作用，就形成了二向应力状态。
一般来说，二向应力状态可以分为各向同性的和各向异性的两种情况。
各向同性是指材料在各个方向上的性能均相同，而各向异性则是指材料在不同方向上的性能存在差异。
在工程实践中，需要根据具体情况来判断材料的二向应力状态，以便正确求解主应力。
3.一般二向应力状态下求解主应力方法一般二向应力状态下求解主应力的方法可以分为数学方法和实验方法两种。
3.1 数学方法数学方法是通过数学推导和计算来求解主应力的方法。
在一般二向应力状态下，可以采用坐标变换的方法将二向应力状态转化为主应力状态。
具体步骤如下：（1）确定材料受力情况并获取二向应力状态的数值；（2）根据材料的各向同性或各向异性特点，选择合适的坐标系，进行坐标变换；（3）利用坐标变换后的应力矩阵，通过数学运算求解出主应力的数值。
3.2 实验方法实验方法是通过实验手段来求解主应力的方法。
在一般二向应力状态下，可以采用应变片法或光栅法来进行主应力的实验测量。
具体步骤如下：（1）利用应变片或光栅在材料表面进行应力测量；（2）根据实验测量结果，计算出主应力的数值。
4.应用举例为了更好地理解一般二向应力状态下求解主应力的方法，我们可以举一个具体的应用例子。
某种材料同时受到水平和垂直方向的应力作用，需要求解主应力。
可以采用数学方法进行坐标变换，将二向应力状态转化为主应力状态，再通过数学计算求解主应力的数值。
5.总结一般二向应力状态下求解主应力是工程实践中的重要课题。
通过数学方法和实验方法的结合，可以准确求解出材料在二向应力状态下的主应力，为工程设计和材料应用提供重要依据。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.以CD为基准线，沿反时针方向另取角度2 ，得一射线，与 圆交于G点 ,
6.按比例尺量出 , 值，即为单元体 斜面上的正应力和剪
应力 ,
三.验证 , 的正确性
由应力圆可得：
y y yx
xy x
n
x x xy
yx y
B1 B O 2
G1' ,E
D(x, xy)
2 2 A1
C L A 1
MPa
22.5
0
00
222.5222.或5.51或12或.15112.152.5
max 105
max
min
x
-
2
y
2
+
2 x
85MPa
min 65
点面对应
y
y
A x
x
a
c
转向对应、二倍角对应
n
b
2 a
c
某单元体应力如图所示，其铅垂方向和水平方向各平面 上的应力已知，互相垂直的二斜面ab和bc的外法线分别与x
轴成300和－600角，试求此二斜面ab和bc上的应力。
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面，说明 低碳钢拉伸时发生屈服的主要原因。
-450
+ max
断开的。因此，可以认为这种脆性破
坏是由最大拉应力引起的。
450 0
例题4:图示一矩形截面简支梁,在跨中有集中力作用。已 知:P=100KN,L=2m,b=200mm,h=600mm,=400。求：
离左支座L/4处截面上C点在400斜截面上的应力。
P
h/4
L/4 L/4 L/2
低碳钢拉伸时，其上任意一点都是单向应力状态。
x
x + y
2
+ x - y cos 2
2
- x sin 2
x
2
+ xy
2
cos 2
x - y sin 2
2
+ x cos 2
450
450
x
2
450
x
2
max
x
2
sin
2
低碳钢试样拉伸至屈服时沿45o 表面出现滑移线，是由最大切 应力引起的。
2
+
4
2 x
z
25mm
1
2
3
2
4
h
1
3
3
Fs 4 2、计算各点主应力
1点
Iz
2点
bh3 500cm4 12
(处于纯剪状态)
1
My Iz
11000M10P3a 50 500 104
1 2 0 3 -100MPa
max
3 2
Fs A
330M12P0a103 2 60100
1 30MPa 2 0
§8.2.1 二向应力状态分析——解析法
平面应力状态的解析法
• 确定任意方向面上的应力 • 应用平衡的方法
正负号规则 平衡原理的应用— 微元局部的平衡方程
应力变换及其实质
平面应力状态的解析法
正
x
x
负
正
号
应
规
力
则
x
x
拉为正
压为负
平面应力状态的解析法
正负号规则
x'y'
xy
yx
剪 应力
使微元或 其局部顺时针 方向转动为正 ；反之为负。
- y (dAsin q) cos q 0
y´
x'y' x´
x q
x'
xy dA yx
y
平面应力状态的解析法
化简得到以下两个方程：
x' x cos2 q + y sin2 q - xy sinq cosq - yx sinq cosq x' y' x sinq cosq - y sinq cosq + xy cos2 q - yx sin2 q
0.469MPa
C C
C
§8-2-3 平面应力状态下的最大应力，主应力
y y
y
B1 B O 2
G1' ,E
D(x,xy)
2 20
CF A
A1 1
D’ (y, yx) G2 "
tg- 20
DDAF CCAF
tg 2 0
- 2 x x - y
max
A1
OC
+
CA 1
x
+ y
2
+
x
-
利用三角恒等式，整理得
x'
x
+ y
2
+x
- y
2
cos 2q
- xy sin 2q
x'y' x - y sin 2q + xy cos 2q
2
平面应力状态的解析法
应力变换的实质——同一点的应力
状态可以有各种各样的描述方式：
y
yx
y
xy
x
x
y'
y'x'
y'
x' y' x'
x'
y''
3点
3
(一般平面状态)
Fs
S
* z
My Iz
10103 25
50MPa 500 10
4
Izb
1 58.6MPa
2122.50M51P00a03 160042650 37.5
2 0 3 -8.6MPa
3 -30MPa
4点1 100MPa
2 0 3 0
自受力构件内取一单元体,其上承受应力如图示,
单位：MPa
解：(一)使用解析法求解
x 80MPa, y -40MPa
x 80MPa, y -40MPa
x -60MPa, = 30
x10-x26M+2x0+2PMayP+ay ,+x-2x=-2y
30
coys
2 - x
cos 2
sin
-
2
x sin
2
1x0-2M yPsain 2
平面应力状态的解析法
正负号规则
q角
由 x正向反 时针转到x'正 向者为正；反 之为负。
y' y
x'
q
x
平衡原理的应用—微元局部的平衡方程
• 平衡对象——用q 斜截
面截取的微元局部
y´
参加平衡的量——应力 乘以其作用的面积
平衡方程——
x'y' x´
x q
x'
xy dA yx
Fx 0 Fy 0
D(x, xy)
2
2
A1
C L A 1
yx y
D’ (y, yx) G2 "
目录
３、几种对应关系
y
y
x D
x
A
c o
(y d,y)
a (x ,x)
点面对应——应力圆上某一点的坐标值对应着单元 体某一方向面上的正应力和切应力；
转向对应——半径旋转方向与斜截面法线旋转方向 一致；
二倍角对应——半径转过的角度是斜截面旋转角度 的两倍。
2
y
2
+
2 x
min
B
1
OC
-
CB1
x
+ y
2
-
x
-
2
y
2
+
2 x
圆A1、B1两点位于应力圆上同一直径的两端，即最大正 应力所在截面与最小正应力所在截面互相垂直，故，应力圆
中各正应力极值所在截面的方位可表示如下：
y
y
m in
max x
x
0 max
m in
B1 B O 2
G1',E
分析圆轴扭转时最大切应力的作用面，说明铸铁圆 试样扭转破坏的主要原因。
450
min
x + y
2
+ x - y cos 2
2
- x sin 2
- sin 2
max
x - y sin 2
2
+ x cos 2
cos 2
450
max
-
铸铁圆试样扭转试验时，正是沿着
最大拉应力作用面（即45o螺旋面）
D’ (y, yx) G2 "
EL CE sin2 + 2 CEsin 2 cos2 + cos2 sin 2 CD cos2 sin 2 + CD sin 2 cos2
CAsin 2 + DAcos2
y
y yx
xy x
n
x x xy
B1 B O 2
G1' ,E
D(x, xy)
2 2
y
平面应力状态的解析法
Fx 0
x
'dA
-
x
(dA
cos
q
)
cosq
+ xy(dAcos q) sin q
+yx (dAsin q) cos q
- y (dAsin q) sin q 0
y´
x'y' x´
x q
x'
xy dA yx
y
平面应力状态的解析法
Fy 0
-x'y'dA +x (dAcos q) sin q +xy (dAcos q) cos q -yx (dAsin q) sin q
6.按比例尺量出 , 值，即为单元体 斜面上的正应力和剪
应力 ,
三.验证 , 的正确性
由应力圆可得：
y y yx
xy x
n
x x xy
yx y
B1 B O 2
G1' ,E
D(x, xy)
2 2 A1
C L A 1
MPa
22.5
0
00
222.5222.或5.51或12或.15112.152.5
max 105
max
min
x
-
2
y
2
+
2 x
85MPa
min 65
点面对应
y
y
A x
x
a
c
转向对应、二倍角对应
n
b
2 a
c
某单元体应力如图所示，其铅垂方向和水平方向各平面 上的应力已知，互相垂直的二斜面ab和bc的外法线分别与x
轴成300和－600角，试求此二斜面ab和bc上的应力。
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面，说明 低碳钢拉伸时发生屈服的主要原因。
-450
+ max
断开的。因此，可以认为这种脆性破
坏是由最大拉应力引起的。
450 0
例题4:图示一矩形截面简支梁,在跨中有集中力作用。已 知:P=100KN,L=2m,b=200mm,h=600mm,=400。求：
离左支座L/4处截面上C点在400斜截面上的应力。
P
h/4
L/4 L/4 L/2
低碳钢拉伸时，其上任意一点都是单向应力状态。
x
x + y
2
+ x - y cos 2
2
- x sin 2
x
2
+ xy
2
cos 2
x - y sin 2
2
+ x cos 2
450
450
x
2
450
x
2
max
x
2
sin
2
低碳钢试样拉伸至屈服时沿45o 表面出现滑移线，是由最大切 应力引起的。
2
+
4
2 x
z
25mm
1
2
3
2
4
h
1
3
3
Fs 4 2、计算各点主应力
1点
Iz
2点
bh3 500cm4 12
(处于纯剪状态)
1
My Iz
11000M10P3a 50 500 104
1 2 0 3 -100MPa
max
3 2
Fs A
330M12P0a103 2 60100
1 30MPa 2 0
§8.2.1 二向应力状态分析——解析法
平面应力状态的解析法
• 确定任意方向面上的应力 • 应用平衡的方法
正负号规则 平衡原理的应用— 微元局部的平衡方程
应力变换及其实质
平面应力状态的解析法
正
x
x
负
正
号
应
规
力
则
x
x
拉为正
压为负
平面应力状态的解析法
正负号规则
x'y'
xy
yx
剪 应力
使微元或 其局部顺时针 方向转动为正 ；反之为负。
- y (dAsin q) cos q 0
y´
x'y' x´
x q
x'
xy dA yx
y
平面应力状态的解析法
化简得到以下两个方程：
x' x cos2 q + y sin2 q - xy sinq cosq - yx sinq cosq x' y' x sinq cosq - y sinq cosq + xy cos2 q - yx sin2 q
0.469MPa
C C
C
§8-2-3 平面应力状态下的最大应力，主应力
y y
y
B1 B O 2
G1' ,E
D(x,xy)
2 20
CF A
A1 1
D’ (y, yx) G2 "
tg- 20
DDAF CCAF
tg 2 0
- 2 x x - y
max
A1
OC
+
CA 1
x
+ y
2
+
x
-
利用三角恒等式，整理得
x'
x
+ y
2
+x
- y
2
cos 2q
- xy sin 2q
x'y' x - y sin 2q + xy cos 2q
2
平面应力状态的解析法
应力变换的实质——同一点的应力
状态可以有各种各样的描述方式：
y
yx
y
xy
x
x
y'
y'x'
y'
x' y' x'
x'
y''
3点
3
(一般平面状态)
Fs
S
* z
My Iz
10103 25
50MPa 500 10
4
Izb
1 58.6MPa
2122.50M51P00a03 160042650 37.5
2 0 3 -8.6MPa
3 -30MPa
4点1 100MPa
2 0 3 0
自受力构件内取一单元体,其上承受应力如图示,
单位：MPa
解：(一)使用解析法求解
x 80MPa, y -40MPa
x 80MPa, y -40MPa
x -60MPa, = 30
x10-x26M+2x0+2PMayP+ay ,+x-2x=-2y
30
coys
2 - x
cos 2
sin
-
2
x sin
2
1x0-2M yPsain 2
平面应力状态的解析法
正负号规则
q角
由 x正向反 时针转到x'正 向者为正；反 之为负。
y' y
x'
q
x
平衡原理的应用—微元局部的平衡方程
• 平衡对象——用q 斜截
面截取的微元局部
y´
参加平衡的量——应力 乘以其作用的面积
平衡方程——
x'y' x´
x q
x'
xy dA yx
Fx 0 Fy 0
D(x, xy)
2
2
A1
C L A 1
yx y
D’ (y, yx) G2 "
目录
３、几种对应关系
y
y
x D
x
A
c o
(y d,y)
a (x ,x)
点面对应——应力圆上某一点的坐标值对应着单元 体某一方向面上的正应力和切应力；
转向对应——半径旋转方向与斜截面法线旋转方向 一致；
二倍角对应——半径转过的角度是斜截面旋转角度 的两倍。
2
y
2
+
2 x
min
B
1
OC
-
CB1
x
+ y
2
-
x
-
2
y
2
+
2 x
圆A1、B1两点位于应力圆上同一直径的两端，即最大正 应力所在截面与最小正应力所在截面互相垂直，故，应力圆
中各正应力极值所在截面的方位可表示如下：
y
y
m in
max x
x
0 max
m in
B1 B O 2
G1',E
分析圆轴扭转时最大切应力的作用面，说明铸铁圆 试样扭转破坏的主要原因。
450
min
x + y
2
+ x - y cos 2
2
- x sin 2
- sin 2
max
x - y sin 2
2
+ x cos 2
cos 2
450
max
-
铸铁圆试样扭转试验时，正是沿着
最大拉应力作用面（即45o螺旋面）
D’ (y, yx) G2 "
EL CE sin2 + 2 CEsin 2 cos2 + cos2 sin 2 CD cos2 sin 2 + CD sin 2 cos2
CAsin 2 + DAcos2
y
y yx
xy x
n
x x xy
B1 B O 2
G1' ,E
D(x, xy)
2 2
y
平面应力状态的解析法
Fx 0
x
'dA
-
x
(dA
cos
q
)
cosq
+ xy(dAcos q) sin q
+yx (dAsin q) cos q
- y (dAsin q) sin q 0
y´
x'y' x´
x q
x'
xy dA yx
y
平面应力状态的解析法
Fy 0
-x'y'dA +x (dAcos q) sin q +xy (dAcos q) cos q -yx (dAsin q) sin q