三角函数单调区间
(完整版)求三角函数的单调性的基本方法[推荐]
![(完整版)求三角函数的单调性的基本方法[推荐]](https://img.taocdn.com/s3/m/05d36b82a216147916112878.png)
求三角函数的单调性的基本方法:函数 sin()y A x k ωϕ=++的单调区间的确定,首先要看A 、ω是否为正,若ω为负,则先应用诱导公式化为正,然后将ωx +φ看作一个整体,化为最简式,再结合A 的正负,在22,22k x k k z ππππ-≤≤+∈和322,22k x k k z ππππ+≤≤+∈两个区间内分别确定函数的单调增减区间。
1、求函数)213sin(x y -=π在区间[-2π,2π]的单调增区间。
解:⑴利用诱导公式把函数转化为标准函数(sin(),0,0y A x A ωϕω=+>>)的形式:)321sin()213sin(ππ--=-=x x y⑵把标准函数转化为最简函数(sin y A x =)的形式:令123z x π=-,原函数变为1sin()sin 23y x z π=--=-⑶讨论最简函数sin y z=-的单调性:从函数sin y z=-的图像可以看出,sin y z=-的单调增区间为3[2,2]22k k ππππ++,Z ∈K 。
所以32222K z K ππππ+≤≤+,Z ∈K 即πππππ23232122+≤-≤+K x K , Z ∈K ∴ππππ3114354+≤≤+K x K , Z ∈K⑷计算k=0,k=±1时的单调增区间:当k=0时,ππ31135≤≤x当k=1时,222333xππ≤≤当k=-1时,ππ3137-≤≤-x⑸在要求的区间内[-2π,2π]确定函数的最终单调增区间:因为[2,2]xππ∈-,所以该函数的单调增区间为ππ312-≤≤-x和ππ235≤≤x2、求函数)26sin(2xy-=π在区间[0,π]的单调增区间。
解:⑴利用诱导公式把函数转化为标准函数(sin(),0,0y A x Aωϕω=+>>)的形式:sin(2)sin(2)66y x xππ=-=--⑵把标准函数转化为最简函数(siny A x=)的形式:令26z xπ=-,原函数变为sin(2)sin6y x zπ=--=-⑶讨论最简函数sin y z=-的单调性:从函数sin y z=-的图像可以看出,sin y z=-的单调增区间为3[2,2]22k k ππππ++,Z ∈K 。
三角函数的单调性
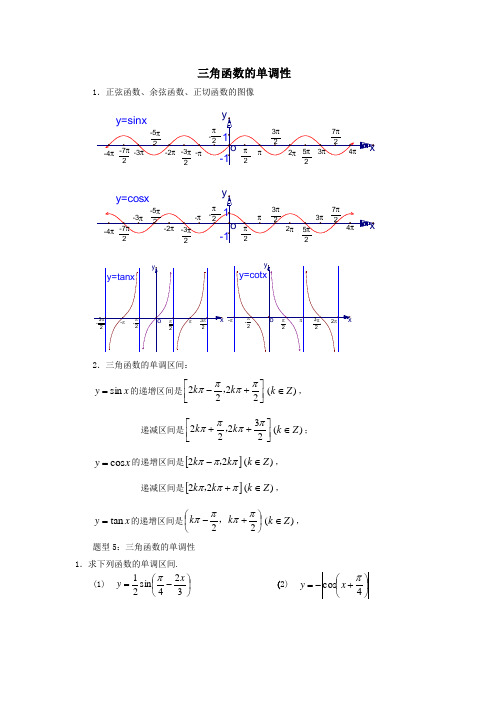
三角函数的单调性1.正弦函数、余弦函数、正切函数的图像2.三角函数的单调区间:x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ,)(Z k ∈,递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ,)(Z k ∈; x y cos =的递增区间是[]πππk k 22,-)(Z k ∈,递减区间是[]πππ+k k 22,)(Z k ∈,x y tan =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ,)(Z k ∈,题型5:三角函数的单调性 1.求下列函数的单调区间.(1) ⎪⎭⎫ ⎝⎛-=324sin 21x y π (2) ⎪⎭⎫ ⎝⎛+-=4cos πx y解:(1).原函数变形为⎪⎭⎫⎝⎛--=432sin 21πx y 令432π-=x u ,则只需求u y sin =的单调区间即可.2243222sin πππππ+≤-=≤-=k x u k u y 在 ,(Z k ∈)上 即893833ππππ+≤≤-k x k ,(Z k ∈)上单调递增, u y sin =在)(,23243222Z k k x u k ∈+≤-=≤+πππππ,上 即)(,8213893Z k k x k ∈+≤≤+ππππ,上单调递减 故⎪⎭⎫ ⎝⎛-=324sin 21x y π的递减区间为:,893,833⎥⎦⎤⎢⎣⎡+-ππππk k ()k Z ∈ 递增区间为:)(,8213,893Z k k k ∈⎥⎦⎤⎢⎣⎡++πππ.(2)原函数的增减区间即是函数⎪⎭⎫ ⎝⎛+=4cos πx y 的减增区间,令4π+=x u由函数u y cos =的图象可知:周期π=T 且 u y cos =在,42ππππk x u k ≤+=≤-上,即Z k k x k ∈-≤≤-,443ππππ上递增, 在24ππππ+≤+=≤k x u k 即在Z k k x k ∈+≤≤-,44ππππ上递减故所求的递减区间为⎥⎦⎤⎢⎣⎡--4,43ππππk k ,递增区间为,44k k ππππ⎡⎤-+⎢⎥⎣⎦(Z k ∈) 2.函数y =2sin x的单调增区间是( ) A .[2k π-2π,2k π+2π](k ∈Z )B .[2k π+2π,2k π+23π](k ∈Z ) C .[2k π-π,2k π](k ∈Z ) D .[2k π,2k π+π](k ∈Z )解析:A ;函数y =2x为增函数,因此求函数y =2sin x的单调增区间即求函数y =sin x 的单调增区间。
三角函数画图技巧与单调区间快速求解

()φω+=x A y sin 函数的画图技巧与单调区间快速求解新疆克拉玛依第十三中学 韩兴平(834009)画图能力一向是作为高中学生的基本工,而“数形结合思想”是解决数学问题的基本思想之一它有着不可替代的直观性。
在三角函数这一部分考题中画三角函数草图解题是常用的方法,那么,怎么又快又准确的画出三角函数的草图呢?还有就是不用图像怎么又快又准确写出()φω+=x A y sin 函数的单调区间呢?首先、经过第一轮教学同学们就应该从宏观上认识到()φω+=x A y sin 函数是周期函数(周期T=||2ωπ),图像似波浪线,在两个相邻最大(最小)值之间有一半是增函数、有一半减函数。
从零点起移动四分之一个周期会得最值、再移动四分之一周期会得零点、继续移动四分之一个周期会得最值、接着再一四分之一个周期得零点(整个移动就是一个周期)。
认识到这些我们就很容意又快又准确的画草图,写单调区间。
例如:1、画函数⎪⎭⎫ ⎝⎛+=32sin πx y 的草图 【解析】分析因为()φω+=x A y sin 函数从零点起移动四分之一个周期会得最值、再移动四分之一周期会得零点、继续移动四分之一个周期会得最值、接着再一四分之一个周期得零点所以我们可以先找一个零点(遵循距离原点越近越好的原则) 画法:第一步;画x 轴(不画0点)第二步;画波浪线(大致形状保证)由式子看趋势标一个零点C (),06π-。
为什么要找C点?(因为C 点在草图中部且C 点右方函数值大于零;当然点A 、E第三步;画y 轴定原点和标其它关键点O (0,0),A )0,6(-,B 3(-,0) C (),0π-,D )0,(π,E )0,5(π,F )0,4(π等。
(利用中点坐标公式或平移距离标最值点横坐标)X2、写出函数⎪⎭⎫ ⎝⎛-=x y 24sin 3π的单调区间 【解析】:这里有部分同学用换元法去求解发现答案看起来不好看,形式上与标准答案区别大。
三角函数单调区间w为负数 复合函数

【文章标题】深入探讨三角函数单调区间与复合函数1.引言在数学领域里,三角函数和复合函数都是非常重要且常见的概念。
三角函数是代表角度关系的函数,而复合函数则是由一个函数和另一个函数结合而成的新函数。
本文将深入探讨三角函数的单调区间和复合函数的相关知识,帮助读者更好地理解这两个概念之间的联系和应用。
2.三角函数单调区间的概念在数学中,单调性是指函数图像的走势是否是单调上升或者单调下降的。
而三角函数则是以角度为自变量的函数。
要求三角函数的单调区间首先需要了解三角函数的图像走势。
以正弦函数为例,它的单调递增区间是在\[2kπ,(2k+1)π\],单调递减区间是在\[(2k+1)π,(2k+2)π\],其中k为整数。
而余弦函数的单调递增区间是在\[(2k+1)π/2,(2k+3)π/2\],单调递减区间是在\[(2k-1)π/2,(2k+1)π/2\],其中k为整数。
3.三角函数单调区间w为负数三角函数单调区间与w为负数之间的联系在于w的取值对角度的影响。
当w为负数时,求出的角度与w的取值有关。
在三角函数中,角度并不仅限于180度内,而是可以通过周期性关系,延伸至整个实数轴上。
当w为负数时,三角函数的单调区间也会相应地发生变化。
需要特别注意的是,在求解三角函数单调区间时,对w的取值要进行严谨的分析和计算,以确保得出准确的单调区间。
4.复合函数的概念复合函数是由两个或者多个函数按照一定顺序组合而成的新函数。
这个概念的提出,是为了更好地描述和分析多项式函数、三角函数及其他函数之间的复杂关系。
在实际问题中,很多情况下都需要用到复合函数的概念,以便更好地处理和分析复杂的函数关系。
5.深入探讨三角函数单调区间与复合函数的关系三角函数单调区间和复合函数在某种程度上是相关的。
当我们要求解复合函数的单调区间时,有时需要用到三角函数的单调区间知识。
尤其是当复合函数中涉及到三角函数的情况,更需要对三角函数的单调区间进行全面的分析和理解。
高中数学三角函数的单调性知识分析

高中数学三角函数的单调性知识分析卢玉玺(安徽省临泉第二中学㊀236400)摘㊀要:纵观近几年的高考数学卷ꎬ我们不难发现三角函数这部分的知识已经成为了数学高考中的一大 风景点 .但是在实际解题中ꎬ很多学生对这部分知识中的应用能力并不特别强.因此ꎬ本文中将以 三角函数中的单调性 类题目的解法为例ꎬ与同学们一起寻找此类题目的解题规律.关键词:高中数学ꎻ三角函数ꎻ单调性中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)13-0024-02收稿日期:2020-02-05作者简介:卢玉玺(1979.12-)ꎬ男ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.㊀㊀一㊁正弦函数的单调区间在高中数学的学习中ꎬ函数问题较为常见ꎬ其中三角函数作为同学们整个高中阶段函数学习的重点更是具有着不容忽视的地位ꎬ在三角函数类的解题中ꎬ以正弦函数的单调性类题目为例ꎬ为更好求解正弦函数的单调区间我们就可以借助诱导公式的方法.例1㊀求函数y=sin(π3-2x)的单调区间.思路分析㊀分析题目ꎬ我们可以发现ꎬ此题中函数的ω<0ꎬ因此在本题中我们就可以先利用诱导公式将函数中x的系数化为正值ꎬ然后再根据正弦函数的单调区间求出此题答案.根据这一思路我们就可以将原函数转化为y=-sin(2x-π3)ꎬ此时所求函数的增区间就是y=sin(2x-π3)的减区间ꎻ所求函数的减区间就是y=sin(2x-π3)的增区间.之后ꎬ再根据正弦函数的单调区间求法ꎬ我们就可以得到2kπ+π2ɤ2x-π3ɤ2kπ+3π2(kɪZ)ꎬ解得kπ+5π12ɤxɤkπ+11π12(kɪZ).故所求函数的增区间为[kπ+5π12ꎬkπ+11π12](kɪZ).同理ꎬ在求原函数的减区间时ꎬ我们也可以沿用这种思路ꎮ在本题中ꎬ通过分析y=sin(2x-π3)的增区间ꎬ我们可知2kπ-π2ɤ2x-π3ɤ2kπ+π2(kɪZ)ꎬ解得kπ-π12ɤxɤkπ+5π12(kɪZ).故所求函数的减区间为[kπ-π12ꎬkπ+5π12](kɪZ).方式评注㊀在求三角函数的单调区间时ꎬ当不好直接对题目进行分析时就可以先借助诱导公式对其变形处理ꎬ然后再根据相应原理进行解题分析ꎬ以此提高我们的解题效率ꎬ让我们更准确地找出问题的解答策略.㊀㊀二㊁正切函数的单调区间本部分中我将以数形结合思想为例ꎬ带领大家探究利用数形结合思想求正切函数单调区间的具体方法.例2㊀求函数y=tan|x|的单调区间.思考方式:我们可以发现题目中的正切函数是一个绝对值函数ꎬ因而在此题中我们就可以利用数形结合的方法进行求解.在解题中ꎬ我们可以先根据题目要求及已有数学经验作出y=tan|x|的函数图象ꎬ因为函数y=tan|x|是一个偶函数ꎬ所以它的图象应该关于y轴对称.通过作图分析的方式我们可以知道:当x>0时ꎬy=tanxꎬ其增区间为(0ꎬπ2)ꎬ(kπ-π2ꎬkπ+π2)ꎬkɪN∗ꎻ当x<0时ꎬy=-tanxꎬ其减区间为(-π2ꎬ0)ꎬ(kπ-3π2ꎬkπ-π2)ꎬk为非正整数.故此题的答案应为:y=tan|x|的增区间为(0ꎬπ2)ꎬ(kπ-π2ꎬkπ+π2)ꎬkɪN∗ꎻ减区间为(-π2ꎬ0)ꎬ(kπ-3π2ꎬkπ-π2)ꎬk为非正整数.方式评注㊀在三角函数的单调性类题目中这种图象42解题的方法较为常见ꎬ在如例题中的题目里ꎬ同学们就可以利用图象的方法ꎬ通过作图分析ꎬ从左到右观察图象ꎬ按照 图象中呈上升趋势的区间为增区间㊁呈下降趋势的区间为减区间 这一理念进行题目求解.㊀㊀三㊁余弦函数的单调区间三角函数的单调性部分是三角函数的主要性质之一ꎬ本部分中ꎬ我将与同学们一起探索余弦函数的单调区间求取方法.例3㊀求函数y=cos(2x+π6)的单调区间.思考方式㊀本题中的函数是一个余弦函数ꎬ我们可以利用余弦函数的单调性进行求解.在解题过程中我们可以先将2x+π6看成一个整体ꎬ然后根据余弦函数的单调增区间求解方法就可以得到2kπ-πɤ2x+π6ɤ2kπ(kɪZ)ꎬkπ-7π12ɤxɤkπ-π12(kɪZ).故所求函数y=cos(2x+π6)的增区间应为[kπ-7π12ꎬkπ-π12](kɪZ).在求函数的单调递减区间时ꎬ我们也可以用这种方法ꎬ先将2x+π6看成一个整体ꎬ然后通过对题目的分析可得2kπɤ2x+π6ɤ2kπ+π(kɪZ)ꎬkπ-π12ɤxɤkπ+5π12(kɪZ).故所求函数y=cos(2x+π6)的减区间应为[kπ-π12ꎬkπ+5π12](kɪZ).方式评注㊀对于一些比较复杂的函数ꎬ同学们就可以使用这种方法先将原函数中的式子视为一个整体ꎬ然后再利用相关定理求解.总之ꎬ在高中数学中三角函数的单调性部分的解题过程中ꎬ同学们应该注意挖掘典型题目的具体特征ꎬ并不断总结㊁不断反思ꎬ以期形成一套完整的数学解题思路ꎬ并合理地通过知识迁移及相关题目的变式练习将自己的思路运用到实际解题中ꎬ以此达到事半功倍的学习效果.㊀㊀参考文献:[1]孙月.对高中函数单调性的解析策略研究[J].新课程(中学)ꎬ2015(10):68.[2]张先龙ꎬ肖凌戆.基于数学核心素养的教学设计 以函数的单调性新授课为例[J].中学数学教学参考ꎬ2017(z1):16-19.[责任编辑:李㊀璟]一题多解一题多变在切线方程中的运用探究伍锡浪(江西省九江第一中学㊀332000)摘㊀要:本文通过对2013年高考数学山东卷理科第22题的研究ꎬ引发了对圆锥曲线的切线方程的探究ꎬ体现了导数的工具性作用ꎬ进一步表明了数学教学中应提倡一题多解一题多变的探究ꎬ从而大力提高学生的探索能力和创造能力.关键词:一题多解ꎻ一题多变ꎻ圆锥曲线ꎻ切线方程ꎻ斜率ꎻ导数中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)13-0025-02收稿日期:2020-02-05作者简介:伍锡浪ꎬ江西省九江人ꎬ硕士ꎬ高级教师ꎬ从事高中数学教学研究.基金项目:江西省教育科学 十三五 规划2018年度ꎬ课题«一题多解一题多变在教学中的运用研究»编号:18PTYB036㊀㊀«普通高中数学课程标准(实验)»指出: 学生的数学学习活动不应只限于接受㊁记忆㊁模仿和练习ꎬ高中数学课程还应倡导自主探究㊁动手实践㊁合作交流㊁阅读自学等学习数学的方式. 这就要求我们在教学中重在为学生创设良好的思维情境ꎬ让学生在自主探究和合作交流的过程中体验数学发现和创造的历程ꎬ学会研究问题㊁解决问题ꎬ做到举一反三㊁触类旁通.从而大力提高学生的探索能力和创造能力.㊀㊀一㊁真题铺路㊀引出课题(2013年高考数学山东卷理科第22题)椭圆C:x2a2+y2b2=1(a>b>0)的左㊁右焦点分别为F1㊁F2ꎬ离心率为32ꎬ过点52。
三角函数的图象、定义域、最值(值域)、单调性

[学习要求] 1.能画出 y = sin x , y = cos x , y =tan x 的图象. 2.理解
正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小
值、图象与 x 轴的交点等). 3.理解正切函数在区间
π
π
− ,
2
2
上的性质.
π
π
− <<
2
2
由题意得 y = cos x ·|tan x |=ቐ
的大致图象是(
sin,0 ≤
π
< ,
2
π
−sin, − <
2
所以其图象的大致形状如选项C所示.
< 0,
C )
2. 已知函数 f ( x )= sin x +2| sin x |, x ∈[0,2π],若直线 y = k
与其仅有两个不同的交点,则 k 的取值范围为
, k ∈Z,
2
2
π
π
π
+ ≥ + 2π,
4
2
所以ቐ 2
k ∈Z,
π
3π
π+ ≤ + 2π,
4
2
1
5
解得4 k + ≤ω≤2 k + , k ∈Z.
2
4
1
5
5
又由4 k + - 2+ ≤0, k ∈Z,且2 k + >0, k ∈Z,解得 k =0,
2
4
4
1
5
所以ω∈ , .
2
4
方法总结
A. [-1,1]
令 sin x = t , t ∈[-1,1],
则 y = t 2+ t -1=
1 2
三角函数及反三角函数
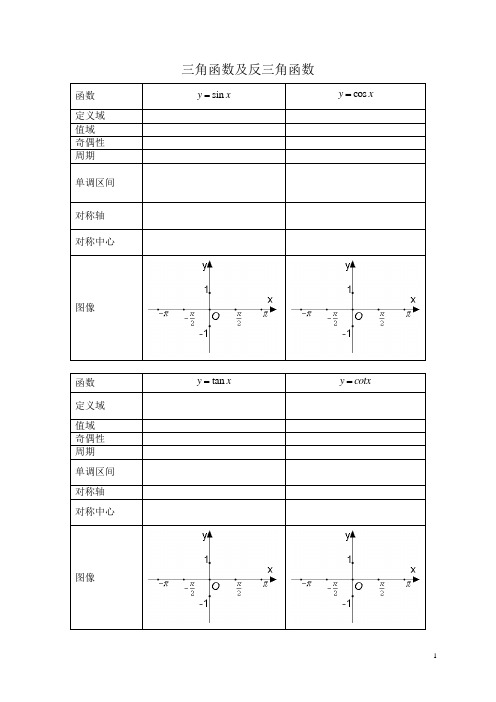
三角函数及反三角函数221.sin 2sin cos 3cos ,222.sincos 3363.sin 2cos 2, .634.y=2sin 1,,54y x x x x x R y x x y x m x x m x x x ππππω=++∈⎛⎫=++ ⎪⎝⎭=+=-⎛⎫⎛⎤+-+ ⎪ ⎥⎝⎭⎝⎦例求函数的对称轴方程以及对称中心坐标.例求函数的图像相邻的两条对称轴之间的距离.例函数的一条对称轴为则的值为例函数在区间, .x R ω∈内恰有两个对称中心则=()()()[]2sin .,0,sin ,cos .sin cos ,sin cos ||,||sec ,0,2||,||csc ,,0||cos ,0,.2y A x B y at bt c a t x x x x t t x x x a x a x a x a x a ωϕωϕωϕπθθπθθθθπ=++=++≠++⎡⎫±=≥=∈⎪⎢⎣⎭⎡⎫≤-=∈-=∈⎪⎢⎣⎭二、三角函数的值域或最值①利用公式化为的形式②可以整理为为等③令用对进行换元可令可令可令等等[]sin ,0,cos ,,.63a x by ac c x dx πππ+≠+⎡⎫-⎪⎢⎣⎭④形如=可化为①来解,也可以利用万能公式代换,还可以构造斜率.注:上述几种形式中的都可以取实数集的真子集,如0,等()()()()225.cos cos ,0,2,.26.sin 2cos 2,.1117.2,0,.sin cos sin cos 28.219.f x x x x a a R x f x a y m x x m N N g m y x x x x x y x y x x y ππ⎡⎤=++∈∈⎢⎥⎣⎦=+--⎛⎫=+++∈ ⎪⎝⎭=+=-+≥=例设函数若时的最小值为求的值例若函数的最大值为求=的函数表达式例求函数的值域例求函数①的值域例求函数.()()[]()()sin 0,0,||20,0?.10.sin 00150 11.2sin 1,0||01,0,22,112.|sin |y Ax B A A y x y x y x πωϕωϕωωωωππωϕωϕπ=++>><>>=>⎡⎤=+->≤⎢⎥⎣⎦⎛⎫- ⎪⎝⎭=+三、的图像,注:为什么要限定说明理由例为使函数在区间,上至少出现个最大值,则的最小值是多少?例函数经过,点且在区间内单调递减,函数图像3关于对称,求函数解析式.4例求作函数()()()()22|cos |.13.,32,,2cos ,().14.,.15.()sin 2(1)sin cos 5cos 2,x y f x y x y f x f x f x x a x x x a a x R a πππ====-=-+--+-∈的图像例将函数的图像向右平移个单位再将所得图像上各点的横坐标伸长为原来的倍纵坐标不变最后将所得图像向上平移个单位,得到曲线与函数的图像重合求的解析式例讨论函数并在,内作出它的图像例设①若1,()sin |()|6,.y f x y x a f x x R a ===≤∈说明的图像可由的图像经过怎样的变换得到?②已知常数使得不等式对任意恒成立求实数的取值范围()()[][]()1sin arcsin cos(arccos ),1,1;tan(arctan )(),1sin(arccos )cos(arcsin )1,1;tan()(arctan ),02arcsin(sin ),2,[,],22ar x x x x x cot arccotx x x Rx x x arccotx cot x x xy x T y πππ==∈-==∈==∈-==≠==-=四、反三角函数的几个等式值域单调区间同正弦函数;(连续的折线)()[]ccos(cos ),2,[0,],;arctan(tan ),,((),,;(31,1,arcsin arccos ;,arctan arccot .22216.sin ,x T y x T y arccot cotx T x x x x R x x y x x πππππππ=====∈-+=∈+==∈值域单调区间与余弦函数相反(连续的折线)其值域和单调区间同正切函数;不连续的线段)其值域和单调区间与余切函数相反不连续的线段)当时当时例求函数①2212123,2arcsin(1).3217.arccos()218.arccos(sin ),arcsin(1)arccos 2.3319.,sin cos 0,0,arctan arctan .y x y x x y x x y x x x x x x x x ππππαααπ⎡⎫=-+⎪⎢⎣⎭=+=-<<=-+-+=<<+②的反函数例求函数的定义域、单调区间、值域.例求函数①②的值域例是方程的两个根且求的值22220.:lg(25)21.:arccos 3arcsin arcsin(1)arcsin(1)222.:3cos 4sin 33sin cos 1sin sin 2sin()0323.y y x x x x x x x xx x x x yx ππ==-++≥-+--==+--==五、三角方程或三角不等式例求下列函数的定义域①例解不等式①②例解下列方程①②③六、三角函数和反三角函数的应用例求函数(){}(){}212.24.|4,,|2cos 3sin ,,,.25.cos sin cos ,,log 410,.M z z t t i t R i N z z i R M N D x D y x y x θλθθλαβαβ==+-∈==++∈=∅+=+∈=+ 例设集合为虚数单位,若求实数的取值范围例已知的取值范围是若求函数最小值并求取得最小值时的值()()121226.,,120,,1.2,A B C ABCD l A B BC AB CD ABC l AB BC CD S Sl l '''∆''''∆=+=∠=++= 例已知水渠在过水面积为定值时,过水湿周越小其流量越大,现有两种设计,其纵断面如图:甲过水断面为等腰,过水湿周乙为等腰梯形,过水湿周=求和的最小值为使流量最大给出最佳设计方案.'图乙。
三角函数的单调区间公式

三角函数的单调区间公式三角函数的单调区间公式1、在0°~90°,正弦函数y=sin x从0递增到1:2、在90°~180°,正弦函数y=sin x从1递减到0:3、在180°~270°,正弦函数y=sin x从0递减到-1:4、在270°~360°,正弦函数y=sin x从-1递增到0:5、在0°~90°,余弦函数y=cos x从1递增到0:6、在90°~180°,余弦函数y=cos x从0递减到-1:7、在180°~270°,余弦函数y=cos x从-1递增到0:8、在270°~360°,余弦函数y=cos x从0递增到1:9、在0°~90°,正切函数y=tan x从0递增到无穷大:10、在90°~180°,正切函数y=tan x从无穷大递减到0:11、在180°~270°,正切函数y=tan x从0递减到无穷大负值:12、在270°~360°,正切函数y=tan x从无穷负大增动0:在数学中,三角函数是一组非常重要的函数,它们需要更具体的说明,即相应的函数的单调区间的范围。
这些单调区间的范围,也就是函数y = sin x, y = cos x和y = tan x的单调区间是其中三种最常见的三角函数。
关于三角函数的单调区间的公式有一对数学的一对概念,它们是:1、函数的单调性:2、函数的极值点:具体到三角函数,它们的单调性指的是它们在某一区间上在增加或减小,而极值点指的是在某一区间上他们的值没有继续增加或减少了。
根据上述概念,三角函数的单调区间可以总结为:1、在0°~90°,正弦函数y=sin x从0递增到1:2、在90°~180°,正弦函数y=sin x从1递减到0:3、在180°~270°,正弦函数y=sin x从0递减到-1:4、在270°~360°,正弦函数y=sin x从-1递增到0:5、在0°~90°,余弦函数y=cos x从1递增到0:6、在90°~180°,余弦函数y=cos x从0递减到-1:7、在180°~270°,余弦函数y=cos x从-1递增到0:8、在270°~360°,余弦函数y=cos x从0递增到1:9、在0°~90°,正切函数y=tan x从0递增到无穷大:10、在90°~180°,正切函数y=tan x从无穷大递减到0:11、在180°~270°,正切函数y=tan x从0递减到无穷大负值:12、在270°~360°,正切函数y=tan x从无穷负大增动0:由于三角函数的单调性和极值点的关系,所以可以用来推导各种需要求解三角函数的实际问题中依据函数计算出函数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数单调区间
三角函数单调区间是数学中的一个重要概念,是弧度和角度转换
的依据。
它在微积分中也得到了广泛的应用。
所谓三角函数单调区间,指的是某一函数在一定区间上是单调递
增或者单调递减的函数,即在这个区间内不存在最大值和最小值。
具
体而言,三角函数单调区间主要指的是正弦、余弦和正切三个函数的
单调区间,它们分别表示从反正弦、反余弦和反正切得到的变量。
三角函数单调区间的表达形式主要有二类。
第一类是基于函数x (x∈R)的单调性变换。
它把有界函数y=f(x)的单调性变换为有界函
数y=f(x+δ)和y=f(x-δ)。
其中δ表示单调性变化的距离,正
值表示函数增大,负值表示函数减小。
这种变换后的函数即为三角函
数单调区间。
第二类是采用延迟矩阵来表示三角函数单调区间。
延迟矩阵也称
滞后矩阵,它能够具有简洁优雅的表达形式,但它也比较复杂,并且
表达的结果有一定的误差。
因此,应用延迟矩阵来表示三角函数单调
区间一般会产生一定的误差。
总结一下,三角函数单调区间是一类有界函数的单调性的表示形式,它是微积分中的重要概念,正弦、余弦和正切函数的变量是三角
函数单调区间的核心,通常可以用单调性变换和延迟矩阵来表示它们。
