离散信源熵信道容量实验报告
实验二 离散信道及其容量

实验二离散信道及其容量一、[实验目的]1、理解离散信道容量的内涵;2、掌握求二元对称信道(BSC)互信息量和容量的设计方法;3、掌握二元扩展信道的设计方法并会求其平均互信息量。
二、[实验环境]windows XP,MATLAB 7三、[实验原理]若某信道输入的是N 维序列x ,其概率分布为q(x ),输出是N 维序列y ,则平均互信息量记为I(X ;Y ),该信道的信道容量C 定义为()max (X;Y)q x C I =。
四、[实验内容]1、给定BSC 信道,信源概率空间为信道矩阵0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦求该信道的I(X;Y)和容量,画出I(X;Y)和ω、C 和p 的关系曲线。
2、编写一M 脚本文件t03.m,实现如下功能:在任意输入一信道矩阵P 后,能够判断是否离散输出对称信道。
3、对题1求其二次扩展信道的平均互信息I(X;Y)。
五、[实验过程]每个实验项目包括:1)设计思路1、信道容量()max (X;Y)q x C I =,因此要求给定信道的信道容量,只要知道该信道的最大互信息量,即求信道容量就是求信道互信息量的过程。
程序代码:clear all,clc;w=0.6;w1=1-w;p=0.01;XP 010.60.4=p1=1-p;save data1p p1;I_XY=(w*p1+w1*p)*log2(1/(w*p1+w1*p))+(w*p+w1*p1)*log2(1/(w*p+w1*p1))-...(p*log2(1/p)+p1*log2(1/p1));C=1-(p*log2(1/p)+p1*log2(1/p1));fprintf('互信息量:%6.3f\n信道容量:%6.3f',I_XY,C);p=eps:0.001:1-eps;p1=1-p;C=1-(p.*log2(1./p)+p1.*log2(1./p1));subplot(1,2,1),plot(p,C),xlabel('p'),ylabel('C');load data1;w=eps:0.001:1-eps;w1=1-w;I_XY=(w.*p1+w1.*p).*log2(1./(w.*p1+w1.*p))+(w.*p+w1.*p1).*log2(1./(w.*p+w1.*p1))-.. .(p.*log2(1./p)+p1.*log2(1./p1));subplot(1,2,2),plot(w,I_XY)xlabel('w'),ylabel('I_XY');实验结果:互信息量:0.891信道容量:0.919I(X;Y)和ω、C和p的关系曲线图:CX2、离散对称信道:当离散准对称信道划分的子集只有一个时,信道关于输入和输出对称。
中北大学信息论实验报告(离散信道容量计算)

信息与通信工程学院实验报告
(软件仿真性实验)
课程名称:信息论基础
实验题目:离散信道容量计算 指导教师:
班级: 学号: 学生姓名:
一、实验目的和任务
1.掌握离散信道的信道容量的计算方法。
2.学会利用MATLAB 计算离散信道的信道容量。
3.学会依据所绘制的信道容量曲线,分析其物理意义。
二、实验内容及原理
1)实验内容:
离散信道容量的计算与分析
2)实验原理:
1.信道容量定义为平均互信息量的最大值:
)},({max )
(Y X I C x p = 2.对称DMC 信道,其信道容量计算公式为:
ij m
j ij i p p m a Y H m C log log )(log 1∑=+=-=丨
3.准对称DMC 信道,其信道容量计算公式为:
k k k M N n C log log k
1∑=-=
成绩
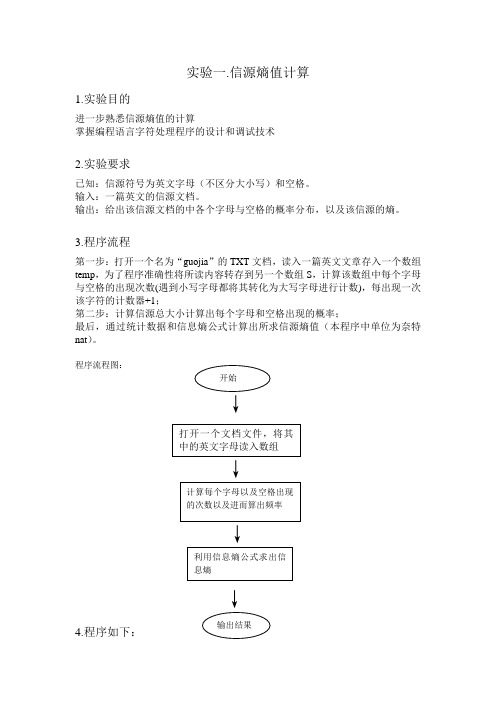
三、实验步骤或程序流程
以matlab软件为基础,通过编程:计算对称信道的信道容量。
四、实验数据及程序代码
1.离散信道的信道容量的计算
假设信道转移概率矩阵为
则该信道容量为:
2.绘制信道容量曲线
程序代码:
五、实验数据分析及处理
该函数曲线的物理意义为:
由信道容量曲线可知,当概率为0或1时,信道容量达到最大即由干扰造成的信息损失为0.
六、实验结论与感悟(或讨论)
通过本次试验,掌握了离散信道容量的计算与分析,学会了依据所绘制的信道容量曲线,分析其物理意义。
离散信源熵信道容量实验报告

离散信源熵信道容量实验报告实验目的:通过模拟离散信源熵和信道容量的实验,掌握熵和信道容量的概念及计算方法。
实验原理:离散信源:离散信源是指其输出符号集合为有限的离散符号集合,通常用概率分布来描述其输出符号的概率分布,称为离散概率分布。
离散信源的熵是度量这一离散概率分布的不确定度的量度,其单位是比特。
离散信源的熵公式为:H(S)=-Σpi×log2pi其中,H(S)为离散信源的熵,pi为消息符号i出现的概率,log2为以2为底的对数。
信道容量:信道容量是指在某一固定的信噪比下,能够传送的最大信息速率。
信道容量的大小决定了数字通信系统的最高可靠传输速率。
离散无记忆信道的信道容量公式为:C=max{I(X;Y)}其中,X为输入符号,Y为输出符号,I为信息熵。
实验步骤:1. 生成随机概率分布对于3种不同的符号数量,生成随机的符号及其概率分布。
在生成时,要求概率之和为1。
2. 计算离散信源的熵根据所生成的随机概率分布计算离散信源的熵。
3. 构建离散无记忆信道构建一个离散的2进制对称信道,并存储在一个概率矩阵中,利用生成的概率分布对该矩阵进行初始化。
4. 计算信道容量根据所构建的离散无记忆信道计算其信道容量。
实验结果分析:以下是实验结果分析,其中H(S)表示离散信源的熵,C表示离散无记忆信道的信道容量。
符号数量为3时:符号概率a 0.2b 0.3c 0.5H(S) = 1.485构建的离散无记忆信道的概率矩阵为:| 0 | 1 |--------------------------a | 0.20 | 0.80 |--------------------------b | 0.60 | 0.40 |--------------------------c | 0.80 | 0.20 |--------------------------C = 0.823从实验结果可以看出,当符号数量增加时,熵的值也会随之增加,这是由于符号集合增加,随机性增强所导致的。
《信息论基础》实验报告-实验1

信息与通信工程学院实验报告(软件仿真性实验)课程名称:信息论基础实验题目:绘制信源熵函数曲线指导教师:班级:1605XXXX学号:XX 学生姓名:王小明一、实验目的和任务1.掌握离散信源熵的原理和计算方法。
2.熟悉Matlab软件的基本操作,练习应用Matlab软件进行信源熵函数曲线的绘制。
3.理解信源熵的物理意义,并能从信源熵函数曲线图上进行解释其物理意义。
二、实验内容及原理(1)离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
假定X是一个离散随机变量,即它的取值范围R={x1,x2,x3,…}是有限或可数的。
设第i个变量xi发生的概率为p i=P{X=x i}。
则:定义一个随机事件的自信息量I(x i)为其对应的随机变量x i出现概率对数的负值。
即:I(xi )= -log2p(xi)定义随机事件X的平均不确定度H(X)为离散随机变量x i出现概率的数学期望,即:∑∑-==i ii ii ixpxpxIxpXH)(log)()()()(单位为 比特/符号 或 比特/符号序列。
平均不确定度H (X )的定义公式与热力学中熵的表示形式相同,所以又把平均不确定度H (X )称为信源X 的信源熵。
必须注意以下几点:某一信源,不管它是否输出符号,只有这些符号具有某些概率特性,必有信源的熵值;这熵值是在总体平均上才有意义,因而是个确定值,一般写成H (X ),X 是指随机变量的整体(包括概率分布)。
信息量则只有当信源输出符号而被接收者收到后,才有意义,这就是给与信息者的信息度量,这值本身也可以是随机量,也可以与接收者的情况有关。
熵是在平均意义上来表征信源的总体特征的,信源熵是表征信源的平均不确定度,平均自信息量是消除信源不确定度时所需要的信息的量度,即收到一个信源符号,全部解除了这个符号的不确定度。
或者说获得这么大的信息量后,信源不确定度就被消除了。
信源熵和平均自信息量两者在数值上相等,但含义不同。
信源熵值计算实验报告
result=-result;
printf("信息熵为:%f",result);
printf("\n");
return 0;
}
运行结果如下:
其中guojia.txt中的文档如下:
There is no hate without fear. Hate is crystallized fear, fear’s dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity and our dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.
fread(temp,1, 486, f);}
fclose(f);
s[0]=*temp;
for(i=0;i<strlen(temBiblioteka );i++){
s[i]=temp[i];
}
for(i=0;i<strlen(s);i++)
{
if(s[i]==' ')
num[26]++;
else if(s[i]>='a'&&s[i]<='z')
5.程序优点:
本程序可以打开文档进行统计,不必运行程序时重新输入文档,节省时间并且避免了一定的输入错误。
中南大学信息论实验报告

中南大学信息论与编码课实验报告专业班级:指导老师:张祖平姓名:学号:实验一 关于信源熵的实验一、实验目的1. 掌握离散信源熵的原理和计算方法。
2. 熟悉matlab 软件的基本操作,练习使用matlab 求解信源的信息熵。
3. 自学图像熵的相关概念,并应用所学知识,使用matlab 或其他开发工具求解图像熵。
4. 掌握Excel 的绘图功能,使用Excel 绘制散点图、直方图。
二、实验原理1. 离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
随机事件的自信息量I (x i )为其对应的随机变量x i 出现概率对数的负值。
即:I (x i )= -log 2 p (x i )随机事件X 的平均不确定度(信源熵)H (X )为离散随机变量x i 出现概率的数学期望,即:∑∑-==iii i i i x p x p x I x p X H )(log )()()()(2. 信源的信息熵设信源符号集X ={a1,a2,…,ar},每个符号发生的概率分别为p (a1)=p 1,p (a2)=p 2,…,p (ar),即信源的概率空间为,⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)(...... )2(2 )1(1ar p ar a p a a p a P X则该信源的信源熵为:H (X ) = - p (a1) log p (a1) –p (a2) log p (a2) –…–p (ar) log p (ar)3. 信道的数学模型与相关熵的计算• 单符号离散无噪声无损信道的信道容量4. MATLAB 二维绘图用matlab 中的命令plot(x , y )就可以自动绘制出二维图来。
例1-2,在matlab 上绘制余弦曲线图,y = cos x ,其中0 ≤ x ≤ 2π。
>>x =0:0.1:2*pi ; %生成横坐标向量,使其为0,0.1,0.2,…,6.2 >>y =cos(x ); %计算余弦向量 >>plot(x ,y ) %绘制图形 5. MATLAB 求解离散信源熵求解信息熵过程:1) 输入一个离散信源,并检查该信源是否是完备集。
离散无记忆信道的信道容量计算实验报告

感谢聆听!
2.信道容量算法
信道容量是互信息的最大值,首先要将信道容量求极值得问题表示 为二重交替优化问题。
(1)
运行结果
(2)
实验结果(1):输入概率转移矩阵是之前例题中的概率转移矩阵,迭代 次数为11和70次,经验证,迭代程序结果比例题中的一般信道容量算 法更为精确。
实验结果(2):迭代次数为4,迭代结果为1.3219,经验算发现此输入概 率转移矩阵的实际结果为1.329,误差不大,符合要求,另外精度越高, 结果越接近。
离散无记忆信道的迭代运算
一、为什么要迭代?
(1)解方程组求出的输入分布 {P(x)}可能不唯一,因为可能有多个 极值点;
(2)需要验证求出的输入分布序列 是否符合要求。
二、Blahut-Arimoto算法
1.交替优化
(2)、通过轮流固定f的其中一个自变量,对另一个没固定的 自变量求极值,由此来确定受此自变量影响下的最值。下一 次对另一个自变量也如此操作,循环往复形成迭代。
程序部分
程序设计思路
(1)参数输入模块
(2)判断模块
判断矩阵中的元素是否 >=0且<=1
判断矩阵的行相加是否 都为1
(3)迭代模块1
(4)迭代模块2
(5)输出模块
P116 4.3 (b)
一般的王育民、李晖 .《信息论与编码理论第二版》[M]北京:高等教育出版社,2013.4 96-101 [2]辛英.《离散信道容量的迭代算法及其实现》[D]山东:山东工商学院,1994 [3]徐伟业 耿苏燕 马湘蓉 冯月芹.《任意DMC信道容量的计算与仿真》[D]南京:南京工程学院 2017
实验三_信源熵及信道容量特性

实验三信源熵及信道容量极值性研究一、实验目的验证信源熵及信道容量的极值特性,理解相关参数的变化对信源熵及信道容量的影响。
二、实验原理二元信源的熵H(X)=[wlog2(1/w)+(1-w)log2(1/(1-w))]这时信息熵H(X)是w的函数,通常用H(w)表示,w取值[0,1]。
当固定某信道时,选择不同的信源(其概率分布不同)与信道连接,在信道输出端接收道每个符号获得的信息量是不同的。
而且对于每一个固定信道,一定存在有一种信源(某一种概率分布P(x)),使输出获得的平均信息量为最大。
当信源固定后,选择不同的信道传输同一信源符号时,在信道的输出端获得关于信源的信息量是不同的。
信道输出端获得关于信源的信息量是信道传递概率的U型凸函数。
三、程序信源熵的程序:w=[0.000001:0.01:1];H=w.*log2(1./w)+(1-w).*log2(1./(1-w));plot(w,H);title('信源熵函数H(w)');xlabel('w');ylabel('H(w)');固定二元对称信道的互信息和固定二元信源的互信息:w=[0:0.01:1];p=0.2;h=-p.*log2(1./p)-(1-p).*log2(1./(1-p));H=(w.*(1-p)+(1-w).*p).*log2(1./(w.*(1-p)+(1-w).*p))-(1-(w.*(1-p)+ (1-w).*p)).*log2(1-(w.*(1-p)+(1-w).*p));I=H+h;subplot(2,1,1);plot(w,I);title('固定二元对称信道的互信息');xlabel('w');ylabel('I(X;Y)');p=[0.000001:0.01:1];w=0.2;h=-p.*log2(1./p)-(1-p).*log2(1./(1-p));H=(w.*(1-p)+(1-w).*p).*log2(1./(w.*(1-p)+(1-w).*p))-(1-(w.*(1-p)+ (1-w).*p)).*log2(1-(w.*(1-p)+(1-w).*p));I=H+h;subplot(2,1,2);plot(p,I);title('固定二元信源的互信息'); xlabel('p');ylabel('I(X;Y)');四、实验结果图1图2五、实验分析由图1可知,如果二元信源的输出时确定的(~w=1-w=0或w=1),则该信源不提供任何信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算离散信源熵、离散信道容量
1 实验任务和目的
实验任务:
(1)简要总结信源的熵、信道容量的物理意义,概念;
(2)写出离散信源熵、离散信道容量计算的基本步骤,画出实现离散信源熵、离散信道容量计算的程序流程图;
(3)讨论信源的熵的大小与前后符号之间相关性的关系,讨论信道容量与信源先验概率及信道转移概率的关系。
实验目的:
掌握信源的熵、信道容量的物理意义,概念;熟练掌握离散信源熵、离散信道容量的计算方法步骤;利用Matlab 编写离散信源熵、离散信道容量的计算程序;验证程序的正确性。
2 实验过程和结果 2.1 实验过程
1、简要总结信源的熵、信道容量的物理意义,概念。
信源熵的物理意义是指信源中的各个符号的平均不确定性;熵是信源符号的平均信息量,是信源符号的平均不确定度。
信道容量 概念:在信道可以传输的基本前提下,对信源的一切可能的概率分布而言,信道能够传输的最大(接收)熵速率称为信道容量。
意义:求出了某个信道的信道容量,也就找到了信源的最佳概率分布。
从而指导人们改造信源,使之最大可能地利用信道的传输能力。
2、写出离散信源熵、离散信道容量计算的基本步骤,画出实现离散信源熵、离散信道容量计算的程序流程图;
离散信源熵的计算步骤:
()()()11log log ()q
r r r i i i i H X E p a a p a =⎛⎫
==- ⎪⎝⎭
∑
信道容量的计算步骤:()
(){}()符号/;max bit Y X I C X
P =
3、(1)讨论信源的熵的大小与前后符号之间相关性的关系,讨论信道容量与信源先验概率及信道转移概率的关系。
信源的相关性是信源符号间的依赖程度的度量。
由于信源输出符号间的依赖关系也就是 信源的相关性使信源的实际熵减小。
信源输出符号间统计约束关系越长,信源的实际熵越小。
当信源输出符号间彼此不存在依赖关系且为等概率分布时,信源的实际熵等于最大熵。
(2)信道容量与信源先验概率及信道转移概率的关系。
信道容量是信道的一个参数,反映了信道所能传输的最大信息量,其大小与信源无关。
对不同的输入概率分布,互信息一定存在最大值。
我们将这个最大值定义为信道的容量。
一但转移概率矩阵确定以后,信道容量也完全确定了。
尽管信道容量的定义涉及到输入概率分布,但信道容量的数值与输入概率分布无关。
我们将不同的输入概率分布称为试验信源,对不同的试验信源,互信息也不同。
其中必有一个试验信源使互信息达到最大。
这个最大值就是信道容量。
实验结果
计算离散信源熵:
否
是
()()⎪⎭
⎫ ⎝⎛=+=+⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡=∑∑∑i i i
i i j i i j i i j i j i a n n C a x p n n C x y p x p x y p x y p a max ln ,1)(ln ,1)/()()/(ln )/(exp 21 ()()ε
<+-+n n C n n C ,1,121()n n C C ,11+= ∑=i i i i i i a x p a x p x p )()()( 输入)()()0(i i x p x p = 结束
计算离散信道容量:
3实验总结和心得
通过本次的试验,让我加深了对信息论与编码这门课知识点的认识,学会了怎么样去计算信源熵以及信道容量,怎样去把它具体实现出来。
在此次实验过程中,让我认识到了做实验之前预习是很重要的,通过查找资料可以解决一些我们不能解决的问题的方法。
还有就是不懂的问题及时问老师,能解决的问题随堂解决。
4附录(代码)
计算信道容量:
clc;clear all;
N = input('输入信源符号X的个数N=');
M = input('输出信源符号Y的个数M=');
p_yx=zeros(N,M); %程序设计需要信道矩阵初始化为零fprintf('输入信道矩阵概率\n')
for i=1:N
for j=1:M
p_yx(i,j)=input('p_yx=');%输入信道矩阵概率if p_yx(i)<0
error('不符合概率分布')
end
end
end
for i=1:N %各行概率累加求和
s(i)=0;
for j=1:M
s(i)=s(i)+p_yx(i,j);
end
end
for i=1:N %判断是否符合概率分布
if (s(i)<=0.999999||s(i)>=1.000001)
error('不符合概率分布')
end
end
b=input('输入迭代精度:');%输入迭代精
度 for i=1:N
p(i)=1.0/N; %取初始概率为均匀分布
end
for j=1:M %计算q(j)
q(j)=0;
for i=1:N
q(j)=q(j)+p(i)*p_yx(i,j);
end
end
for i=1:N %计算a(i) d(i)=0;
for j=1:M
if(p_yx(i,j)==0) d(i)=d(i)+0; else d(i)=d(i)+p_yx(i,j)*log(p_yx(i,j)/q(j)); end
end
a(i)=exp(d(i)); end u=0;
for i=1:N %计算u
u=u+p(i)*a(i); end
IL=log2(u); %计算IL
IU=log2(max(a));%计算IU n=1;
while((IU-IL)>=b) %迭代计算
for i=1:N
p(i)=p(i)*a(i)/u; %重新赋值p(i)
end
for j=1:M %计算q(j)
q(j)=0;
for i=1:N
q(j)=q(j)+p(i)*p_yx(i,j);
end
end for i=1:N %计算a(i)
d(i)=0;
for j=1:M
if(p_yx(i,j)==0)
d(i)=d(i)+0;
else
d(i)=d(i)+p_yx(i,j)*log(p_yx(i,j)/q(j)); end
end
a(i)=exp(d(i)); end u=0;
for i=1:N %计算u
u=u+p(i)*a(i);
end
IL=log2(u); %计算IL
IU=log2(max(a));%计算IU n=n+1;
end
fprintf('信道矩阵为:\n'); disp(p_yx);
fprintf('迭代次数n=%d\n',n);
fprintf('信道容量C=%f比特/符号',IL);
计算离散信源熵:
%用MA TLAB编程实现单符号离散无记忆信源熵的计算
function H = entropy(p)
%该函数用来计算包含任意多个符号的信源熵(比特)
%p为DMS的概率分布,行向量
if sum(p)~=1 %判断是否满足概率完备性(~= 不等于的意思)
error('!!!不满足概率完备性,请重新输入信源分布')
return;
else
L = length(p) %得到信源符号的个数
H=0; %熵值初始化为零
for i=1:L
H=H-p(i)*log2(p(i)); %累加熵函数各个子项
end
end
%sum(A):求数组A的元素之和
%length(X):求矢量X的长度
%log2(X):计算以2为底X的对数
%error:显示错误信息。
