奥数讲座搭配问题
人教版数学二年级下册奥数专讲:搭配问题教案
- PPT:制作精美的PPT,通过图文并茂的方式,展示搭配问题的概念、方法和案例,帮助学生理解和记忆。
-视频:播放一些与搭配问题相关的视频,如实际场景的搭配问题解决过程,让学生更直观地理解和应用搭配问题的解决方法。
-在线工具:利用在线工具,如数学软件或在线教育平台,学生可以进行搭配问题的练习和测试,及时获得反馈和指导。
技能训练:
设计实践活动或游戏,让学生在实践中体验搭配问题的应用,提高实践能力。
在搭配问题的新课呈现结束后,对搭配问题的知识点进行梳理和总结。
强调搭配问题的关键点和解决方法,帮助学生形成完整的知识体系。
(四)巩固练习(预计用时:5分钟)
随堂练习:
随堂练习题,让学生在课堂上完成,检查学生对搭配问题的掌握情况。
2.学生的学习兴趣、能力和学习风格:学生对动手操作和实践性的活动通常比较感兴趣,因此通过实物操作和游戏等互动方式进行教学能够激发他们的学习兴趣。在学习能力方面,二年级的学生具备一定的思维能力和问题解决能力,但仍然需要具体的实例和直观的展示来帮助他们理解和掌握概念。学生的学习风格各异,有的喜欢通过听讲来学习,有的则更倾向于通过实践和操作来学习。
1.逻辑推理:通过解决搭配问题,学生能够培养运用逻辑推理的能力,从具体的事物中抽象出搭配关系的规律,形成初步的逻辑思维。
2.数学建模:在解决搭配问题时,学生需要建立适当的数学模型来描述问题,并通过枚举法等方法找到解决问题的策略,从而培养数学建模的能力。
3.问题解决:学生将运用已有的知识和方法,通过分析、综合、判断等思维过程,解决实际的搭配问题,提高问题解决的能力。
-实际应用:搭配问题在实际生活中有很多应用,如服装搭配、食物搭配等。
④搭配问题的拓展
三下奥数思维训练搭配教案

三下奥数思维训练搭配教案奥数思维训练搭配教案。
一、教学目标。
1.通过奥数思维训练,培养学生的逻辑思维能力和数学解决问题的能力。
2.激发学生对数学的兴趣,提高学生学习数学的积极性。
3.通过搭配教案,引导学生在解决问题时灵活运用奥数思维方法。
二、教学重点。
1.培养学生的逻辑思维能力。
2.引导学生在解决问题时灵活运用奥数思维方法。
三、教学难点。
1.如何引导学生在解决问题时灵活运用奥数思维方法。
2.如何激发学生对数学的兴趣。
四、教学方法。
1.启发式教学法,通过引导学生解决实际问题,激发学生的思维能力。
2.案例教学法,通过具体案例分析,引导学生灵活运用奥数思维方法。
五、教学过程。
1.导入,通过一个生活中的实际问题引入奥数思维训练的教学内容,激发学生的兴趣。
2.讲解,向学生介绍奥数思维训练的方法和技巧,引导学生理解奥数思维的重要性和应用。
3.案例分析,通过具体案例分析,引导学生灵活运用奥数思维方法,解决问题。
4.练习,设计一些练习题,让学生在课堂上进行练习,巩固所学的奥数思维方法。
5.讨论,组织学生进行讨论,分享他们在解决问题时的思路和方法,互相学习,互相提高。
6.总结,对本节课的内容进行总结,强调奥数思维训练的重要性,鼓励学生在日常学习中多多运用奥数思维方法。
六、教学反思。
通过奥数思维训练搭配教案的教学实践,我发现学生在解决数学问题时能够更加灵活运用奥数思维方法,提高了他们的解决问题的能力。
同时,学生对数学的兴趣也得到了激发,积极性也有所提高。
但是在教学中也发现,有些学生在灵活运用奥数思维方法时还存在一定的困难,需要我们在后续的教学中加强引导和训练。
希望通过我们的努力,能够培养出更多数学思维敏捷、解决问题能力强的学生。
二年级奥数(间隔、搭配问题)

二年级奥数间隔问题例1 丽丽住的这幢楼共七层,每层楼梯20级,她家在五楼,你知道丽丽走多少级楼梯才能到自己的家吗?例2 把一根粗细均匀的木头锯成5段,每锯一次要5分钟,一共要多少分钟?例3 少先队员在操场的一旁每隔5米栽一棵树,起点和终点都栽了,一共栽了21棵树,操场长多少米?例4 学校门前一条路长56米,为迎接国庆节,从头到尾都要插彩旗,每隔7米插一面,一共要插彩旗多少面?例5 圆形花圃的周长是27米,现在每隔3米栽一棵树,一共要栽多少棵树?例6 时钟两点钟敲2下,2秒敲完。
五点钟敲5下,几秒钟敲完?例7 校门口的一条路长20米,路的两边从头到尾都栽树,每隔2米栽一棵,一共要栽多少棵?课后练习:1、小红家住七楼,她从一楼到三楼要用2分钟,那么他从一楼到七楼要用几分钟?2、王师傅家住六楼,他从一楼到三楼要走40级台阶,那么他从一楼到六楼要走多少级台阶?3、把一根粗细均匀的木料锯成5段,每锯一次要5分钟,一共要多少分钟?4、一根铁丝长25厘米,把它剪成5厘米长的小段,要剪几次?5、一条河堤长40米,每隔4米栽一棵树,从头到尾一共要栽多少棵?6、校门口的一条路长10米,路的两边从头到尾都要插彩旗,每隔一米插一面,一共要插多少面?7、一个圆形花坛的周长是24米,在它的边上每隔4米放一盆月季花,一共要花多少盆月季花?8、时钟三点钟敲3下,需要4秒钟,那么十一点钟敲11下,需要几秒钟?9、一条路长25米,少先队员在路的两旁栽树,起点终点都栽,一共栽了12棵树,那么每两棵树之间相隔多少米?10、两栋楼之间相距12米,每隔两米栽一棵树,一共栽了几棵树?二年级奥数搭配方法例1 芳芳有三件衬衣,两条裙子,一共有几种穿法?例2 四个男同学和两个女同学进行乒乓球单打比赛,如果每个男同学和女同学都打一盘,那么一共要打几盘?例3 用数字1,2,3可以组成多少个没有重复数字的三位数?例4 从上海到南京要停9个站(包括上海和南京)。
二年级下奥数《搭配问题》试卷有答案

二年级例1.(1)红红有3件上衣,2条裙子,一共有几种穿法?2×3=6(种)(2)学校食堂今天午餐的菜谱上有2个肉菜和2个素菜,小明想买1个肉菜和1个素菜,问共有几种的搭配方法? 2×2=4(种)(3)4个男同学和3个女同学进行乒乓球单打比赛,如果每个男同学和每个女同学都打1盘,一共要打几盘?4×3=12(盘)例2.(1)花花有1件白上衣,1条黄裤子,1条蓝裤子,1双黑皮鞋和1双红皮鞋,花花参加活动时要求上衣、裤子和皮鞋全部配齐,花花共有多少种搭配方法? 1×2×2=4(种)(2)学校为艺术节选送节目,要从3个合唱节目中选出2个,2个舞蹈节目中选出1个。
一共有多少种选送方案?3×2=6(种)例3. 如图,从甲地到乙地有2条路可走,从乙地到丙地有3条路可走,从甲地到丙地共有4条不同的路可走,问从甲地到丙地共有多少种不同的走法?2×3+4=10(种)例4. 下图中,要读出“数学比赛”,共有多少种不同的读的顺序?数学 学比 比 比赛 赛 赛 赛 1×2×3×4=24(种)练 习:1. 学校二年级5个班举行班级排球比赛,规定每班与其它各班都赛1场。
问这次比赛一共要赛几场?4+3+2+1=10(场) 或5×4÷2=10(场)2. 要从某班数学学习优秀的甲、乙、丙、丁四个同学中选两个同学参加数学竞赛,有多少种不同的选法?3+2+1=6(种)3. 如图中有5个点、6条线段。
一只甲虫从A 点出发,要沿着某几条线段爬到D 点,行进中,同一点或同一条线段只能经过一次,这只甲虫最多有几种不同的走法? 2×2=4 (种)4. 小明和爸爸、妈妈看完演出后,每人都想和4位独唱演员各照一张合影。
请问一共要照多少张?4×3=12(张)5.如下图,从甲地到乙地有2条路,从乙地到丙地有4条路,从甲地到丁地有3条路,从丁地到丙地也有3条路,问:从甲地到丙地共有多少种不同的走法?2×4+3×3=17(种)。
二年级奥数第2讲:搭配问题-课件
12
3种
3
3种
3种
2+1=3(种) 3×3=9(种) 答:一共有9种不同的扎法。
练习五(选做)
为了让大家的伙食更丰富,芭啦啦综合教育学校食堂提
供了以下几种食物和水果,每个学生可以从中选择2种食物
和1种水果,有多少种不同的选择?
4种
3种
5种
2种
1种
4+3+2+1=10(种)
10×5=50(种)
答:有50种不同的选择。
5次 4次 3次 2次 1次
1
2
3
4
5
6
5+4+3+2+1=15(场) 答:一共要进行15场比赛。
小结
解决组合问题的主要方法是用列举法。 一般可以借助图形来描述,更加生动形象清 晰,并且不容易遗漏。
密码要求:
(1)是两位数。 (2)十位上的数字是3、4中的任意一个,个位上的数
字是2、5中的任意一个。 (3)必须要把组成的两位数全找齐了,才能通过密码。
搭配问题
例题一
阿派准备放学后回家换上运动鞋再去爬山,已知从学校 有2条路可以回家,从家有4条路可以去爬山。阿派有多少种 不同的走法? (学校、家、山的位置如下图)
学校
1 2
家
3
4 5 6
山
4种 4种
4×2=8(种) 答:阿派有8种不同的走法。
练习一
欧拉回乡下看望奶奶,从家到中转站有3种公交可以 选择,从中转站到奶奶家有2种公交可以选择,那么欧拉去 奶奶家有多少条不同的路线?
择孩
在子
冬是
天荷
开花
放,
选
择
在
三年级奥数搭配问题及解析

三年级奥数搭配问题及解析
在三年级的奥数学习中,搭配问题是一个重要的考点。
下面将介绍一些搭配问题及其解法。
1. 现在有5个红球、4个蓝球和3个绿球,请问从中任选两个球,有多少种不同的组合方式?
解析:总共有12个球,从中任选2个球的组合方式共有C(12,2) = 66种。
2. 小明有7本不同的书,他想从中选出3本,问有多少种不同的选法?
解析:小明从7本书中选出3本的选法共有C(7,3) = 35种。
3. 班级里有10个男生和8个女生,从中任选3个同学组成一个小组,请问有多少种不同的组合方式?
解析:首先从10个男生中选出1个同学,再从8个女生中选出2个同学,共有C(10,1) × C(8,2) = 280种组合方式。
4. 现在有4个小球,每个小球上写着一个不同的数字,从1到4。
请问从中任选2个小球,有多少种不同的组合方式?
解析:从4个小球中任选2个小球的组合方式共有C(4,2) = 6种。
5. 有5个小球,每个小球上写着一个不同的数字,从1到5。
请问从中任选3个小球,有多少种不同的组合方式?
解析:从5个小球中任选3个小球的组合方式共有C(5,3) = 10种。
以上是一些三年级奥数搭配问题及其解法,希望能对同学们的奥数学习有所帮助。
二年级奥数有趣的搭配带答案

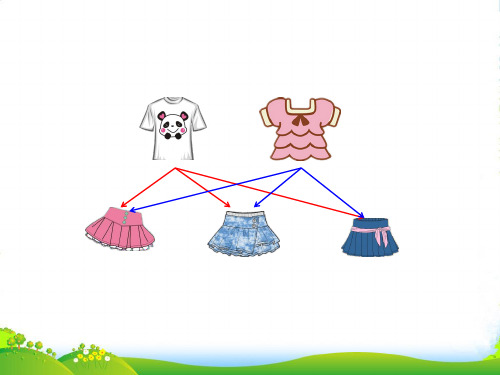
本讲我们将探索简单事物组合、排列的规律,培养有顺序地、全面地思考问题的意识.来看看最简单的搭衣服吧.上下装搭配的每种穿法需要两步来确定,一步是上装的选择,一步是下装的选择,一件上装搭配一件下装就是一种穿法.知识分类一:生活中的搭配小熊要穿衣服,它共有3件不同的上衣和4条不同的裤子.那么,小熊共有多少种不同的穿法?【提示】红色上衣可以和哪几条裤子搭配成一身衣服呢?用笔连一连.【解答】:3×4=12(种)答:小熊一共有12种穿法。
淘淘去餐厅点餐,看到菜单上写着,饮料有:可乐、橙汁;点心有:玉米、汉堡、薯条.如果饮料和点心只能各选一种,搭配成一份套餐,一共有多少种不同的搭配方法?【解答】:2×3=6(种)答:一共有6种不同的搭配方案。
知识分类二:路线问题小狗要去小猪家,必须经过小兔家,它一共有多少种不同的走法?【解答】:3×4=12(种)答:它一共有12种不同的走法。
丫丫从家到学校有3条路,从学校到少年宫有2条路,丫丫从家要到少年宫,中途必须经过学校,一共有多少种不同的走法?家少年宫学校【解答】:2×2=4(种)答:一共有4种不同的走法。
知识分类三:比赛和握手问题小明、小平、小丽、小花四个小朋友进行乒乓球单打比赛,要求每两个同学比赛一场,这次比赛一共要进行多少场?【解答】:3+2+1=6(种)答:这场比赛一共要进行6场。
白雪公主和7个小矮人在一起玩,每两个人都要握一次手,一共握了多少次手?【解答】:7+6+5+4+3+2+1=28(次)答:一共握了28次手。
体育课上,老师让小华去体育室拿3个球.体育室中有一个足球、一个篮球、一个排球和一个橄榄球.请问,小华共有多少种不同的拿法?【提示】当选好3个球之后,体育室中还剩余几个球?【解答】:4种。
跳跳的家里共有A、B、C、D、E这5盏吊灯.妈妈让跳跳关掉其中的4盏,请问,跳跳共有多少种不同的关灯方法?【解答】:5种。
知识分类四:搭配问题中的倒推法有一些游客去海边游玩,海边共停靠着7艘不同的快艇.如果这些游客要从中选出5艘快艇去游玩,那么共有多少种不同的选法?【提示】先把这7艘快艇编上序号吧!从7艘中选出5艘,那么会剩下几艘呢?【解答】:6+5+4+3+2+1=21(种)答:共有21种不同的选法熊老师有8个不同的礼物要奖励给6个优秀的学生(每人一个礼物),请问熊老师一共有多少种选法?【解答】:7+6+5+4+3+2+1=28(种)答:熊老师一共有28种选法。
四年级下册数学奥数教案-6 搭配问题(第二课时) 全国通用

师:说得非常好,那同学们你们知道选2本数学类的书,1本文学类的书有几种选法了吗?
生:6×3=18(种)
师:对,说说你是怎么想的?
生:数学类的2本可以是①②,①③,①④;②③,②④,③④,
那么如果①②,搭配一本文学类的书,分别为《鲁滨逊漂流记》、《安徒生童话》、《儿童文学》,共有3种;如果①③,搭配一本文学类的书,分别为《鲁滨逊漂流记》、《安徒生童话》、《儿童文学》,共有3种;……,共有6×3=18(种)。
答案:
(1)6+5+4+3+2+1=21(种)
答:乐乐想从中任选2本,共有21种选法。
教案
教材版本:实验
2课时
课 题
第6讲—搭配问题
教材分析
本讲的内容是合理搭配的问题,主要是让学生掌握通过示意图和列举来解决搭配问题,利用列举法计算要按照一定顺序才能保证不重不漏。
例1和例2较简单学生独立完,师适当提示。例3,例4需要学生分组协作完成。大胆闯关1,2,4的题目都是例题1,2,4的变式,采取小组积分的形式,学生自己独立完成,学生讲解教师适当引导
(1)学生独立完成,然后指定学生说说自己答案。
(2)师主意提示学生“互赠贺卡”最后要乘2。
5.托尼爷爷买了3件玩具,要送给卡卡、罗拉、小豆丁每人一件。其中卡卡想从智力拼图和积木中选一件,罗拉想从玩偶和积木中选一件。那么托尼爷爷送出这3件玩具共有多少种不同的方法?
师适当提示学生:
师:通过读题,你能发现什么呢?
教学难点:
如何把搭配原理迁移到其他类似的问题中去
教学准备
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
432 423
3 × 2 = 6 (种) 最大数是 432 ,最小数是 234
ቤተ መጻሕፍቲ ባይዱ
.
6
例2.用0、 1 、 2 、 3 能写出多少个不 同的四位数?其中最大的是多少?最小 的是多少?
1023 1032 1203 1230 1320 1302 2031 2013 2103 2130 2310 2301 3012 3021 3201 3210 3120 3102
可以组成 4 十 6 + 4 十 1 .二 15 (种)不同的币值1。1
6.要从某班数学学习优秀的 5 个同学中,选 出 4 个同学参加一次数学竞赛,间共有多少 种不同的选法?
ABC DE
ABCD BCDE CDEA
DEAB EABC
共5种
.
12
7.从甲地到乙地有 2 条路可走,从乙地到丙地有 3 条路可走,从丙地到丁地有 4 条路可走,试问 从甲地到丁地共有多少种不同的走法?
共有车票的种数是: 8×9 = 72 (种)。
.
14
例6. 有 6 个小朋友,要互相通一次电话, 你能算出,他们一共打了多少次电话?
【 思路分析 】我们把 6 个小朋友分别编号 :A、B、C、D、E、F。 A 应与其他小朋友打电话 5 次,这 5 次是 : A一B , A 一 C , A一D , A一E , A一F 。 同样, B 也应打 5 次电话, B 打的 5 次电话是: B一A , B一C , B一D , B一E , B一F 。
(3)以武汉为起点站,则终点站是(北京 )
(郑州 )(广州 ),有( 3 )种不同车票:
.
2
(4)以广州为起点站,则终点站是(北京) (郑州)(武汉),有( 3 )种不同车票:
( 5 )一个起点和一个终点间对应一种车票, 因此,这四个车站间的往返火车票共需( ) ×(3 ) = ( 4 )1(2种)不同的车票。
3×6=18(个)
最大数是 3210 ,最小数是 1023。
.
7
例3.用 3 、 0 、 0 、 5 四个数字可以组成 多少个不同的四位数?请你全部写出来?
可以组成 6 个不同的四位数,它们分别是:
3005 、 3050 、 3500 、 5003 、5030 、 5300 。
.
8
例4.小青有两件毛衣:一件黄的、一件白的; 她有 3 条裤子:一条蓝的、一条咖啡色的、 一条红的。算一算,要使她的毛衣和裤子有 不同的搭配,能有几种搭配方法?
2×3 = 6 (种)
因为上衣有两种不同的选择方法,裤 子有 3 种不同的选择方法。
.
9
4.四块不同颜色的木块:红、蓝、黄、白, 取出三块排成一横排,共有多少种不同的取 法?
以红色的作为第一块,可以排出: 3×2 =6 (种)不同的形式。 这四种颜色的木块都可作为第一块,而且 各种颜色作为第一块时都可以排出 6 种不 同形式。因此不同的取法共有:
.
3
1.5 个小朋友,互相握一次手,他 们共握多少次手?
4+3+2+1=10(次)
.
4
2.小英有 8 本不同的书, 小莉向她借 2 本,有几种 不同的借法?
7+6+5+4+3+2+1
=28(种)
.
5
3.用 2 、 3 、 4 能写出多少个不同的三位 数?其中最大的是多少?最小的是多少?
234 243 324 342
6×4 = 24 (种)。
.
10
5.有一张 10 元、一张 5 元、一张 2 元、一张 1 元的人民币,可以组成多少种不同的币值?
( 1)四张人民币就有四种币值: 1 元、 2 元、 5 元、 10 元。 ( 2 )每次取两张人民币,可以组成的币值有:
1 + 2 = 3 (元)、 1 + 5 二 6 (元)、 1 + 10 = 11 (元)、 2 + 5 = 7 (元)、 2 + 10 = 12 (元)、 5 + 10 = 15 (元) ; ( 3 )每次取 3 张人民币,可以组成的币值有: 1 + 2 + 5 = 8(元)、 2 + 5 + 10 = 17 (元)、 1 + 2 + 10 = 13 (元)、 l + 5 + 10 = 16 (元) ; ( 4 )每次取四张人民币,有一种币值: 1 + 2 十 5 + 10 = 18 (元)所以,
.
15
同样, C 、 D 、 E 、 F 也应该各打 5 次电话 。这样, 6 个小朋友,一共要打: 5 x6 = 30 (次)电话。但是,题目要求两个小朋 友之间只能通一次电话,当 A 打电话给 B 时( A -B ) , A 、 B 两人已通了一次电话, B 没有必 要再打电话给 A (去掉 B -A 这一次)。如果把 打电话的情况排列出来,我们就会发现,这 30 次 电话中,有一半是重复计算的。所以实际打电话的
2 × 3×4 = 24 (条)
.
13
例5. 从上海到南京有 9 个火车站(包括上海和 南京)。各火车站售票处要为这条路线准备几种不 同的火车票?(往返车票是不相同的。)
【 思路分析]我们假设这些火车站的编号分别是 1 号、 2 号、 3 号、 4 号、 5 号、 6 号、 7 号、 8 号、 9 号。那么 1 号站到其他车站的车票有8种。 如:1 一 2 , 1一 3 , 1一 4 , 1 一 5 , 1一 6 ,
1一 7 , 1一 8 , 1一 9 。同样, 2 号站到其他车站的车票也有 8 种。
如 2 ? 1 , 2 一 3 , 2 一 4 , 2一 5 , 2 一 6 , 2一 7 , 2一 8 , 2一 9 。(注意 1一 2 , 2一 1 的车票是 不相同的。)每个车站必须准备 8 种不同的车票。所以,
搭配问题
.
1
例1.北京到广州的火车如果只考虑京广铁路上 的北京、郑州、武汉、广州这 4 个车站,那么 这 4 个车站间的往返火车票共需多少种?这 4 个车站中,任何一个车站既可以作起点站也可以 作终点站。
( 1 )以北京为起点站,则终点站是(郑州 ) ( 武汉)(广州 ),有( 3)种不同的票;
( 2 )以郑州为起点站,则终点站是( 北京) (武汉 )(广州 ),有(3 )种不同车票:
次数是:
5 ×6 ÷ 2 = 15 (次)。
解: 5 ×6 ÷ 2 = 15 (次)
答:他们一共打了 15 次电话。
