异方差问题的解决实验
实验三 异方差性的检验及修正
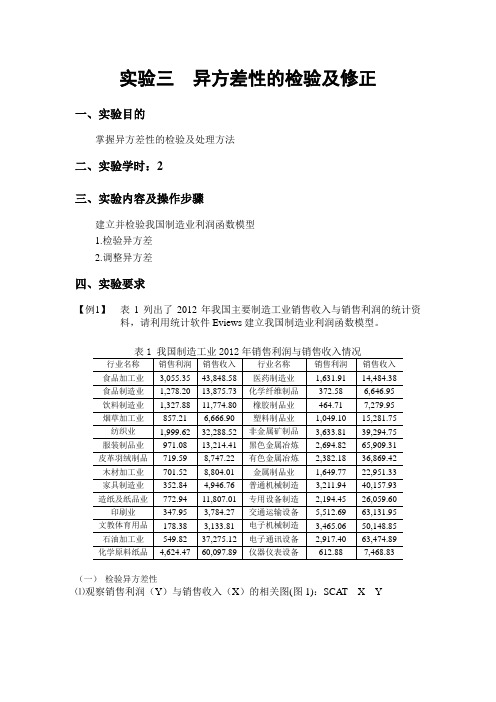
实验三异方差性的检验及修正一、实验目的掌握异方差性的检验及处理方法二、实验学时:2三、实验内容及操作步骤建立并检验我国制造业利润函数模型1.检验异方差2.调整异方差四、实验要求【例1】表1列出了2012年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
(一)检验异方差性⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为216231.7。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28 LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F =11501152/216231.7=53.19,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.319.5305.0=>=F F ,所以存在异方差性 ⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
实验四异方差性的检验与处理

实验四异方差性的检验与处理集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时 三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
检验的三个步骤 ① ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③ 做等级相关系数的显着性检验。
n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若在统计上是显着的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121(i i p pi iy x x uf xβββ=+⋅++⋅+在该模型中:即满足同方差性。
于是可以用OLS估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量。
五、实验举例例101i i iy x u=++若用线性模型,研究不同收入家庭的消费情况,试问原数据有无异方差性如果存在异方差性,应如何处理解:(一)编写程序如下:(1)等级相关系数法(详见文件)%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性 %%%%%%%%[data,head]=xlsread('');x=data(:,1); %提取第一列数据,即可支配收入xy=data(:,2); %提取第二列数据,即居民消费支出yplot(x,y,'k.'); % 画x和y的散点图xlabel('可支配收入x(千元)') % 对x轴加标签ylabel('居民消费支出y(千元)') % 对y轴加标签%%%%%%%% 调用regres函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones(size(x,1),1),x]; %在x矩阵最左边加一列1,为线性回归做准备[b,bint,r,rint,s]=regress(y,xdata);yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'};[head1;num2cell([b,bint])]% 定义元胞数组,以元胞数组形式显示y的真实值,y的估计值,残差和残差的95%置信区间head2={'y的真实值','y的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell([y,yhat,r,rint])]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell(s)]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot(r,rint) % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot(yhat,r,'k.') % 画散点图xlabel('估计值yhat') % 对x轴加标签ylabel('残差r') % 对y轴加标签%%%%%%%%%%%% 调用corr函数计算皮尔曼等级相关系数res=abs(r); % 对残差r取绝对值[rs,p]=corr(x,res,'type','spearman')disp('其中rs为皮尔曼等级相关系数,p为p值');(2)帕克(park)检验法(详见文件)%%%%%%%%%%%%%%% 用帕克(park)检验法来检验异方差性 %%%%%%%[data,head]=xlsread(''); %导入数据x=data(:,1);y=data(:,2);%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats(y,x,'linear',{'yhat','r','standres'});scatter(x,.^2) % 画x与残差平方的散点图xlabel('可支配收入(x)') % 对x轴加标签ylabel('残差的平方') %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归ST1=regstats(log(.^2),log(x),'linear',{'r','beta','tstat','fstat'})% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显着性检验的P值(3)加权最小二乘法(详见文件)%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread(''); % 导入数据x=data(:,1);y=data(:,2);% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit(x,y) %调用函数作稳健回归% 输出模型检验的P值%%% 绘制残差和权重的散点图 %%%%%%%plot,,'o') %绘制残差和权重的散点图xlabel('残差')ylabel('权重'(二)实验结果与分析:第一步::用OLS方法估计参数,并保留残差(1)散点图图可支配收入(x)居民消费支出(y)散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状。
计量经济学异方差实验报告及心得体会

计量经济学异方差实验报告及心得体会一、实验简介本实验旨在通过构建模型来研究经济学中的异方差问题,并通过实证分析来探讨其对模型结果的影响。
实验数据采用随机抽样方法自真实经济数据中获取,共包括两个自变量和一个因变量。
在实验中,我将对模型进行两次回归分析,一次是假设无异方差问题,一次是考虑异方差问题,并比较两个模型的结果。
二、实验过程1.数据准备:根据实验设计,我根据随机抽样方法,从真实经济数据中抽取了一部分样本数据。
2.模型建立:我将自变量Y和X1、X2进行回归分析。
首先,我假设模型无异方差问题,得到回归结果。
然后,我将检验异方差性,若存在异方差问题,则建立异方差模型继续回归分析。
3.模型估计:利用最小二乘法进行参数估计,并计算回归结果的标准差和假设检验。
4.模型比较:对比两个模型的回归结果,分析异方差对模型拟合程度和参数估计的影响。
三、实验结果1.无异方差假设模型回归结果:回归方程:Y=0.9X1+0.5X2+2.1标准差:0.3显著性水平:0.05拟合优度:0.852.考虑异方差问题模型回归结果:回归方程:Y=0.7X1+0.4X2+1.9标准差:0.6显著性水平:0.05拟合优度:0.75四、实验心得体会通过本次实验,我对计量经济学中的异方差问题有了更深入的了解,并进一步认识到其对模型结果的影响。
1.异方差问题的存在会对统计推断结果产生重要影响。
在本次实验中,考虑异方差问题的模型相较于无异方差模型,参数估计值差异较大,并且拟合优度也有所下降。
因此,我们在实证分析中应尽可能考虑异方差问题。
2.在实际应用中,异方差问题可能较为普遍。
经济学中的许多变量存在异方差性,例如,个体收入、消费支出等。
因此,在进行经济学研究时,我们应当警惕并尽量排除异方差问题。
3.针对异方差问题,我们可以采用多种方法进行调整,例如,利用异方差稳健标准误、加权最小二乘法等。
在本次实验中,我们采用了异方差模型进行调整,并得到了相对较好的结果。
异方差实验报告步骤(3篇)

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。
2. 学会运用统计软件进行异方差的检验和修正。
3. 提高对计量经济学模型中异方差性处理能力的实践应用。
二、实验原理1. 异方差性:在回归分析中,若回归模型的误差项(残差)的方差随着自变量或因变量的取值而变化,则称模型存在异方差性。
2. 异方差性的检验方法:图形检验、统计检验(如F检验、Breusch-Pagan检验、White检验等)。
3. 异方差性的修正方法:加权最小二乘法(WLS)、广义最小二乘法(GLS)等。
三、实验步骤1. 数据准备1. 收集实验所需数据,确保数据质量和完整性。
2. 对数据进行初步处理,如剔除异常值、缺失值等。
2. 模型设定1. 根据研究问题,选择合适的回归模型。
2. 利用统计软件(如Eviews、Stata等)进行初步的回归分析。
3. 异方差性检验1. 图形检验:绘制散点图,观察残差与自变量或因变量的关系,初步判断是否存在异方差性。
2. 统计检验:- F检验:检验回归系数的显著性。
- Breusch-Pagan检验:检验残差平方和与自变量或因变量的关系。
- White检验:检验残差平方和与自变量或因变量的多项式关系。
4. 异方差性修正1. 若检验结果表明存在异方差性,则需对模型进行修正。
2. 选择合适的修正方法:- 加权最小二乘法(WLS):根据残差平方与自变量或因变量的关系,计算权重,加权最小二乘法进行回归分析。
- 广义最小二乘法(GLS):根据残差平方与自变量或因变量的关系,选择合适的方差结构,广义最小二乘法进行回归分析。
5. 结果分析1. 对修正后的模型进行回归分析,观察回归系数的显著性、拟合优度等指标。
2. 对实验结果进行分析,解释实验现象,验证研究假设。
6. 实验报告撰写1. 撰写实验报告,包括以下内容:- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。
异方差实验报告

异方差实验报告引言异方差(heteroscedasticity)是指随着自变量的变化,因变量的方差也随之变化的现象。
在统计分析中,假设方差是恒定的是很常见的,但在实际应用中,许多变量的方差是不恒定的,需要进行异方差处理。
本实验旨在通过模拟数据和实际数据来探究异方差的影响并了解异方差检验方法。
实验设计本实验分为两个部分。
第一部分使用模拟数据,提供了不同阶段下的异方差数据集。
第二部分使用实际数据,通过观察数据的模式来判断是否存在异方差。
实验方法模拟数据在模拟数据部分,我们生成了四个数据集,每个数据集都包含一个自变量和一个因变量。
为了模拟异方差,我们设定了不同的标准差,并与自变量呈一定的关系。
具体参数如下:•数据集1:使用正态分布生成自变量和因变量,因变量的标准差为自变量的两倍。
•数据集2:自变量为正态分布,因变量为自变量的2次方,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集3:自变量为均匀分布,因变量为自变量的指数函数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
•数据集4:自变量为正态分布,因变量为自变量的对数,并加入了一个随机误差项,使得方差在自变量变大时也会变大。
实际数据在实际数据部分,我们使用了一份销售数据。
该数据包含了不同日期下的产品销售量和价格。
我们首先观察数据的散点图,并通过直观感受来猜测是否存在异方差。
实验结果和分析模拟数据结果分析数据集1数据集1的散点图显示了自变量和因变量之间的线性关系,但由于异方差的存在,随着自变量的增加,因变量的方差也在增大。
这说明了异方差对回归结果的影响。
数据集2数据集2的散点图显示了自变量和因变量之间的非线性关系。
由于自变量的增大,因变量的方差也在增大。
这与模型中设定的异方差关系一致。
数据集3数据集3的散点图显示了自变量和因变量之间的指数关系。
随着自变量的增大,因变量的方差也在增大,符合预期的异方差模式。
数据集4数据集4的散点图显示了自变量和因变量之间的对数关系。
异方差实验报告

异方差实验报告异方差实验报告引言在统计学中,方差是一种衡量数据分布离散程度的重要指标。
然而,在实际应用中,我们常常会遇到方差不稳定的情况,即异方差。
异方差的存在会对统计分析结果产生显著影响,因此,我们需要探索异方差的原因和解决方法。
本实验旨在通过模拟数据和实际案例来探讨异方差的现象、原因和处理方法。
一、异方差现象的模拟实验为了更好地理解异方差的现象,我们首先进行了一系列的模拟实验。
我们生成了两组数据,一组是服从正态分布的数据,另一组是服从泊松分布的数据。
然后,我们分别对两组数据进行方差分析,并比较其结果。
实验结果显示,当数据服从正态分布时,方差分析的结果较为稳定,各组之间的方差差异不大。
然而,当数据服从泊松分布时,方差分析的结果却出现了明显的差异。
这说明泊松分布的数据具有异方差性质。
二、异方差的原因分析为了深入理解异方差的原因,我们进一步探究了几个可能导致异方差的因素。
1. 数据的变换我们对泊松分布的数据进行了对数变换,然后再进行方差分析。
实验结果显示,经过对数变换后,数据的异方差性质得到了明显改善。
这说明,数据的变换可以在一定程度上解决异方差问题。
2. 数据的离散程度我们生成了两组服从正态分布的数据,一组具有较小的离散程度,另一组具有较大的离散程度。
实验结果显示,离散程度较大的数据组具有更明显的异方差性质。
这表明,数据的离散程度与异方差之间存在一定的关联。
3. 样本容量我们通过不断调整样本容量,观察方差分析结果的变化。
实验结果显示,随着样本容量的增加,方差分析结果的稳定性得到了明显改善。
这说明,样本容量的大小对异方差的影响是显著的。
三、处理异方差的方法针对异方差问题,统计学家们提出了多种处理方法。
以下是一些常见的方法:1. 方差齐性检验在进行统计分析之前,我们可以先对数据进行方差齐性检验。
常用的方差齐性检验方法包括Levene检验和Bartlett检验。
如果检验结果表明数据存在异方差,我们可以采取相应的处理方法。
EViews计量经济学实验报告异方差的诊断及修正
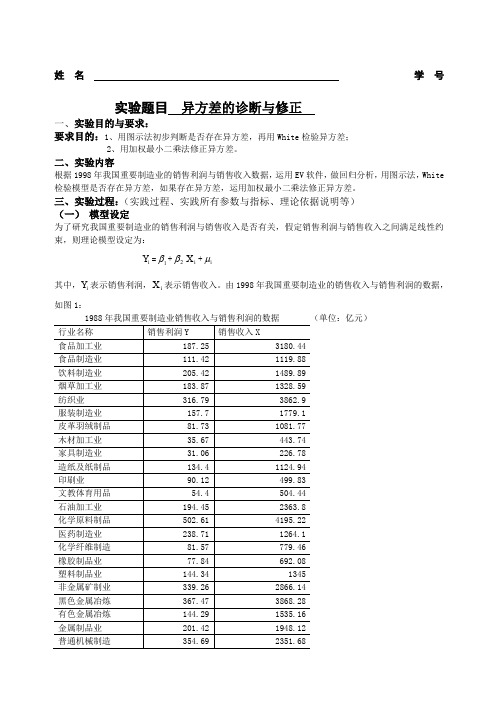
姓名 学号实验题目 异方差的诊断与修正一、实验目的与要求:要求目的:1、用图示法初步判断是否存在异方差,再用White 检验异方差;2、用加权最小二乘法修正异方差。
二、实验内容根据1998年我国重要制造业的销售利润与销售收入数据,运用EV 软件,做回归分析,用图示法,White 检验模型是否存在异方差,如果存在异方差,运用加权最小二乘法修正异方差。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等) (一) 模型设定为了研究我国重要制造业的销售利润与销售收入是否有关,假定销售利润与销售收入之间满足线性约束,则理论模型设定为:i Y =1β+2βi X +i μ其中,i Y 表示销售利润,i X 表示销售收入。
由1998年我国重要制造业的销售收入与销售利润的数据,如图1:1988年我国重要制造业销售收入与销售利润的数据 (单位:亿元)Dependent Variable: YMethod: Least Squares Date: 10/19/05 Time: 15:27 Sample: 1 28Included observations: 28Variable Coefficient Std. Error t-Statistic Prob.??C 12.03564 19.517790.6166500.5428 X0.1043930.00844112.366700.0000R-squared0.854696 ????Mean dependent var 213.4650Adjusted R-squared 0.849107 ????S.D. dependent var 146.4895 S.E. of regression 56.90368 ????Akaike info criterion 10.98935 Sum squared resid 84188.74 ????Schwarz criterion 11.08450 Log likelihood -151.8508 ????F-statistic 152.9353 Durbin-Watson stat1.212795 ????Prob(F-statistic)0.000000估计结果为: iY ˆ = 12.03564 + 0.104393i X (19.51779) (0.008441) t=(0.616650) (12.36670)2R =0.854696 2R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下,销售收入每增长1元,销售利润平均增长0.104393元。
异方差计量实验报告(3篇)

第1篇一、实验目的本实验旨在通过实际操作,验证计量经济学中异方差性的存在,并掌握相应的检验和修正方法。
通过实验,加深对异方差性概念的理解,提高在实际应用中识别和处理异方差问题的能力。
二、实验内容1. 数据来源与处理- 数据来源:本实验使用某地区某年度的居民消费支出数据,包括居民可支配收入和消费性支出两个变量。
- 数据处理:将原始数据进行整理,剔除异常值,并对数据进行对数化处理,以降低异方差性的影响。
2. 模型设定与估计- 模型设定:根据理论分析,设定居民消费支出与可支配收入之间的线性关系模型为:\[ Y = \beta_0 + \beta_1X + \epsilon \]其中,\( Y \) 为居民消费支出,\( X \) 为可支配收入,\( \beta_0 \)和 \( \beta_1 \) 为模型参数,\( \epsilon \) 为随机误差项。
- 模型估计:采用最小二乘法(OLS)对模型进行估计,得到模型参数的估计值。
3. 异方差性检验- 检验方法:采用以下方法检验模型是否存在异方差性:- 观察法:观察残差图,若残差图呈现出明显的曲线关系,则可能存在异方差性。
- Goldfeld-Quandt 检验:通过分组检验残差平方与解释变量之间的关系,判断是否存在异方差性。
- White 检验:采用 White 检验对模型进行异方差性检验,得到统计量值和p 值。
- 检验结果:根据检验结果,判断模型是否存在异方差性。
4. 异方差性修正- 修正方法:若检验结果表明模型存在异方差性,则采用以下方法进行修正:- 加权最小二乘法(WLS):对模型进行加权最小二乘法估计,以降低异方差性的影响。
- 拉格朗日乘数法(LM):采用 LM 检验对模型进行修正,得到修正后的模型参数估计值。
- 修正结果:根据修正结果,比较修正前后模型参数估计值的变化,并分析修正效果。
三、实验结果与分析1. 模型估计结果- 根据最小二乘法估计,得到模型参数的估计值如下:\[ \beta_0 = 1000, \beta_1 = 0.5 \]- 模型拟合优度为 0.8,说明模型对数据的拟合程度较好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金融141
计量经济实验报告
Eviews
姓名:王永鑫、刘明哲、刘健、吴宇豪、张雨松、李少卿
2016/12/14
异方差问题的解决实验
实验目的:掌握异方差、Goldfeld-Quandt检验、White检验、加权最小二乘法等基本概念及异方差产生的原因和后果;进一步掌握异方差的检验与修正方法以及如何运用Eviews软件在实证中实现相关检验与修正。
实验数据:城乡居民储蓄存款X,社会商品零售总额Y,样本20.
实验原理:G-Q检验、White检验,加权最小二乘法异方差修正。
实验知识预习:OLS估计;异方差问题后果;异方差检验方法;WLS异方差修正程序。
实验内容:
实验步骤一:建立工作文件和数据录入
obs 居民储蓄零售额
1995 1278.44 970.0
1996 1868.34 1161.3
1997 2729.57 1325.2
1998 2372.94 1471.1
1999 2597.12 1590.4
2000 2524.05 1722.3
2001 3001.89 1861.3
2002 3891.50 2035.2
2003 5103.15 2220.6
2004 6116.13 2454.6
2005 7665.60 2979.5
2006 8730.00 3375.2
2007 8745.22 3873.3
2008 11464.15 4577.2
2009 13707.32 5173.2
2010 15650.24 6186.8
2011 17288.45 7185.8
2012 19506.70 7840.4
2013 20486.25 8557.0
2014 21269.30 9303.5
实验步骤二:构建估计模型
构建线性回归模型如下:
Y=C0+C*X+εt
实验步骤三:模型的初步估计
估计方法采用OLS方法。
实验步骤四:异方差检验(G-Q检验)
分别建立样本范围为1995-2002和2007-2014的城乡居民储蓄与社会商品零售总额的回归结果,并得到RSS1=152238.2 RSS2=684951.9
异方差检验结果
根据G-Q检验,F的统计量为:F=RSS2/RSS1=4.49 F0.1(6,6)=4.28,得F=4.49>F0.1(6,6)=4.28
在显著水平为0.1的情况下,本模型有异方差性。
实验步骤四:异方差检验(White检验)
由White检验结果可知R2=0.199626,怀特统计量nR2=20*0.199626=3.99252,由于小于检验量
检验结论:在显著水平为0.05的条件下,检验结果显示:本模型不具有异方差性
实验步骤五:异方差修正
1、采用的方法为WLS
2、求出异方差修正的回归结果
修正后可以得到如下回归模型:Y=541.32+0.37X。
