Boost变换器的CCM小信号传递函数
反激变换器小信号模型Gvd(s)推导__1210

一、反激变换器小信号模型的推导 1.1 DCM1.1.1 DCM buck-boost 小信号模型的推导根据状态空间平均法推导DCM buck-boost 变换器小信号模型如下:+-v in (t)v o (t)一般开关网络图1 1理想Buck-Boost 变换器开关网络1231d d d ++= (1)首先,定义开关网络的端口变量1122,,,v i v i ,建立开关周期平均值1122,,,ssssT T T T v i v i 之间的关系:11()sg T g pk s s v t v i d T d T LL<>==(2)根据工作模态:113()()()0s s s L T g T T v t d v t d v t d <>=<>+<>+ (3)[]11()()()sss t T t T L T L s ttsssdi Lv t v d Ld i t T i t T T d T τττ++<>===+-⎰⎰(4) DCM 下,()()0s i t T i t +==,所以()0s L T v t <>=,结合(3)式:11()()0s s g T T d v t d v t <>+<>= (5)21()(t)=-(t)()s sg T T v t d d v t <><> (6)根据工作模态:1123()()0()(()())()()s s s s T g T T g T v t d t d t v t v t d t v t <>=+<>-<>+<>(7) 消去上式的2d 和3d 得:1()()s s T g T v t v t <>=<> (8)根据工作模态:2123()()(()())()0(())s s s s T g T T g T v t d t v t v t d t d v t <>=<>-<>++-<>(9)消去上式的2d 和3d 得:2()()s s T T v t v t <>=-<> (10)21111111()()()22ss s t T s T pk T tsd T i t i t d i v t T L+<>===<>⎰(11)于是输入端口的方程可表示为:111()()()ss T T e v t i t R d <><>= (12)1212()e sLR d d T =(13) 222111222212()()11()()22()()()ss s s s st T T T s T pk tsT e T v t v t d T i t i t d i T L v t R d v t +<><><>====<><>⎰(14)于是输出端口的输出功率可以表示为:21221()()()()s s s T T T e v t i t v t R d <><><>=(15)可见输出端口的输出功率等于输入端口的输入功率。
boost传递函数 交流小信号推导

看看确实推导过程都没写,不过确实因为推导太复杂了,要整理成word真不容易,开个手稿版的,其实都是按照张卫平那本书中的方法和步骤推导的,不过那本书中只对buck拓扑进行了推导,所以我真的没有抄哦。
由上面的两个式子就可以推导出Gvd(s)和Gid(s),过程就略过了,直接给出结果:而Gvg(s)和Gig(s)的推导则令交流小信号等效电路中d(s)微变量为零,即涉及到的电压源短路,电流源开路,同样根据变压器两边电压电流的关系可列出两个式子基本上,CCM模式的boost主回路Gvd(s)均可以套用这个公式,大家可以结合自己接触过的项目用mathcad绘制这个函数的波特图,对于主回路的传递函数其实有四个式子,这个当然是最关键的,因为是占空比到输出电压的传递函数,关于这个函数主要注意点是:品质因数Qc、ESR造成的零点和右半平面零点,明天再做具体分析。
最后一张图②中的交流小信号等效电路,那个方法不懂,麻烦楼主再讲一下为什么d'(t) < Vo(t) >Ts就分离为那四部分了?我也是按照那个书上《开关变换器的建模与控制》的方法来推导的,我的理解是那种分离方法是针对小信号扰动进行,其实就相当于用d'(t) < Vo(t) >Ts对t求导数,<Vo(t)>Ts指的是开关周期内输出电压的平均值,自然就是Vo了,d`(t)在开关周期内的平均值自然就是D`,该式对时间求一阶导数的话就是那四个分式啦不晓得有没有解释清楚其实你可以看看那本书,我推传递函数的方法和步骤基本都是按照那本书的方法进行的d'(t)<Vo(t)>Ts不就是d(t)<Vo(t)>Ts对时间t 求导了么?,还是说这里的d' 表示的和D‘差不多的意思?其实应该是(1-d(t))<Vo(t)>Ts对时间求导,所以式子中有很多匪夷所思的负号那个d(t)<vo(t)>Ts是平均分量表达式,然后把平均分量分解成直流分量与交流小信号分量之和。
14、boost变换器DCM小信号建模
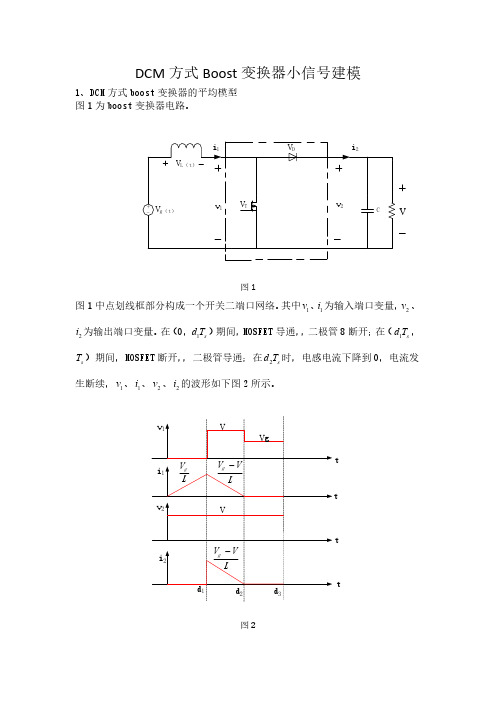
f1( v1(t) TS , v2 (t) TS , d (t))
将该式在静态工作点附近作泰勒级数展开得到:
I1 iˆ1
f1(V1,V2, D) vˆ1
f1 (v1 ,V2 dv1
,
D)
|v1 V1
vˆ2
f1(V1, v2 , dv2
D)
|v2
V2
dˆ (t )
f1 (V1 ,V2 dd
,
D)
|v2 V2
(M
1 1)2
Re
j1
df1(V1,V2, d ) dd
|d D
2MV1 D(M 1)2 Re
类似的,对输出端口作同样处理,输出端口方程为:
i2 (t)
TS
d12Ts 2L
*
v1(t) v2 (t) TS
2 TS
v1(t)
TS
f2 ( v1(t) TS , v2 (t) TS , d (t))
i1 (t )
TS
d12Ts 2L
*
v2 (t) TS v2 (t) TS
* v1(t) TS v1(t) TS
i2 (t)
TS
d12Ts 2L
*
v1(t) v2 (t) TS
2 TS
v1(t)
TS
首先引入扰动,即令
d (t) D d (t)
v1
(t
)
Ts
V1
v1
(t
)
iv12((tt))TTs sIV1 2i1v(t2)(t
j2
df2 (V1,V2 , d ) dd
|d D
2V1 D(M 1)Re
根据上式,DCM 方式下 boost 变换器的小信号模型如图 5 所示
Boost变换器阻抗特性及其稳定性分析

Boost变换器阻抗特性及其稳定性分析摘要:在以光伏发电单元为主微源的直流微电网中,光伏发电单元的阻抗特性及稳定性是研究的关键。
此处将Boost 变换器的输出阻抗作为研究对象,对连续导电模式(CCM)下的Boost 变换器进行小信号建模,得到变换器的开环输出阻抗。
对光伏发电单元采用电压下垂控制方式进行控制,分析了在该控制方式下变换器的闭环输出阻抗。
最后依据阻抗比判据,分析了线路中不同的寄生电容对光伏发电单元稳定性的影响,总结出规律性结论,对直流微电网进行稳定性分析,实验结果验证了上述理论分析的正确性。
关键词:微电网;下垂控制;稳定性分析1 引言为便于将分布式发电单元连接到电网上,出现了微电网的概念。
随着光伏电池成本降低,它已被作为主要的分布式发电单元而得到广泛应用。
由于光伏电池是直流源,因此在与电网及直流负载的连接中,直流微电网将成为最合适的构架。
为提高微电网冗余性和可靠性,将发电单元模块化已成为解决方案之一。
模块化后的发电单元的输入、输出阻抗将成为微电网的研究重点。
已有文献只是利用阻抗匹配准则对Buck 变换器在单电压闭环控制时的输出阻抗和稳定性进行分析,而未考虑发电单元的实际工作情况,故此处以光伏发电单元为背景,首先对光伏发电单元变换器进行小信号建模,求取其开环输出阻抗,其次引入电压下垂控制,分析了在该控制方式下微源变换器闭环输出阻抗,最后根据阻抗比禁止区判据对光伏发电单元的稳定性进行判断。
2 原理与设计图1 为所研究的直流微电网结构图,其微源包括光伏发电单元、蓄电池储能单元及负载。
其中光伏发电单元是直流微电网的主要发电单元,储能单元作为能量管理单元,在微电网孤岛运行模式下,调节微源与负载间的功率平衡。
当光伏发电。
反激变换器小信号模型Gvd(s)推导

一、反激变换器小信号模型的推导 1.1 DCM1.1.1 DCM buck-boost 小信号模型的推导根据状态空间平均法推导DCMbuck-boost 变换器小信号模型如下:+-v in (t)v o (t)一般开关网络图1 1理想Buck-Boost 变换器开关网络1231d d d ++=(1)首先,定义开关网络的端口变量1122,,,v i v i ,建立开关周期平均值1122,,,ssssT T T T v i v i 之间的关系:11()sg T g pk s s v t v i d T d T LL<>==(2)根据工作模态:113()()()0s s s L T g T T v t d v t d v t d <>=<>+<>+(3) []11()()()sss t T t T L T L s ttsssdi Lv t v d Ld i t T i t T T d T τττ++<>===+-⎰⎰(4) DCM 下,()()0s i t T i t +==,所以()0s L T v t <>=,结合(3)式:11()()0s s g T T d v t d v t <>+<>=(5) 21()(t)=-(t)()s sg T T v t d d v t <><>(6)根据工作模态:1123()()0()(()())()()s s s s T g T T g T v t d t d t v t v t d t v t <>=+<>-<>+<> (7) 消去上式的2d 和3d 得:1()()s s T g T v t v t <>=<>(8)根据工作模态:2123()()(()())()0(())s s s s T g T T g T v t d t v t v t d t d v t <>=<>-<>++-<>(9)消去上式的2d 和3d 得:2()()s s T T v t v t <>=-<>(10)21111111()()()22ss s t T s T pk T tsd T i t i t d i v t T L+<>===<>⎰(11)于是输入端口的方程可表示为:111()()()ss T T e v t i t R d <><>=(12)1212()e sLR d d T =(13) 222111222212()()11()()22()()()ss s s s st T T T s T pk tsT e T v t v t d T i t i t d i T L v t R d v t +<><><>====<><>⎰(14)于是输出端口的输出功率可以表示为:21221()()()()s s s T T T e v t i t v t R d <><><>=(15)可见输出端口的输出功率等于输入端口的输入功率。
PFC的数字设计总结

1 0.002424 3.3 1 电流环反馈系数: K i g cur _ sen g AD 0.24 0.0725 3.3 1 电压环反馈系数: K o g vo _ sen g AD 0.0066 0.002 3.3
前馈电压系数:
K in g vin _ sen g AD 0.008
根据假设①和②有
(7)
I in kVinVc
其中 k 为比例因子,与输入电压有效值有关,Vc 为电压控制器的输出。 在稳态条件下,定义电压增益 M 和输出阻抗 ro 为
(8)
Vo M V in r Vo o Io
(9)
联立(7),(8)两式,加入扰动项,并线性化参数,忽略高次项,可以得到以下 小信号方程:
函数时,可以得到
o ro // Z v gc 1 sCro // Z vc
根据假设④,负载 Z
Vo ro ,传函可以转化为: Io
(12)
Gvc ( s )
由(8)式,可以得到
iL K m
o v 1 gc c sC v
(13)
K in | vin | Vc K K I L in 2 m Vc 2 K i ( K ffVin ) K i K ff Vin
(2)电压环的设计
由(13)式,可知 PFC 的电压功率级电路的低频等效模型是一个电流源驱 动的电容器,可等效为一个积分器,它的增益特性在超过转折频率以上时,衰减 比例为 20dB,所以不加电压补偿电路系统也能稳定,但考虑到系统的电压环对 电流参考信号的影响,采用 PI 电压调节器,使电压环的带宽通常取 5~25Hz。
L
+
ˆ i
20170715-Buckboost变换器在电阻负载下的小信号传递函数
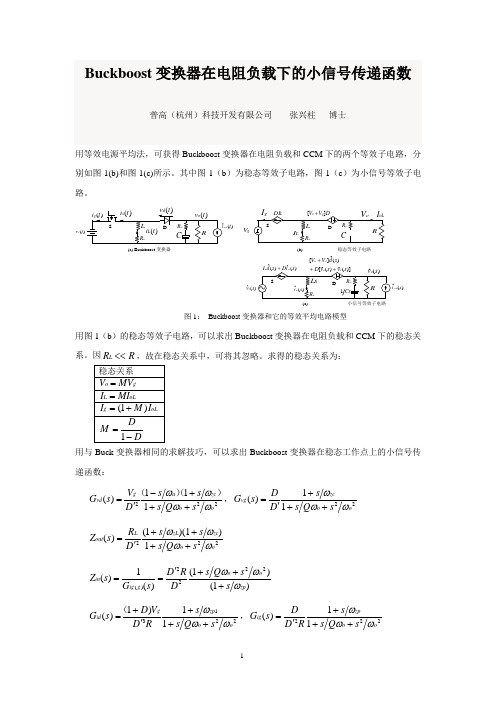
Buckboost 变换器在电阻负载下的小信号传递函数普高(杭州)科技开发有限公司 张兴柱 博士用等效电源平均法,可获得Buckboost 变换器在电阻负载和CCM 下的两个等效子电路,分别如图1(b)和图1(c)所示。
其中图1(b )为稳态等效子电路,图1(c )为小信号等效子电路。
)(t v g )(tgV(ˆs vg )(ˆ][s dV V g o +)(ˆs oL图1: Buckboost 变换器和它的等效平均电路模型用图1(b )的稳态等效子电路,可以求出Buckboost 变换器在电阻负载和CCM 下的稳态关系。
因R R L <<,故在稳态关系中,可将其忽略。
求得的稳态关系为:Buckboost 变换器在稳态工作点上的小信号传递函数:222111)(o o zc a g vd s Q s s s D V s G ωωωω+++−′=)()(,2211)(o o zc vg s Q s s D Ds Gωωω+++′= 2221)1)(1()(oo zc zL L out s Q s s s D R s Z ωωωω++++′=)1()1()(1)(2222)(zp o o g ig in s s Q s D R D s G s Z ωωω+++′== 221311)1)(o o zp g id s Q s s R D V D s G ωωω+++′+=(,22211)(oo zpig s Q s s R D D s G ωωω+++′=22111)(o o zcii s Q s s D s G ωωω+++′=其中:D D −=′1,LC D o ′=ω,])([122C D R R R D L Q L c o ′++′=ω,DL R D a 2′=ω L R L zL =ω,C R C zc 1=ω,RC zp 1=ω,RCD zp +=11ω有两个小信号传递函数,即)()(s G g id ,)()(s G g ii 没有给出,有兴趣的读者,可以作为作业自己去推导。
20170808-峰值电流型控制Boost等效功率级的小信号传递函数

峰值电流型控制Boost 等效功率级的小信号传递函数
普高(杭州)科技开发有限公司 张兴柱 博士
Boost 变换器在峰值电流型控制下的等效功率级小信号传递函数(CCM ): )
1)(1()1()1()(220n n p p zc a vc vc s Q s s s s G s G ωωωωω++++−′≈′ )1)(1()1)(1()(220
n n p p zc a vg vg s Q s s s s G s G ωωωωω++++′+′≈′ )
1()1()(0p zc out s s R s Z ωω++′≈′ 其中:10F D R R G i vc ′=′,120F F L RT G s vg =′,1
0F R R =′ 11F RC p =ω,L R D a 2′=ω,)5.0(1−′=D m Q c p π,C R c zc 1=ω,s
n T πω= a a D F ωω×′=′22,)]5.0(21[231−′+=c s m D L RT F ,]5.0[22−′+′′=D m RT D L D F c s
n e c S S m +=1,i g n R L
V S ×=
Boost 的峰值电流控制等效功率级小信号传递函数,与Buck 的差别是在控制电压到输出电压这个小信号传递函数中增加了一个右半平面零点,其它的特性很类似,但由于其极点数少了一阶,所以相比于电压型控制而言,它的补偿电路也是比较容易设计的。
1。
