高中数学试卷
2023-2024学年河北省部分高中高二(上)期中数学试卷【答案版】

2023-2024学年河北省部分高中高二(上)期中数学试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.直线l :2x +√3y −1=0的斜率为( ) A .−2√33B .−√32C .2√33D .√322.若方程x 2+y 2+4x +2y ﹣m =0表示一个圆,则m 的取值范围是( ) A .(﹣∞,﹣5)B .(﹣5,+∞)C .(﹣∞,5)D .(5,+∞)3.已知F 1,F 2分别是椭圆E :x 29+y 25=1的左、右焦点,P 是椭圆E 上一点,若|PF 1|=2,则|PF 2|=( )A .1B .2C .3D .44.如图,在三棱锥P ﹣ABC 中,P A ⊥平面ABC ,AB ⊥AC ,且PD →=3DC →,则BD →在AC →方向上的投影向量为( )A .34AC →B .−23AC →C .−34AC →D .23AC →5.若圆O 1:x 2+y 2=25与圆O 2:(x ﹣7)2+y 2=r 2(r >0)相交,则r 的取值范围为( ) A .[2,10]B .(2,10)C .[2,12]D .(2,12)6.若A (2,2,1),B (0,0,1),C (2,0,0),则点A 到直线BC 的距离为( ) A .2√305B .√305C .2√55D .√557.已知双曲线C :x 2a 2−y 2b2=1(a >0,b >0)的右焦点为F ,过F 作双曲线C 的其中一条渐近线l 的垂线,垂足为A (第一象限),并与双曲线C 交于点B ,若FB →=BA →,则l 的斜率为( ) A .2B .1C .12D .−748.已知实数x ,y 满足2x ﹣y +2=0,则√(x −9)2+y 2+√x 2+y 2−4x −4y +8的最小值为( ) A .3√13B .10+√13C .108D .117二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别是AB ,BC 的中点,则( )A .BC →−A 1A →=AD 1→B .BC →−A 1A →=2AD 1→C .EF →=12A 1C 1→D .EF →=A 1C 1→10.在同一直角坐标系中,直线l :y =mx +1与曲线C :x 2+my 2=1的位置可能是( )A .B .C .D .11.已知F 1,F 2分别是椭圆E :x 2a2+y 2b 2=1(a >b >0)的左、右焦点,P 是椭圆E 上一点,且|PF 1|=43|PF 2|,cos ∠PF 2F 1=35,则下列结论正确的有( ) A .椭圆E 的离心率为57B .椭圆E 的离心率为45C .PF 1⊥PF 2D .若△PF 1F 2内切圆的半径为2,则椭圆E 的焦距为1012.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两层等高的几何体,其中上层EFGH ﹣NPQM 是正四棱柱,下层底面ABCD 是边长为4的正方形,E ,F ,G ,H 在底面ABCD 的投影分别为AD ,AB ,BC ,CD 的中点,若AF =√5,则下列结论正确的有( )A .该几何体的表面积为32+8√2+4√6B .将该几何体放置在一个球体内,则该球体体积的最小值为36πC .直线CP 与平面ABF 所成角的正弦值为√63D .点M 到平面BFG 的距离为√63三、填空题:本题共4小题,每小题5分,共20分.13.已知点N 是点M (3,3,4)在坐标平面Oxz 内的射影,则|ON →|= . 14.若双曲线C :x 2m+1+y 2m 2−m−2=1的实轴长与虚轴长相等,则m = .15.过点M(√3,0)作圆C :x 2+(y ﹣1)2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为 .16.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,AM =2MB ,N 为DD 1的中点,记平面CMN 与平面ADD 1A 1的交线为l ,则直线l 与直线AC 1所成角的余弦值为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知直线l 1:x +ay ﹣a +2=0与l 2:2ax +(a +3)y +a ﹣5=0. (1)当a =1时,求直线l 1与l 2的交点坐标; (2)若l 1∥l 2,求a 的值.18.(12分)如图,在正四棱锥P ﹣ABCD 中,E ,F 分别为P A ,PC 的中点,DG →=2GP →. (1)证明:B ,E ,G ,F 四点共面.(2)记四棱锥P ﹣BEGF 的体积为V 1,四棱锥P ﹣ABCD 的体积为V 2,求V 1V 2的值.19.(12分)已知P 是圆C :x 2+y 2=12上一动点,过P 作x 轴的垂线,垂足为Q ,点M 满足PQ →=2PM →,记点M 的轨迹为E . (1)求E 的方程;(2)若A ,B 是E 上两点,且线段AB 的中点坐标为(−85,25),求|AB |的值.20.(12分)如图,这是某圆弧形山体隧道的示意图,其中底面AB 的长为16米,最大高度CD 的长为4米,以C 为坐标原点,AB 所在的直线为x 轴建立直角坐标系. (1)求该圆弧所在圆的方程;(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)21.(12分)如图,在斜三棱柱ABC ﹣A 1B 1C 1中,△ABC 是边长为2的等边三角形,M ,Q 分别为AC ,A 1B 1的中点,且MQ ⊥AB . (1)证明:MC 1⊥AB .(2)若BB 1=4,MQ =√15,求平面MB 1C 1与平面MC 1Q 夹角的余弦值.22.(12分)如图,已知F 1(−√10,0),F 2(√10,0)分别是双曲线E :x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点,P(−2√103,√63)是E 上一点. (1)求E 的方程.(2)过直线l :x =1上任意一点T 作直线l 1,l 1与E 的左、右两支相交于A ,B 两点.直线l 1关于直线l 对称的直线为l 2(与l 1不重合),l 2与E 的左、右两支相交于C ,D 两点.证明:∠ABD =∠ACD .2023-2024学年河北省部分高中高二(上)期中数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.直线l :2x +√3y −1=0的斜率为( ) A .−2√33B .−√32C .2√33D .√32解:将l 的方程转化为y =−2√33x +√33,则l 的斜率为−2√33. 故选:A .2.若方程x 2+y 2+4x +2y ﹣m =0表示一个圆,则m 的取值范围是( ) A .(﹣∞,﹣5)B .(﹣5,+∞)C .(﹣∞,5)D .(5,+∞)解:因为方程x 2+y 2+4x +2y ﹣m =0表示一个圆,所以42+22+4m >0,解得m >﹣5. 故选:B .3.已知F 1,F 2分别是椭圆E :x 29+y 25=1的左、右焦点,P 是椭圆E 上一点,若|PF 1|=2,则|PF 2|=( )A .1B .2C .3D .4解:椭圆E :x 29+y 25=1,可知a =3,因为P 是椭圆E 上一点,所以|PF 1|+|PF 2|=2a =6,所以|PF 2|=6﹣|PF 1|=4. 故选:D .4.如图,在三棱锥P ﹣ABC 中,P A ⊥平面ABC ,AB ⊥AC ,且PD →=3DC →,则BD →在AC →方向上的投影向量为( )A .34AC →B .−23AC →C .−34AC →D .23AC →解:因为P A ⊥平面ABC ,AB ⊥AC ,所以P A ⊥AB ,P A ⊥AC ,故以A 为坐标原点,AB ,AC ,P A 所在直线分别为x ,y ,z 轴建立空间直角坐标系,令AB =a ,AC =b ,P A =c ,则A (0,0,0),B (a ,0,0),C (0,b ,0),D(0,34b ,14c), 则AC →=(0,b ,0),BD →=(−a ,34b ,14c),所以BD →在AC →方向上的投影向量为AC →⋅BD →|AC →|⋅AC →|AC →|=34b 2|b|⋅AC →|b|=34AC →.故选:A .5.若圆O 1:x 2+y 2=25与圆O 2:(x ﹣7)2+y 2=r 2(r >0)相交,则r 的取值范围为( ) A .[2,10]B .(2,10)C .[2,12]D .(2,12)解:∵O 1与O 2相交, ∴|r ﹣5|<|O 1O 2|<|r +5|, 又|O 1O 2|=7,∴|r ﹣5|<7<|r +5|,解得2<r <12. 故选:D .6.若A (2,2,1),B (0,0,1),C (2,0,0),则点A 到直线BC 的距离为( ) A .2√305B .√305C .2√55D .√55解:由题意得,BA →=(2,2,0),BC →=(2,0,−1),则BA →在BC →上的投影向量的模为|BA →⋅BC →||BC →|=√5,则点A 到直线BC 的距离为√|BA →|2−(|BA →⋅BC →||BC →|)2=√(√8)2−(4√5)2=2√305. 故选:A .7.已知双曲线C :x 2a 2−y 2b2=1(a >0,b >0)的右焦点为F ,过F 作双曲线C 的其中一条渐近线l 的垂线,垂足为A (第一象限),并与双曲线C 交于点B ,若FB →=BA →,则l 的斜率为( )A .2B .1C .12D .−74解:由已知直线l 的方程为y =b ax ,即bx ﹣ay =0,点F (c ,0),则|FA|=|bc|√b +(−a)2=b ,因为FB →=BA →,所以B 为线段AF 的中点,则|BF|=b2, 设双曲线C 的左焦点为F 1,则|BF 1|=2a +b2, 在△BFF 1中,由余弦定理可得:cos ∠BFF 1=|BF|2+|FF 1|2−|BF 1|22|BF||FF 1|=b 24+4c 2−(2a+b 2)22×b2×2c=2b−ac, 又cos ∠BFF 1=bc ,所以a =b ,故l 的斜率为1, 故选:B .8.已知实数x ,y 满足2x ﹣y +2=0,则√(x −9)2+y 2+√x 2+y 2−4x −4y +8的最小值为( ) A .3√13B .10+√13C .108D .117解:√(x −9)2+y 2+√x 2+y 2−4x −4y +8=√(x −9)2+y 2+√(x −2)2+(y −2)2, 该式表示直线l :2x ﹣y +2=0上一点到P (9,0),Q (2,2)两点距离之和的最小值. 而P ,Q 两点在l 的同一侧,设点P 关于l 对称的点P ′(x 0,y 0),则{y 0−0x 0−9=−122×x 0+92−y 0+02+2=0,解得{x 0=−7y 0=8,∴P ′(﹣7,8),故√(x −9)2+y 2+√x 2+y 2−4x −4y +8≥|P′Q|=√(−7−2)+(8−2)2=3√13. 故选:A .二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别是AB ,BC 的中点,则( )A .BC →−A 1A →=AD 1→B .BC →−A 1A →=2AD 1→C .EF →=12A 1C 1→D .EF →=A 1C 1→解:BC →−A 1A →=AD →+AA 1→=AD 1→,A 正确,B 不正确,又因为EF →=12A 1C 1→,故C 正确,D 不正确. 故选:AC .10.在同一直角坐标系中,直线l :y =mx +1与曲线C :x 2+my 2=1的位置可能是( )A .B .C .D .解:A .取m =1,则直线l :y =x +1与曲线C :x 2+y 2=1满足图中的位置关系,因此A 正确; B .联立{y =mx +1x 2+my 2=1,化为(1+m 3)x 2+2m 2x +m ﹣1=0,若直线l :y =mx +1与曲线C :x 2+my 2=1有交点,则Δ=4m 4﹣4(1+m 3)(m ﹣1)=m 3﹣m +1>0. 由曲线C :x 2+my 2=1结合图形,则0<1m <1,∴m >1,满足Δ>0,因此B 正确;C .由曲线C :x 2+my 2=1结合图形,则0<1m <1,∴m >1,直线l 与椭圆应该有交点,因此C 不正确;D .由图可知:直线l 经过点(1,0),则m =﹣1,联立{y =−x +1x 2−y 2=1,化为x =1,y =0,即直线l 与双曲线的交点为(1,0),因此D 正确. 故选:ABD .11.已知F 1,F 2分别是椭圆E :x 2a2+y 2b 2=1(a >b >0)的左、右焦点,P 是椭圆E 上一点,且|PF 1|=43|PF 2|,cos ∠PF 2F 1=35,则下列结论正确的有( ) A .椭圆E 的离心率为57B .椭圆E 的离心率为45C .PF 1⊥PF 2D .若△PF 1F 2内切圆的半径为2,则椭圆E 的焦距为10解:A 、B 选项,由椭圆的定义得,|PF 1|+|PF 2|=2a ,已知|PF 1|=43|PF 2|,解得|PF 1|=87a ,|PF 2|=67a ,由cos ∠PF 2F 1=|PF 2|2+|F 1F 2|2−|PF 1|22|PF 2||F 1F 2|=4c 2−47a 2247ac=35, 整理得5a 2+18ac ﹣35c 2=0,即(a +5c )(5a ﹣7c )=0,则a =﹣5c (舍去)或a =75c ,即c a=57,故椭圆E 的离心率为57,故A 正确,B 不正确;C 选项,由a =75c ,得|F 1F 2|=2c =107a ,则|PF 1|2+|PF 2|2=|F 1F 2|2,故PF 1⊥PF 2,故C 正确; D 选项,由PF 1⊥PF 2,△PF 1F 2内切圆的半径为2,得2c =2a ﹣4,因为a =75c ,所以c =5,即椭圆E 的焦距为10,故D 正确. 故选:ACD .12.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两层等高的几何体,其中上层EFGH ﹣NPQM 是正四棱柱,下层底面ABCD 是边长为4的正方形,E ,F ,G ,H 在底面ABCD 的投影分别为AD ,AB ,BC ,CD 的中点,若AF =√5,则下列结论正确的有( )A .该几何体的表面积为32+8√2+4√6B .将该几何体放置在一个球体内,则该球体体积的最小值为36πC .直线CP 与平面ABF 所成角的正弦值为√63D .点M 到平面BFG 的距离为√63解:设F ,G 在平面ABCD 的投影分别为AB ,BC 的中点R ,S ,由于AF =√5,AB =4,所以F 到平面ABCD 的距离为FR =√AF 2−(12AB)2=1, 由于上、下两层等高,所以P 到平面ABCD 的距离为2,又FG =RS =12AC =2√2,由于GS =FR =1,BS =RB =12×4=2 所以BG =GC =√GS 2+BS 2=√5=BF =AF ,所以△AFB ≌△BGC ,同理可得△CDH ≌△ADE ≌△AFB ≌△BGC ,△BFG ≌△CHG ≌△DEH ≌△AEF , 则点B 到FG 的距离为√BF 2−(12FG)2=√(√5)2−(√2)2=√3,则△ABF 的面积为12AB ⋅FR =12×4×1=2,△BFG 的面积为12×2√2×√3=√6,故该几何体的表面积4×2+4×√6+4×4+2√2×2√2+2√2×4=32+8√2+4√6,故A 正确; 将该几何体放置在一个球体内,要使该球体体积最小,则球心在该几何体上下底面中心所连直线上, 且A 、B 、C 、D ,N 、P 、Q 、M 均在球面上,设球心到下底面ABCD 的距离为x , 由于四边形MNPQ 为边长为2√2的正方形,四边形ABCD 为边长为4的正方形, 则其对角线长度分别为4,4√2,则(2√2)2+x 2=22+(2−x)2,解得x =0,则该球体的半径为2√2,体积为4π3×(2√2)3=64√2π3,故B 错误;以A 为坐标原点建立如图所示的空间直角坐标系,则C (4,4,0),P (2,0,2),B (4,0,0),F (2,0,1),G (4,2,1),M (2,4,2),CP →=(−2,−4,2),BF →=(﹣2,0,1),BG →=(0,2,1),BM →=(﹣2,4,2), 平面ABF 的一个法向量为m →=(0,1,0),则cos <CP →,m →>=−42√6=−√63,设直线CP 与平面ABF 所成角为θ,则sinθ=|cos <CP →,m →>|=√63,故直线CP 与平面ABF 所成角的正弦值为√63,故C 正确; 设平面BFG 的法向量为n →=(x 1,y 1,z 1),则{n →⋅BF →=−2x 1+z 1=0n →⋅BG →=2y 1+z 1=0,令x 1=1,得n →=(1,﹣1,2), 则点M 到平面BFG 的距离为|n →⋅BM →||n →|=222=√63,故D 正确. 故选:ACD .三、填空题:本题共4小题,每小题5分,共20分.13.已知点N 是点M (3,3,4)在坐标平面Oxz 内的射影,则|ON →|= 5 . 解:由题可知,N (3,0,4),则ON →=(3,0,4),∴|ON →|=√32+42=5. 故答案为:5.14.若双曲线C :x 2m+1+y 2m 2−m−2=1的实轴长与虚轴长相等,则m = 1 .解:由题可知(m +1)+(m 2﹣m ﹣2)=0,解得m =1或m =﹣1(舍去),∴m =1. 故答案为:1.15.过点M(√3,0)作圆C :x 2+(y ﹣1)2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为 √3x −y =0 .解:圆C :x 2+(y ﹣1)2=1①,则圆心C (0,1), 以C (0,1),M (√3,0)为直径的圆的方程为:(x −√32)2+(y −12)2=1②,①﹣②可得,√3x −y =0,故直线AB 的方程为√3x −y =0. 故答案为:√3x −y =0.16.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,AM =2MB ,N 为DD 1的中点,记平面CMN 与平面ADD 1A 1的交线为l ,则直线l 与直线AC 1所成角的余弦值为7√111111.解:设I ∩AA 1=P ,连接NP ,MP ,直线NP 即为直线l .易证得MP ∥CN ,由AM =2MB ,N 为DD 1的中点,得AP =13AA 1,以D 为坐标原点,DA .DC ,DD 1所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,设AB =6,则得:N (0,0,3),P (6,0,2),A (6,0,0),C 1(0,6,6), NP →=(6,0,﹣1),AC 1→=(﹣6,6,6), 所以得:|cos <NP →,AC 1→>|=|NP →⋅AC 1→||NP →|⋅|AC 1→|=37×63=7√111111,故直线与直线 AC 1 所成角的余弦值为7√111111.故答案为:7√111111. 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知直线l 1:x +ay ﹣a +2=0与l 2:2ax +(a +3)y +a ﹣5=0. (1)当a =1时,求直线l 1与l 2的交点坐标; (2)若l 1∥l 2,求a 的值. 解:(1)因为a =1,所以l 1:x +y +1=0,l 2:2x +4y ﹣4=0,即x +2y ﹣2=0, 联立{x +y +1=0x +2y −2=0解得{x =−4y =3,故直线l 1与l 2的交点坐标为(﹣4,3).(2)因为l 1∥l 2,所以2a 2﹣a ﹣3=0,解得a =﹣1或a =32, 当a =﹣1时,l 1与l 2重合,不符合题意. 当a =32时,l 1与l 2不重合,符合题意. 故a =32.18.(12分)如图,在正四棱锥P ﹣ABCD 中,E ,F 分别为P A ,PC 的中点,DG →=2GP →. (1)证明:B ,E ,G ,F 四点共面.(2)记四棱锥P ﹣BEGF 的体积为V 1,四棱锥P ﹣ABCD 的体积为V 2,求V 1V 2的值.解:(1)证明:因为E ,F 分别为P A ,PC 的中点, 所以BE →=12BA →+12BP →,BF →=12BC →+12BP →, 所以BG →=BD →+DG →=BD →+23DP →=BD →+23(BP →−BD →)=13BD →+23BP →=13BA →+13BC →+23BP →=23(12BA →+12BP →)+23(12BC →+12BP →)=23BE →+23BF →, 故B ,E ,G ,F 四点共面;(2)由正四棱锥的对称性知,V 1=2V E ﹣PBG ,V 2=2V A ﹣PBD , 设点E 到平面PBG 的距离为d 1,点A 到平面PBD 的距离为d 2,由E 是P A 的中点得d 2=2d 1, 由DG →=2GP →得S △PBD =3S △PBG ,所以V 1V 2=V E−PBG V A−PBD=13S △PBG ⋅d 113S △PBD ⋅d 2=16.19.(12分)已知P 是圆C :x 2+y 2=12上一动点,过P 作x 轴的垂线,垂足为Q ,点M 满足PQ →=2PM →,记点M 的轨迹为E . (1)求E 的方程;(2)若A ,B 是E 上两点,且线段AB 的中点坐标为(−85,25),求|AB |的值. 解:(1)设M (x ,y ),则Q (x ,0), 因为PQ →=2PM →,则P (x ,2y ), 因为P 在圆C 上,所以x 2+(2y )2=12, 故E 的方程为x 212+y 23=1.(2)设A (x 1,y 1),B (x 2,y 2),若A ,B 是E 上两点,则{x 1212+y 123=1x 2212+y 223=1, 两式相减得x 12−x 2212+y 12−y 223=0,即y 1−y 2x 1−x 2=−x 1+x 24(y 1+y 2).因为线段AB 的中点坐标为(−85,25),所以y 1−y 2x 1−x 2=−x 1+x 24(y 1+y 2)=1,所以k AB =1,则直线AB 的方程为y =x +2.联立方程组{y =x +2x 212+y 23=1,整理得5x 2+16x +4=0,其中Δ>0, 则x 1+x 2=−165,x 1x 2=45, |AB|=√1+12√(x 1+x 2)2−4x 1x 2=4√225. 20.(12分)如图,这是某圆弧形山体隧道的示意图,其中底面AB 的长为16米,最大高度CD 的长为4米,以C 为坐标原点,AB 所在的直线为x 轴建立直角坐标系. (1)求该圆弧所在圆的方程;(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)解:(1)由圆的对称性可知,该圆弧所在圆的圆心在y轴上,由图形可得A(﹣8,0),B(8,0),D(0,4),设该圆的半径为r米,则r2=82+(r﹣4)2,解得r=10,圆心为(0,﹣6),故该圆弧所在圆的方程为x2+(y+6)2=100.(2)设与该种汽车等高且能通过该隧道的最大宽度为d米,则(d2)2+(6+1.6)2=102,解得d=2√42.24.若并排通过4辆该种汽车,则安全通行的宽度为4×2.5+3×0.5=11.5<2√42.24.隧道能并排通过4辆该种汽车;若并排通过5辆该种汽车,则安全通行的宽度为5×2.5+4×0.5=14.5>2√42.24,故该隧道不能并排通过5辆该种汽车.综上所述,该隧道最多可以并排通过4辆该种汽车.21.(12分)如图,在斜三棱柱ABC﹣A1B1C1中,△ABC是边长为2的等边三角形,M,Q分别为AC,A1B1的中点,且MQ⊥AB.(1)证明:MC1⊥AB.(2)若BB1=4,MQ=√15,求平面MB1C1与平面MC1Q夹角的余弦值.(1)证明:因为△A1B1C1是等边三角形,Q为A1B1的中点,所以C1Q⊥A1B1,又AB∥A1B1,所以C1Q⊥AB,因为MQ⊥AB,C1Q∩MQ=Q,所以AB⊥平面MC1Q,又MC1⊂平面C1MQ,所以MC1⊥AB;(2)解:取AB靠近点A的四等分点N,连接MN,NQ,易证得MN∥C1Q,则MN⊥AB,且MN=√32,由BB 1=4,得QN =3√72,因为MQ =√15,所以MQ 2+MN 2=QN 2, 即MQ ⊥MN ,又MQ ⊥AB ,从而MQ ⊥平面ABC ,以M 为坐标原点,MN 所在直线为x 轴,MQ 所在直线为z 轴,建立如图所示的空间直角坐标系,则M (0,0,0),B 1(0,1,√15),C 1(−√3,0,√15), 则MB 1→=(0,1,√15),MC 1→=(−√3,0,√15), 设平面MB 1C 1的法向量为m →=(x ,y ,z ),则有{m →⋅MB 1→=y +√15z =0m →⋅MC 1→=−√3x +√15z =0,令z =1,得m →=(√5,−√15,1),由图可知,n →=(0,1,0)是平面MC 1Q 的一个法向量,设平面MB 1C 1与平面MC 1Q 的夹角为θ,则cosθ=|m →⋅n →||m →||n →|=√1521=√357.22.(12分)如图,已知F 1(−√10,0),F 2(√10,0)分别是双曲线E :x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点,P(−2√103,√63)是E 上一点. (1)求E 的方程.(2)过直线l :x =1上任意一点T 作直线l 1,l 1与E 的左、右两支相交于A ,B 两点.直线l 1关于直线l 对称的直线为l 2(与l 1不重合),l 2与E 的左、右两支相交于C ,D 两点.证明:∠ABD =∠ACD .解:(1)∵F 1(−√10,0),F 2(√10,0)分别是双曲线E :x 2a 2−y 2b 2=1(a >0,b >0)的左、右焦点,P(−2√103,√63)是E 上一点,∴{a 2+b 2=10409a2−69b2=1,解得a 2=4,b 2=6,∴E 的方程为x 24−y 26=1.(2)证明:设T (1,m ),由题意得直线l 1的斜率存在且不等于0, 设直线l 的方程为y ﹣m =k (x ﹣1),则直线l 2的方程为y ﹣m =﹣k (x ﹣1), 设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),D (x 4,y 4), 联立方程组{y −m =k(x −1)x 24−y 26=1,整理得(3﹣2k 2)x 2+(4k 2﹣4km )x ﹣2k 2+4km ﹣2m 2﹣12=0,Δ=(4k 2﹣4km )2﹣(12﹣8k 2)(﹣2k 2+4km ﹣2m 2﹣12)=﹣72k 2﹣48km +24m 2+144>0, 则x 1+x 2=4k 2−4km 2k 2−3,x 1x 2=2k 2−4km+2m 2+122k 2−3,|AT |=√1+k 2|x 1−1|,|BT |=√1+k 2|x 2﹣1|,|CT |=√1+k 2|x 3﹣1|,|DT |=√1+k 2|x 4﹣1|, ∴|AT ||BT |=(1+k 2)|(x 1﹣1)(x 2﹣1)|=(1+k 2)|x 1x 2﹣(x 1+x 2)+1| =(1+k 2)|2k 2−4km+2m 2+122k 2−3−4k 2−4km 2k 2−3+1|=(1+k 2)|2m 2+92k 2−3|,同理,|CT ||DT |=(1+k 2)|2m 2+92k 2−3,∴|AT||DT|=|CT||BT|,∴△ACT ∽△DBT ,∴∠ABD =∠ACD .。
福建省部分优质高中2024-2025学年高二上学期第一次阶段性质量检测数学试卷

福建省部分优质高中2024-2025学年高二上学期第一次阶段性质量检测数学试卷一、单选题1.已知2b a c =+,则直线0ax by c ++=恒过定点( ) A .(1,2)- B .(1,2) C .(1,2)-D .(1,2)--2.已知两点()3,2A -,()2,1B ,过点()0,1P -的直线l 与线段AB (含端点)有交点,则直线l 的斜率的取值范围为( ) A .(][),11,-∞-+∞U B .[]1, 1-C .[)1,1,5⎛⎫-∞-⋃+∞ ⎪⎝⎭D .1,15⎡⎤-⎢⎥⎣⎦3.下列命题中正确的是( )A .点()3,2,1M 关于平面yOz 对称的点的坐标是()3,2,1--B .若直线l 的方向向量为()1,1,2e =-r ,平面α的法向量为()6,4,1m =-r,则l α⊥C .若直线l 的方向向量与平面α的法向量的夹角为120o ,则直线l 与平面α所成的角为30oD .已知O 为空间任意一点,A ,B ,C ,P 四点共面,且任意三点不共线,若12OP mOA OB OC =-+u u u r u u u r u u u r u u u r ,则12m =-4.已知{},,a b c r r r为空间的一个基底,则下列各组向量中能构成空间的一个基底的是( )A .a b +r r ,c b +r r ,a c -r rB .2a b +r r,b r ,a c -r r C .2a b +r r,2c b +r r ,a b c ++r r rD .a b +r r ,a b c ++r r r ,c r5.过点()1,4A 的直线在两坐标轴上的截距之和为零,则该直线方程为( ) A .30x y -+=B .50x y +-=C .40x y -=或50x y +-=D .40x y -=或30x y -+=6.如图,在平行六面体1111ABCD A B C D -中,底面ABCD 是菱形,侧面11A ADD 是正方形,且1120A AB ∠=︒,60DAB ∠=︒,2AB =,若P 是1C D 与1CD 的交点,则异面直线AP 与DC 的夹角的余弦值为( )A B C D 7.在棱长为2的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA ,1BB 的中点,G 为棱11A B 上的一点,且()102AG λλ=<<,则点G 到平面1D EF 的距离为( )A B C D 8.平面几何中有定理:已知四边形ABCD 的对角线AC 与BD 相交于点E ,且AC BD ⊥,过点E 分别作边AB ,BC ,CD ,DA 的垂线,垂足分别为1P ,2P ,3P ,4P ,则1P ,2P ,3P ,4P 在同一个圆上,记该圆为圆F .若在此定理中,直线AB ,BC ,AC 的方程分别为0x y -=,20x y +=,2x =,点()43,1P ,则圆F 的方程为( )A .()221252416x y ⎛⎫-+-=⎪⎝⎭B .()22113239x y ⎛⎫-+-= ⎪⎝⎭C .()221412416x y ⎛⎫-++= ⎪⎝⎭ D .()22125239x y ⎛⎫-++= ⎪⎝⎭二、多选题9.已知向量()1,1,0a =-r ,()1,0,1b =-r ,()2,3,1c =-r,则( ) A .6a b -=rr B .()()37a b b c +⋅+=r r rrC .()4a b c +⊥r r rD .()a b c -r rr ∥10.给出下列命题正确的是( )A .直线l 的方向向量为()3,1,2a =-r,平面α的法向量为12,1,2b ⎛⎫=- ⎪⎝⎭r ,则l 与α平行B .直线()()()1213m x m y m m -+-=-∈R 恒过定点()5,2-C .已知直线()2210a x ay ++-=与直线320ax y -+=垂直,则实数a 的值是43-D .已知,,A B C 三点不共线,对于空间任意一点O ,若212555OP OA OB OC =++u u u r u u u r u u u r u u u r,则,,,P A B C 四点共面11.如图,平行六面体1111ABCD A B C D -的所有棱长均为2,AB ,AD ,1AA 两两所成夹角均为60o ,点E ,F 分别在棱1BB ,1DD 上,且12BE B E =,12D F DF =,则( )A .A ,E ,1C ,F 四点共面B .1AA u u u r 在1AC uuu r 方向上的投影向量为113AC u u u urC .EF u u u rD .直线1AC 与EF三、填空题12.1:30l x y -+=,与直线2:220l x my +-=平行,则直线1l 与2l 的距离为.13.已知{},,a b c r r r是空间向量的一个基底,{},,a b a b c +-r r r r r 是空间向量的另一个基底,若向量p r 在基底{},,a b c r r r 下的坐标为()4,2,3,则向量p r在基底{},,a b a b c +-r r r r r 下的坐标为.14.“曼哈顿距离”是人脸识别中的一种重要测距方式,其定义如下:设()11,A x y ,()22,B x y ,则A ,B 两点间的曼哈顿距离()1212,d A B x x y y =-+-.已知()4,6M ,点N 在圆22:640C x y x y +++=上运动,若点P 满足(),2d M P =,则PN 的最大值为.四、解答题15.如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为矩形,且12,,AA AB AD E F ==分别为111,C D DD 的中点.(1)证明://AF 平面1A EB .(2)求平面11A B B 与平面1A BE 夹角的余弦值.16.已知ABC V 的顶点()1,2,A AB 边上的中线CM 所在直线的方程为210,x y ABC +-=∠的平分线BH 所在直线的方程为y x =. (1)求直线BC 的方程和点C 的坐标; (2)求ABC V 的面积.17.设直线1:230l x y -+=和直线2:30l x y ++=的交点为P .(1)若直线l 经过点P ,且与直线250x y ++=垂直,求直线l 的方程; (2)若直线m 与直线250x y ++=关于点P 对称,求直线m 的方程. 18.在空间几何体ABC DEF -中,四边形,ABED ADFC 均为直角梯形,π2FCA CAD DAB ABE ∠=∠=∠=∠=,4,5,6AB AC CF AD BE =====.(1)如图1,若π2CAB ∠=,求直线FD 与平面BEF 所成角的正弦值; (2)如图2,设π02CAB θθ⎛⎫∠=<< ⎪⎝⎭(ⅰ)求证:平面BEF ⊥平面DEF ;(ⅱ)若二面角E BF D --cos θ的值.19.已知圆C 经过坐标原点O 和点()2,2G -,且圆心C 在直线20x y +-=上. (1)求圆C 的方程;(2)设PA PB 、是圆C 的两条切线,其中,A B 为切点. ①若点P 在直线20x y --=上运动,求证:直线AB 经过定点; ②若点P 在曲线214y x =(其中4x >)上运动,记直线PA PB 、与x 轴的交点分别为 M N 、, 求PMN V 面积的最小值.。
2023年全国统一高考数学试卷(新高考II)(解析版)

2023年全国统一高考数学试卷(新高考Ⅱ)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共计40分。
每小题给出的四个选项中,只有一个选项是正确的。
请把正确的选项填涂在答题卡相应的位置上。
1.(5分)在复平面内,(1+3i)(3﹣i)对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解答】解:(1+3i)(3﹣i)=3﹣i+9i+3=6+8i,则在复平面内,(1+3i)(3﹣i)对应的点的坐标为(6,8),位于第一象限.故选:A.2.(5分)设集合A={0,﹣a},B={1,a﹣2,2a﹣2},若A⊆B,则a=( )A.2B.1C.D.﹣1【答案】B【解答】解:依题意,a﹣2=0或2a﹣2=0,当a﹣2=0时,解得a=2,此时A={0,﹣2},B={1,0,2},不符合题意;当2a﹣2=0时,解得a=1,此时A={0,﹣1},B={1,﹣1,0},符合题意.故选:B.3.(5分)某学校为了了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有( )A.种B.种C.种D.种【答案】D【解答】解:∵初中部和高中部分别有400和200名学生,∴人数比例为400:200=2:1,则需要从初中部抽取40人,高中部取20人即可,则有种.故选:D.4.(5分)若f(x)=(x+a)为偶函数,则a=( )A.﹣1B.0C.D.1【答案】B【解答】解:由>0,得x>或x<﹣,由f(x)是偶函数,∴f(﹣x)=f(x),得(﹣x+a)ln=(x+a),即(﹣x+a)ln=(﹣x+a)ln()﹣1=(x﹣a)ln=(x+a),∴x﹣a=x+a,得﹣a=a,得a=0.故选:B.5.(5分)已知椭圆C:的左焦点和右焦点分别为F1和F2,直线y=x+m与C交于点A,B两点,若△F1AB面积是△F2AB面积的两倍,则m=( )A.B.C.D.【答案】C【解答】解:记直线y=x+m与x轴交于M(﹣m,0),椭圆C:的左,右焦点分别为F1(﹣,0),F2(,0),由△F1AB面积是△F2AB的2倍,可得|F1M|=2|F2M|,∴|﹣﹣x M|=2|﹣x M|,解得x M=或x M=3,∴﹣m=或﹣m=3,∴m=﹣或m=﹣3,联立可得,4x2+6mx+3m2﹣3=0,∵直线y=x+m与C相交,所以Δ>0,解得m2<4,∴m=﹣3不符合题意,故m=.故选:C.6.(5分)已知函数f(x)=ae x﹣lnx在区间(1,2)上单调递增,则a的最小值为( )A.e2B.e C.e﹣1D.e﹣2【答案】C【解答】解:对函数f(x)求导可得,,依题意,在(1,2)上恒成立,即在(1,2)上恒成立,设,则,易知当x∈(1,2)时,g′(x)<0,则函数g(x)在(1,2)上单调递减,则.故选:C.7.(5分)已知α为锐角,cosα=,则sin=( )A.B.C.D.【答案】D【解答】解:cosα=,则cosα=,故=1﹣cosα=,即==,∵α为锐角,∴,∴sin=.故选:D.8.(5分)记S n为等比数列{a n}的前n项和,若S4=﹣5,S6=21S2,则S8=( )A.120B.85C.﹣85D.﹣120【答案】C【解答】解:等比数列{a n}中,S4=﹣5,S6=21S2,显然公比q≠1,设首项为a1,则=﹣5①,=②,化简②得q4+q2﹣20=0,解得q2=4或q2=﹣5(不合题意,舍去),代入①得=,所以S8==(1﹣q4)(1+q4)=×(﹣15)×(1+16)=﹣85.故选:C.二、选择题:本大题共小4题,每小题5分,共计20分。
河北省石家庄市2024届高三教学质量检测(三)数学试卷

石家庄市2024年普通高中学校毕业年级教学质量检测(三)数学(本试卷满分150分,考试时间120分钟)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数2ii z -=,则|z |=()A.B.C.3D.5【答案】B 【解析】【分析】根据复数的除法运算化简复数,再求复数的模长即可.【详解】由已知得2i (2i)i 2i 112i i i i 1z --+====--⨯-,所以z ==,故选:B.2.已知圆221:1C x y +=和圆2226890C x y x y +--+=:,则两圆公切线的条数为()A.1B.2C.3D.4【答案】C 【解析】【分析】根据圆与圆的位置关系求两圆圆心距及两圆半径,从而可判断两圆位置关系,即可得公切线条数.【详解】圆221:1C x y +=的圆心为()10,0C ,半径11r =,圆2226890C x y x y +--+=:的圆心()23,4C ,半径24r =,则12125C C r r ===+,故两圆外切,则两圆公切线的条数为3.故选:C.3.已知等差数列{}n a 的前n 项和为195,1,627n S a S a ==+,则5S =()A.25 B.27C.30D.35【答案】A 【解析】【分析】借助等差数列及其前n 项和的性质计算可得公差,结合等差数列求和公式计算即可得.【详解】设等差数列{}n a 的公差为d ,则有()()1117894262a a d a d ++⨯++=,又11a =,则()()62714914d d =⨯+++,解得2d =,则()511425252S ++⨯⨯==.故选:A.4.已知双曲线()2222:10,0y x C a b a b-=>>其上焦点到双曲线的一条渐近线的距离为3,则双曲线C 的渐近线方程为()A.y =B.33y x =±C.32y x =±D.233y x =±【答案】B 【解析】【分析】设双曲线()2222:10,0y x C a b a b-=>>的上焦点为(0,)c ,由题意可得3=,可求b ,由已知可求a ,可求渐近线方程.【详解】设双曲线()2222:10,0y x C a b a b-=>>的上焦点为(0,)c ,双曲线的渐近线方程为0by ax ±=,由点到直线的距离公式可得3b ===,又双曲线()2222:10,0y x C a b a b-=>>a =所以双曲线C 的渐近线方程为30y ±=,即3y x =±.故选:B.5.设,,αβγ是三个不同的平面,,m l 是两条不同的直线,则下列命题为真命题的是()A.若,,m l αβαβ⊥⊂⊥,则m l ∥B.若,,m l αβαβ⊂⊂ ,则m l∥C.若,,m l m αβαβ⊥⋂=⊥,则l β⊥ D.若,,l m l m αβγ⋂=⊥ ,则αγ⊥【答案】D 【解析】【分析】根据线面位置关系依次讨论各选项即可得答案.【详解】对于A 选项,若,,m l αβαβ⊥⊂⊥,则//l α或l ⊂α,无法确定m 与l 的关系,错误;对于B 选项,根据面面平行的性质定理,缺少m l ∥的条件,它们可能平行或异面,错误;对于C 选项,根据面面垂直的性质定理,缺少条件l ⊂α,,l β平行、相交或l β⊂均有可能,错误;对于D 选项,若,,l m l m αβγ⋂=⊥ ,则l γ⊥,由面面垂直的判定定理可得αγ⊥,正确.故选:D6.某项活动在周一至周五举行五天,现在需要安排甲、乙、丙、丁四位负责人值班,每个人至少值班一天,每天仅需一人值班,已知甲不能值第一天和最后一天,乙要值班两天且这两天必须相邻,则不同安排方法的种数为()A.24B.10C.16D.12【答案】D 【解析】【分析】分乙值前两天,乙值后两天及乙不值第一天和最后一天进行讨论即可得.【详解】若乙值前两天,则甲有两种选择,共有1222C A 4=,若乙值后两天,则甲有两种选择,共有1222C A 4=,若乙不值第一天和最后一天,共有1222C A 4=,共有44412++=种不同安排方法.故选:D .7.已知角,αβ满足()1tan ,2sin cos sin 3αβαβα==+,则tan β=()A.13B.16C.17D.2【答案】C 【解析】【分析】借助()βαβα=+-对已知化简,可求出()tan αβ+的值,再由()()tan tan βαβα=+-可解.【详解】因为()2sin cos sin βαβα=+,即()()2sin cos sin αβααβα⎡⎤+-=+⎣⎦,所以()()()2sin cos 2cos sin cos sin αβααβααβα+-+=+,整理得()()2sin cos 3cos sin αβααβα+=+,变形得()31tan tan 22αβα+==,所以()()()tan tan 1tan tan 1tan tan 7αβαβαβααβα+-⎡⎤=+-==⎣⎦++.故选:C8.已知抛物线2:8C y x =的焦点为F ,斜率为()0k k >的直线过F 与C 交于,P Q 两点,若FP FQ -=,则k 的值为()A.1B.C.2D.3【答案】C 【解析】【分析】设出直线方程,联立曲线后得到横坐标有关韦达定理,结合焦半径公式计算即可得解.【详解】由2:8C y x =可得()2,0F ,则():2PQ l y k x =-,()11,P x y ,()22,Q x y ,联立()228y k x y x⎧=-⎨=⎩,得()22224840k x k x k -++=,42421664641664640k k k k ∆=++-=+>,212224884k x x k k++==+,124x x =,由焦半径公式可得1122p FP x x =+=+,2222pFQ x x =+=+,则12FP FQ x x -=-=,则有21284422k x k ++==+,22284422k x k -+==+,21224254x x k ⎛⎫=+-= ⎪⎝⎭,解得2k =±,又0k >,故2k =.故选:C.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.某校“五一田径运动会”上,共有12名同学参加100米、400米、1500米三个项目,其中有8人参加“100米比赛”,有7人参加“400米比赛”,有5人参加“1500米比赛”,“100米和400米”都参加的有4人,“100米和1500米”都参加的有3人,“400米和1500米”都参加的有3人,则下列说法正确的是()A.三项比赛都参加的有2人B.只参加100米比赛的有3人C.只参加400米比赛的有3人D.只参加1500米比赛的有1人【答案】ABD 【解析】【分析】根据总人数和各个项目的人数,可求出三项比赛都参加的人数,从而可判定各选项.【详解】根据题意,设A ={x x 是参加100米的同学},B ={x x 是参加400米的同学},C ={x x 是参加1500米的同学},则()()()card 8,card 7,card 5,A B C ===且()()()card 4,card 3,card 3,A B A C B C === 则()()()card 128754332A B C ⎡⎤=-++-++=⎣⎦ ,所以三项比赛都参加的有2人,只参加100米比赛的有3人,只参加400米比赛的有2人,只参加1500米比赛的有1人.故选:ABD10.函数()()ππ4sin 02,22f x x ωϕωϕ⎛⎫=+<≤-<< ⎪⎝⎭的部分图象如图所示,则下列说法中正确的是()A.π6ϕ=-B.()f x 的图象关于直线πx =对称C.()12π4cos 23f x x ⎛⎫=- ⎪⎝⎭D.若方程()2f x =在()0,m 上有且只有5个根,则26π,10π3m ⎛⎤∈ ⎥⎝⎦【答案】ACD 【解析】【分析】根据图象可求得函数()f x 的解析式,再根据三角函数的性质依次判断各选项.【详解】对于A ,由()02f =-,得4sin 2ϕ=-,即1sin 2ϕ=-,又ππ22ϕ-<<,π6ϕ∴=-,故A 正确;对于C ,又()f x 的图象过点π,03⎛⎫⎪⎝⎭,则π03f ⎛⎫= ⎪⎝⎭,即ππsin 036ω⎛⎫-= ⎪⎝⎭,πππ36k ω∴-=,即得132k ω=+,k ∈Z ,又02ω<≤,12ω∴=,所以()1ππ12π12π4sin 4sin 4cos 2622323f x x x ⎛⎫⎛⎫⎛⎫⎛⎫=-=+-=- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭,故C 正确;对于B ,因为()1π4sin 26f x x ⎛⎫=-⎪⎝⎭,而()ππππ4sin 4sin 263f ⎛⎫=-== ⎪⎝⎭故直线πx =不是函数()f x 的对称轴,故B 错误;对于D ,由()2f x =,得12π1cos 232x ⎛⎫-=⎪⎝⎭,解得2π4πx k =+或2π4π3k +,Z k ∈,方程()2f x =在()0,m 上有5个根,从小到大依次为:2π14π26π,2π,,6π,333,而第7个根为10π,所以26π10π3m <≤,故D 正确.故选:ACD.11.如图,在棱长为2的正方体1111ABCD A B C D -中,M 为11B C 的中点,则下列说法正确的有()A.若点O 为BD 中点,则异面直线MO 与1CC 所成角的余弦值为5B.若点N 为线段BC 上的动点(包含端点),则MN DN +C.若点P 为CD 的中点,则平面AMP 与四边形11CDD C D.若点Q 在侧面正方形11ADD A 内(包含边界)且1MQ AC ⊥,则点Q 【答案】BD 【解析】【分析】取BC 中点E ,连接,,ME MO OE ,OME ∠为异面直线MO 与1CC 所成角,可判断A ;将侧面11BCC B 延BC 旋转至与平面ABCD 共面,根据两点间线段最短可判断B ;对于C ,如图以点D 为原点,以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系,取11A B 靠近1B 的四等分点,则可证明//MF AP ,判断C ;并确定点Q 的轨迹为直线1x z +=在正方形11ADD A 内的线段,判断D.【详解】对于A ,取BC 中点E ,连接,,ME MO OE ,则1//CC ME ,所以OME ∠为异面直线MO 与1CC 所成角,在Rt OEM △中,25cos 5ME OME OM ∠==,故A 错误;对于B ,将侧面11BCC B 延BC 旋转至与平面ABCD 共面,如图连接DM ,交BC 与点N ,此时MN DN +最小,且MN DN DM +===B 正确;对于C ,如图,以点D 为原点,以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系,则()()()2,0,0,0,1,0,1,2,2,A P M 因为平面//ABCD 平面1111D C B A ,所以平面AMP 与平面1111D C B A 的交线为过点M 且平行于AP 的直线,取11A B 靠近1B 的四等分点F ,连接FM ,并延长交11C D 于点S ,连接SP ,交1CC 于点T ,由32,,22F ⎛⎫⎪⎝⎭,所以()11,,0,2,1,02MF AP ⎛⎫=-=- ⎪⎝⎭ ,则12MF AP =-,则//MF AP ,所以MF 为平面AMP 与平面1111D C B A 的交线,则SP 为平面AMP 与平面11CDD C 的交线,所以TP 为平面AMP 与四边形11CDD C 的交线,由于11Rt Rt FB M SC M ≅ ,所以1112SC FB ==,又1Rt Rt SC T PCT ,所以43CT =,则53PT ==,故C 错误;对于D ,因为点Q 在侧面正方形11ADD A 内,设(),0,Q x z ,则()()12,2,2,1,2,2A C MQ x z =--=---,因为1MQ AC ⊥,所以()()214220x z -----=,化简为1x z +=,则点Q 的轨迹为直线1x z +=在正方形11ADD A,故D 正确.故选:BD【点睛】关键点睛:本题选项D 为空间动点轨迹的探索问题,解答本题的关键是利用空间直角坐标系探索出动点的轨迹.三、填空题:本题共3小题,每小题5分,共15分.12.为了解全市高三学生的体能素质情况,在全市高三学生中随机抽取了1000名学生进行体能测试,并将这1000名学生的体能测试成绩整理成如下频率分布直方图.则直方图中实数a 的值为______.【答案】0.015【解析】【分析】利用直方图直方块总面积为1,进行运算解出a 即可.【详解】由直方图可知:组距为10,所以()100.0050.0200.0400.0201a ⨯++++=,解得0.015a =.故答案为:0.015.13.给定函数()()21,f x x x g x x x=+=+,用()M x 表示()(),f x g x 中的较大者,记()()(){}max ,M x f x g x =.若函数()y M x =的图象与y a =有3个不同的交点,则实数a 的取值范围是______.【答案】()10,2,4⎛⎫+∞ ⎪⎝⎭【解析】【分析】在同一坐标系下画出()()21,f x x x g x x x=+=+的图象,求出交点坐标;结合图象再做出满足条件的直线y a =,进而求出a 的取值范围即可.【详解】由()()()2221010x x x x f x x x x x x ⎧+≤-≥⎪=+=⎨---<<⎪⎩或,()1g x x x =+,因为()()(){}max ,M x f x g x =,所以图象变为:其中()()2max1104x xx +=-≤≤,当且仅当12x =-时取最大值;且设两函数在第一象限的交点为P ,即当0,0x y >>,()()21f x x xg x x x ⎧=+⎪⎨=+⎪⎩,解得:()1,2P ,由题意y a =与函数()y M x =的图象有3个不同的交点,由数形结合易知:10a 4<<,或2a >,故答案为:()10,2,4∞⎛⎫⋃+ ⎪⎝⎭.14.已知数列{}n a 满足:12211,2,2n n n a a a a a ++==-=,定义:()mod4a b ≡表示整数a 除以4的余数与整数b 除以4的余数相同,例:()()19mod4,622mod4≡≡.设()()42,0mod4,123mod4kk k k a b k a ⎧⎪≡=⎨≡⎪⎩或或,其中*k ∈N ,数列{}n b 的前n 项和为n S ,则4b =______;满足2024m S ≥的m 最小值为______.【答案】①.2②.40【解析】【分析】由12211,2,2n n n a a a a a ++==-=,可得当n 为4的倍数时,n a 也是4的倍数,当n 不为4的倍数时,n a 也不是4的倍数,则得当k 是4的倍数时,42kk b =,当k 不是4的倍数时,k b k =,即可得4b ,取()*4n s s =∈N,计算出nS后,再计算40S 及39S 即可得解.【详解】由212n n n a a a ++-=,则3415a =+=,410212a =+=,则1a 、2a 、3a 都不是4的倍数,4a 是4的倍数,5432a a a =+,不是4的倍数,65443252a a a a a =+=+,不是4的倍数,76543434321042125a a a a a a a a a =+=+++=+,不是4的倍数,87643434322410522912a a a a a a a a a =+=+++=+,是4的倍数,依次可得当n 为4的倍数时,n a 也是4的倍数,当n 不为4的倍数时,n a 也不是4的倍数,由()()42,0mod4,123mod4kk k k a b k a ⎧⎪≡=⎨≡⎪⎩或或,则有当k 是4的倍数时,42kk b =,当k 不是4的倍数时,k b k =,则44422b ==;当()*4n s s =∈N,12123256722snS=+++++++++ ()212344222484s s s =+++++++++-+++ ()()()212144442122ss s s s -+⨯+=+--21221822222622s s s s s s s ++=++---=+-,当40n =,即10s =时,有14021610226002048226462024S =⨯+-=+-=>,01040394264622646102416222024S b S =-=-=-=<,故满足2024m S ≥的m 最小值为40.故答案为:2;40.【点睛】关键点点睛:本题关键点在于借助题意,得到当k 是4的倍数时,42kkb =,当k 不是4的倍数时,k b k =,从而可通过计算当()*4n s s =∈N 时的n S .四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC 中,角、、A B C 所对的边分别为,4,9a b c c ab ==、、.(1)若2sin 3C =,求sin sin A B ⋅的值;(2)求ABC 面积的最大值.【答案】(1)14(2)【解析】【分析】(1)根据正弦定理可得sin ,sin 66a bA B ==,从而可求sin sin A B ⋅的值;(2)利用基本不等式可得22218a b ab +≥=,再根据余弦定理可得cos C 的范围,从而可得sin C 的范围,结合三角形面积公式,即可得ABC 面积的最大值.【小问1详解】由正弦定理6sin sin sin c b a C B A ===,可得sin ,sin 66a bA B ==,91sin sin 66364a b A B ∴⋅=⋅==【小问2详解】9ab = ,22218a b ab ∴+≥=,由余弦定理可得2222161cos 2189a b c ab C ab +--=≥=,1cos 19C ∴≤<,()28001cos 81C ∴<-≤,0sin 9C ∴<≤,19sin sin 22S ab C C ∴==≤,当且仅当3a b ==时,等号成立,此时ABC 面积取得最大值16.在推动电子制造业高质量发展的大环境下,某企业统筹各类资源,进行了积极的改革探索.下表是该企业每月生产的一种核心产品的产量()315x x ≤≤(件)与相应的生产总成本y (万元)的四组对照数据.x57911y200298431609企业研究人员建立了y 与x 的两种回归模型,利用计算机算得近似结果如下:经验回归方程①:311733ˆx y =+;经验回归方程②:26860ˆ1yx =-.其中经验回归方程①的残差图如图所示(残差=观测值-预测值):(1)在下表中填写经验回归方程②的残差,根据残差分析,判断哪一个经验回归方程更适宜作为y 关于x 的回归方程,并说明理由;x57911y200298431609ˆe(2)从该企业在过去几年生产的该产品中随机抽取100件,优等品有60件,合格品有40件.每件优等品利润为20万元,每件合格品利润为15万元.若视频率为概率,该企业某月计划生产12件该产品,记优等品件数为X ,总利润为Y .(ⅰ)求Y 与X 的关系式,并求()E X 和()E Y ;(ⅱ)记该月的成本利润率p ,在(1)中选择的经验回归方程下,求p 的估计值.(结果保留2位小数)附:成本利润率=总利润总成本.【答案】(1)残差数据表见解析,经验回归方程①更适宜作为y 关于x 的回归方程(2)(ⅰ)1805Y X =+,()7.2E X =,()216E Y =;(ⅱ)0.29【解析】【分析】(1)先列出经验回归方程②的残差数据表以及经验回归方程②的残差图,对比回归方程①进行选择,并给出理由即可;(2)对于(ⅰ),先求出优等品的概率,分析得出()12,0.6X B ~,进而得出求Y 与X 的关系式,并解出()E X 和()E Y 即可;对于(ⅱ),由(ⅰ)知总利润为216万元,总成本估计值319ˆ12173743y =+=(万元),再求出p 的估计值即可.【小问1详解】经验回归方程②的残差数据如下表:x57911y200298431609ˆe 2018-21-21经验回归方程②的残差图如图所示:经验回归方程①更适宜作为y 关于x 的回归方程.(以下理由或其他合理的理由,说出一条即可得分):理由1:经验回归方程①这4个样本点的残差的绝对值都比经验回归方程②的小.理由2:经验回归方程①这4个样本的残差点落在的带状区域比经验回归方程②的带状区域更窄.理由3:经验回归方程①这4个样本的残差点比经验回归方程②的残差点更贴近x 轴.【小问2详解】(ⅰ)由题意知,每件产品为优等品的概率0600.6100P ==,则()12,0.6X B ~,因此()120.67.2E X =⨯=,由()2015125180Y X X X =+⨯-=+,则()()5180216E Y E X =+=;(ⅱ)由(ⅰ)知总利润为216万元,总成本估计值319ˆ12173743y =+=(万元),则2160.29749p =≈.17.已知函数()()()211ln 02f x x a x a x a =-++>.(1)讨论函数()f x 的单调性;(2)当2a =时,若函数()()211e 2x g x f x x -=-+,求函数()g x 极值点的个数.【答案】(1)答案见解析(2)2【解析】【分析】(1)求导得()()21x a x af x x'-++=,分类讨论当01a <<,1a >,1a =时分别确定导函数的符合从而得函数单调性即可;(2)求导得()12e 3x g x x --+'=,令()12e 3x h x x-=-+,求导确定其单调性与最值,从而可得()g x 的单调与极值情况.【小问1详解】()()()211x a x a a f x x a x x-++=-++='()()1,0x x a x x --=>,当01a <<时,当()()0,,1,x a x ∞∈∈+时,()()0,f x f x '>单调递增;当(),1x a ∈时,()()0,f x f x '<单调递减.当1a >时,当()()0,1,,x x a ∞∈∈+时,()()0,f x f x '>单调递增;当()1,x a ∈时,()()0,f x f x '<单调递减;当1a =时,()()0,f x f x '≥在()0,∞+单调递增.【小问2详解】2a =时,()()112e32ln ,e 3x x g x x x g x x--=-+-+'=,设()()()11222e3,e ,x x h x h x h x x x--=-+-''=在区间()0,∞+单调递增.因为()()1110,2e 02h h ''=-=-,所以存在唯一()01,2x ∈使得()00h x '=,当()00,x x ∈时,()()0,h x h x '<单调递减,即()g x '单调递减;当()0,x x ∞∈+时,()()0,h x h x '>单调递增,即()g x '单调递增.()10g '=,且()g x '在()01,x 单调递减,所以()00g x '<,又()2e 20g ='->因此()g x '在区间()0,2x 存在唯一零点t当()()0,1,,x x t ∞∈∈+时,()()0,g x g x '>单调递增;当()1,x t ∈时,()()0,g x g x '<单调递减;所以()g x 极值点为1,t ,因此()g x 极值点个数为2.18.如图,在五棱锥S ABCDE -中,平面SAE ⊥平面AED ,,AE ED SE AD ⊥⊥.(1)证明:SE ⊥平面AED ;(2)若四边形ABCD 为矩形,且1,3SE AB AD ===,2BN NC =.当直线DN 与平面SAD 所成的角最小时,求三棱锥D SAE -体积.【答案】(1)证明见解析(2)34【解析】【分析】(1)借助面面垂直的性质定理与线面垂直的判定定理推导即可得;(2)建立适当空间直角坐标系,借助空间向量可得当直线DN 与平面SAD 所成的角最小时EAD ∠的大小,结合体积公式计算即可得解.【小问1详解】因为平面SAE ⊥平面,,AED DE EA DE ⊥⊂平面AED ,平面SAE 平面AED AE =,所以DE ⊥平面SAE ,又SE ⊂平面SAE ,所以DE SE ⊥,又因为,SE AD ED AD D ⊥= ,且,AD DE ⊂平面AED ,所以SE ⊥平面AED ;【小问2详解】以E 为坐标原点,分别以,,EA ED ES 为,,x y z轴建立空间直角坐标系,设π0,2EAD θθ⎛⎫⎛⎫∠=∈ ⎪ ⎪⎝⎭⎝⎭,则()()()3cos ,0,0,0,3sin ,0,0,0,1A D S θθ,可得CD 与y 轴夹角为θ,所以()sin ,cos ,0DC θθ=,()1cos ,sin ,03CN DA θθ==-,()sin cos ,cos sin ,0DN DC CN θθθθ=+=+-,()()3cos ,0,1,0,3sin ,1SA SD θθ=-=- ,平面SAD 的法向量记为(),,n x y z =,由00n SA n SD ⎧⋅=⎪⎨⋅=⎪⎩,得3cos 03sin 0x z y z θθ-=⎧⎨-=⎩,令3sin cos z θθ=,得()sin ,cos ,3sin cos n θθθθ=,22cos ,DN n =,即26cos ,13DN n =,当π4θ=时,等号成立,此时,直线DN 与平面SAD 的所成的角取得最小值,此时119313344D SAE ADE V S SE -=⋅=⋅⋅= .19.已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为12(F F O 为坐标原点,直线l 与C 交于,A B 两点,点A 在第一象限,点B 在第四象限且满足直线OA 与直线OB 的斜率之积为14-.当l 垂直于x 轴时,1232F A F B =- .(1)求C 的方程;(2)若点P 为C 的左顶点且满足(0,0)OP OA OB λμλμ=+<<,直线PA 与OB 交于1B ,直线PB 与OA交于1A .①证明:22λμ+为定值;②证明:四边形11AB A B 的面积是AOB 面积的2倍.【答案】(1)2214x y +=(2)①证明见解析;②证明见解析【解析】【分析】(1)取l 垂直x 轴特殊情况研究,由直线OA 与直线OB 的斜率之积为14-,且1232F A F B ⋅=- 求出A 点坐标,再代入椭圆方程待定系数法求解即可;(2)①由OP OA OB λμ=+建立,,P A B 坐标之间关系,利用,,P A B 在椭圆上及直线OA 与直线OB 的斜率之积为14-消去1122,,,x y x y ,即可得证;②设()()()()1122133144,,,,,,,,:A x y B x y A x y B x y l x my n =+,利用韦达定理将直线OA 与直线OB 的斜率之积为14-表示出来即可得到,m n 的关系2224n m =+,再表示出AOB 面积11sin 2S OA OB AOB =⋅⋅∠,四边形11AB A B 的面积2111sin 2S A A B B AOB =⋅⋅∠;若要证212S S =,只需证112A A B B OA OB ⋅=⋅.转化为证明3142122y y y y y y -⋅-=⋅,由题将,y y 34用12,y y 表示,化简即可.【小问1详解】当l 垂直x 轴时,由直线OA 与直线OB 的斜率之积为14-,故11:,:22OA y x OB y x ==-,设()()()2,,2,0A t t B t t t ->,则22212343332F A F B t t t ⋅=--=-=- ,解得2t =,即22A ⎫⎪⎪⎝⎭,则222221123a b a b ⎧+=⎪⎨⎪-=⎩,解得224,1a b ==,故C 的方程为2214x y +=;【小问2详解】(2)①设()()()1122,,,,2,0A x y B x y P -,由OP OA OB λμ=+ 知121220x x y y λμλμ-=+⎧⎨=+⎩①②,将224+⨯①②得()()22121244x x y y λμλμ+++=,即()()()2222221122121244244xy x y x x y y λμλμ+++++=.由,A B 为C 上点,则2222112244,44x y x y +=+=.又直线OA 与直线OB 的斜率之积为14-,故121214y y x x =-,即121240x x y y +=.因此221λμ+=;②由题直线l 斜率不为0,设()()()1122:,,,,,2,0l x my n A x y B x y P =+-由①联立2244x y x my n⎧+=⎨=+⎩,消去x 得()()222224240,Δ1640m y mny n m n+++-==+->,212122224,44mn n y y y y m m -+=-=++,由()()12121212440x x y y my n my n y y +=+++=,即()()()()2212121212440my n my n y y m y y mn y y n +++=++++=,即2224n m =+.因此有()()22212121212122244,,42m n y y y y y y y y y y n n n-+=-=-=+-=.AOB 面积11sin 2S OA OB AOB =⋅⋅∠,四边形11AB A B 的面积2111sin 2S A A B B AOB =⋅⋅∠,即若要证212S S =,只需证112A A B B OA OB ⋅=⋅.设()()133144,,,A x y B x y ,故只需证3142122y y y y y y -⋅-=⋅即可.直线12122:2,:x xPA x y OB x y y y +=-=,联立解得()12124122212122222y y y y y x y y x y n y y y ==+--+,同理得()12123211121212222y y y y y x y y x y n y y y ==+--+.故()()()()()2222123142121212222212121224222482824n n y y n y y y y y y y y y y n n n y y n y y y y n n ++⋅--⋅-=⋅⋅=⋅⋅=⋅+-----+-+故问题得证.【点睛】关键点点睛:本题解题的关键是将212S S =表示为112A A B B OA OB ⋅=⋅后将同一直线上的弦长比值问题转化为纵坐标的比值问题,即证明3142122y y y y y y -⋅-=⋅,而,y y 34可以用12,y y 表示出来,从而达到消元化简的目的.。
2024年高中数学高考试卷

2024年高中数学高考试卷一、单项选择题(本题共8小题,每小题5分,共40分)1. 设集合A = {xx^2 - 3x + 2 = 0},B={xx>1},则A∩ B = (_ )A. {1}B. {2}C. {1,2}D. varnothing2. 复数z=(2i)/(1 - i)(i为虚数单位)的共轭复数¯z=(_ )A. -1 - iB. -1 + iC. 1 - iD. 1 + i3. 已知向量→a=(1,2),→b=(x,1),若→a⊥→b,则x = (_ )A. -2B. -(1)/(2)C. (1)/(2)D. 24. 函数y = sin(2x+(π)/(3))的最小正周期是T = (_ )A. πB. 2πC. (π)/(2)D. (2π)/(3)5. 在等差数列{a_n}中,a_1 = 1,d = 2,则a_10=(_ )A. 19B. 20C. 21D. 226. 若log_a2(a>0且a≠1),则a的取值范围是(_ )A. (0,1)B. (1,+∞)C. (0,2)D. (2,+∞)7. 从5名男生和3名女生中选3人参加某项活动,要求至少有1名女生,则不同的选法有(_ )种。
A. 46B. 56C. 64D. 728. 已知双曲线frac{x^2}{a^2}-frac{y^2}{b^2} = 1(a>0,b>0)的一条渐近线方程为y=(3)/(4)x,则双曲线的离心率e = (_ )A. (5)/(4)B. (5)/(3)C. (√(7))/(2)D. (√(7))/(3)二、多项选择题(本题共4小题,每小题5分,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分)9. 下列函数中,在区间(0,+∞)上单调递增的是(_ )A. y = x^(1)/(2)B. y=ln xC. y = 2^xD. y=(1)/(x)10. 已知函数f(x)=Asin(ω x+φ)(A>0,ω>0,φ<(π)/(2))的部分图象如图所示,则(_ )A. A = 2B. ω = 2C. φ=(π)/(6)D. f(x)的图象关于直线x=(π)/(3)对称。
2024年高考数学真题试卷(天津卷)附详细解答
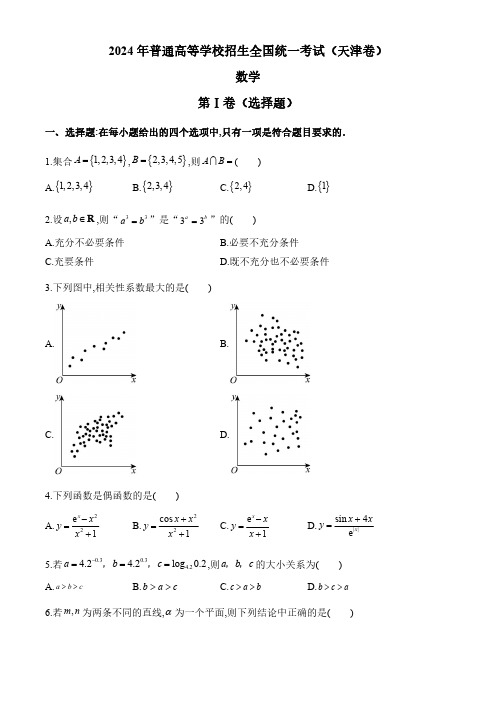
2024年普通高等学校招生全国统一考试(天津卷)数学第Ⅰ卷(选择题)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A.{}1,2,3,4 B.{}2,3,4 C.{}2,4 D.{}12.设,a b ∈R ,则“33a b =”是“33a b =”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.下列图中,相关性系数最大的是()A. B.C. D.4.下列函数是偶函数的是()A.22e 1x x y x -=+ B.22cos 1x x y x +=+ C.e 1x x y x -=+ D.||sin 4e x x x y +=5.若0.30.3 4.24.2 4.2log 0.2a b c -===,,,则a b c ,,的大小关系为()A.a b c>> B.b a c>> C.c a b>> D.b c a>>6.若,m n 为两条不同的直线,α为一个平面,则下列结论中正确的是()A.若//m α,n ⊂α,则//m nB.若//,//m n αα,则//m nC.若//,αα⊥m n ,则m n⊥ D.若//,αα⊥m n ,则m 与n 相交7.已知函数()()πsin303f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π.则函数在ππ,126⎡⎤-⎢⎥⎣⎦的最小值是()A.32-B.32-C.0D.328.双曲线22221()00a x y a bb >-=>,的左、右焦点分别为12.F F P 、是双曲线右支上一点,且直线2PF 的斜率为2.12PF F △是面积为8的直角三角形,则双曲线的方程为()9.一个五面体ABC DEF -.已知AD BE CF ∥∥,且两两之间距离为1.并已知123AD BE CF ===,,.则该五面体的体积为()A.6B.33142+ C.32D.33142-第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.10.已知i 是虚数单位,复数))i 2i ⋅=______.11.在63333x x⎛⎫+ ⎪⎝⎭的展开式中,常数项为______.12.22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为______.13.,,,,A B C D E 五种活动,甲、乙都要选择三个活动参加.(1)甲选到A 的概率为______;已知乙选了A 活动,他再选择B 活动的概率为______.14.在边长为1的正方形ABCD 中,点E 为线段CD 的三等分点,1,2CE DE BE BA BC ==+uur uur uuu r λμ,则λμ+=______;若F 为线段BE 上的动点,G 为AF 中点,则AF DG ⋅的最小值为______.15.若函数()21f x ax =--+有唯一零点,则a 的取值范围为______.三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在ABC 中,92cos 5163a Bbc ===,,.(1)求a ;(2)求sin A ;(3)求()cos 2B A -.17.已知四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,1A A ⊥平面ABCD ,AD AB ⊥,其中12,1AB AA AD DC ====.N 是11B C 的中点,M 是1DD 的中点.(1)求证1//D N 平面1CB M ;(2)求平面1CB M 与平面11BB CC 的夹角余弦值;(3)求点B 到平面1CB M 的距离.18.已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =.左顶点为A ,下顶点为B C ,是线段OB 的中点,其中ABC S =△.(1)求椭圆方程.(2)过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ,.在y 轴上是否存在点T 使得0TP TQ ⋅≤ 恒成立.若存在求出这个T 点纵坐标的取值范围,若不存在请说明理由.19.已知数列{}n a 是公比大于0的等比数列.其前n 项和为n S .若1231,1a S a ==-.(1)求数列{}n a 前n 项和n S ;(2)设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩,11b =,其中k 是大于1的正整数.(ⅰ)当1k n a +=时,求证:1n k n b a b -≥⋅;(ⅱ)求1nS i i b =∑.20.设函数()ln f x x x =.(1)求()f x 图象上点()()1,1f 处的切线方程;(2)若()(f x a x ≥-在()0,x ∞∈+时恒成立,求a 的取值范围;(3)若()12,0,1x x ∈,证明()()121212f x f x x x -≤-.2024年普通高等学校招生全国统一考试(天津卷)数学答案解析一、选择题.1.【答案】B【解析】因为集合{}1,2,3,4A =,{}2,3,4,5B =所以{}2,3,4A B = 故选:B 2.【答案】C【解析】根据立方的性质和指数函数的性质,33a b =和33a b =都当且仅当a b =,所以二者互为充要条件.故选:C.3.【答案】A【解析】观察4幅图可知,A 图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较好,呈现明显的正相关,r 值相比于其他3图更接近1.故选:A 4.【答案】B【解析】对A,设()22e 1x x f x x -=+,函数定义域为R ,但()112e 1f ---=,()112e f -=,则()()11f f -≠,故A 错误;对B,设()22cos 1x x g x x +=+,函数定义域为R 且()()()()()2222cos cos 11x x x x g x g x x x -+-+-===+-+,则()g x 为偶函数,故B 正确;对C,设()e 1x xh x x -=+,函数定义域为{}|1x x ≠-,不关于原点对称,则()h x 不是偶函数,故C 错误;对D,设()||sin 4e x x x x ϕ+=,函数定义域为R,因为()sin141e ϕ+=,()sin141eϕ---=则()()11ϕϕ≠-,则()x ϕ不是偶函数,故D 错误.故选:B.5.【答案】B【解析】因为 4.2x y =在R 上递增,且0.300.3-<<所以0.300.30 4.2 4.2 4.2-<<<所以0.30.30 4.21 4.2-<<<,即01a b <<<因为 4.2log y x =在(0,)+∞上递增,且00.21<<所以 4.2 4.2log 0.2log 10<=,即0c <所以b a c >>故选:B 6.【答案】C【解析】对于A,若//m α,n ⊂α,则,m n 平行或异面,故A 错误.对于B,若//,//m n αα,则,m n 平行或异面或相交,故B 错误.对于C,//,αα⊥m n ,过m 作平面β,使得s βα= 因为m β⊂,故//m s ,而s α⊂,故n s ⊥,故m n ⊥,故C 正确.对于D,若//,αα⊥m n ,则m 与n 相交或异面,故D 错误.故选:C.7.【答案】A【解析】()()πsin3sin 3πsin 33f x x x x ωωω⎛⎫=+=+=- ⎪⎝⎭,由2ππ3T ω==得23ω=即()sin2f x x =-,当,126⎡⎤∈-⎢⎣⎦ππx 时,ππ2,63x ⎡⎤∈-⎢⎥⎣⎦画出()sin2f x x =-图象,如下图由图可知,()sin2f x x =-在ππ,126⎡⎤-⎢⎥⎣⎦上递减所以,当π6x =时,()min πsin 32f x =-=-故选:A 8.【答案】C【解析】如下图:由题可知,点P 必落在第四象限,1290F PF ∠=︒,设2PF m=211122,PF F PF F θθ∠=∠=,由21tan 2PF k θ==,求得12sin 5θ=因为1290F PF ∠=︒,所以121PF PF k k ⋅=-,求得112PF k =-,即21tan 2θ=21sin 5θ=由正弦定理可得:121212::sin :sin :sin 902:1:5PF PF F F θθ=︒=则由2PF m =得1122,25PF m F F c m ===由1212112822PF F S PF PF m m =⋅=⋅= 得2m =则21122,2,210,10PF PF F F c c =====由双曲线第一定义可得:1222PF PF a -==222,8a b c a ==-=所以双曲线的方程为22128x y -=.故选:C 9.【答案】C【解析】用一个完全相同的五面体HIJ LMN -(顶点与五面体ABC DEF -一一对应)与该五面体相嵌,使得,D N ;,E M ;,F L 重合因为AD BE CF ∥∥,且两两之间距离为1.1,2,3AD BE CF ===则形成的新组合体为一个三棱柱该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为1322314+=+=+=2132211311422ABC DEF ABC HIJ V V --==⨯⨯⨯⨯=.故选:C.第Ⅱ卷二、填空题.10.【答案】7【解析】))i 2i 527+⋅=+-+=-.故答案为:7.11.【答案】20【解析】因为63333x x ⎛⎫+ ⎪⎝⎭的展开式的通项为()63636216633C 3C ,0,1,,63rr r r r r r x T x r x ---+⎛⎫⎛⎫===⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭令()630r -=,可得3r =所以常数项为0363C 20=.故答案为:20.12.【答案】45【解析】圆22(1)25-+=x y 的圆心为()1,0F ,故12p =即2p =由()2221254x y y x⎧-+=⎪⎨=⎪⎩可得22240x x +-=,故4x =或6x =-(舍)故()4,4A ±,故直线()4:13AF y x =±-即4340x y --=或4340x y +-=故原点到直线AF 的距离为4455d ==故答案为:4513.【答案】①.35②.12【解析】设甲、乙选到A 为事件M ,乙选到B 为事件N则甲选到A 的概率为()2435C 3C 5P M ==;乙选了A 活动,他再选择B 活动的概率为()()()133524351C 2C C P MN C P N M P M ===故答案为:35;1214.【答案】①.43②.518-【解析】因为12CE DE =,即23CE BA =uur uur ,则13BE BC CE BA BC =+=+uuu r uur u uu ur r uuu r 可得1,13λμ==,所以43λμ+=;由题意可知:1,0BC BA BA BC ==⋅= 因为F 为线段BE 上的动点,设[]1,0,13BF k BE k BA k BC k ==+∈ 则113AF AB BF AB k BE k BA k BC ⎛⎫=+=+=-+ ⎪⎝⎭又因为G 为AF 中点,则1111112232DG DA AG BC AF k BA k BC ⎛⎫⎛⎫=+=-+=-+- ⎪ ⎪⎝⎭⎝⎭可得11111113232AF DG k BA k BC k BA BC ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⋅=-+⋅-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 22111563112329510k k k k ⎛⎫⎛⎫⎛⎫=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又因为[]0,1k ∈,可知:当1k =时,AF DG ⋅ 取到最小值518-;15.【答案】()(1- 【解析】令()0f x =,即21ax =--由题可得20x ax -≥当0a =时,x ∈R ,有211=--=,则2x =±,不符合要求,舍去;当0a >时,则23,2121,ax x a ax ax x a ⎧-≥⎪⎪=--=⎨⎪-<⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩有唯一交点由20x ax -≥,可得x a ≥或0x ≤当0x ≤时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得)()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =时,即410x +=,即14x =-当()0,2a ∈,12x a =-+或102x a =>-(正值舍去)当()2,a ∈+∞时,102x a =-<+或102x a=<-,有两解,舍去即当(]0,2a ∈时,210ax -+=在0x ≤时有唯一解则当(]0,2a ∈时,210ax -+=在x a ≥时需无解当(]0,2a ∈,且x a ≥时由函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在12,a a ⎛⎫ ⎪⎝⎭上单调递减,在23,a a ⎛⎫ ⎪⎝⎭上单调递增令()g x y ==,即2222142a x y a a⎛⎫- ⎪-⎭=⎝故x a ≥时,()g x 图象为双曲线()222214y x a a-=右支的x 轴上方部分向右平移2a 所得由()222214y x a a -=的渐近线方程为22a y x xa =±=±即()g x 部分的渐近线方程为22a y x ⎛⎫=- ⎪⎝⎭,其斜率为2又(]0,2a ∈,即()23,21,ax x a h x ax x a⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a ≥时的斜率(]0,2a ∈令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a +∞上单调递增故有13aaaa ⎧<⎪⎪⎨⎪>⎪⎩,解得1a <<,故1a <<符合要求;当a<0时,则23,2121,ax x aax ax x a⎧-≤⎪⎪=--=⎨⎪->⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a⎧-≤⎪⎪=⎨⎪->⎪⎩有唯一交点由20x ax -≥,可得0x ≥或x a ≤当0x ≥时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得()()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =-时,即410x -=,即14x =当()2,0a ∈-,102x a =-<+(负值舍去)或102x a =-当(),2a ∈-∞时,102x a =->+或102x a =>-,有两解,舍去即当[)2,0a ∈-时,210ax --+=在0x ≥时有唯一解则当[)2,0a ∈-时,210ax --+=在x a ≤时需无解当[)2,0a ∈-,且x a ≤时由函数()23,21,ax x a h x ax x a ⎧-≤⎪⎪=⎨⎪->⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在21,a a ⎛⎫ ⎪⎝⎭上单调递减,在32,a a ⎛⎫ ⎪⎝⎭上单调递增同理可得:x a ≤时,()g x 图象为双曲线()222214y x a a -=左支的x 轴上方部分向左平移2a 所得()g x 部分的渐近线方程为22a y x ⎛⎫=-+ ⎪⎝⎭,其斜率为2-又[)2,0a ∈-,即()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a <时的斜率[)2,0a ∈-令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a -∞上单调递减故有13a a a a⎧>⎪⎪⎨⎪<⎪⎩,解得1a <<-,故1a <<-符合要求;综上所述,()(11,a ∈- .故答案为:()(1-⋃.三、解答题.16.【答案】(1)4(2)74(3)5764【小问1详解】设2,3a t c t ==,0t >,则根据余弦定理得2222cos b a c ac B=+-即229254922316t t t t =+-⨯⨯⨯,解得2t =(负舍);则4,6a c ==.【小问2详解】因为B 为三角形内角,所以57sin 16B ===再根据正弦定理得sin sin a b A B =,即4sin 5716A =,解得7sin 4A =【小问3详解】因为9cos 016B =>,且()0,πB ∈,所以π0,2B ⎛⎫∈ ⎪⎝⎭由(2)法一知57sin 16B =因为a b <,则A B <,所以3cos 4A ==则7337sin 22sin cos 2448A A A ==⨯⨯=,2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭()19573757cos 2cos cos 2sin sin 281616864B A B A B A -=+=⨯+⨯=.17.【答案】(1)证明见解析(2)22211(3)21111【小问1详解】取1CB 中点P ,连接NP ,MP由N 是11B C 的中点,故1//NP CC ,且112NP CC =由M 是1DD 的中点,故1111122D M DD CC ==,且11//D M CC 则有1//D M NP 、1D M NP=故四边形1D MPN 是平行四边形,故1//D N MP又MP ⊂平面1CB M ,1D N ⊄平面1CB M故1//D N 平面1CB M ;【小问2详解】以A为原点建立如图所示空间直角坐标系有()0,0,0A 、()2,0,0B 、()12,0,2B 、()0,1,1M 、()1,1,0C 、()11,1,2C 则有()11,1,2CB =- 、()1,0,1CM =- 、()10,0,2BB = 设平面1CB M 与平面11BB CC 的法向量分别为()111,,m x y z = 、()222,,n x y z = 则有111111200m CB x y z m CM x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ,1222122020n CB x y z n BB z ⎧⋅=-+=⎪⎨⋅==⎪⎩ 分别取121x x ==,则有13y =、11z =、21y =,20z =即()1,3,1m = 、()1,1,0n =则cos ,11m n m n m n ⋅===⋅ 故平面1CB M 与平面11BB CC 的夹角余弦值为22211;【小问3详解】由()10,0,2BB = ,平面1CB M 的法向量为()1,3,1m =则有111BB m m ⋅== 即点B 到平面1CB M 的距离为21111.18.【答案】(1)221129x y +=(2)存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.【小问1详解】因为椭圆的离心率为12e =,故2a c =,b =,其中c 为半焦距所以()()32,0,0,,0,2A c B C ⎛⎫-- ⎪ ⎪⎝⎭,故13332222ABC S c c =⨯⨯=△故c =所以a =,3b =,故椭圆方程为:221129x y +=.【小问2详解】若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率存在,则可设该直线方程为:32y kx =-设()()()1122,,,,0,P x y Q x y T t 由22343632x y y kx ⎧+=⎪⎨=-⎪⎩可得()223412270k x kx +--=故()222Δ144108343245760k k k =++=+>且1212221227,,3434k x x x x k k+==-++而()()1122,,,TP x y t TQ x y t =-=- 故()()121212123322TP TQ x x y t y t x x kx t kx t ⎛⎫⎛⎫⋅=+--=+---- ⎪⎪⎝⎭⎝⎭ ()()22121233122k x x k t x x t ⎛⎫⎛⎫=+-++++ ⎪ ⎪⎝⎭⎝⎭()22222731231342342k k k t t k k ⎛⎫⎛⎫⎛⎫=+⨯--+⨯++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭()2222222327271812332234k k k t t t k k ⎛⎫----++++ ⎪⎝⎭=+()22223321245327234t t k t k ⎛⎫⎡⎤+--++- ⎪⎣⎦⎝⎭=+因为0TP TQ ⋅≤ 恒成立,故()223212450332702t t t ⎧+--≤⎪⎨⎛⎫+-≤⎪ ⎪⎝⎭⎩,解得332t -≤≤.若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率不存在,则()()0,3,0,3P Q -或()()0,3,0,3P Q -此时需33t -≤≤,两者结合可得332t ≤≤.综上,存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.19.【答案】(1)21n n S =-(2)①证明见详解;②()131419n n S i i n b =-+=∑【小问1详解】设等比数列{}n a 的公比为0q >因为1231,1a S a ==-,即1231a a a +=-可得211q q +=-,整理得220q q --=,解得2q =或1q =-(舍去)所以122112nn n S -==--.【小问2详解】(i )由(1)可知12n n a -=,且N*,2k k ∈≥当124k k n a +=≥=时,则111221111k k k k k a n n a a -++⎧=<-=-⎨-=-<⎩,即11k k a n a +<-<可知12,1k k n a b k -==+()()()1111222121k k k n a k k b b a a k k k k --+=+--⋅=+-=-可得()()()()1112112122120k n k n k k k k k k k k b k a b ---=--+=--≥--=-⋅≥-当且仅当2k =时,等号成立所以1n k n b a b -≥⋅;(ii )由(1)可知:1211n n n S a +=-=-若1n =,则111,1S b ==;若2n ≥,则112k k k a a -+-=当1221k k i -<≤-时,12i i b b k --=可知{}i b 为等差数列可得()()()111211112221122431434429k k k k k k k k i i b k k k k k -------=-⎡⎤=⋅+=⋅=---⎣⎦∑所以()()()232113141115424845431434499n n S n n i i n b n n -=-+⎡⎤=+⨯-⨯+⨯-⨯+⋅⋅⋅+---=⎣⎦∑且1n =,符合上式,综上所述:()131419n n S i i n b =-+=∑.20.【答案】(1)1y x =-(2){}2(3)证明过程见解析【小问1详解】由于()ln f x x x =,故()ln 1f x x ='+.所以()10f =,()11f '=,所以所求的切线经过()1,0,且斜率为1,故其方程为1y x =-.【小问2详解】设()1ln h t t t =--,则()111t h t t t'-=-=,从而当01t <<时()0h t '<,当1t >时()0h t '>.所以()h t 在(]0,1上递减,在[)1,+∞上递增,这就说明()()1h t h ≥,即1ln t t -≥,且等号成立当且仅当1t =.设()()12ln g t a t t =--,则()((ln 12ln f x a x x x a x x a x g ⎛⎫-=-=-=⋅ ⎪⎭⎝.当()0,x ∞∈+时的取值范围是()0,∞+,所以命题等价于对任意()0,t ∞∈+,都有()0g t ≥.一方面,若对任意()0,t ∞∈+,都有()0g t ≥,则对()0,t ∞∈+有()()()()112012ln 12ln 1212g t a t t a t a t at a t t t ⎛⎫≤=--=-+≤-+-=+-- ⎪⎝⎭取2t =,得01a ≤-,故10a ≥>.再取t =,得2022a a a ≤--=--=-,所以2a =.另一方面,若2a =,则对任意()0,t ∞∈+都有()()()212ln 20g t t t h t =--=≥,满足条件.综合以上两个方面,知a 的取值范围是{}2.【小问3详解】先证明一个结论:对0a b <<,有()()ln 1ln 1f b f a a b b a -+<<+-.证明:前面已经证明不等式1ln t t -≥,故ln ln ln ln ln ln ln 1ln 1b b b a a a b a a a b b b b b a b a a--=+=+<+---且1lnln ln ln ln ln ln ln 1ln 11a a b b a a b b b a b b a a a a a a b a b a b b ⎛⎫--- ⎪--⎝⎭=+=+>=+----所以ln ln ln 1ln 1b b a a a b b a -+<<+-,即()()ln 1ln 1f b f a a b b a-+<<+-.由()ln 1f x x ='+,可知当10e x <<时()0f x '<,当1ex >时()0f x '>.所以()f x 在10,e ⎛⎤ ⎥⎝⎦上递减,在1e ,⎡⎫+∞⎪⎢⎣⎭上递增.不妨设12x x ≤,下面分三种情况(其中有重合部分)证明本题结论.情况一:当1211e x x ≤≤<时,有()()()()()()122122121ln 1f x f x f x f x x x x x x -=-<+-<-<结论成立;情况二:当1210ex x <≤≤时,有()()()()12121122ln ln f x f x f x f x x x x x -=-=-.对任意的10,e c ⎛⎤∈ ⎥⎝⎦,设()ln ln x x x c c ϕ=--则()ln 1x x ϕ=++'由于()x ϕ'单调递增,且有1111111ln 1ln 11102e 2e e c c ϕ⎛⎫ ⎪=++<+=-= ⎪⎝⎭'且当2124ln 1x c c ≥-⎛⎫- ⎪⎝⎭,2c x >时,2ln 1c ≥-可知()2ln 1ln ln 102c x x c ϕ⎛⎫=++>++=-≥ ⎪⎝⎭'.所以()x ϕ'在()0,c 上存在零点0x ,再结合()x ϕ'单调递增,即知00x x <<时()0x ϕ'<,0x x c <<时()0x ϕ'>.故()x ϕ在(]00,x 上递减,在[]0,x c 上递增.①当0x x c ≤≤时,有()()0x c ϕϕ≤=;②当00x x <<时,112221e e f f c ⎛⎫=-≤-=< ⎪⎝⎭,故我们可以取1,1q c ⎫∈⎪⎭.从而当201c x q <<-时,>可得()1ln ln ln ln 0x x x c c c c c c q c ϕ⎫=--<--<--=-<⎪⎭.再根据()x ϕ在(]00,x 上递减,即知对00x x <<都有()0x ϕ<;综合①②可知对任意0x c <≤,都有()0x ϕ≤,即()ln ln 0x x x c c ϕ=--.根据10,e c ⎛⎤∈ ⎥⎝⎦和0x c <≤的任意性,取2c x =,1x x =,就得到1122ln ln 0x x x x --≤.所以()()()()12121122ln ln f x f x f x f x x x x x -=-=-≤.情况三:当12101ex x <≤≤<时,根据情况一和情况二的讨论,可得()11e f x f ⎛⎫-≤≤ ⎪⎝⎭,()21e f f x ⎛⎫-≤≤ ⎪⎝⎭而根据()f x 的单调性,知()()()1211e f x f x f x f ⎛⎫-≤- ⎪⎝⎭或()()()1221e f x f x f f x ⎛⎫-≤- ⎪⎝⎭.故一定有()()12f x f x -≤成立.综上,结论成立.。
福建省高中名校2024学年高三年级第一学期期末数学试卷(附答案)

福建省高中名校2024学年高三年级第一学期期末试卷数 学一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数2i1i z =+,则z z -=( )A 2B. 2i -C. 2-D. 2i2. 已知集合{}2680A x x x =-+>,{}30B x x =-<,则A B = ( ) A. (2,3)B. (3),-∞C. (,2)-∞D. (4,)+∞3. 已知向量(3,5)a =r,(1,21)b m m =-+,若//a b,则m =( )A. 8B.8- C. 213-D. 87-4. 已知0.3log 2a =,0.23b =,0.30.2c =,则( ) A. b c a >>B. b a c >>C. c b a >>D. c a b >>5. 已知函数()ππcos 44f x x x ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭,要得到函数2()sin 22cos 1g x x x =-+的图象,只需将()f x 的图象( ) A. 向左平移π8个单位长度 B. 向左平移3π4个单位长度 C. 向右平移3π4个单位长度D. 向右平移3π8个单位长度6. 抛物线2:2(0)C y px p =>的焦点为F ,M 是抛物线C 上的点,O 为坐标原点,若OFM △的外接圆与抛物线C 的准线相切,且该圆的面积为36π,则p =( )A 4B. 8C. 6D. 107. 已知ABC 是边长为8的正三角形,D 是AC 的中点,沿BD 将BCD △折起使得二面角A BD C --为π3,则三棱锥C ABD -外接球的表面积为( ) A. 52π B. 52π3 C. 208π3D.103π38. 在数列{}n a 中,11a =,且1n n a a n +=,当2n ≥时,1231112n n na a a a a λ++++≤+- ,则实数λ的..取值范围为( )A. (,1]-∞B. [1,)+∞C. (0,1]D. (,4]-∞二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 下列结论正确的是( ) A. 若0a b <<,则22a ab b >> B. 若x ∈R ,则22122x x +++最小值为2 C. 若2a b +=,则22a b +的最大值为2 D. 若(0,2)x ∈,则1122x x+≥- 10. 《黄帝内经》中的十二时辰养生法认为:子时(23点到次日凌晨1点)的睡眠对一天至关重要.相关数据表明,入睡时间越晚,沉睡时间越少,睡眠指数也就越低.根据某次的抽样数据,对早睡群体和晚睡群体的睡眠指数各取10个.如下表:编号 1 2 3 4 5 6 7 8 9 10 早睡群体睡眠指数 65 68 75 85 85 85 88 92 9295 晚睡群体睡眠指数35405555556668748290根据样本数据,下列说法正确的是( )A. 早睡群体的睡眠指数一定比晚睡群体的睡眠指数高B. 早睡群体的睡眠指数的众数为85C. 晚睡群体的睡眠指数的第60百分位数为66D. 早睡群体的睡眠指数的方差比晚睡群体的睡眠指数的方差小 11. 已知点()0,5A,()5,0B -,动点P 在圆C :()()22348x y ++-=上,则( )A. 直线AB 截圆C 所得的弦长为B. PAB 的面积的最大值为15C. 满足到直线AB 的P 点位置共有3个D. PA PB ⋅的取值范围为22⎡---+⎣12. 已知定义在R 上的函数()f x 满足(2)()(2026)f x f x f ++=,且(1)1f x +-是奇函数.则( )的A. (1)(3)2f f +=B. (2023)(2025)(2024)f f f +=C. (2023)f 是(2022)f 与(2024)f 等差中项D.20241()2024i f i ==∑三、填空题:本题共4小题,每小题5分,共20分.13. 若函数21()2e 2x f x x x a =--的图象在点(0,(0))f 处的切线平行于x 轴,则=a _________. 14. 如图,在长方体1111ABCD A B C D -中,8AB =,6AD =,异面直线BD 与1AC所成角的余弦值为10,则1CC =_________.15. 某美食套餐中,除必选菜品以外,另有四款凉菜及四款饮品可供选择,其中凉菜可四选二,不可同款,饮品选择两杯,可以同款,则该套餐的供餐方案共有_________种.16. 法国数学家加斯帕·蒙日被称为“画法几何创始人”“微分几何之父”.他发现椭圆的两条互相垂直的切线的交点的轨迹是以该椭圆的中心为圆心的圆,这个圆被称为该椭圆的蒙日圆.若椭圆2222:1(0)x y C a b a b+=>>的蒙日圆为22273x y b +=,则C 的离心率为_________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知数列{}n a 的前n 项和n S 满足210n n S a +-=. (1)求{}n a 的通项公式;(2)设27log n n b a =,求数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T . 18. 已知某公司生产的风干牛肉干是按包销售的,每包牛肉干的质量M (单位:g )服从正态分布()2250,N σ,且(248)0.1P M <=.(1)若从公司销售的牛肉干中随机选取3包,求这3包中恰有2包质量不小于248g 的概率;(2)若从公司销售的牛肉干中随机选取K (K 为正整数)包,记质量在248g ~252g 内的包数为X ,且的()320D X >,求K 的最小值.19. 在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,a =,πsin sin 3a B b A ⎛⎫=+ ⎪⎝⎭. (1)求角A ;(2)作角A 的平分线与BC 交于点D ,且AD =,求b c +.20. 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PO ⊥平面ABCD ,垂足为O ,E 为PC 的中点,//OE 平面PAD .(1)证明:PC PD =;(2)若24==A D A B ,OC OD ⊥,PC 与平面ABCD 所成的角为60°,求平面PBC 与平面PCD 夹角的余弦值.21. 已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率为6,且其焦点到渐近线的距离为1.(1)求C 的方程;(2)若动直线l 与C 恰有1个公共点,且与C 的两条渐近线分别交于,P Q 两点,O 为坐标原点,证明:OPQ △的面积为定值.22. 已知函数ln ()x af x x+=,[1,)x ∈+∞. (1)讨论()f x 的单调性.(2)是否存在两个正整数1x ,2x ,使得当12x x >时,()12121212x x x x x x x x -=?若存在,求出所有满足条件1x ,2x 的值;若不存在,请说明理由.的答案解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数2i1i z =+,则z z -=( )A. 2B. 2i -C. 2-D. 2i【答案】D 【答案解析】【详细分析】根据条件,利用复数的运算即可求出结果. 【答案详解】因为2i 2i(1i)1i 1i (1i)(1i)z -===+++-,所以1i z =-,故2i z z -=, 故选:D.2. 已知集合{}2680A x x x =-+>,{}30B x x =-<,则A B = ( ) A. (2,3)B. (3),-∞C. (,2)-∞D.(4,)+∞【答案】C 【答案解析】【详细分析】解一元二次不等式化简集合A ,结合交集的概念即可得解.【答案详解】因为{4A x x =>或}2x <,{}3B x x =<,所以{}2A B x x ⋂=<. 故选:C.3. 已知向量(3,5)a =r ,(1,21)b m m =-+ ,若//a b ,则m =( )A. 8B.8- C. 213-D. 87-【答案】B 【答案解析】【详细分析】由平面向量平行的充要条件即可得解.【答案详解】因为//a b ,所以3(21)5(1)m m +=-,所以8m =-.故选:B.4. 已知0.3log 2a =,0.23b =,0.30.2c =,则( ) A. b c a >>B. b a c >>C. c b a >>D.c a b >>【答案】A 【答案解析】【详细分析】引入中间量,利用函数的单调性,进行大小的比较.【答案详解】因为0.30.3log 2log 10a =<=,0.20331b =>=,0.30.2(0,1)=∈c ,所以b c a >>.故选:A5. 已知函数()ππcos 44f x x x ⎛⎫⎛⎫=+-⎪ ⎪⎝⎭⎝⎭,要得到函数2()sin 22cos 1g x x x =-+的图象,只需将()f x 的图象( )A. 向左平移π8个单位长度 B. 向左平移3π4个单位长度 C. 向右平移3π4个单位长度D. 向右平移3π8个单位长度【答案】D 【答案解析】【详细分析】先把()f x ,()g x 的答案解析式都化成()sin y A x ωϕ=+或()cos y A x ωϕ=+的形式,再用图象的平移解决问题.【答案详解】()πππππcos sin 2244442f x x x x x x x⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-=++=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,()2π3πsin 22cos 1sin 2cos 22244g x x x x x x x ⎛⎫⎛⎫=-+=-=-=- ⎪ ⎪⎝⎭⎝⎭,故将()f x 的图象向右平移38π个单位长度可得3π3π2284y x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,即为()g x 的图象. 故选:C6. 抛物线2:2(0)C y px p =>的焦点为F ,M 是抛物线C 上的点,O 为坐标原点,若OFM △的外接圆与抛物线C 的准线相切,且该圆的面积为36π,则p =( ) A. 4 B. 8C. 6D. 10【答案】B 【答案解析】【详细分析】综合应用三角形外接圆的性质和抛物线的性质即得答案. 【答案详解】因为OFM △的外接圆与抛物线C 的准线相切, 所以OFM △的外接圆的圆心到准线的距离等于圆的半径. 因为圆的面积为36π,所以圆的半径为6, 又因为圆心在OF 的垂直平分线上,||2pOF =, 所以OFM △的外接圆的圆心到准线的距离624p p+=,可得8p =.故选:B.7. 已知ABC 是边长为8的正三角形,D 是AC 的中点,沿BD 将BCD △折起使得二面角A BD C --为π3,则三棱锥C ABD -外接球的表面积为( ) A. 52πB. 52π3 C. 208π3D.103π3【答案解析】【详细分析】根据给定条件,结合球的截面圆性质确定球心位置,再求出球半径即得. 【答案详解】在三棱锥C ABD -中,,,,,BD AD BD CD AD CD D AD CD ⊥⊥=⊂ 平面ACD ,由二面角A BD C --为π3,4AD CD ==,得ACD 是正三角形,令其外接圆圆心为O ',则2πsin 333O D AD '==,令三棱锥C ABD -外接球的球心为O ,球半径为R , 则OO '⊥平面ACD ,即有//OO BD ',显然球心O 在线段BD 的中垂面上,令线段BD 的中垂面交BD 于E ,则OE BD ⊥,显然O D BD '⊥,于是//OE O D ',四边形OEDO '是平行四边形,且是矩形,而12==DE BD22222252(33R OD OE DE ==+=+=, 所以三棱锥C ABD -外接球的表面积22084ππ3S R ==. 故选:C8. 在数列{}n a 中,11a =,且1n n a a n +=,当2n ≥时,1231112n n na a a a a λ++++≤+- ,则实数λ的取值范围为( ) A. (,1]-∞B. [1,)+∞C. (0,1]D.(,4]-∞【答案解析】【详细分析】先根据递推关系得到111n n na a a +-=-,把条件转化为22λ≤,从而可得答案. 【答案详解】因为1n n a a n +=,11a =,所以21a =,且当2n ≥时,11n n a a n -=-, 所以111n n n n a a a a +--=,所以111n n na a a +-=-, 所以3142531123111n n na a a a a a a a a a a +-+++=-+-+-++-= 12112n n n n a a a a a a ++--++=+-.因为1231112n n na a a a a λ++++≤+- , 所以1122n n n n a a a a λ+++-≤+-,所以22λ≤,故1λ≤. 故选:A.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 下列结论正确的是( ) A. 若0a b <<,则22a ab b >> B. 若x ∈R ,则22122x x +++的最小值为2 C. 若2a b +=,则22a b +最大值为2 D. 若(0,2)x ∈,则1122x x+≥- 【答案】AD 【答案解析】【详细分析】利用作差法比较大小判断A ,利用基本(均值)不等式判断BCD ,要注意“一正二定三相等”.【答案详解】因为2()0a ab a a b -=->,所以2a ab >, 的因为2()0=->-b a b ab b ,所以2ab b >,所以22a ab b >>,故A 正确; 因为221222x x ++≥+的等号成立条件22122x x +=+不成立,所以B 错误; 因为222122a b a b ++⎛⎫≥= ⎪⎝⎭,所以222a b +≥,故C 错误;因为11111121(2)2(22)2222222xx x x x x x x x x -⎛⎫⎛⎫+=+-+=++≥+= ⎪ ⎪---⎝⎭⎝⎭,当且仅当112x x=-,即1x =时,等号成立,所以D 正确. 故选:AD10. 《黄帝内经》中的十二时辰养生法认为:子时(23点到次日凌晨1点)的睡眠对一天至关重要.相关数据表明,入睡时间越晚,沉睡时间越少,睡眠指数也就越低.根据某次的抽样数据,对早睡群体和晚睡群体的睡眠指数各取10个.如下表:编号 1 2 3 4 5 6 7 8 9 10 早睡群体睡眠指数 65 68 75 85 85 85 88 92 92 95 晚睡群体睡眠指数35405555556668748290根据样本数据,下列说法正确的是( )A. 早睡群体的睡眠指数一定比晚睡群体的睡眠指数高B. 早睡群体的睡眠指数的众数为85C. 晚睡群体的睡眠指数的第60百分位数为66D. 早睡群体的睡眠指数的方差比晚睡群体的睡眠指数的方差小 【答案】BD 【答案解析】【详细分析】由样本数据可判断A ;样本数据的集中程度可判断D ;由众数的概念可判断B ;由百分位数的概念可判断C.【答案详解】因为早睡群体的睡眠指数不一定比晚睡群体的睡眠指数高,所以A 错误; 因为早睡群体的睡眠指数的10个样本数据中85出现次数最多,所以B 正确;因为晚睡群体的睡眠指数的第60百分位数为6668672+=,所以C 错误; 由样本数据可知,早睡群体的睡眠指数相对比较稳定,所以方差小,故D 正确. 故选:BD. 11. 已知点()0,5A,()5,0B -,动点P 在圆C :()()22348x y ++-=上,则( )A. 直线AB 截圆C所得的弦长为 B. PAB 的面积的最大值为15C. 满足到直线AB的P 点位置共有3个 D. PA PB ⋅的取值范围为22⎡---+⎣【答案】BCD 【答案解析】【详细分析】根据点到直线的距离公式,结合勾股定理即可求解弦长判断A ,根据三角形的面积公式,结合圆的性质即可求解B ,根据圆上的点到直线的距离的范围,即可求解C ,根据向量的数量积的运算量,结合坐标运算即可求解D.【答案详解】对于A ,因为()0,5A ,()5,0B -,所以直线AB 的方程为50x y -+=,圆心()3,4C -到直线AB 的距离为d ==,又因为圆C 的半径r =所以直线AB 截圆C所得的弦长为2=A 错误.对于B,易知AB =PAB 的面积最大,只需点P 到直线AB 的距离最大,而点P到直线AB的距离的最大值为r d +==, 所以PAB的面积的最大值为1152⨯=,B 正确. 对于C ,当点P 在直线AB 上方时,点P到直线AB 的距离的范围是(0,r +,即(,由对称性可知,此时满足到直线AB 的P 点位置有2个.当点P 在直线AB 下方时,点P到直线AB 的距离的范围是(0,r,即(,此时满足到直线AB的P 点位置只有1个.综上所述,满足到直线AB的P 点位置共有3个,C 正确.对于D ,由题意知()()()2PA PB PC CA PC CB PC PC CA CB CA CB ⋅=+⋅+=+⋅++⋅.又因为()0,5A ,()5,0B -,()3,4C -,所以()3,1CA = ,()2,4CB =--, 故()()321410CA CB ⋅=⨯-+⨯-=- ,()1,3CA CB +=-.设点()00,D x y 满足CA CB CD +=,则()003,4CD x y =+- ,故0031,43,x y +=⎧⎨-=-⎩解得002,1,x y =-⎧⎨=⎩即()2,1D -,CD =所以()28cos ,10PA PB PC PC CA CB CA CB PC CD PC CD ⋅=+⋅++⋅=+⋅⋅-2,2,PC CD PC CD =-+=-+ .又因为,PC CD ⎡∈-⎣,所以2,22PC CD ⎡-+∈---+⎣ ,即PA PB ⋅取值范围为[2--,2-+,D 正确.故选:BCD12. 已知定义在R 上的函数()f x 满足(2)()(2026)f x f x f ++=,且(1)1f x +-是奇函数.则( )A. (1)(3)2f f +=B. (2023)(2025)(2024)f f f +=的C. (2023)f 是(2022)f 与(2024)f 的等差中项D.20241()2024i f i ==∑【答案】ACD 【答案解析】【详细分析】由(2)()(2026)f x f x f ++=,可推出()f x 的周期为4,由(1)1f x +-是奇函数可推出(1)1f =,通过赋值及函数的周期性可逐个判断各个选项. 【答案详解】因为(2)()(2026)f x f x f ++=, 所以(4)(2)(2026)f x f x f +++=, 两式相减得(4)()f x f x +=, 所以()f x 的周期为4. 因为(1)1f x +-是奇函数,所以(1)1(1)1f x f x -+-=-++,所以(1)(1)2f x f x -+++=, 即()(2)2f x f x -++=, 令=1x -,得(1)1f =.因为(2)()(2026)(2)f x f x f f ++==, 令2x =,得(4)(2)(2)f f f +=, 所以(4)0f =,即(0)0f =. 因为()(2)2f x f x -++=, 令0x =,得(0)(2)2f f +=, 所以(2)2f =,所以(2)()2f x f x ++=, 所以(3)(1)2f f +=,故A 正确. 因为()(2)2f x f x -++=,所以(1)(3)2f f -+=,即(3)(3)2f f +=,所以(3)1f =.因为(2023)(2025)(3)(1)2f f f f +=+=,(2024)(0)0f f ==,所以B 错误. 因为(2022)(2024)(2)(0)2f f f f +=+=,(2023)(3)1f f ==, 所以(2022)(2024)2(2023)f f f +=,所以(2023)f 是(2022)f 与(2024)f 的等差中项,故C 正确.因为(1)(2)(3)(4)f f f f +++()(1)(3)(2)(4)f f f f =+++2204=++=,所以20241()506[(1)(2)(3)(4)]50642024i f i f f f f ==+++=⨯=∑,故D 正确故选:ACD【点评】关键点评:本题的关键是通过其奇偶性得到其周期性,再结合等差中项的含义以及赋值法一一详细分析选项即可.三、填空题:本题共4小题,每小题5分,共20分.13. 若函数21()2e 2x f x x x a =--的图象在点(0,(0))f 处的切线平行于x 轴,则=a _________. 【答案】2- 【答案解析】【详细分析】求出函数的导数,根据导数的几何意义,即可求得答案. 【答案详解】由题意得()2e x f x x a '=--, 由函数21()2e 2x f x x x a =--的图象在点(0,(0))f 处的切线平行于x 轴, 可得(0)20f a '=--=,得2a =-, 故答案为:-214. 如图,在长方体1111ABCD A B C D -中,8AB =,6AD =,异面直线BD 与1AC 所成角的余弦值为10,则1CC =_________. .【答案】【答案解析】【详细分析】利用直线的平移,把两条异面直线所成的角转化为平面角,再解三角形求角. 【答案详解】连接AC ,交DB 于点O ,取1CC 的中点E ,连接OE ,BE . 因为1//AC OE ,所以BD 与1AC 所成的角为∠BOE (或其补角). 令EC x =,在BEO △中,由8AB =,6AD =,得5OB =.又OE =,BE =cos 10BOE ∠=, 由余弦定理得22222225536210x x OE OB BE OE OB ++-++-==⋅,解得x =1CC =.故答案为:15. 某美食套餐中,除必选菜品以外,另有四款凉菜及四款饮品可供选择,其中凉菜可四选二,不可同款,饮品选择两杯,可以同款,则该套餐的供餐方案共有_________种. 【答案】60 【答案解析】【详细分析】先选菜品,再选饮品,结合分步计数原理可得答案.【答案详解】由题意可知凉菜选择方案共有24C 6=种,饮品选择方案共有2144C C10+=种,因此该套餐的供餐方案共有61060⨯=种. 故答案为:6016. 法国数学家加斯帕·蒙日被称为“画法几何创始人”“微分几何之父”.他发现椭圆的两条互相垂直的切线的交点的轨迹是以该椭圆的中心为圆心的圆,这个圆被称为该椭圆的蒙日圆.若椭圆2222:1(0)x y C a b a b+=>>的蒙日圆为22273x y b +=,则C 的离心率为_________. 【答案】12##0.5 【答案解析】【详细分析】根据蒙日圆的定义得出点(,)a b 一定在其蒙日圆上,从而可得离心率. 【答案详解】由题意可知点(,)a b 一定在其蒙日圆上,所以22273a b b +=, 所以234b a ⎛⎫= ⎪⎝⎭,故椭圆C的离心率为12c e a ===. 故答案为:12四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知数列{}n a 的前n 项和n S 满足210n n S a +-=. (1)求{}n a 的通项公式; (2)设27log n n b a =,求数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)13nn a ⎛⎫= ⎪⎝⎭(2)91n nT n =+ 【答案解析】【详细分析】(1)根据条件,利用n a 与n S 间的关系,得到13n n a a -=,从而得出数列{}n a 为等比数列,即可求出结果;(2)由(1)得出3n nb =-,从而得出111191n n b b n n +⎛⎫=- ⎪+⎝⎭,再利用裂项相消法即可求出结果.【小问1答案详解】因为210n n S a +-=,所以当1n =时,113a =, 当2n ≥时,11210n n S a --+-=,两式相减得13n n a a -=,又1103=≠a , 所以数列{}n a 是以13为首项,13为公比的等比数列, 则1111333n nn a -⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭. 【小问2答案详解】因为27271log log (33nn n n b a ===-, 所以119119(1)1n n b b n n n n +⎛⎫==- ⎪++⎝⎭, 所以1111111119991122334111n n T n n n n ⎛⎫⎛⎫=-+-+-++-=-=⎪ ⎪+++⎝⎭⎝⎭ . 18. 已知某公司生产的风干牛肉干是按包销售的,每包牛肉干的质量M (单位:g )服从正态分布()2250,N σ,且(248)0.1P M <=.(1)若从公司销售的牛肉干中随机选取3包,求这3包中恰有2包质量不小于248g 的概率; (2)若从公司销售的牛肉干中随机选取K (K 为正整数)包,记质量在248g ~252g 内的包数为X ,且()320D X >,求K 的最小值. 【答案】(1)0.243 (2)2001 【答案解析】【详细分析】(1)根据正态分布的性质求出(248)P M ≥的值,再结合二项分布的概率计算,即可得答案;(2)根据正态分布的对称性求出(248252)P M <<的值,确定~(,0.8)X B K ,结合正态分布的方差公式,列出不等式,即可求得答案. 【小问1答案详解】由题意知每包牛肉干的质量M (单位:g)服从正态分布()2250,N σ,且(248)0.1P M <=, 所以(248)10.10.9P M ≥=-=,则这3包中恰有2包质量不小于248g 的概率为223C 0.90.10.243⨯⨯=.【小问2答案详解】因为(248)0.1P M <=,所以(248252)(0.50.1)20.8P M <<=-⨯=, 依题意可得~(,0.8)X B K ,所以()0.8(10.8)0.16D X K K =⨯⨯-=, 因为()320D X >,所以0.16320,2000K K >>, 又K 为正整数,所以K 的最小值为2001.19. 在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c,a =,πsin sin 3a B b A ⎛⎫=+ ⎪⎝⎭. (1)求角A ;(2)作角A 的平分线与BC 交于点D,且AD =,求b c +.【答案】(1)π3(2)6 【答案解析】【详细分析】(1)由正弦定理边角互化,化简后利用正切值求角即得;(2)充分利用三角形的角平分线将三角形面积进行分割化简得b c cb +=,再运用余弦定理解方程即得. 【小问1答案详解】 因πsin sin 3a B b A ⎛⎫=+⎪⎝⎭,由正弦定理可得:1sin sin cos sin sin 022B A A A B ⎛⎫+-= ⎪ ⎪⎝⎭,即1sin cos sin 022B A A ⎛⎫-= ⎪ ⎪⎝⎭.因(0,π)B ∈,故sin 0B ≠,则有1cos sin 22A A =,即tan A =, 因(0,π)A ∈,故π3A =. 【小问2答案详解】因为AD 为角平分线,所以DAB DAC ABC S S S += , 所以111sin sin sin 222AB AD DAB AC AD DAC AB AC BAC ⋅∠+⋅∠=⋅∠. 因π3BAC ∠=,6πDAB DAC ∠=∠=,AD =,则444AB AC AB AC +=⋅, 即AB AC AB AC +=⋅,所以b c cb +=. 又由余弦定理可得:2222π2cos()33a b c bc b c bc =+-=+-,把a =,b c cb +=分别代入化简得:2()3()180b c b c +-+-=, 解得:6b c +=或3b c +=-(舍去),所以6b c +=.20. 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PO ⊥平面ABCD ,垂足为O ,E 为PC 的中点,//OE 平面PAD .(1)证明:PC PD =;(2)若24==A D A B ,OC OD ⊥,PC 与平面ABCD 所成的角为60°,求平面PBC 与平面PCD 夹角的余弦值. 【答案】(1)证明见答案解析(2)17. 【答案解析】【详细分析】(1)根据线线平行可得面面平行,进而根据面面平行的性质可得//OF AD ,线线垂直可求证线面垂直,进而根据线面垂直的性质即可求证, (2)建立空间直角坐标系,利用法向量的夹角即可求解. 【小问1答案详解】证明:取CD 的中点F ,连接EF ,PF ,OF ,因为E 为PC 的中点,所以//EF PD . 又EF ⊄平面PAD ,PD ⊂平面PAD ,所以//EF 平面APD . 因为//OE 平面PAD ,OE EF E = ,,OE EF ⊂平面OEF , 所以平面//OEF 平面PAD .因为平面ABCD ⋂平面OEF OF =,平面ABCD ⋂平面PAD AD =,所以//OF AD . 因为AD CD ⊥,所以OF CD ⊥.由PO ⊥平面ABCD ,CD ⊂平面ABCD ,可得PO CD ⊥.又PO OF O ⋂=,,PO OF ⊂平面POF ,所以CD ⊥平面POF ,PF ⊂平面POF , 从而PF CD ⊥.因为PF 是CD 的中垂线,所以PC PD =.【小问2答案详解】因为PO ⊥平面ABCD ,所以PC 与平面ABCD 所成的角为60PCO ∠=︒, 又OC OD ⊥,OC OD =,2AB CD ==,所以OC OD PO ====.作OG BC ⊥,垂足为G ,分别以OG,OF ,OP 的方向为x ,y ,z 轴的正方向,建立如图所示的空间直角坐标系,则()1,1,0D -,()1,3,0B -,()1,1,0C,(P ,()0,4,0BC =,(1,1,PC = ,()2,0,0DC =uuu r .设平面PBC 的法向量为()111,,m x y z =,则111140,0,m BC y m PC x y ⎧⋅==⎪⎨⋅=+=⎪⎩ 令11z =,得)m = .设平面PCD 的法向量为()222,,x n y z =,则222220,0,n DC x n PC x y ⎧⋅==⎪⎨⋅=+-=⎪⎩令2y =,得()n = .所以1cos ,7m n m n n m ⋅===,即平面PBC 与平面PCD 夹角的余弦值为17.21. 已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率为6,且其焦点到渐近线的距离为1.(1)求C 的方程;(2)若动直线l 与C 恰有1个公共点,且与C 的两条渐近线分别交于,P Q 两点,O 为坐标原点,证明:OPQ △的面积为定值.【答案】(1)2216x y -=(2)证明见答案解析 【答案解析】【详细分析】(1)由点到直线的距离公式、离心率公式以及平方关系再结合已知即可求解. (2)当直线l 的斜率存在时,不妨设:l y kx m =+,且6k ≠±.动直线l 与C 相切可得Δ0=即2261k m =+,再由弦长公式、点到直线的距离公式表示出三角形面积,结合2261k m =+即可得解.【小问1答案详解】设右焦点为(),0F c ,一条渐近线方程为0bx ay -=,1b ==.因为222,6c e c a b a ===+,所以a c ==. 故C 的方程为2216x y -=.【小问2答案详解】当直线l 的斜率不存在时,l的方程为x =,此时12,22OPQ PQ S ==⨯= . 当直线l 的斜率存在时,不妨设:l y kx m =+,且6k ≠±. 联立方程组22,1,6y kx m x y =+⎧⎪⎨-=⎪⎩得()2221612660k x mkx m ----=. 由()()2222Δ144416660m k km=+-+=,得2261k m =+.联立方程组6y kx m y x =+⎧⎪⎨=⎪⎩,得x =. 不妨设l与,66y x y x ==-的交点分别为,P Q,则P x =同理可求Q x =P Q PQ x =-=因为原点O 到l的距离d =,所以221216OPQS PQ d k=⋅=- . 因为2261k m =+,所以OPQ S =.故OPQ △.22 已知函数ln ()x af x x+=,[1,)x ∈+∞. (1)讨论()f x 的单调性.(2)是否存在两个正整数1x ,2x ,使得当12x x >时,()12121212x x x x x x x x -=?若存在,求出所有满足条件的1x ,2x 的值;若不存在,请说明理由. 【答案】(1)答案见答案解析 (2)14x =,22x = 【答案解析】【详细分析】(1)求得()f x ',分 1a ≥,1a <讨论()f x 的单调性. (2)将问题转化为()121212ln ln ln x x x x x x -=+,根据ln ()x f x x=的值域确定122x x -=,分别就13,4,x =⋅⋅⋅详细分析是否满足题意. 【小问1答案详解】21ln ()a xf x x'--=, 当1a ≥时,()0f x '≤,()f x 在[1,)+∞上单调递减. 当1a <时,令()0f x '=,得1e a x -=.)11,e a x -⎡∈⎣,()0f x '>,则()f x 在)11,e a-⎡⎣上单调递增, ()1e ,a x ∞-∈+,()0f x '<,则()f x 在()1e ,a ∞-+上单调递减.【小问2答案详解】由(1)知,令0a =,得ln ()xf x x=在[1,e)上单调递增,在(e,)+∞上单调递减,则11()(e)e 2f x f ≤=<. 因为121x x >≥,所以()12211212x x x x x x x x -=,即()12122112ln ln ln x x x x x x x x -=+, 即()121212ln ln ln x x x x x x -=+, .因为1x ,2x 为正整数,所以121x x -≥.当121x x -=时,21121x xx x =,因为21x ≥,12x ≥,所以21121x x x x >,这与21121x xx x =矛盾,不符合题意.当121x x ->时,因11ln 12x x <,22ln 12x x <,所以()121212ln ln ln 1x x x x x x -=+<, 所以12e x x -<,得122x x -=,即1212ln ln ln 2x x x x =+. 经检验,当21x =,13x =时,不符合题意, 当22x =,14x =时,符合题意,当23x =,15=x 时,因为53153037532763528<==⨯,所以ln3ln5ln 235+<, 当24x ≥时,11ln ln 6ln565x x ≤<,22ln ln 4ln343x x ≤<, 所以1212ln ln ln5ln3ln 253x x x x +<+<. 综上,仅存在14x =,22x =满足条件.【点评】关键点评:本题关键点在于根据ln ()xf x x =的值域确定12x x -的范围,再根据12,x x 为正整数得122x x -=,从而就12,x x 的取值讨论即可为。
福建省部分达标高中2024-2025学年高三上学期11月期中考试 数学含答案

高三半期考数学试卷(答案在最后)注意事项:1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:集合与常用逻辑用语、等式与不等式、函数与导数、三角函数与解三角形、平面向量与复数。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{13}A x x =-<≤∣,{}1,2,3,4B =,则A B = ()A .{}2,3B .{}1,2C .{}1,2,3D .{}12.函数41tan 3y x π⎛⎫=-⎪⎝⎭的最小正周期为()A .4B .22πC .8D .24π3.在中国传统的十二生肖中,马、牛、羊、鸡、狗、猪为六畜,则“甲的生肖不是马”是“甲的生肖不属于六畜”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知复数()32z =-+,则z 的虚部为()A .-B .C .10-D .105.在梯形ABCD 中,5BC AD = ,AC 与BD 交于点E ,则ED =()A .1166AD AB-B .1177AD AB-C .1166AB AD-D .1177AB AD-6.将函数()cos y x ϕ=+图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数()y f x =的图象.若()y f x =的图象关于点7,03π⎛⎫- ⎪⎝⎭对称,则ϕ的最小值为()A .3πB .23πC .6πD .56π7.已知22111x y+=,则221169x y --的最大值为()A .35-B .49-C .42-D .48-8.若2sin cos 2tan3sin cos 1tan 3αααααα-=+-,则α的值可以为()A .12π-B .20π-C .10πD .5π二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.若()f x 与()g x 分别为定义在R 上的偶函数、奇函数,则函数()()()h x f x g x =的部分图象可能为()A .B .C .D .10.如图,在ABC 中,3AB AC ==,2BC =,点D ,G 分别边AC ,BC 上,点E ,F 均在边AB 上,设DG x =,矩形DEFG 的面积为S ,且S 关于x 的函数为()S x ,则()A .ABC 的面积为B .()13S =C .()S x 先增后减D .()S x 11.已知向量a ,b ,c 满足6a = ,1b = ,,3a b π= ,()()3c a c b -⋅-= ,则()A .a b -=B .cC .a c - 的最小值为2D .a c - 的最大值为62三、填空题:本题共3小题,每小题5分,共15分.12.log =________.13.已知14ω>,函数()sin 4f x x π⎛⎫=- ⎪⎝⎭在[]0,ωπ上单调递增,则ω的最大值为________.14.已知函数()e x x f x m =-,()2exg x m =-,若()f x 与()g x 的零点构成的集合的元素个数为3,则m 的取值范围是________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin cos sin sin c A B a B C =.(1)求角B ;(2)若3a =,ABC 的面积为92,求b .16.(15分)已知函数()3f x x x =--.(1)求曲线()y f x =在点()()4,4f 处的切线方程;(2)若()ln f x m >恒成立,求m 的取值范围.17.(15分)已知函数()14sin sin 3f x x x π⎛⎫=--⎪⎝⎭.(1)将()f x 化成()()sin 0,0,2f x A x B A πωϕωϕ⎛⎫=++>><⎪⎝⎭的形式;(2)求()f x 在0,4π⎡⎤⎢⎥⎣⎦上的值域;(3)将()f x 的图象向左平移6π个单位长度后得到函数()h x 的图象,求不等式()0h x ≥的解集.18.(17分)已知函数()f x ,()g x 满足()2e exxf x ax -=-+,()()()2212e 1e 2e 2e x x f x g x a -⎛⎫+=-+-+ ⎪⎝⎭.(1)若()f x 为R 上的增函数,求a 的取值范围.(2)证明:()f x 与()g x 的图象关于一条直线对称.(3)若a ≥-,且关于x 的方程()()()e 22xf x f mg x +-=-在[]1,1-内有解,求m 的取值范围.19.(17分)若存在有限个0x ,使得()()00f x f x -=,且()f x 不是偶函数,则称()f x 为“缺陷偶函数”,0x 称为()f x 的偶点.(1)证明:()5h x x x =+为“缺陷偶函数”,且偶点唯一.(2)对任意,x y ∈R ,函数()f x ,()g x 都满足()()()()22f x f y g x g y x y++-=+①若()g x y x=是“缺陷偶函数”,证明:函数()()F x xg x =有2个极值点.②若()32g =1x >时,()()21ln 12g x x >-.参考数据:1ln0.4812+≈ 2.236≈.高三半期考数学试卷参考答案1.C因为{13}A x x =-<≤∣,{}1,2,3,4B =,所以{}1,2,3A B = .2.D 函数41tan 3y x π⎛⎫=- ⎪⎝⎭的最小正周期244T πππ==.3.B若甲的生肖不是马,则甲的生肖未必不属于六畜;若甲的生肖不属于六畜,则甲的生肖一定不是马.故“甲的生肖不是马”是“甲的生肖不属于六畜”的必要不充分条件.4.A因为()()()321210z =-+=--+=+,所以z的虚部为-.5.A 因为5BC AD = ,所以AD BC ,且15DE AD BE BC ==,所以()11116666ED BD AD AB AD AB ==-=- .6.A 依题意可得()1cos 2f x x ϕ⎛⎫=+⎪⎝⎭.因为()y f x =的图象关于点7,03π⎛⎫- ⎪⎝⎭对称,所以()17232k k ππϕπ⎛⎫⨯-+=+∈ ⎪⎝⎭Z ,即()53k k πϕπ=+∈Z ,所以ϕ的最小值为5233πππ-=.7.D因为22111x y+=,所以()2222222222119161691692525249y x x y x y xy x y ⎛⎫+=++=++≥+ ⎪⎝⎭,当且仅当2222916y x x y=,即274x =,273y =时,等号成立.故221169x y --的最大值为14948-=-.8.B因为sin cos tan 1tan sin cos tan 14αααπαααα--⎛⎫==-⎪++⎝⎭,22tan3tan61tan 3ααα=-,且2sin cos 2tan3sin cos 1tan 3αααααα-=+-,所以()64k k πααπ-=+∈Z ,所以()205k k ππα=--∈Z ,所以α的值可以为20π-.9.AC因为()f x 与()g x 分别为定义在R 上的偶函数、奇函数,所以()()f x f x -=,()()g x g x -=-,所以()()()()h x f x g x h x -=--=-,则()h x 为奇函数,其图象关于原点对称,故选AC .10.ACD取BC 的中点N ,连接AN ,则AN BC ⊥,且AN ==,所以ABC的面积为122⨯⨯=,A 正确.过C 作CH AB ⊥,垂足为H ,设CH 与DG 交于点M ,由等面积法可得1 2AB CH⋅=3CH=.由CM DGCH AB=,得9CH DGCMAB⋅==,则3MH CH CM=-=9-,所以()()2233992S x DG DE DG MH x x x⎛⎫=⋅=⋅=-=--+<⎪⎝⎭3)x<,则()19S=,则() S x在30,2⎛⎫⎪⎝⎭上单调递增,在3,32⎡⎫⎪⎢⎣⎭上单调递减,所以()S x,B错误,C,D均正确.11.BC a b-==A错误.建立平面直角坐标系xOy,不妨假设()6,0a OA==,1,22b OB⎛⎫== ⎪⎪⎝⎭,设(),c OC x y==,则()6,c a x y-=-,1,22c b x y⎛-=--⎝⎭,代入()()3c a c b-⋅-=,整理得221343444x y⎛⎛⎫-+-=⎪⎝⎭⎝⎭,所以点C在以13,44M⎛⎫⎪⎪⎝⎭为圆心,2为半径的圆上.因为该圆经过坐标原点,所以cB正确.因为22133143604444⎛⎛⎫-+-=<⎪⎝⎭⎝⎭,所以点A在圆M内,因为a c AC-=,2AM=,所以a c-的最小值为43312,a c-的最大值为43312+,C正确,D错误.12.1525221515log log8log8222===.13.34因为[]0,x ωπ∈,所以,444x πππωπ⎡⎤-∈--⎢⎣⎦,又14ω>,所以04πωπ->,所以42ππωπ-≤,解得34ω≤,则ω的最大值为34.14.222210,,e e e ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭ 令()0f x =,得e x x m =,令()0g x =,得2e xm =.设()e x x h x =,()1exxh x -=',则()h x 在()0,1上单调递增,在()1,+∞上单调递减,所以()()max11e h x h ==.当0x >时,()0h x >,所以结合()h x ,()2exk x =的图象(图略)及()()22122e e h k ==<,得m 的取值范围是222210,,e e e ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭.15.解:(1)因为sin cos sin sin c A B a B C =,所以sin sin cos sin sin sin C A B A B C =,2分因为sin 0A >,sin 0C >,所以cos sin B B =,4分所以tan 1B =.6分又()0,B π∈,所以4B π=.7分(2)因为193sin 242c π⨯=,所以c =,9分所以2222cos 918292b ac ac B =+-=+-⨯=,12分解得3b =.13分16.解:(1)()231f x x=--'2分所以()4481146f =--='.3分因为()4644852f =--=,所以曲线()y f x =在点()()4,4f 处的切线方程为()52464y x -=-,即46132y x =-.6分(2)()231f x x=--'()0,+∞上单调递增.8分因为()10f '=,9分所以当()0,1x ∈时,()0f x '<,()f x 单调递减,当()1,x ∈+∞时,()0f x '>,()f x 单调递增,11分所以()()min ln 14m f x f <==-,13分解得410e m <<,故m 的取值范围为410,e ⎛⎫ ⎪⎝⎭.15分17.解:(1)()2114sin 4sin 12sin cos 22f x x x x x x x ⎛⎫=-⨯-⨯=-+ ⎪ ⎪⎝⎭1分1cos212cos22sin 226xx x x x π-⎛⎫=-⨯+=+=+ ⎪⎝⎭.4分(2)由0,4x π⎡⎤∈⎢⎥⎣⎦,得22,663x πππ⎡⎤+∈⎢⎥⎣⎦.5分当266x ππ+=时,()f x 取得最小值,最小值为2sin 16π=;6分当262x ππ+=时,()f x 取得最大值,最大值为2sin 22π=.7分故()f x 在0,4π⎡⎤⎢⎥⎣⎦上的值域为[]1,2.8分(3)由题意可得()2sin 22sin 22cos26662h x f x x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+= ⎪ ⎪ ⎪⎢⎝⎭⎝⎭⎝⎭⎣⎦,11分则不等式()0h x ≥即为2cos20x ≥,得()22222k x k k ππππ-+≤≤+∈Z ,13分解得()44k x k k ππππ-+≤≤+∈Z ,即不等式()0h x ≥的解集为(),44k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z .15分18.(1)解:因为()f x 为R 上的增函数,所以()2e e 0x x f x a -=++≥'恒成立,2分因为()f x a a ≥=',3分当且仅当2e e xx-=,即1ln22x =-时,等号成立,4分所以0a ≥,即a ≥-,a 的取值范围为)⎡-+∞⎣.5分(2)证明:因为()2e exxf x ax -=-+,()()()2212e 1e 2e 2e x x f x g x a -⎛⎫+=-+-+ ⎪⎝⎭,所以()222e e 2x x g x a ax --=-+-,7分所以()()()()222ee 22x xg x a x f x ---=-+-=-,9分则()f x 与()g x 的图象关于直线1x =对称.10分(3)解:因为()()()e 22xf x f mg x +-=-,所以由(2)知()()()e 2xf x f m f x +-=,即()()e xf m f x -=.12分由(1)知,当a ≥-时,()f x 为R 上的增函数,所以e xm x -=,即e x m x =-.13分设()()e 11x h x x x =--≤≤,则()()e 111x h x x '=--≤≤,当10x -≤<时,()0h x '<,当01x <≤时,()0h x '>,14分所以()()min 01h x h ==,又()111eh -=+,()()11e 1h h =-+>-,所以()()max 1e 1h x h ==-.16分故m 的取值范围是[]1,e 1-.17分19.证明:(1)由()()h x h x -=,得()55x x x x -+-=+,则()()542210x xx x +=+=,1分解得0x =,所以()h x 只有1个偶点,且偶点为0,所以()5h x x x =+为“缺陷偶函数”,且偶点唯一.3分(2)由题意得()()()()22f x g x x f y g y y +-=-++对,x y ∈R 恒成立,4分所以存在常数a ,使得()()()()22f x g x x f y g y y a +-=-++=.5分令y x =,得()()()()2,2,f x g x x a f x g x x a ⎧+-=⎪⎨-++=⎪⎩解得()223x x a g x -+=.6分①()21333g x x a y xx ==+-,由()()g x g x x x -=-,得2033x ax+=,即()220x a x =-≠,则20a ->,即0a <.7分()()3223x x ax F x xg x -+==,()23223x x aF x -+=',因为4240a ∆=->,所以()0F x '=必有两根1x ,2x (设12x x <),8分当1x x <或2x x >时,()0F x '>,当12x x x <<时,()0F x '<,所以函数()()F x xg x =有2个极值点1x ,2x .9分②若()62323ag +==,则0a =,()23x x g x -=,10分当1x >时,要证()()21ln 12g x x >-,只需证()223ln 12x x x ->-,因为()()223420x x x x ---=-≥,所以234x x x -≥-,所以只需证()2334ln 12x x ->-.12分设函数()()()2334ln 112p x x x x =--->,则()()()()22231631121x x xp x x x x '--=-=>--,当112x <<时,()0p x '<,当12x +>时,()0p x '>,14分所以()min12p x p ⎛+= ⎝⎭,211122⎛++-= ⎝⎭,所以()min 3353153 2.236534ln 0.4810.132522222p x ++⨯-=--≈-⨯=,16分所以()min 0p x >,从而()()2334ln 102p x x x =--->,故当1x >时,()()21ln 12g x x >-.17分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012.7.14
平面向量
班级 姓名 学号 成绩
一、选择题(本大题共8小题,每小题5分,共40分)
1.若向量a =(x +3,x 2-3x -4)与AB →相等,其中A (1,2),B (3,2),则x 等于( )
A.1
B.0
C.-1
D.2
2.已知命题正确的个数是 ( )
①若a ·b =0,则a =0或b =0 ②(a ·b )·c =a ·(b ·c ) ③若a ·b =b ·c (b ≠0),则a =c
④a ·b =b ·a ⑤若a 与b 不共线,则a 与b 的夹角为锐角
A.1
B.2
C.3
D.4
3.下面几个有关向量数量积的关系式:
①0·0=0 ②|a ·b |≤a ·b ③a 2=|a |2 ④a ·b |a |2 =b a
⑤(a ·b )2=a 2·b 2 ⑥(a -b )2=a 2-2a ·b +b 2 其中正确的个数是 ( )
A.2
B.3
C.4
D.5
4.已知a =(x ,y ),b =(-y ,x )(x ,y 不同时为零),则a ,b 之间的关系是 ( )
A.平行
B.不平行也不垂直
C.垂直
D.以上都不对
5.已知两点A (2,3),B (-4,5),则与AB →共线的单位向量是 ( )
A.e =(-6,2)
B.e =(-6,2)或(6,-2)
C.e =(-31010,1010)
D.e =(-31010,1010)或(31010,-1010
) 6.若|a |=|b |=1,a ⊥b ,且2a +3b 与k a -4b 也互相垂直,则k 的值为 ( )
A.-6
B.6
C.3
D.-3
7.已知e 1,e 2是夹角为60°的两个单位向量,则a =2e 1+e 2;b =-3e 1+2e 2的夹角是( )
A.30°
B.60°
C.120°
D.150°
8.若|a -b |=41-20 3 ,|a |=4,|b |=5,则a 与b 的数量积为 ( )
A.10 3
B.-10 3
C.10 2
D.10
二、填空题(本大题共6小题,每小题5分,共30分)
9.若a 与b 、c 的夹角都是60°,而b ⊥c ,且|a |=|b |=|c =1,则(a -2c )·(b +c )=_____.
10.已知A (3,0),B (0,4),点P 在线段AB 上运动(P 可以与A 、B 重合),O 是坐标原点,则|OP →|的取
值范围为_____________.
11.已知a =(λ,2),b =(-3,5)且a 与b 的夹角是钝角,则实数λ的取值范围是_______.
12.已知OP 1→+OP 2→+OP 3→=0,|OP 1→|=|OP 2→|=|OP 3→|=1,则OP 2→,OP 3→的夹角为_______.
13.等边△ABC 的边长为1,AB →=a ,BC →=b ,CA →=c ,那么a ·b +b ·c +c ·a 等于
14.若对n 个向量a 1,a 2,…,a n ,存在n 个不全为零的实数k 1,k 2,……,k n ,使得等式
k 1a 1+k 2a 2+…+k n a n =0成立,则称向量a 1,a 2,…,a n “线性相关”,请写出使得a 1=(1,0),a 2=(1,-1),a 3=(2,2)“线性相关”的一组实数k 1,k 2,k 3的值,即k 1=_________,k 2=___________,k 3=_____________.(答案不唯一)
三、解答题(本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分10分)已知a 和b 的夹角为60°,|a |=10,|b |=8,求:
(1)|a +b |; (2)a +b 与a 的夹角θ的余弦值.
16.(本小题满分10分)已知△ABC 中,A (2,-1),B (3,2),C (-3,-1),BC 边上的高为AD ,求点
D 和向量AD →.
17. (本小题满分10分)已知a =(3,4),b =(4,3),c =x a +y b ,且a ⊥c ,|c |=1,求x 和y 的值.
2012.7.14
平面向量(答案)
一、选择题(本大题共8小题,每小题5分,共40分)
1.C 2.A 3.B 4.C 5.D 6.B 7.C 8.A
二、填空题(本大题共6小题,每小题5分,共30分)
9.-1 10.[125 ,4] 11.(103 ,+∞) 12.120° 13.-32 14.4 ,-2 , -1 三、解答题(本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分10分)已知a 和b 的夹角为60°,|a |=10,|b |=8,求:
(1)|a +b |;(2)a +b 与a 的夹角θ的余弦值.
【解】 (1)|a +b |=(a +b )2 =a 2+2a ·b +b 2 =|a |2+|b |2+2|a ||b |cos600 =102+82+2×10×8×12
=261 (2)cos θ=a ·(a +b )|a ||a +b | =a 2+a ·b 10×261
=76161. 16.(本小题满分10分)已知△ABC 中,A (2,-1),B (3,2),C (-3,-1),BC 边上的高为AD ,求点
D 和向量AD →.
【解】 设D (x 0,y 0),则AD →=(x 0-2,y 0+1),BC →=(-6,-3),BD →=(x 0-3,y 0-2)
∵⎩⎨⎧AD →⊥BC →BC →∥BD
→ , ∴⎩⎨⎧-6(x 0-2)-3(y 0+1)=0-6(y 0-2)+3(x 0-3)=0
解得,⎩⎨⎧x 0=1y 0=1
, ∴D (1,1),AD →=(-1,2)
17. (本小题满分10分)已知a =(3,4),b =(4,3),c =x a +y b ,且a ⊥c ,|c |=1,求x 和y 的值.
【解】 设c =(c 1,c 2), 则:
∵a ⊥c ,a =(3,4)
∴3c 1+4c 2=0,c 2=-34
c 1 ∴c (c 1,-34
c 1),又∵|c |=1 ∴c 12+(-34 c 1)2=1 c 1=±45
∴⎩⎨⎧c 1=45 c 2=-35 或⎩⎨⎧c 1=-4
5
c 2=35 , ∴c (45 ,-35 )或c (-45 ,35
)
又已知c =x a +y b =(3x +4y ,4x +3y ) ∴⎩⎨⎧3x +4y =45 4x +3y =-35 或⎩⎨⎧3x +4y =-45 4x +3y =35
, 解得:⎩⎨⎧x =-2435 y =57 或⎩
⎨⎧x =2435 y =-57。
