直方图的均衡化
图像处理中直方图均衡化的使用教程

图像处理中直方图均衡化的使用教程图像处理中的直方图均衡化是一种常用的增强图像对比度的方法。
通过对图像的像素值进行重新分布,直方图均衡化可以使图像中的明暗区域更具有对比度,从而提高图像的质量和清晰度。
本文将介绍直方图均衡化的原理、应用场景以及具体的步骤。
1. 直方图均衡化的原理直方图均衡化的原理基于对图像的灰度级进行重新分布。
它通过将原始图像的像素值映射到新的像素值上,使得直方图在整个灰度范围内得到均匀分布。
这样就能够增强图像中的低对比度区域,提高图像的视觉效果。
2. 直方图均衡化的应用场景直方图均衡化在图像处理领域有着广泛的应用。
下面列举了一些常见的应用场景:- 增强图像的对比度:直方图均衡化可以使得图像中的亮度值更加均匀分布,提高图像的对比度,使得图像变得更加清晰。
- 增强图像的细节:直方图均衡化通过增强图像中的低对比度区域,可以使得细节更加显著,提高图像的可视化效果。
- 降低图像的噪声:直方图均衡化可以将图像中的噪声分布均匀化,从而减少噪声对图像质量的影响。
3. 直方图均衡化的步骤下面是使用直方图均衡化对图像进行处理的具体步骤:步骤 1: 将彩色图像转换为灰度图像如果原始图像是彩色图像,我们需要将其转换为灰度图像。
这是因为直方图均衡化是针对灰度级进行处理的。
步骤 2: 计算原始图像的像素值分布使用图像处理工具,计算原始图像中每个像素值的出现频率。
这样可以得到一个直方图,该直方图显示了原始图像中像素值的分布情况。
步骤 3: 计算累积分布函数通过对原始图像的直方图进行累积求和,得到一个累积分布函数。
该函数显示了每个像素值的累积出现频率。
步骤 4: 计算新的像素值根据累积分布函数,计算每个像素值的新的映射像素值。
这个计算公式可以根据具体的图像处理工具而有所不同。
步骤 5: 创建均衡化后的图像使用新的像素值替换原始图像中的像素值,将得到的图像称为均衡化后的图像。
4. 注意事项在使用直方图均衡化时,需要考虑以下几个注意事项:- 直方图均衡化可能会改变图像的整体亮度。
直方图均衡化计算
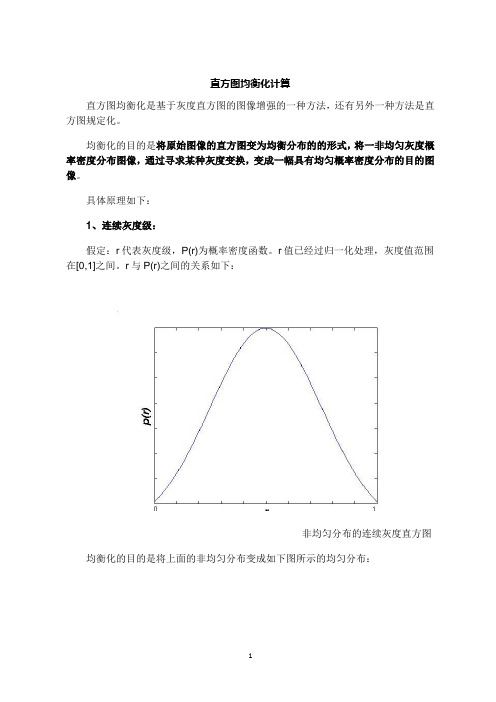
直方图均衡化计算直方图均衡化是基于灰度直方图的图像增强的一种方法,还有另外一种方法是直方图规定化。
均衡化的目的是将原始图像的直方图变为均衡分布的的形式,将一非均匀灰度概率密度分布图像,通过寻求某种灰度变换,变成一幅具有均匀概率密度分布的目的图像。
具体原理如下:1、连续灰度级:假定:r代表灰度级,P(r)为概率密度函数。
r值已经过归一化处理,灰度值范围在[0,1]之间。
r与P(r)之间的关系如下:非均匀分布的连续灰度直方图均衡化的目的是将上面的非均匀分布变成如下图所示的均匀分布:均匀分布的连续灰度直方图我们接下来要做的是要找到一种变换S=T(r)使直方图变平直,为使变换后的灰度仍保持从黑到白的单一变化顺序,且变换范围与原先一致,以避免整体变亮或变暗,需要有如下规定:(1)在0 <= r <= 1中,T(r)是单调递增函数,且0 <= T(r) <= 1;(2)反变换r=(s),(s)也为单调递增函数,且0 <= s <= 1。
直方图均衡化变换公式推导图示因为灰度变换不影响像素的位置分布,而且也不会增减像素数目,所以有如下的推导公式:2、离散灰度级:设一幅图像的像素总数为n,分为L个灰度级,其中::表示第K个灰度级出现的个数。
:第K个灰度级出现的概率。
(0<=<=1, k=0,1,2,...,L-1),公式如下:计算的基本步骤如下:(1)求出图像中所包含的灰度级,一般都经过归一化处理,范围在[0,1]之间,也可以定在[0,L-1]之间。
(2)统计各灰度级的像素数目(k=0,1,2,...,L-1)。
(3)计算图像直方图。
(4)计算变换函数,即:(5)用变换函数计算映射后输出的灰度级。
(6)统计映射后新的灰度级的像素数目。
(7)计算输出图像的直方图。
根据上面推导出来的公式以及计算步骤,我们可以结合栗子来加深理解~~~eg:设图像有64*64=4096的像素,有8个灰度级,灰度分布如下所示:由上图我们知道该图像的,和,下一步我们要做的就是通过变换函数求,即:依次可求得,,,,。
直方图均衡化原理

直方图均衡化原理直方图均衡化是一种用于增强图像对比度的经典方法,它通过重新分布图像的像素值来实现增强图像的对比度和亮度。
在本文中,我们将介绍直方图均衡化的原理,包括其基本概念、算法步骤和应用场景。
直方图均衡化的基本概念是通过重新分布图像的像素值,使得原始图像的像素值分布更加均匀,从而增强图像的对比度和亮度。
这种方法的核心思想是将原始图像的灰度直方图进行变换,使得变换后的直方图更加平坦,从而实现对比度的增强。
直方图均衡化的算法步骤可以简单概括为以下几步,首先,计算原始图像的灰度直方图,即统计图像中每个像素值的出现次数;然后,根据原始图像的灰度直方图计算累积分布函数(CDF),用于描述像素值的累积分布情况;接着,根据CDF对原始图像的像素值进行映射,得到变换后的图像;最后,根据映射后的像素值重新构建图像,实现对比度增强。
直方图均衡化的应用场景非常广泛,包括但不限于医学图像处理、遥感图像处理、数字摄影等领域。
在医学图像处理中,直方图均衡化可以帮助医生更清晰地观察病灶,提高诊断准确性;在遥感图像处理中,直方图均衡化可以增强图像的细节信息,提高图像的可视化效果;在数字摄影中,直方图均衡化可以改善照片的曝光不足或曝光过度的问题,提高照片的质量。
总之,直方图均衡化作为一种经典的图像增强方法,具有重要的理论意义和实际应用价值。
通过重新分布图像的像素值,直方图均衡化可以有效地增强图像的对比度和亮度,提高图像的质量和可视化效果。
在实际应用中,我们可以根据具体的需求选择合适的直方图均衡化算法,从而实现对图像的有效增强和优化。
希望本文对直方图均衡化的原理有所了解,对读者有所帮助。
如果您对直方图均衡化还有其他疑问或者需要进一步的了解,欢迎继续阅读相关的文献资料或者咨询相关领域的专业人士。
感谢您的阅读!。
直方图的均衡化

三、例题演示
设有1幅64x64,8bit灰度图像,其直方 图见图1,所用均衡化变换函数(即累积 直方图)见图2,均衡化后的直方图见图 3。
直方图均衡化计算列表
序号
运算
1 列出原始图灰度级Sk,k=0,1,…7
0
1
2
2 统计原始直方图各灰度级象素数Nk 790 1023 850
3 用式1计算原始直方图(图1)
对图像空间域点的增强过程是通过增强函数t=EH(s)来完成的, t、s分别为目标图像和原始图像上的像素点(x,y)处的灰度值。
在进行均衡化处理时,增强函数EH需要满足两个条件: 1)、增强函数EH(s)在0≤s≤L-1的范围内是一个单调递增函数,
这个条件保证了在增强处理时没有打乱原始图像的灰度排列次序; 2)、对于0≤s≤L-1应当有0≤EH(s)≤L-1,它保证了变换过程
0 sk 1
k=0,1,…L-1
公式(2)
根据该方程可以由原图像的各像素灰度值直接得到直方图均衡化后各 像素的灰度值。
在实际处理变换时,一般先对原始图像的灰度情况进行统计分析,并
计算出原始直方图分布,然后根据计算出的累计直方图分布 t k ,按式 tkint[(L1)tk0.5]对其取整扩展并得出原灰度s k 到 t k 的灰度映
%step1:get histogram
for i=1:m;
for j=1:n;
k=plane(i,j);
tmhist(k)=tmhist(k)+1;
end
end
四、直方图均衡化的原理程序(lm2.m)
%step2:get cdf
cdf(1)=tmhist(1);
for i=2:256
▪ 其实在MATLAB中,用imhist函数求图像直方图,histeq函数可 以实现直方图均衡化操作(histogram equalization)。
《直方图的均衡化》课件
直方图均衡化的效果评估
直方图均衡化的效果可以通过比较处理前后的直方图、对比度和视觉效果来 评估,通常希望处理后的图像具有更均匀的像素值分布和更好的对比度。
结论和总结
直方图的均衡化是一种有效的图像增强技术,在图像处理和计算机视觉中具有广泛的应用,能够改善图 像的质量和视觉效果。
《直方图的均衡化》PPT 课件
直方图的均衡化是什么
直方图的均衡化是一种图像增强技术,通过调整图像的亮度分布,使得图像中的像素值更均匀地分布在 整个灰度范围内,从而改善图像的对比度和视觉效果。
直方图的基本概念
直方图是用于表示图像中像素值分布的统计图,横坐标表示像素值,纵坐标 表示该像素值对应的像素数量。
直方图的均衡化原理
直方图均衡化的原理是通过对图像的像素值进行变换,使得原始图像的像素值分布更均匀,同时增强图 像的对比度。
直Байду номын сангаас图均衡化的应用场景
直方图均衡化广泛应用于图像增强、图像处理、计算机视觉等领域,可以改 善图像的质量、增强图像的细节和对比度。
直方图均衡化的步骤
直方图均衡化的步骤包括计算原始图像的像素值累计分布函数、对像素值进 行映射,以及将映射后的像素值替换到原始图像中。
直方图均衡化

直方图均衡化
0≤r≤1 • T (r) 满足下列两个条件: (1) 在区间0≤r≤1中为单值且单调递增 (2)当0≤r≤1时,0≤ ≤1 • 条件(1)保证原图各灰度级在变换后仍保
定义(2):
一个灰度级在范围[0,L-1]的数字图像的直 方图是一个离散函数
p(rk ) nk rk / n
n 是图像的像素总数
nk是图像中灰度级为rk的像素个数
rk是第 个灰度级, = 0,1,2,…,L-1
比较两种定义
h(rk ) nk
p(rk ) nk / n
其中,定义(2)
定义(1) 定义(2)
直方图均衡化
对于离散值:
pr
(rk
)
nk n
已知变换函数的离散形式为:
sk 称作直方图均衡化
将输入图像中灰度级为 rk(横坐标)的像素映射到
输出图像中灰度级为 s k(横坐标)的对应像素
得到:
即:
sk
T(rk )
k j0
pr (rj )
k j0
nj n
• 使函数值正则化到[0,1]区间,成为实数函数
• 函数值的范围与象素的总数无关
• 给出灰度级 rk 在图像中出现的概率密度统
计
图像直方图的定义举例
直方图均衡化
• 直方图应用举例——直方图均衡化 • 希望一幅图像的像素占有全部可能的灰度级 且分布均匀,能够具有高对比度
• 使用的方法是灰度级变换:s T (r)
持从黑到白(或从白到黑)的排列次序
• 条件(2)保证变换前后灰度值动态范围的 一致性
直方图均衡化的原理和作用

直方图均衡化的原理和作用直方图均衡化是一种常见的图像处理技术,用于增强图像的对比度和视觉效果。
它的原理是通过重新分布图像的灰度级别,使得图像中的像素灰度值分布更加均匀,从而改善图像的视觉效果。
在进行直方图均衡化时,首先需要获取图像的灰度直方图,然后根据灰度直方图的累积概率密度函数对图像的像素进行重新分配。
直方图均衡化的作用主要体现在以下几个方面:1. 增强图像的对比度:直方图均衡化可以有效地增强图像的对比度,使得图像中不同区域的灰度级别更加明显,从而使得图像的细节更加清晰。
2. 提高图像的视觉效果:通过直方图均衡化,图像的灰度级别分布更加均匀,可以使得图像看起来更加自然和真实,同时增强了图像的视觉效果,使得观看者更容易理解和分析图像内容。
3. 抑制背景噪声:在图像处理中,背景噪声往往会影响图像的清晰度和质量。
通过直方图均衡化可以有效地抑制背景噪声,使得图像更加清晰和易于分析。
4. 增强图像的细节:直方图均衡化可以增强图像的细节,使得图像中的纹理和结构更加清晰和突出,同时也能够凸显出图像中的一些微弱的特征。
直方图均衡化的原理是基于图像的灰度级别分布的重新分配,其具体操作过程如下:1. 获取图像的灰度直方图:首先需要对图像进行灰度化处理,然后统计不同灰度级别的像素点数量,从而得到图像的灰度直方图。
2. 计算灰度直方图的累积概率密度函数:根据图像的灰度直方图,可以计算出每个灰度级别对应的累积概率密度函数,即将原始的灰度级别映射到新的灰度级别上。
3. 根据累积概率密度函数对像素进行重新分配:根据计算得到的累积概率密度函数,可以将图像中的每个像素的灰度级别重新映射到新的灰度级别上,从而得到均衡化后的图像。
通过以上操作,可以实现直方图均衡化,从而改善图像的对比度和视觉效果。
需要注意的是,直方图均衡化可能会增强图像中的噪声和细小的纹理,因此在实际应用中需要结合具体的图像特性进行调整,以达到最佳的效果。
总之,直方图均衡化是一种有效的图像处理技术,通过重新分配图像的灰度级别,可以增强图像的对比度,改善图像的视觉效果,并抑制背景噪声,使得图像更加清晰和易于分析。
直方图均衡化处理

实验1.直方图均衡化程序的原理及步骤直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某灰度区间变成在全部灰度范围内的均匀分布。
直方图均衡化的原理:直方图均衡化是把原图像的直方图通过灰度变换函数修正为灰度均匀分布的直方图,然后按均衡直方图修正原图像,其变换函数取决于图像灰度直方图的累积分布函数。
概括地说,就是把一已知灰度概率分布的图像,经过一种变换,使之演变成一幅具有均匀概率分布的新图像。
当图像的直方图为一均匀分布时,图像的信息熵最大,此时图像包含的信息量最大,图像看起来更清晰。
灰度直方图用各灰度值出现的相对频数(该灰度级的像素数与图像总像素数之比)表示。
直方图表示数字图像中每一灰度级与其出现频数的的统计关系,用横坐标表示灰度级,纵坐标表示频数。
直方图就能给出该图像的概貌性描述,例如图像的灰度范围、每个灰度级的频数和灰度的分布、整幅图像的亮度和平均明暗对比度等,由此可得出进一步处理的重要依据。
计算每个灰度级出现的概率为:P r (r k )=N k /N k=0,1,2,…,L-1上式中, P r (r k )表示第k 个灰度级出现的概率,N k 为第 k 个灰度级出现的频数,N 为图像像素总数,L 为图像中可能的灰度级总数。
由此可得直方图均衡化变换函数,即图像的灰度累积分布函数Sk 为:1,...,2,1,0)()(00-====∑∑==L k r P r T s kj NN k j j r k k j 上式中, S k 为归一化灰度级。
这个变换映射称做直方图均衡化或直方图线性化。
直方图均衡化过程如下:(1) 输出原图像;(2) 根据公式P r (r k )=n k /m*n ( k=0,1,2,…,L-1)计算对应灰度级出现的概率,绘制原图像的直方图。
(3) 计算原图象的灰度级累积分布函数:sk=Σp r (r k );(4) 取整Sk=round((S1*256)+0.5);将Sk 归一到相近的灰度级,绘制均衡化后的直方图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
射关系。重复上述步骤,得到所有的原图像各灰度级到目标图像各灰
度级的映射关系,再按照新的映射关系对原图像各点像素进行灰度转
换,即可完成对原图的直方图均衡化。下面例题是按照上述算法实现
的。
1.为什么cdf是均衡化的变化函数
tk EH
sk
k i0
ni n
k i0
ps (si )
0 sk 1
k=0,1,…L-1
公式(2)
根据该方程可以由原图像的各像素灰度值直接得到直方图均衡化后各 像素的灰度值。
在实际处理变换时,一般先对原始图像的灰度情况进行统计分析,并
计算出原始直方图分布,然后根据计算出的累计直方图分布 tk ,按式
仙也。名之者/谁?太守/自谓也。太守与客来饮/于此,饮少/辄醉,而/年又最高,故/自号曰/醉翁也。醉翁之意/不在酒,在乎/山水之间也。山水之乐,得之心/而寓之酒也。节奏划分思考“山行/六七里”为什
么不能划分为“山/行六七里”?
明确:“山行”意指“沿着山路走”,“山行”是个状中短语,不能将其割裂。“望之/蔚然而深秀者”为什么不能划分为“望之蔚然/而深秀者”?明确:“蔚然而深秀”是两个并列的词,不宜割裂,“望
形成一片浓荫,秋天风高气爽,霜色洁白,冬日水枯而石底上露,如此,就是山中的四季。【教学提示】翻译有直译与意译两种方式,直译锻炼学生用语的准确性,但可能会降低译文的美感;意译可加强译
文的美感,培养学生的翻译兴趣,但可能会降低译文的准确性。因此,需两种翻译方式都做必要引导。全文直译内容见《我的积累本》。目标导学四:解读文段,把握文本内容1.赏析第一段,说说本文是如
总结
从实现算法上也可以看出其优点主要在于能自动增强 整幅图像的对比度,但具体的增强效果也因此不易控 制,只能得到全局均衡化处理的直方图。
直方图均衡法虽能扩大视觉的动态范围但是以牺牲图 像细节为代价。
新的直方图均衡法:是将改进后的直方图均衡算法和 局部对比度增强法结合起来。前者使图像外貌较好, 后者能增强图像细节。
%step1:get histogram
for i=1:m;
for j=1:n;
k=plane(i,j);
tmhist(k)=tmhist(k)+1;
end
end
四、直方图均衡化的原理程序(lm2.m)
%step2:get cdf
cdf(1)=tmhist(1);
for i=2:256
乎山水之间也。醉能同其乐,醒能述以文者,太守也。这种情绪是作者遭贬谪后的抑郁,作者并未在文中袒露胸怀,只含蓄地说:“醉能同其乐,醒能述以文者,太守也。”此句与醉翁亭的名称、“醉翁之
直方图均衡化计算列表
序号
运算
1 列出原始图灰度级Sk,k=0,1,…7
0
1
2
2 统计原始直方图各灰度级象素数Nk 790 1023 850
3 用式1计算原始直方图(图1)
0.19 0.25 0.21
4 计算累积直方图(图2)
0.19 0.44 0.65
5 取整扩展:Tk=int[(L-1)*Tk+0.5]
划分。2.以四人小组为单位,组内互助解疑,并尝试用“直译”与“意译”两种方法译读文章。3.教师选择疑难句或值得翻译的句子,请学生用两种翻译方法进行翻译。翻译示例:若夫日出而林霏开,云
归而岩穴暝,晦明变化者,山间之朝暮也。野芳发而幽香,佳木秀而繁阴,风霜高洁,水落而石出者,山间之四时也。直译法:那太阳一出来,树林里的雾气散开,云雾聚拢,山谷就显得昏暗了,朝则自暗
何引出“醉翁亭”的位置的,作者在此运用了怎样的艺术手法。
明确:首先以“环滁皆山也”五字领起,将滁州的地理环境一笔勾出,点出醉翁亭坐落在群山之中,并纵观滁州全貌,鸟瞰群山环抱之景。接着作者将“镜头”全景移向局部,先写“西南诸峰,林壑尤美”,
醉翁亭坐落在有最美的林壑的西南诸峰之中,视野集中到最佳处。再写琅琊山“蔚然而深秀”,点山“秀”,照应上文的“美”。又写酿泉,其名字透出了泉与酒的关系,好泉酿好酒,好酒叫人醉。“醉翁
这个条件保证了在增强处理时没有打乱原始图像的灰度排列次序; 2)、对于0≤s≤L-1应当有0≤EH(s)≤L-1,它保证了变换过程
中灰度值的动态范围的一致性。同样的,对于反变换过程 s=EH-1(t),在0≤t≤1时也必须满足上述两个条件。
可以证明累积分布函数就是满足上述条件,通过该函数可以完成s到t 的均匀分布转换,即使直方图均衡化的灰度变化函数是累积分布函数 (概率分部函数)。离散情况下的增强转换方程为:
而明,暮则自明而暗,或暗或明,变化不一,这是山间早晚的景色。野花开放,有一股清幽的香味,好的树木枝叶繁茂,形成浓郁的绿荫。天高气爽,霜色洁白,泉水浅了,石底露出水面,这是山中四季的
景色。意译法:太阳升起,山林里雾气开始消散,烟云聚拢,山谷又开始显得昏暗,清晨自暗而明,薄暮又自明而暗,如此暗明变化的,就是山中的朝暮。春天野花绽开并散发出阵阵幽香,夏日佳树繁茂并
直方图的特点
它只反映该图中不图灰度值出现的次数(或频率), 未反映某以灰度值象素所处的位置。
一幅图各子区的直方图之和就等于该图全图的直方图。 图像直方图覆盖0~255全部灰度级(即256个灰度级
的到了恰当利用)时图像对比度好。但许多图像对应 的直方图并未有效利用动态范围(集中在一侧或中间) 那么其对比度就较差,由此我们引入了一种图像处 理——通过改变原始图像各像素在各灰度级上的概率 分布来实现的图像的灰度变换处理方法——直方图的 均衡化。
二、直方图的均衡化
直方图均衡化处理的中心思想是把原始图像的灰度直方图从比较 集中的某个灰度区间变成在全部灰度范围内的均匀分布。
对图像空间域点的增强过程是通过增强函数t=EH(s)来完成的, t、s分别为目标图像和原始图像上的像素点(x,y)处的灰度值。
在进行均衡化处理时,增强函数EH需要满足两个条件: 1)、增强函数EH(s)在0≤s≤L-1的范围内是一个单调递增函数,
从概率的观点来理解,灰度出现的频率可看作 其出现的概率,这样直方图就对应于概率密度 函数pdf,而概率分布函数就是直方图的累积 和,即概率密度函数的积分,如下图所示:
r
dP(r)
P(r) p(r)dr
0
,
p(r)
dr
若直接从代表每种灰度的 象素数目的直方图来观察, 常用如下的表示:
五、用MATLAB实现直方图的均衡化
其实在MATLAB中,用imhist函数求图像直方图,histeq函数可 以实现直方图均衡化操作(histogram equalization)。
程序为:(lm1.m)
t0=imread(‘f:\ljm\plane1.gif’); %打开一个图像
Imshow(t0) ;
1
3
5
6 确定映射对应关系(Sk-->Tk) 0-》1 1-》3 2-》5
7 统计新直方图各灰度级象素数Nk
790
8 用式计算新直方图(图3)
0.19
步骤和结果
3
4
656 329
0.16 0.08
0.81 0.89
6
6
3,4-》6
1023
0.25
5
6
7
245 122 81
0.06 0.03 0.02
之”是总起词语,故应从其后断句。【教学提示】引导学生在反复朗读的过程中划分朗读节奏,在划分节奏的过程中感知文意。对于部分结构复杂的句子,教师可做适当的讲解引导。目标导学三:结合注释,
翻译训练1.学生结合课下注释和工具书自行疏通文义,并画出不解之处。【教学提示】节奏划分与明确文意相辅相成,若能以节奏划分引导学生明确文意最好;若学生理解有限,亦可在解读文意后把握节奏
cdf(i)=cdf(i-1)+tmhist(i);
End
bar(t,cdf);
%step3:run point operation
for i=1:m
for j=1:n
k=plane(i,j);
plane_equ(i,j)=cdf(k)*256/(m*n);
end
end
醉是为山水之乐而醉,更是为能与百姓同乐而醉。体现太守与百姓关系融洽,“政通人和”才能有这样的乐。5.第四段主要写了什么?明确:写宴会散、众人归的情景。目标导学五:深入解读,把握作者思
想感情思考探究:作者以一个“乐”字贯穿全篇,却有两个句子别出深意,不单单是在写乐,而是另有所指,表达出另外一种情绪,请你找出这两个句子,说说这种情绪是什么。明确:醉翁之意不在酒,在
0
0.3 0.25
0.2 0.15
0.1 0.05
0
0.19
0.25
0.21
0.24
0.11
0
0
0
0.3 0.25
0.2 0.15
0.1 0.05
0
注:由于不能将同一个灰度值的各个象素变换到不 同灰度级,所以数字图像直方图均衡化的结果一般 只是近似均衡的直方图。如图4中的折线是实际均 衡化的结果,而理想均衡化是求平均值,图为一条 水平直线。
设灰度变换 s=f (r) 为斜率有
限的非减连续可 微函数,它将输 入图象A(x,y)转 换为输出图象 B(x,y),输入图 象的直方图为 HA(r),输出图象 的直方图为HB(s), 则它们的关系可 由如下过程导出:
三、例题演示
设有1幅64x64,8bit灰度图像,其直方 图见图1,所用均衡化变换函数(即累积 直方图)见图2,均衡化后的直方图见图 3。
