2019年辽宁省沈阳市中考数学试卷及解析
2019年辽宁省沈阳市中考数学试卷及答案解析
2019年辽宁省沈阳市中考试卷数 学一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分) 1.(2分)5-的相反数是( ) A.5B.5-C.15D.15-2.(2分)2019年1月1日起我国开始贯彻《国务院关于印发个人所得税专项附加扣除暂行办法的通知》的要求,此次减税范围广,其中有6 500万人减税70%以上,将数据6 500用科学记数法表示为( ) A.26.510⨯B.36.510⨯C.36510⨯D.40.6510⨯3.(2分)如图是由五个相同的小立方块搭成的几何体,这个几何体的俯视图是 ( )A.B.C.D.4.(2分)下列说法正确的是( )A. 若甲、乙两组数据的平均数相同,20.1S =甲,20.04S =乙,则乙组数据较稳定B.如果明天降水的概率是50%,那么明天有半天都在降雨C.了解全国中学生的节水意识应选用普查方式D.早上的太阳从西方升起是必然事件 5.(2分)下列运算正确的是( )则这12名队员年龄的众数和中位数分别是( ) A.15岁和14岁 B.15岁和15岁C.15岁和14.5岁D.14岁和15岁7.(2分)已知ABC A B C '''∽,AD 和A D ''是它们的对应中线,若10AD =,6A D ''=,则ABC 与A B C '''的周长比是( ) A.3:5B.9:25C.5:3D.25:98.(2分)已知一次函数(1)y k x b =++的图象如图所示,则k 的取值范围是 ( )A.0k <B.1k <-C.1k <D.1k >-9.(2分)如图,AB 是O 的直径,点C 和点D 是O 上位于直径AB 两侧的点,连接AC ,AD ,BD ,CD ,若O 的半径是13,24BD=,则sinACD ∠的值是 ( )A.1213B.125C.512D.51310.(2分)已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论正确的是( )-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________________________ ___________A.0abc <B.240b ac -<C.0a b c -+<D.20a b +=二、填空题(每小题3分,共18分)11.(3分)因式分解:2244x y xy --+= .12.(3分)二元一次方程组32325x y x y -=⎧⎨+=⎩的解是 .13.(3分)一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有 个白球.14.(3分)如图,在四边形ABCD 中,点E ,F ,G ,H 分别是AB ,CD ,AC ,BD的中点,若AD BC ==EGFH 的周长是 .15.(3分)如图,正比例函数11y k x =的图象与反比例函数22(0)ky x x=>的图象相交于点A ,点B 是反比例函数图象上一点,它的横坐标是3,连接OB ,AB ,则AOB 的面积是 .16.(3分)如图,正方形ABCD 的对角线AC 上有一点E ,且4CE AE =,点F 在DC 的延长线上,连接EF ,过点E 作EG EF ⊥,交CB 的延长线于点G ,连接GF 并延长,交AC 的延长线于点P ,若5AB =,2CF =,则线段EP 的长是 .三、解答题(第17小题6分,第18、19小题各8分,共22分) 17.(6分)计算:201()2cos301(π 2 019)2-︒-+-+-.18.(8分)为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A ,B ,C ,D 依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.(1)小明从中随机抽取一张卡片是足球社团B 的概率是 .(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D 的概率.19.(8分)如图,在四边形ABCD 中,点E 和点F 是对角线AC 上的两点,AE CF =,DF BE =,且DF BE ∥,过点C 作CG AB ⊥交AB 的延长线于点G .(1)求证:四边形ABCD 是平行四边形;(2)若2tan 5CAB ∠=,°45CBG ∠=,BC =则ABCD 的面积是 .四、(每小题8分,共16分)20.(8分)“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x 小时,将做家务的总时间分为五个类别:(010)A x ≤<,(1020)B x ≤<,(2030)C x ≤<,(3040)D x ≤<,(40)E x ≥.并将调查结果制成如下两幅不完整的统计图:根据统计图提供的信息,解答下列问题:(1)本次共调查了 名学生;(2)请根据以上信息直接在答题卡中补全条形统计图;(3)扇形统计图中m 的值是 ,类别D 所对应的扇形圆心角的度数是 度;(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.21.(8分)2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元. (1)求甲种树苗每棵多少元? (2)若准备用3 800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?五、(本题10分)22.(10分)如图,AB 是O 的直径,BC 是O 的弦,直线MN 与O 相切于点C ,过点B 作..于点D .(1)求证:ABC CBD ∠=∠;(2)若BC =,4CD =,则O 的半径是 .毕业学校_____________ 姓名________________ 考生号________________ ________________ ___________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------六、(本题10分)23.(10分)在平面直角坐标系中,直线4(0)y kx k =+≠交x 轴于点(8,0)A ,交y 轴于点B .(1)k 的值是 ;(2)点C 是直线AB 上的一个动点,点D 和点E 分别在x 轴和y 轴上. ①如图,点E 为线段OB 的中点,且四边形OCED 是平行四边形时,求OCED 的周长;②当CE 平行于x 轴,CD 平行于y 轴时,连接DE ,若CDE 的面积为334,请直接写出点C 的坐标. 七、(本题12分) 24.(12分)思维启迪:(1)如图1,A ,B 两点分别位于一个池塘的两端,小亮想用绳子测量A ,B 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B 点的点C ,连接BC ,取BC 的中点P (点P 可以直接到达A 点),利用工具过点C 作CD AB ∥交AP 的延长线于点D ,此时测得200CD =米,那么A ,B 间的距离是米. 思维探索:(2)在ABC 和ADE 中,AC BC =,AE DE =,且AE AC <,°90ACB AED ∠==,将ADE 绕点A 顺时针方向旋转,把点E 在AC 边上时ADE 的位置作为起始位置(此时点B 和点D 位于AC 的两侧),设旋转角为α,连接BD ,点P 是线段BD 的中点,连接PC ,PE . ①如图2,当ADE 在起始位置时,猜想:PC 与PE 的数量关系和位置关系分别是 ;②如图3,当°90α=时,点D 落在AB 边上,请判断PC 与PE 的数量关系和位置关系,并证明你的结论;③当150α=︒时,若3BC =,DE l =,请直接写出2PC 的值.八、(本题12分)25.(12分)如图,在平面直角坐标系中,抛物线22(0)y ax bx a =++≠与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,抛物线经过点(2,3)D --和点(3,2)E ,点P 是第一象限抛物线上的一个动点.(1)求直线DE 和抛物线的表达式;(2)在y 轴上取点(0,1)F ,连接PE ,PB ,当四边形OBPF 的面积是7时,求点P 的坐标;(3)在(2)的条件下,当点P 在抛物线对称轴的右侧时,直线DE 上存在两点M ,N (点M 在点N 的上方),且MN =动点Q 从点P 出发,沿P M N A →→→的路线运动到终点A ,当点Q 的运动路程最短时,请直接写出此时点N 的坐标.2019年辽宁省沈阳市中考试卷数学答案解析C 、了解全国中学生的节水意识应选用抽样调查方式,故本选项错误;D 、早上的太阳从西方升起是不可能事件,故本选项错误; 故选A .【考点】方差,概率,全面调查,抽样调查,随机事件 5.【答案】 B【解析】根据合并同类项、幂的乘法除法、幂的乘方、完全平方公式分别计算即可. 解:A .325235m m m +=,不是同类项,不能合并,故错误; B .32m m m ÷=,正确;C .237()m m m =,故错误;D .222()()()2m n n m m n n m mn --=--=--+,故错误.故选B .【考点】整式的运算 6.【答案】C【解析】众数就是出现次数最多的数,而中位数就是大小处于中间位置的数,根据定义即可求解.解:在这12名队员的年龄数据里,15岁出现了5次,次数最多,因而众数是145. 14.5.故选C .【考点】众数和中位数的概念 7.【答案】C【解析】相似三角形的周长比等于对应的中线的比. 解:∵ABC A B C ''',AD 和A D ''是它们的对应中线,10AD =,6A D ''=, ∴ABC 与A B C '''的周长比AD =:10A D ''=:65:3=.故选C .【考点】相似三角形的性质 8.【答案】B【解析】根据一次函数的增减性确定有关k 的不等式,求解即可.∵O的半径是213AB=⨯由勾股定理得:sinADBAB∠=∴0a b c-+>,C错误;∵2b a=-,D正确;故选D.【考点】二次函数的图象及性质二、填空题11.【答案】2(2)x y--【解析】先提取公因式1-,再套用公式完全平方公式进行二次因式分解.解:2244x y xy--+,22(44)x y xy=-+-,2(2)x y=--.【考点】利用完全平方公式分解因式12.【答案】21.5xy=⎧⎨=⎩【解析】通过观察可以看出y的系数互为相反数,故①+②可以消去y,解得x的值,再把x的值代入①或②,都可以求出y的值.解:2352 3x yx y-=⎨+=⎧⎩①②,①+②得:48x=,解得2x=,把2x=代入②中得:225y+=,解得 1.5y=,所以原方程组的解为21.5xy=⎧⎨=⎩.【考点】二元一次方程组的解法13.【答案】3【解析】从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息.这时,我们用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.轴交OA 于点D ,结合点的坐标,再根据三角形的面积公式即可求出AOB 的面积. 1222AOBABD OBDSSS=+=⨯⨯CEF △FEP ,EC EP ,由此即可解决问题.解:如图,作FH PE ⊥于H .52EH =, tEFH R 中,2EF =∵CFE FEP∠=∠,∴CEF FEP∽,EP,52132242EP==.【考点】正方形的性质,相似三角形的判定和性质,解直角三角形等知识据全等三角形的性质得到AD CB=,DAF∠)根据已知条件得到BCG是等腰直角三角形,求得∵DF BE=,∴()ADF CBE SAS≌,∴四边形ABCD是平行四边形;2)解:∵CG AB⊥,90G∠=︒,∵45CBG∠=︒,∴BCG是等腰直角三角形,∴6AB=,∴ABCD的面积=2)B类人数:12(人)类人数:8(人)(2)B类人数:,D类人数:,168五、(本题10分)22.【答案】(1)CBD ABC∠=∠(2)5【解析】(1)连接OC,由切线的性质可得OC MN⊥,即可证得OC BD∥,由平行线的性质和等腰三角形的性质可得CBD BCO ABC∠=∠=∠,即可证得结论;(2)连接AC,由勾股定理求得BD,然后通过证得ABC CBD,求得直径AB,从而求得半径.(1)证明:连接OC,∵MN为O的切线,∴OC MN⊥,t BCDR中,BC=是O的直径,90ACB=︒,ACB CDB=∠,∵ABC CBD∠=∠,∴ABC CBD,10,∴O的半径是5.上点的坐标特征可得出点的坐标,由平行四边形的性质结合点E为OB的中点可得出是ABO的中位线,结合点的长,在t DOER中,利用勾股再利用平行四边形的周长公式即可求出OCED的周长;2CDE的面积为334可得出关于1)将(8,0)A代入y1k=-(2)①由(1)可知直线当0x=时,y=-AC,是ABO的中位线,4OD CE==,OC DE=t DOER中,DOE∠=2225OD OE+=1 4CDESCE ==-280x +8x +330=无解;22七、(本题12分) 即可证明ABP DCP ≅,,易证()FBP EDP SAS ≌可得EFC 是等腰直角三角PC PE =,PC PE ⊥.②作CF ,易证()FBP EDP SAS ≅,结合已()FBP EAC SAS ≅,可得EFC 是等腰直角三角形,延长线于点F ,连接CE 、CF ,过E 点作EH 在ABP 和DCP 中,BP APB B =⎧⎪∠⎨⎪∠=⎩∴()ABP DCP SAS ≅,200AB =米.200CD =米.2)①PC 与PE 的数量关系和位置关系分别是理由如下:如解图1,延长EP 交BC 于F , )理,可知∴()FBP EDP SAS ≌,又∵90ACB ∠=︒, ∴EFC 是等腰直角三角形,理由如下:如解图2,作BF DE ∥,交EP 同①理,可知()FBP EDP SAS ≌,,在FBC 和EAC 中,BF CBE BC =⎧⎪∠⎨⎪=⎩∴()FBC EAC SAS ≌,90ACB ∠=︒, ∴90FCE ∠=︒, ∴FCE 是等腰直角三角形,EP FP =,③如解图2,作BF ∥CA 延长线于H 点,当角的锐角为30°,150FBC EAC α=∠==︒ 同②可得()FBP EDP SAS ≅,同②FCE 是等腰直角三角形,tAHE R 中,EAH ∠12,32AE =,3AC AB ==,332AH =+,222EC AH HE =+=110+【考点】几何变换综合题,旋转的性质,全等三角形的判定和性质,等腰直角三角形性质,勾股定理,30°直角三角形性质 142OBF PFB S S +=⨯运动的路径最短,即可求解.1142OBF PFBS S+=⨯2或35(,)28;线DE的对称点A'',连接PA''交直线DE于点M,此时,点Q运动的路径最短,。
辽宁省沈阳市2019年中考数学试题含答案【Word版】

2019年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1。
0这个数是( )A 。
正数 B.负数 C.整数 D 。
无理数2.2019年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8。
5×104C.0.85×105 D 。
8.5×105 3。
某几何体的三视图如图所示,这个几何体是( )A.圆柱 B 。
三棱柱 C.长方体 D 。
圆锥4。
已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6 C 。
平均数是4 D 。
方差是55。
一元一次不等式x —1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条 B 。
4条 C.6条 D.8条7.下列运算正确的是( )A.()623x x -=- B 。
844x x x =+ C 。
632x x x =⋅ D.()34y xy xy -=-÷8。
如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( ) A 。
7。
5 B 。
10 C 。
15 D 。
20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q, PM ⊥l 于点P , 若∠1=50°,则∠2=________°. 12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________。
2019年辽宁省沈阳市中考数学试题及答案(Word版)

2019年沈阳中考数学试卷 考试时间:120分钟,试卷满分150分, 参考公式:参考公式:抛物线2y ax bx c =++的顶点坐标是24(,)24b ac b a a--. 对称轴是直线2b x a =-,一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题3分,共24分)1.2019年第一季度,沈阳市公共财政预算收入完成196亿元(数据来源:4月16日《沈阳日报》),讲196亿用科学记数法表示为( )A .81.9610⨯B .819.610⨯C .101.9610⨯D .1019.610⨯2.右图是一个几何体的三视图,这个几何体的名称是( )A .圆柱体B .三棱锥C .球体D .圆锥体3.下面计算一定正确的是( )A .3362b a b +=B .222(3)9pq p q -=-C .3585315y y y ⋅= D .933b b b ÷= 4.如果71m =-,那么m 的取值范围是( )A .01m <<B .12m <<C .23m <<D .34m <<5.下列事件中,是不可能事件的是( )A .买一张电影票,座位号是奇数B .射击运动员射击一次,命中9环.C .明天会下雨D .度量三角形的内角和,结果是360°6. 计算2311x x+-- 的结果是( ) A .11x - B .11x - C .51x - D .51x - 7、在同一平面直角坐标系中,函数1y x =-与函数1y x=的图象可能是( )8.如图,ABC ∆中,AE 交BC 于点D ,C E ∠=∠,AD=4,BC=8,BD:DC=5:3,则DE 的长等于( )A .203B .154C .163D .174二、填空题(每小题4分,共32分)9.分解因式: 2363a a ++= _________.10.一组数据2,4,x ,-1的平均数为3,则x 的值是 =_________.11.在平面直角坐标系中,点M (-3,2)关于原点的对称点的坐标是 _________.12.若关于x 的一元二次方程240x x a +-=有两个不相等的实数根,则a的取值方位是 _________.13.如果x=1时,代数式2234ax bx ++的值是5,那么x= -1时,代数式2234ax bx ++的值 _________.14.如图,点A 、B 、C 、D 都在⊙O 上,ABC ∠=90°,AD=3,CD=2,则⊙O的直径的长是_________.15.有一组等式:22222222222222221233,2367,341213,452021++=++=++=++=…… 请观察它们的构成规律,用你发现的规律写出第8个等式为_________16.已知等边三角形ABC 的高为4,在这个三角形所在的平面内有一点P ,若点P 到AB 的距离是1,点P 到AC 的距离是2,则点P 到BC 的最小距离和最大距离分别是 _________三、解答题(第17、18小题各8分,第19小题10分.共26分) 17.计算:2016sin 30282-⎛⎫-︒++- ⎪⎝⎭(-2)18.一家食品公司将一种新研发的食品免费送给一些人品尝,并让每个人按A (不喜欢)、B (一般)、C (比较喜欢)、D (非常喜欢)四个等级对该食品进行评价, 图①和图②是该公司采集数据后,绘制的两幅不完整的统计图。
【中考真题】2019年辽宁省沈阳市中考数学真题试卷(附答案)
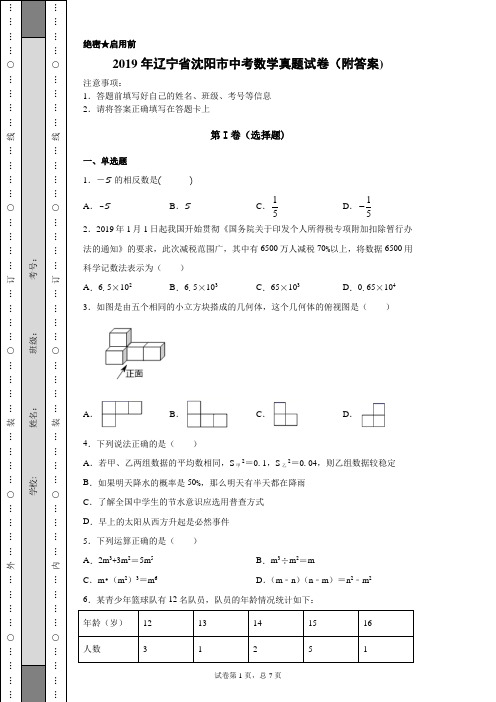
5
1
则这12名队员年龄的众数和中位数分别是( )
A.15岁和14岁B.15岁和15岁
C.15岁和14.5岁D.14岁和15岁
7.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A.3:5B.9:25C.5:3D.25:9
故选:A.
【点睛】
本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
4.A
【解析】
【分析】
根据方差、概率、全面调查和抽样调查以及随机事件的意义分别对每一项进行分析即可得出答案.
【详解】
A、∵S甲2=0.1,S乙2=0.04,∴S甲2>S乙2,∴乙组数据较稳定,故本选项正确;
B、明天降雨的概率是50%表示降雨的可能性,故此选项错误;
【详解】
A.2m3+3m2,不是同类项,不能合并,故错误;
B.m3÷m2=m,正确;
C.m•(m2)3=m7,故错误;
D.(m﹣n)(n﹣m)=﹣(m﹣n)2=﹣n2﹣m2+2mn,故错误.
故选B.
【点睛】
本题考查了整式的运算,熟练掌握合并同类项、幂的乘除法、幂的乘方、完全平方公式是解题的关键.
6.C
(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB= ,∠CBG=45°,BC=4 ,则▱ABCD的面积是.
20.“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
2019年辽宁省沈阳市中考数学试卷-答案

2019年辽宁省沈阳市中考试卷数学答案解析故选A .【考点】方差,概率,全面调查,抽样调查,随机事件 5.【答案】B【解析】根据合并同类项、幂的乘法除法、幂的乘方、完全平方公式分别计算即可. 解:A .325235m m m +=,不是同类项,不能合并,故错误; B .32m m m ÷=,正确; C .237()m m m =,故错误;D .222()()()2m n n m m n n m mn --=--=--+,故错误. 故选B .【考点】整式的运算 6.【答案】C【解析】众数就是出现次数最多的数,而中位数就是大小处于中间位置的数,根据定义即可求解. 解:在这12名队员的年龄数据里,15岁出现了5次,次数最多,因而众数是145. 解:∵ABC A B C ''',AD 和∴ABC 与A B C '''的周长比AD =故选C .【考点】相似三角形的性质 【答案】B【解析】根据一次函数的增减性确定有关∵O的半径是AB=⨯213由勾股定理得:B 面积公式即可求出AOB 的面积.)∵正比例函数11y k x =的图象与反比例函数133k =,1222AOBABD OBDSSS=+=⨯⨯CEF △FEP ,可得EC EP ,R中,2t EFHEF==∠=90GEF GCF,G,F,C四点共圆,EFG ECG=∠=45∽,∴CEF FEPEF EC=,EP EF2=,EF EC EP52132EP==.2)根据已知条件得到BCG是等腰直角三角形,求得平行四边形的面积公式即可得到结论.CF,,∴()ADF CBE SAS ≌,AD CB =,DAF BCE ∠=∠AD CB ∥,∴四边形ABCD 是平行四边形;∴BCG 是等腰直角三角形,42BC =, 4BG CG ==, 2tan 5CAB ∠=, ∴ABCD 的面积=【考点】平行相交线的判定和性质,全等三角形的判定和性质,解直角三角形四、(每小题8分,共20.【答案】(1)5 2)B 类人数:12(人)168五、(本题10分) 22.【答案】(1)CBD ABC ∠=∠ (2)5【解析】(1)连接OC ,由切线的性质可得OC MN ⊥,即可证得OC BD ∥,由平行线的性质和等腰三角形的性质可得CBD BCO ABC ∠=∠=∠,即可证得结论;(2)连接AC ,由勾股定理求得BD ,然后通过证得ABC CBD ,求得直径1)证明:连接OC , MN 为O 的切线, OC MN ⊥, BD MN ⊥, t BCD R 中,BC =, 是O 的直径,90ACB =︒,ACB CDB =∠∴ABC CBD ,AB CBBC BD =,即45845AB =10AB =, ∴O 的半径是5.六、(本题10分)是ABO 的中位线,结合点tDOE R 中,利用勾股定理可求出的长,再利用平行四边形的周长公式即可求出OCED 的周长;②设点C 的坐标为(,x 142x =-+,利用三角形的面积公式结合CDE 的面积为334可得出关于x 的方程,解之即可得出结论.(1)将(8,0)A 代入4y kx =+,得:08=解得:12k =-. )①由(1)可知直线AB 是ABO 的中位线,142OA =. ∵四边形OCED 是平行四边形,4CE =,OC DE =t DOE R 中,DOE ∠22DE OD OE =+=2(OCED OD =平行四边形1 4CDE S CD CE ==-0或28x +22七、(本题12分)即可证明ABP DCP ≅,即可得AB 易证()FBP EDP SAS ≌可得EFC 是等腰直角三角形,即可证明PC ,交EP 延长线于点F ,连接CE 、CF ,易证()FBP EDP SAS ≅,结合已知,再证明()FBP EAC SAS ≅,可得EFC 是等腰直角三角形,即可证明PC =,交EP 延长线于点F ,连接CE 、CF ,过E 点作EH AC ⊥交CA 延长线于150=︒,DE 与BC 所成夹角的锐角为30°,得FBC EAC ∠=∠,同②可证可得再由已知解三角形∴22EC AH =+在ABP 和DCP 中,BP APB B =⎧⎪∠⎨⎪∠=⎩∴()ABP DCP SAS ≅,DC AB =.200AB =米.200CD =米.1,延长EP 交BC 于F ,)理,可知∴()FBP EDP SAS ≌,DE =,AE DE =,∴EFC 是等腰直角三角形,EP FP =,PC PE =,PC ⊥PC 与PE 的数量关系和位置关系分别是理由如下:如解图2,作BF DE ∥,交EP 同①理,可知()FBP EDP SAS ≌,,12PE PF EF ==, ,,在FBC 和EAC 中,BF CBE BC =⎧⎪∠⎨⎪=⎩∴()FBC EAC SAS ≌,CF CE =,FCB ECA ∠=∠90ACB ∠=︒,90FCE ∠=︒,∴FCE 是等腰直角三角形,EP FP =, CP EP ⊥,CP EP =③如解图2,作B F D E ∥150FBC EAC α=∠==︒同②可得()FBP EDP SAS ≅, 同②FCE 是等腰直角三角形,CP t AHE R 中,30EAH ∠=︒,AE 12HE =,32AE =, 3AC AB ==,332AH =+, 22八、(本题12分)142OBF PFB S S +=⨯M AN ∥,过作点A (2)如图1,连接BF ,过点P 作PH y ∥轴交BF 于点H ,1142OBF PFB S S +=⨯或32,。
辽宁沈阳2019中考试题数学卷解析版

分)一、选择题(下列各题的备选答案中,只有一个答案是正确的。
每小题2分,共20 )1.下列各数是无理数的是(. D0 BA..﹣1 C. C.【答案】【解析】3是无理数,故是有理数,,﹣1,试题分析:无理数是无限不循环小数,由此可得027 C.答案选考点:无理数.)42.如图是由个大小相同的小立方块搭成的几何体,这个几何体的俯视图是(A.【答案】考点:简单组合体的三视图.全市房地产开发企业提供房源的参展面积达到.3在我市2016年春季房地产展示交易会上,)用科学记数法表示为(5400000平方米,将数据54000007 756.5.4×10C.5.4×10B.54×10DA.0.54×10 .【答案】C 【解析】n的值为n为整数,<的形式,其中1≤|a|10,n10a试题分析:科学记数法的表示形式为×6.105400000=5.41这个数的整数位数减,所以×,故答案选C.考点:科学记数法1k(x>0)图象上的一点,分别过点4.如图,在平面直角坐标系中,点P是反比例函数y=x P 作PA⊥x轴于点A,PB⊥y轴于点B.若四边形OAPB的面积为3,则k的值为()D.﹣3 B.﹣3 C.A.A. 【答案】【解析】k轴于xP作PA是反比例函数y=⊥(x>0)图象上的一点,分别过点试题分析:已知点P x k=的面积OAPBS=|k|=3,所以B,四边形OAPB的面积为3,可得矩形轴于点点A,PB⊥y .故答案选A.±3.又因反比例函数的图象在第一象限,即可得k=3 考点:反比例函数系数k的几何意义.)5.“射击运动员射击一次,命中靶心”这个事件是(D.不确定事件.确定事件 B.必然事件 C.不可能事件A .D【答案】考点:随机事件.)6.下列计算正确的是(2 2328 36 263 44yx﹣)=x﹣)(﹣.(xxxA.+x=2xB.?x=xC.(y)=xyDxyyD. 【答案】【解析】.考点:整式的运算2),下列说法正确的是(6,7,8,87.已知一组数据:3,4,7 .中位数是6 D.中位数是A.众数是2 B.众数是8 CB. 【答案】【解析】故6.5.88,8的众数为,中位数为试题分析:根据众数和中位数的定义可得数据3,4,6,7, B.答案选.考点:众数;中位数2 x)﹣4x=12的根是( 8.一元二次方程=6 x.x=2,﹣.x=2,x=﹣6 D,﹣.Ax=2,x=6 B.x=﹣2x=6 C22211211B. 【答案】【解析】2,,x=6)=0,解得x=﹣26试题分析:方程整理得x4x﹣﹣12=0,分解因式得(x+2)(x﹣21B.故答案选.考点:解一元二次方程)中,∠C=90°,∠B=30°,AB=8,则BC的长是( 9.如图,在Rt△ABC33 4 DA. B.4 C..8D. 【答案】【解析】×AB=8,由锐角三角函数可得BC=cosBC=90试题分析:在Rt△ABC中,∠°,∠B=30°,3D. .AB=cos30°×故答案选8=4.考点:解直角三角形2,B(x),xy=x.在平面直角坐标系中,二次函数3+2x﹣的图象如图所示,点A(,y10211)≤0,则下列结论正确的是(x<)是该二次函数图象上的两点,其中﹣3≤xy 21234 的最小值是﹣y的最小值是﹣3 D.<A.yyB.y>yC.y2 2 11D.【答案】考点:二次函数图象上点的坐标特征;二次函数的最值.二、填空题2. 11.分解因式:2x ﹣4x+2=).【答案】2(x﹣【解析】22)2,再利用完全平方公式进行二次分解即2x﹣﹣4x+2=2(x2x+1 21试题分析:先提取公因式2 =2(x﹣1)..考点:分解因式边形. 12.若一个多边形的内角和是540°,则这个多边形是5. 【答案】【解析】 2=540°,)?180°试题分析:设多边形的边数是n,根据多边形的内角和公式可得(n ﹣ n=5.解得. 考点:多边形的内角1.化简:(1﹣.)?(m+1)= 131m?m. 【答案】【解析】11?m?=m.)m+1试题分析:原式?(=1?m.考点:分式的运算.是最大的一个,这三个数的和为 14.三个连续整数中,n【答案】3n ﹣3.【解析】试题分析:用n表示出最小的数为n-2,中间的整数为n-1,则这三个数的和为n﹣2+n﹣1+n=3n ﹣3.4.考点:列代数式,两地之间,甲,乙两车分别从A地位于A, BA15.在一条笔直的公路上有,B,C三地,C地的过程,甲、乙CCB两地出发,沿这条公路匀速行驶至地停止.从甲车出发至甲车到达)之间的函数关系如图表示,当甲车出t(h(两车各自与C地的距离ykm)与甲车行驶时间. h时,两车相距350km发3. 【答案】2.考点:一次函数的应用BCM是边DE中,∠A=90°,AB=AC,BC=20,是△ABC的中位线,点16.如图,在Rt△ABC.若△OMN相交于点DNO与MEME,点上一点,BM=3N是线段MC上的一个动点,连接DN,,是直角三角形,则DO的长是.2550或.【答案】613 5. 考点:三角形综合题三、解答题12﹣027..计算:(π﹣174))+|3﹣tan60°|﹣(+232.【答案】【解析】负整数指数幂试题分析:先根据零指数幂的性质以及绝对值的性质和特殊角的三角函数值、的性质、二次根式的性质分别化简后合并即可求出答案.3334+3=2﹣,试题解析:原式=1+3.﹣.考点:实数的运算《三.为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,18这三个CB,,,字经》,《弟子规》(分别用字母A,BC依次表示这三个诵读材料),将A张卡片背面朝上洗匀后放在桌面3把这字母分别写在3张完全相同的不透明卡片的正面上,记录下卡片上的内容,小明和小亮参加诵读比赛,上.比赛时小明先从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比放回后洗匀,再由小亮从中随机抽取一张卡片,赛. 1)小明诵读《论语》的概率是;()请用列表法或画树状图(树形图)法求小明和小亮诵读两个不同材料的概率.(221.)2)1(【答案】;(33 6)列表得:(2小明CB A 小亮 C)(A,A,A)(A,B)A ( C)((B,A)) B,,(BBB)(C,B C CC(,A))(C,种.种等可能性结果,其中小明和小亮诵读两个不同材料结果有由表格可知,共有9626 .所以小明和小亮诵读两个不同材料的概率=39.考点:概率.求证:DE19.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接)∠CEB=∠CBE;(1 2()四边形BCED是菱形.. 【答案】详见解析【解析】)2CBE;(CBE=∠ABD,即可得∠CEB=∠,∠)根据已知条件易证∠试题分析:(1CEB=∠ABD CEDB是菱形即可.判定四边形易证明四边形CEDB是平行四边形,再根据BC=BD ,≌△)∵△ABCABD试题解析:证明;(1 ,∠ABD∴∠ABC= ,∥∵CEBD ,∠∴∠CEB=DBE7是菱形.∴四边形CEDB考点:全等三角形的性质;菱形的判定.跳大绳和踢毽球四种项目(2016?沈阳)我市某中学决定在学生中开展丢沙包、打篮球、20.(每m名学生最喜欢的一种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校,并将调查结果绘制成如下的不完整的统计图名学生必选且只能选择四种活动项目的一种)表:学生最喜欢的活动项目的人数统计表百分比学生数(名)项目10% 20 丢沙包p% 60 打篮球40% n 跳大绳20%40踢毽球根据图表中提供的信息,解答下列问题: p= ;(1)m= ,n= ,)请根据以上信息直接补全条形统计图;(2 名学生中有多少名学生最喜欢跳大绳.)根据抽样调查结果,请你估计该校(32000 8800.3);(2)详见解析;(,【答案】(1)20080,30名学生最喜欢跳大绳.800答:估计该校2000名学生中有考点:条形统计图;用样本估计总体.,E,BD=CDAC分别于BC,相交于点D,为直径的⊙O在△ABC21.(2016?沈阳)如图,中,以AB F.D作⊙O的切线交边AC于点过点)求证:DF⊥AC;(1,∠CDF=30°,求的长(结果保留的半径为(2)若⊙O5π).5? 2)详见解析;(【答案】1().3 9D为切点,∵DF是⊙O的切线,∴OD⊥DF,∴∠ODF=90°. OA=OB,∵BD=CD,是△ABC的中位线,∴OD ∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.)解:∵∠CDF=30°,(2 )得∠ODF=90°,由(1 ∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,?5560???∴的长.=3180考点:切线的性质;弧长的计算.B,B.倡导健康生活,推进全民健身,某社区要购进A,两种型号的健身器材若干套,A22且每种型号健身器材必须整套购元,460310两种型号健身器材的购买单价分别为每套元,买.10 (1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?【答案】(1)购买A种型号健身器材20套,B型器材健身器材30套;(2)A种型号健身器材至少要购买34套.【解析】试题分析:(1)设购买A种型号健身器材x套,B型器材健身器材y套,根据题目中的“A,B 两种型号的根据题意,得:310m+460(50﹣m)≤18000,,解得:m≥33 为整数,∵m ,的最小值为34∴m 套.种型号健身器材至少要购买34答:A 考点:二元一次方程组的应用;一元一次不等式的应用.),点,0为坐标原点,点A的坐标为(4O23.如图,在平面直角坐标系中,△AOB的顶点轴的正半轴上,连接在xOBDE的顶点EAB0,1),点C 为边的中点,正方形B的坐标为( CE.,CD,CO ;)线段OC的长为 1()求证:△CBD≌△COE;(2的对应点,E, B,D,其中点O3)将正方形OBDE沿x轴正方向平移得到正方形BDEO(1111的a≠2,△CD),其中EE的坐标为(a,0CE,连接D,分别为点OB,,ECD,,设点111111 S.面积为 a之间的函数表达式;Sa<<2时,请直接写出与1①当1的值.aS=②在平移过程中,当时,请直接写出4 11175131.S=)①S=﹣a+1【答案】(1);②当时,a=或(2);详见解析;(322224的坐标为(0,1),A试题解析:(1)∵点的坐标为(4,0),点B OA=4,,OB=1∴°,∵∠AOB=9022 AB=∴,17OA OB为边AB的中点,∵点C117∴OC=AB=;22的中点,C是AB)证明:∵∠(2AOB=90°,点1,∴OC=BC=AB2,∠∴∠CBO=COB 1212,)∴点C的坐标为:(2,<20),1<a∵点E的坐标为(a,,﹣a∴CH=2111a+1;a)=﹣E?CH=×1×(∴S=2﹣D1122211﹣S=<2时,1a+1=,②当<a243解得:a=;2,﹣2a>2时,同理:CH=a当111,a=﹣11CH=××(a﹣2S=∴)?DE1122211S=∴, a﹣1=245,解得:a=2531.a=时,或S=综上可得:当22413考点:四边形综合题.按顺时针方向旋转,得到△ADE,旋转角A,将△ABC绕点.在△ABC中,AB=6,AC=BC=524 BE.E的对应点为点,连接BD,为α(0°<α<180°),点B的对应点为点D,点C F.BE交AD于点(1)如图,当α=60°时,延长①求证:△ABD是等边三角形; AF=DF;②求证:BF⊥AD, BE的长;③请直接写出,当∠DAG=∠ACB,CE,垂足为点G,连接D2)在旋转过程中,过点作DG垂直于直线AB(的值.AE无公共点时,请直接写出BE+CE且线段DG与线段温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.3﹣4;(2)13①②详见解析;③【答案】(1).3BE=5,即可得答案.试题解析:(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,∴AB=AD,∠BAD=60°,∴△ABD是等边三角形;②由①得△ABD是等边三角形,∴AB=BD,∵△ABC绕点A顺时针方向旋转60°得到△ADE,∴AC=AE,BC=DE,又∵AC=BC,∴EA=ED,143;﹣∴BE=BF﹣EF=34 )如图所示,(2,DAE=∠BAC,∠∵∠DAG=∠ACB ABC=180°,∠∠∠∠∠∴∠ACB+BAC+ABC=DAG+DAE+15∴BE+CE=13.考点:三角形综合题.25.如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正32x ﹣3x+m与yy=轴相交于点A,抛物线的对称轴与x轴半轴上,OC=8,OE=17,抛物线20 K.,与CD交于点相交于点B 上的点F处.OOCDE沿AB折叠,点恰好落在边CD(1)将矩形的长,CK B①点的坐标为(、),BK的长是;是的坐标;②求点F ③请直接写出抛物线的函数表达式;,折OG上的点)将矩形(2OCDE沿着经过点E的直线折叠,点O恰好落在边CDG处,连接GH痕与OG相交于点,点M是线段EH上的一个动点(不与点H重合),连接MO,过点MG,N至与点H从点E开始沿线段EH向点运动,,于点P作GP⊥OM于点,交EHN,连接ON点M(即?S的运动过程中,S,在点和重合时停止,△MOG和△NOG的面积分别表示为SSM2121的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这SS与21个值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.32x﹣3x+5.(2)不变.S?S=189y=84108010(1)【答案】①,,,;②(,);③.2120【解析】16,CK=OB=10,KB=OC=8∴,10.0故答案分别为10,,8 ,BK=OC=8,②在RT△FBK中,∵∠FKB=90°,BF=OB=10 FK==6∴,22BKBF?FK=4,﹣∴CF=CK 8).∴点F坐标(4, OA=AF=x,③设222=AF+CFACF 中,∵AC,在RT△222)=x+4,x∴(8﹣∴x=5,32,3x+m得0∴点A坐标(,5),代入抛物线y=m=5x﹣2032﹣∴抛物线为y=3x+5.x20.?(2)不变.SS=18921△EDG中,∵GE=EO=17,ED=8,中,在理由:如图2RT2222,∴=15DG=8?DE?17GE? DG=2,∴CG=CD﹣222217 =2∴,OG=28CGOC??? 171112 17=2892.?)?(???=??S∵S?OGHNOGHM=21222.考点:二次函数综合题18。
2019年沈阳中考数学试题以及答案解析

2019年沈阳市中考数学试卷及答案一、选择题1、在“朗读者”节目的影响下,某中学开展了“好书伴我成长”读书活动、为了解5月份八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示: 册数 0 1 2 3 4 人数41216171关于这组数据,下列说法正确的是( ) A 、中位数是2 B 、众数是17 C 、平均数是2 D 、方差是22、将直线23y x =-向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( ) A 、24y x =- B 、24y x =+ C 、22y x =+ D 、22y x =- 3、一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( ) A 、108° B 、90° C 、72° D 、60° 4、若一组数据2,3,,5,7的众数为7,则这组数据的中位数为( )A 、2B 、3C 、5D 、75、已知二次函数y =ax 2+bx +c ,且a>b>c ,a +b +c =0,有以下四个命题,则一定正确命题的序号是( )①x=1是二次方程ax 2+bx +c=0的一个实数根; ②二次函数y =ax 2+bx +c 的开口向下;③二次函数y =ax 2+bx +c 的对称轴在y 轴的左侧; ④不等式4a+2b+c>0一定成立、 A 、①②B 、①③C 、①④D 、③④6、如图,在⊙O 中,AE 是直径,半径OC 垂直于弦AB 于D ,连接BE ,若AB=27,CD=1,则BE 的长是( )A 、5B 、6C 、7D 、87、如图,四个有理数在数轴上的对应点M ,P ,N ,Q ,若点M ,N 表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )A 、点MB 、点NC 、点PD 、点Q8、下面的几何体中,主视图为圆的是( )A 、B 、C 、D 、9、如图,直线//AB CD ,AG 平分BAE ∠,40EFC ∠=,则GAF ∠的度数为( )A 、110B 、115C 、125D 、130 10、已知关于x 的方程2x+a-9=0的解是x=2,则a 的值为A 、2B 、3C 、4D 、511、为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( ) 捐款数额 10 20 30 50 100 人数24531A 、众数是100B 、中位数是30C 、极差是20D 、平均数是3012、下列分解因式正确的是( ) A 、24(4)x x x x -+=-+ B 、2()x xy x x x y ++=+ C 、2()()()x x y y y x x y -+-=-D 、244(2)(2)x x x x -+=+-二、填空题13、某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是______元。
辽宁省沈阳市2019年中考数学试题含答案【Word版】

2019年沈阳市中考数学试卷试题满分150分 考试时间120分钟参考公式:抛物线2y ax bx c =++的顶点是24(,)24b ac b a a --,对称轴是直线2b x a =-. 一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题4分,共24分)1.0这个数是( )A.正数B.负数C.整数D.无理数2.2019年端午节小长假期间,沈阳某景区接待游客约为85000人,将数据85000用科学记数法表示为( )A.85×103B.8.5×104C.0.85×105D.8.5×105 3.某几何体的三视图如图所示,这个几何体是( )A.圆柱B.三棱柱C.长方体D.圆锥4.已知一组数据:1,2,6,3,3,下列说法正确的是( )A.众数是3B.中位数是6C.平均数是4D.方差是55.一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A B C D6.正方形是轴对称图形,它的对称轴有( )A.2条B.4条C.6条D.8条7.下列运算正确的是( )A.()623x x -=-B.844x x x =+C.632x x x =⋅D.()34y xy xy -=-÷8.如图,在△ABC 中,点D 在边AB 上,BD=2AD ,DE ∥BC 交AC 于点E ,若线段DE=5,则线段BC 的长为( )A.7.5B.10C.15D.20二、填空题(每小题4分,共32分)9.计算:=9___________10.分解因式:2m 2+10m=___________11.如图,直线a ∥b ,直线l 与a 相交于点P ,与直线b 相交于点Q , PM ⊥l 于点P , 若∠1=50°,则∠2=________°. 12.化简:=⋅⎪⎭⎫ ⎝⎛-+xx 1111___________ 13.已知一次函数y=x+1的图象与反比例函数x k y =的图象相交,其中有一个交点的横坐标是2,则k 的值为________.14.如图,△ABC 三边的中点D ,E ,F 组成△DEF ,△DEF 三边的中点M ,N ,P 组成△MNP ,将△FPM 与△ECD 涂成阴影.假设可以随意在△ABC 中取点,那么这个点取在阴影部分的概率为________.15.某种商品每件进价为20元,调查表明:在某段时间内若以每件x 元(20≤x ≤30,且x 为整数) 出售,可卖出(30-x)件.若使利润最大,每件的售价应为________元16.如图,□ABCD 中,AB>AD ,AE ,BE ,CM ,DM 分别为∠DAB ,∠ABC ,∠BCD ,∠CDA 的平分线,AE 与DM 相交于点F ,BE 与CM 相交于点H ,连接EM ,若□ABCD 的周长为42cm ,FM=3cm ,EF=4cm ,则EM=①cm ,AB=②cm.三、解答题(第17、18小题各8分,第19小题10分,共26分)17.先化简,再求值:()()a b a b a ⋅--+22,其中a=-1,b=5.18.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=O F.19.在一个不透明的盒子里有红球、白球、黑球各一个,它们除了颜色外其余都相同.小明从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图(树形图)法求小明两次摸出的球颜色不同的概率.四、(每小题10分,共20分)20.2019年世界杯足球赛于北京时间6月13日2时在巴西开幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:根据统计图表提供的信息,解答下列问题:(1)a=________,b=________;(2)根据以上信息,请直接..在答题卡中补全条形统计图;(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.21.某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.五、(本题10分)22.如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD ,BD ,CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.六、(本题12分)23.如图,在平面直角坐标系中,四边形OABC 的顶点O 为坐标原点,点C 在x 轴的正半轴上,且BC ⊥OC 于点C ,点A 的坐标为 (2,32),AB=34,∠B=60°,点D 是线段OC 上一点,且OD=4,连接AD.(1)求证:△AOD 是等边三角形;(2)求点B 的坐标;(3)平行于AD 的直线l 从原点O 出发,沿x 轴正方向平移.设直线l 被四边形OABC 截得的线段长为m ,直线l 与x 轴交点的横坐标为t.①当直线l 与x 轴的交点在线段CD 上(交点不与点C ,D 重合)时,请直接..写出m 与t 的函数关系式(不必写出自变量t 的取值范围)②若m=2,请直接..写出此时直线l 与x 轴的交点坐标.七、(本题12分)24.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM. (1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=3AM;(3)连接EM,若△AEM的面积为40,请直接..写出△AFM的周长.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.八、(本题14分)25.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC.(1)点B 的坐标为________,点C 的坐标为________;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP(点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n. ①如图2,当AC n 21<时,求证:△PAM ≌△NCP ; ②直接..用含n 的代数式表示线段PQ 的长; ③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接..写出此时二次函数表达式温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.。
